Abstract
We propose a wide-band metamaterial perfect absorber (MPA), using the coupling in the near-field of a quadruple split-ring resonator concentric with crossed ellipses. We designed the MPA with a metal–insulator-metal (MIM) structure for use in thermal energy harvesting. A gradient-based optimization approach was carried out to maximize the absorption of infrared (IR) radiation around 10 μm. Owing to the near-field coupling of resonators with optimal design parameters, the peaks of the absorption responses approach each other, thus broadening the overall bandwidth with almost unity absorptivity. The proposed design has a resonance at 10 μm resulting from magnetic polaritons (MPs) and thus maintains high absorption above 99% up to a range of incident-angles greater than 60° and exhibits a polarization-free behavior due to symmetry. When the optimal design was numerically examined to fabrication tolerances, it showed negligible sensitivities in the absorptivity with respect to design parameters. The strong electric field enhancement inside the split-ring gaps and between the ends of the cross arms and the surrounding ring enables designing MIM diodes to rectify the harvested thermal radiations at 288 K. MIM diodes can be built by the deposition of thin insulators to sit in these gaps. The MIM diode and MPA work together to harvest and rectify the incident IR radiation in a manner similar to the operation of rectennas. The MPA outperforms the traditional nano-antennas in impedance matching efficiency because of its higher resistance. Also, its dual-polarization reception capability doubles the rectenna efficiency. Our proposed MPA retained absorptivity more than 99% when coupled with MIM diodes whose resistances are in the range of 500 Ω–1 MΩ.
Similar content being viewed by others
Introduction
The current patterns of climate change have attracted considerable attention to the hidden costs of conventional energy sources such as fossil fuel. Renewable energy sources including solar, wind, geothermal and biomass have substantially less harmful impact on the environment by most measures1. One of the serious impacts of fossil fuels is global warming driven by increasing concentrations of greenhouse gas emissions2. These emissions decrease the thermal back-radiations leaving the atmosphere, thus leading to an energy imbalance between the earth and the sun and consequently warmer temperatures. The thermal energy emitted back from earth is considered an intact energy source in the infrared (IR) regime. The peak of these IR radiations corresponding to an average earth surface temperature of 288 K lies at wavelength of ~ 10 μm according to Wien's equation3.
Attempts to harvest the IR electromagnetic radiations with wavelengths around 10 μm, i.e. a frequency ~ 30 THz, were reported4,5,6,7,8,9. These efforts include using thermoelectric materials that can directly transform the thermal heat into dc voltages through the Seebeck effect4,5. However, their relatively high cost and low conversion efficiency at lower temperatures impedes their use at large scale10. A promising technique is the rectifying antennas (rectennas) which have been implemented successfully in the microwave regime with high efficiency11. The rectenna is comprised of a rectifying element which is the diode connected to the terminals of a receiving antenna designed to resonate around the peak of the incoming electromagnetic radiation9. The antenna can be considered as an absorbing element for the incoming electromagnetic radiation. It is capable of strongly enhancing the localized electromagnetic fields inside a tiny gap, i.e. hot spot, where the diode, the rectifying element, is situated. Metamaterials-based absorbers have been widely suggested for several applications including thermophotovoltaics12, spectroscopy13, and stealth technology14 due to their tunability for near unity absorption of electromagnetic radiations.
Metamaterials-based absorbers are engineered materials and structures that exhibit exotic properties in terms of absorption peaks and wavelengths through matching their equivalent permittivity and permeability with that of the surrounding medium15,16,17,18,19,20. A popular configuration of these metamaterials-based absorbers is the periodic metal–insulator-metal (MIM) structures21,22. The metal-dielectric interfaces allow the excitation of the plasmonic phenomenon which in turn manipulates the absorption at certain wavelengths to reach near unity where these MIM structures realize a nearly perfect absorber22. Therefore, building a metamaterial perfect absorber (MPA) with few nanometers gaps can replace the antenna in the rectenna device. The MIM-based MPA structure encompasses a repeatedly distributed metallic pattern at the top, another metallic layer in the bottom, and a thin dielectric film is sandwiched between these two metallic layers. The metallic patterns on top and the dielectric layer determine the number, peak and width of the absorption bands23, while the bottom metallic layer is to impede the transmission from occuring24.
The MIM-based MPA requires an ultra-fast diode that can follow the captured ultra-high frequency signal of the incident IR radiation at 30 THz8. MIM diodes offer this opportunity owing to their ultra-thin dielectric layers that result in tunneling as the dominant conduction mechanism9. The operation of the MPA in a rectenna for IR energy harvesting requires a small gap in the range of few nanometers to accommodate the MIM diode. One of the advantages of building MIM diodes within the MPA structure is the possibility of growing the dielectric layer in both structures simultaneously, which in turn simplifies the fabrication process.
In this work, we present metallic crossed ellipses (CE) concentric with a quadruple split-ring resonator (QSRR). The metallic top layer sandwiches a thin dielectric layer with the other metallic bottom layer. The MIM-based MPA structure is optimized to achieve near unity absorption with a wide-band response. This design can absorb IR radiation with both polarizations due to its symmetry and also offers a wide-angle of reception that surpasses the traditional antennas such as dipoles or bow-ties. Sensitivity analysis to the design geometry parameters shows insignificant change in the overall performance within the expected fabrication tolerances. The strong electric field enhancement inside all the gaps has broad bandwidth characteristics which in turn increase the amount of harvested IR radiation. The choice of Au/TiO2/Au and Au/TiO2/Ti allows for the use of simple fabrication techniques to build the proposed MIM structure. The proposed rectenna-like structure shows insensitive absorptivity to changes in the MIM diode’s resistance.
MIM structure optimal design for IR energy harvesting
Crossed-ellipses coincide with quadruple split-ring-resonator
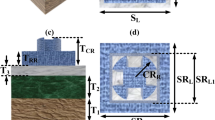
First, the concept of building a perfect absorber that is compatible with MIM diodes integration through few-nanometers gaps was implemented. The selection of the quadruple split-ring-resonator (QSRR) successfully achieves near-unity absorption at 10 μm wavelength. In addition, the gaps of SRR formed 4 MIM diodes within the design. The arrangement of the designed perfect absorber combined with the diode resulted in a rectenna-like element capable of perfectly absorbing IR radiation and transforming it into useful DC power. To improve the rectification process, we designed crossed ellipses (CEs) concentric with the QSRR. The crossed ellipses exhibit an additional absorption band that is controllable through the major and minor axes of the ellipse. By adding this cross absorber, 4 more tiny gaps were formed within the inner perimeter of the SRR, which in turn double the rectification capability. A schematic diagram of one cell of the array of the metamaterial perfect absorber (MPA) based on a metal–insulator-metal architecture is shown in Fig. 1a. Gold is used to build the top resonators and the ground plane, while TiO2 is chosen to form the dielectric layer in between. The top view of the designed MPA showing the geometric parameters of both resonators is depicted in Fig. 1b. Additionally, the cross- section of the MPA is shown in Fig. 1c with the thicknesses for each layer as additional design parameters.
The proposed metamaterial perfect absorber (MPA) structure (a) 3D isometric view, (b) top view showing the design parameters of the split-ring-resonator (SRR) and crossed ellipses, (c) Cross-sectional view of the MPA showing the metal–insulator-metal (MIM) 3-layers with thicknesses as design parameters. (ANSYS HFSS 2018, https://www.ansys.com/).
The initial dimensions of both QSRR and CEs were determined to form a wide-band absorber around 10 μm. The resonance wavelength of QSRR can be approximated analytically using an inductor-capacitor (LC) circuit model25:
where c is the speed of light, Lk and Lm are the kinetic and magnetic inductances, respectively, and Cs and Cgap are the surface and gap capacitances25, respectively. These equivalent inductances and capacitances are functions that are dependent on the radius, width, thickness of the circular ring, in addition to the gap width and Gold plasma frequency at the resonant frequency. The \(\mathop \lambda \nolimits_{QSSR}\) is substituted by 10 μm. The cross resonator is considered an electric ring resonator (ERR)26 that is able to strongly manipulate the incident IR radiations. The major and minor axes of the designed CEs control the electric response while the magnetic response is tuned by the thickness of the dielectric layer27. The resonant frequency of a regular cross resonator, i.e. crossed rectangles, can be estimated from the microwave regime using the formula28:
where l and w represent the arm length and width of the cross respectively which can be replaced for simplicity by 2a and 2b, as shown in Fig. 1b. The parameter tm is the cross thickness as depicted in Fig. 1c. λCE is desired to be close enough to that of QSRR. Therefore, it was selected to be 9.5 μm in order to allow the wide-band operation. The relative permittivity of TiO2 at 9.5–10 μm is almost 1.929. The dimensions resulting from the above formulas are presented in Table 1. These are taken as initial values towards realizing a wide-band metamaterial perfect absorber around 10 μm. The reflectivity of the MPA structure forms the objective function W = (1 − A), where A is the absorptivity, for the gradient-based optimization algorithm as described below. The MPA dimensions constitute the vector of design parameters, u = [G, R, w, a, b, td, tm]T for this objective function. The gradient of the objective function, i.e., absorptivity, is provided for the optimizer through adjoint sensitivities to allow for faster convergence30. The optimization problem is given by:
where λi represent the selected wavelength points between 9.7 μm and 10 μm to maximize the absorptivity within this range.
Magnetic resonance in CEs and QSRR to achieve wide incident-angle and polarization-insensitive perfect absorber
The resonance wavelengths and the magnitude of the absorptivity peaks depend on the polarization of the incident IR radiation. In IR rectennas, the MPA is important to absorb the randomly polarized incoming radiation. This requires the design to be polarization insensitive to overcome the polarization-dependence of conventional antennas. Therefore, the proposed MPA was designed to retain symmetry to prevent the absorption characteristics from changing under different polarization directions. It is also preferable to account for the dependence of the absorption characteristics on the angle of incidence of the impinged electromagnetic waves.
To keep the energy harvesting functionality of the perfect absorber at a wide range of incident angles, the resonance peak is required to be held around 10 μm. Therefore, the interest to excite magnetic polaritons (MPs) from both resonators around this desirable wavelength is vital26. The cross resonators array that is built with a layered MIM structure usually provides two bands of absorption. One of these bands is attributed to the propagation of surface plasmon polaritons (SPPs) while the other is related to MPs and occurs at longer wavelengths27. The SPPs are excited at the interface between the top resonator and the dielectric layer while MPs arise from the coupling mechanism between the incident IR radiations and magnetic resonances inside the absorber23. The periodicity of the crossed-ellipses array is directly proportional to the SPP resonance wavelength14. Therefore, the periodicity G is designed to induce SPPs resonances at a shorter wavelength far from 10 μm, thus enabling a remarkably insensitive absorption band with respect to the angle of incidence around this resonance wavelength.
The proposed metamaterial perfect absorber shown in Fig. 1 was optimally designed to retain absorption bands resulting from MPs resonances of the quadruple split-ring resonator and crossed-ellipses close together, and to create a broadband absorption around 10 μm. The symmetry of the design and the MPs excitation allow for a wide-angle absorption with a polarization-insensitive response.
Results and discussions
Dimensions of the quadruple split-ring resonator and crossed-ellipses
The initial dimensions of QSRR and CE are determined using the inductor-capacitor (LC) circuit models as explained earlier. These values were used to simulate the MPA structure using the finite element method (FEM) through ANSYS HFSS. The complex permittivity of gold is defined according to the model31, while another model29 is used for TiO2. The absorptivity corresponding to these parameters was calculated and plotted in Fig. 2a. Although absorption peaks exist around 10 μm, their magnitude barely approaches an absorptivity of 83%.
(a) The absorptivity of the proposed MPA structure calculated at the initial (dotted) and optimal (solid) design parameters; the bandwidth of the optimal response is ~ 1.7 times the initial one with flat near-unity absorption. (b) The convergence of the optimization algorithm measured with the objective function (reflectivity = 1-absorptivity) versus the iteration number. The algorithm approaches the optimal values after 43 steps.
We utilized an adjoint-sensitivity based optimization approach that is able to start from this initial design and achieve a broader band of absorption and near-unity peaks. The optimal parameters’ values are shown in Table 1 and the corresponding absorptivity is plotted in Fig. 2a. The absorption band increased from 11% initially to 18% for the optimal design. Also, the absorption band is almost flat near unity in the range between 9.6 and 10.2 μm which is equivalent to 29.4–31.3 THz. The convergence of the optimization algorithm is illustrated in Fig. 2b, where the objective function in the algorithm is defined by the absorber reflectivity. Therefore, the algorithm sought to obtain zero reflectivity, i.e. unity absorption, around the wavelength of interest. It took the algorithm 43 steps to approach this local minimum, as shown in Fig. 2b. The absorption peaks were calculated to be above 99% at 9.7 μm and 10 μm. The high absorptivity of these two wavelengths are attributed to the resonance wavelengths of each metallic resonator. The shorter resonant wavelength of 9.7 μm is attributed to the smaller resonator, i.e. crossed-ellipses, while the quadruple split-ring resonator contributes to the longer wavelength of 10 μm, as will be discussed later.
The optimization results revealed a preferred dielectric thickness, td of 0.56 μm, i.e. λ/17, which in turn allows for building thinner MPA. The ground plane thickness, tg, is designed to be fixed at 200 nm, which is several skin depths at this wavelength range in order to ensure approximately zero transmission. By comparing the initial and optimal values of design parameters, it is noted that the larger changes occurred mainly in 3 parameters: R, a, td which represent the inner radius of the QSRR, the ellipse’s major-axis of the CE, and the thickness of the dielectric layer, respectively. This agrees with the theoretical predictions, where in the ring resonator, the response is more dependent on the ring radius25. As for the cross resonator, the arm length, i.e. twice the ellipse major axis, is more dominant28. Also, the insulator thickness tunes the coupling within the MIM structure. Owing to all parameters’ variations, the absorption band was tailored efficiently, and hence the required performance was realizable.
By taking fabrication tolerances into account at this nanometer scale, the absorption sensitivities with respect to all design parameters were calculated at the two wavelengths of 9.7 μm and 10 μm. These sensitivities, obtained through adjoint sensitivity calculations by considering 10% change in each parameter, are presented in Table 1. Most of the values are relatively small which in turn enables acceptable performance at predictable and unavoidable tolerances. From the last two rows in Table 1, the largest expected variation in the absorptivity at the 9.7 μm peak, which is 0.022, is attributed to the ellipses’ major axis, a, while the other peak at 10 μm is almost insensitive. Moreover, a slight change of 0.004, at this shorter wavelength peak, is associated with the 10% change in the thickness of the dielectric layer with almost no impact at the longer wavelength. As for the longer wavelength peak, a relatively small change of 0.005 is expected due to variations in the radius of the ring resonator, with lesser impact on the shorter wavelength peak.
Electromagnetic field distributions at MP resonances of the polarization insensitive MPA
We calculated the magnetic field distributions in the cross-sections of the MPA structure at the wavelengths of 9.7 μm and 10 μm, where the absorption peaks reach 99.99%. These calculations were obtained using FEM simulations in both ANSYS HFSS and COMSOL Multiphysics, and the corresponding field distributions are presented in Fig. 3(a-f). In the simulations, a normal incident electromagnetic wave impinged the MPA structure directed from top to bottom, i.e. z-direction, with the electric field polarized in the x-direction. The magnetic field intensity |H|2 was investigated in the XY plane, parallel to the top cross-section at the interface between the top gold resonators and the TiO2 dielectric layer underneath. Figures 3a,b show the magnetic resonances at 9.7 μm and 10 μm, respectively. The magnetic field is confined around the arm of the crossed ellipses that is parallel to the incident electric field at 9.7 μm, as depicted in Fig. 3a. At 10 μm, the magnetic field is concentrated within the top and bottom parts of the QSRR, as shown in Fig. 3b.

source of the resonance occurs at each absorption peak; the left one shows the field beneath the crossed ellipses resonance is dominating, while the right one reveals the domination of QSRR resonance. (ANSYS HFSS 2018, https://www.ansys.com/, COMSOL Multiphysics 5.3 ).
The distribution of the magnetic field intensity |H|2 of the proposed MPA structure calculated at two peaks of 9.7 μm and 10 μm, respectively. (a, b) at the cross section at the interface between the top resonators and the dielectric layer below, where the darker color represents higher magnetic field intensity, all plots at the same scale. (c, d) the grey scale spectrum maps the magnetic field intensity at XZ-plane cross-section, while the red arrows show the electric field distribution at both resonance wavelengths emphasizing the creation of magnetic resonances. The cross-section is cut along the CE arm in (c), while it passes through the circumference of the QSRR in (d). (e, f) YZ-plane cross-section illustrates the dominant
Figures 3c,d illustrate the electric field and magnetic field distributions across the XZ plane cross-sections. At 9.7 μm, the electric field vectors form circles that exhibit a strong magnetic resonance that is shown in Fig. 3c. At the other wavelength of 10 μm, the XZ cross-section was selected at the perimeter of the QSRR, where the electric fields are arranged to compose a confined magnetic resonance around the QSRR, as illustrated in Fig. 3d. The YZ cross-sections plotted in Figs. 3e,f show an enhanced magnetic field in the dielectric layer below each top resonator according to Lenz’s law. The magnetic field confinement shown in Fig. 3a–e indicates the strong MPs excited by the CE and the QSRR at 9.7 μm and 10 μm, respectively.
Electric field enhancement in the gaps of the metamaterial perfect absorber and energy harvesting capabilities
The designed metamaterial perfect absorber is featured with multiple gaps that promote the integration with diodes, i.e. rectifiers. This integration allows the MPA to harvest the absorbed energy from IR radiation and simultaneously transform it into a useful DC current. The electric field intensity enhancement |E/E0|2 at the center of each gap is depicted in Fig. 4a. The gaps are categorized into two groups; the gaps between the crossed ellipses arms and the surrounding ring resonator, and the other gaps formed by splits of the ring resonator itself. The electric field enhancement of the first category is blue shifted, as expected from the resonance characteristics resulting from the crossed ellipses which are around 9.7 μm as shown in Fig. 4a. The electric field enhancement at the center of the other gaps inside the ring resonator’s splits is confined almost around 10 μm as presented in the same figure. These electric field intensities are normalized and plotted with the absorptivity of the proposed metamaterial perfect absorber. The figures illustrate the capability of each group of those tiny gaps to confine the absorbed fields. Both groups of gaps work simultaneously to trap the incoming IR radiations and cover the whole absorption band as shown in Fig. 4a.
(a) The absorptivity of the optimal MPA design in dotted black line and the normalized electric field intensity enhancement |E/E0|2 at the center of the gap between the CE and QSRR and center of the slits of the QSRR in red and blue solid lines, respectively. The electric field intensity distribution at 9.7 μm and 10 μm, respectively, (b, c) through the XY cross-section, and (d, e) through the YZ cross-section. (COMSOL Multiphysics 5.3 https://www.comsol.com/).
The distribution of the electric field intensity is plotted in Fig. 4b–e. The top views of the electric field intensity in the XY plane of PMA structure exhibit a strong electric field confinement at the gaps located between the CE arms and the surrounding QSRR combined with a weaker resonance inside the splits of QSRR at 9.7 μm, as depicted in Fig. 4b. While the electric field is mostly confined inside the splits of QSRR at 10 μm as presented in Fig. 4c. Figure 4d–e illustrate the electric field confinement distribution across the YZ plane cross section which agrees with the previous results, where the electric field is noticeably confined inside the gaps between CE arms and QSRR inner perimeter at the shorter wavelength of 9.7 μm.
Energy harvesting using MPA combined with MIM diodes
The strong electric field confined inside the MPA gaps promotes its applicability and suitability to efficiently replace the nano-antennas in the rectenna system for energy harvesting. The developed MPA design offers a polarization insensitive performance due to the symmetry. Owing to the excitation of MPs through both top resonators, i.e. CE and QSRR, the proposed MPA exhibits almost insensitive absorption peaks to incident angle variations up to 60°, as illustrated in Fig. 5a. The shift in the resonance wavelength in this range is at most 2%, which falls in the absorption band of interest. These characteristics support the use of the proposed MPA rather than regular nano-antennas that lack at least one of these features, for thermal energy harvesting.
(a) Incident angle sensitivity of the absorptivity of the optimal MPA structure through calculating absorptivity peaks for TE and TM polarizations. (b) The absorptivity of the optimal MPA structure using a gold ground compared to the titanium. (c) The resistance and reactance of the MPA structure, (d) Diode’s resistance sensitivity, resistances range from 500 Ω up to 1 MΩ.
The metal–insulator-metal (MIM) diodes are the best candidate that can work with the proposed perfect absorber in the IR region. Due to the dominance of the tunneling current through thin dielectric barriers with a few nanometers thickness, the MIM diodes can rectify the ultra-high frequency AC signal captured by the MPA structure. Additionally, the fabrication of the MPA structure combined with an MIM diode would reduce the complexity as compared to the integration of MIM diodes with nano-antennas. To reduce the complexity of the manufacturing, we designed the metallic ground plane to be made of titanium instead of gold. The resulted absorptivity of the Ti-based MPA structure is compared to the Au-based one as depicted in Fig. 5b. A slight shift in absorption band due the change of the ground materials is noticed because of different optical permittivities. In addition, a small increase in the absorption bandwidth is achieved. The choice of Ti as a ground plane facilitates forming the TiO2 layer on top of it.
One of the main shortcomings of recent IR rectennas is the impedance mismatching between the MIM diode and the nano-antenna. The MIM diodes possess a wide range of diode resistance from few hundreds up to several Mega Ohms8 depending on the materials’ properties of the diode including barrier heights, dielectric constants and their corresponding thicknesses, and area9. Nano-antennas, on the other hand, generally have a small resistance in the range of few tens of ohms9. The diode’s resistance is considered the load of the nano-antenna and thus a small portion of the power received by the nano-antenna can reach the diode terminals to be rectified. Experimental attempts were carried out to improve this matching by selecting diodes’ dielectric materials with ultra-thin thicknesses to achieve smaller diode’s resistance. However, this matching should be accomplished through both rectenna elements, i.e. diode and nano-antenna, simultaneously. We calculated the impedance of our MPA structure and presented the results in Fig. 5c. The resistance is greater than 500Ω over the absorption bandwidth, which is higher than that of the dipole and bowtie nano-antennas32. This consequently improves the matching efficiency9.
The wide range of possible diode’s resistance drives the investigation of the sensitivity of the proposed MPA absorptivity to this range of resistances. The MIM diode’s resistance was varied from a 500 Ω up to 1 MΩ. The absorptivity shows insensitive response for diode resistances greater than 1 kΩ as illustrated in Fig. 5d. For resistances of 1kΩ or less, the rectenna shows a perfect absorption but with a little reduction in the flat absorption band while the absorption bandwidth increased. Additionally, the MIM diodes are connected in series through the proposed rectenna-like design and consequently decrease the capacitance of the equivalent diode. This reduction in turns allows for attaining a shorter time constant and hence a higher cut-off frequency. This also leads to further improvement in the rectenna performance. The final rectenna structure will employ the proposed MPA with the MIM diode as a unit cell in a large 2D array with the corresponding interconnections as represented in Fig. 6a.
(a) A schematic representation for the array of connected rectennas using the proposed MPA structure with control lines in green (horizontal) and red (vertical), (ANSYS HFSS 2018, https://www.ansys.com/) (b) The absorption efficiency of the proposed MPA structure calculated for the substrate (green), load (blue) and metal (red) of the MPA with PI substrate.
The absorbed power per each layer of the MIM structure can be determined by considering the corresponding complex permittivity of each material at this wavelength range33. Therefore, the absorption efficiency can be calculated as the ratio of power absorbed by each layer to the total absorbed power34,35. By considering that the extinction coefficient, k, of TiO2 is ~ 0.14 around 10 μm wavelength29, the power loss in the substrate is expected to be large and will dominate the absorption efficiency. However, building the MIM structure using a low-loss substrate such as polyimide (PI), where k ~ 20 × 10–3, allows for a drastic reduction in substrate losses compared to TiO2 case36. The absorption efficiency is estimated using the PI layer and presented in Fig. 6b, where most of the absorbed power is delivered to the load.
The proposed metamaterial perfect absorber (MPA) design in this work is built as a metal–insulator-metal (MIM) structure composed of a crossed ellipse (CE) concentric with a quadruple split-ring resonator (QSRR). The structure is optimized, around 10 μm, using an adjoint sensitivity approach to achieve near unity wide-band absorptivity. The proposed MPA supports wide reception-angle up to 60°. The strong electric field enhancement inside the gaps of the structure allows for simple integration with MIM diodes to form a complete rectenna for thermal energy harvesting around 10 μm. The optimal design shows insensitive performance with different MIM diode’s resistances, and accordingly provides more flexibility in selecting the diodes’ materials. Finally, this proposed work offers a scalable approach to design MPA at different resonance wavelengths.
Methods
Numerical simulations
We employed an LC circuit model to determine the initial parameter values for the wide incident-angle and polarization insensitive MIM absorber structure. An FEM method using ANSYS HFSS simulator software was used to verify the circuit model results. It was integrated within a MATLAB-based optimization algorithm. At each optimization step, the absorptivity and the corresponding adjoint sensitivities with respect to all design parameters were calculated using ANSYS HFSS and then passed to MATLAB to move forward. Another FEM model was built in COMSOL Multiphysics to study the performance at different incident angles. Periodic boundary conditions were applied in x and y directions of the unit cell with perfectly matched layer in the top of the structure along z-axis. The incident IR consisted of TM-mode plane waves. The mesh was set to be with a minimum 2 nm in the vicinity of the tiny gaps and inside the top metal structures.
References
Quaschning, V. V. Renewable Energy and Climate Change (Wiley, Hoboken, 2019).
Harvey, L. D. D. Global Warming (Routledge, Abingdon, 2018).
Tiwari, G. N. Solar Energy: Fundamentals, Design, Modelling and Applications (Alpha Science Int’l Ltd., Oxford, 2002).
Couderc, E. Thermoelectrics: invisible harvest. Nat. Energy 2, 17137 (2017).
Zhu, T., Fu, C., Xie, H., Liu, Y. & Zhao, X. High efficiency half-Heusler thermoelectric materials for energy harvesting. Adv. Energy Mater. 5, 1500588 (2015).
Jayaswal, G. et al. Optical rectification through an Al2O3 based MIM passive rectenna at 28.3 THz. Mater. Today Energy 7, 1–9 (2018).
Dasgupta, A. et al. Optical wireless link between a nanoscale antenna and a transducing rectenna. Nat. Commun. 9, 1992 (2018).
Gadalla, M. N., Abdel-Rahman, M. & Shamim, A. Design, optimization and fabrication of a 28.3 THz nano-rectenna for infrared detection and rectification. Sci. Rep. 4, 4270 (2014).
Elsharabasy, A. Y., Negm, A. S., Bakr, M. H. & Deen, M. J. Global optimization of rectennas for IR energy harvesting at 10.6 μm. IEEE J. Photovolt. 9, 1232–1239 (2019).
Guan, M., Wang, K., Xu, D. & Liao, W.-H. Design and experimental investigation of a low-voltage thermoelectric energy harvesting system for wireless sensor nodes. Energy Convers. Manag. 138, 30–37 (2017).
Assimonis, S. D., Fusco, V., Georgiadis, A. & Samaras, T. Efficient and sensitive electrically small rectenna for ultra-low power RF energy harvesting. Sci. Rep. 8, 15038 (2018).
Farhat, M. et al. Mirror-backed dark alumina: a nearly perfect absorber for thermoelectronics and thermophotovotaics. Sci. Rep. 6, 19984 (2016).
Okamoto, K. et al. Surface-plasmon-enhanced light emitters based on InGaN quantum wells. Nat. Mater. 3, 601 (2004).
Zheludev, N. I. & Kivshar, Y. S. From metamaterials to metadevices. Nat. Mater. 11, 917 (2012).
Landy, N. I., Sajuyigbe, S., Mock, J. J., Smith, D. R. & Padilla, W. J. Perfect metamaterial absorber. Phys. Rev. Lett. 100, 207402 (2008).
Yong, Z., Zhang, S., Gong, C. & He, S. Narrow band perfect absorber for maximum localized magnetic and electric field enhancement and sensing applications. Sci. Rep. 6, 24063 (2016).
Gong, C. et al. Broadband terahertz metamaterial absorber based on sectional asymmetric structures. Sci. Rep. 6, 32466 (2016).
Sreekanth, K. V. et al. A multiband perfect absorber based on hyperbolic metamaterials. Sci. Rep. 6, 26272 (2016).
Aydin, K., Ferry, V. E., Briggs, R. M. & Atwater, H. A. Broadband polarization-independent resonant light absorption using ultrathin plasmonic super absorbers. Nat. Commun. 2, 517 (2011).
Baranov, D. G., Krasnok, A., Shegai, T., Alù, A. & Chong, Y. Coherent perfect absorbers: linear control of light with light. Nat. Rev. Mater. 2, 17064 (2017).
Chen, K., Dao, T. D., Ishii, S., Aono, M. & Nagao, T. Infrared aluminum metamaterial perfect absorbers for plasmon-enhanced infrared spectroscopy. Adv. Funct. Mater. 25, 6637–6643 (2015).
Dao, T. D. et al. Infrared perfect absorbers fabricated by colloidal mask etching of Al–Al2O3–Al trilayers. Acs Photonics 2, 964–970 (2015).
Ogawa, S. & Kimata, M. Metal-insulator-metal-based plasmonic metamaterial absorbers at visible and infrared wavelengths: a review. Materials (Basel) 11, 458 (2018).
Watts, C. M., Liu, X. & Padilla, W. J. Metamaterial electromagnetic wave absorbers. Adv. Mater. 24, OP98–OP120 (2012).
Delgado, V. et al. Analytical circuit model for split ring resonators in the far infrared and optical frequency range. Metamaterials 3, 57–62 (2009).
Padilla, W. J. et al. Electrically resonant terahertz metamaterials: theoretical and experimental investigations. Phys. Rev. B 75, 41102 (2007).
Li, Y. et al. Surface-enhanced molecular spectroscopy (SEMS) based on perfect-absorber metamaterials in the mid-infrared. Sci. Rep. 3, 2865 (2013).
Cheng, Y., Nie, Y., Wang, X. & Gong, R. Adjustable low frequency and broadband metamaterial absorber based on magnetic rubber plate and cross resonator. J. Appl. Phys. 115, 64902 (2014).
Kischkat, J. et al. Mid-infrared optical properties of thin films of aluminum oxide, titanium dioxide, silicon dioxide, aluminum nitride, and silicon nitride. Appl. Opt. 51, 6789–6798 (2012).
Bakr, M. Nonlinear Optimization in Electrical Engineering with Applications in MATLAB (Institution of Engineering and Technology, London, 2013).
Rakić, A. D., Djurišić, A. B., Elazar, J. M. & Majewski, M. L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 37, 5271–5283 (1998).
González, F. J. & Boreman, G. D. Comparison of dipole, bowtie, spiral and log-periodic IR antennas. Infrared Phys. Technol. 46, 418–428 (2005).
Assimonis, S. D. & Fusco, V. Polarization insensitive, wide-angle, ultra-wideband, flexible, resistively loaded, electromagnetic metamaterial absorber using conventional inkjet-printing technology. Sci. Rep. 9, 1–15 (2019).
Almoneef, T. S. & Ramahi, O. M. Metamaterial electromagnetic energy harvester with near unity efficiency. Appl. Phys. Lett. 106, 153902 (2015).
Zhong, H.-T., Yang, X.-X., Tan, C. & Yu, K. Triple-band polarization-insensitive and wide-angle metamaterial array for electromagnetic energy harvesting. Appl. Phys. Lett. 109, 253904 (2016).
Wang, Y., Abe, Y., Matsuura, Y., Miyagi, M. & Uyama, H. Refractive indices and extinction coefficients of polymers for the mid-infrared region. Appl. Opt. 37, 7091–7095 (1998).
Author information
Authors and Affiliations
Contributions
A.E., M.B. and J.D. wrote the manuscript. A.E. did the design and simulations. A.E., M.B. and J.D. analyzed the simulations and interpreted the results. All three authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Elsharabasy, A., Bakr, M. & Deen, M.J. Wide-angle, wide-band, polarization-insensitive metamaterial absorber for thermal energy harvesting. Sci Rep 10, 16215 (2020). https://doi.org/10.1038/s41598-020-73368-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-73368-7
This article is cited by
-
Dumbbell shaped structure loaded modified circular ring resonator based perfect metamaterial absorber for S, X and Ku band microwave sensing applications
Scientific Reports (2024)
-
Level set methods for gradient-free optimization of metasurface arrays
Scientific Reports (2024)
-
Selective-wavelength perfect infrared absorption in Ag@ZnO conical metamaterial structure
Scientific Reports (2024)
-
Si3N4 Dielectric Hemi-sphere Arrayed Plasmonic Metasurface With Top Metal Coating for Multiresonant Absorption in NIR Regime
Plasmonics (2024)
-
Metamaterial Wave Absorber for Harvesting Electromagnetic Energy with Dispersion Characteristics Using Palm Oil Frond Graphitic Carbon
Journal of Electronic Materials (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.