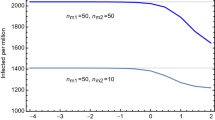
Abstract
A second wave pandemic constitutes an imminent threat to society, with a potentially immense toll in terms of human lives and a devastating economic impact. We employ the epidemic Renormalisation Group (eRG) approach to pandemics, together with the first wave data for COVID-19, to efficiently simulate the dynamics of disease transmission and spreading across different European countries. The framework allows us to model, not only inter and extra European border control effects, but also the impact of social distancing for each country. We perform statistical analyses averaging on different level of human interaction across Europe and with the rest of the World. Our results are neatly summarised as an animation reporting the time evolution of the first and second waves of the European COVID-19 pandemic. Our temporal playbook of the second wave pandemic can be used by governments, financial markets, the industries and individual citizens, to efficiently time, prepare and implement local and global measures.
Similar content being viewed by others
Introduction
A second wave pandemic constitutes an imminent threat to society, with an immense toll in terms of human lives and a devastating economic impact. The disease diffusion dynamics is traditionally modelled via compartmental1 or complex network diffusion techniques2,3,4. These models provide a fairly accurate description of the time evolution of the number of affected individuals. However, it is a hurdle to predict the future evolution of a pandemic5 and to account for the diffusion across different regions of the World. Here we show that the epidemic Renormalisation Group framework6,7 is a simple and effective method to provide robust projections of the time evolution of a pandemic across regions. We apply it to the COVID-19, calibrating it on the first wave data, to efficiently simulate an incumbent second wave across Europe. We perform statistical analyses averaging on different levels of human interaction across Europe and with the rest of the world, finding that the second wave will occur between July 2020 and January 2021. Our results demonstrate that our method can be employed to describe pandemic dynamics beyond the European example. We anticipate that our results can be functional to a more quantitative understanding of future pandemics, which are expected to become a recurrent threat to our society. Our temporal playbook of the second wave pandemic can be used by governments, financial markets, the industries and individual citizens, to efficiently time, prepare and implement local and global measures.
Pandemics are increasingly becoming a constant menace to the human race, with COVID-198,9 being the latest example. A second wave is creeping back in Europe and is poised to rage across the continent by fall 2020. In this letter we provide a statistical analysis of the temporal evolution of the second wave of infected cases, with the impact for various European countries. To model the spreading, we employ the epidemic Renormalisation Group (eRG) framework6,7. It can be mapped7,10 into a time-dependent compartmental model of the SIR type1. The Renormalisation Group approach11,12 has a long history in physics with impact from particle to condensed matter physics and beyond. Its application to epidemic dynamics is complementary to other approaches2,3,4,13,14,15,16,17,18,19,20.
The eRG approach consists in a set of first order differential equations apt to describe the time-evolution of the infected cases in a specific isolated region. It has been extended7 to include interactions among multiple regions of the World, without the need for powerful numerical simulations. The set of equations7 reads
with \({{\mathscr {I}}}_i (t)\) being the total number of infected cases per million inhabitants for region i and \(\ln \) indicating its natural logarithm. These equations embody, within a small number of parameters, the pandemic spreading dynamics across coupled regions of the World via the temporal evolution of \(\alpha _i\), which resembles the energy dependence of the couplings appearing in fundamental interactions of particle physics.
The first term of the right-hand side in Eq.(1) characterises the epidemic evolution within a given region of the World. The infection rate \(\gamma _i\), measured in inverse weeks, is responsible for how quickly the epidemic evolves in the i-th region. Besides depending on the intrinsic virulent character of the epidemic, the size of \(\gamma _i\) can be controlled via social-distancing measures, with a flatter epidemic curve associated to smaller \(\gamma _i\). It is well understood1 that epidemic diffusion curves generally lead to plateaus in the total number of infected cases at late times. This is encoded in the parameter \(a_i\), equal to the natural logarithm (ln) of the total number of infected cases (per million) at the end of the epidemic wave.
The second term of the right-hand side in Eq.(1), first introduced here7, is a source-term that takes into account human interaction across different regions of the World. Here, \(n_{mi}\) is the population of region-i in millions and \(k_{ij}\) represents the number of reciprocal travellers per week from region i to region j and vice-versa in units of million people. For a single country, i.e. France, we illustrate diagrammatically the connections given by the \(k_{ij}\) couplings in Fig. 1. We also consider an extra-source of infection modelled as a new region that we call Region-X (\(i=0\)). We can interpret this region in various ways: for instance, this may represent an inflow of infections coming from outside of the regions of the World included in the simulation or, alternatively, Region-X may represent the effect of local hotspots of infections. Of course, it could also be a combination of the two effects.
Illustration of the connections \(k_{ij}\) between, i.e., France and the other countries considered in this study. Each line represents the exchange of infected cases. The line pointing outside the map represents the connection with Region-X, representing an inflow from a source outside the pool of countries in the simulation and/or the presence of hotspots in the concerned country. Figure created with Wolfram Mathematica.
To simulate the second wave diffusion in Europe, we take, as reference, the values of the parameters \(\gamma _i\) and \(a_i\) to the first wave fits, which provides a reasonable benchmark for quantities that are very hard to predict5. The couplings \(k_{ij}\), are randomly generated within the range \(10^{-3}\)–\(10^{-2}\), which has been shown7 to give reasonable timing for the peak diffusion. We will consider five scenarios, which differ for the values given to the couplings to Region-X: (a) we use the randomly generated \(k_{0i} = k_{i0}\), in the range \(10^{-2} - 10^{-3}\); (b) we divide the \(k_{0i}\) by a factor of ten, implying a 90% reduction of the interaction with Region-X; (c) we divide the \(k_{0i}\) by a factor of hundred, i.e. a 99% reduction; (d) for unrestricted \(k_{i0}\), we allow the \(\gamma _i\)’s to vary within \(14\%\) of the first wave fit value; (e) all the \(k_{0i}\) are set to zero except for a set of 10 countries, which already show signs of a second wave as of the 5th of August, 2020. For these countries, which are Belgium, Bosnia, Croatia, Czechia, Greece, the Netherlands, Serbia, Slovakia, Slovenia and Spain, the \(k_{i0}\) and other parameters are tuned in order to fit the available data from the second wave, as detailed in the section “Methods”. We consider this case (e) as the most realistic one.
In all cases, the simulation starts in week 25, where no country is yet in the second wave. For the first four cases, we average over the 100 simulated matrices \(k_{ij}\) to extract the location of the peak of the newly infected cases for the second wave per each country and the relative error. In case (d), we also include the error coming from the variation of \(\gamma _i\). Finally, for case (e), the error comes from a \(10\%\) variation for \(\gamma \)’s of all countries. The results are summarised in the last five columns of Table 1 with the errors representing one standard deviation. The time is given in 2020 calendar weeks.
Results
We first discuss the results for the simulations in case (e), which are more realistic vis à vis the current situation in Europe, as of week 32 (i.e., the 5th of August). As already mentioned, we tuned the \(k_{i0}\) and other parameters (\(\gamma _i\) and \(a_i\)) for the second wave simulation in order to reproduce the data available between week 25 (the start of the simulation) and week 32. This was done to render the simulation more realistic. As an example, in Fig. 2 we show the outcome for Croatia compared to the actual data points (from www.worldometers.info). We also include the first wave from the fit. To obtain this result, we fixed \(k_{i0} = 0.1\), and for the second wave we rescaled \(\gamma \) and a respectively by 0.6 and 1.06 for Croatia alone. This implies that Croatia has already internal hotspots (as indicated by the large value of the coupling \(k_{i0}\) with Region-X) and the second wave shows a smaller infection rate. For Croatia we also observe, however, that the total number of infected cases for the second wave is higher than for the first wave. It would be interesting to learn, from future data, whether this worrisome trend is followed by other European countries. The figure demonstrates that the result of our simple simulation can be tuned to reproduce the beginning of the second wave already observed in some countries. We have repeated the same tuning for Belgium, Bosnia, Czechia, Greece, the Netherlands, Serbia, Slovakia, Slovenia and Spain.
As an example of our prognoses for the remaining countries, we show in Fig. 3 the epidemic dynamics of the first and second wave for three representatives: Italy, France and the UK. The top panel shows the number of infected cases not normalised per million. The central panel shows the number of new infected cases while the lower panel displays an estimate for the effective reproduction rate R. The number of recovered cases \({{\mathscr {R}}}(t)\) is calculated by solving the following SIR-inspired equation7:
where we fix the recovery rate \(\epsilon =0.1\) in the numerical solutions. The effective reproduction rate R is estimated by computing the ratio of the new infected cases over the new recoveries within the susceptible population, from the theoretical model. The susceptible population is here defined as the total number of people infected at late time for the first and second waves independently. A more accurate result could be obtained using a generalised eRG approach10, at the expense of introducing more parameters. The plots are obtained using the simulations for case (e). Note that we used the same \(\gamma \)’s and a’s stemming from the first wave fit with the main error on the curve deriving from allowing a \(10\%\) variation for the infection rates \(\gamma \)’s. One can also modify the values of a’s which will not modify the general temporal picture and trend of the second wave pandemic.
Result of case (e) for France, Italy and the UK. We show the time evolution of the total number of infected cases in the top panel, the new infected in the central panel and the derived effective reproduction rate R in the bottom panel. The number of cases refer to the total population of the countries. The bands are generated by varying the infection rates \(\gamma _i\) within \(10\%\).
To study the dependence of the peak timing on \(k_{ij}\), \(\gamma _i\) and \(a_i\), we can use the results from cases (a–c) from Table 1, as visualised in Fig. 4. Here we show the average peak time in calendar weeks versus \(\gamma \) for all the countries in this study. Comparing the results in each set of simulations, we discover a clear correlation between the timing of the peak and the infection rate \(\gamma _i\) of each country. The higher is the infection rate the sooner the peak is reached, as expected6. Furthermore, comparing the results for the three cases, we show that reducing the coupling with Region-X systematically delays the peaks, in accordance with previous results7. Quantitatively a reduction of a factor ten in the coupling to Region-X delays the peaks by about three weeks. We recall that, following the possible interpretations of Region-X, a reduction of the couplings to this region can be seen as the effect of travel bans and/or better control of local hotspots. Overall the peak timing ranges from end of July 2020 to beginning 2021. We did not find any correlation between the peak timing and the value of \(a_i\) across the countries we studied. We also notice that the second wave peak timing for the countries without early signs of a second wave in case (e), indicated by un-starred values in Table 1, is close to the result found for case (c). This can be explained by the values of the \(k_{ij}\) we use in case (e) simulation, which are close to the \(k_{i0}\) used in case (c). The countries with early signs of a second wave act as a effective “Region-X” for the others.
The results from the first three simulations show a fairly small error in the peak time prediction due to the uncertainty on our knowledge of the \(k_{ij}\) couplings. We recall that we vary the couplings within a factor of 10. However, the peak position also depends crucially on the value of the infection rates \(\gamma _i\)6. In this study, we use as a benchmark the values obtained by fitting the first wave. However, such values can depend crucially on the social distancing measures imposed in each country, so important variations are expected. For instance, it was shown in the eRG framework that reduction of individual mobility may lead to a decrease in \(\gamma \) by \(20\%\) or more21. For analogous analyses within compartmental models, see22,23. To study the robustness of our results with respect to a change in \(\gamma \), we performed the simulation in case (d), where the \(k_{ij}\) are as for case (a) while we allow the \(\gamma _i\) to vary around the first wave value by \(15\%\), following a Normal distribution. The results are shown in the second-to-last column of Table 1: while the central values agree with case (a), as expected, the error is substantially increased. This results proves that it is the value of \(\gamma \) that can mostly influence the position of the second wave peak, thus highlighting the importance of timely social distancing measures. For the realistic simulation of case (e), we include a variation of \(\gamma _i\)’s by 10%, resulting in the intervals reported in the last column of Table 1. This can be considered our prognosis for the second wave in Europe. It should be clear that the a’s and the \(\gamma \)’s chosen for the simulation can, and will, be different from the first wave values we used. Nevertheless, we expect the dynamics to be still well represented by the framework and that these values give a reasonable indication for the second wave European pandemic.
Discussion and video simulation
We employed the epidemic Renormalisation Group approach to simulate the dynamics of disease transmission and spreading across different European countries for the second COVID-19 wave. Since it has been demonstrated10 that the framework can be mapped into other compartmental models, our results are sufficiently general. The approach allows to model inter and extra European border control effects while taking into account the impact of social distancing for each country. To reduce the number of unknowns in the simulation, we used the information from the first wave. This information is encoded in the infection rate and the logarithm of the number of total infected cases per each country. Going beyond this hypothesis is straightforward in our approach, but such parameter tuning is not the point of this work. Nevertheless we allowed variations of the central value of \(\gamma \)’s by up to 15% to estimate the impact on the second wave pandemic and shown that the general overall trend remains unchanged. We then performed statistical analyses averaging on different level of cross Europe interactions and with the rest of the World. The role of the rest of the World and possibly local hotspots has been attributed to a Region-X, which acts as a source of infection coupled to all or only few European countries. By calibrating on the current European situation that shows early signs of the second wave, we provided a temporal playbook of the second wave pandemic. Our results can be employed by governments, financial markets and the industry world to implement local and global measures.
The main results show that the temporal position of the second wave peak, once started, is rather solid and will occur between July 2020 and January 2021. As an example, we show in Fig. 5 our prognosis for the nordic countries, Denmark, Finland, Norway and Sweden. The precise timing for each country can be controlled via travel and social distancing measures. The sensitivity of the second peak prognosis on the value of the infection rates gives a clear indication that social distancing measures and responsible individual behaviour can have a strong effect if implemented early on. The predictions given by our model can, therefore, be easily updated to take into account the current situation in each country.
In the added material, we also include two animations representing the time evolution of the first and second wave of the European COVID-19 pandemic resulting from our simulations, extracted from case (a) and case (e) respectively, tuned to give the most realistic results and taking into account early signs of a second wave in some countries, as of the 5th of August, 2020. The simplicity of the eRG approach is such that the simulations take only a few seconds on an average personal laptop, thus providing a practical and accurate tool for the understanding of a second (and third, and so on) wave pandemic. The temporal playbook we provide is a useful tool for governments, financial markets, the industries and individual citizens to prepare in advance and possibly counter the threat of recurring pandemic waves.
Note added
At the time of publication, many of the countries we considered in this study did enter a second wave of COVID-19 infections. By comparing the current data to our simulation case (e), we found that the second wave has started roughly 4 weeks earlier, compatible with case (a), for the countries that did not have signs of a second wave as of the 5th of August. Case (a) corresponds to values of the couplings \(k_{ij}\) an order of magnitude larger than those used in case (e). One can see from Table 1 that the peak timing expected in case (a) reproduces better the observed data. To better appreciate this fact, in Fig. 6 we show the epidemiological data for six countries, adjourned to the 30th of August, compared to the simulation.
Methods
To simulate the European second wave, we use as input parameters the values of \(\gamma _i\) and \(a_i\) stemming from the first wave. Predicting these parameters for the second wave is hard, as shown, for instance, via a stochastic SEIR model where very large fluctuations are found5. This is one of the reasons why we choose for our simulations the parameters coming from the first wave. Additionally this choice has the advantage of endowing us with reasonable benchmark values. These parameters depend on social distancing measures enacted by each country during the first wave. The methodology of the fit for \(\gamma _i\) and \(a_i\) is described in6,7. The values are reported in the first three columns of Table 1 at 90% confidence level. For the simulations we used the central values. The countries selected for this study, as listed in Table 1, are the ones whose data gives a good fit on the first wave and have a population above 3 millions to improve on the statistics. Some countries included in the study, namely Belgium, Bosnia, Croatia, Czechia, Greece, the Netherlands, Serbia, Slovakia, Slovenia and Spain, already show signs of a second wave starting between week 25 and week 32 (the 5th of August). Fur these countries we limit the data in the fit to the first wave. For the same reason, we started the simulation at week 25.
We now move to the interaction across the different European countries encoded in the matrix \(k_{ij}\). We generate the entries of the matrix randomly with each value in the interval \(10^{-3} - 10^{-2}\) and a flat probability. This translates in a range of 1k to 10k travellers per week across countries. In our earlier work7 this interval was shown to be able to account for the peak delay in between countries. As mentioned earlier, we also consider the extra-source of infection Region-X (\(i=0\)) with a fixed number of infected cases. This region couples to the different European countries with randomly generated \(k_{0i} = k_{i0}\) in the same range as above. To Region-X we can assign different interpretations. One could be that of an extra-European source (say the rest of the World) that still couples to some or all European countries we consider. Another interpretation is that the coupling \(k_{0i}\) to Region-X represents an internal source of infection inside the i-th region. To provide a sensible value for the initial source, we considered the current number of total infected (5.2 millions) normalised to the world population in millions.
Specifically, for the simulations cases (a–c), we randomly generate 100 copies of the matrix \(k_{ij}\) to be used to repeat the simulation. The initial time of the second wave simulations is the calendar week 25, where we set the initial values for \(\alpha _i = 0\) (while \(\alpha _0 = \mathrm{constant}\)). The 100 simulations are repeated, with the same set of \(k_{ij}\) matrices for the first four cases described in the main text.
For case (d), we additionally include a variation in the values of the \(\gamma _i\)’s for the European countries. To do so, we generate randomly 100 sets of scaling factors \(\epsilon _i\), one per country. The values of \(\epsilon _i\) are generated randomly following a Normal distribution with mean 1 and standard deviation \(\sigma = 0.15\). This allows for an uncertainty of \(15\%\) on the value of the second wave \(\gamma \) for each country.
Epidemiological data (red), adjourned to the 30th of August, for six sample countries compared to an updated simulation. For all countries, except Croatia, the second wave from case (e) simulation is anticipated by 4 weeks, thus in agreement with the results of case (a). To match the slow growing phase in between the two waves, we added a linearly growing term, in line to what we did for the calibration of the case (e) simulations. The bands are generated by varying the infection rates \(\gamma _i\) within \(10\%\).
For the realistic simulation, case (e), our strategy is a bit different. We fix \(k_{ij} = 0.5 \times 10^{-3}\) for the couplings intra European countries. Furthermore, all \(k_{i0} = k_{0i} = 0\), except for the 10 countries that already show a second wave start. For these countries we find the values of \(k_{i0}\) and rescale the \(\gamma \) and a parameters to fit the data adjourned to the 5th of August, 2020. One example of the fit is show in Fig. 2 for Croatia. Many countries, after reaching the peak of the first wave, feature a period with a linear growth of the infected cases. To better fit the second wave data, we included such a period, by adding the following term to the solution at the time when the first wave reaches the plateau:
The values of the \(k_{i0}\), rescaling of \(\gamma \), a, and the parameters of the linear growth for the 10 countries in this study are as follows:
Belgium | Bosnia | Croatia | Czechia | Greece | Netherland | Serbia | Slovakia | Slovenia | Spain | |
|---|---|---|---|---|---|---|---|---|---|---|
\(k_{i0}\) | 0.01 | 0.12 | 0.3 | 0.1 | 0.01 | 0.01 | 0.5 | 0.02 | 0.035 | 0.3 |
\(\gamma _i\) scaling | 1 | 0.7 | 0.6 | 0.6 | 1 | 1 | 0.7 | 0.8 | 0.6 | 0.85 |
\(a_i\) scaling | 1 | 1.3 | 1.06 | 1.06 | 1 | 1 | 1.05 | 1 | 0.95 | 1 |
\(\theta _i\) | 60 | 0 | 0 | 40 | 7 | 35 | 35 | 1 | 1 | 30 |
\(t_{\mathrm{pl}}\) | 20 | − | − | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
Plots comparing our theory curve with the data are provided in the additional material.
Data availability
For the simulations, we used a code written for Wolfram Mathematica. The data of the simulations and a Mathematica code for their analysis can be made available upon request. The data for the COVID-19 infected cases in Europe are extracted from the worldometer.info repository.
References
Kermack, W. O., McKendrick, A. & Walker, G. T. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 115, 700–721. https://doi.org/10.1098/rspa.1927.0118 (1927).
Perc, M. et al. Statistical physics of human cooperation. Phys. Rep. 687, 1–51. https://doi.org/10.1016/j.physrep.2017.05.004 (2017).
Wang, Z., Andrews, M. A., Wu, Z.-X., Wang, L. & Bauch, C. T. Coupled disease-behavior dynamics on complex networks: A review. Phys. Life Rev. 15, 1–29. https://doi.org/10.1016/j.plrev.2015.07.006 (2015).
Wang, Z. et al. Statistical physics of vaccination. Phys. Rep. 664, 1–113. https://doi.org/10.1016/j.physrep.2016.10.006 (2016).
Faranda, D. & Alberti, T. Modelling the second wave of COVID-19 infections in france and italy via a stochastic seir model (2020). arXiv:2006.05081.
Della Morte, M., Orlando, D. & Sannino, F. Renormalization group approach to pandemics: The COVID-19 case. Front. Phys. 8, 144. https://doi.org/10.3389/fphy.2020.00144 (2020).
Cacciapaglia, G. & Sannino, F. Interplay of social distancing and border restrictions for pandemics (COVID-19) via the epidemic renormalisation group framework (2020). arXiv:2005.04956.
Hâncean, M.-G., Perc, M. & Juergen, L. Early spread of COVID-19 in Romania: Imported cases from Italy and human-to-human transmission networks. R. Soc. Open sci. 7, 200780. https://doi.org/10.1098/rsos.200780 (2020).
Perc, M., Gorišek Miksić, N., Slavinec, M. & Stožer, A. Forecasting COVID-19. Front. Phys. 8, 127. https://doi.org/10.3389/fphy.2020.00127 (2020).
Morte, M. D. & Sannino, F. Renormalisation group approach to pandemics as a time-dependent sir model (2020). arXiv:2007.11296.
Wilson, K. G. Renormalization group and critical phenomena. 1. Renormalization group and the Kadanoff scaling picture. Phys. Rev. B 4, 3174–3183. https://doi.org/10.1103/PhysRevB.4.3174 (1971).
Wilson, K. G. Renormalization group and critical phenomena. 2. Phase space cell analysis of critical behavior. Phys. Rev. B 4, 3184–3205. https://doi.org/10.1103/PhysRevB.4.3184 (1971).
Li, L. et al. Analysis of transmission dynamics for zika virus on networks. Appl. Math. Comput. 347, 566–577. https://doi.org/10.1098/rspa.1927.01180 (2019).
Zhan, X.-X. et al. Coupling dynamics of epidemic spreading and information diffusion on complex networks. Appl. Math. Comput. 332, 437–448. https://doi.org/10.1098/rspa.1927.01181 (2018).
Danby, J. M. A. Computing applications to differential equations modelling in the physical and social sciences (Reston Publishing Company, Reston, 1985).
Brauer, F. Early estimates of epidemic final sizes. J. Biol. Dyn. 13, 23–30. https://doi.org/10.1080/17513758.2018.1469792 (2019).
Miller, J. C. A note on the derivation of epidemic final sizes. Bull. Math. Biol. 74, 2125–2141. https://doi.org/10.1098/rspa.1927.01183 (2012).
Murray, J. D. Mathematical biology. Interdisciplinary applied mathematics 3rd edn. (Springer, New York, 2002).
Fishman, D., Khoo, E. & Tuite, A. Early epidemic dynamics of the West African. Ebola outbreak: Estimates derived with a simple two-parameter model. PLOS Curr. Outbreaks.https://doi.org/10.1371/currents.outbreaks.89c0d3783f36958d96ebbae97348d571 (2014).
Pell, B., Kuang, Y., Viboud, C. & Chowell, G. Using phenomenological models for forecasting the 2015 Ebola challenge. Epidemics 22, 62–70. https://doi.org/10.1016/j.epidem.2016.11.002 (2018) (The RAPIDD Ebola Forecasting Challenge).
Cacciapaglia, G., Cot, C. & Sannino, F. Mining google and apple mobility data: Twenty-one shades of european social distancing measures for COVID-19 (2020). arXiv:2008.02117.
Lai, S. et al. Effect of non-pharmaceutical interventions for containing the COVID-19 outbreak in China. Nature. https://doi.org/10.1038/s41586-020-2405-7 (2020).
Flaxman, S. et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature. https://doi.org/10.1038/s41586-020-2293-x (2020).
Acknowledgements
G.C. and C.C. acknowledge partial support from the Labex-LIO (Lyon Institute of Origins) under grant ANR-10-LABX-66 (Agence Nationale pour la Recherche), and FRAMA (FR3127, Fédération de Recherche “André Marie Ampère”).
Author information
Authors and Affiliations
Contributions
This work has been designed and performed conjointly and equally by the authors. G.C., C.C. and F.S. have equally contributed to the writing of the article.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Video of early second wave peaks, based on simulations a
Video of late second wave peaks, based on simulations e
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cacciapaglia, G., Cot, C. & Sannino, F. Second wave COVID-19 pandemics in Europe: a temporal playbook. Sci Rep 10, 15514 (2020). https://doi.org/10.1038/s41598-020-72611-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-72611-5
This article is cited by
-
Counting the uncounted: estimating the unaccounted COVID-19 infections in India
Nonlinear Dynamics (2024)
-
The impact of non-pharmaceutical interventions on the first COVID-19 epidemic wave in South Africa
BMC Public Health (2023)
-
Genetic determination of regional connectivity in modelling the spread of COVID-19 outbreak for more efficient mitigation strategies
Scientific Reports (2023)
-
A real-world data validation of the value of early-stage SIR modelling to public health
Scientific Reports (2023)
-
Multiple waves of COVID-19: a pathway model approach
Nonlinear Dynamics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.