Abstract
Algorithms based on Empirical Mode Decomposition (EMD) and Iterative Filtering (IF) are largely implemented for representing a signal as superposition of simpler well-behaved components called Intrinsic Mode Functions (IMFs). Although they are more suitable than traditional methods for the analysis of nonlinear and nonstationary signals, they could be easily misused if their known limitations, together with the assumptions they rely on, are not carefully considered. In this work, we examine the main pitfalls and provide caveats for the proper use of the EMD- and IF-based algorithms. Specifically, we address the problems related to boundary errors, to the presence of spikes or jumps in the signal and to the decomposition of highly-stochastic signals. The consequences of an improper usage of these techniques are discussed and clarified also by analysing real data and performing numerical simulations. Finally, we provide the reader with the best practices to maximize the quality and meaningfulness of the decomposition produced by these techniques. In particular, a technique for the extension of signal to reduce the boundary effects is proposed; a careful handling of spikes and jumps in the signal is suggested; the concept of multi-scale statistical analysis is presented to treat highly stochastic signals.
Similar content being viewed by others
Introduction
Nonstationary processes and signals generated by nonlinear dynamics are ubiquitous in real life. Their time-frequency analysis and features extraction can help in solving open problems in many fields of research.
However, when dealing with nonlinear and nonstationary time series, neither the standard Fourier transform1 nor the wavelet Transform represent the best approach. In fact, all of them produce linear decompositions, whereas real life data sets are in many cases generated by nonlinear phenomena. Furthermore, all the aforementioned methods have troubles providing an accurate time-frequency representation of the data2 due to the well known Heisenberg uncertainty principle3. For all these reasons, several methods have been proposed to increase the accuracy of the time-frequency representation produced by the previously mentioned methods, like the Short Time Fourier Transform (STFT)3, the Synchrosqueezed Wavelet Transform4,5 or the ConceFT method6.
Two decades ago a different kind of method called Empirical Mode Decomposition (EMD) was introduced by Huang and his collaborators in the seminal work published in 19987. This method is aimed at the decomposition of nonstationary and nonlinear signals in order to unravel their hidden quasi-periodicity and features. It is a local and adaptive data-driven method which makes it a much more suitable technique for nonlinear and nonstationary data analysis.
Furthermore, it has a divide et impera approach which allows to bypass the Heisenberg-Gabor uncertainty principle8. First, the signal is divided into several simple components via the so called sifting approach, which boils down to the calculation of the signal moving average via envelopes connecting its extrema. Then, each component is analysed separately in the time-frequency domain9.
While the EMD method proved to be extremely powerful in extracting simple components from a given signal, it is unstable to perturbations10 and susceptible to mode splitting and mode mixing11. These are the reasons why the Ensemble Empirical Mode Decomposition (EEMD) method10 first, and then several alternative noise-assisted EMD-based methods (e.g. the complementary EEMD12, the complete EEMD13, the partly EEMD14, the noise assisted multivariate EMD (NA-MEMD)15, and fast multivariate EMD (FMEMD)16) have been proposed.
While these newly developed methods are based on EMD, they all address the so called mode mixing problem and guarantee the stability of the decomposition with respect to noise9. However, mode splitting is still an open problem for all these methods and, more importantly, their mathematical analysis is by no means complete9.
An alternative technique for signal decomposition, based on iterations like the EMD, is the so called Iterative Filtering (IF) method, proposed by Lin et al. in 200917. The IF algorithm structure is based on the EMD one, but it differs from it in the way it computes the signal moving average, which is derived as a point by point local weighted average. This is obtained convolving the signal with an a priori chosen “filter function”, which is simply any positive and compactly supported function whose area equals one. To guarantee a priori the convergence of this method it has been recently proved that it is sufficient to consider a filter function obtained as convolution of another filter function with itself18.
IF method allows to produce results similar to the EMD-based algorithms, but with the important advantage that it is possible to guarantee a priori its convergence and stability. This is due to the moving average computation based on convolution, which has opened the door to the mathematical analysis of IF and derived algorithms18,19,20,21,22. Furthermore, IF mathematical analysis has also led to its acceleration via Fast Fourier Transform (FFT) in what is called the Fast Iterative Filtering (FIF) method18,23.
We point out that IF and FIF methods do not suffer of mode mixing24, whereas mode splitting can be easily avoided by tuning the value of the stopping criterion parameter2.
The IF algorithm has been generalized to tackle highly nonstationary signals (leading to the Adaptive Local Iterative Filtering (ALIF)25,26), and, as for EMD, multidimensional signals27,28, and multivariate ones29.
Both the EMD- and IF-based algorithms yield a decomposition of any signal in simpler components, known as Intrinsic Mode Functions (IMFs) which fulfill two conditions: the envelopes connecting the minima and maxima of an IMF have a local average which equals zero; the IMF extrema number differs from the number of its zero crossing of at most one. Differently from the sine and cosine components of the Fourier transform, the IMFs are oscillatory modes whose amplitude and frequency can vary over time. Their instantaneous frequency estimation done, for instance, via Hilbert transform30, provides an accurate time-frequency representation of a nonstationary and nonlinear signal.
The versatility of these techniques has opened the door to their application in many applied fields. As a matter of fact, they are largely implemented in geophysical studies30,31,32, with applications in Seismology (data denoising and/or detrending33,34,35, pre-seismic signal analysis36,37,38, earthquake-induced co/post-seismic anomalies analysis39), Exploration Seismology (for improving signal-to-noise ratio in seismic data processing routines40,41 or for seismic interpretation42), Geomagnetism43,44,45,46,47,48,49, Engineering Seismology (mainly for analysing ground motion data50,51,52,53,54), climate, atmospheric and oceanographic sciences55,56,57,58,59,60. Their use is also common in Physics (for data analysis61,62,63,64,65, data denoising and/or detrending66,67,68, to assess causal relationships between two time series69, or to extract information on multiple time scales70); Medicine and Biology71,72,73,74,75,76,77,78,79; Engineering80,81,82,83,84,85; Economics and Finance87,86,88; Computer vision89,90,91.
Although the EMD- and IF-based techniques are more suitable than traditional methods for the analysis of non-linear and nonstationary data sets, they could easily be misused if their known limitations21,92, together with the assumptions they rely on, are not carefully considered. The endeavor of this study is to call attention to the main pitfalls encountered when implementing these techniques. Specifically, by examining a large number of studies pertaining to different fields, we have detected three critical factors that are often neglected or underestimated: boundary effects; presence of spikes/jumps in the original signal; signals generated by processes containing a high degree of stochasticity.
This paper is structured as follows: in “Problems with the boundaries” and “Spike pulses and jumps in the signal” we discuss the issues related to the boundary effects and to the presence of spikes/jumps, respectively. For each issue, we critically analyze a study that, in our opinion, represents a clear example of how either boundary conditions or spike/jumps should not be handled. In “Stochastic signals decomposition” we address the problem of the suitability of the EMD- and IF-based methods for the multiscale analysis of a stochastic signal.
In all the subsequent sections we present numerical examples, comparing the performance of the EMD, EEMD and IF algorithms. It is important to remind that, although in many instances the original EMD method produces results that are similar to those derived by its more evolved variants, we strongly discourage its usage. As we recalled previously, this method is particularly sensitive to noise and mode mixing. We suggest to implement either enhanced versions of the EMD technique10,12,13,14,15,16, or alternative methods such as the IF-based algorithms17,18,23,25,27,29.
Problems with the boundaries
Like any signal processing technique, boundary conditions must be carefully addressed when implementing EMD and IF algorithms and their variants. This is equivalent to make assumptions about right and left extension of the signal, i.e. to extrapolate the time series beyond its boundaries. If not properly handled, end effects could arise, which result in anomalously high amplitudes of the IMFs and artifact wave peaks towards the boundaries.
We remark that identifying these errors is not always straightforward. This is because the IMFs are produced by subsequent subtraction from the original signal. Therefore, their sum always equals the original signal.
This problem was already pointed out by Huang and collaborators in their seminal work on the EMD7, and many approaches have been published since then to address it. Huang himself proposed the characteristic wave method93 and the extremum continuation method94. Other authors proposed, among many ones, the slope method95, the extremum image continuation method96, the artificial neural network method97, mirror extension coupled with support vector machine method98, and the extremum sequence extension99.
It is important to stress that is particularly difficult to estimate a priori the error contributions coming from the boundaries when implementing the EMD and derived methods, since a mathematical analysis of these techniques is still missing. To make things worst, there exist many alternative versions of these algorithms, each of which has its own peculiar way of handling boundaries. We mention here, for instance, the version by Yung-Hung Wang and collaborators (Fast EMD/EEMD Code https://in.ncu.edu.tw/~ncu34951/FEEMD.rar Research Center for Adaptive Data Analysis (RCADA), National Central University, Taiwan), the Patrick Flandrin and collaborators version (Matlab/C codes for EMD and EEMD http://perso.ens-lyon.fr/patrick.flandrin/emd.html Laboratoire de Physique, Ecole Normale Supérieure de Lyon, France), or the Mathworks Matlab official code (https://it.mathworks.com/help/signal/ref/emd.html). So far, there is no consensus on which version should be adopted to properly handle boundaries.
Regarding the IF-based methods, conversely, it is possible to a priori estimate the errors introduced by a specific boundary extension and to evaluate how they affect each IMF, since a complete and deep mathematical analysis of IF-based methods has been recently presented18. In particular, it is now possible to choose an optimal extension based on the specific features of the signal under study when we deal with the IF-based decompositions, reducing de facto the end effect errors in the decomposition. This is what it has been been done in21 for the periodical, symmetric (reflective), and anti-symmetric (anti-reflective) boundary extensions.
For the EMD-based methods, since a mathematically rigorous analysis of these methods is still missing, it is not possible to prove any general optimality of a given extension technique with respect to the others. Only a case by case analysis can be conducted at this stage. However, we can use the results derived from the rigorous mathematical analysis on the optimal pre-extension of a given signal for the IF-based methods, to extend the same signal also for the EMD-based algorithms.
Nevertheless, after pre-extension, the newly obtained data set \(s_{\text {ext}}\) will be still finite. Therefore, some end effects may be present in the decomposition yet. One possibility is to force the extended signal to become periodical at the newly generated boundaries. In fact both IF and FIF are designed to decompose properly periodical signals without introducing any numerical error. Hence, we propose the following technique (Signal Extension Algorithm code available at www.cicone.com):
Signal extension algorithm
-
1.
Subtract from the signal s its mean value m
-
2.
Extend \(s-m\) outside the boundaries in the preferred or optimal way, producing an extended signal \(s_{\text {ext}}\) which is \(\nu\) times longer than the original one
-
3.
Multiply \(s_{\text {ext}}\) by a characteristic function \(\chi\) which has value one in the interval corresponding to the original signal s and goes smoothly to zero as we approach the new boundaries of \(s_{\text {ext}}\)
-
4.
Add back the mean value m of the original signal
$$\begin{aligned} s_{\text {new}}=\chi \cdot s_{\text {ext}} + m \end{aligned}$$
The produced signal \(s_{\text {new}}\) is now periodical at the boundaries.
This approach allows to reduce the boundary errors in the IF-based algorithms, as known from the theory21, and in the EMD-based methods and shown by the following numerical simulations on synthetic and real life signals.
We point out that the proposed approach is similar in nature to a time-domain windowing technique. The main difference is that now we first pre-extend the signal and then apply a time-domain window. This window is constructed specifically to preserve unaltered the values at the center of the extended signal, which correspond to the original data. The proposed Signal Extension Algorithm allows to preserve and make use of all the information contained in the original data set, meanwhile reducing boundary effects errors.
Regarding the signal extension, step 2 of the proposed extension algorithm, in a recent paper21, as we mentioned previously, three kinds of extensions have been studied and compared: periodical, symmetric (reflective), and anti-symmetric (anti-reflective). In particular, they show the dependence of the end effects on the phase of the signal at the boundary. The result can be summarized as follows. If the slope of the signal at the boundary is close to zero, it is better to extend in a symmetric way. Whereas, when the slope is maximal in absolute value, it is better to extend in an anti-symmetrical way.
However, there are infinitely many other possible ways of extending a signal outside its boundaries besides periodical, symmetric and anti-symmetric extensions. What is the actual best or optimal way to properly extend a signal for IF-based methods remains, to the best of our knowledge, an open question. In this work we consider only these three kind of extensions and we choose for each example the optimal one among these three as suggested in21. The identification of the actual global optimal extension for each given signal for the IF-based methods and a detailed comparison with extension approaches proposed in the literature for the EMD-based techniques is out of the scope of this paper and we plan to tackle it in a future work.
Finally, regarding the choice of \(\nu\), the number of times that we replicate the signal, its choice is a compromise between the need to reduce the border effects, and that of limiting the total length of the signal, keeping the computing time reasonable. In21 it was shown that border effects decrease exponentially with the distance from the edges of the signal. From this observation it follows that it sufficient to extend the signal with a \(\nu\) from 0.5 to 5 of the original signal. The choice of the actual \(\nu\) depends on the length of the original signal, the longer the signal the smaller we choose \(\nu\), and on how low are the frequency we want to preserve, the lower are the frequency of interest the longer we extend the signal.
Synthetic example
We consider the signal plotted in the top row of Fig. 1 which is given by
We first run the EMD algorithm included in matlab distribution 2018a and later versions, and produce the decomposition shown in the left panel of Fig. 1. To better visualize the end effects, we plot the first 1000 points only. Similar behaviors are present on the left boundary.
Boundary problems Synthetic Example. EMD results are compared with the analytical solution (“ground truth”). Left: EMD decomposition of the original signal (we show the first 1000 points). There are clear errors induced by EMD nearby the boundary. Right: EMD decomposition after pre-extending symmetrically left and right and made periodical the original signal, as described in “Problems with the boundaries”.
Issues are clearly visible nearby the boundary and they become more severe as the IMF frequency decreases. In order to reduce these end effects, we pre-extend the original signal. We make it five times longer than the original one, following the procedure presented above, since in this case the original signal is short enough and the computational complexity does not increase significantly in this way. We point out that in this case, since the signal has zero slope both on the right and left boundary, we opt to extend it symmetrically.
We feed this pre-extended signal to the EMD method to produce the decomposition shown in the right panel of Fig. 1. The end effects are visibly reduced.
Similar results are obtained using EEMD or FIF on this signal. The interested reader can find more details in the online supplementary material100.
In Table 1, we report the total computational time for the two EMD decompositions and the 2-norm of the relative differences between the ground truth and each IMF as well as the trend. This 2-norm quantifies the misfit between the ground truth and the IMF components produced via EMD.
This synthetic example shows that end effects mainly consist of artifact wave peaks at the onset (or at the end) of the IMFs: the higher the IMF index (i.e. the lower its frequency), the longer the wavelength of the spurious signal. It follows that such artifact can be recognized as a fictitious wave “propagating” towards the middle of the IMF, as one considers higher IMFs indexes. Additionally, end effects may also result into IMFs amplitude being larger than the original signal or even, in some cases, in the appearance of new IMFs containing frequencies not at all present in the original signal.
Real life example
There is a huge amount of papers published in a wide variety of fields of research in which EMD-like methods are used to decompose signals. In some instances, we have identified a clear role of end effects in the derived decomposition59,101,102,103,104.
In the following, we examine, as an example, the results presented by Sarlis et al.103 where the authors themselves notice that some end effects are showing up in the decomposition. In that work, the analysed signal is the magnitude time series of the global seismicity for events of magnitude \(M \ge 5.0\) .
In the left panel of Fig. 2, adapted from Fig. 1 in the original article, we use red boxes to pinpoint potential boundary effects, i.e. artifact wave peaks and anomalous amplitudes. Specifically, from IMF seven on, we notice the appearance of oscillations nearby the boundaries that have amplitudes different from the rest of the IMF and, more importantly, from the original signal. As an example, both the twelfth and thirteenth IMFs have values clearly oscillating in the interval \([-10,\ 10]\), whereas the original signal has values varying in the interval \([4.3,\ 9.08]\).
Boundary problems Real Life Example. Left: Adapted from Sarlis et al. paper103. EMD decomposition of the magnitude time-series of GCMT collected from 1 January 1976 to 1 October 2014. The red boxes highlight artifact wave peaks at the boundaries of the IMFs, while the blue asterisks pinpoint anomalous IMFs amplitudes (larger than the original signal). Right: Decomposition of the GCMT magnitude time-series from January 1st 1976 to October 1st 2014 produced using the EEMD function released on March 04 2009 by Zhaohua Wu. The red line in each panel represents the zero reference line. Total computational time: 213.9069 s.
In order to reproduce their findings, we downloaded the catalog of global earthquakes (\(M\ge 5.0\)) from the Global Centroid Moment Tensor (CMT) Project (https://www.globalcmt.org/)105,106, for the period January 1, 1976–October 1, 2014. The global earthquake magnitude time series is shown in the top row of Fig. 2. We run the decomposition of this signal using both the EMD algorithm, included in matlab distribution 2018a and later versions, and the eemd algorithm (it can be downloaded from the official website of the Taiwanese Research Center for Adaptive Data Analysis https://in.ncu.edu.tw/~ncu34951/research1.htm and is contained in the repository https://in.ncu.edu.tw/~ncu34951/Matlab_runcode.zip) written by Zhaohua Wu in 200910. This time we opt to set the number of elements in the ensemble to be 100 to speed up the calculations. The standard deviation is set, as suggested by the authors of the technique10, to 0.2. The outcome of these decompositions are pretty similar. We report in the right panel of Fig. 2 the one obtained via EEMD. The interested reader can find the EMD and FIF decomposition in the online supplementary material100.
In this case, no pre-extension of the signal was performed here, because the signal is highly erratic, and hence pseudo-periodic, as far as the border effects are concerned.
It is evident from the right panel of Fig. 2 that this decomposition do not contain the end effects obtained by Sarlis et al. (left panel of Fig. 2). The possible explanation is that they used some implementation of the EMD method which handles the boundaries in a way that induces the observed oscillations.
We point out that the authors of the original work also provided in their supplementary material103 the decomposition obtained using the EEMD code released by the Taiwanese Research Center for Adaptive Data Analysis. The decomposition they produced is compatible with the one shown in the right panel of Fig. 2.
Spike pulses and jumps in the signal
If jumps or spikes are present in the time series, they can substantially affect the signal decomposition. As a matter of fact, when the EMD- and IF-based techniques are applied to a signal containing an impulsive change, their decompositions introduce oscillations at any frequency (ref. “Synthetic example” and “Real life example”). This is, mathematically speaking, expected and meaningful because any jump and spike can be represented locally as the summation of infinitely many frequencies. However, this way of representing a jump or spike is not necessarily meaningful from a physical point of view. Specifically, we warn that a physical interpretation of the derived decomposition could likely bring to conclusions apparently in contradiction with the causality principle.
Caveats regarding the causality principle in analysing IMFs
A slippery problem is represented by the application of decomposition techniques, such as the EMD- and IF-based algorithms, to the identification of possible precursors of abrupt high-magnitude events like spikes and jumps. In many fields, as seismology, medical science, space weather or meteorology, guessing in advance when “catastrophic events” occur is very desirable. However, we warn the reader that using EMD- and IF-based decomposition techniques may be very misleading.
The key point is that every abrupt change in amplitude, that necessarily is concentrated around some instant \(t_{0}\) and takes place at small scales, can also be represented as the superposition of many components of different scales. In order to visualize this, just imagine to Fourier-decompose a peak as Dirac’s \(\delta \left( t-t_{0}\right)\): a namely infinite assortment of frequencies will be necessary, hence involving also very large period components. The same thing happens for locally-characterized decompositions, like the ones produced using EMD- and IF-based methods, as shown in Fig. 3 of the following synthetic example: any peak around \(t_{0}\) of a given original signal \(x\left( t\right)\), appearing as a narrow bump in the original time series, will “broaden” on larger and larger intervals around \(t_{0}\) when larger scale components are considered. In particular, if at some given “small” time scale \(\ell\) the signal component \(x_{\ell }\left( t\right)\) peaks within some interval \(\left( t_{0}-\epsilon ,t_{0}+\eta \right)\), at some larger scale \(\ell '>\ell\) the increment of the component \(x_{\ell '}\left( t\right)\) will take place all along the interval \(\left( t_{0}-\epsilon ',t_{0}+\eta '\right)\), with \(\epsilon '\ge \epsilon\) and \(\eta '\ge \eta\). All of this might induce the not-enough-careful scientist to imagine that, observing the large scale component \(x_{\ell '}\left( t\right)\), a peaky behaviour can be already guessed to appear soon at time \(t_{0}-\epsilon '\le t_{0}-\epsilon <t_{0}\), namely anticipating what the original signal \(x\left( t\right)\), peaking at time \(t_{0}\), will behave like. This is clearly a mistake: it would be as understanding that the \(\delta\)-like pulse force bouncing back a rubber ball from a wall is “sensed” at some distance from the solid wall by observing the time series of the force \(F\left( t\right) =F\delta \left( t-t_{0}\right)\) exerted on the flying ball, being \(t_{0}\) the precise time at which the collision takes place. This is blatantly false, as the force cannot be sensed in any way before the collision takes place. One can argue that, still, the “signal” \(F\left( t\right) =F\delta \left( t-t_{0}\right)\) is indeed composed by all the large scale IMF addenda “anticipating” the impact, which is indeed true. The logical way out of this conundrum is the following: the time series of the \(\delta\)-like peak can be mathematically represented as the summation of components which apparently extend their influence further back in time as the scale size increases. However, from a physical stand point, this second interpretation makes no sense. A travelling ball cannot sense the presence of a wall in advance in any way. In particular, the large scale components produced in the mathematical decomposition of the force F(t) applied on the flying ball once it touches the wall, cannot be used as precursor of the collision.
The examples reported in the following “Synthetic example” and “Real life example” all clearly suffer from this problem. It is actually incorrect to use information from the large scale components to infer the occurrence time of the peak, before it has occurred. This is because those low frequency components, necessary from a mathematical stand point to re-produce the spike or jump a posteriori, do not have the same aspect if the original signal \(x\left( t\ll t_{0}\right)\) does not show any peak yet, as shown in Fig. 4.
This does not mean that multiscale decomposition of some time series \(x\left( t\right)\), being it performed via EMD- or IF-like methods, or even the standard wavelet or Fourier transform, cannot be of use in investigating the physical properties of the process producing the time series. What multiscale decomposition and their study can be of use for is the detection of behaviour and statistics within the time interval sampled: so, as a time series represents what a probe encounters as the phenomenon evolves in a given time interval \(\left[ t_{\mathrm {i}},t_{\mathrm {f}}\right]\), multiscale statistics of the time series reveals what has taken place at the different scales in the whole \(\left[ t_{\mathrm {i}},t_{\mathrm {f}}\right]\): this may be of great use in understanding, e.g., whether, turbulence47,48,49,107, intermittency46 or critical behaviour108 have taken place in \(\left[ t_{\mathrm {i}},t_{\mathrm {f}}\right]\). We will come back on this topic in “Stochastic signals decomposition”.
In the following we first show, by numerical simulation, how the presence of a spike may influence the decomposition (“Synthetic example”). Then, we examine one of the literature studies to stress the caveats about spikes and jumps proper handling in the decomposition of a signal (“Real life example”).
Synthetic example
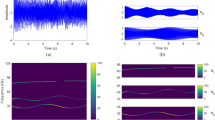
We start showing, by means of a simple numerical simulation, how the presence of even a single spike may influence the signal decomposition. Specifically, we simulate a constant-amplitude signal with a impulsive spike, shown in the top row of Fig. 3, and then we decompose it by means of both the EEMD and the FIF techniques. For the EEMD method we set the standard deviation to 0.2 and the dimension of the ensemble to 800, to reduce as much as possible the noise-related IMFs. Results are shown in Fig. 3.
We point out that this example allows to understand also how a jump, or multiple ones, can influence the decomposition of a signal. In fact, if we imagine covering with our hand the second half of Fig. 3 left or right panels, what we see is the beginning of a jump and its corresponding decomposition. In fact a spike can be viewed as two consecutive jumps, one going up and the other going down. From this observation it follows that there is no need to present here a separate example to show the influence of a jump in the decomposition of a signal. At the same time, it is important to underline that the idea of interpreting a spike as two consecutive jumps is not a practical way of dealing with spikes contained in a data set. The actual handling of spikes and jumps present in a data set differs widely, in fact, as explained in the following section.
One of the most important lesson that we can learn from this example is that the information contained in a single spike diffuses quickly far away in time/space from the location of the spike when we decompose it. Furthermore, from Fig. 3 we observe that, if we consider the peak values in each IMF component, the errors are distributed practically uniformly over all frequencies. The lower is the frequency the more far away from the spike location we have an impact in the decomposition. Researchers could be tempted to assume that such impact regards only low frequency IMF components. But there is not a single frequency which is not impacted in the decomposition by the presence of even a single spike, and the more the spikes are, the worse the situation becomes. So, regardless the context in which the signal is generated, it is always strongly advisable to decompose both the signal as it is and the signal after an appropriate pre-processing in order to understand and estimate the impact of spikes and jumps in the decomposition.
Real life example
We have found several studies published in the literature where signals containing spikes or jumps are not carefully handled38,109,110,111,112.
The proper identification of spikes position in signals has been already studied in the literature, for instance in113,114, and for the jumps the so called essentially non-oscillatory (ENO) technique was developed in computational fluid dynamics to capture shock positions25,115, and it can be adopted in this context. If on the one hand some approaches have been proposed on how to remove spikes, on the other hand the question of how to properly handle jumps have never been raised in the context of EMD- and IF-based methods decompositions, to the best of the authors knowledge.
For this reason, in the following, we focus on the jump handling. In particular we examine, as an example, one of the decompositions presented by Chen et al.110, where the authors analyse the number of daily earthquakes time series (\(M_{L} \ge 3.0\)) occurred in Taiwan in the period 1978-2008, which present naturally jumps.
In Fig. 4 (left and center left panels, adapted from Fig. 3 in the original article) we use red boxes to pinpoint jump effects, i.e. artifact waves “propagating” throughout all the IMFs.
Spikes and jumps real life example. Adapted from Chen et al.110. Left: From top to bottom, the first six IMFs of the non-stacked data of the number of daily earthquakes from the Taiwanese catalog for events of magnitude \(M_{L} \ge 3.0\) from 1978 to 2008. Center Left: The top row shows the temporal variations in theoretical Earth tides at the center of Taiwan with a period of 1462 days (red) and the stacked data of daily earthquake numbers (blue). The second to seventh row display the first six IMFs that were extracted from the stacked time series by Chen et al. In both panels, red boxes highlight the artifacts induced by a jump, in the original time series, which “propagates” through all the IMFs. Center Right and Right: Comparisons of the IMFs produced using EMD and FIF, respectively. The time signal in the first panel is zoomed in to highlight the jump. In red the decompositions obtained using the original stacked data set, and in black the ones obtained after splitting the time series into two disjoint subsets. In particular, we split it at the highest jump, in position 988. We use symmetric extension to produce all the results. Total computational time: 0.3479 s (EMD—splitted signal), 0.0511 s (EMD—original data set), 0.3243 s (FIF—splitted signal), 0.0526 s (FIF—original data set).
In the following, we consider the stacked data set analysed by the authors of the original work, which is shown in the top row of Fig. 4 center left panel. Here, the highest jumps correspond to the sequences of events triggered by the largest earthquakes.
We decompose this signal using both EMD (we used the EMD algorithm included in matlab distribution 2018a and later versions) and FIF (available at www.cicone.com) in two ways: without any “pre-processing”, as in the original article110, and with a “pre-processing”, which consists in splitting the time series in “before” and “after” the jump, and symmetrically extending the two disjoint subsets. Regarding the jumps and spikes identification and their localization, as we mentioned previously, many works have been published in the literature where different techniques have been proposed, e.g.113,114. Therefore in this work we assume that their localization is known.
The outcome of these decompositions are shown in Fig. 4, center right and right panels. Here we plot in red the decompositions produced using the original stack data set, and in black the decomposition after splitting and symmetrically extending the two disjoint subsets.
It is evident from these results that an improper handling of the jump can severely affect the returned decomposition at time \(t<t_0\). Specifically, the lower the IMF frequency, the further the jump has influence back in time.
Based on these evidences, we suggest to always compare the decomposition obtained before and after “pre-processing” the signal. Regarding the pre-processing, if a jump is present we propose to split the signal in two subsets, before and after the jump. Whereas, if one or more spikes are present, they can be localized and removed following what has been already suggested in the literature, e.g.113,114.
We also observe that the presence of the main jumps and spikes in a signal can be detected looking at the IMF components of the original signal in time domain all together, ref. Figs. 3 and 4. However this approach is not enough robust to help in the identification of secondary spikes and jumps which can affect badly the signal decomposition and mask other nonstationarities. So it is always advisable to use an ad hoc method for the spikes and jumps identification and removal, and to compare the decomposition before and after pre-processing.
Stochastic signals decomposition
When dealing with real data, the first question we should ask ourselves is: can we apply these decomposition techniques to the signal under analysis?
The EMD- and IF-based methods proved to be well suited for the analysis of signals coming from diffusion processes like heat or wave equations and, more in general, systems whose behavior can be described by differential equations with oscillatory solutions. Whereas, a stochastic signal is missing enough regularity to be described by a mathematical model based on ordinary or partial differential equations. It is therefore an open problem to assess whether the techniques, on which this paper is focused, can successfully reproduce the features of the signal at different scales. In fact, while it is always possible to decompose a signal by EMD- and IF-based methods, a physical interpretation of the derived IMFs and their features has to be done with care, even in the case of deterministic signals; the stochastic signal case may appear even more uncertain.
As a first observation, one should point out that stochastic signals can be analysed sensibly with two purposes: either, to separate from the signal a deterministic part of it, that could be used to model part of the phenomenon via non-stochastic tools (e.g., systems of differential equations); or to study statistical characteristics of the signal. The application we want to discuss here pertains to this latter purpose.
Here the EMD and FIF techniques are applied to a synthetic stochastic time series largely used to mimic turbulent signals, both in fluid and plasma dynamics, namely the p-model (see, for instance:116 and117). Even if EMD and FIF decomposition is generally used to recognize and reconstruct the mathematical form of different components of a time series, so to understand the different contributions to a given phenomenon, this is not the aim here. Indeed, the p-model is constructed by summing functions that do not meet the characteristics of the components that can be reconstructed via EMD or via FIF. Still, decomposing the p-model signal via such techniques, in order to study its statistical properties at diffrent scales, allows to provide meaningful insights in the data sets, as shown below.
The p-model is a simple branching model: still, it is extremely powerful in mimicking the irregular and intermittent distribution of energy in turbulent media (118,119).
The p-model construction starts from the distribution
i.e., a piecewise constant distribution that is equal to E in the interval \(I=\left[ 0,L\right]\) and zero outside. The \(\theta\)s are Heavyside step functions. Then, the interval I is divided into two subintervals \(I_{11}=\left[ 0,\frac{L}{2}\right]\) and \(I_{12}=\left[ \frac{L}{2},L\right]\), and the quantity E, contained in the whole original interval, is distributed “randomly” in \(I_{11}\) and \(I_{12}\), so that the overall amount remains the same. In order to do so, a parameter \(p\in \left[ 0,1\right]\) is defined, and two weights \(w_{11}\) and \(w_{12}\) are chosen, whose value is randomly chosen between 2p and \(2\left( 1-p\right)\), so that \(\left( w_{11}+w_{12}\right) \frac{E}{2}=E\). In doing so we define the distribution
The \(u_{1}\left( x\right)\) distribution is zero outside \(I=\left[ 0,L\right]\) and it is considered “the first generation” of the p-model. The branching process \(u_{0}\mapsto u_{1}\) is repeated as \(u_{1}\mapsto u_{2}\), by subdividing \(I_{11}\overset{\mathrm {def}}{=}\left[ 0,\frac{L}{2}\right]\) and \(I_{12}\overset{\mathrm {def}}{=}\left[ \frac{L}{2},L\right]\) into two halves each, and repeating the random assignment of the weights 2p and \(2\left( 1-p\right)\) to each half of \(I_{11}\) and of \(I_{12}\). By recursively repeating the previous steps, at the n-th step the distribution \(u_{n}\left( x\right)\) is derived. This is constant on each of the \(2^{n}\) intervals \(I_{n,i=1,2^{n}}\), each of which has length \(\ell _{n}=\frac{L}{2^{n}}\), and has the same integral as all the other ones: \(\int u_{n}\left( x\right) dx=E,\ \forall n\). For a thorough explanation of the branching process just sketched, with explicit calculation, the interested reader can refer to the paper by Materassi et al.120
The profiles \(u_{n}\left( x\right)\) produced at a suitably high value of n by the p-model were proved to be useful to mimic the distribution of kinetic energy in fluid turbulence118,119, or that of magnetic energy in MHD or ionospheric turbulence121,122,123. Moreover, the choice of the parameter p, with which we defined the weights \(w_{11}\) and \(w_{12}\) in (3), tunes the degree of intermittency of the final result \(u_{n}\left( x\right)\), as it regulates how uneven the partition of the amount E is from the \(\left( n-1\right)\)-th to the n-th generation: \(p=\frac{1}{2}\) reproduces Kolmogorov’s non-intermittent K41 theory119, while \(p\rightarrow 0\) and \(p\rightarrow 1\) gives rise to more and more intermittent distributions, with a mirror symmetry between \(p\in \left[ 0,\frac{1}{2}\right)\) and \(p\in \left[ \frac{1}{2},1\right]\). Last, but not least, the p-model distribution shows a well known multi-fractal singularity spectrum122,124,125. All those reasons render the p-model series a suitable test bed for multiscale analysis techniques, as EMD and IF, because the ground truth is an intermittent signal of perfectly known characteristics, and the extent to which those are retrieved by the various analysis tools clearly emerges.
In the following, we consider a signal \(p\left( x\right)\) obtained from the summation of \(n=12\) generations \(u_{k=0,...,12}\), each representing a different realization of a p-model \(p\left( x\right) =\sum _{k=0}^{12}u_{k}\left( x\right)\). In doing so we produce a signal which contains several scales which are enough “orthogonal” (i.e. independent) to each other. The sum \(p\left( x\right)\) clearly contains information about each of the kth generations corresponding to \(n=12\) different p-models, from the 0th to the 12th one, because it is formed by these addenda.
As a next step, we decompose this signal via the DWT, using both “Haar” and “Daubechies 4” (db4) bases, EMD and FIF algorithms. In this work we compare the performance of the EMD- and IF-based methods with that of the discrete wavelet, since wavelets are a very well established tools in the study of turbulent signals126. Moreover, regarding the choice of the wavelet bases, the “Haar” wavelets are particularly suited to treat stepwise-function based signals, as the single components \(u_k\) are; whereas the use of “Daubechies” decomposition is well established in fluctuation analysis127. We call \(\left\{ \psi _{h}\right\}\) the set of functions along which the signal is decomposed, so that \(p\left( x\right) =\sum _{h}c_{h}\psi _{h}\left( x\right)\). In our analysis, the functions \(\psi _{h}\) are DWT generated levels, EMD or FIF IMF functions. The hth-scale filtered component of the true signal \(p\left( x\right)\) is defined as \(p_{h}(x)\overset{\mathrm {def}}{=}c_{h}\psi _{h}\left( x\right)\). We show these decompositions in Fig. 5. It is evident that none of the aforementioned techniques is able to extract components which resemble the corresponding ground truth \(u_{k}\) generations, and on the other hand we already anticipated that retrieving those addenda is not the purpose of our analysis.
Stochastic signals—P-model Example. From Top left to Bottom right corner, Haar and db4 Wavelet, EMD and FIF decompositions, respectively. In solid red the corresponding ground truth \(u_{k}\) generations. In each panel, the x-axis plots the sample points, and the y-axis the IMFs ordered from top to bottom.
One may argue that, for real life data sets, probability distributions, such as the exponential one, represent the large-scale randomness which could arise from the superposition of nonrandom processes at smaller scales. While this could be correct in theory, the previous simulation shows that DWT, EMD- and IF-based algorithms might not help researchers in identifying the exact origin of a data set. These techniques will always produce a decomposition of the signal, no matter what the process behind it is.
Finally, we compare the ability of all these techniques in reconstructing multiscale statistical features of the given signal, compared to the ground truth ones. We study, in particular, the standard deviation \(\sigma \left( p_{h}(x)\right)\), the skewness \(S\left( p_{h}(x)\right)\) and the excess of kurtosis \(K\left( p_{h}(x)\right)\), as a function of the scale h. Moreover, we include the total energy pertaining to the h-th scale \(\mathscr {E}\left( p_{h}(x)\right)\), and the inner product between two nearby scales \(\mathscr {C}\left( p_{h}(x)\right)\), which we calculate as:
The derived multiscale statistics are presented in Fig. 6.
Stochastic signals—P-model Example. From Top to Bottom rows, multiscale statistical analysis of the Haar and Daubechies 4 Wavelet, EMD, and FIF decompositions, respectively. Different statistical quantities are plotted with respect to the IMF number, from left to right columns: standard deviation (sigma), skewness, kurtosis, power and inner product of two subsequent levels. In dashed red the ground truth values.
A stochastic multi-scale (multifractal) signal as the p-model, or any highly turbulent natural signal, can be conveniently characterized by the statistical properties it shows when it is zoomed in at different time or space scales. For instance, multi-scale analysis of the statistical properties of turbulent signals in geophysics and plasma science may unveil which dynamical processes are at work to produce what the instruments measure. The purpose here is to show what happens when the “zoom-in” tool are EMD- and IF-based techniques, and the result is that the multi-scale statistical properties recognized are in agreement with what found via other more traditional (and literature-consolidated) techniques. From Fig. 6 we see that the behavior, scale by scale, of signal variance, skewness and kurtosis, and the scalar product between adjacent scales, is caught rather well when we filter the signal with EMD and FIF methods. In particular these techniques prove to help in reconstructing the trend of \(\sigma (p_h)\), \(S(p_h)\) or \(K(p_h)\) functions, which is the main objective in real life turbulence study.
We observe that the DWT has troubles regardless the basis we select in reproducing the exact multiscale statistical features values, but it provides the right trends. EMD and FIF decompositions, instead, prove to be more accurate in replicating the standard deviation and power of the different components. The skewness values, as expected, are close to zero. These methods, in fact, decompose signals into simple and pseudo-sinusoidal IMFs which are symmetric with respect to the horizontal axis. Furthermore, the inner products between subsequent IMFs tends to zero since the EMD and FIF methods produces components which tend to be almost orthogonal each other, as the ground truth levels which have been obtained by different p-models. Regarding the kurtosis, EMD and FIF, as well as DWT, are all able to properly reproduce its trend as a function of the scale. We therefore conclude that all the multiscale analysis tools compared in this example are able to detect the intermittency of the signal under analysis119.
Furthermore, the previous example shows that either DWT, or EMD or FIF techniques leave their characteristic signatures in the multiscale analysis of a given signal. Like, for instance, in the case of the skewness values for the IMFs produced using EMD- and IF-based methods. We explain, in fact, that these techniques are designed to produce simple components which have symmetric envelopes with respect to the horizontal axis. Nevertheless, both EMD and FIF provide a meaningful insight in the multiscale statistical analysis and trends of the signal under study, even in presence of strong stochasticity.
Physical signals may not only be stochastic, but also result out of the superposition of a deterministic part with noise. In general, as far as “noise” is expected to be a high frequency component, EMD and FIF techniques should separate it from low frequency deterministic parts, and then treated as here described. The case of superposition of noise and high frequency deterministic parts should be treated in more specific ways, see for instance128.
This example should have clarified the limits as well as the potentialities of these techniques when analysing signals characterized by some degree of stochasticity. As already reported, in real-life applications particular care must be taken when interpreting IMFs in physical terms. Based on the results proposed in this section, we discourage to blindly decompose and analyse a signal when its degree of stochasticity is not well known.
Conclusions
The EMD- and IF-based methods proved to be more suitable than traditional methods for the analysis of nonlinear and nonstationary signals. Their relevance is witnessed by the large number of studies employing them. However, like any other technique, these methods rely on assumptions and have limitations that, if neglected, can severely affect any interpretation based on the returned decomposition. In this work, we examine the main pitfalls and provide caveats for the proper use of the EMD- and IF-based algorithms. Specifically, we address the problems related to boundary errors, to spikes and jumps in the signal and to the analysis of highly-stochastic data sets.
-
Boundary conditions may influence the decomposition of a signal to an extent that increases with the component scale. If not properly handled, they could lead to an artefact-prone decomposition of the original signal. This problem has been studied rigorously in the literature21 for the IF-based methods, but not for the EMD-based algorithms. However, based on the results obtained so far for the IF-based methods, we can reduce the impact of the possible boundary errors for both IF- and EMD-based algorithms by properly pre-extending the signal under study. For this reason, here we propose a new approach for the pre-extension of a given signal. This method is based on the assumption that the optimal way to extend the signal at the boundaries is known. So far, the only extensions studied rigorously in the literature are the periodical, symmetrical and anti-symmetrical ones for the IF-based methods. How to optimally extend in general a signal outside its boundaries is still an open problem that we leave to a future research project.
-
Spikes, including outliers and jumps, can have a big impact on the decomposition, as shown in the examples presented in this work. We show that they could lead, as for the boundary conditions, to an artefact-prone decomposition of the original signal. Moreover, we encourage researchers to be extremely careful when conducting any precursory analysis based on signal decomposition techniques, such as EMD and IF methods. When dealing with a signal containing spikes, the optimal solution would be to study its decomposition before and after removing the spikes from the signal itself. Whereas, when a jump is present in the data set, a good practice would be to split it into before and after the jump, analyse the two portions separately, and compare the outcome of this decomposition with the one of the original signal.
-
In this work, we raise the question of whether the EMD- and IF-based methods are suitable for the analysis of highly stochastic signals. Although the derived decomposition is always correct from a mathematical stand point, it may be the case that there is not a corresponding evident physical meaning of each IMF.
As a matter of fact, when the signal is originated by processes whose behavior can be described by differential equations with oscillatory solutions, EMD- and IF-based techniques produce a decomposition which is meaningful from both a mathematical and a physical standpoint. Whereas, when the process underlying the signal that we want to analyse is characterized by a high degree of stochasticity, the ability of these techniques in separating properly the different scales becomes less clear. In this paper we consider, as an example, the multiscale statistical analysis of the decompositions produced by the DWT-, EMD- and IF-based methods of a stochastic signal obtained as solution of a p-model. This model has been proposed and used in the literature to generate signals which mimic the behavior of irregular and intermittent distribution of energy in turbulent media. The EMD- and IF-based methods proved to have good performance from a multiscale statistical analysis prospective. It remains, however, an open problem to understand up to which degree of stochasticity these techniques are able to reproduce with a good accuracy the single components contained in a given signal. We plan to study this matter in a forthcoming work.
From all these results it is evident that it can be risky to blindly run the decomposition of a nonstationary signals by means of the EMD- and IF-based techniques and using the results without carefully considering the aforementioned limitations. However, the right handling of these techniques allows the users to fully exploit their potentialities in the analysis of nonstationary signals.
References
Bracewell, R. . N. & Bracewell, R. . N. The Fourier transform and its applications Vol. 31999 (McGraw-Hill, New York, 1986).
Cicone, A. Nonstationary signal decomposition for dummies. in Advances in Mathematical Methods and High Performance Computing 69–82 (Springer, New York, 2019).
Cohen, L. Time-frequency analysis Vol. 778 (Prentice hall, New York, 1995).
Daubechies, I., Lu, J. & Wu, H. T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmonic Anal. 30, 243–261. https://doi.org/10.1016/j.acha.2010.08.002 (2011).
Auger, F. et al. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 30, 32–41. https://doi.org/10.1109/MSP.2013.2265316 (2013).
Daubechies, I., Wang, Y. & Wu, H. T. Conceft: Concentration of frequency and time via a multitapered synchrosqueezed transform. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 374, 20150193. https://doi.org/10.1098/rsta.2015.0193 (2016).
Huang, N. E. et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 454, 903–995. https://doi.org/10.1098/rspa.1998.0193 (1998).
Flandrin, P. Time-frequency/time-scale analysis Vol. 10 (Academic press, London, 1998).
Huang, N. E. Introduction to the Hilbert-Huang transform and its related mathematical problems (World Scientific, Singapore, 2014).
Wu, Z. & Huang, N. E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv. Adapt. Data Anal. 1, 1–41. https://doi.org/10.1142/S1793536909000047 (2009).
ur Rehman, N., Park, C., Huang, N. . E. & Mandic, D. . P. Emd via memd: multivariate noise-aided computation of standard emd. Adv. Adapt. Data Anal. 5, 1350007 (2013).
Yeh, J. R., Shieh, J. S. & Huang, N. E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2, 135–156. https://doi.org/10.1142/S1793536910000422 (2010).
Torres, M. E., Colominas, M. A., Schlotthauer, G. & Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. in 2011 IEEE international conference on acoustics, speech and signal processing (ICASSP), 4144–4147, https://doi.org/10.1109/ICASSP.2011.5947265 (IEEE, New York, 2011).
Zheng, J., Cheng, J. & Yang, Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing. Signal Process. 96, 362–374. https://doi.org/10.1016/j.sigpro.2013.09.013 (2014).
Ur Rehman, N. & Mandic, D. . P. Filter bank property of multivariate empirical mode decomposition. IIEEE Trans. Signal Process. 59, 2421–2426 (2011).
Lang, X. et al. Fast multivariate empirical mode decomposition. IEEE Access 6, 65521–65538. https://doi.org/10.1109/ACCESS.2018.2877150 (2018).
Lin, L., Wang, Y. & Zhou, H. Iterative filtering as an alternative algorithm for empirical mode decomposition. Adv. Adapt. Data Anal. 1, 543–560. https://doi.org/10.1142/S179353690900028X (2009).
Cicone, A. & Zhou, H. Numerical analysis for iterative filtering with new efficient implementations based on fft. Numer. Math. (2020).
Huang, C., Yang, L. & Wang, Y. Convergence of a convolution-filtering-based algorithm for empirical mode decomposition. Adv. Adapt. Data Anal. 1, 561–571. https://doi.org/10.1142/S1793536909000205 (2009).
Wang, Y. & Zhou, Z. On the convergence of iterative filtering empirical mode decomposition. Excursions Harmonic Anal. 2, 157–172, https://doi.org/10.1007/978-0-8176-8379-5_8 (Birkhäuser, Boston, 2013).
Cicone, A. & Dell’Acqua, P. Study of boundary conditions in the iterative filtering method for the decomposition of nonstationary signals. J. Comput. Appl. Math. 373, 112248, https://doi.org/10.1016/j.cam.2019.04.028 (2020).
Cicone, A., Garoni, C. & Serra-Capizzano, S. Spectral and convergence analysis of the discrete alif method. Linear Algebra Appl. 580, 62–95. https://doi.org/10.1016/j.laa.2019.06.021 (2019).
Cicone, A. Iterative filtering as a direct method for the decomposition of nonstationary signals. Numer. Algorithms, https://doi.org/10.1007/s11075-019-00838-z (2020).
Cicone, A. & Zhou, H. One or two frequencies? the iterative filtering answers. Preprint (2020).
Cicone, A., Liu, J. & Zhou, H. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl. Comput. Harmonic Anal. 41, 384–411. https://doi.org/10.1016/j.acha.2016.03.001 (2016).
Cicone, A. & Wu, H.-T. Convergence analysis of adaptive locally iterative filtering and sift method. Submitted (2020).
Cicone, A. & Zhou, H. Multidimensional iterative filtering method for the decomposition of high-dimensional non-stationary signals. Numer. Math. Theory Methods Appl. 10, 278–298. https://doi.org/10.4208/nmtma.2017.s05 (2017).
Papini, E. et al. Multidimensional iterative filtering: a new approach for investigating plasma turbulence in numerical simulations. J. Plasma Phys. (2020).
Cicone, A. Multivariate fast iterative filtering for the decomposition of nonstationary signals. Preprint (2020).
Huang, N. E. & Wu, Z. A review on hilbert-huang transform: Method and its applications to geophysical studies. Rev. Geophys. 46, https://doi.org/10.1029/2007RG000228 (2008).
Bowman, D. C. & Lees, J. M. The Hilbert-Huang transform: A high resolution spectral method for nonlinear and nonstationary time series. Seismol. Res. Lett. 84, 1074–1080. https://doi.org/10.1785/0220130025 (2013).
Tary, J. B., Herrera, R. H., Han, J. & van der Baan, M. Spectral estimation–what is new? what is next?. Rev. Geophys. 52, 723–749. https://doi.org/10.1002/2014RG000461 (2014).
Baykut, S., Akgül, T., İnan, S. & Seyis, C. Observation and removal of daily quasi-periodic components in soil radon data. Radiat. Meas. 45, 872–879. https://doi.org/10.1016/j.radmeas.2010.04.002 (2010).
Tsolis, G. S. & Xenos, T. D. A qualitative study of the seismo-ionospheric precursors prior to the 6 April 2009 earthquake in l’aquila, Italy. Nat. Hazards Earth Syst. Sci. 10, 133–137, https://doi.org/10.5194/nhess-10-133-2010 (2010).
Huang, J. Y. et al. Coseismic deformation time history calculated from acceleration records using an emd-derived baseline correction scheme: A new approach validated for the 2011 Tohoku earthquake. Bull. Seismol. Soc. Am. 103, 1321–1335. https://doi.org/10.1785/0120120278 (2013).
Chen, C. H. et al. Surface deformation and seismic rebound: implications and applications. Surv. Geophys. 32, 291. https://doi.org/10.1007/s10712-011-9117-3 (2011).
Barman, C., Ghose, D., Sinha, B. & Deb, A. Detection of earthquake induced radon precursors by Hilbert Huang transform. J. Appl. Geophys. 133, 123–131. https://doi.org/10.1016/j.jappgeo.2016.08.004 (2016).
Wang, D., Hwang, C. & Shen, W. Investigations of anomalous gravity signals prior to 71 large earthquakes based on a 4-years long superconducting gravimeter records. Geodesy Geodyn. 8, 319–327. https://doi.org/10.1016/j.geog.2017.07.002 (2017).
Chen, C. et al. Identification of earthquake signals from groundwater level records using the hht method. Geophys. J. Int. 180, 1231–1241. https://doi.org/10.1111/j.1365-246X.2009.04473.x (2010).
Battista, B. M., Knapp, C., McGee, T. & Goebel, V. Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data. Geophysics 72, H29–H37. https://doi.org/10.1190/1.2437700 (2007).
Chen, Y. Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter. Geophys. J. Int. 206, 457–469. https://doi.org/10.1093/gji/ggw165 (2016).
Vasudevan, K. & Cook, F. A. Empirical mode skeletonization of deep crustal seismic data: Theory and applications. J. Geophys. Res. Solid Earth 105, 7845–7856. https://doi.org/10.1029/1999JB900445 (2000).
Roberts, P. H., Yu, Z. J. & Russell, C. T. On the 60-year signal from the core. Geophys. Astrophys. Fluid Dyn. 101, 11–35. https://doi.org/10.1080/03091920601083820 (2007).
Jackson, L. P. & Mound, J. E. Geomagnetic variation on decadal time scales: What can we learn from empirical mode decomposition?. Geophys. Res. Lett. 37, https://doi.org/10.1029/2010GL043455 (2010).
Yu, Z. G., Anh, V., Wang, Y., Mao, D. & Wanliss, J. Modeling and simulation of the horizontal component of the geomagnetic field by fractional stochastic differential equations in conjunction with empirical mode decomposition. J. Geophys. Res. Space Phys. 115, https://doi.org/10.1029/2009JA015206 (2010).
Materassi, M. et al. Stepping into the equatorward boundary of the auroral oval: preliminary results of multi scale statistical analysis. Ann. Geophys. 61, 55. https://doi.org/10.4401/ag-7801 (2019).
Spogli, L. et al. Role of the external drivers in the occurrence of low-latitude ionospheric scintillation revealed by multi-scale analysis. J. Space Weather Space Clim. 9, A35, https://doi.org/10.1051/swsc/2019032 (2019).
Piersanti, M. et al. Adaptive local iterative filtering: A promising technique for the analysis of nonstationary signals. J. Geophys. Res. Space Phys. 123, 1031–1046. https://doi.org/10.1002/2017JA024153 (2018).
Spogli, L. et al. Role of the external drivers in the occurrence of low-latitude ionospheric scintillation revealed by multi-scale analysis. 2019 URSI Asia-Pacific Radio Science Conference, AP-RASC 2019, 8738254 (2019).
Huang, N. E. et al. A new spectral representation of earthquake data: Hilbert spectral analysis of station tcu129, Chi-Chi, Taiwan, 21 September 1999. Bull. Seismol. Soc. Am. 91, 1310–1338. https://doi.org/10.1785/0120000735 (2001).
Loh, C. H., Wu, T. C. & Huang, N. E. Application of the empirical mode decomposition-Hilbert spectrum method to identify near-fault ground-motion characteristics and structural responses. Bull. Seismol. Soc. Am. 91, 1339–1357. https://doi.org/10.1785/0120000715 (2001).
Zhang, R. R., Ma, S., Safak, E. & Hartzell, S. Hilbert-Huang transform analysis of dynamic and earthquake motion recordings. J. Eng. Mech. 129, 861–875. https://doi.org/10.1061/(ASCE)0733-9399(2003)129:8(861) (2003).
Zhang, R. R., Ma, S. & Hartzell, S. Signatures of the seismic source in emd-based characterization of the 1994 Northridge, California, earthquake recordings. Bull. Seismol. Soc. Am. 93, 501–518. https://doi.org/10.1785/0120010285 (2003).
Yang, J. N., Lei, Y., Lin, S. & Huang, N. Identification of natural frequencies and dampings of in situ tall buildings using ambient wind vibration data. J. Eng. Mech. 130, 570–577. https://doi.org/10.1061/(ASCE)0733-9399(2004)130:5(570) (2004).
Franzke, C. Multi-scale analysis of teleconnection indices: Climate noise and nonlinear trend analysis. Nonlinear Process. Geophys. 16, 65–76. https://doi.org/10.5194/npg-16-65-2009 (2009).
Lee, T. & Ouarda, T. B. M. J. Prediction of climate nonstationary oscillation processes with empirical mode decomposition. J. Geophys. Res. Atmos. 116, https://doi.org/10.1029/2010JD015142 (2011).
Ezer, T. & Corlett, W. B. Is sea level rise accelerating in the Chesapeake Bay? A demonstration of a novel new approach for analyzing sea level data. Geophys. Res. Lett. 39, https://doi.org/10.1029/2012GL053435 (2012).
Franzke, C. Nonlinear trends, long-range dependence, and climate noise properties of surface temperature. J. Clim. 25, 4172–4183. https://doi.org/10.1175/JCLI-D-11-00293.1 (2012).
Ezer, T., Atkinson, L. . P., Corlett, W. . B. & Blanco, J. . L. Gulf stream’s induced sea level rise and variability along the u.s. mid-atlantic coast.. J. Geophys. Res. Oceans 118, 685–697. https://doi.org/10.1002/jgrc.20091 (2013).
Duffy, D. G. The application of hilbert-huang transforms to meteorological datasets. Hilbert-Huang Transform Appl. 203–221, https://doi.org/10.1142/9789814508247_0009 (World Scientific, 2014).
Huang, N. E., Shen, Z. & Long, S. R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 31, 417–457. https://doi.org/10.1146/annurev.fluid.31.1.417 (1999).
Terradas, J., Oliver, R. & Ballester, J. L. Application of statistical techniques to the analysis of solar coronal oscillations. Astrophys. J. 614, 435 (2004).
Morton, R. J., Erdélyi, R., Jess, D. B. & Mathioudakis, M. Observations of sausage modes in magnetic pores. Astrophys. J. Lett. 729, L18. https://doi.org/10.1088/2041-8205/729/2/L18 (2011).
Hofmann-Wellenhof, B., Lichtenegger, H. & Wasle, E. GNSS-global navigation satellite systems: GPS, GLONASS, Galileo, and more (Springer, New York, 2007).
Ghobadi, H. et al. Disentangling ionospheric refraction and diffraction effects in gnss raw phase through fast iterative filtering technique. GPS Solut. (2020).
Hillier, A., Morton, R. J. & Erdélyi, R. A statistical study of transverse oscillations in a quiescent prominence. Astrophys. J. Lett. 779, L16. https://doi.org/10.1088/2041-8205/779/2/L16 (2013).
Wang, C. et al. Deconvolution of subcellular protrusion heterogeneity and the underlying actin regulator dynamics from live cell imaging. Nat. Commun. 9, https://doi.org/10.1038/s41467-018-04030-0 (2018).
Cicone, A., Liu, J. & Zhou, H. Hyperspectral chemical plume detection algorithms based on multidimensional iterative filtering decomposition. Phil. Trans. R. Soc. A: Math. Phys. Eng. Sci. 374, 2015.0196, https://doi.org/10.1098/rsta.2015.0196 (2016).
Yang, A. C., Peng, C. K. & Huang, N. E. Causal decomposition in the mutual causation system. Nat. Commun. 9, 3378. https://doi.org/10.1038/s41467-018-05845-7 (2018).
Costa, M., Goldberger, A. L. & Peng, C. K. Broken asymmetry of the human heartbeat: Loss of time irreversibility in aging and disease. Phys. Rev. Lett. 95, 198102. https://doi.org/10.1103/PhysRevLett.95.198102 (2005).
Cicone, A. & Wu, H.-T. How nonlinear-type time-frequency analysis can help in sensing instantaneous heart rate and instantaneous respiratory rate from photoplethysmography in a reliable way. Front. Physiol. 8, 701 (2017).
Cummings, D. A. et al. Travelling waves in the occurrence of dengue haemorrhagic fever in Thailand. Nature 427, 344. https://doi.org/10.1038/nature02225 (2004).
Liang, H., Bressler, S. L., Buffalo, E. A., Desimone, R. & Fries, P. Empirical mode decomposition of field potentials from macaque v4 in visual spatial attention. Biol. Cybernet. 92, 380–392. https://doi.org/10.1007/s00422-005-0566-y (2005).
Yang, A. C., Huang, N. E., Peng, C. K. & Tsai, S. J. Do seasons have an influence on the incidence of depression? The use of an internet search engine query data as a proxy of human affect. PLOS ONE 5, https://doi.org/10.1371/journal.pone.0013728 (2010).
Wu, C. H. et al. Frequency recognition in an ssvep-based brain computer interface using empirical mode decomposition and refined generalized zero-crossing. J. Neurosci. Methods 196, 170–181. https://doi.org/10.1016/j.jneumeth.2010.12.014 (2011).
Gregoriou, G. G., Gotts, S. J. & Desimone, R. Cell-type-specific synchronization of neural activity in fef with v4 during attention. Neuron 73, 581–594. https://doi.org/10.1016/j.neuron.2011.12.019 (2012).
Hu, K., Lo, M. T., Peng, C. K., Liu, Y. & Novak, V. A nonlinear dynamic approach reveals a long-term stroke effect on cerebral blood flow regulation at multiple time scales. PLoS Comput. Biol. 8, e1002601. https://doi.org/10.1371/journal.pcbi.1002601 (2012).
Zheng, Y., Wang, G., Li, K., Bao, G. & Wang, J. Epileptic seizure prediction using phase synchronization based on bivariate empirical mode decomposition. Clin. Neurophysiol. 125, 1104–1111. https://doi.org/10.1016/j.clinph.2013.09.047 (2014).
Hassan, A. R. & Bhuiyan, M. I. H. Automatic sleep scoring using statistical features in the emd domain and ensemble methods. Biocybernet. Biomed. Eng. 36, 248–255. https://doi.org/10.1016/j.bbe.2015.11.001 (2016).
Parey, A., El Badaoui, M., Guillet, F. & Tandon, N. Dynamic modelling of spur gear pair and application of empirical mode decomposition-based statistical analysis for early detection of localized tooth defect. J. Sound Vib. 294, 547–561. https://doi.org/10.1016/j.jsv.2005.11.021 (2006).
Liu, H., Chen, C., Tian, H. Q. & Li, Y. F. A hybrid model for wind speed prediction using empirical mode decomposition and artificial neural networks. Renewable Energy 48, 545–556. https://doi.org/10.1016/j.renene.2012.06.012 (2012).
Wei, Y. & Chen, M. C. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks. Transp. Res. Part C-Emerg. Technol. 21, 148–162. https://doi.org/10.1016/j.trc.2011.06.009 (2012).
An, N., Zhao, W., Wang, J., Shang, D. & Zhao, E. Using multi-output feedforward neural network with empirical mode decomposition based signal filtering for electricity demand forecasting. Energy 49, 279–288. https://doi.org/10.1016/j.energy.2012.10.035 (2013).
Sfarra, S. et al. Improving the detection of thermal bridges in buildings via on-site infrared thermography: The potentialities of innovative mathematical tools. Energy and Build. 182, 159–171. https://doi.org/10.1016/j.enbuild.2018.10.017 (2019).
Lei, Y., Lin, J., He, Z. & Zuo, M. J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 35, 108–126. https://doi.org/10.1016/j.ymssp.2012.09.015 (2013).
Yu, L., Wang, S. & Lai, K. K. Forecasting crude oil price with an emd-based neural network ensemble learning paradigm. Energy Econ. 30, 2623–2635. https://doi.org/10.1016/j.eneco.2008.05.003 (2008).
Zhang, X., Lai, K. K. & Wang, S. Y. A new approach for crude oil price analysis based on empirical mode decomposition. Energy Econ. 30, 905–918. https://doi.org/10.1016/j.eneco.2007.02.012 (2008).
Zhang, X., Yu, L., Wang, S. & Lai, K. K. Estimating the impact of extreme events on crude oil price: An emd-based event analysis method. Energy Econ. 31, 768–778. https://doi.org/10.1016/j.eneco.2009.04.003 (2009).
Abdelouahad, A. A., El Hassouni, M., Cherifi, H. & Aboutajdine, D. Reduced reference image quality assessment based on statistics in empirical mode decomposition domain. Signal Image Video Process. 8, 1663–1680 (2014).
Xia, Y., Zhang, B., Pei, W. & Mandic, D. P. Bidimensional multivariate empirical mode decomposition with applications in multi-scale image fusion. IEEE Access 7, 114261–114270 (2019).
Li, X., Su, J. & Yang, L. Building detection in sar images based on bi-dimensional empirical mode decomposition algorithm. in IEEE Geoscience and Remote Sensing Letters (2019).
Rato, R. T., Ortigueira, M. D. & Batista, A. G. On the hht, its problems, and some solutions. Mech. Syst. Signal Process. 22, 1374–1394 (2008).
Huang, N. E. Empirical mode decomposition apparatus, method and article of manufacture for analyzing biological signals and performing curve fitting (2004). US Patent 6738734.
Huang, N. E. et al. A confidence limit for the empirical mode decomposition and hilbert spectral analysis. Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 459, 2317–2345 (2003).
Dätig, M. & Schlurmann, T. Performance and limitations of the hilbert-huang transformation (hht) with an application to irregular water waves. Ocean Eng. 31, 1783–1834 (2004).
Rilling, G., Flandrin, P., Goncalves, P. et al. On empirical mode decomposition and its algorithms. In IEEE-EURASIP workshop on nonlinear signal and image processing, Vol. 3, 8–11 (NSIP-03, Grado (I), 2003).
Liu, Z. A novel boundary extension approach for empirical mode decomposition. In International Conference on Intelligent Computing, 299–304 (Springer, New York, 2006).
Wang, J., Liu, W. & Zhang, S. An approach to eliminating end effects of emd through mirror extension coupled with support vector machine method. Pers. Ubiquit. Comput. 23, 443–452 (2019).
Meng, E. et al. A robust method for non-stationary streamflow prediction based on improved emd-svm model. J. Hydrol. 568, 462–478 (2019).
Stallone, A., Cicone, A. & Materassi, M. New insights and best practices for the successful use of empirical mode decomposition, iterative filtering and derived algorithms. Supplementary material. Sci. Rep. (2020).
Briongos, J. V., Aragón, J. M. & Palancar, M. C. Phase space structure and multi-resolution analysis of gas-solid fluidized bed hydrodynamics: Part I–the emd approach. Chem. Eng. Sci. 61, 6963–6980. https://doi.org/10.1016/j.ces.2006.07.023 (2006).
Sweeney-Reed, C. M. & Nasuto, S. J. A novel approach to the detection of synchronisation in eeg based on empirical mode decomposition. J. Comput. Neurosci. 23, 79–111. https://doi.org/10.1007/s10827-007-0020-3 (2007).
Sarlis, N. V., Skordas, E. S., Mintzelas, A. & Papadopoulou, K. A. Micro-scale, mid-scale, and macro-scale in global seismicity identified by empirical mode decomposition and their multifractal characteristics. Sci. Rep. 8, 9206. https://doi.org/10.1038/s41598-018-27567-y (2018).
Yun, S. M. et al. Analyzing groundwater level anomalies in a fault zone in Korea caused by local and offshore earthquakes. Geosci. J. 23, 137–148. https://doi.org/10.1007/s12303-018-0062-8 (2019).
Dziewonski, A. M., Chou, T. A. & Woodhouse, J. H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. Solid Earth 86, 2825–2852. https://doi.org/10.1029/JB086iB04p02825 (1981).
Ekström, G., Nettles, M. & Dziewoński, A. M. The global cmt project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Interiors 200, 1–9. https://doi.org/10.1016/j.pepi.2012.04.002 (2012).
Materassi, M. & Mitchell, C. Wavelet analysis of gps amplitude scintillation: A case study. Radio Sci. 42 (2007).
Alberti, T. et al. Time scale separation in the solar wind-magnetosphere coupling during st. patrick’s day storms in 2013 and 2015. J. Geophys. Res. Space Phys. 122, 4266–4283. https://doi.org/10.1002/2016JA023175 (2017).
Pan, N., Mang, V. & Un, M. P. Accurate removal of baseline wander in ecg using empirical mode decomposition. in 2007 Joint Meeting of the 6th International Symposium on Noninvasive Functional Source Imaging of the Brain and Heart and the International Conference on Functional Biomedical Imaging, 177–180 (IEEE, 2007).
Chen, H. J., Chen, C. C., Tseng, C. Y. & Wang, J. H. Effect of tidal triggering on seismicity in Taiwan revealed by the empirical mode decomposition method. Nat. Hazards Earth Syst. Sci. 12, 2193. https://doi.org/10.5194/nhess-12-2193-2012 (2012).
Matcharashvili, T., Telesca, L., Chelidze, T., Javakhishvili, Z. & Zhukova, N. Analysis of temporal variation of earthquake occurrences in caucasus from 1960 to 2011. Tectonophysics 608, 857–865. https://doi.org/10.1016/j.tecto.2013.07.033 (2013).
Fan, X. & Lin, M. Multiscale multifractal detrended fluctuation analysis of earthquake magnitude series of Southern California. Phys. A: Stat. Mech. Appl. 479, 225–235. https://doi.org/10.1016/j.physa.2017.03.003 (2017).
Nenadic, Z. & Burdick, J. W. Spike detection using the continuous wavelet transform. IEEE Trans. Biomed. Eng. 52, 74–87 (2004).
Yang, H.-W. et al. A minimum arclength method for removing spikes in empirical mode decomposition. IEEE Access 7, 13284–13294 (2019).
Harten, A., Engquist, B., Osher, S. & Chakravarthy, S. R. Uniformly high order accurate essentially non-oscillatory schemes, III. in Upwind and high-resolution schemes, 218–290 (Springer, 1987).
Meneveau, C. & Sreenivasan, K. The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484 (1991).
Macek, W. M. & Wawrzaszek, A. Multifractal turbulence at the termination shock. in AIP Conference Proceedings, Vol. 1216, 572–575 (American Institute of Physics, 2010).
Meneveau, C. & Sreenivasan, K. R. The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484 (1991).
Frisch, U. & Kolmogorov, A. N. Turbulence: the legacy of AN Kolmogorov (Cambridge University Press, Cambridge, 1995).
Materassi, M., Wernik, A. W. & Yordanova, E. Statistics in the p-model. Chaos Solit. Fractals 30, 642–655 (2006).
Marsch, E. & Tu, C.-Y. Intermittency, non-Gaussian statistics and fractal scaling of mhd fluctuations in the solar wind. Nonlinear Process. Geophys. 4, 101–124 (1997).
Macek, W. M. Multifractality and intermittency in the solar wind. Nonlinear Process. Geophys. 14, 695–700 (2007).
Grzesiak, M. Analysis of random cascade processes in the earth magnetospheric cusps. Acta Geophys. Polon. 48, 241–261 (2000).
Muzy, J.-F., Bacry, E. & Arneodo, A. The multifractal formalism revisited with wavelets. Int. J. Bifurcation Chaos 4, 245–302 (1994).
Macek, W. M. & Wawrzaszek, A. Multifractal two-scale cantor set model for slow solar wind turbulence in the outer heliosphere during solar maximum. Nonlinear Process. Geophys. 18, 287 (2011).
Farge, M. Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 24, 395–458 (1992).
González, A. O., Junior, O. M., Menconi, V. E. & Domingues, M. O. Daubechies wavelet coefficients: a tool to study interplanetary magnetic field fluctuations. Geofís. Int. 53, 101–115 (2014).
Kampers, G. et al. Disentangling stochastic signals superposed on short localized oscillations. Phys. Lett. A 384, 126307 (2020).
Acknowledgements
Antonio Cicone is a member of the Italian “Gruppo Nazionale di Calcolo Scientifico” (GNCS) of the Istituto Nazionale di Alta Matematica “Francesco Severi” (INdAM). He thank the INdAM for the financial support under the “Progetto Premiale FOE 2014” “Strategic Initiatives for the Environment and Security– SIES”, and the Italian Space Agency for the financial support under the contract ASI “LIMADOU scienza” no. 2016-16-H0. Massimo Materassi would like to stress that this work was benefited from discussions within the International Space Science Institute (ISSI) Team # 455 “Complex Systems Perspectives Pertaining to the Research of the Near-Earth Electromagnetic Environment”.
The authors want to thank Haomin Zhou (Georgia Tech) and Emanuele Papini (University of Florence) for the interesting discussions and all the advises they gave on the topic. We thank the authors of the work110 for sharing with us their data sets that we used in “Real life example”.
Author information
Authors and Affiliations
Contributions
A.S. and A.C. managed the literature search and the manuscript and developed “Problems with the boundaries” and “Spike pulses and jumps in the signal”; M.M. managed the manuscript,contributed to “Spike pulses and jumps in the signal” and developed “Stochastic signals decomposition”. All the authors approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stallone, A., Cicone, A. & Materassi, M. New insights and best practices for the successful use of Empirical Mode Decomposition, Iterative Filtering and derived algorithms. Sci Rep 10, 15161 (2020). https://doi.org/10.1038/s41598-020-72193-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-72193-2
This article is cited by
-
Stabilization and variations to the adaptive local iterative filtering algorithm: the fast resampled iterative filtering method
Numerische Mathematik (2024)
-
Spatiotemporal subsidence feature decomposition and hotspot identification
Environmental Earth Sciences (2024)
-
High resolution seafloor thermometry for internal wave and upwelling monitoring using Distributed Acoustic Sensing
Scientific Reports (2023)
-
Understanding the Constraints to the Correct Application of the Upward Continuation Operation in Gravity Data Processing
Pure and Applied Geophysics (2023)
-
Detection of intermuscular coordination based on the causality of empirical mode decomposition
Medical & Biological Engineering & Computing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.