Abstract
We demonstrate the magnetically-induced transparency (MIT) effect in Y\(_3\)Fe\(_5\)O\(_{12}\)(YIG)/Permalloy (Py) coupled bilayers. The measurement is achieved via a heterodyne detection of the coupled magnetization dynamics using a single wavelength that probes the magneto-optical Kerr and Faraday effects of Py and YIG, respectively. Clear features of the MIT effect are evident from the deeply modulated ferromagnetic resonance of Py due to the perpendicular-standing-spin-wave of YIG. We develop a phenomenological model that nicely reproduces the experimental results including the induced amplitude and phase evolution caused by the magnon–magnon coupling. Our work offers a new route towards studying phase-resolved spin dynamics and hybrid magnonic systems.
Similar content being viewed by others
Introduction
Hybrid magnonic systems are becoming rising contenders for coherent information processing1,2,3,4, owing to their capability of coherently connecting distinct physical platforms in quantum systems as well as the rich emerging physics for new functionalities5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. Magnons have been demonstrated to efficiently couple to cavity quantum electrodynamics systems including superconducting resonators and qubits5,6,7,8,9; magnonic systems are therefore well-positioned for the next advances in quantum information. In addition, recent studies also revealed the potential of magnonic systems for microwave-optical transduction23,24,25,26,27,28,29, which are promising for combining quantum information, sensing, and communication.
To fully leverage the hybrid coupling phenomena with magnons, strong and tunable couplings between two magnonic systems have attracted considerable interests recently30,31,32,33. They can be considered as hosting hybrid magnonic modes in a “magnonic cavity” as opposed to microwave photonic cavity in cavity-magnon polaritons (CMPs)1,2,3, which allows excitations of forbidden modes and high group velocity of spin waves owing to the state-of-the-art magnon bandgap engineering capabilities31,34. The detuning of the two magnonic systems can be easily engineered by the thickness of the thin films, which set the wavenumbers and the corresponding exchange field. Furthermore, in such strongly coupled magnetic heterostructures, both magneto-optical Kerr and Faraday effects can be utilized for light modulation, in terms of light reflection by metals and/or transmission in insulators, respectively. In this architecture, the freedom of lateral dimensions is maintained for device fabrication and large-scale, on-chip integration.
To date, both magnon–photon and magnon–magnon couplings are predominantly investigated by the cavity ferromagnetic resonance (FMR) spectroscopy, i.e. microwave transmission and/or reflection measurements, typically involving a vector-network analyzer (VNA) or a microwave diode5,7,8,9,10,11,12,13,30,31,32,33,35. Strong magnon–magnon couplings have been observed in yttrium iron garnet (Y\(_3\)Fe\(_5\)O\(_{12}\), YIG) coupled with ferromagnetic (FM) metals, where exchange spin waves were excited by a combined action of exchange, dampinglike, and/or fieldlike torques that are localized at the interfaces30,31,32,33.
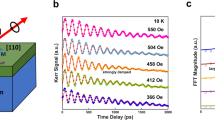
(a) Schematic illustration of the experimental setup. Modulated and linearly-polarized 1550-nm light enter the sample at a polarization angle (1); dynamic Faraday effect of the YIG causes the polarization to rotate (2); dynamic Kerr effect of the Py causes polarization to further rotate (3); the reflected light, upon the returning path, picks up again the Faraday effect and causes the polarization to further rotate (4), before entering light detection and analysis. The applied dc magnetic field is parallel to the ground–signal–ground (G–S–G) lines of the CPW. (b) Example signal trace for YIG/Py (solid) and YIG/SiO\(_2\)/Py (dashed) measured at 5.85 GHz, showing the in-phase X (top) and quadrature Y (middle), and the total amplitude, \(\sqrt{X^2+Y^2}\) (bottom). (c) Plotting and the fitting of the observed PSSW modes versus the resonance fields.
In this work, we investigate the magnon–magnon coupling in YIG/Permalloy (Py) bilayers by a phase-resolved, heterodyne optical detection method. We reveal the coupled magnon modes in the regime exhibiting the magnetically-induced transparency (MIT) effect, i.e. the magnetic analogy of electromagnetically induced transparency (EIT)11,36,37,38,39,40, akin to a spin-wave induced suppression of FMR. In the hybrid magnon–photon systems, the MIT effect arises when the coupling strength, \(g/2\pi\) is larger than the photon dissipation rate \(\kappa _\text {p}/2\pi\) but smaller than the magnon dissipation rate \(\kappa _\text {m}/2\pi\)11. Under such a condition, the mode hybridization leads to an abrupt suppression of the microwave transmission at a certain frequency range. A transparency window, whose bandwidth is determined by the low-loss mode, can be observed in the broad resonance of the other lossy mode. Such resonant transparency can be controlled by an external magnetic field. Our measurement is achieved via detecting the coupled magnetization dynamics of the insulating and metallic FMs using a single 1550-nm telecommunication wavelength. Unlike the ultrafast optical pump-probes27, the method herein is a continue-wave (cw), heterodyne technique in which the 1550-nm laser light is modulated at the FMR frequencies (in GHz range) simultaneously with the sample’s excitation. This feature makes the method effectively an optical “lock-in” type measurement, akin to the electrical lock-in detection41,42,43. The phase information between the Py and YIG FMRs, as well as the YIG perpendicular standing spin waves (PSSWs) can be obtained by simultaneously analyzing both the Kerr and Faraday responses.
Samples and measurements
The commercial YIG films (from MTI Corporation) used in this work are 3-\(\mu\)m thick, single-sided grown on double-side-polished Gd\(_3\)Ga\(_5\)O\(_{12}\) (GGG) substrates via liquid phase epitaxy (LPE). The Py films (t\(_{Py}\) = 10 nm and 30 nm) were subsequently deposited on the YIG films using magnetron sputtering following earlier recipes33. To ensure the strong coupling, we used in situ Ar gas rf-bias cleaning for 3 min, to clean the YIG surface before depositing the Py layer. Reference samples of GGG/YIG/SiO\(_2\)(3-nm)/Py(10-nm) GGG/YIG/Cu(3-nm)/Py(10-nm) were also prepared at the same growth condition.
Figure 1a illustrates the measurement configuration. The modulated and linearly-polarized 1550-nm light passes through the transparent GGG substrates and detects the dynamic Faraday and Kerr signals upon their FMR excitation. As the light travels through the YIG bulk, the dynamic Faraday rotation due to the YIG FMR is picked up. Similarly, the dynamic Kerr rotation caused by the Py FMR is then picked up, when the light reaches the Py layer. The Py layer also serves as a mirror and reflects the laser light. Upon reflection, the dynamic Faraday effect from the YIG is picked up again, making the effective YIG thickness 6-\(\it \upmu\)m, i.e. twice the film thickness. It should be noted that the Faraday rotations for the incoming and returning light add up as opposed to cancel, due to the inversion of both the chirality of the Faraday rotation and the projection of the perpendicular magnetization of YIG along the wavenumber direction, whose mechanism is akin to a commercial “Faraday rotator” often encountered in fiber optics.
The YIG/Py samples are chip-flipped on a coplanar waveguide (CPW) for microwave excitation and optical detection, as depicted in Fig. 1a. An in-plane magnetic field, H, along the y-direction saturates both the YIG and Py magnetizations. We scan the frequency (from 4 to 8 GHz) and the magnetic field, and then measure the optical responses using a lock-in amplifier’s in-phase X (Re[\(V_\text {O}\)]) and quadrature Y (Im[\(V_\text {O}\)]) channels as well as the microwave transmission using a microwave diode. A detailed description of the measurement setup is in the Supplemental Materials (SM), Figure S1.
Results and discussions
Figure 1b compares the optical rectification signals between the 10-nm-Py sample and the YIG/SiO\(_2\)/Py reference sample measured at 5.85 GHz. The 10-nm-Py sample (solid line) shows the representative features of the detected FMR and hybridized PSSW modes. The complete fine-scan including the FMR diode dataset are summarized in the SM, Fig. S2. The optical signals with the phase information are obtained by the lock-in’s in-phase X (Re[\(V_\text {O}\)], top panel) and quadrature Y (Im[\(V_\text {O}\)], middle panel), which are further used to calculate the total amplitude, \(\sqrt{X^2+Y^2}\), (bottom panel). The technical details of the measured signal versus the optical and electrical phases are summarized in the SM.
The YIG FMR signal at \(\sim\)1.3 kOe is accumulated from the Faraday effect corresponding to the spatially uniform precession of the YIG magnetization. The FMR dispersion is described by the Kittel formula: \(\omega ^2/\gamma ^2= H_\text {FMR}(H_\text {FMR}+M_s)\), where \(\omega\) is the mode frequency, \(\gamma /2\pi =(g_\text {eff}/2) \times\) 28 GHz/T is the gyromagnetic ratio, \(g_\text {eff}\) is the g-factor, \(H_\text {FMR}\) is the resonance field, and \(M_s\) is the magnetization. The excitation of the YIG PSSW modes introduces an additional exchange field \(H_{ex}\) to the Kittel equation, as \(\mu _0 H_\text{ex} = (2A_\text{ex}/M_s) (n\pi /d_{\mathrm{YIG}})^2\), which defines the mode splitting between the PSSW modes and the uniform mode. Here \(A_\text{ex}\) is the exchange stiffness, and \(d_{\mathrm{YIG}}\) is the YIG film thickness. A total of more than 30 PSSW modes can be identified for the 10-nm-Py sample. In Fig. 1c, the quadratic increase of \(H_\text{ex}\) with the mode number n confirms the observation of the PSSWs. Fittings to the Kittel equation and the exchange field expression yield \(M_s\) = 1.97 kOe and \(A_\text{ex}\) = 3.76 pJ/m, which are in good agreement with the previously reported values30,31,32,33.
In Fig. 1b, the Py FMR at \(\sim\)0.6 kOe is strongly modulated by the YIG PSSWs, exhibiting the MIT effect, due to the formation of hybrid magnon modes. Besides, the YIG PSSW signals near the Py FMR regime (\(n>25\)) are much stronger than the off-resonance regime (\(n<25\)), which indicates the important role of the Py/YIG coupling in exciting the relevant PSSW modes and resonantly enhancing the magnetization dynamics. As a comparison, no apparent PSSW modes are observed for the Py/SiO\(_2\)/YIG reference sample, in Fig. 1b (dashed line), indicating that only the Py but not the YIG PSSWs couples to the microwave drive in the MIT regime. The Py resonance linewidth also is much narrower.
(a) Theoretical signal trace of the MIT effect of the YIG/Py bilayer. 7 hybrid PSSW modes are shown as an example. (b) Example fitting of the complex optical singals, |VO|, at 6 GHz for the 30-nm-Py sample. (c) Full scan of the signals, |VO|, as a function of the magnetic field and frequency. (d) Theoretical calculated dispersion using the fitting parameters, reproducing the experimental data in (c). (e, f) are the fine-scans at smaller field and frequency steps corresponding to the boxes in (c,d) (5.7–6.3 GHz).
Our experimental configuration, similar to previously reported30,31,32,33, is relevant to the Schlömann excitation mechanism of spin wave44 with a dynamic pinning at the interface45. The interfaces of two distinct, coupled magnetic layers have been recently recognized as an interesting source of spin dynamics generation and manipulation46,47. In particular, the critical role of the microwave susceptibilities of the distinct magnetic layers has been theoretically laid out48,49 that are directly relevant to the magnon-magnon coupled experiments30,31,32,33. Here, we introduce a phenomenological model by considering a series of YIG oscillators coupled with a Py oscillator, and using practical experimental fitting parameters, with which the measured complex optical signal, \(V_\text {O}\), can be expressed as:
where A is the total signal amplitude, \(H_\text{FMR}^{\mathrm{Py}}\) and \(H_\text {PSSW}^{\mathrm{YIG}}\) is the resonance field of Py and YIG-PSSWs, respectively, \(\Delta H_{\mathrm{YIG(Py)}}\) is the half-width-half-maximum linewidth, and g is the fieldlike coupling strength from the interfacial exchange. This model disregards the linear frequency-dependent phase (exists in the Re[\(V_\text {O}\)] and Im[\(V_\text {O}\)] signals) but directly analyzes the total optical signal.
Figure 2a plots the theoretically predicated MIT effect according to Eq. 1, showing the lineshape of the Py FMR mode that is coupled to the YIG PSSW modes. The center curve with a zero resonance detuning is a characteristic of the MIT effect. The magnon–magnon coupling induces a set of sharp dips in the spectra. Such dips in the optical reflection means a peak in their transmission, which is referred to as a “transparency window” in quantum optics, resembling the EIT phenomenon in photonics38 and optomechanics39,40. Using a single g value, the amplitude and phase of the hybrid modes display a clearly evolution with respect to the different Py-YIG resonance detuning. Away from the Py FMR, the lineshape appears to be more antisymmetric, whilst around the Py FMR, the hybrid mode appears to be more symmetric. Such a phase evolution is contained in the Eq. 1 and is not a fit parameter. Figure 2b is an example fitting result of a signal trace at 6 GHz. The fittings nicely reproduce the lineshapes arising from the coupled YIG PSSW modes and the Py FMR, including the phase evolution across the involved PSSW modes (n). Our model allows extracting the YIG and Py magnon dissipation rates, \(\Delta H_\text {YIG}\) = 1.8 Oe, \(\Delta H_\text {Py}\) = 43.3 Oe, and the coupling strength: g = 18.7 Oe. In the frequency domain, these values correspond to \(g/2\pi = 90\) MHz, \(\kappa _\text {YIG}/2\pi = 6\) MHz, and \(\kappa _\text {Py}/2\pi = 308\) MHz. The numbers satisfy the condition for the MIT effect: \(\Delta H_\text {YIG}< g < \Delta H_\text {Py}\).
The YIG/Py interfacial exchange coupling can be also found from the \(H^\text {Py}_\text {FMR}\) shift comparing to the YIG/SiO\(_2\)/Py reference sample. As shown in Fig. 1b, the Py resonance occurs at a higher field when Py is in direct contact with YIG due to the interfacial exchange coupling. The increase of \(H^\text {Py}_\text {FMR}\) suggests that the YIG/Py interface induces a negative effective field onto Py, which agrees well with the antiferromagnetic coupling in the previous reports30,33. We find a resonance offset of \(H^\text {Py}_\text {FMR,ofst}=0.17\) kOe from Fig. 1b, which further yields a fieldlike coupling strength from the interfacial exchange33, \(g =H^\text {Py}_\text {FMR,ofst}\times 0.9\sqrt{M_\text {Py}t_\text {Py}/M_\text {YIG}t_\text {YIG}}\). Taking \(M_\text {YIG}=1.97\) kOe, \(M_\text {Py}=10\) kOe, \(t_\text {Py}=10\) nm and \(t_\text {YIG}=3\) \(\it \upmu\)m, we estimate \(g = 19.8\) Oe. This value is in good agreement with that obtained earlier from the MIT effect.
Figure 2c,d compare the experimental and theoretical spin-wave dispersion using the total amplitude signal (\(\sqrt{X^2+Y^2}\)), whilst the individual channels, X and Y, as well as the corresponding theoretical plots, are included in the SM, Fig. S3. To better analyze the hybrid PSSW modes, we show the zoom-in scan between 5.7 and 6.3 GHz and 0.2 to 0.9 kOe in Fig. 2e,f, which covers the Kittel dispersion of the Py. We clearly identify the distinct PSSW modes strongly “chopping” the Py FMR line. In particular, the Py resonance is attenuated to nearly the background level (non-absorption condition) at the PSSW resonance dips.
The same measurements are also performed for the reference samples, YIG/SiO\(_2\)/Py and YIG/Cu/Py, as summarized in the SM, Fig. S4. Despite the observation of the YIG and Py FMR modes, we do not measure any signal of the hybrid PSSW modes, reconfirming that the excitation of the PSSW modes are primarily via the interfacial exchange coupling, rather than the dipolar interactions.
(a) The Re[\(V_\text {O}\)] signal at a representative frequency window (5.85–6.1 GHz) for the 10-nm-Py sample. b YIG PSSW lineshape (12 mode series near the Py resonance are labeled and analyzed, n = 32–43) after subtracting the Py resonance profile. The highlighted section is an example series at n = 39. (c) Resonance field, \(H^\text {YIG}_\text {PSSW}\) of the PSSW series and the \(H^\text {Py}_\text {FMR}\) envelope. The shaded area reflects the Py linewidth. (d) The extracted YIG PSSW linewidth \(\Delta H_\text {YIG}\) versus the \(\Delta H_\text {res}\) at each frequency and for all the PSSW series.
To further examine the detuning range and its characteristics, we separate the Py resonance envelope with the YIG PSSW modes. Such analysis can be made via fitting either the raw Re[\(V_\text {O}\)] or Im[\(V_\text {O}\)] data. Figure 3a shows the raw Re[\(V_\text {O}\)] signal of the hybrid modes at a representative frequency window (5.85–6.1 GHz) for the 10-nm-Py sample. After subtracting the Py resonance profile (details are in the SM, Fig. S5), we can fit each PSSW series (labeled \(n =\) 32–43) to a phase-shifted Lorentzian function yielding the resonance and linewidth for each PSSWs, as shown in Fig. 3b (where the highlighted section shows an example series at \(n = 39\)). We define a “resonance distance”, \(\Delta H_\text {res}\) = \([H^\text {YIG}_\text {PSSW} - H^\text {Py}_\text {FMR}]\), which represents their frequency detuning and the coupling efficiency.
Figure 3c shows the resonance field \(H^\text {YIG}_\text {PSSW}\) of the PSSW series (thin lines, from \(n =\) 32–43) comparing to the \(H^\text {Py}_\text {FMR}\) (single thick line). The shaded area indicates the Py linewidth, which is centered at the \(H^\text {Py}_\text {FMR}\) and is also much enhanced as compared to the case without the mode coupling (in the YIG/SiO\(_2\)/Py sample). Next, we plot the \(\Delta H_\text {res}\) at each frequency and for all the PSSW series with the corresponding YIG PSSW linewidth, \(\Delta H_\text {YIG}\), in Fig. 3d. We clearly observe a modulation effect of the YIG linewidth, \(\Delta H_\text {YIG}\), from \(\sim\) 2 Oe to \(\sim\) 10 Oe, spanning across the magnon–magnon coupling regime. This observation provides strong evidence that the MIT linewidth is broadened due to the additional energy dissipation by coupling the YIG PSSW modes to the Py FMR mode, also known as the Purcell regime2,3,11. From the theoretical model in Eq. 1, we obtain a relationship between the YIG linewidth broadening due to a finite g and the overlapped resonance:
where the derivation is included in the SM. Since the MIT regime is within a relatively narrow frequency window from 5.7 to 6.6 GHz, we take the average of the Py linewidth within this frequency window, as \(\Delta H_\text {Py} = 60 \pm 8\) Oe from Fig. 3c. For YIG, we take the same linewidth as in Fig. 2b, \(\Delta H_{\text {YIG},j} = 1.8\) Oe, therefore leaving g as the only fitting parameter. The best fit yields \(g = 17.7 \pm 1.2\) Oe, with a fitting curve indicated in Fig. 3d, dashed line. This value agrees with the lineshape fitting results of 18.7 Oe as discussed above.
Finally, the observed multiple PSSW modes and their coupling to a “magnonic cavity” are similar to the multi-mode coupling in the magnon–photon system50, in which the profiles and properties of each PSSW mode are greatly modified as compared to the free-space conditions. We envisage that a stronger coupling condition may be fulfilled by combining an appropriately designed optical cavity such as the whispering gallery modes24, or replacing the Py with a low damping ferromagnetic material with reduced dissipation rate30.
Conclusion
In summary, we report the observation of the magnetically-induced transparency in YIG/Py bilayers exhibiting magnon-magnon coupling. The use of the thin-film YIG system shows great potential in practical applications. The series of standing waves in YIG may allow to build an evenly distributed resonance array in a single YIG device, which may lead to relevant applications such as memory and comb generation[51,52,53]. In addition, compared with the so-far widely used hybrid magnonic systems that utilize the ferromagnetic resonances, our results pave the way towards building more complex hybrid systems with spin-waves. Our measurement is achieved via a simultaneous and stroboscopic detection of the coupled magnetization dynamics using a single wavelength, therefore avoids the possible artifacts due to multiple probes. Our work, performed in a planar structure as opposed to 3D cavities, also paves the way towards solving strong magnon–magnon couplings by the state-of-the-art spin-orbitronic toolkits54,55, involving emerging materials such as antiferromagnets56,57,58, 2D monolayers59,60,61,62, and topological insulators63,64.
References
Lachance-Quirion, D., Tabuchi, Y., Gloppe, A., Usami, K. & Nakamura, Y. Hybrid quantum systems based on magnonics. Appl. Phys. Exp. 12, 070101 (2019).
Harder, M., Hu, C. -M. Cavity Spintronics: an early review of recent progress in the study of magnon–photon level repulsion. in Solid State Physics, Vol. 70 (eds Stamps, R. & Camley R.) 47–121 (Academic Press, 2018).
Bhoi, B., Kim, S. -K. Photon-magnon coupling: historical perspective, status, and future directions. in Solid State Physics, Vol. 69 (eds Stamps, R. & Schultheiss, H.) 1–77 (Academic Press, 2019).
Li, Y., Zhang, W., Tyberkevych, V., Kwok, W. K., Hoffmann, A., Novosad, V. Hybrid magnonics: physics, circuits and applications for coherent information processing. arXiv: 2006.16158
Tabuchi, Y. et al. Coherent coupling between a ferromagnetic magnon and a superconducting qubit. Science 349, 405 (2015).
McKenzie-Sell, L. et al. Low-impedance superconducting microwave resonators for strong coupling to small magnetic mode volumes. Phys. Rev. B 99, 140414 (2019).
Li, Y. et al. Strong coupling between magnons and microwave photons in on-chip ferromagnet-superconductor thin-film devices. Phys. Rev. Lett. 123, 107701 (2019).
Hou, J. T. & Liu, L. Strong coupling between microwave photons and nanomagnet magnons. Phys. Rev. Lett. 123, 107702 (2019).
Huebl, H. et al. High cooperativity in coupled microwave resonator ferrimagnetic insulator hybrids. Phys. Rev. Lett. 111, 127003 (2013).
Bai, L. et al. Spin pumping in electrodynamically coupled magnon–photon systems. Phys. Rev. Lett. 114, 227201 (2015).
Zhang, X., Zou, C.-L., Jiang, L. & Tang, H. X. Strongly coupled magnons and cavity microwave photons. Phys. Rev. Lett. 113, 156401 (2014).
Zhang, X. et al. Magnon dark modes and gradient memory. Nat. Commun. 6, 8914 (2015).
Cao, Y., Yan, P., Huebl, H., Goennenwein, S. T. B. & Bauer, G. E. W. Exchange magnon-polaritons in microwave cavities. Phys. Rev. B 91, 094423 (2015).
Harder, M. et al. Level attraction due to dissipative magnon–photon coupling. Phys. Rev. Lett. 121, 137203 (2018).
Bhoi, B. et al. Abnormal anticrossing effect in photon-magnon coupling. Phys. Rev. B 99, 134426 (2019).
Winchester, M. N., Norcia, M. A., Cline, J. R. K. & Thompson, J. K. Magnetically induced optical transparency on a forbidden transition in strontium for cavity-enhanced spectroscopy. Phys. Rev. Lett. 118, 263601 (2017).
Zhang, D., Luo, X.-Q., Wang, Y.-P., Li, T.-F. & You, J. Q. Observation of the exceptional point in cavity magnon-polaritons. Nat. Commun. 8, 1368 (2017).
Tabuchi, Y. et al. Hybridizing ferromagnetic magnons and microwave photons in the quantum limit. Phys. Rev. Lett. 113, 083603 (2014).
Kikkawa, T. et al. Magnon polarons in the spin Seebeck effects. Phys. Rev. Lett. 117, 207203 (2016).
Zhang, X., Zou, C.-L., Jiang, L. & Tang, H. X. Cavity magnomechanics. Sci. Adv. 2, e1501286 (2016).
Bai, L., Harder, M., Hyde, P., Zhang, Z. & Hu, C. M. Cavity mediated manipulation of distant spin currents using a cavity-magnon-polariton. Phys. Rev. Lett. 118, 217201 (2017).
Andrich, P. et al. Long-range spin wave mediated control of defect qubits in nanodiamonds. NPJ Quantum Inf. 3, 28 (2017).
Osada, A. et al. Cavity optomagnonics with spin-orbit coupled photons. Phys. Rev. Lett. 116, 223601 (2016).
Zhang, X., Zhu, N., Zou, C.-L. & Tang, H. X. Optomagnonic whispering gallery microresonators. Phys. Rev. Lett. 117, 123605 (2016).
Hisatomi, R. et al. Bidirectional conversion between microwave and light via ferromagnetic magnons. Phys. Rev. B 93, 174427 (2016).
Haigh, J. A., Nunnenkamp, A., Ramsay, A. J. & Ferguson, A. J. Triple-resonant Brillouin light scattering in magneto-optical cavities. Phys. Rev. Lett. 117, 133602 (2016).
Kirilyuk, A., Kimel, A. V. & Rasing, Th. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 82, 2731 (2010).
Li, J., Zhu, S. Y. & Agarwal, G. S. Magnon-poton-phonon entanglement in cavity magnomechanics. Phys. Rev. Lett. 121, 203601 (2018).
Lachance-Quirion, D. et al. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 367, 425 (2020).
Klingler, S. et al. Spin-torque excitation of perpendicular standing spin waves in coupled YIG/Co heterostructures. Phys. Rev. Lett. 120, 127201 (2018).
Chen, J. et al. Strong interlayer magnon–magnon coupling in magnetic metal–insulator hybrid nanostructures. Phys. Rev. Lett. 120, 217202 (2018).
Qin, H., Hamalainen, S. J. & van Dijken, S. Exchange-torque-induced excitation of perpendicular standing spin waves in nanometer-thick YIG films. Sci. Rep. 8, 5755 (2018).
Li, Y. et al. Coherent spin pumping in a strongly coupled magnon–magnon hybrid system. Phys. Rev. Lett. 124, 117202 (2020).
Kruglyak, V. V., Demokritov, S. O. & Grundler, D. Magnonics. J. Phys. D Appl. Phys. 43, 264001 (2010).
An, K. et al. Coherent long-range transfer of angular momentum between magnon Kittel modes by phonons. Phys. Rev. B 101, 060407(R) (2020).
Miroshnichenko, A. E., Flach, S. & Kivshar, Y. S. Fano resonance in nanoscale structures. Rev. Mod. Phys. 82, 2257 (2010).
Limonov, M. F., Rybin, M. V., Poddubny, A. N. & Kivshar, Y. S. Fano resonances in photonics. Nat. Photonics 11, 543 (2017).
Peng, B., Ozdemir, S. K., Chen, W., Nori, F. & Yang, L. What is and what is not electromagnetically induced transparency in whispering-gallery microcavities. Nat. Commun. 5, 5082 (2014).
Weis, S. et al. Optomechanically induced transparency. Science 330, 1520 (2010).
Safavi-Naeini, A. H. et al. Electromagnetically induced transparency and slow light with optomechanics. Nature 472, 69 (2011).
Yoon, S., Liu, J. & McMichael, R. D. Phase-resolved ferromagnetic resonance using a heterodyne detection method. Phys. Rev. B 93, 144423 (2016).
Li, Y. et al. Simultaneous optical and electrical spin-torque magnetometry with phase-sensitive detection of spin precession. Phys. Rev. Appl. 11, 034047 (2019).
Li, Y. et al. Optical detection of phase-resolved ferromagnetic resonance in epitaxial FeCo thin films. IEEE Trans. Magn. 55, 6100605 (2019).
Schlömann, E. Generation of spin waves in nonuniform magnetic field. I. Conversion of electromagnetic power into spinwave power and vice versa. J. Appl. Phys. 35, 159 (1964).
Wigen, P. E., Kooi, C. F., Shanabarger, M. R. & Rossing, T. D. Dynamic pinning in thin-film spin-wave resonance. Phys. Rev. Lett. 9, 206 (1962).
Kruglyak, V. V. et al. Formation of the band spectrum of spin waves in 1D magnonic crystals with different types of interfacial boundary conditions. J. Phys. D Appl. Phys. 50, 094003 (2017).
Verba, R., Tiberkevich, V. & Slavin, A. Spin-wave transmission through an internal boundary: beyond the scalar approximation. Phys. Rev. B 101, 144430 (2020).
Poimanov, V. D., Kuchko, A. N. & Kruglyak, V. V. Emission of coherent spin waves from a magnetic layer excited by a uniform microwave magnetic field. J. Phys. D Appl. Phys. 52, 135001 (2019).
Poimanov, V. D., Kuchko, A. N. & Kruglyak, V. V. Magnetic interfaces as sources of coherent spin waves. Phys. Rev. B 98, 104418 (2018).
Zhang, X., Zou, C., Jiang, L. & Tang, H. X. Superstrong coupling of thin film magnetostatic waves with microwave cavity. J. Appl. Phys. 119, 023905 (2016).
Sundaresan, N. M. et al. Beyond strong coupling in a multimode cavity. Phys. Rev. X 5, 021035 (2015).
Moores, B. A., Sletten, L. R., Viennot, J. J. & Lehnert, K. W. Cavity quantum acoustic device in the multimode strong coupling regime. Phys. Rev. Lett. 120, 227701 (2018).
Kostylev, N., Goryachev, M. & Tobar, M. E. Superstrong coupling of a microwave cavity to yttrium iron garnet magnons. Appl. Phys. Lett. 108, 062402 (2016).
Zhang, W. et al. Spin pumping and inverse spin Hall effects—insights for future spin-orbitronics. J. Appl. Phys. 117, 172610 (2015).
Ramaswamy, R., Lee, J. M., Cai, K. & Yang, H. Recent advances in spin-orbit torques: moving towards device applications. Appl. Phys. Rev. 5, 031107 (2018).
Baltz, V. et al. Antiferromagnetic spintronics. Rev. Mod. Phys. 90, 015005 (2018).
Zhang, W. & Krishnan, K. M. Epitaxial exchange-bias systems: from fundamentals to future spin-orbitronics. Mater. Sci. Eng. R Rep. 105, 1–20 (2016).
Liensberger, L. et al. Exchange-enhanced ultrastrong magnon–magnon coupling in a compensated ferrimagnet. Phys. Rev. Lett. 123, 117204 (2019).
MacNeill, D. et al. Control of spinorbit torques through crystal symmetry in WTe2/ferromagnet bilayers. Nat. Phys. 13, 300 (2017).
Zhang, W. et al. Spin transfer torques in permalloy on monolayer MoS2. APL Mater. 4, 032302 (2016).
Li, Y. et al. Gate-tuned temperature in a hexagonal boron nitride-encapsulated 2-D semiconductor device. IEEE Trans. Electron Devices 65, 4068 (2018).
Zhang, X. Characterization of layer number of two-dimensional transition metal diselenide semiconducting devices using Si-peak analysis. Adv. Mater. Sci. Eng. 2019, 7865698 (2019).
Mellnik, A. R. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449 (2014).
Li, P. et al. Magnetization switching using topological surface states. Sci. Adv. 5, eaaw3415 (2019).
Acknowledgements
W.Z. acknowledges useful discussions with V. Tyberkevych and A. Slavin. This work, including apparatus buildup, experimental measurements, and data analysis, was supported by AFOSR under Grant No. FA9550-19-1-0254, National Science Foundation under Grants No. DMR-1808892 and ECCS-1933301 . Work at Argonne, including sample preparation, was supported by U.S. DOE, Office of Science, Materials Sciences and Engineering Division. M.H. acknowledges the Michigan Space Grant Consortium Student Fellowship for financial support.
Author information
Authors and Affiliations
Contributions
Y.L. and W.Z. conceived the idea. Y.X., M.H., R.B., W.Z. performed the experiment. J.S., X.Z., and Y.L. developed the theoretical model. J.P., A.H., and V.N. participated in the thin-film sample fabrication. G.S. and H.Q. participated in the microwave measurement. Y.L., X.Z., J.S., and W.Z. prepared the figures and manuscript draft. All authors discussed the results and participated in the writing and finalizing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xiong, Y., Li, Y., Hammami, M. et al. Probing magnon–magnon coupling in exchange coupled Y\(_3\)Fe\(_5\)O\(_{12}\)/Permalloy bilayers with magneto-optical effects. Sci Rep 10, 12548 (2020). https://doi.org/10.1038/s41598-020-69364-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-69364-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.