Abstract
Surface plasmon polaritons (SPPs) are collective excitations of free electrons propagating along a metal-dielectric interface. Although some basic quantum properties of SPPs, such as the preservation of entanglement, the wave-particle duality of a single plasmon, the quantum interference of two plasmons, and the verification of entanglement generation, have been shown, more advanced quantum information protocols have yet to be demonstrated with SPPs. Here, we experimentally realize quantum state teleportation between single photons and SPPs. To achieve this, we use polarization-entangled photon pairs, coherent photon–plasmon–photon conversion on a metallic subwavelength hole array, complete Bell-state measurements and an active feed-forward technique. The results of both quantum state and quantum process tomography confirm the quantum nature of the SPP mediated teleportation. An average state fidelity of \(0.889\pm 0.004\) and a process fidelity of \(0.820\pm 0.005\), which are well above the classical limit, are achieved. Our work shows that SPPs may be useful for realizing complex quantum protocols in a photonic-plasmonic hybrid quantum network.
Similar content being viewed by others
Introduction
The hybrid light-matter nature of surface plasmon polaritons (SPPs) allows light to be confined below the diffraction limit, opening up the possibility of subwavelength photonic device integration1. The quantum properties of SPPs originate from quantized surface plasma waves, and several quantum models have been proposed to describe the electromagnetic field of a plasmon2,3. The quantization of SPPs has motivated many researchers to explore the fundamental quantum phenomena associated with them, for example, plasmon-assisted transmission of entangled photons4,5, single-plasmon state generation and detection6,7, quantum statistics and interference in plasmonic systems8,9,10,11,12,13, quantum logic operations14, anti-coalescence of SPPs in the presence of losses15 and quantum plasmonic N00N state for quantum sensing16. For reviews, see Ref.17,18. Recently, some quantum properties of new plasmonic metamaterials have also been explored, such as coherent perfect absorption in plasmonic metamaterials with entangled photons19, testing hyper-complex quantum theories with negative refractive index metamaterials20 and the active control of plasmonic metamaterials operating in the quantum regime21.
These works motivate us to study and utilize the quantum properties of SPPs in more advanced quantum information protocols. Quantum teleportation uses entanglement as a resource to faithfully transfer unknown quantum states between distant nodes. Ever since it was first introduced by Bennett et al.22 and experimentally realized using photonic qubits23,24, quantum teleportation has become the essential protocol for establishing worldwide quantum networks25,26. The teleportation distance has increased significantly over the last two decades27,28,29,30,31 and has recently been successfully extended to more than a thousand kilometres from the ground to a satellite32. To build a quantum network with more functionalities, various physical systems are required with individual advantages in terms of transferring and processing the quantum state.
Results
The conceptual scheme of SPP mediated quantum teleportation
We experimentally realize the quantum state teleportation of a single photon to a single SPP, which is a single qubit consisting of collective electronic excitations typically involving \({\sim }10^{6}\) electrons17. Our scheme is based on three qubits, which is first proposed by Popescu33 and realized in experiment by Boshi et al.24. The conceptual framework of our experiment with the three-qubit scheme is shown in Fig. 1a. The entanglement between qubits 1 (Q1) and 2 (Q2), serving as the quantum channel, is generated from the entangled photon-pair source and distributed to Alice and Bob. An input state of qubit 0 (Q0) is sent to Alice. Alice performs a Bell-state measurement (BSM)24, projecting Q0 and Q1 randomly into one of the four Bell states, each with a probability of 25%. Then, the outcomes of the BSM are sent to Bob through a classical communication (CC) channel. Q2 is sent to a subwavelength hole array sample patterned on a gold film at Bob’s site to facilitate the photon–SPP–photon conversion34. There, the quantum state of Q2 is transferred to qubit 3 (Q3), carried by a single SPP. This SPP propagates along the surface of the sample and subsequently couples to an optical photon (Q4), which radiates towards detectors in the far field. According to the outcomes of the BSM, the corresponding unitary transformations (UTs) are applied to Q4. Finally, we perform quantum state tomography (QST)35,36 on Q4 and verify whether the quantum state teleportation from a single photon to a single SPP is successful by evaluating the quantum state fidelities of Q4 to Q0 and the quantum process fidelity of the whole procedure.
Subwavelength hole array and its characterization
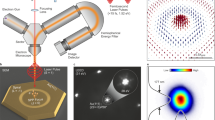
Figure 1b shows a scanning electron microscopy (SEM) image of the subwavelength hole array used in our experiment. The gold film is perforated over a square area of \(189\times 189\, \upmu \hbox {m}^2\) with periodic hole arrays by using a focused ion beam. The hole diameter and the period are 200 nm and 700 nm, respectively. The thickness of our metal film is 150-nm. Although the hole array reduces the direct photon transmission, it allows resonant excitation of the SPP34.
The transmission spectrum of our sample is shown in Fig. 1c and has a peak centred at approximately 809 nm with a full width at half maximum (FWHM) of \({\sim }70\hbox { nm}\). The peak transmittance of the sample at 809 nm is approximately 0.8%. The extraordinary optical transmission (EOT) observed in the subwavelength hole arrays is a typical resonant tunneling phenomenon which results from the constructive interference when the photons go through the holes34,37. Compared with other works4,34, the total transmittance of our sample is slightly lower. The reason is that the transmission spectrum is very sensitive to the geometrical parameters of the system37,38. The imperfections during the fabrication can lead to the hole shape, period of the lattice as well as thickness and smoothness of the gold film departure from the nominal settings, thus resulting in the low transmission39. Even setting the same parameters, the transmission of samples fabricated at different times has some obvious differences and is lower than 3% due to the fabrication imperfections4. However, we only utilize the frequency information, i.e. peak position, instead of the transmittance in our teleportation experiment. Although our overall transmission is smaller than 2.5%, it is still larger than the value predicted by the standard aperture theory34, which indicates that the EOT does happen in our sample. The transmission curves for different light polarizations are similar, indicating that our sample is nearly polarization-independent. The polarization insensitivity is due to the symmetry of the square lattice, as have been demonstrated in previous works38,40,41. A numerical calculation based on the geometry of the array and the wavevector matching shows that this peak is associated with the (\(\pm 1,\pm 1\)) SPP modes at the glass-metal interface42. These modes can excite the SPPs propagating along the four diagonal directions. We experimentally measure the SPP propagation with a laser and a charge-coupled device (CCD), as shown in Fig. 1d. By fitting to the SPP propagation along the diagonal direction, we estimate the 1/e decay length of the plasmonic mode to be \({\sim }4.48\pm 0.50\, \upmu \hbox {m}\). See the Supplementary Information for more details on the numerical simulation, design of the hole array and characterizations of this device.
Realizing quantum teleportation between photon and SPP
Figure 1e presents a layout of our experimental setup. The entangled photon pairs are generated from spontaneous parametric down conversion, which is realized by embedding a periodically poled \(\hbox {KTiOPO}_4\) (PPKTP) crystal in a Sagnac interferometer43,44. The quantum state of photons A and B is similar to the singlet state:
which has a fidelity of approximately \(98\%\). \(|H\rangle _{A}\) (\(|V\rangle _{A}\)) denotes the horizontal (vertical) polarization state of photon A. The same notation is used for photon B. We obtain coincidence counts at a rate of approximately 100 kHz with a pump power of 20 mW.
Experimental layout of the surface plasmon polariton (SPP) mediated quantum teleportation. (a) The conceptual framework of our experiment. At Alice’s site, the input states are prepared using qubit 0 (Q0). An Einstein-Podolsky-Rosen (EPR) source generates two entangled qubits, Q1 and Q2. Q1 is sent to Alice for a Bell-state measurement (BSM)24. Q2 is sent to Bob to excite the SPP qubit, Q3. Through the photon–plasmon–photon conversion, the quantum states of the SPPs are transformed back to a photonic qubit, Q4. The outcomes of the BSM are sent to Bob using the classical communication (CC). Bob then applies a unitary transformation (UT) to Q4. As a result, the output state \(|\phi \rangle ^4_B\) is identical to \(|\phi \rangle ^0_A\); hence, teleportation is accomplished. (b) The SEM image of the subwavelength hole arrays with 200 nm diameter and 700 nm period. (c) Transmission spectrum of the hole arrays. The resonance at approximately 809 nm (dashed line) is the (\(\pm 1\),\(\pm 1\)) mode, corresponding to the SPPs propagating along the diagonal direction. (d) The far-field image shows the SPP propagation mode. The units ‘counts’ (cnts) is labelled below the colorbar. (e) Sketch of the experimental setup. The polarization-entangled source uses a type-II down-conversion Sagnac interferometer, where a \(\chi ^{(2)}\) nonlinear crystal (periodically poled \(\hbox {KTiOPO}_4\), PPKTP) is coherently pumped by 405 nm laser light from clockwise and counter-clockwise directions. The central wavelength of the entangled signal (A) and idler (B) photons is approximately 810 nm. Photon A is sent to Alice. The polarization degree of freedom (DOF) (Q0) of photon A is used for preparing the six input states. The four Bell states are constructed using the path (Q1) and polarization (Q0) DOF of photon A. Photon B is sent to Bob. The polarization of photon B (Q2) is used to excite the SPPs. After undergoing a photon–plasmon–photon conversion, the quantum state of the SPPs (Q3) is transferred back to the photon (Q4). The results of the BSM (00, 01, 10, 11) are sent to Bob by CC and subsequently used to trigger the electro-optic modulators (EOMs, \(\sigma _x\), \(\sigma _z\)) to apply the corresponding UTs (\(I, \sigma _z, \sigma _x, i\sigma _y\)). The quantum state is finally analysed through quantum state tomography (QST). HWP: half-wave plate; QWP: quarter-wave plate; BD: beam displacer; DM: dichromatic mirror; d-PBS: dual-wavelength polarizing beam splitter.
We employ the two-photon three-qubit scheme to realize the SPP mediated quantum teleportation24,29. The two-photon three-qubit scheme has the advantages that it avoids the very low detection rates caused by the simultaneous detection of three photons and allows a 100% Bell state measurement24,29,33. We note that two-photon scheme of teleportation has limitation as one can’t use this scheme to teleport the quantum state of an independent photon which comes from outside. In our experiment, photons A and B are sent to Alice and Bob through single-mode fibre (SMF), respectively. We use photon A’s polarization as Q0 and its path state as Q1. Photon B’s polarization acts as Q2. First, we swap the entanglement between Q0 and Q2 (see Eq. (1)) to Q1 and Q2. We achieve this by sending photon A through a beam displacer (BD1 in Fig. 1e), which makes the horizontal polarized component undergo a lateral displacement into the left path mode (denoted as \(|l\rangle \)) and transmits the vertically polarized component directly (denoted as \(|r\rangle \)). The two-photon (A and B) three-qubit (Q0, Q1 and Q2) state can be written as
Note that the superscripts are labelled for the qubit and the subscripts are labelled for the photon. Then, a \(45^\circ \)-oriented HWP (HWP@45\(^\circ \) in Fig. 1e) rotates the horizontal component (\(|H\rangle _A\)) to the vertical polarization (\(|V\rangle _A\)) in the left path, \(|l\rangle \). Along the right path, \(|r\rangle \), a \(90^\circ \)-oriented HWP (HWP@90\(^\circ \) in Fig. 1e) is used for phase compensation. After these two HWPs, the polarization state of photon A (qubit 0) is in \(|V\rangle \) and is factorized out. The full state is as follows:
Consequently, the initial entanglement between the polarization states of photons A and B is swapped into the path state of photon A (qubit 1) and the polarization state of photon B (qubit 2)45,46.
The combination of HWP2 and QWP2 are then used to create the polarization state to be teleported (see Sect. S5 of Supplementary Information), i.e. \(|\phi \rangle ^{0}_{A}=\alpha |H\rangle ^{0}_{A}+\beta |V\rangle ^{0}_{A}\), where \(\alpha \) and \(\beta \) are two complex numbers satisfying \(|\alpha |^2+|\beta |^2=1\). This process can be expressed as follows:
Here the polarization (Q0) and path states (Q1) of photon A are used to construct the four Bell states: \(|\Psi ^{\pm }\rangle ^{01}_A=\frac{1}{\sqrt{2}}(|V\rangle _{0}|l\rangle _{1} \pm |H\rangle _{0}|r\rangle _{1})\) and \(|\Phi ^{\pm }\rangle ^{01}_A=\frac{1}{\sqrt{2}}(|H\rangle _{0}|l\rangle _{1} \pm |V\rangle _{0}|r\rangle _{1})\). Alice realizes a complete BSM using the polarization (Q0) and path (Q1) DOF of photon A with BD2 and BD3 (see Sect. S5 of Supplementary Information for details). The outcomes of the BSM are sent from Alice to Bob via coaxial cables.
Photon B (Q2) is delayed by a 222-m-long (corresponding to a temporal delay of \({\sim }1110\) ns) SMF and then sent to Bob. At Bob’s site, Q2 is focused on the subwavelength hole arrays and converted to a single surface plasmon (Q3). As a result, we coherently transmit the quantum state of Q2 to Q3, which is carried by the single-mode collective electronic excitations of the SPP. Then, the SPP propagates along the surface of the sample and subsequently couples out to an optical photon (Q4), radiating into the far field. After the BSM is performed by Alice, the quantum state of Q4 is projected into a pure state and equals the input state \(|\phi \rangle ^{0}_{A}\) up to a local UT according to the BSM result (see Eq. (4)). The local UTs are realized with two EOMs, which perform the required \(\sigma _x\) and \(\sigma _z\) operations. Collectively, the EOMs perform the \(i\sigma _y\) operation. After these local UTs, the output state of Q4 is: \(|\phi \rangle ^{4}_{B}=\alpha |H\rangle ^{4}_{B}+\beta |V\rangle ^{4}_{B}\). Finally, we collect the photons into an SMF and perform QST on Q4.
The results of quantum state and process tomography
We prepare six input states of qubit 0: \(|H\rangle \), \(|V\rangle \), \(|D\rangle \), \(|A\rangle \), \(|R\rangle \), and \(|L\rangle \) (see Fig. 2a). Note that \(|D\rangle =(|H\rangle +|V\rangle )/\sqrt{2}\)/\(|A\rangle =(|H\rangle -|V\rangle )/\sqrt{2}\), and \(|R\rangle =(|H\rangle -i|V\rangle )/\sqrt{2}\)/\(|L\rangle =(|H\rangle +i|V\rangle )/\sqrt{2}\) stand for the diagonal/anti-diagonal linearly and right/left circularly polarized states of single photons, respectively.
Reconstructed density matrices of the six teleported states. (a) The initial prepared states are \(|H\rangle \), \(|V\rangle \), \(|D\rangle \), \(|A\rangle \), \(|R\rangle \), and \(|L\rangle \) and are indicated by coloured dots on the Bloch sphere. (b,d,f,h,j,l) Real parts of the reconstructed density matrices for the six states. (c,e,g,i,k,m) Imaginary parts of the reconstructed density matrices for the six states. The ideal density matrix is shown as the wire grid. The representative data here are for experiments with a \(|\Phi ^{+}\rangle \) Bell-state measurement outcome with SPP. The reconstructed density matrices of the six states for all four Bell-state measurement outcomes are provided in the Supplementary Information.
To characterize the quantum teleportation mediated by the SPP, we perform single-qubit QST measurements on the teleported quantum states. In Fig. 2b–m, we show the real and imaginary parts of the reconstructed density matrices for different input states. With the reconstructed density matrices, we calculate the state fidelity \(F={}_{ideal}{\left\langle \phi \right| }\rho |\phi \rangle _{ideal}\), where \(\rho \) is the reconstructed density matrix and \(|\phi \rangle _{ideal}\) is the ideal quantum state. The results of the quantum state fidelity after quantum teleportation are shown in Fig. 3. For a comparison, we present the state fidelities both without and with photon–SPP–photon conversion. We can see from Fig. 3 that all the fidelities are well above the limit of 2/3 that can be achieved using a classical strategy without employing entanglement47. By averaging the single photon fidelities over all input states, we obtain an average fidelity of \(92.67\pm 0.32\%\) (without SPP) and \(88.91\pm 0.38\%\) (with SPP) for the retrieved initial states, including active feed-forward operations, which exceed the classical limit of 2/3 by more than 81-\(\sigma \) and 58-\(\sigma \) standard deviations47. We note that the difference in the state fidelities between the cases without the SPP and with the SPP is mainly caused by: The excited SPP distorts the beam pattern and then leads to a lower contrast of the phase flip of the two EOMs. Quantitative analysis of the reduction in the achievable fidelity can be found in the Supplementary Information (Sect. S7).
Quantum state fidelities of quantum teleportation for the six different input states: \(|H\rangle \), \(|V\rangle \), \(|D\rangle \), \(|A\rangle \), \(|R\rangle \) and \(|L\rangle \) with four Bell-state measurement results: \(|\Psi ^{-}\rangle \), \(|\Psi ^{+}\rangle \), \(|\Phi ^{-}\rangle \) and \(|\Phi ^{+}\rangle \). The different BSM outcomes are denoted with different colours. (a) The fidelities measured without the SPP involved. We perform this measurement by moving the subwavelength hole array out from the setup. (b) The fidelities measured with the SPP involved. All the fidelities exceed the classical limit of 2/3 (dashed line). The error bars are calculated using a Monte Carlo routine assuming Poissonian statistics.
Results of quantum process tomography for the teleportation procedure. (a) The real part of the reconstructed process matrix \(\chi \) without the SPP (W.O. SPP). The ideal process matrix has only one nonzero component \((\chi _{ideal})_{00}\)=1, and we obtain a process fidelity of \(F_{proc}=\text {Tr}(\chi _{ideal}\chi )=(89.80\pm 0.45)\%\). (b) The real part of the reconstructed process matrix \(\chi \) with the SPP (With SPP). The process fidelity is \(F_{proc}=\text {Tr}(\chi _{ideal}\chi )=(82.01\pm 0.50)\%\). (c,d) Bloch sphere representations of the process without (W.O.) (c) and with (d) the SPP involved. The plot shows how the input states lying on the surface of the initial Bloch sphere (meshed surface) are transformed by our teleportation protocol, with the output states lying on the solid surface.
Since quantum teleportation is a quantum process, it is natural to quantitatively describe the whole process with quantum process tomography48. The reconstructed density matrices of the teleported quantum states allow us to fully characterize the teleportation procedure by quantum process tomography. We choose four input states (\(\rho _{in} = |H\rangle \langle H|, |V\rangle \langle V|, |D\rangle \langle D|, |L\rangle \langle L|\)) and their corresponding output states \(\rho _{out}\) to benchmark the process of quantum teleportation. The effect of teleportation on \(\rho _{in}\) is determined by the process matrix \(\chi \), which is defined by \(\rho _{out} = \sum _{l,k = 0}^3 \chi _{lk} \sigma _l \rho _{in} \sigma _k\), where \(\sigma _{i}\) are the Pauli matrices with \(\sigma _{0}\) being the identity operator. A perfect process matrix of quantum teleportation has only one nonzero component, \(\chi _{00}=1\), indicating that the input state is faithfully teleported without a reduction in the state fidelity. The real parts of the process matrix \(\chi \) for the two situations (without and with the SPP) are shown in Fig. 4a (without SPP) and Fig. 4b (with SPP), respectively. The quantum process fidelities, i.e. \(\mathscr {F}_{proc}=\text {Tr}(\chi _{ideal}\chi )\), for our experiment without and with the SPP are 0.898±0.005 and 0.820±0.005, respectively. These fidelities correspond to 80-\(\sigma \) and 64-\(\sigma \) violations over the classical bound of 0.531,49. A single-qubit quantum process, including quantum teleportation, can be represented graphically by a deformation of the Bloch sphere subjected to the quantum process48. As shown in Figs. 4c (without SPP) and d (with SPP), the ideal input states of Q0 are denoted as the states lying on the meshed surface of the Bloch sphere. After the photon-to-SPP quantum teleportation, the initial Bloch spheres are deformed into anisotropic ellipsoids as shown in the solid blue-yellow colour, corresponding to the final output states.
Discussion
Note that the transmission losses reduce the coincidence count rate in our experiment. Therefore, we have to increase the integration time to obtain enough coincidence counts (see Table S7 in the Supplementary Information) for obtaining statistical significance. However, the advantages of plasmonic systems are that they are very suitable for making miniaturized quantum devices. Their sizes can be reduced such that the quantum logic operations can be finished below the propagation distances before plasmons are lost14. Recently, the new techniques of material growth and structure design have helped in greatly minimize or mitigate the influence of losses on the plasmonic devices50,51,52. In some cases, the losses can provide new insights into quantum physics, such as the lossy beam splitter exhibiting fermionic anti-coalescence behavior using surface plasmons15,53.
In our present experiment, the average teleportation fidelity for the retrieved initial states is smaller for the case with SPP than that without SPP. As have been explained in Sect. S7 of the Supplementary Information, the reduction of fidelity is caused by the low contrast of feed-forward operations. With EOMs of higher extinction ratio, it is possible to improve the fidelity. In addition, the fabrication techniques can also be optimized to improve the quality of the sample and alleviate the deterioration of the light beam. We would like to elaborate on the motivation of our work from two different perspectives: 1, From a fundamental perspective: although quantum teleportation has been demonstrated with many different physical systems, to the best of our knowledge, it has never been implemented with the plasmonic system, a system consisting of \(10^6\) electrons. It would be interesting to see if the quantum teleportation could work between two systems with such dramatic particle number difference, namely one photon vs \(10^6\) electrons. 2, From the application perspective, plasmonic devices allow us to implement quantum operation with orders-of-magnitude smaller dimension14 comparing to \(\hbox {SiO}_2\) or Si integrated devices54. However, to realize more complicated quantum information protocols, such as quantum teleportation of quantum gates55 or quantum teleportation based quantum computation56 with plasmonic systems, we have to firstly experimentally verify the feasibility of quantum teleportation via plasmons. We view our work as the decisive step towards that goal, as the average state fidelity of the teleportation mediated by SPP we obtained exceeds the classical limit of 2/3 by more than 58-\(\sigma \) standard deviations, which shows the plasmonic system is robust against the reduction of fidelity.
In summary, we demonstrate faithful teleportation of quantum states from one qubit of a single photon to another qubit of an SPP. The photon-to-SPP quantum teleportation is completely characterized by quantum state and process tomography. The fidelities of the six teleported states all exceed the classical limit with tens of standard deviations. The process fidelities also exceed the classical limit with tens of standard deviations. These results conclusively confirm the quantum nature of teleportation from arbitrary unknown quantum states of a single photon to a single SPP. Our work is a further step towards exploring the fascinating quantum behaviours of SPPs. The comprehensive utilization of the quantum properties of SPPs in more advanced protocols will promote the rapid development of future quantum information processing with quantum plasmonic devices.
Data availability
The data used in current study are available from the corresponding author upon reasonable request.
References
Ozbay, E. Plasmonics: merging photonics and electronics at nanoscale dimensions. Science 311, 189–193 (2006).
Ritchie, R. H. Plasma losses by fast electrons in thin films. Phys. Rev. 106, 874–881 (1957).
Hopfield, J. J. Theory of the contribution of excitons to the complex dielectric constant of crystals. Phys. Rev. 112, 1555–1567 (1958).
Altewischer, E., van Exter, M. P. & Woerdman, J. P. Plasmon-assisted transmission of entangled photons. Nature 418, 304–306 (2002).
Fasel, S. et al. Energy-time entanglement preservation in plasmon-assisted light transmission. Phys. Rev. Lett. 94, 110501 (2005).
Akimov, A. et al. Generation of single optical plasmons in metallic nanowires coupled to quantum dots. Nature 450, 402–406 (2007).
Heeres, R. W., Kouwenhoven, L. P. & Zwiller, V. Quantum interference in plasmonic circuits. Nature Nanotech. 8, 719–722 (2013).
Kolesov, R. et al. Wave-particle duality of single surface plasmon polaritons. Nature Phys. 5, 470–474 (2009).
Di Martino, G. et al. Quantum statistics of surface plasmon polaritons in metallic stripe waveguides. Nano Lett. 12, 2504–2508 (2012).
Di Martino, G. et al. Observation of quantum interference in the plasmonic Hong-Ou-Mandel effect. Phys. Rev. Appl. 1, 034004 (2014).
Cai, Y.-J. et al. High-visibility on-chip quantum interference of single surface plasmons. Phys. Rev. Appl. 2, 014004 (2014).
Fakonas, J. S., Lee, H., Kelaita, Y. A. & Atwater, H. A. Two-plasmon quantum interference. Nature Photon 8, 317–320 (2014).
Dheur, M.-C. et al. Single-plasmon interferences. Sci. Adv. 2, e1501574 (2016).
Wang, S. M. et al. A 14\(\times \)14 \(\mu \)m\(^{\rm 2}\) footprint polarization-encoded quantum controlled-NOT gate based on hybrid waveguide. Nature Commun. 7, 11490 (2016).
Vest, B. et al. Anti-coalescence of bosons on a lossy beam splitter. Science 356, 1373 (2017).
Chen, Y. et al. Quantum plasmonic n00n state in a silver nanowire and its use for quantum sensing. Optica 5, 1229–1235 (2018).
Tame, M. S. et al. Quantum plasmonics. Nature Phys. 9, 329–340 (2013).
Ming, L., Yang, C., Guang-Can, G. & Xi-Feng, R. Recent progress of the application of surface plasmon polariton in quantum information processing. Acta Phys. Sin. 66, 144202 (2017).
Altuzarra, C. et al. Coherent perfect absorption in metamaterials with entangled photons. ACS Photon. 4, 2124–2128 (2017).
Procopio, L. M. et al. Single-photon test of hyper-complex quantum theories using a metamaterial. Nat. Commun. 8, 15044 (2017).
Uriri, S. A. et al. Active control of a plasmonic metamaterial for quantum state engineering. Phys. Rev. A 97, 053810 (2018).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Boschi, D., Branca, S., De Martini, F., Hardy, L. & Popescu, S. Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 80, 1121–1125 (1998).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead. Science 362, eaam9288 (2018).
Marcikic, I., de Riedmatten, H., Tittel, W., Zbinden, H. & Gisin, N. Long-distance teleportation of qubits at telecommunication wavelengths. Nature 421, 509–513 (2003).
Ursin, R. et al. Communications: Quantum teleportation across the danube. Nature 430, 849 (2004).
Jin, X.-M. et al. Experimental free-space quantum teleportation. Nature Photon. 4, 376–381 (2010).
Yin, J. et al. Quantum teleportation and entanglement distribution over 100-kilometre free-space channels. Nature 488, 185–188 (2012).
Ma, X.-S. et al. Quantum teleportation over 143 kilometres using active feed-forward. Nature 489, 269–273 (2012).
Ren, J.-G. et al. Ground-to-satellite quantum teleportation. Nature 549, 70–73 (2017).
Popescu, S. An optical method for teleportation. arXiv: 9501020 (1995).
Ebbesen, T. W., Lezec, H. J., Ghaemi, H. F., Thio, T. & Wolff, P. A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 391, 667–669 (1998).
Leonhardt, U. Quantum-state tomography and discrete wigner function. Phys. Rev. Lett. 74, 4101–4105 (1995).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Martín-Moreno, L. et al. Theory of extraordinary optical transmission through subwavelength hole arrays. Phys. Rev. Lett. 86, 1114–1117 (2001).
Koerkamp, K. J. K., Enoch, S., Segerink, F. B., van Hulst, N. F. & Kuipers, L. Strong influence of hole shape on extraordinary transmission through periodic arrays of subwavelength holes. Phys. Rev. Lett. 92, 183901 (2004).
Altewischer, E. Sub-wavelength hole arrays, surface plasmons and quantum entanglement. Ph.D. thesis, Universiteit Leiden (2005).
Ren, X.-F., Guo, G.-P., Huang, Y.-F., Wang, Z.-W. & Guo, G.-C. Influence of unsymmetrical periodicity on extraordinary transmission through periodic arrays of subwavelength holes. Appl. Phys. Lett. 90, 161112 (2007).
Ren, X.-F. et al. Polarization properties of subwavelength hole arrays consisting of rectangular holes. Appl. Phys. B 91, 601–604 (2008).
Ghaemi, H. F., Thio, T., Grupp, D. E., Ebbesen, T. W. & Lezec, H. J. Surface plasmons enhance optical transmission through subwavelength holes. Phys. Rev. B 58, 6779–6782 (1998).
Kim, T., Fiorentino, M. & Wong, F. N. C. Phase-stable source of polarization-entangled photons using a polarization sagnac interferometer. Phys. Rev. A 73, 012316 (2006).
Fedrizzi, A., Herbst, T., Poppe, A., Jennewein, T. & Zeilinger, A. A wavelength-tunable fiber-coupled source of narrowband entangled photons. Opt. Express 15, 15377–15386 (2007).
Giacomini, S., Sciarrino, F., Lombardi, E. & De Martini, F. Active teleportation of a quantum bit. Phys. Rev. A 66, 030302 (2002).
Takeda, S., Mizuta, T., Fuwa, M., van Loock, P. & Furusawa, A. Deterministic quantum teleportation of photonic quantum bits by a hybrid technique. Nature 500, 315–318 (2013).
Massar, S. & Popescu, S. Optimal extraction of information from finite quantum ensembles. Phys. Rev. Lett. 74, 1259–1263 (1995).
Nielsen, M. .A. & Chuang, I. .L. Quantum Computation and Quantum Information (Cambridge University Press, UK, 2010).
Nielsen, M. A. A simple formula for the average gate fidelity of a quantum dynamical operation. Phys. Lett. A 303, 249–252 (2002).
Boriskina, S. V. et al. Losses in plasmonics: from mitigating energy dissipation to embracing loss-enabled functionalities. Adv. Opt. Photon. 9, 775–827 (2017).
Baburin, A. S. et al. Silver-based plasmonics: golden material platform and application challenges. Opt. Mater. Express 9, 611–642 (2019).
Haffner, C. et al. Low-loss plasmon-assisted electro-optic modulator. Nature 556, 483–486 (2018).
Faccio, D. Plasmons that won’t stick. Science 356, 1336–1337 (2017).
Wang, J., Sciarrino, F., Laing, A. & Thompson, M. G. Integrated photonic quantum technologies. Nature Photon. 1, 1–12 (2019).
Gao, W.-B. et al. Teleportation-based realization of an optical quantum two-qubit entangling gate. Proc. Nat. Acad. Sci. USA. 107, 20869–20874 (2010).
Gottesman, D. & Chuang, I. L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390–393 (1999).
Acknowledgements
The authors thank Tong Wu for help in designing the optical circuitry of the BSM. This work was supported by the National Key Research and Development Program of China (Nos. 2017YFA0303704 and 2019YFA0308704), the National Natural Science Foundation of China (Nos. 11674170 and 11690032), NSFC-BRICS (No. 61961146001), the Natural Science Foundation of Jiangsu Province (No. BK20170010), the Leading-edge technology Program of Jiangsu Natural Science Foundation (No. BK20192001), the program for Innovative Talents and Entrepreneur in Jiangsu, and the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Contributions
X.-H.J., P.C. and K.-Y.Q. contributed equally to this work. X.-H.J., P.C., K.-Y.Q. and X.-S.M. designed and performed the experiment. X.-H.J., K.-Y.Q. and S.-Q.X. fabricated and characterized the SPP samples with the help of Y.-B.X. P.C. and X.-H.J. designed and tested the BSM module. Z.-Z.C. designed and characterized the photon source. X.-H.J. and K.-Y.Q. set up the SPP module and carried out classical measurements for the sample. X.-H.J. analysed the data. X.-H.J., P.C., K.-Y.Q. and X.-S.M. wrote the manuscript with input from all authors. S.-N.Z. and X.-S.M. conceived the work and supervised the whole project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jiang, XH., Chen, P., Qian, KY. et al. Quantum teleportation mediated by surface plasmon polariton. Sci Rep 10, 11503 (2020). https://doi.org/10.1038/s41598-020-67773-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-67773-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.