Abstract
The Josephson junction (JJ) is the corner stone of superconducting electronics and quantum information processing. While the technology for fabricating low Tc JJ is mature and delivers quantum circuits able to reach the “quantum supremacy”, the fabrication of reproducible and low-noise high-Tc JJ is still a challenge to be taken up. Here we report on noise properties at RF frequencies of recently introduced high-Tc Josephson nano-junctions fabricated by mean of a Helium ion beam focused at sub-nanometer scale on a YBa2Cu3O7 thin film. We show that their current-voltage characteristics follow the standard Resistively-Shunted-Junction (RSJ) circuit model, and that their characteristic frequency fc = (2e/h)IcRn reaches ~300 GHz at low temperature. Using the “detector response” method, we evidence that the Josephson oscillation linewidth is only limited by the thermal noise in the RSJ model for temperature ranging from T ~ 20 K to 75 K. At lower temperature and for the highest He irradiation dose, the shot noise contribution must also be taken into account when approaching the tunneling regime. We conclude that these Josephson nano-junctions present the lowest noise level possible, which makes them very promising for future applications in the microwave and terahertz regimes.
Similar content being viewed by others
Introduction
The astonishing recent evolution of Information and Communication Technologies (ICTs) is based on an accurate control of quantum properties of semiconductors at sub-micron scales. As some limitations appear, new paradigms emerge to further improve the performances of ICT devices, based on coherent quantum states and nano-scale engineering. Superconductivity is a very interesting platform which provides robust quantum states that can be entangled and controlled to realize quantum computation and simulation1, or classical computation at very high speed using the so called SFQ (Single Flux Quantum) logic2. This platform can also be used to make detectors of electromagnetic fields and photons operating at the quantum limit, i.e. with unsurpassed sensitivity and resolution. These quantum sensors can be used for classical or quantum communications3, THz waves detection and imaging4, sensitive high frequency magnetic fields measurements5,6. Impressive results have been achieved in the recent years with devices based on Low critical Temperature (Tc) Superconductors (LTS) working at liquid helium temperature, and well below for Quantum Computing.
The main building block of this superconducting electronics is the Josephson Junction (JJ), a weak link between two superconducting reservoirs. While the technology for LTS JJ of typically 1 μm in size required for complex systems is mature2, other ways are explored to downsize the JJ using Carbon Nano-Tubes7, Copper nanowires8 or LaAlO3/SrTiO3 interfaces9 for examples. The complexity and the cost of the needed cryogenic systems are clearly obstacles for large scale applications of such devices. High-Tc superconductors (HTS) operating at moderate cryogenic temperature (≤40 K) appear as an interesting alternative solution, provided reliable JJ are available.
Different routes to make HTS JJ with suitable and reproducible characteristics are explored10,11. One of them relies on the extreme sensitivity of HTS materials such as YBa2Cu3O7 (YBCO) to disorder, which first reduces Tc and then makes it insulating. High energy ion irradiation (HEII) have been used to introduce disorder in YBCO thin films through e-beam resist masks with apertures at the nanometric scale (20–40 nm), to make JJ12,13,14 and arrays15,16,17 with interesting high frequencies properties, from microwaves to THz ones. Recently, Cybart et al. successfully used a Focused Helium Ion Beam (He FIB) to locally disorder YBCO thin films and make JJ18. In this technique, a 30 keV He+ ion beam of nominal size 0.7 nm is scanned onto a thin film surface to induce disorder. It has been used to engineer nanostructures in two-dimensional (2D) materials19,20,21, magnetic ones22 or to make plasmonic nano-antennas for instance23. Superconducting nano-structures and JJ have been fabricated with cuprate superconductors24,25,26,27,28, MgB229 and pnictides30. While mainly DC properties of HTS JJ made by this technique have been reported to date, the present work aims at exploring their dynamic behavior, by studying the Josephson oscillation linewidth in the tens of GHz frequency range. This characterization, which gives access to the intrinsic noise of the JJ, is essential for high frequency applications of JJ such as mixers and detectors14,16,17 and to study unconventional superconductivity31.
Depending on the ion dose, HTS JJs made by the He FIB technique behave as Superconductor/Normal metal/Superconductor (SNS) JJs or Superconductor/Insulator/Superconductor (SIS) ones18. Müller et al.28 evidenced scaling relations obeyed by the characteristic parameters Ic (critical current) and Rn (normal resistance), which are typical of highly disordered materials and known for a long time in HTS Grain-Boundary (GB) JJ32 for example. The large density of localized electronic defect states at the origin of this behavior is a source of 1/f low-frequency noise33,34, which broadens the Josephson oscillation linewidth at much higher frequency35. To assess the potential performances of HTS Josephson devices made with He FIB, we directly measured the Josephson linewidth up to 40 GHz.
Results
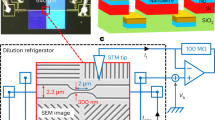
To fabricate HTS JJ, we begin with a commercial 50 nm-thick c-oriented YBCO thin film on a sapphire substrate36 capped in-situ with 250 nm of gold for electrical contacts. After removing the Au layer by Ar+ ion etching everywhere except at contact pads, we structure 4 μm wide and 20 μm long channels using the HEII technique12. An e-beam resist mask protects the film from a 70 keV oxygen ion irradiation at a dose of 1 × 1015 ions/cm2 to keep it superconducting. The unprotected part becomes insulating. In a second step, samples are loaded into a Zeiss Orion NanoFab Helium/Neon ion microscope and the 30 keV He+ beam (current ~1.15 pA) was scanned across the 4 μm-wide superconducting bridges to form JJs. A single line is used in these experiments, whose trace can be imaged directly in the microscope28 (Fig. 1(a)). Imaging with the He+ beam creates disorder, which adds to the one used to make the JJ. This is why we did not image the channels that we measured in the present study. On the same YBCO chip, we irradiated different channels with different doses ranging from 200 to 1000 ions/nm. The samples were then measured in a cryogen-free cryostat with a base temperature of 2 K, equipped with filtered DC lines. The RF illumination is performed via a broadband spiral antenna placed 1 cm above the chip, and connected to a generator in a Continuous Wave (CW) mode at frequency f. To measure the “detector response” described below, the RF signal is electrically modulated at low frequency (fmod = 199 Hz). The output signal Vdet is measured via a lock-in amplifier synchronized on this frequency.
(a) Image of a JJ using the imaging mode of the He-FIB microscope. The light grey area in between dashed lines is the superconducting channel defined by HEII The horizontal line is the 600 ions/nm dose irradiated zone, which corresponds to the barrier of the JJ. (b) Sketch of the circuit used to measure the detector response signal Vdet. A RF signal whose amplitude is modulated at the frequency fmod is sent onto the JJ via an antenna. Vdet is measured with a lock-in amplifier at fmod. The JJ is described according to the RSJ model, as a junction in parallel with a resistance Rn. (c) R vs T curves (solid lines) for JJ made using different irradiation doses: 200 ions/nm (blue), 400 ions/nm (green) and 600 ions/nm (red). Same color code for panels (c,d). Below TJ, Rn (symbols) is extracted from RSJ fits. Dashed lines show the linear decrease of R(T) curves below TJ. (d) Ic vs T for different irradiation doses. Dashed lines are quadratic fits. inset: I − V characteristics of a 200 ions/nm JJ. Blue line are data and black line is the RSJ fit. (e) IcRn product vs T for different irradiation doses. Colored areas are calculated from the dashed lines in (c,d), and correspond to the Josephson regimes.
Figure 1(c) shows the resistance R as a function of temperature T for samples irradiated with a dose of 200, 400 and 600 ions/nm. Below the Tc of the reservoirs (Tc = 84 K), a resistance plateau develops till a transition to a zero-resistance state takes place, corresponding to the Josephson coupling through the irradiated part of the channel. Let TJ be this coupling temperature, which decreases as the dose is increased as already reported18,28. The resistance above TJ increases with disorder as expected, from \(\lesssim \)1 Ω (200 ions/nm) to ~3 Ω (600 ions/nm). For irradiation dose higher than 1000 ions/nm, an insulating behavior is observed down to the lowest temperature. For the samples studied here (doses between 200 and 600 ions/nm), we measured the current-voltage (I − V) characteristics below TJ. The inset of Fig. 1(d) shows the I − V curve of the 200 ions/nm sample recorded at T = 73 K, which can be accurately fitted with the Resistively-Shunted-Junction (RSJ) model including thermal noise (black line), as already reported18,28.
This model accounts for Josephson weak links and Superconductor-Normal Metal-Superconductor (SNS) junctions, where the quasiparticle current is in parallel with the superconducting one, in the limit of small junction capacitance37,38. Finite temperature effect is introduced by mean of a noise current whose power spectral density corresponds to the Johnson noise of the normal state resistance Rn35,39 (see Methods section for more detail and numerical calculation).
The RSJ fits are still valid when the dose and the temperature are varied, as proved by extended fits shown in Fig. 2. From these fits, we extracted the temperature-dependent normal-state resistance Rn(T) and the critical current Ic(T) presented in Fig. 1(c,d), respectively, with an uncertainty of typically a few percents, indicated by error bars in the figures. The former roughly follows the R(T) curve measured above TJ, decreases linearly with temperature (dashed lines) and goes to zero at the superconducting temperature of the irradiated part where the Josephson regime ends. The latter has a quadratic temperature dependence (dashed lines) as expected for SNS JJ12,40. Its absolute value can exceed 1 mA (200 and 400 ions/nm doses), which corresponds to critical current densities larger than 500 kA/cm2 28. We show in Fig. 1(e) the IcRn product as a function of temperature for the different irradiation doses.
I − V characteristics of (a) a 200 ions/nm JJ, (b) a 400 ions/nm JJ and (c) a 600 ions/nm JJ, with (red) and without (blue) 10 GHz irradiation. Solid lines are data and dashed lines RSJ fits. Color-plot of Rd as a function of I and VRF at f = 10 GHz for (d) a 200 ions/nm JJ and (e) a 400 ions/nm JJ (Color-scale at the bottom). (f) Same plot for a 600 ions/nm JJ (Color scale on the right).
At low doses, it shows a maximum, characteristic of SS’S junctions (where S’ is a superconductor with a Tc lower than the one of S) as observed with HEII HTS JJ14. However, for the highest dose (600 ions/nm), it raises monotonically as the temperature is lowered. Its maximum value (IcRn ~ 600 μV at 4 K) lies in between the values reported by Cybart et al.18 and Müller et al.28. The corresponding characteristic frequency \({f}_{c}={I}_{c}{R}_{n}{/\Phi }_{0} \sim 300\) GHz (\({\Phi }_{0}=h/2e\) the flux quantum) is higher than the one obtained by the HEII technique, which is promising for operations up to the THz frequency range14.
We now focus on properties of these JJ at frequencies f much lower than fc, and more specifically on the Shapiro steps which appear on I − V characteristics at voltages \({V}_{n}=n\cdot f\cdot {\Phi }_{0}\) (n is an integer). Figure 2(a) shows the I − V curves of the 200 ions/nm JJ measured at T = 72 K without (blue) and with (red) RF irradiation at f = 10 GHz, where we observe clear Shapiro steps. Both curves are well fitted with the RSJ model (dashed lines) with the following parameters: Rn = 0.5 Ω, Ic = 133 μA and for the RF curve: IRF = 133 μA (the RF current). For this temperature close to TJ = 75 K, Rn does not depend on the bias current I, contrary to the HEII HTS JJ15,41. Sweeping both the RF voltage VRF and the bias current I, we recorded the I − V curves from which we computed numerically the differential resistance \({R}_{d}=\frac{dV}{dI}\). The result is presented in color-scale in Fig. 2(d). The observation of well-defined and high-index (up to n = 12) Shapiro steps attests the quality of this SNS JJ. Similar measurements were performed on the other JJs. The results are shown in Fig. 2(b,c) for the 400 ions/nm JJ and the 600 ions/nm, respectively. In each case, the measurement temperature (T = 60 K and T = 30 K) are close to their respective TJ. In this regime, all the curves are very well fitted with the RSJ model with the following parameters: Rn = 0.68 Ω, Ic = 205 μA and IRF = 143.5 μA for the 400 ions/nm JJ, and Rn = 2.9 Ω, Ic = 32.5 μA and IRF = 26.2 μA for the 600 ions/nm one. It is important to note that the RSJ fits were performed while taking a noise temperature equals to the bath temperature. Figure 2(e,f) show color-plot for the corresponding samples. In both cases, pronounced oscillations with RF voltage corresponding to high order Shapiro steps are observed.
Shapiro steps unveil the internal Josephson oscillation that is produced when a JJ is biased beyond its critical current. The width of the steps is the linewidth of the Josephson oscillation35. Within the RSJ model, Likharev and Semenov35,39 calculated the voltage power spectral density SV(f) and the resulting Josephson oscillation linewidth Δf as follows:
This thermal Δf is the minimum Josephson linewidth which can be measured, as any other noise source will increase this intrinsic linewidth. Divin et al. showed that Δf can be measured experimentally from the Shapiro steps by mean of the “detector response” method42,43,44. The JJ is DC biased while the RF illumination is modulated at low frequency (fmod)45. The “detector response” signal Vdet is measured with a lock-in amplifier synchronized at fmod, and plotted as a function of the DC voltage V converted into a frequency f through the Josephson relation \(f=V\,{/\Phi }_{0}\). Centered on the Josephson frequency, i.e. on the Shapiro step, an odd-symmetric structure appears, whose width (distance between the extrema) corresponds to Δf. To be more precise, Divin et al.42 showed that the inverse Hilbert transform of the quantity \(g(V)=(8/\pi )\cdot ({V}_{\det }/{R}_{d})\cdot I\cdot V\) is directly SV(f), a Lorentzian of width Δf centered at the Josephson frequency f. This procedure, successfully used in LTS43 and HTS44 materials, allows to extract the Josephson linewidth accurately.
We measured the Josephson oscillation linewidth of the different JJ irradiated at f = 40 GHz using the “detector response” method. Figure 3(a) (bottom panel) shows Vdet (left axis) as a function of the frequency (\(f=V{/\Phi }_{0}\)) for the 200 ions/nm JJ. Around 40 GHz, the characteristic double-peak structure predicted by Divin42 is observed, from which we extracted the Josephson linewidth (Δf = 4.87 GHz). It is worth noticing that this method is highly sensitive, since the Shapiro steps cannot be seen in the I − V curve simultaneously recorded (top panel). We then computed SV through the above explained procedure, and plotted it on the same graph (Fig. 3(a) (bottom panel, right axis). Two peaks are observed, corresponding to the first an second Shapiro steps, that can be fitted with Lorentzian to extract the corresponding Josephson oscillation linewidths. For the first step (index n = 1), the value is exactly the same as the one calculated above. Depending on the experimental conditions, we could accurately measure the Josephson linewidth of the first two Shapiro steps, or only of one of them.
(a) I − V characteristics of the 200 ions/nm JJ under f = 40 GHz irradiation. Vdet vs \(f=V{/\Phi }_{0}\). The distance Δf between the extrema corresponds to the Josephson oscillation linewidth. SV extracted from the inverse Hilbert transform of the the normalized response g(V) (pink), whose width is Δf (grey). (b) Vdet vs V for a 400 ions/nm JJ measured at different temperatures under f = 40 GHz irradiation. (c) Δf vs T for different irradiation doses. Solid symbols correspond to the first Shapiro step, open symbols to the second one. Solid lines (blue, green, red) are calculated from the RSJ model for n = 1 (200 and 400 ions/nm) and n = 2 (600 ions/nm), the black one from the tunneling one. (d) Δf vs ΔfRSJ (left panel) and vs ΔfTunnel (right panel, 600 ions/nm JJ (n = 2) for \(T\le 26\,K\)). The slope of the dashed lines is one. inset: Δf vs Ic for the 600 ions/nm JJ (n = 2) for \(T\le 26\,K\). Dashed lines are best fits with a power-law exponent 1 (purple) and 1.35 (orange).
We measured Vdet as a function of V at different temperatures, as for example reported in Fig. 3(b) for the 400 ions/nm JJ. The odd-symmetric structure at V = 82.7 μV (corresponding to 40 GHz, dashed line) widens with increasing temperature as expected for thermal noise. We extracted Δf as a function of temperature for the different samples. The result is shown in Fig. 3(c). Open (respectively solid) symbols correspond to measurements on the first (respectively second) Shapiro step. On the same graph, we added the linewidth ΔfRSJ calculated for the thermal noise in the RSJ model using Eq. 135,39, with no adjustable parameter. The agreement is excellent for the 200 and 400 ions/nm JJ at all temperatures. For the 600 ions/nm, data are well reproduced at high temperature, but strongly depart from the calculation below T = 20 K. In Fig. 3(d), we made a parametric plot of the same data: the experimental Δf as a function of the calculated ΔfRSJ in the RSJ model with thermal noise (left panel). All data align along the dashed line of slope 1, which means that noise in He FIB JJ is purely thermal, except for 600 ions/nm JJ at low temperature.
This indicates that an extra source of noise takes place below T = 20 K in this JJ. We notice that this temperature corresponds to an up-turn in the R(T) curve (Fig.1(c)).
This thermally activated electronic transport, characteristic of a disorder-induced Anderson insulator where charge carriers hop between localized states46, is well known for ion-irradiated cuprates47. It has been reported by Cybart et al.18 in YBCO JJ made by the He FIB technique for a sample slightly more irradiated than our 600 ions/nm one. They showed that a SIS junction is formed, and they observed a structure in the conductance related to the superconducting gap, as expected in tunnel junctions where the differential conductance is proportional to the Density of States of the reservoirs in first approximation. It is worth noting that in this regime, and contrary to the SS’S one, both Ic and Rn increase as the temperature is lowered, and so does the IcRn product (see Fig. 1e)) to reach an interesting high value (~600 μV). In that case, the tunneling approach proposed by Dahm et al.48 is more appropriate than the RSJ one to calculate the Josephson oscillation linewidth, which includes the non-linear superposition of thermal and shot noises in these JJ at intermediate damping35,48. They show that:
We calculated Δf for the 600 ions/nm JJ with this expression, and obtained a very good agreement with the data as shown in Fig. 3(c)(black line), once again with no adjustable parameter. The excess noise comes therefore from the shot noise contribution when approaching the tunneling limit. The parametric plot of the experimental Δf as a function of the calculated ΔfTunnel including the shot noise (Fig. 3(d) right panel) clearly shows that there is no additional noise source in our JJ.
Discussion
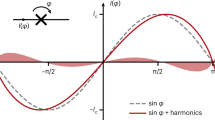
This seems quite surprising, given the recent result from Müller et al. pointing towards highly disordered JJ28, which are usually associated with strong 1/f Flicker noise33. They measured the low-frequency noise of SQUIDs made with low-irradiation dose JJ (230 ions/nm). A clear 1/f noise component is observed up to ~100 kHz. These measurements have been performed on JJ fabricated on the so-called “LSAT” substrate, which have much lower Ic and IcRn products than the others for the same dose. The role of the substrate on the JJ characteristics is not understood yet, but it is clear that the microstructure of the film matters for final JJ performances, and more specifically for noise properties related to defects. This has been evidenced long ago on YBCO Grain-Boundary JJ by annealing experiments49. Our samples grown on sapphire may have therefore less fluctuating centers at the origin of Flicker noise than others. Past studies showed that this noise in HTS JJ is often induced by enhanced critical current fluctuations in inhomogeneous barriers50,51,52, and that the maximum 1/f noise power in the vicinity of Ic scales with it (\({S}_{{Vmax}}\propto {I}_{c}^{2.7}\))52,53. This noise translates into a broader Josephson linewidth at high frequency, especially when f < fc, i.e. for DC bias current close to Ic44. It has been evaluated by Hao et al.52 as:
where f0 is a low frequency cut-off of the 1/f noise (typically f0 ~ 1 Hz). Through the above mentioned scaling relation, Δf should thus increase as \({I}_{c}^{1.35}\) or so. The data on our 600 ions/nm sample below T = 20 K are compatible with this relation (inset Fig. 3(d)), but we cannot make a quantitative fit since we do not know the value of SV(f0). Moreover, the same data can be fitted with the shot noise model as well (inset Fig. 3(d)), since the latter states that Δf ~ Ic close to Ic (derived from the above equation). This model fits quantitatively the evolution of Δf with temperature with no adjustable parameter, and qualitatively the one with the critical current. We therefore conclude that the shot noise contribution fully explains the low temperature data of the most irradiated JJ, and that there is no evidence of strong Flicker noise in the present study.
Conclusion
We fabricated HTS JJ by the He FIB technique, and studied their DC and RF properties in the 10 to 40 GHz range. Their IcRn product reaches 300 GHz at low temperature, which is higher than for HEII JJ. We showed that Shapiro steps in the I − V characteristics that appear under RF irradiation are well described by the RSJ model for SNS junctions with thermal noise. Using the “detector response” method, we determined the Josephson oscillation linewidth, and showed that it corresponds to the sole Johnson-Nyquist thermal noise in the RSJ model for the low-dose irradiated JJ. Below T = 20 K, the high-dose irradiated sample has a SIS character. We demonstrated that the associated enhanced noise is due to shot noise when approaching the tunneling regime. We did not evidenced any Flicker noise component, which means that the barrier is rather homogeneous in these JJ. This study paves the way for using He FIB JJ in high frequency applications53.
Methods
Resistively shunted junction (RSJ) model
Calculation of the I–V curve at finite temperature
The Resistively Shunted Junction (RSJ) model describes the equivalent circuit of a Josephson Junction (JJ) as two elements in parallel (the junction described by the two Josephson equations written below and its normal state resistance Rn as sketched in Fig. 1(b)), biased with a current I37,38. In this “overdamped” limit, the capacitance of the junction is neglected. The Josephson equations state:
where IJ is the bias current and V the voltage of the JJ, Ic its critical current, φ the quantum phase difference across it, and \({\varPhi }_{0}\) the superconducting flux quantum.
The time evolution of the current is therefore:
The voltage is given by Eq. 5.
These equations are valid in the limit of zero-temperature. At finite temperature, the Johnson noise of the resistance must be added. The power spectral density of the current fluctuations at temperature T is35,39:
We introduce a noise current δIn(t) whose power spectral density is given by Eq. 7. It has therefore a Gaussian variation in time with a variance:
where Δt is the time interval considered.
The time evolution of the current is now:
To get the DC I-V curve, one needs to time average this equation.
I–V curve in a presence of RF irradiation
If the JJ is submitted to a time varying current (RF irradiation) \({I}_{RF}={I}_{RF0}\,\cos (2\pi {\nu }_{RF}t)\) at finite temperature, the time evolution of the JJ is given by:
and Eq. 5. After time averaging, the I-V curves present current (Shapiro) steps at voltages \({V}_{n}=n{\Phi }_{0}{\nu }_{RF}\), where n is an integer. The width of the transition from one step to the next one is given by the thermal noise.
I–V curve simulation
In practice, the simulation of an IV curve consists in solving the Eqs. 5 and 10 by numerical integration using the Euler method. Hence the system to be numerically solved is:
where the bracket notation means discrete time steps of pace δτ, and n is the step index. For each current bias I, a voltage vector is thus found by iteration, for each step δτ from τ = 0 to τ = τMax, starting with a random initial phase and V[0] = 0. The Gaussian noise δIn is a random variable changed at every step, whose variance is given by Eq. 8 (Δt = δτ).
The system is numerically heavy to solve: first because one needs a sufficiently small δτ to account for the rapid variation of the voltage oscillations, especially at low bias, and at the same time one needs a sufficiently high τMax in order to have enough oscillations to average. In practice, δτ must be much smaller than 1/vRF, and τMax should be sufficiently high to average enough oscillations. We typically have vectors of 200000 points, and δτ ~ 1 · 10−12 s. Second, because the presence of the (actually pseudo random) noise also requires to average the calculation of each VDC over several iterations of the same IV curve, typically 10 times.
References
Wendin, G. Quantum information processing with superconducting circuits: a review. Reports on Progress in Physics 80, 106001–51 (2017).
Tolpygo, S. K. Superconductor digital electronics: Scalability and energy efficiency issues (Review Article). Low Temperature Physics 42, 361–379 (2016).
Holzman, I. & Ivry, Y. Superconducting Nanowires for Single-Photon Detection: Progress, Challenges, and Opportunities. Advanced Quantum Technologies 2, 1800058–28 (2019).
Sizov, F. Terahertz radiation detectors: the state-of-the-art. Semiconductor Science and Technology 33, 123001–27 (2018).
Clarke, J. & Braginski, A. I. The SQUID Handbook, Fundamentals and Technology of SQUIDS and SQUID Systems (Wiley, 2005).
Mukhanov, O., Prokopenko, G. & Romanofsky, R. Quantum Sensitivity: Superconducting Quantum Interference Filter-Based Microwave Receivers. IEEE Microwave Magazine 15, 57 (2014).
Cleuziou, J. P., Wernsdorfer, W., Bouchiat, V., Ondarçuhu, T. & Monthioux, M. Carbon nanotube superconducting quantum interference device. Nature Nanotechnology 1, 53–59 (2006).
Skryabina, O. V. et al. Josephson coupling across a long single-crystalline Cu nanowire. Applied Physics Letters 110, 222605–6 (2017).
Goswami, S. et al. Quantum interference in an interfacial superconductor. Nature Nanotechnology 11, 861–865 (2016).
Mitchell, E. E. & Foley, C. P. YBCO step-edge junctions with high IcRn. Superconductor Science and Technology 23, 065007 (2010).
Divin, Y. Y., Poppe, U., Jia, C. L., Shadrin, P. M. & Urban, K. Structural and electrical properties of YBa2Cu3O7-X [1 0 0]-tilt grain boundary Josephson junctions with large IcRn products. Physica C: Superconductivity 372–376, 115 (2002).
Bergeal, N. et al. High-quality planar High Tc Josephson junctions. Applied Physics Letters 87, 102502 (2005).
Bergeal, N. et al. Using ion irradiation to make High Tc Josephson junctions. Journal Of Applied Physics 102, 083903 (2007).
Malnou, M. et al. High-Tc superconducting Josephson mixers for terahertz heterodyne detection. Journal Of Applied Physics 116, 074505 (2014).
Ouanani, S. et al. High-Tc superconducting quantum interference filters (SQIFs) made by ion irradiation. Superconductor Science and Technology 29, 094002 (2016).
Pawlowski, E. R. et al. Static and radio frequency magnetic response of High Tc superconducting quantum interference filters made by ion irradiation. Superconductor Science and Technology 31, 095005 (2018).
Couedo, F. et al. High- T csuperconducting detector for highly-sensitive microwave magnetometry. Applied Physics Letters 114, 192602–6 (2019).
Cybart, S. A. et al. Nano Josephson superconducting tunnel junctions in YBCO directly patterned with a focused helium ion beam. Nature Nanotechnology 10, 598–602 (2015).
Iberi, V. et al. Nanoforging Single Layer MoSe2 Through Defect Engineering with Focused Helium Ion Beams. Scientific Reports 1–9 (2016).
Stanford, M. G. et al. Focused helium-ion beam irradiation effects on electrical transport properties of few-layer WSe2 : enabling nanoscale direct write homo-junctions. Scientific Reports 1–10 (2016).
Zhou, Y. et al. Precise milling of nano-gap chains in graphene with a focused helium ion beam. Nanotechnology 27, 325302–7 (2016).
Gusev, S. A. et al. The modification of the structure of multilayer Co/Pt films by the irradiation with a focused helium ion beam. AIP Conference Proceedings 1748, 030002–8 (2016).
Scholder, O. et al. Helium focused ion beam fabricated plasmonic antennas with sub-5 nm gaps. Nanotechnology 24, 395301–7 (2013).
Cho, E. Y. et al. YBa2Cu3O7-X superconducting quantum interference devices with metallic to insulating barriers written with a focused helium ion beam. Applied Physics Letters 106, 252601–5 (2015).
Gozar, A., Litombe, N. E., Hoffman, J. E. & Bozovic, I. Optical Nanoscopy of High Tc-Cuprate Nanoconstriction Devices Patterned by Helium Ion Beams. Nano Letters 17, 1582–1586 (2017).
Cho, E. Y. et al. Direct-coupled micro-magnetometer with Y-Ba-Cu-O nano-slit SQUID fabricated with a focused helium ion beam. Applied Physics Letters 113, 162602–4 (2018).
Cho, E. Y., Zhou, Y. W., Cho, J. Y. & Cybart, S. A. Superconducting nano Josephson junctions patterned with a focused helium ion beam. Applied Physics Letters 113, 022604–5 (2018).
Müller, B. et al. Josephson junctions and SQUIDs created by focused helium ion beam irradiation of YBa2Cu3O7. Physical Review Applied 11, 044082 (2019).
Kasaei, L. et al. MgB2 Josephson junctions produced by focused helium ion beam irradiation. AIP Advances 8, 075020–7 (2018).
Kasaei, L. et al. Normal-state and superconducting properties of Co-doped BaFe2 As2 and MgB2 thin films after focused helium ion beam irradiation. Superconductor Science and Technology 32, 095009–10 (2019).
Kwon, H. J., Sengupta, K. & Yakovenko, V. M. Fractional ac Josephson effect in p- and d-wave superconductors. The European Physical Journal B 37, 349–361 (2004).
Gross, R., Chaudhari, P., Kawasaki, M. & Gupta, A. Scaling behavior in electrical transport across grain boundaries in YBCO superconductors. Physical review B 42, 10735–10737 (1990).
Marx, A. & Gross, R. Scaling behavior of 1/fnoise in high-temperature superconductor Josephson junctions. Applied Physics Letters 70, 120–122 (1997).
Gustafsson, D., Lombardi, F. & Bauch, T. Noise properties of nanoscale YBa2Cu3O7-X Josephson junctions. Physical review B 84, 184526–10 (2011).
Likharev, K. Dynamics of Josephson junctions and circuits (1986).
Stewart, W. C. Current-Voltage characteristics of Josephson junctions. Applied Physics Letters 12, 277–280 (1968).
Barone, A. & Paterno, G. Physics and applications of Josephson effect (Wiley, 1982).
Likharev, K. & Semenov, V. K. Fluctuation spectrum in superconducting point junctions 15, 442 (1972).
De Gennes, P. G. Boundary EfFects in Superconductors. Review of Modern Physics 36, 225 (1964).
Kahlmann, F. et al. Superconductor–normal–superconductor Josephson junctions fabricated by oxygen implantation into YBa2Cu3O7-X. Applied Physics Letters 73, 2354–2356 (1998).
Divin, Y., Polyanskii, O. & Shul’Man, A. Pisma Zh. Tekh. Fiz. 6, 1056 (1980).
Divin, Y. Y. & Mordovets, N. A. Width of the Josephson-generation line in the far-IR region. Sov. Tech. Phys. Lett. 9, 108 (1983).
Sharafiev, A. et al. Josephson oscillation linewidth of ion-irradiated YBa2Cu3O7 junctions. Superconductor Science and Technology 29, 1–6 (2016).
Anderson, P. W. Absence of diffusion in certain random lattices. Physical Review 109, 1492 (1958).
Lesueur, J., Dumoulin, L., Quillet, S. & Radcliffe, J. Ion-Beam-Induced Metal-Insulator-Transition in YBCO Films. Journal of Alloys and Compounds 195, 527–530 (1993).
Dahm, A. J. et al. Linewidth of the Radiation Emitted by a Josephson Junction. Physical Review Letters 22, 1416–1420 (1969).
Kawasaki, M., Chaudhari, P. & Gupta, A. 1/f Noise in YBa2Cu3O7-X Superconducting Bicrystal Grain-Boundary Junctions. Physical Review Letters 68, 1065–1068 (1992).
Miklich, A. H., Clarke, J., Colclough, M. S. & Char, K. Flicker (1/f) noise in biepitaxial grain boundary junctions of YBa2Cu3O7-X. Applied Physics Letters 60, 1899–1901 (1992).
Divin, Y. Y., Mygind, J., Pedersen, N. F. & Chaudhari, P. Linewidth of Josephson oscillations in YBa2Cu3O7-X grain-boundary junctions. Applied Superconductivity, IEEE Transactions on 3, 2337–2340 (1993).
Hao, L., Macfarlane, J. C. & Pegrum, C. M. Excess noise in thin film grain boundary Josephson junctions and devices. Superconductor Science and Technology 9, 678–687 (1996).
Marx, A., Fath, U., Ludwig, W., Gross, R. & Amrein, T. 1/f noise in BSCCO crystal grainboundary Josephson junctions. Physical review B 51, 6735–6738 (1995).
Hao, L. & Macfarlane, J. C. Estimation of the noise temperature of YBaCuO grain boundary Josephson junctions. Physica C 292, 315–321 (1997).
Cortez, A. T. et al. Tuning Y-Ba-Cu-O Focused Helium Ion beam Josephson Junctions for use as THz Mixers. IEEE Transactions On Applied Superconductivity 29, 1102305 (2019).
Acknowledgements
The authors thank Yann Legall (ICUBE laboratory, Strasbourg) for ion irradiations. This work has been supported by the QUANTUMET ANR PRCI program (ANR-16-CE24-0028-01), the T-SUN ANR ASTRID program (ANR-13-ASTR-0025-01), the SUPERTRONICS ANR PRCE program (ANR-15-CE24-0008-03), the Emergence Program from Ville de Paris, the Région Ile-de-France in the framework of the DIM Nano-K and Sesame programs, the Délégation Générale à l’Armement (P. A. DGA PhD grant 2016) and the National Science Foundation Singapore (NRF2016-NRF-ANR004).
Author information
Authors and Affiliations
Contributions
F.C. designed the samples with the help of Y.K.S. and R.S., and fabricated them with the help of P.A., C.F.-P. and C.U.F.C. performed the measurements with N.B. and C.F.-P., and most of the data analysis with J.L.J.L. and F.C. wrote the initial draft of the manuscript. All the authors contributed to the ideas behind the project, and to discussions and revisions of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Couëdo, F., Amari, P., Feuillet-Palma, C. et al. Dynamic properties of high-Tc superconducting nano-junctions made with a focused helium ion beam. Sci Rep 10, 10256 (2020). https://doi.org/10.1038/s41598-020-66882-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-66882-1
This article is cited by
-
Josephson radiation threshold detector
Scientific Reports (2024)
-
Single-photon detection using high-temperature superconductors
Nature Nanotechnology (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.