Abstract
We present an extensive study of vortex dynamics in a high-quality single crystal of HgBa2CuO4+δ, a highly anisotropic superconductor that is a model system for studying the effects of anisotropy. From magnetization M measurements over a wide range of temperatures T and fields H, we construct a detailed vortex phase diagram. We find that the temperature-dependent vortex penetration field Hp(T), second magnetization peak Hsmp(T), and irreversibility field Hirr(T) all decay exponentially at low temperatures and exhibit an abrupt change in behavior at high temperatures T/Tc >~ 0.5. By measuring the rates of thermally activated vortex motion (creep) S(T, H) = |dlnM(T, H)/dlnt|, we reveal glassy behavior involving collective creep of bundles of 2D pancake vortices as well as temperature- and time-tuned crossovers from elastic (collective) dynamics to plastic flow. Based on the creep results, we show that the second magnetization peak coincides with the elastic-to-plastic crossover at low T, yet the mechanism changes at higher temperatures.
Similar content being viewed by others
Introduction
Interest in copper-oxide superconductors (cuprates) is fueled by their technological potential and the outstanding mystery of the mechanism governing high-temperature superconductivity, which stifles prediction of new superconductors. It is known that, in cuprates, superconductivity is hosted in the crystallographic ab-planes. This induces anisotropy γ between the in-plane (ab) and out-of-plane (c-axis) fundamental superconducting parameters, such as the penetration depth λab = λc/γ and coherence length ξab = γξc. When evaluating the potential of superconductors for technological applications, high anisotropy compels considerations beyond the typical metrics of high critical temperature Tc, critical current density Jc, and upper critical field Hc2. This is because thermal fluctuations profoundly impact anisotropic materials’ electronic and magnetic properties, which are significantly influenced by the dynamics of vortices. Consequently, thermally activated vortex motion (creep) is fast and Jc vanishes at an irreversibility field Hirr that can be much less than Hc2, potentially negating the otherwise advantageous properties of these materials. Understanding vortex dynamics in cuprates is not only technologically relevant, but also can substantially contribute to the debate over the degree to which superconductivity in cuprates is conventional1.
Magnetic flux penetrates superconductors immersed in fields greater than the lower critical field Hc1. This does not quench superconductivity in high-Tc materials provided that the field remains below Hc2. In layered cuprates, interior flux can appear as stacks of weakly-coupled 2D pancake vortices, each localized on a Cu-O plane. Pancake vortices within a stack are not necessarily aligned and interact both magnetically (owing to their moments) and through Josephson coupling between pancakes in adjacent planes. If this coupling is sufficiently strong, the stacks may behave as continuous strings, hence be considered 3D vortex lines. The differing dynamics of 2D pancakes and 3D vortex lines should therefore play a major role in determining the phase diagram in highly anisotropic materials.
The superconductor HgBa2CuO4+δ (Hg1201) is recognized as ideal for systematically studying the effects of high anisotropy. This is because its clean microstructure enables probing intrinsic, rather than sample-dependent, properties associated with high anisotropy2. Specifically, Hg1201 crystals do not contain common defects, such as twin-boundaries and rare-earth-oxide precipitates3,4,5. Furthermore, it has a simple tetragonal structure and optimally doped Hg1201 has the highest Tc among single Cu-O layer materials, permitting thorough studies of the effects of thermal fluctuations on the superconducting state. Despite these desirable characteristics, the paucity of research on Hg1201 results from the challenges of growing large, high-quality single crystals.
In this paper, we identify vortex phase boundaries and glassy regimes in the vortex phase diagram of a clean, optimally doped Hg1201 single crystal. We find that the temperature-dependent vortex penetration field Hp(T), second magnetization peak Hsmp(T), and irreversibility field Hirr(T) all decay exponentially at low temperatures and exhibit an abrupt change in behavior at high temperatures. We present complementary vortex creep measurements over a wide range of the phase diagram that reveal the broad extent to which the dynamics of pancake vortices determine the magnetic properties in our sample. Our main findings from these measurements are as follows: First, the crystal hosts a vortex glass state characterized by collective creep of large bundles of pancake vortices at low temperatures T/Tc ≤ 0.4 and applied fields μ0H < 0.5 T. The glass state persists at higher fields, yet the bundle size shrinks. Second, we find temperature-tuned crossovers from elastic (collective) dynamics to plastic flow. By measuring at the crossover temperature over an extended time frame, we additionally capture a transition from elastic to plastic dynamics over time. Last, we show that the second magnetization peak does not originate from elastic-to-plastic crossovers over most of the phase diagram; these crossovers only coincide with the second magnetization peak at low temperatures T/Tc < 0.2.
Results
Critical temperature and anisotropy
Two of the sample’s key characteristics, the critical temperature Tc and the anisotropy γ, were extracted from temperature- and field-dependent magnetization measurements as summarized in Fig. 1. The temperature sweeps M(T) in a field of 5 Oe yielded a critical temperature of Tc ≈ 95.9 K, see Fig. 1(a), consistent with near optimal doping2,6. To determine the anisotropy, we measured the ratio of the transverse (MT) to the longitudinal (ML) magnetization at various field orientations (θ) relative to the c axis in the reversible (vortex liquid) regime. The raw data is plotted in Fig. 1(b,c). As shown in Fig. 1(d), a least squares fit of the data to Eq. (1), the Kogan model7,8,
(a) Temperature dependent magnetization M(T) measured at H = 5 Oe after zero-field cooling, revealing Tc ≈ 95.9 K, consistent with expectations for optimally doped Hg1201. Angular dependence of the (b) transverse (MT) and (c) longitudinal (ML) components of the magnetization, and (d) the ratio MT/ML in an applied field of 0.1 T and temperatures 80 K and 85 K. Note that in (d), the data for the two temperatures overlap and the black curve is a fit of the 80 K data to Eq. (1) that yields an anisotropy factor γ ≈ 32.
produces an anisotropy of γ ≈ 32. This is consistent with previous work on optimally doped Hg1201 single crystals. Specifically, angle dependent torque magnetometry studies9,10,11,12 found γ ≈ 27−30. Additionally, a study13 that measured the magnetization at two field orientations, perpendicular (M⊥) and parallel (M||) to the CuO2 planes, found γ ≈ 30 using a self-consistency equation from anisotropic Ginzburg-Landau theory M⊥(H) = γM||(γH).
Irreversible Magnetization
Isothermal magnetization loops were recorded for H||c and at T = 5−65 K. Select curves are displayed in Fig. 2. In all cases, the field was first swept to −3 or −4 T (not shown) to establish the critical state (full flux penetration throughout the sample). The lower branch of the loop was subsequently measured as the field was ramped from 0 T to 7 T, and the upper branch was collected as the field was swept back down. All curves exhibit a distinct shape with two conspicuous features: a dip in the magnitude of M near the onset field Hon and a second magnetization peak (SMP) at Hsmp. In general, this shape and the magnitude of the magnetization is indicative of a weak vortex pinning regime at low fields (\(H\lesssim {H}_{on}\)) and stronger pinning at higher fields. We observed similar results in measurements of our other Hg1201 crystals. The source of pinning is likely point defects in the Hg-O layer—specifically, oxygen interstitials and mercury vacancies3,4,5, and this should be the main source of disorder in the bulk that hinders thermal wandering of vortices.
In high-temperature superconducting crystals, a surface barrier—called the Bean-Livingston (BL) barrier—often plays a significant role in determining the magnetic properties and shaping the M(H) loops14,15,16,17. It originates from competing effects: vortices are repelled from the surface by Meissner shielding currents and attracted by a force arising from the boundary conditions (usually modeled as the attraction between the vortex and an image antivortex18). Disappearing at the penetration field Hp ≈ κHc1/lnκ, the BL barrier impedes vortex entry and exit from the sample in fields less than Hp > Hc1, where Hc1 is the lowest field at which flux penetration is thermodynamically favorable. The contribution of the barrier is magnified in materials with high Ginzburg-Landau parameters κ = λ/ξ and diminished by surface imperfections. Creep of pancake vortices over the barrier produces the exponential temperature dependence17
where T0 = ε0dln(t/t0), \({\varepsilon }_{0}={\Phi }_{0}^{2}/4\pi {\mu }_{0}{\lambda }_{ab}^{2}\) is the vortex line energy or tension, d is the spacing between CuO2 planes, t is the time scale of the measurement, t0 ~ 10−10–10−8 s relates to the vortex penetration time19, and the thermodynamic critical field is \({H}_{c}={\Phi }_{0}/2\sqrt{2}\pi {\xi }_{ab}{\lambda }_{ab}\).
To investigate the relevance of surface barriers in our sample, we measured the field at which vortices first penetrate into the sample peripheries Hp by collecting the zero-field cooled M(H) isotherms shown in Fig. 3(a): we defined Hp as the field at the departure from linearity. Figure 3(a) inset shows the extraction technique and the phase diagram in Fig. 4 contains the resulting temperature dependence. We find that Hp(T) follows Eq. (2) at low temperatures T/Tc < 0.55, and a least squares fit produces T0 = 21.3 ± 0.7 K and Hc = 0.06 T. The experimentally extracted T0 is reasonably close to the estimate T0 = 26 K, calculated assuming t ~ 100 s, t0 = 10−10 s, d ≈ 9.5 Å13, and λab ≈ 162 nm20.
(a) M versus H at low fields after zero field cooling. Hp is the field at which each curve deviates from a linear fit to the Meissner slope (black line). Inset shows the deviation ΔM from the Meissner slope and the black horizontal line indicates the criterion used for defining Hp (a deviation of a tenth of the standard deviation σ ≈ 0.003 from the linear fit). (b) Magnification of magnetization loops plotted in Fig. 2 (collected after full flux penetration) showing a weak pinning regime at low fields in which M is low and weakly sensitive to magnetic field. (c) Temperature dependence of the magnetization showing transition from the irreversible regime to the reversible regime to the normal state. The upper (lower) branches were collected after the critical state was prepared by sweeping the field to >Δ4H* above (below) the indicated fields. The irreversibility point (Tirr, Hirr) is defined as the point at which the upper and lower branches merge.
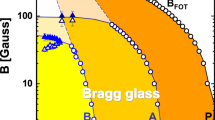
Vortex phase diagram for our Hg1201 crystal, determined by behavior extracted from fits to data shown in Fig. 3. The solid blue line is a fit to Eq. (2), while the dashed blue line is a fit to \({H}_{c1}(T)=[{\Phi }_{0}/(4\pi {\lambda }_{ab}^{2}(T)\)\((1-N))]\,\mathrm{ln}\,\kappa \). The solid red line is a fit of the low temperature second magnetization peak data to ~e−AT for constant A. Lastly, the solid purple line is a fit to \({e}^{-T/{T}_{0}}\) and the dashed purple curve is a fit to (1−T/Tc)m.
To accurately assess the field of first penetration, we must account for local field enhancements due to demagnetizing effects by multiplying our extracted value by 1/(1 − N), where N is the effective demagnetizing factor. Expressing the field enhancement in terms of a demagnetizing factor formally exclusively applies to samples with elliptic cross-section (per refs. 21,22). For samples with rectangular cross-section (width w and thickness δ, \(w\gg \delta \)), we must account for the fact that the field of first penetration is retarded by a geometrical barrier23,24. This barrier is associated with a parametrically lower field enhancement at the sample edge as compared to an elliptic slab with the same dimensions. In this case, accurate values of the effective demagnetizing factors for rectangular prisms have been calculated numerically25. Following the calculations from ref. 26, we find N ≈ 0.75 which yields Hc = 0.24T and hence a coherence length ξab(0) ~ 1.5 nm, similar to the value of ξab(0) ~ 2.0 ± 0.4 nm measured by Hofer et al.11. We attribute the deviation of the penetration field at low temperature from the expected scaling of Hc1(T), see Fig. 4 for T/Tc < 0.55, to the increasing importance of thermal creep to overcome the surface/geometric barriers.
Agreement of our Hp(T < 0.55Tc) data with Eq. (2) indicates that, at low T, vortices enter as pancakes (as evinced by creep measurements, see discussion in the next section) and are thermally activated over the BL barrier. At T/Tc ~ 0.55, the temperature dependence of Hp abruptly changes, suggestive of a different mechanism for vortex penetration at higher temperatures. Similar crossovers have been observed in other layered superconductors16,27,28,29,30,31 around T/Tc ~ 0.5. We anticipate such a crossover when Hp(T) from Eq. (2) falls below Hc1: in this case, we would expect Hp(T) to be bound by \((1-N){H}_{c1}(T)=[{\Phi }_{0}/(4\pi {\lambda }_{ab}^{2}(T))]\,\mathrm{ln}\,\kappa \) for T above the crossover. Considering the two-fluid approximation, λab(T) = λab(0)[1−(T/Tc)4]−1/2, and a T-independent κ, this expression indeed fits the data for Hc1 = 300Oe, see Fig. 4. A competing scenario for the crossover—based on a transition of creep of pancakes to creep of vortex half-loops17,31—fails to produce the correct temperature dependence for T/Tc > 0.55. From this value for Hc1 we extract λab(0) = 154 nm, which is comparable with published data11,20.
For fields above Hp, but below Hsmp, |M| dips to an ill-defined minimum and increases again at Hon. Figure 3(b) magnifies this low-field plateau and Hon(T) is plotted in Fig. 4. Previous studies have related Hon to a transition between an ordered vortex lattice at low fields and an entangled lattice created by point disorder at higher fields, tuned by competition between thermal, pinning, and elastic energies. For example, FeSe1−x Tex single crystals showed evidence of a Bragg glass (quasi-ordered vortex solid) below Hon32 and a presumed disordered vortex solid above Hon. Additionally, YBa2Cu3O7−δ, Nd1.85Ce0.15CuO4−δ, and Bi2Sr2CaCu2O8+δ all demonstrate disorder induced phase transitions that show a signature in the M(H) loops33.
In applied magnetic fields above Hon, the magnetization apexes at the second magnetization peak Hsmp. Second magnetization peaks have been reported in studies of most classes of superconductors, including low-Tc34,35, iron-based32,36,37,38,39,40, and highly anisotropic28,41 materials, as well as YBa2Cu3O7−δ (YBCO) single crystals42. In fact, this peak has also been observed in a few previous studies20,43,44,45,46 of Hg1201 single crystals grown by two research groups4,45, though the peak is far more pronounced in our samples. This feature is typically either attributed to a crossover between vortex pinning regimes or a structural phase transition47,48 in the vortex lattice. Below, we will revisit the discussion of the second magnetization peak because creep measurements are requisite to evaluate possible origins of the SMP.
At sufficiently high fields, the loops close as the system transitions into the reversible regime at the irreversibility field Hirr. Instead of extracting Hirr from the isothermal magnetization loops M(H), we extract it from isomagnetic M(T) sweeps. This is more precise than measurements involving sweeping the field: temperature sweeps tend to induce less noise than field sweeps and, at the transition, the upper and lower branches of M(T) not only converge, but also exhibit a sharp change in slope. Figure 3(c) contains select M(T) datasets showing the extraction technique and the resulting irreversibility line is shown in Fig. 4.
For T/Tc < 0.6, we find that Hirr(T) ∝ \({e}^{-T/{T}_{0}}\) (shown in Fig. 4), which yields T0 = 19.7 ± 0.6 K, produced by a least squares fit. Notice that T0 is close to the value T0 ≈ 21 K, extracted in the fit of our Hp data to Eq. (2) and identical to the value (T0 = 19.7 ± 0.4 K) extracted in another study on Hg1201 single crystals45. At higher temperatures T > T*, the shape of the irreversibility line changes. Similar trends in Hirr(T) have been found in grain-aligned Hg1201 samples49 and single crystals45.
Although the field of first penetration seems to be dominated by surface barrier effects, we conclude from the symmetric magnetization loops that bulk pinning is the dominant pinning source in our Hg1201 crystal after field penetration. Otherwise, i.e. if the contribution of bulk pinning were relatively insignificant, we would observe asymmetry between the upper and lower branches of the magnetization loops 18. Despite the observation of bulk pinning dominance, it remains unclear whether the similar exponential temperature scaling of Hp and Hirr have a common ground. Compiling the aforementioned results, Fig. 4 shows the resulting phase diagram on a semilog plot. In the following sections, we use magnetic relaxation measurements to learn more about the nature of vortex dynamics in the gray region of Fig. 4. The following sections present our main result – a more detailed understanding of vortex behavior derived from extensive vortex creep measurements.
Vortex creep
The disorder landscape defines potential energy wells in which vortices will preferentially localize to reduce their core energies by a pinning energy U0. An applied or induced current tilts this energy landscape. This reduces the energy barrier that a pinned vortex must surmount to escape from a well to a current-dependent value U(J). The time required for thermal activation over such a barrier can be approximated by the Arrhenius form
At low temperatures (\(T\ll {T}_{c}\)) and fields, the simple linear relationship U(J) = U0(1 − J/Jc0) proposed in the Anderson-Kim model50,51 is often accurate. However, because this model neglects vortex elasticity and vortex-vortex interactions, its relevance is often further limited to the early stages of the relaxation process (\(J\lesssim {J}_{c0}\)). In the later stages \(J/{J}_{c0}\ll 1\), collective creep theories, which consider vortex elasticity, predict an inverse power law form for the energy barrier U(J) = U0[(Jc0/J)μ]. Here, the glassy exponent μ is sensitive to the size of the vortex bundle that hops during the creep process and its dimensionality. To capture behavior for a broad range of J, we invoke a commonly used interpolation between the two regimes
where μ = −1 recovers the Anderson-Kim result. It is now straightforward to combine Eqs. (3) and (4) to determine the expected decay in the persistent current over time J(t) and subsequently the vortex creep rate S:
and
Creep measurements are a useful tool for determining the size of the energy barrier and its dependence on current, field, and temperature. Such measurements further probe the vortex state, revealing the existence of glassy behavior, collective creep regimes, or plastic flow. This is because, as evident in Eq. (6), creep provides access to both U0 and μ. Table 1 summarizes expected values of μ for collective creep of 3D flux lines and 2D pancake vortices.
To shed light on the Hg1201 phase diagram, we measured creep rates in a wide range of temperatures (5–60 K) and magnetic fields (0.1–5 T) using standard methods19, summarized here. We first establish the critical state by sweeping the field 4H* above the field at which creep will be measured H, where H* is the minimum field at which magnetic flux will fully penetrate the sample. Second, the field is swept to H, such that the magnetization M(H) coincides with its value on the upper branch of a magnetization loop. [If the magnitude of the initial field sweep were not sufficiently high, M(H) would instead fall inside the loop, vortices would not fully penetrate the entire sample and the previously discussed models would be inapplicable.] Third, the magnetization M(t) ∝ J(t) is subsequently recorded every ~15 s for an hour. We also briefly measure M(t) in the lower branch to determine the background arising from the sample holder, subtract this, and adjust the time to account for the difference between the initial application of the field and the first measurement (maximize correlation coefficient). Lastly, the normalized creep rate S(T, H) is extracted from the slope of a linear fit to lnM−lnt.
Figure 5 shows the field dependence of the creep rate. In low fields, S decreases as H increases, a trend that reverse above ~0.5 T. This change in behavior may be related to a different source of vortex pinning at low than at high fields. It roughly coincides with the low-field change in shape of the M(H) loops around Hon ~ 0.5 T. This trend is apparent in the inset, which compares the temperature dependencies of Hon (open symbols) and the field at which the minimum in creep S(H) occurs (closed symbols). Because of this, in the following section, we will separately analyze low-field and high-field measurements. We will first present S(T) and an analysis of the vortex state in the low-field regime, and then proceed to analyze the high-field regime.
Glassy vortex dynamics and elastic-to-plastic crossovers
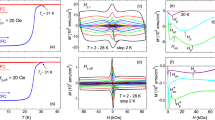
To study the dynamics in the low-field weak pinning regime, exemplified in Fig. 3(b), we measured vortex creep for μ0H < 0.5 T, shown in the main panel of Fig. 6(a). The creep rates in fields of 0.1–0.3 T are similar over the entire temperature range, plateauing at S ~ 0.06 for T < 40 K then sharply rising at higher temperatures. Such behavior is akin to S(T) in YBCO samples, which typically exhibit a plateau around S ~ 0.02–0.03519,52,53. In YBCO, the plateau appears because \({U}_{0}\ll \mu T\,\mathrm{ln}(t/{t}_{0})\) such that \(S \sim {[\mu {k}_{B}\mathrm{ln}(t/{t}_{0})]}^{-1}\) becomes T-independent. It is often associated with glassy vortex dynamics because μ ≈ 1 considering S ~ 0.035 and ln(t/t0) ≈ 27 for a typical measurement window of t ~ 1 hour19,53.
Temperature dependence of the vortex creep rate in applied magnetic fields of (a) 0.1–0.4 T and (c) 0.7–5 T. The inset to (a) shows the energy scale U* ≡ kBT/S versus 1/J. The lines are linear fits to the data for temperatures 5–25 K, and the slopes yield the glassy exponents μ ≈ 1 at 0.4 T and μ ≈ 0.5 for 0.1–0.3 T. (b) Magnetization (M) collected every ~15 s for 67 hours at 20 K and 0.3 T. The black curve is a fit to Eq. (5) using μ = 0.5, where J(t) ∝ M(t). (d) Energy scale U* plotted against 1/J for applied field 0.7–1.8 T. The lines are linear fits, and the change from a positive to negative slope suggests a crossover from elastic vortex dynamics to plastic flow at Hcr. The dashed lines show examples of how the glassy exponents μ, displayed in the phase diagram in Fig. 7(a), were extracted.
Similarly, for our Hg1201 sample, if \({U}_{0}\ll \mu {k}_{B}T\,\mathrm{ln}(t/{t}_{0})\) were true, the S ~ 0.05 plateau would yield μ ~ 0.6. However, in our sample, we do not yet know the comparative magnitudes of U0 and μkBTln(t/t0). To extract μ without the need for assumptions regarding U0, it is common practice37,54,55,56,57,58 to define an experimentally accessible auxiliary energy scale U* ≡ kBT/S. From Eq. (6), we see that U* = U0 + μkBTln(t/t0) and, combined with Eq. (5), find that
Hence, μ can be directly obtained from the slope of U* versus 1/J on a log − log plot. As shown in the Fig. 6(a) inset, μ = 0.5 for fields of 0.1–0.3 T. We reinforce this result with a complementary 67 hour long relaxation study shown in Fig. 6(b) and fitting the resulting M(t) to the interpolation formula Eq. (5). For free parameters Jc0, U0, and μ, the best fit again produces μ = 0.5, which is expected for collective creep of large bundles of 2D pancake vortices (see Table 1)59.
The presence of large bundles in these small fields is suggestive of a clean pinning landscape in which long-range 1/r vortex-vortex interactions are only weakly perturbed by vortex-defect interactions. Furthermore, this result is consistent with the evidence from Hirr(T) (shown in Fig. 4) of a 2D vortex state over a wide low temperature \(T/{T}_{c}\ll 0.6\) region of the phase diagram. We have now ascertained that, though the plateau in S(T) appears at a higher S than in YBCO, it again correlates with glassiness.
At 0.4 T, S(T) is non-monotonic, reaching a local minimum around 30 K (see Fig. 6(a)). As shown in the Fig. 6(a) inset, we extract μ ≈ 1, which is close to the μ = 13/16 expectation for creep of medium bundles of pancake vortices (see Table 1). So, the system transitions from creep of large bundles at low fields μ0H < 0.4 T to medium bundles at 0.4 T. This change in μ occurs roughly around Hon (compare to Fig. 3(b)) and the minimum in S(H) (compare to Fig. 5). In many systems, the bundle size increases with increasing H51. Hence, this scenario is not standard, but is consistent with our suspected mechanism for Hon: as H increases, the strength of pinning suddenly increases around Hon causing the lattice to become more entangled, the bundle size to decrease, and we see both Jc and μ increase.
Collective creep theory only considers elastic deformations of the vortex lattice and neglects dislocations. At high temperatures and/or fields, the elastic pinning barrier becomes quite high and plastic deformations of the vortex lattice can become more energetically favorable. Plastic creep60 involves the motion of a channel of vortices constrained between two edge dislocations of opposite sign (dislocation pairs) and requires surmounting a diverging plastic barrier Upl ~ J−μ for small driving force \(J\ll {J}_{c0}\). It manifests as a negatively sloped region in a U*(1/J) plot: in Eq. 7, μ < 0 is conventionally represented using the notation p, such that the auxiliary quantity U* scales as U0(Jc0/J)p in the plastic regime. Note that the true potential barrier U(J) in Eq. (4) remains monotonically decreasing with increasing current.
Figure 6(c) displays creep rates at fields H > 0.5 T. Representing the data as U*(1/J), plotted in Fig. 6(d), the slopes exhibit a distinct sign change, revealing elastic (μ > 0) to plastic (μ < 0 → p) crossovers for H ≤ 2 T. Figure 6(d) displays the 1 T data for fields of 0.7–1.8 T. From the data, we extract the exponents μ displayed in the vortex phase diagram show in Fig. 7(a). We see, for example, that at 1 T the sample hosts creeping small bundles of pancake vortices in the elastic regime T < 20. To investigate the dynamics at the crossover temperature Tcr = 20 K, we perform a 6-hour measurement of M(t) that is plotted in the Fig. 7(b) and fit the data to Eq. (5). To reduce the number of free parameters (Jc0 and U0), we obtain μ from the slope of 1/S plotted against lnt, see Eq. (6) and the Fig. 7(b) inset. Clearly, the early stages of relaxation is glassy. The bundle size evolves over time, manifesting as a change in μ. In the latter stages, we observe a transition to plastic flow.
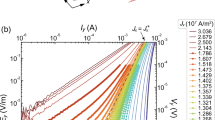
(a) Vortex phase diagram determined from creep measurements overlaid with position of second magnetization peak. (b) 1/S versus lnt determined from the time-dependent magnetization M(t) data shown in the inset. M(t) was collected every ~15 s for 6 hours at 20 K and 1 T, at the elastic-to-plastic crossover. The data points in the main panel represent S extracted from subsets of the data over intervals Δt. Dashed lines are linear fits. The red, green, and blue curves in the inset are fits to Eq. (5), where J(t) ∝ M(t), using μ = 0.9, μ = 0.5, and μ → p = −0.3, respectively. (c) Upper branch of M(H) loop at T = 20 K constructed from magnetic relaxation data, where M(ti) represents the magnetization a time ti after the critical state was formed. The inset demonstrates the extraction technique and how the first measurement collected by the magnetometer occurs at approximately ti = 100 s.
Discussion
Elastic-to-plastic crossovers are considered the cause of the second magnetization peak in many superconductors32,37,38,40. However, the origin of the SMP in Hg1201 is controversial. Daignère et al.43,61 found no correlation between the SMP and elastic-to-plastic crossovers in Hg1201 single crystals, and concluded that the SMP merely arises from competition between an increase in Jc and decrease in pinning energy with increasing magnetic field. On the contrary, Pissas et al.44 showed that though Hcr < Hsmp, a correlation between the two fields does indeed exist, therefore the peak is possibly associated with collective-to-plastic transitions. That study reconciled the lack of coincidence between the two fields as caused by very fast creep at low fields and slower creep at high fields. To understand their reasoning, it is important to note that magnetization measurements are not collected instantaneously with the application of a magnetic field. That is, there is a 10−100 s lag between establishing the field and measuring M due to the time required for setting the magnet in persistent mode and translating the sample through the magnetometer SQUID detection coils. Consequently, by the time M is recorded during magnetization loop measurements, J is much less than Jc0 at low fields where creep is fast and closer to Jc0 at higher fields where creep is slow. This idea was further supported by a demonstration that measuring the loop faster shifts Hsmp to lower fields, towards Hcr44.
To explore this issue, we overlay our measurements of Hsmp and Hcr in the phase diagram in Fig. 7(a). Figure 6(d) show examples of how Hcr was extracted from U*(1/J). At low temperatures T/Tc < 0.2, the appearance of the SMP coincides with the elastic-to-plastic crossover whereas Hcr < Hsmp at higher temperatures. Given this discrepancy, we now consider the previous argument that fast creep rates make measurements of Hsmp from loops inaccurate.
As described above, we typically create a magnetization loop by measuring M once at each field as the field is ramped up in steps. Constructing the loop instead from magnetic relaxation data enables us to set a consistent time scale for all M values. We achieve this by extracting M from a linear fit to logM − logt at a predetermined time ti after formation of the critical state, exemplified in the inset to Fig. 7(c). This also allows us to estimate M before the first measurement. The main panel shows how M(H) changes with ti. We find that a faster measurement increases Hsmp, moving it away from Hcr, contrary to the observation in Pissas et al.44.
Conversely, the time scale associated with our determination of the elastic-to-plastic crossover is arguably the 1 hour duration of our creep measurements, therefore, an appropriate comparison requires Hsmp to be determined from ti = 1 hour. As shown in Fig. 7(a,c), though this reduces Hsmp, it remains significantly larger than Hcr. We can therefore conclude that the elastic-to-plastic crossover is not the source of the SMP at high temperatures. The SMP could be caused by a transition in the structure of the vortex lattice. As the conditions for this transition would depend on anisotropy, this could be clarified through a comprehensive study comparing magnetization in Hg1201 crystals having different anisotropies, achieved by varying the doping, or through neutron scattering studies47.
To summarize, we have studied the field- and temperature- dependent magnetization and vortex creep in an HgBa2CuO4+δ single crystal to understand the effects of anisotropy on vortex dynamics in superconductors. We reveal glassy behavior involving collective creep of bundles of 2D pancake vortices over a broad range of temperatures and fields as well as temperature- and time-tuned crossovers from elastic dynamics to plastic flow. The isothermal magnetization loops exhibit distinct second magnetization peaks that have also been observed in previous studies of Hg1201, and Hsmp(T) decays exponentially at low temperatures then exhibits an abrupt change in behavior above T/Tc = 0.5. The origin of the second magnetization peak in superconductors can be controversial, and is often attributed to an elastic-to-plastic crossover. Here we clearly show that the second magnetization in Hg1201 is not caused by an elastic-to-plastic crossover at T/Tc > 0.2 and occurs within the plastic flow regime.
Methods
Hg1201 single crystals were grown using an encapsulated self-flux method62 at Los Alamos National Laboratory. The crystals were subsequently heat-treated at 350 °C in air and quenched to room temperature to achieve near optimal doping6. The high-quality of the synthesized crystals is evinced by the observation of large quantum oscillations in other samples from the same growth batch. Multiple crystals were measured to verify reproducibility. The results presented in this manuscript were collected on a crystal with dimensions 1.28 × 0.84 × 0.24 mm3 and mass of 1.9 mg, shown in the Fig. 1(a) inset.
All measurements were performed using a Quantum Design superconductor quantum interference device (SQUID) magnetometer equipped with two independent sets of detection coils to measure the magnetic moment in the direction of (mL) and transverse to (mT) the applied magnetic field. For measurements requiring manipulating the field orientation, the crystal was placed on a rotating sample mount. Most measurements, however, were conducted with the field aligned with the sample c-axis (H||c), in which case the sample was mounted on a delrin disk inside a straw.
References
Berthod, C., Maggio-Aprile, I., Bruér, J., Erb, A. & Renner, C. Observation of Caroli-de Gennes-Matricon Vortex States in YBa 2Cu3O7−δ. Phys. Rev. Lett 119, 237001 (2017).
Barišić, N. et al. Demonstrating the model nature of the high-temperature superconductor HgBa2CuO4+δ. Phys. Rev. B 78, 054518 (2008).
Wagner, J. et al. Structure and superconductivity of HgBa2CuO4+δ. Phys. C 210, 447–454 (1993).
Pelloquin, D., Hardy, V., Maignan, A. & Raveau, B. Single crystals of the 96 K superconductor (Hg, Cu)Ba 2CuO4+δ: growth, structure and magnetism. Phys. C 273, 205–212 (1997).
Viallet, V. et al. Superconductivity, X-ray structure and non stoichiometry of HgBa2Cu4+δ. Phys. C 282–287, 1073–1074 (1997).
Yamamoto, A., Hu, W.-Z. & Tajima, S. Thermoelectric power and resistivity of HgBa2CuO4+δ over a wide doping range. Phys. Rev. B 63, 024504 (2000).
Kogan, V. G., Fang, M. M. & Mitra, S. Reversible magnetization of high- T c materials in intermediate fields. Phys. Rev. B 38, 11958–11961 (1988).
Mosqueira, J., Rey, R. I. & Vidal, F. Magnetization vector in the reversible region of the highly anisotropic cuprate superconductor Tl 2Ba2Ca2Cu3O10: Anisotropy factor and the role of two-dimensional vortex fluctuation. Phys. Rev. B 81, 174509 (2010).
Xia, D. D. et al. Temperature and field dependence of the anisotropy parameter for the high-temperature superconductor HgBa 2CuO4+δ. Supercond. Sci. Technol. 25, 115010 (2012).
Hofer, J. et al. Torque magnetometry on single-crystal high-temperature superconductors near the critical temperature: A scaling approach. Phys. Rev. B 62, 631–639 (2000).
Hofer, J. et al. Doping dependence of superconducting parameters in HgBa 2CuO4+δ single crystals. Phys. C 297, 103–110 (1998).
Hofer, J. et al. Angular-dependent torque magnetometry on single-crystal HgBa 2CuO4+y near the critical temperature. Phys. Rev. B 60, 1332–1339 (1999).
Le Bras, G. et al. Superconducting properties and anisotropy of a HgBa 2CuO4+δ single crystal. Physica C 271, 205–213 (1996).
Konczykowski, M., Burlachkov, L., Yeshurun, Y. & Holtzberg, F. Evidence for surface barriers and their effect on irreversibility and lower-critical-field measurements in Y-Ba-Cu-O crystals. Phys. Rev. B 43, 13707–13710 (1991).
Bean, C. P. & Livingston, J. D. Surface Barrier in Type-II Superconductors. Phys. Rev. Lett. 12, 14–16 (1964).
Kopylov, V. N., Koshelev, A. E., Schegolev, I. & Togonidze, T. G. The role of surface effects in magnetization of high-Tc superconductors. Physica C 170, 291–297 (1990).
Burlachkov, L., Geshkenbein, V. B., Koshelev, A. E., Larkin, A. I. & Vinokur, V. M. Giant flux creep through surface barriers and the irreversibility line in high-temperature superconductors. Phys. Rev. B 50, 16770 (1994).
Burlachkov, L. Magnetic relaxation over the Bean-Livingston surface barrier. Phys. Rev. B 47, 8056–8064 (1993).
Yeshurun, Y., Malozemoff, A. P. & Shaulov, A. Magnetic relaxation in high-temperature superconductors. Rev. Mod. Phys. 68, 911–949 (1996).
Villard, G., Daignere, A., Pelloquin, D. & Maignan, A. Effect of underdoping on the superconductivity of (Hg, Cu)Ba 2CuO4+δ ‘1201’ single crystals. Physica C 314, 196–204 (1999).
Klemm, R. Demagnetization effects upon the lower critical field of an anisotropic type II superconductor of ellipsoidal shape. J. Low Temp. Phys. 39, 589601 (1980).
Osborn, J. A. Demagnetizing Factors of the General Ellipsoid. Phys. Rev. 67, 351 (1945).
Zeldov, E. et al. Geometrical Barriers in High-Temperature Superconductors. Phys. Rev. Lett. 73, 1428–1431 (1994).
Willa, R., Geshkenbein, V. B. & Blatter, G. Suppression of geometric barrier in type-II superconducting strips. Phys. Rev. B 89, 104514 (2014).
Brandt, E. Geometric edge barrier in the Shubnikov phase of type-II superconductors. Low Temp. Phys. 27, 723–731 (2001).
Pardo, E., Chen, D. X. & Sanchez, A. Demagnetizing factors for completely shielded rectangular prisms. J. Appl. Phys. 96, 5365 (2004).
Chowdhury, P., Kim, H.-J., Gupta, S. K. & Lee, S.-I. Field dependent creep characteristics in Tl 2Ba2CuO6 single crystals. J. Phys.: Condens. Matter 16, 6727–6736 (2004).
Chowdhury, P., Kim, H.-J., Jo, I.-S. & Lee, S.-I. Peak anomaly and irreversible magnetization in Tl 2Ba2CaCu2O8 single crystals. Physica C 384, 411–418 (2003).
Chikumoto, N., Konczykowski, M., Motohira, N., Kishio, K. & Kitazawa, K. The first magnetic penetration field in BSCCO single crystals, temperature dependence and electron irradiation effect. Physica C 185–189, 1835–1836 (1991).
Zeldov, E. et al. Nature of the Irreversibility Line in Bi 2Sr2CaCu2O8. Eur. Lett. 30, 367–372 (1995).
Nideröst, M. et al. Lower critical field H and barriers for vortex entry in Bi 2Sr2CaCu2O8+δ crystals. Phys. Rev. Lett. 81, 3231–3234 (1998).
Miu, D., Noji, T., Adachi, T., Koike, Y. & Miu, L. On the nature of the second magnetization peak in FeSe1−xTex single crystals. Supercond. Sci. Technol. 25, 115009 (2012).
Giller, D., Shaulov, A., Yeshurun, Y. & Giapintzakis, J. Vortex solid-solid phase transition in an untwinned YBa 2Cu3O7−δ crystal. Phys. Rev. B 60, 106–109 (1999).
Banerjee, S. S. et al. Peak effect, plateau effect, and fishtail anomaly: The reentrant amorphization of vortex matter in 2 H-NbSe2. Phys. Rev. B 62, 11838 (2000).
Zuo, F., Khizroev, S., Jiang, X., Peng, J. L. & Greene, R. L. Surface barriers and two-dimensional-collective pinning in single crystal Nd 1.85Ce0.15CuO4−δ superconductors. J. Appl. Phys. 76, 6953 (1994).
Fang, L. et al. Doping- and irradiation-controlled pinning of vortices in BaFe 2(As1−xPx)2 single crystals. Phys. Rev. B 84, 140504 (2011).
Zhou, W., Xing, X., Wu, W., Zhao, H. & Shi, Z. Second magnetization peak effect, vortex dynamics, and flux pinning in 112-type superconductor Ca0.8La0.2Fe1−xCoxAs2. Sci. Rep. 6, 22278 (2016).
Salem-Sugui, S. et al. Flux dynamics associated with the second magnetization peak in the iron pnictide Ba1−xKxFe2As2. Phys. Rev. B 82, 054513 (2010).
Pramanik, A. K. et al. Fishtail effect and vortex dynamics in LiFeAs single crystals. Phys. Rev. B 83, 094502 (2011).
Shen, B. et al. Flux dynamics and vortex phase diagram in Ba(Fe1−xCox)2As2 single crystals revealed by magnetization and its relaxation. Phys. Rev. B 81, 014503, https://doi.org/10.1103/PhysRevB.81.014503 (2010).
Konczykowski, M. et al. Magnetic relaxation in the vicinity of second magnetization peak in BSCCO crystals. Phys. C 332, 219–224 (2000).
Boudissa, M., Halimi, R., Frikach, K. & Senoussi, S. Fishtail effect in twinned and detwinned YBCO single crystals. Phys. Stat. Sol. (c) 3, 3044–3047 (2006).
Daignere, A., Aouaroun, T. & Simon, C. Absence of dynamical crossover in the vortex creep near by the second peak effect in superconducting Hg-1201 single crystals. Eur. Phys. J. B 16, 397–402 (2000).
Pissas, M. et al. Magnetic relaxation measurements in the region of the second magnetization peak in a HgBa 2CuO4+δ single crystal. Phys. Rev. B 59, 12121–12126 (1999).
Pissas, M. et al. Irreversibility line in superconducting HgBa 2CuO4+δ single crystals. Phys. Rev. B 58, 9536–9542 (1998).
Stamopoulos, D. & Pissas, M. Hysteretic behavior of the vortex lattice at the onset of the second peak for the HgBa 2CuO4+δ. Phys. Rev. B 65, 134524 (2002).
Gilardi, R. et al. Direct Evidence for an Intrinsic Square Vortex Lattice in the Overdoped High- T c Superconductor La1.83Sr0.17CuO4+δ. Phys. Rev. Lett. 88, 217003 (2002).
Rosenstein, B. et al. Peak effect and square-to-rhombic vortex lattice transition in La2−xSrxCuO4. Phys. Rev. B 72, 144512 (2005).
Lewis, J. A., Vinokur, V. M., Wagner, J. & Hinks, D. Surface-barrier effects in grain-aligned HgBa 2CuO4+δ, HgBa2CaCu2O6+δ, and HgBa 2Ca2Cu3O8+δ compounds. Phys. Rev. B 52, 3852–3855 (1995).
Anderson, P. W. & Kim, Y. B. Hard superconductivity: Theory of the motion of Abrikosov flux lines. Rev. Mod. Phys. 36, 39–43 (1964).
Blatter, G., Feigel’man, M. V., Geshkenbein, V. B., Larkin, A. I. & Vinokur, V. M. Vortices in high-temperature superconductors. Rev. Mod. Phys. 66, 1125–1388 (1994).
Malozemoff, A. P. & Fisher, M. P. A. Universality in the current decay and flux creep of Y-Ba-Cu-O high-temperature superconductors. Phys. Rev. B 42, 6784–6786 (1990).
Kwok, W.-K. et al. Vortices in high-performance high-temperature superconductors. Rep. Prog. Phys. 79, 116501 (2016).
Sun, Y. et al. Enhancement of critical current density and mechanism of vortex pinning in H+ -irradiated FeSe single crystal. APEX 8, 113102 (2015).
Sun, Y. et al. Critical current density, vortex dynamics, and phase diagram of single-crystal FeSe. Phys. Rev. B 92, 144509 (2015).
Haberkorn, N. et al. Strong pinning and elastic to plastic vortex crossover in Na-doped CaFe 2As2 single crystals. Phys. Rev. B 84, 094522 (2011).
Miu, L. et al. High Vortex Depinning Temperatures in YBCO Films with BZO Nanorods. J. Supercond. Nov. Magn. 26, 1167–1173 (2013).
Sundar, S. et al. Plastic pinning replaces collective pinning as the second magnetization peak disappears in the pnictide superconductor Ba 0.75K0.25Fe2As2. Phys. Rev. B 95, 134509 (2017).
Vinokur, V. M., Kes, P. H. & Koshelev, A. E. The 2D collective creep exponents reconsidered. Physica C 248, 179–184 (1995).
Kierfeld, J., Nordborg, H. & Vinokur, V. M. Theory of plastic vortex creep. Phys. Rev. Lett. 85, 4948–4951 (2000).
Daignere, A., Maignan, A., Hardy, V. & Simon, C. Pinning properties in (Hg0.8Cu0.2)Ba2CuO4+δ single crystals: relaxation and irradiation studies. Supercond. Sci. Technol. 14, 659–662 (2001).
Zhao, X. et al. Crystal growth and characterization of the model high-temperature superconductor HgBa 2CuO4+δ. Adv. Mater. 18, 3243–3247 (2006).
Acknowledgements
We would like to thank V.M. Vinokur for useful discussions regarding the plastic flow regime. This material is based upon work supported by the National Science Foundation under Grant No. 1905909 (data analysis and manuscript composition) and the U.S. Department of Energy, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, projects Towards a Universal Description of Vortex Matter in Superconductors (experimental measurements), Science at 100 T (crystal synthesis) and Quantum Fluctuations in Narrow Band Systems (crystal synthesis). R.W. acknowledges funding support from the Swiss National Science Foundation through its Early Postdoc.Mobility program.
Author information
Authors and Affiliations
Contributions
S.E. conceived the experiments, M.K.C. and E.D.B. grew the samples, S.E. and L.C. performed magnetization measurements, S.E., R.W., and L.C. analyzed and interpreted the results, R.W. provided theoretical support, S.E. and R.W wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Eley, S., Willa, R., Chan, M.K. et al. Vortex phases and glassy dynamics in the highly anisotropic superconductor HgBa2CuO4+δ. Sci Rep 10, 10239 (2020). https://doi.org/10.1038/s41598-020-65224-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-65224-5
This article is cited by
-
Order–disorder phase transition and elastic-to-plastic vortex creep crossover in a triclinic iron pnictide superconductor (Ca\(_{0.85}\)La\(_{0.15}\))\(_{10}\)(Pt\(_3\)As\(_8\))(Fe\(_2\)As\(_2\))\(_5\)
Scientific Reports (2023)
-
Second magnetization peak, anomalous field penetration, and Josephson vortices in KCa\(_2\)Fe\(_4\)As\(_4\)F\(_2\) bilayer pnictide superconductor
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.