Abstract
The presence of Magnéli phases in titanium oxide nanotubes (NTs) can open up frontiers in many applications owing to their electrical and optical properties. Synthesis of NTs with Magnéli phases have posed a challenge due to the degradation and loss of morphology in NTs upon high-temperature treatments (>600 °C) in a reducing environment. This study reports on the synthesis of anodically formed NTs containing Magnéli phases through a double annealing route: oxygen (O2) annealing followed by annealing in 2% hydrogen with a nitrogen balance (2%H2-N2). The nucleation, growth, and transformation of anodized amorphous NTs into crystalline phases was investigated. The NTs obtained through this route were highly ordered and composed of mixed phases of anatase, rutile, and the Magnéli phase (Ti4O7). Experimental results from scanning electron microscopy (SEM), X-ray diffraction (XRD), scanning transmission electron microscopy (S/TEM), and Raman spectroscopy were combined with first principle calculations to develop an understanding of the sequential phase transformations during annealing. A predictive model was developed using density functional theory (DFT) to potentially predict the titanium oxides formed and their stability with reference to the mole fraction of oxygen. The change in the density of states (DOS), band structure, optical properties, and stability of phases are also discussed using DFT simulations. The combination of experimental characterization and modelling helped to understand the nucleation of anatase and rutile and the reorganization of these phases to form Magnéli phases on the anodized amorphous NTs through annealing treatment.
Similar content being viewed by others
Introduction
Magnéli phases are substoichiometric titanium oxide with chemical formula TinO2n−1 where n ranges from 4–91. Magnéli phases are highly desirable because of their inertness in aggressive media2 and their conductance3; for example, at room temperature they are stable in 4 mol dm−3 sulfuric acid (H2SO4) with a projected half-life of 50 years4. Magnéli phases are semi-metallic in nature with electrical properties comparable to carbon1,2. There has been a significant amount of research on Magnéli materials due to the increasing demand for chemically inert, conductive materials5. Much of the research has been focused on the synthesis of Magnéli phase titanium oxide by reducing rutile under high temperatures 600–1000 °C1. Annealing in a reducing environment produces a number of defects in the TiO2 crystal structure, including oxygen vacancies (Vo). The increasing number of Vo alters the Ti and O ratio, resulting in the formation of different suboxides (i.e., Magnéli compounds). Magnéli phases form from TiO2 according to the following reaction6:
These structural changes and oxygen deficiencies reduce the resistance of the oxides results in delocalized electrons that assist in electron pathway, thus increasing the conductivity1,7.
The formation of Magnéli phases by annealing in a 2% hydrogen gas with a nitrogen balance (2%H2-N2) is a sequential process; starting with anodized amorphous NTs, annealing initially nucleates anatase crystals that transform to rutile during high temperature treatment. After prolonged treatments in reducing environment, defects are introduced in rutile leading to thermodynamic instability and subsequent atomic reorganization into the stable Magnéli phases under the high temperature treatments. However, using this technique to form Magnéli phases within anodically formed NTs is challenging because of the structural changes encountered within the NTs at high temperatures. During annealing, the NTs are prone to atomic rearrangement with formation of Vo with concurrent morphology changes due to sintering, as nucleation and growth occurs within the NTs and at the NT-Ti substrate interface. These changes degrade the highly-ordered, thin walled (<10 nm) NTs until they are completely degraded onto the titanium substrate.
The present work introduces an annealing route that enables the formation of Magnéli phases while maintaining the morphology of the nanotubes. This double annealing route consist of oxygen (O2) annealing at 500 °C followed by annealing in a 2%H2-N2 environment at 600 °C. This route ensures the formation of Magnéli phases while preserving the NTs morphology. A predictive model was first developed using density functional theory simulations for predicting suboxide (Magnéli compound) formation at specific mole fractions of oxygen. Experimental investigations of the relationship between process and structure were then performed to validate the model.
Results and Discussion
The annealing of as-anodized NTs causes the amorphous structure to undergo extensive changes that depend on the processing path and temperature. This link between processing and structure was used to successfully develop the double annealing route for obtaining NTs containing Magnéli suboxide, while preserving the nanotubular morphology. The key driving force behind the formation of the Magnéli phase was found to be the formation of oxygen vacancies (Vo), which is also the major driver in the degradation of the NTs. In order to form Magnéli phases within NTs while maintaining their nanotubular structure, the changes in the morphology and crystalline phases with varying temperature and gaseous atmosphere (O2 and 2%H2-N2) was investigated. A successful route to obtain the desirable phase while maintain morphology was found by annealing in O2 at 500 °C with a subsequent anneal in 2%H2-N2 at 600 °C. Annealing in O2 enabled the nucleation of anatase and transformation of almost half of the nucleated anatase to rutile. Subsequent annealing in 2%H2-N2 at 600 °C then transforms some of the rutile into the Magnéli phases. Without the initial annealing in O2 (i.e., directly annealing in 2%H2-N2 from the amorphous state), the lack of oxygen creates so many Vo that the nanotubes begin to degrade, and the underlying titanium substrate over which the NTs are grown reduces and consumes the NTs.
Density functional theory (DFT) for formation of magnéli phases
DFT was used to predict what TiO2 compounds would form based on the relative phase stability of unit cells of Magnéli phase in comparison to the stable TiO2 phase at ambient temperature. Figure 1c shows the DFT model that calculates and predicts thermodynamically stable Ti-O oxides by comparing the relative energies of different oxides to the end members Ti and O which was used as a reference for zero energy (0 eV). The model gives an inverse trend between the phase stability and the amount of oxygen vacancy Vo for the Ti-O oxides. From the first principle calculations, the formation energy of the unit cell was calculated based on the Linear Combination of Atomic Orbitals (LCAO) calculator8,9:
where
Crystal structure and relative stability of Magnéli phases. The 2 × 2 × 2 supercell (primitive unit cell) of tetragonal crystal (a) rutile and (b) anatase, and the triclinic crystal of the Magnéli phases (d) Ti4O7 and (e) Ti5O9. Ti atoms form a green octahedra surrounded by red coloured O atoms at the corners of the octahedra. The Magnéli phase Ti4O7 crystal system made of rutile chains along the c direction and Ti2O3 corundum bounded along the (001) planes (d). Likewise, the Magnéli phase Ti5O9 is composed of rutile chains and Ti3O5 corundum. Corundum in these Magnéli phases refer to shear planes which are induced due to depletion of O atoms. The relative stability of the Magnéli phases (c) in the TiO2 system for unit cell structures as calculated from DFT calculations. The stability diagram shows that Ti5O9 and Ti4O7 are the most stable Magnéli phases in the TiO2 system.
By dividing the total formation energy by the number of atoms in the unit cell to obtain the formation energy/atom, it was shown that the higher the formation energy/atom, the higher the stability of the structure. Figure 1c shows the relative stability of the non-stoichiometric Magnéli phases as a function of the mole fraction of O. The DFT calculation revealed that the most stable phase is TiO2 which showed a formation energy of −3.51 eV/atom. Amongst the sub oxides, the Magnéli phases of Ti5O9 and Ti4O7 were calculated to have highest stability of −3.44 eV and −3.42 eV, respectively. The Magnéli phases are derived from the natural occurring anatase and rutile (Fig. 1a,b)10. Ti4O7 (Fig. 1d) is comprised of periodic arrangement of rutile chains along the c-direction with a Ti2O3 structure along its boundary. The Ti2O3 corundum is made of TiO6 octahedral blocks that share faces. In this structure, the corundum bounds the rutile chains and represents the planes of crystallographic shear in Magnéli phase formed by the occurrence of O vacancies (i.e., the plane of defects)11,12. This Magnéli phase crystallizes in a triclinic structure with a P \(\bar{1}\) space group. The Magnéli phase Ti5O9 has the subtle difference from the Ti4O7 in that the rutile planes are comprised of one extra plane of TiO6 atoms (Fig. 1e). The presence of Vo in the unit cell increases the volume of Ti4O7 (237.72 Å3) to Ti5O9 (302.38 Å3), which occurs when concentration of Vo formed becomes high enough to induce a shear operation in the rutile planes (121) \(\frac{1}{2}\) [0 \(\bar{1}\) 1], resulting in subsequent displacements of atoms in the rutile plane13,14. This shear operation is associated with a dislocation in the direction [0 \(\bar{1}\) 1] of the rutile structure along with shifting of the atoms along the c direction lying above the (121) plane. This dislocation increases the lattice constant c in these Magnéli phases as shown in Table 16. Reduction in the Ti-O bond distances (4,6 pairs) from Ti4O7 (1.87 Å) and Ti5O9 (1.86 Å) respectively are observed (Fig. 2e–h). The difference between the DFT calculated unit cell lattice parameters and experimental values were within 6% of each other15.
DFT based optimized unit cell, band structure and Density of States (DOS) diagram of TiO2 and Magnéli phases. The Normalized DOS diagram for (a) rutile (b) anatase (c) Ti4O7 (d) Ti5O9. Quantum Expresso based PBE optimization (without spin orbit coupling (SOC)) for unit cells of (e) rutile (f) anatase (g) Ti4O7 (h) Ti5O9. DFT based band structures of (i) rutile (j) anatase (k) Ti4O7 (l) Ti5O9. The band structures were calculated along the high symmetry directions of \(\Gamma \to \) X \(\to {\rm{M}}\to \Gamma \to {\rm{Z}}\to {\rm{R}}\to {\rm{A}}\to {\rm{Z}}\) for the tetragonal systems of rutile and anatase, symmetry direction of \({\rm{Q}}\to {\rm{Z}}\to \Gamma \to {\rm{V}}\) for triclinc systems of Magnéli phases of Ti4O7 and Ti5O9.
The normalized electron DOS for rutile, anatase, Ti4O7 and Ti5O9 are presented in Fig. 2. As shown in Fig. 2a and b for both rutile and anatase, the conduction band is mainly comprised of Ti 3d states, whereas the valence band from both is composed of O 2p electrons. However, in the case of Ti4O7 and Ti5O9, Vo tend to form an intermediate band comprised of pseudo-point defects16. This intermediate band forms in a reduced atmosphere when Ti4+ interstitials in the conduction band are converted into Ti3+, which are shallow donor states located below the conduction band minima (CBM). For Ti4O7 and Ti5O9, the intermediate band encompasses the zone of zero energy (Fermi level), thereby reducing the band gap to zero (i.e., semi-metallic).
The electronic DOS results are consistent with our band structure calculations (Fig. 2i–l). The band structure for rutile shows a direct band gap (1.74 eV) in the point of the Brillouin zone (Fig. 2i). However, in the case of anatase, the valence band minima (VBM) occurs at the M point of the Brillouin zone, whereas the conduction band maxima occur at the M point resulting in a non-direct band gap (2.06 eV). The DFT predicted band gaps of anatase and rutile were found to be lower as compared to their experimental band gaps of 3.2 and 3 eV respectively, which is expected since GGA-PBE exchange correlation used in our calculations underestimates the band gap17. For both Ti4O7 and Ti5O9, the intermediate band of pseudo defects (Ti3+) brings down the energy of the conduction band below the Fermi level (Fig. 2k,l). This induces semi-metallic states in the Magnéli phases in the Fermi level zone, making the electron behaviour similar to that of metals.
Formation of Magnéli phases with in NTs
NTs are desirable because of their ordered morphology and high surface area, however, if amorphous, their efficacy is limited by the small fraction of the charge carriers (i.e., electrons and holes). Amorphous NTs are considered electrical insulators at room temperature due to their low conduction and amorphous nature18. These traits make them unattractive for numerous applications where faster electron transfer is needed19. Annealing is performed to form a crystal structure within NTs with more desirable properties. Upon subjecting the anodized amorphous NTs (Fig. 4a) to direct annealing in an 2%H2-N2 environment, hydrogen interacts with the TiO2 lattice depending upon the operating temperature range20. At T < 300 °C, hydrogen physically interacts with the adsorbed oxygen of TiO2 lattice20. At T > 300 °C, electrons from hydrogen begin to transfer to the oxygen of TiO2 lattice leading to oxygen abstraction. This combination forms H2O that leaves the TiO2 surface, resulting in oxygen vacancies. At T > 450 °C, interactions between dissociated H and Ti4+ create Ti3+ interstitial defects20. During 2%H2-N2 annealing at T > 600 °C, the NTs begin to deform as the highly reducing environment deteriorates the outer surface whereas the bottom of the NTs begins to be consumed by the titanium oxide substrate (Fig. 4b), resulting in a large decrease in the wall thickness and the length of the NTs: The wall thickness decreases from 22 ± 3.47 nm for the as anodized NTs (Fig. 3a) to 14 ± 1.2 nm for 2%H2-N2 annealed, and the length decreases from 3 ± 0.33 μm to 1.7 ± 0.18 μm (Table 2). The decrease in the wall thickness is attributed to the loss of TiO2 lattice at the surface that are in direct contact with the reducing gas, whereas the decrease in length is due to the consumption of NTs by nucleation of denser crystals within the NTs and at the Ti-TiO2 interface. Additionally, the elevated temperature and inert atmosphere during annealing promote sintering3, which degrades the NTs morphology, resulting in a loss of ordered morphology and surface area.
SEM images of TiO2 nanotubes. SEM images of nanotubes before and after annealing. (a) As anodized nanotubes (b)Nanotubes annealed in 2%H2-N2 at 600 °C, inset shows the nanotubes along the length. (c) Nanotubes annealed in 2%H2-N2 at 700 °C show degraded nanotubes (d) Nanotubes annealed in 2%H2-N2 at 800 °C show complete crystal structure. (e) Nanotubes annealed in O2 at 500 °C. (f) Nanotubes annealed in O2 at 500 °C and subsequent annealed in 2%H2-N2 at 600 °C.
Schematic showing the morphological changes within NTs during annealing. (a) Anodized amorphous NTs (b) NTs annealed in 2%H2-N2 at 600 °C show degraded nanotubes with changes in color, and high density of crystal growth on the NT walls and the Titanium substrate carrying the NTs. (c) NTs annealed in O2 at 500 °C and subsequent annealed in 2%H2-N2 at 600 °C, stable NTs with increased wall thickness and decreased length, very high density of crystal growth and change in color. (d) NTs annealed in O2 at 500 °C showing stable NTs with comparatively smaller crystal growth structure.
The changes in morphology under reducing environment observed in this study are consistent with Sun et al.21. The nucleation and growth of crystals in NTs is a sequential process with anatase forming at T < 400 °C, followed by rutile at T > 400 °C. Once formed the rutile crystallites catalyses the anatase to rutile transformation and causes dimensional changes and deterioration of the NTs22. At even higher temperatures, and under reducing environment, the rutile crystals become highly defect laden and start reorganizing themselves to Magnéli phases. Annealing below T < 600 °C, the NTs only undergo major morphology changes resulting in shorter, thinner walled tubes (Fig. 3b). Above 600 °C, the tops of the tubes start to aggregate (Fig. 3c) and above 700 °C the NTs shrink and form a matted crystal surface resembling a granular structure over the substrate (Fig. 3d). Formation of Magnéli phases within the NTs through direct annealing cannot be attained and only possible by controlling the morphology with the crystal formation and crystal transformation process.
The fractions of anatase and rutile generated during the 2%H2-N2 and O2 annealing is important and this was using the Spurr equation23:
where, FA is a mass fraction of anatase, and IA and IR are the intensities of strongest anatase and rutile peaks, respectively. At 500 °C, 2%H2-N2 NTs were 90% anatase and 10% rutile. The growth of rutile crystals starts degrading the nanotubes by consuming the anatase crystals because rutile is denser than anatase and grows via surface diffusion from tube walls24.
The critical anatase to rutile conversion in the NTs is possible by one of the two routes. One is the conversion of anatase crystallites growing on the nanotube to rutile at elevated temperatures. The other route happens when rutile is nucleating at the Ti-NTs interface, nucleation is much faster at the interface due to the bulk of the material and subsequently these nucleated crystallites at the interface also nucleate and grow into the NTs18. During annealing NTs predominantly have the second route that is the nucleation and growth at Ti-NTs interface similar to previously reported by Zhu et al.24.
To form Magnéli phases within the NTs while preserving the morphology, the NTs were annealed in O2 at 500 °C with a subsequent annealing in 2%H2-N2 at 600 °C. This double annealing route was designed to create NTs that have rutile crystals (during O2 annealing), followed by the introduction of defects that led to the Magnéli phase formation (during 2%H2-N2 annealing). During O2 annealing, oxygen is retained in the titania lattice, which allows for more anatase to rutile conversion (1:1 ratio of rutile to anatase). This transformation preserves the NT morphology (Fig. 4d), in contrast to the defect formation that occurs during 2%H2-N2 annealing. However, the transformation to the denser rutile phase at the Ti-NT interface consumes the amorphous NTs, leading to a decrease in length to 1.2 μm (Fig. 3e). Subsequent annealing in 2%H2-N2 destabilizes the rutile structure as the hydrogen chemically interacts with the oxygen in the lattice to form H2O20. The destabilized rutile crystals transform to stable Magnéli phases. The competition between nanotube consumption and degradation causes a decrease in length to 0.62 ± 0.31 μm and an increase in wall thickness to 34 ± 3 nm (Fig. 3f). While this morphology change is significant (Fig. 4c), the double annealing route enables the creation of Magnéli phases in nanotubular ordered structures.
XRD patterns of the NTs were analysed to verify the crystal phase transformations with the different annealing treatments. The diffraction pattern of NTs before annealing showed peaks corresponding to the titanium substrate (Fig. 5a). The diffraction pattern of NTs annealed in 2%H2-N2 at 500 °C shows a mixture of anatase and rutile with almost 10% rutile (Fig. 5b). Annealing in this same environment at 600 °C, the concentration of rutile increases to approximately 92% (Fig. 5c). Annealing in 2%H2-N2 at T > 600 °C led to the rapid degradation of the nanotube morphology because of this anatase to rutile conversion, which is a reconstructive nucleation and growth process25. Although the anatase to rutile transformation at 600 °C is thermodynamically favourable, 100% rutile was not formed because the 3 hr annealing time is not long for the kinetics of the transformation as it decreases with the rise in temperature26.
XRD patterns of TiO2 nanotubes annealed at different temperatures (°C). (a) Amorphous as anodized TiO2 nanotubes. (b) Patterns of nanotubes annealed in 2%H2-N2 at 500 °C show mixed anatase and rutile nanotubes with prominent peaks from titanium substrate (c) XRD pattern of nanotubes annealed in 2%H2-N2 at 600 °C with much prominent anatase and rutile peaks then titanium substrate peaks (d) XRD pattern of nanotubes annealed in O2 at 500 °C show similar pattern to 2%H2-N2 at 500 °C with mixed anatase and rutile nanotubes and prominent titanium substrate peaks (e) XRD pattern of nanotubes annealed in O2 at 500 °C and subsequent annealed in 2%H2-N2 at 500 °C show mixed anatase and rutile nanotubes 500 °C with prominent peaks for titanium substrate (f) XRD pattern of nanotubes annealed in O2 at 500 °C and subsequent annealed in 2%H2-N2 at 600 °C showing formation of Magnéli phase Ti4O7.
NTs annealed in O2 at 500 °C show more rutile than those annealed in 2%H2-N2 (50% rutile compared to 10%, respectively) because in the absence of the chemical interactions between the NTs and hydrogen, nucleation and growth of rutile can easily proceed (Fig. 5d). Annealing NTs at 600 °C in O2 showed similar results (not shown). Only a slight broadening of the peaks was observed after a subsequent annealing of the O2 annealed NTs in 2%H2-N2 at 500 °C (Fig. 5e). The Magnéli phase Ti4O7 appears after the O2 annealed NTs are subsequent annealed in 2%H2-N2 at 600 °C (Fig. 5f). At this temperature, the rutile become defect laden and destabilized, which enables the reorganizational process where the rutile crystals undergo atomic rearrangements under oxygen depletion, forming Ti4O715.
High-resolution transmission electron microscopy (HR-TEM) was used to confirm the formation of the Magnéli phase and to analyse the effects on the lattice during the double annealing route (O2 at 500 °C followed by 2%H2-N2 at 600 °C, Fig. 6). Figure 6b shows a well-defined lattice structure, indicating crystalline nanotubes. All Magnéli phases possess similar lattice parameters with the same triclinic crystal structure, which have overlying reflective peaks, making it difficult to distinguish between the phases27. Several locations on the HR-TEM image were used to calculate the lattice distance and the results are in good alignment with the XRD diffraction pattern of the same NTs. Lattice distances showed the samples to be a mixture of phases with characteristic anatase (3.5 Å for anatase [101]), rutile (3.2, 2.4 Å for rutile [110], [101]) and Ti4O7 (1.9,1.6 Å for Ti4O7 [2 \(\bar{2}\) 4], [30 \(\bar{4}\)]).
TEM images of double annealed at 600°C nanotubes. (a,b) TEM images of double annealed (O2 annealed at 500 °C followed by 2%H2-N2 at 600 °C) show the ordered NTs, (c) Magnified Magnéli twinned region; observation of Magnéli phase twinned regions (red dashed lines) on HR-TEM image (d) Selected area diffraction pattern showing presence of different crystal phases.
The presence of twinned regions in the lattices of the HR-TEM images helped in developing an understanding of the formation mechanism of Magnéli phases (Fig. 6d). These twinned regions are formed by changes in crystals (anatase, rutile) due to reducing environment resulting in a high density of aperiodic stacking defects (crystallographic shear planes). These defects are ordered by long range ordered Magnéli phases forming the microtwinned Magnéli crystals28.
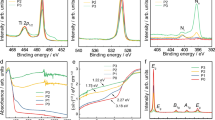
Raman spectroscopy was used to examine the structural difference between the NTs annealed through different routes (Fig. 7). Raman is a useful tool for assessing the TiO2 stoichiometry because the spectra generated is solely from the oxygen stoichiometry3 and this changing stoichiometry assist in determining the phase changes. The decrease in Ti/O ratio causing the formation of Magnéli phases attributes to blue peak shifting around 400 cm−1 and appearance of the broad peak near the anatase peak at 1513. The anatase and the rutile are Raman active between 100–900 cm-129 with tetragonal crystal structure belong to D \(\frac{19}{4h}\) and D \(\frac{14}{4h}\) space groups respectively30. The spectra for as anodized samples showed no crystallinity (Fig. 7). NTs annealed in 2%H2-N2 at 500 °C and 600 °C show similar spectra of a mixed phase with anatase and rutile bands. For the NTs annealed in 2%H2-N2 at 600 °C, the anatase peaks at 166 cm−1 decreased while the rutile peaks intensified. This peak intensification for 2%H2-N2 annealed at 600 °C is a result of the higher fractions of rutile, confirming the XRD results. The spectra of NTs annealed in O2 at 500 °C had the same peak positions as the 2%H2-N2 annealed NTs but intensified peaks, attributed to oxide layer formation on the substrate. Peak shifting, appearance of weak broad peaks and completely new peaks due to formation of Magnéli phases in double annealed NTs are in alignment to previously reported by other researchers3. For the double annealed NTs, the peaks at 166 cm−1 and 390 cm−1 are blue shifted to 170 cm−1 and 399 cm−1, respectively. These peak shifts are due to a reduction in the Ti/O ratio3. The oxygen deficiency is further revealed by a weak broad peak at 200 cm−1. The formation of defects and reduction of Ti/O ratio are due to formation of Magnéli phases. In these NTs, the anatase peak intensity at 170 cm−1 is decreased and the appearance of the new peak at 447 cm−1 is indicative of Magnéli phases.
Raman Spectra of NTs. Raman spectra of amorphous NTs, 2%H2-N2 annealed at 500 °C, 2%H2-N2 annealed at 600 °C, O2 annealed at 500 °C, double annealed at 600 °C. Peak shifting with the peaks at 166 cm−1 and 390 cm−1 for 2%H2-N2 annealed at 500 °C, 2%H2-N2 annealed at 600 °C, O2 annealed at 500 °C samples blue shifted to 170 cm−1 and 399 cm−1 for double annealed NTs, due to a reduction in the Ti-O ratio causing formation of Magnéli phases. The reduction is further revealed by the oxygen deficiency weak broad peak at 200 cm−1. In double annealed NTs, appearance of the new peak at 447 cm−1 was observed indicative of the Magnéli phases.
Conclusion
This study introduced a novel double annealing route (O2 annealing at 500 °C followed by 2%H2-N2 annealing at 600 °C) for the formation of the Magnéli phases within the anodized NTs while preserving their highly ordered morphology. A model was developed using DFT for predicting the stability of titanium oxide phases formed with reference to the mole fraction of oxygen. DFT simulations were also used to estimate the density of states (DOS), band structure, and optical properties of the potential oxides formed. The characterization helped in understanding the morphological, structural, and dimensional changes occurring in the NTs during annealing. The benefits and limitations of annealing the anodized NTs in reducing and oxidizing conditions were analysed. These findings assisted in controlling the process-structure relationship and in developing a synthesis route that allows for the formation of mixed phase NTs with desirable Magnéli phases (Ti4O7) while maintaining their highly ordered morphology.
Materials and Methods
Synthesis of titanium nanotubes
Titanium oxide nanotubes were synthesized according to the electrochemical anodization method from previous work31,32,33. A 99.99% titanium foil (CAS Number 7440-32-6, Alfa Aesar) was used as the starting material for growing NTs. The titanium foil was cut into 2.2 × 2.2 cm strip. Prior to electropolishing and anodization, these foils were ultrasonicated in 15 vol% Hydrochloric acid (CAS Number: 7647-01-0, Sigma-Aldrich) and deionized water (DI). The cleaning and drying was followed by electropolishing. Electropolishing and anodization were carried out at room temperature in a two-electrode electrochemical cell. Titanium foil was used as an anode and platinum gauze was used as a cathode. The electropolishing solution was vinegar with 5% acidity (Kroger white vinegar). During electropolishing the cell was held at 25 volts for 1 minute. The electropolished foils were ultrasonicated in ethanol and DI-water to remove any organic contaminants before subjecting to anodization. Self-aligned nanotubes were grown by anodizing polished foils in an acidic ethylene glycol solution with 96.5 wt% ethylene glycol (CAS Number: 107-21-1, Fisher-Scientific), 0.5 wt% ammonium fluoride (CAS Number: 12125-01-8, Sigma-Aldrich) and 3 wt% DI. For anodization the cell was held at 30 volts for 60 minutes to form NTs. After anodization, the foils with NTs were ultrasonicated in deionized water and air dried overnight32. To improve the properties of these NTs, the amorphous as anodized NTs were subjected to annealing to become crystalline. Direct annealing of the anodized NTs was done in Oxygen (O2) at 500 °C or ultra-pure 2% hydrogen with a nitrogen balance (2%H2-N2) 500 °C. Some of the anodized NTs were subjected to double annealing route, where the NTs were O2 annealing at 500 °C followed by 2%H2-N2 annealing at 600 °C. The annealing furnace was set to reach the desired temperature in 60 minutes and retain the temperature for 180 minutes finally cooling back to room temperature in 60 minutes.
Characterization of nanotubes
Morphology of amorphous and annealed NTs was observed using a field emission scanning electron microscope (FE-SEM, Hitachi, S-4800). The dimensions (Length, wall thickness, diameter) and uniformity of NTs were analysed using ImageJ software. A total of 10 nanotube dimensions for each sample was measured and the standard deviation for each dimension was also calculated. The crystal phases present within the NTs after annealing were observed using x-ray diffractometer (Rigaku MiniFlex 600) with CuKα radiation (λ = 1.54 A) between 2θ = 20°–80° at a rate of 0.025°/s. The XRD pattern were analysed using PDXL software. The Fast Fourier Transform (FFT) and Selected Area electron Diffraction (SAED) patterns were generated using high resolution transmission electron microscope (S/TEM, JEOL JEM-2800), and were analysed using Gatan, and ImageJ. Raman spectra were produced using micro-Raman spectroscopy (WiTec AlphaSNOM).
DFT modelling
The band structures were calculated along the high symmetry directions of \(\Gamma \,\to \) X \(\to {\rm{M}}\,\to \Gamma \to {\rm{Z}}\to {\rm{R}}\to {\rm{A}}\to {\rm{Z}}\) for the tetragonal systems of rutile and anatase, symmetry direction of \({\rm{Q}}\to {\rm{Z}}\to \Gamma \to {\rm{V}}\) for triclinc systems of Magnéli phases of Ti4O7 and Ti5O9. Norm-conserving pseudopotential was used under the framework of General Gradient Approximation (GGA) along with the implementation of Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional for density functional theory calculations16. The plane wave pseudopotential was used within the QUANTUM-ESPRESSO22 package with the aid of BURAI 1.3 as a GUI for the first principle calculations of TiO2 and other Magnéli variants. For each of these compounds, unit cells were used for structural optimizations during which limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm was used and the formation energy per atom total energy was calculated by using PBE exchange-correlation functional34. During the structural cells of TiO2 and other Magnéli variants was then used for band structure and Density of States calculations, keeping the electronic occupation fixed as in case of semiconductors. A dense (5 × 5 × 5) Monkhorst-Pack k-point sampling was used for Brillouin-zone integration. The kinetic energy cut-off for the wave function was 340 Ry and the corresponding value for charge density was 3400 Ry.
Data availability
Data available upon request from Krista Carlson (krista.carlson@utah.edu).
References
Arif, A. F. et al. Highly conductive nano-sized Magnéli phases titanium oxide (TiOx). Sci. Rep. 7, 1–9 (2017).
Walsh, F. C. & Wills, R. G. A. The continuing development of Magnéli phase titanium sub-oxides and Ebonex® electrodes. Electrochim. Acta 55, 6342–6351 (2010).
Li, H., Zhou, T., Hu, S., Su, Z. & Yan, Y. Ti6O11 nanofiber: A new material with robust switching characteristic for memories. Chem. Eng. J. 312, 328–335 (2017).
Kao, W. H., Patel, P. & Haberichter, S. L. Formation enhancement of a lead/acid battery positive plate by barium metaplumbate and Ebonex®. J. Electrochem. Soc. 144, 1907–1911 (1997).
Jemec Kokalj, A. et al. The first comprehensive safety study of Magnéli phase titanium suboxides reveals no acute environmental hazard. Environ. Sci. Nano 6, 1131–1139 (2019).
Padilha, A. C. M., Raebiger, H., Rocha, A. R. & Dalpian, G. M. Charge storage in oxygen deficient phases of TiO2: Defect Physics without defects. Sci. Rep. 6, 2–8 (2016).
Johnson, O. W. Field-enhanced conductivity in TiO2 (Rutile). Appl. Phys. Lett. 13, 338–339 (1968).
Kaasbjerg, K. & Flensberg, K. Strong polarization-induced reduction of addition energies in single-molecule nanojunctions. Nano Lett. 8, 3809–3814 (2008).
Sarswat, P. K., Sarkar, S., Yi, G. & Free, M. L. Phosphorus-Doped SnTe-Type Needle-like Crystals: Band Structure Modifications and Electronic Properties. J. Phys. Chem. C 121, 18263–18273 (2017).
Yang, Y. et al. Discovery and ramifications of incidental Magnéli phase generation and release from industrial coal-burning. Nat. Commun. 8, (2017).
Liborio, L., Mallia, G. & Harrison, N. Electronic structure of the Ti4O7 Magnéli phase. Phys. Rev. B - Condens. Matter Mater. Phys. 79 (2009).
Harada, S., Tanaka, K. & Inui, H. Thermoelectric properties and crystallographic shear structures in titanium oxides of the Magǹli phases. J. Appl. Phys. 108 (2010).
Padilha, A. C. M., Rocha, A. R. & Dalpian, G. M. DFT+U simulation of the Ti4O7-TiO2 interface. Phys. Rev. Appl. 3, 1–5 (2015).
Andersson, S. The Crystal Structure of Ti5O9. Acta Chem. Scand. 14, 1161–1172 (1960).
Padilha, A. C. M., Osorio-Guillén, J. M., Rocha, A. R. & Dalpian, G. M. TinO2n-1 Magnéli phases studied using density functional theory. Phys. Rev. B - Condens. Matter Mater. Phys. 90, 1–7 (2014).
Giannozzi, P. et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, (2009).
Lee, J., Seko, A., Shitara, K., Nakayama, K. & Tanaka, I. Prediction model of band gap for inorganic compounds by combination of density functional theory calculations and machine learning techniques. Phys. Rev. B 93, 1–12 (2016).
Fabregat-Santiago, F., Garcia-Belmonte, G., Bisquert, J., Zaban, A. & Salvador, P. Decoupling of transport, charge-storage, and reaction in the behavior of nanocrystalline TiO2 electrodes in the dark. J. Phys. Chem. B. 106, 334–339 (2002).
Hahn, R. et al. Semimetallic TiO2 nanotubes. Angew. Chemie - Int. Ed. 48, 7236–7239 (2009).
Liu, H. et al. The enhancement of TiO2 photocatalytic activity by hydrogen thermal treatment. Chemosphere 50, 39–46 (2003).
Sun, Y., Yan, K., Wang, G., Guo, W. & Ma, T. Effect of Annealing Temperature on the Hydrogen Production of TiO2 Nanotube Arrays in a Two-Compartment Photoelectrochemical Cell. J. Phys. Chem. C 115, 12844–12849 (2011).
Weissmann, M. & Weht, R. Electronic and magnetic properties of the different phases of Ti4O7 from density functional theory. Phys. Rev. B - Condens. Matter Mater. Phys. 84 (2011).
Padmanabhan, S. C. et al. A simple sol - Gel processing for the development of high-temperature stable photoactive anatase titania. Chem. Mater. 19, 4474–4481 (2007).
Zhu, K., Neale, N. R., Halverson, A. F., Kim, J. Y. & Frank, A. J. Effects of annealing temperature on the charge-collection and light-harvesting properties of TiO2 nanotube-based dye-sensitized solar cells. J. Phys. Chem. C 114, 13433–13441 (2010).
Hanaor, D. A. H. & Sorrell, C. C. Review of the anatase to rutile phase transformation. J. Mater. Sci. 46, 855–874 (2011).
Rao, C. N. R. Kinetics and Thermodynamics of the Crystal Structure Transformation of Spectroscopically Pure Anatase To Rutile. Can. J. Chem. 39, 498–500 (1961).
Gusev, A. A., Avvakumov, E. G. & Vinokurova, O. B. Synthesis of ti4O7magneli phase using mechanical activation. Sci. Sinter. 35, 141–145 (2003).
David, J., Trolliard, G. & Maître, A. Transmission electron microscopy study of the reaction mechanisms involved in the carbothermal reduction of anatase. Acta Mater. 61, 5414–5428 (2013).
Petkov, P., Tsiulyanu, D., Kulisch, W. & Popov, C. Pathways for the Production of Non-stoichiometric Titanium Oxides Perica. Nanosci. Adv. CBRN Agents Detect. Inf. Energy Secur. v–vi, https://doi.org/10.1007/978-94-017-9697-2 (2015).
Ma, H. L. et al. Raman study of phase transformation of TiO2 rutile single crystal irradiated by infrared femtosecond laser. Appl. Surf. Sci. 253, 7497–7500 (2007).
Beeman, M. G. et al. Electrochemical detection of E. Coli O157:H7 in water after electrocatalytic and ultraviolet treatments using a polyguanine-labeled secondary bead sensor. Sensors (Switzerland) 18 (2018).
Carlson, K., Elliott, C., Walker, S., Misra, M. & Mohanty, S. An Effective, Point-of-Use Water Disinfection Device Using Immobilized Black TiO 2 Nanotubes as an Electrocatalyst. J. Electrochem. Soc. 163, H395–H401 (2016).
Huber, J. M., Carlson, K. L., Conroy-Ben, O., Misra, M. & Mohanty, S. K. Development of a field enhanced photocatalytic device for biocide of coliform bacteria. J. Environ. Sci. (China) 44, 38–44 (2016).
Perdew, J. P., Burke, K. & Ernzerhof, M. The stability of ionic crystal surfaces. Journal of Physics C: Solid State Physics, 12(22), 4977. 77, 3865–3868 (1996).
Acknowledgements
This work was made possible by the support of the National Science Foundation (NSF # 1706283) and by the support of the United States Government and the American people through the United States Agency for International Development (USAID). The contents are the sole responsibility of the University of Utah and do not necessarily reflect the views of USAID or the United States Government. The authors would also like to thank “Roger and Dawn Crus Center for Metallurgy Student Research” for financial support for undergraduate student research. This work made use of University of Utah USTAR shared facilities supported, in part, by the MRSEC Program of the NSF under Award No. DMR-1121252.
Author information
Authors and Affiliations
Contributions
H.M. synthesized titanium nanotubes conducted all the experiments and wrote several portions of the manuscript. S.S. performed all the simulations and wrote the manuscript section talking about the DFT, first principal calculations and modelling. K.C. helped in providing the ideas, funds, and wrote several sections of the manuscript. S.M. edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Malik, H., Sarkar, S., Mohanty, S. et al. Modelling and synthesis of Magnéli Phases in ordered titanium oxide nanotubes with preserved morphology. Sci Rep 10, 8050 (2020). https://doi.org/10.1038/s41598-020-64918-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-64918-0
This article is cited by
-
In situ TEM investigation of the oxide/metal interface during the annealing of anodically formed titanium dioxide nanotubes
Journal of Materials Science (2023)
-
Microstructure and Micromechanical Properties of In situ Synthesized TiO2−x Coatings by Plasma Spraying of Bimodal Feedstocks
Journal of Thermal Spray Technology (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.