Abstract
MgAl2O4 spinel is important optical material for harsh radiation environment and other important applications. The kinetics of thermal annealing of the basic electron (F, F+) and hole (V) centers in stoichiometric MgAl2O4 spinel irradiated by fast neutrons and protons is analyzed in terms of diffusion-controlled bimolecular reactions. Properties of MgAl2O4 single crystals and optical polycrystalline ceramics are compared. It is demonstrated that both transparent ceramics and single crystals, as well as different types of irradiation show qualitatively similar kinetics, but the effective migration energy Ea and pre-exponent D0 are strongly correlated. Such correlation is discussed in terms of the so-called Meyer-Neldel rule known in chemical kinetics of condensed matter. The results for the irradiated spinel are compared with those for sapphire, MgO and other radiation-resistant materials.
Similar content being viewed by others
Introduction
Spinel materials based on magnesium aluminate (MgAl2O4) possess unique physical and chemical properties which determines their widespread investigations and attracts increasing interest for their use in various scientific and industrial applications (see1,2 and references therein). In particular, MgAl2O4 single crystals and transparent polycrystalline ceramics (further called as optical ceramics) are planned to be exploited as diagnostics windows in future fusion devices3,4 or to be used as materials for different laser media5, phosphors for solid state lighting and 3D printing6,7, scintillators8, matrices for fiber-optic temperature sensors9,10, and even as a porous material for humidity sensors11,12. MgAl2O4 spinel materials are also used as a substrate for thin film growth13,14, alternative waste immobilization matrices15,16 or target materials in the nuclear transmutation of actinides17. For numerous nuclear applications, an extremely high tolerance against heavy irradiation or prolonged stay in harsh environment with practically no swelling18,19 is of particular importance.
Extremely high tolerance of MgAl2O4 against intense radiation at least partly results from the lattice structure. Stoichiometric magnesium aluminate spinel is an equimolar mixture of MgO and Al2O3. Oxygen ions form face-centered cubic structure, while Al3+ cations with relatively large ionic radius occupy a half of octahedral interstices and small-radius Mg2+ cations are located at every eighth tetrahedral site20. In addition to large empty space in such “normal” MgAl2O4, the cationic sublattice can be easily disordered due to the favorable conditions for the swapping of cation positions and the appearance of cations in “wrong” positions − Mg|Al or Al|Mg. The formation energy of these so-called antisite defects (ADs), which are charged (-1 or +1) with respect to a regular lattice, is significantly lower than that for any other elementary lattice defects21. Just this circumstance explains the presence of a considerable concentration of ADs in as-grown single crystals and optical ceramics, while further irradiation even increases the degree of cation disorder, a kind of structural inversion.
The radiation effects in constituent parts of MgAl2O4 − MgO and Al2O3 binary oxides have been thoroughly studied (see22,23,24,25,26,27,28,29,30,31,32,33,34,35 and references therein) and the results on the microstructure, creation mechanisms and annealing kinetics of Frenkel defects (interstitial-vacancy pairs) and their simplest aggregates have been extended to magnesium aluminate single crystals and optical ceramics (see, e.g.36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52). Note that electron-type primary lattice defects, the F+ and F centers (one or two electrons in the field of an oxygen vacancy) clearly manifest themselves in optical spectra36,38,43,49, while the as-grown and radiation-induced trapped hole V-type centers have been reliably detected by the electron paramagnetic resonance (EPR) method53,54,55,56,57,58. Notably, the main experimental results belong to vacancy-containing structural defects, while complementary oxygen interstitials (not associated with some additional lattice defect/impurity) are still the most “hidden” defects in metal oxides and cation interstitials easily undergo transformation and, as a result, mainly exist in the form of ADs.
In radiation-resistant MgAl2O4, structural defects are mainly formed via the universal displacement mechanism connected with the elastic collisions of incident energetic particles with material atoms/ions. Nevertheless, this impact mechanism is solely responsible for radiation damage in metals and alloys induced by fast neutrons (i.e. neutral particles, see, e.g59. and references therein). The situation is more complicated in case of wide-gap material irradiation with charged particles, which spend a significant part of their energy on the formation of different electronic excitations. According to further studies60,61,62,63,64,65,66,67,68, especially favorable conditions for the creation of structural defects via ionization mechanisms (connected with different electronic excitations) occur within the tracks of ~GeV heavy ions. However, the defect creation mechanisms connected with the decay/recombination of anion excitons/relaxed electron-hole pairs, which ensure radiation damage in model alkali halide crystals (see, e.g.69), are not realized in the majority of metal oxides (including MgAl2O4), where the formation energy of a Frenkel defect pair exceeds the energy gap, EFD > Eg. Therefore, less stable and more energetic electronic excitations (e.g., hot, non-relaxed e-h pairs63,64,66,67,68) could contribute to radiation damage under metal oxide irradiation with swift ions (including protons).
The present paper is devoted to the measuring of the thermal annealing kinetics of structural defects, both electron (F+ and F centers) and hole origin (paramagnetic V centers), induced in MgAl2O4 single crystal and optical ceramics by fast fission neutrons or 100-keV protons with varying fluence. The annealing curves are also simulated in terms of diffusion-controlled bimolecular reactions, and the features of the obtained kinetic parameters are considered and compared with those for other wide-gap materials. It is notable that kinetic parameters provide indirect information just on “poorly studied” oxygen and cation interstitials, which are acting as mobile components in the recombination process with vacancy-containing complementary Frenkel defects.
Note that the present study is a logical continuation of our previous investigations regarding the experimental analysis of electronic excitations and structural defects in magnesium aluminate spinel with different stoichiometry57,58,70,71 as well as a recent phenomenological theory of diffusion-controlled recombination of Frenkel defects in wide-gap materials72,73,74,75,76,77,78.
Methods used
Experimental
Nominally pure MgAl2O4 single crystals (i.e. a stoichiometric spinel) were grown by Union Carbide Corporation using the Czochralski method and irradiated by fast fission neutrons with fluence of Φ = 1017 n/cm2 and Φ = 2.6 × 1018 n/cm2 at Oak Ridge National Laboratory (neutron energy > 1 MeV and irradiation temperature T ≤ 60 °C). Single crystals contained several dozen ppm of iron ions as well as the traces of Cr, Ca, and Mn impurities (see also38).
Transparent polycrystalline ceramics of MgAl2O4 with a grain size of 0.5, 1.4 and 12 μm were sintered by hot isostatic pressing in argon at 1510−1600 °C (lower value for the smallest grain size, upper − for 12-μm grains) at the Fraunhofer Institute for Ceramic Technologies and Systems. The lowest grain size was achieved by addition of a special doping, while a coarser spinel raw powder was used for the highest grain size. Stoichiometric ceramic samples contained impurities below 100 ppm in total, had inversion parameter about 0.4 (estimated on the basis of the lattice parameter determined by XRD78) and were in the form of polished 1-mm thick plates. The similar parameter of cation disorder in single crystals was lower, about 0.1–0.2.
The MgAl2O4 optical ceramics were irradiated with the 100-keV protons and Φ = (1-5) × 1017 p/cm2 using KIIA 500 kV ion implanter of Accelerator Laboratory at the University of Helsinki (see also71). According to SRIM simulation79, the penetration depth of such protons equals about 0.5 μm, while the radiation damage level exceeds ~1 dpa.
The spectra of optical absorption in a spectral region from 1.5 to 6.5 eV were measured by a spectrometer JASCO V-660, while a homemade setup equipped with a vacuum monochromator VMR-2 and the hydrogen discharge source allowed performing measurements up to 10 eV. The EPR measurements were made with an X-band (9.8 GHz) spectrometer Bruker ELEXYS-II E500. This study of paramagnetic centers was performed for a neutron-irradiated (Φ = 2.7 × 1018 n/cm2) single crystal in the form of rectangular parallelepiped, one [110] axis of which was parallel to the magnetic field (see57 for details).
The stepwise thermal annealing of radiation damage was performed in the following way: (i) a porcelain boat with the irradiated samples was placed inside a quartz reactor of a furnace; (ii) heated from room temperature (RT) to a certain temperature Tpr in an argon atmosphere; (iii) kept at this Tpr for 10 min; and then (iv) cooled down by moving the reactor out of the furnace. Multiple “heating-cooling-measuring” cycles were executed under the same conditions with the rise of Tpr by 20–40 K for all samples preliminary irradiated with protons or fast neutrons. Note that all optical absorption and EPR spectra for the samples subjected to the ascribed annealing procedure were measured at RT.
Theoretical
In order to analyze the experimental recombination kinetics, we have recently developed72,73,74,75,76 a simple phenomenological theory that takes into account the mutual diffusion-controlled approach to the electron and hole centers and their recombination. This model allows us to extract the key diffusion parameters – the effective migration energy Ea of more mobile species and the pre-exponential factor X = N0RD0/β, where N0 is initial defect concentration, R recombination radius, D0 pre-exponent for diffusion, and β heating rate upon defect thermal annealing. The typical value of the pre-exponential parameter for a normal solid state diffusion72,74 is X = 101° K−1 if N0 = 1019 cm−3. This theory was successfully applied to sapphire, MgO and MgF2 crystals irradiated by energetic electrons, neutrons, protons or heavy ions72,74,75,76,77 and is used in the present study for MgAl2O4 spinel.
It is also well known that the F center in МgО and Al2O3 is immobile until ca. 1500 K22, so just its complementary defect – an interstitial oxygen ion – is significantly more mobile and reaches the F-type center before mutual recombination72,74. The situation in MgAl2O4 spinel is more unclear. We will try to discuss the contradictory results in this work.
Results
Irradiation of MgAl2O4 crystals by high-energy particles and quanta causes the creation of different color centers/radiation defects responsible for the appearance of several optical absorption bands within the transparency region of virgin (non-irradiated) samples. As a result, the functionality of optical materials/components strongly depends on the radiation damage kinetics − accumulation of radiation defects with the irradiation fluence/dose as well as their annealing (i.e., recovery of optical properties) via a subsequent thermal treatment of the irradiated materials. In the present study, we analyzed the changes in the spectra of optical absorption caused by both the irradiation of MgAl2O4 single crystals/optical ceramics with fast neutrons or 100-keV protons and the subsequent thermal annealing of radiation damage in the irradiated samples.
Figure 1 presents, as an example, the spectra of optical absorption measured in a wide spectral region of 1.5–7.5 eV for a MgAl2O4 sample before (curve 1) and after irradiation (curve 2). The difference between these two absorption spectra has been considered as the radiation-induced optical absorption (RIOA, curve 3) representing the number (concentration) of the corresponding radiation defects. Figure 1a shows the spectra for a single crystal with thickness of d = 0.86 mm exposed to fast fission neutrons (Φ = 1017 n/cm2), while Fig. 1b is related to the irradiation of a transparent ceramic sample with 100-kev protons (Φ = 1017 p/cm2). Note that rather different values of RIOA around 5 eV in parts (a) and (b) reflect the homogeneous coloration through the whole sample thickness in case of neutron irradiation and a rather small amount of F-type centers formed in a thin sample layer (~ 0.5 μm) by 100-keV protons.
According to the literature36,37,38,43,49,53, a broad complex RIOA band peaked around 5.3 eV is mainly connected with electron-type F+ and F centers and the hole-containing color centers are responsible for the RIOA at ~3–4 eV. Note that the existing impurities, mostly Fe, Cr, Mn contribute to the absorption spectra as well (from IR to UV spectral region, see36,37,38,50,51 and references therein). Of particular interest is the origin of optical absorption above 6.5 eV, near the tentative edge of fundamental absorption. Despite the long-term investigations of MgAl2O4, even such fundamental characteristics of an insulating material as the value of the energy gap Eg was not precisely determined. According to the recent studies of MgAl2O4 single crystals and optical ceramics by means of several optical methods70,71, the Eg value at low temperature slightly exceeds 8 eV. In addition, the analysis of the excitation spectra for different emissions and phosphorescence allowed us to conclude that the spectral region of 6.8–7.4 eV is typical of the formation of excitonic-like states, i.e. such exciting photons cause the formation of bound excitons near charged ADs70,71. This suggestion is supported by the peak of RIOA at about 7 eV revealed during the process of thermal annealing of neutron- or proton-irradiated MgAl2O4 samples (see57,71).
Figure 2 demonstrates the complexity of the main RIOA band peaked around 5.25 eV. Figure 2a depicts a difference spectrum that reflects the decrease of RIOA caused by fast-neutron-irradiation as a consequence of a single crystal preheating from 490 to 697 K (see curve with symbols − ooo). This spectrum is decomposed into several elementary Gaussian components, the parameters of which (integrated area S or peak intensity Imax) can be considered to be a measure of the number of corresponding defects. As it has been already stated, we are interested in the annealing kinetics of electron-type F+ and F centers with well-defined characteristics of optical absorption. Therefore, other Gaussian components, a part of which is related to ADs or as-grown impurities and other structural defects, are not a subject of the present paper.
The decomposition of RIOA difference spectra into Gaussian components (thin lines) for an MgAl2O4 single crystal (a) or ceramic sample (b, grain size of 12 μm)) irradiated by fast neutrons and 100-keV protons, respectively. The difference spectra represent the decrease of RIOA caused by the preheated of the irradiated sample from 490 to 697 K (part a) and from 546 to 747 K (b). Symbols (ooo) depict experimental points and solid line − a fitted curve.
In case of predominance of a certain radiation defect (according to Fig. 2 − F centers are such radiation-induced defects in our case), there is a very small difference in thermal annealing curves for the F centers, the number of which has been estimated in three different ways: via Imax (in units of optical density) and S or even as the value of optical density (without decomposition into Gaussians) measured at photon energy where the contribution of a certain defect to RIOA is dominant. This conclusion, important from methodological point of view, has been proved recently for the case of F-type center annealing in MgO single crystals irradiated with swift heavy ions80. The accuracy of the estimation of the number of F+ centers in MgAl2O4 is certainly lower. Nevertheless, it is possible to select a certain hν where just the F+ centers are mainly responsible for optical absorption.
The electronic centers
The results of theoretical analysis of annealing kinetics for the F and F+ centers created by fast neutrons or protons are summarized in Table 1. As one can see, the measurements were performed for both single crystals and optical ceramics with different grain size; moreover, different radiation fluences were used. The annealing kinetics was analyzed for both the electron (F+, F) and hole (V1, V2) centers.
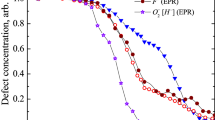
Typical annealing kinetics for the F centers after neutron and proton irradiation are shown in Fig. 3 (curves I-II and III-IV, respectively). These kinetics reveal monotonous and smooth decay of defect number (concentration) with temperature, similar to the previous study for sapphire, MgO and MgF274. Note that the decay kinetics of the F+ centers in spinel samples is very similar to that for F centers and is not presented in Fig. 3. Because of rather large grain size of the used optical ceramics. In addition, there is no noticeable difference in the decay kinetics of F-type centers in our optical ceramics with different but rather large grain size. It is not surprising, because a “grain-size effect” (if any) could be expected in a real nanometer scale region (definitely below 100 nm). Theoretical curves (solid lines) fit very well to the experimental points. This allows us to extract by means of square fitting two key migration parameters, Ea and X with high accuracy.
Kinetics of the F and V2 center annealing in MgAl2O4 samples (see Table 1 for details, only five representative kinetics are plotted here for illustration).
As one can see in Table 1, both parameters reveal considerable variations, dependent on experimental conditions. The most surprising thing is that the parameter X for all experimental conditions is much smaller than that in the previously mentioned estimate for a normal solid-state diffusion, X = 101° K−1 (N0 = 1019 cm−3)72,74. Moreover, these two parameters, Ea and X, show a strong correlation when plotted in the coordinates ln(X) versus Ea (see Fig. 4): the smaller energy, the smaller the relevant pre-exponential. It is noteworthy that bimolecular recombination rate contains a product X·exp(−Ea/kBT), this is why ln(X) instead of X is correlated with Ea. The observed linear correlation is fulfilled very well within eight orders of magnitude in X; the standard Pearson correlation coefficient is almost one. The similar strong correlation of the migration energy and pre-exponential factor we have recently observed in several other radiation-resistant ionic solids – Al2O3, MgO, MgF274,77. This type of correlation is known in chemical kinetics as Mayer-Neldel rule (MNR)81,82,83
where X0 is constant and T0 characteristic temperature. In other words, the diffusion pre-exponent X turns out to be exponentially dependent on the migration energy. As a result, the effective diffusion coefficient now reads:
Despite confirmation of the MNR in this paper, there is considerable difference between spinel samples analyzed here and three above-mentioned ionic solids74. For instance, the obtained interstitial migration energy of 0.89 eV obtained at low fluences in α-Al2O3 is close to the calculated Ea for charged oxygen interstitials in a regular crystal, 0.8–1.0 eV84 (for neutral interstitial atoms the calculated energy barrier is higher, 1.3 eV). Similarly, the migration energy of 1.74 eV obtained in MgO from the experiment at low fluences is again close to the calculated 1.5 eV85. Lastly, for the lowest radiation dose of MgF2, the migration energy is also quite high, 1.74 eV. Moreover, high migration energies are accompanied by large pre-exponetials X: 1.4 × 105 K−1 (for MgO) or 4.8 × 1010 K−1 (for MgF2) comparable to the above-mentioned estimate for a perfect solid, X~1010 K−1. These kinetic parameters corresponding to the low fluences and almost perfect solids are located in the upper right corner of the MNR diagram (see Fig. 4). With the fluence increase, the relevant energies and pre-exponentials move along the line to the low-left corner of the diagram.
However, defects in MgAl2O4 show quite different pattern: for all possible fluences both migration energy and pre-exponential are small and far from those expected for a crystalline solid, e.g. Ea ~ 1.0 eV calculated for interstitial oxygen ions in spinel52. This circumstance indicates to some new defect annealing mechanism. Note that the MNR is typically observed in strongly disordered systems81,82,83. In amorphous solids and liquids86,87, the particle (defect) diffusion jumps over energy barriers are replaced by a collective motion of atoms surrounding the defect; thermal density fluctuations create cavities for particle migration with low energy and low pre-exponential factor (rare events). To some degree, strongly irradiated solids could be considered as partly disordered, which results in MNR observation.
Hole centers
Besides RIOA at 3–4 eV ascribed in the literature to V centers36,37,43, several hole-containing paramagnetic defects complementary to the F-type electron centers have been revealed in neutron-irradiated (Φ = 2.6 × 1018 n/cm2) MgAl2O4 single crystals by means of the EPR method (see also57,58). On the basis of g-factor value, angular dependence of the measured EPR spectra and the modelling program EasySpin88 it was proved that all revealed paramagnetic centers are of hole-type, while a hole is trapped at a regular oxygen ion O2- (forming O- ion) next to some negatively charged defect. In case of so-called V1 and V2 centers, such negative defect, formed under neutron irradiation, appeared to be an aluminium and magnesium vacancy, respectively (VAl and VMg).
The pulse annealing of the EPR signal of these centers with the model of V1 ≡ O–VAl and V2 ≡ O–VMg was performed under the same conditions as the described above thermal annealing of RIOA. It was stated in57,58 that V1 and V2 radiation-induced defects decay irreversibly (as a kind of ionic process) and these structural defects cannot be restored by the subsequent X-ray irradiation (i.e. via recharging of potentially available as-grown cation vacancies by X-ray-induced charge carriers).
Curve V in Fig. 3 presents theoretical fitting (solid line) of the measured (experimental points are given by symbols) pulse annealing curve for the EPR signal of the V2 defects in a neutron-irradiated MgAl2O4 single crystal, whereas Table 1 gives the Ea and X for both hole centers, V1 and V2. According to Table 1 (Nos. 13 and 14), the values of Ea are very close for both hole centers (0.64 eV) but differ from those for F-type centers in the same neutron-irradiated MgAl2O4 crystals (0.44 eV). On the other hand, pre-exponential factors X for these hole centers vary by three orders of magnitude staying again in all cases significantly smaller than a typical value of X = 1010 K−1 72. The difference in Ea values is reasonable because, in contrast to the annealing of F-type centers (see the previous Section), cation interstitials play the role of a mobile recombination component: becoming mobile they reach and fulfil complementary cation vacancies which are constitutive of neutron-induced V1 and V2 centers. It is important to remind that, by energetic reasons, cation interstitials from neutron-induced Frenkel pairs in spinel crystals undergo transformation into antisite defects with the lowest formation energy21. Note that the V2 center decay parameters fit well to the MNR (Fig. 4), which indicates to a strong correlation between the electron and hole center annealing.
Concluding remarks
This study shows that the annealing of the electron centers in spinel, unlike parent binary oxides (MgO, Al2O3), is a multistage process. Based on the EPR-proved microstructure of paramagnetic defects and their thermal stability, we can conclude that, upon heating of the irradiated sample to ~400 K, Al3+ interstitials from Al|Mg are the first defects to become mobile and able to fill-in an aluminum vacancy of the V1 defect producing irreversible decay of these radiation defects. At temperatures above ~500 K, Mg2+ interstitials from Mg|Al antisite defects in their turn become mobile, reach V2 centers and destroy them via fulfilling magnesium vacancies. Probably, the observed energies (Nos. 13 and 14 in Table 1) correspond to these processes.
Note that both decay processes of V1 and V2 defects are accompanied by the decrease of the number of F-type centers (continues attenuation of the corresponding RIOA at T = 380–850 K). After filling the cation vacancies, the holes are released from V1 and V2 centers and could recombine with the electrons from the F and F+ centers. However, the irreversible annealing of RIOA responsible for the F and F+ centers occurs simultaneously and without any sign of recharging of these centers. Note that identical thermal annealing of F+ and F centers takes place in MgO crystals irradiated by swift heavy ions as well80. Therefore, the final destruction of the F and F+ centers or their products requires participation of oxygen interstitials which could be spatially correlated to the F and F+ centers. Alternatively, the mobile holes could release the trapped oxygen interstitials (e.g., at antisite defects) and stimulate their recombination with the F-type centers. However, this would need the energies of the order of 1 eV, much higher than those observed here. Thus, the physical meaning of the energies for the F-type centers in Table 1 remain unclear yet.
Note that the elastic collisions of fast neutrons with crystal atom nuclei lead to the creation of interstitial-vacancy Frenkel pairs in anion and cation sublattice. The involvement of both oxygen and cation interstitials is needed to describe the tentative scenario of the annealing of paramagnetic hole-containing centers in MgAl2O4 single crystal. A search for experimental manifestations of oxygen interstitials in MgAl2O4 (as well as in other binary and complex metal oxides) and the elucidation of their microstructure, preferable charge states, diffusion and trapping mechanisms still lies ahead.
References
Ganesh, I. A review on magnesium aluminate (MgAl2O4) spinel: synthesis, processing and applications. International Materials Reviews. 58, 63–112 (2013).
Rubat du Merac, M., Kleebe, H. J., Müller, M. M. & Reimanis, I. E. Fifty years of research and development coming to fruition; unraveling the complex interactions during processing of transparent magnesium aluminate (MgAl2O4) spinel. Journal of the American Ceramic Society. 96, 3341–3365 (2013).
Ibarra, A. & Hodgson, E. R. The ITER project: the role of insulators. Nucl. Instr. and Meth. B. 218, 29–35 (2004).
Gonzales de Vicente, S. G., Hodgson, E. R. & Shikama, T. Functional materials for tokamak in-vessel systems – status and applications. Nucl. Fusion. 57, 092009 (2017).
Jouini, A., Yoshikawa, A., Brenier, A., Fukuda, T. & Boulon, G. A. Optical properties of transition metal ion‐doped MgAl2O4 spinel for laser application. Physica Status Solidi C. 4, 1380–1383 (2007).
Song, E. et al. Thermally stable narrow-band green-emitting phosphor MgAl2O4:Mn2+ toward Wide Color Gamut Backlight Display Application. J. Mater. Chem. C. 7, 8192–8198 (2019).
Rimpongpisarn, T. et al. (2019). Novel luminescent PLA/MgAl2O4:Sm3+ composite filaments for 3D printing application. Materials Letters. 237, 270–273 (2019).
Chen, C. F. et al. Characterizations of a hot-pressed polycrystalline spinel:Ce scintillator. J. Am. Ceram. Soc. 93, 2399–240 (2010).
Jiang, H. et al. Synthesis and characterization of spinel MgAl2O4 thin film as sapphire optical fiber cladding for high temperature applications. Thin Solid Films. 539, 81–87 (2013).
Aizawa, H. et al. Characteristics of chromium doped spinel crystals for a fiber-optic thermometer application. Review of scientific instruments. 73, 3089–3092 (2002).
Klym, H. et al. Nanoporous characterization of modified humidity-sensitive MgO-Al2O3 ceramics by positron annihilation lifetime spectroscopy method. IOP Conference Series: Materials Science and Engineering. 503, 012019 (2019).
Klym, H. et al. Nanostructural free-volume effects in humidity-sensitive MgO-Al2O3 ceramics for sensor applications. Journal of Materials Engineering and Performance. 25, 866–873 (2016).
Liu, K. et al. Formation of antiphase boundaries in CuFe2O4 films induced by rough MgAl2O4 (001) substrates. Thin Solid Films. 680, 55–59 (2019).
Fukami, N., Wakamatsu, R., Shinozaki, N. & Wasai, K. Wettability between porous MgAl2O4 substrates and molten iron. Materials transactions. 50, 2552–2556 (2009).
Weber, W. J. et al. Radiation effects in crystalline ceramics for the immobilization of high-level nuclear waste and plutonium. Journal of Materials Research. 13, 1434–1484 (1998).
Wang, L. & Liang, T. Ceramics for high level radioactive waste solidification. Journal of Advanced Ceramics. 1, 194–203 (2012).
Wiss, T. & Matzke, H. Heavy ion induced damage in MgAl2O4, an inert matrix candidate for the transmutation of minor actinides. Radiation measurements. 31, 507–514 (1999).
Pells, G. P. & Murphy, M. J. The effects of transmutation products on the radiation-induced swelling of Al2O3 and MgAl2O4. Journal of Nuclear materials. 183, 137–144 (1991).
Kinoshita, C. & Zinkle, S. J. Potential and limitations of ceramics in terms of structural and electrical integrity in fusion environments. Journal of Nuclear materials. 233, 100–110 (1996).
Tropf W. J., Thomas M. E., Magnesium Aluminum Spinel (MgAl2O4), in: E.D. Palik (Ed.), Handbook of Optical Constants of Solids II, Academic Press, 1991, pp. 883-897.
Gilbert, C. A. et al. Theoretical study of intrinsic point defects and defect clusters in magnesium aluminate spinel. J. Phys.: Condens. Matter. 21, 275406 (2009).
Chen Y., Williams R. T., Sibley W. A. Defect cluster centers in MgO. Phys. Rev. 182 (1969) 960-964 (1969).
Evans, B. D. Spectral study of Ne+-bombarded crystalline MgO. Phys. Rev. B 9, 5222–5235 (1974).
Halliburton, L. E. & Kappers, L. A. Radiation-induced oxygen interstitials in MgO. Solid State Commun. 26, 111–114 (1978).
Evans, B. D. A review of the optical properties of anion lattice vacancies, and electrical conduction in α-Al2O3: their relation to radiation-induced electrical degradation. J. Nucl. Mater. 219, 202–223 (1995).
Kotomin, E. A. et al. Calculations of diffusion energies for defects in MgO crystals. Defects and Diffusion Forum. 143-147, 1231–1236 (1997).
Popov, A. I., Monge, M. A., González, R., Chen, Y. & Kotomin, E. A. Dynamics of F-center annihilation in thermochemically reduced MgO single crystals. Solid state communications. 118, 163–167 (2001).
Dolgov, S. et al. (2002). Thermoluminescence centres created selectively in MgO crystals by fast neutrons. Radiation protection dosimetry. 100, 127–130 (2002).
Skuratov, V. A., Zinkle, S. J., Efimov, A. E. & Havancsak, K. Swift heavy ion-induced modification of Al2O3 and MgO surfaces. Nucl. Instrum. Meth. B. 203, 136–140 (2003).
Carrasco, J., Lopez, N. & Illas, F. First principles analysis of the stability and diffusion of oxygen vacancies in metal oxides. Phys. Rev. Lett. 93, 225502 (2004).
Uberuaga, B. P. et al. Dynamical simulations of radiation damage and defect mobility in MgO. Phys. Rev. B. 71, 104102 (2005).
Lushchik, A. et al. Dependence of long-lived defect creation on excitation density in MgO single crystals, Phys. Status Solidi C. 4, 1084–1087 (2007).
Lushchik, A. et al. Stabilization and annealing of interstitials formed by radiation in binary metal oxides and fluorides. Nucl. Instrum. Meth. B. 266, 2868–2871 (2008).
Izerrouken, M. & Benyahia, T. Absorption and photoluminescence study of Al2O3 single crystal irradiated with fast neutrons. Nucl. Instrum. Meth. B 468, 2987–2990 (2010).
Yuan, Y. G. et al. Ab initio molecular dynamics simulation of low energy radiation responses of α-Al2O3. Scientific reports. 7, 3621 (2017).
Summers, G. P., White, G. S., Lee, K. H. & Crawford, J. H. Jr Radiation damage in MgAl2O4. Physical Review B. 21, 2578–2584 (1980).
White, G. S., Jones, R. V. & Crawford, J. H. Jr Optical spectra of MgAl2O4 crystals exposed to ionizing radiation. J. Appl. Phys. 53, 265–270 (1982).
Cain, L. S., Pogatshnik, G. J. & Chen, Y. Optical transitions in neutron-irradiated MgAl2O4 spinel crystals. Physical Review B. 37, 2645–2652 (1988).
Sickafus, K. E. et al. Cation disorder in high dose, neutron-irradiated spinel. Journal of Nuclear Materials 219, 128–134 (1995).
Ibarra, A., Vila, R. & Garner, F. A. Optical and dielectric properties of neutron irradiated MgAl2O4 spinels. Journal of Nuclear Materials. 233, 1336–1339 (1996).
Yasuda, K., Kinoshita, C., Morisaki, R. & Abe, H. Role of irradiation spectrum in the microstructural evolution of magnesium aluminate spinel. Phil. Mag. A. 78, 583–598 (1998).
Wiss, T. et al. Damage produced in magnesium aluminate spinel by high energy heavy ions including fission products of fission energy: Microstructure modifications. Progress in Nuclear Energy 38, 281–286 (2001).
Gritsyna, V. T., Afanasyev-Charkin, I. V., Kazarinov, Y. G. & Sickafus, K. E. Optical transitions in magnesium aluminate spinel crystals of different composition exposed to irradiation. Nucl. Instrum. Meth. B. 218, 264–270 (2004).
Gritsyna, V. T., Kazarinov, Y. G., Kobyakov, V. A. & Reimanis, I. E. Radiation-induced luminescence in magnesium aluminate spinel crystals and ceramics. Nucl. Instrum. Meth. B. 250, 342–348 (2006).
Yasuda, K. et al. Atomic structure and disordering induced by 350 MeV Au ions in MgAl2O4. Nucl. Instrum. Meth. B. 250, 238–244 (2006).
Bacorisen, D. et al. Atomistic simulation of radiation-induced defect formation in spinels: MgAl2O4, MgGa2O4 and MgIn2O4. Phys. Rev B 74, 214105 (2006).
Uberuaga, B. P. et al. Defect kinetics in spinels: long-time simulations of MgAl2O4, MgGa2O4 and MgIn2O4. Phys. Rev. B. 75, 104116 (2007).
Jozwik, I. et al. Ion beam-induced luminescence as method of characterization of radiation damage in polycrystalline materials. Nucl. Intstrum. Methods B. 365, 273–277 (2015).
Costantini, J. M. et al. Color-center production and recovery in electron-irradiated magnesium-aluminate spinel and ceria. J. Phys.: Condens. Matter. 28, 325901 (2016).
Mironova-Ulmane, N. et al. Luminescence and EPR spectroscopy of neutron-irradiated single crystals of magnesium aluminium spinel. Radiat. Meas. 90, 122–126 (2016).
Borges, P. D., Cott, J., Pinto, F. G., Tronto, J. & Scolfaro, L. Native defects as sources of optical transitions in MgAl2O4 spinel. Materials Research Express. 3, 076202 (2016).
Platonenko, A., Gryaznov, D., Zhukovskii, Y. F. & Kotomin, E. A. First principles simulations on migration paths of oxygen interstitials in MgAl2O4. Phys. Status Solidi B. 255, 1800282 (2018).
Ibarra, A., Lopez, F. J. & de Castro, M. J. V centers in MgAl2O4 spinels. Phys. Rev. B. 44, 7256–7262 (1991).
Ibarra, A., Mariani, D. F. & De Castro, M. J. Thermoluminescence processes of MgAl2O4 irradiated at room temperature. Phys. Rev. B. 44, 12158–12165 (1991).
Ibarra, A. et al. Dose dependence of neutron irradiation effects on MgAl2O4 spinels. J. Nucl. Mat. 258−263, 1902–1907 (1998).
Ibarra, A., Bravo, D., Lopez, F. J. & Garner, F. A. High-dose neutron irradiation of MgAl2O4 spinel: effects of post-irradiation thermal annealing on EPR and optical absorption. J. Nucl. Mat. 336, 156–162 (2005).
Lushchik, A. et al. Creation and thermal annealing of structural defects in neutron-irradiated MgAl2O4 single crystals. Nucl. Intstrum. Methods B. 435, 31–37 (2018).
Seeman, V. et al. Fast-neutron-induced and as-grown structural defects in magnesium aluminate spinel crystals with different stoichiometry. Opt. Mater. 91, 42–49 (2019).
Thompson, M., Defects and Radiation Damage in Metals, Univ. Press, Cambridge (1969).
Arnold, G. W., Krefft, G. B. & Norris, C. B. Atomic displacement and ionization effects on the optical absorption and structural properties of ion‐implanted Al2O3. Applied Physics Letters. 25, 540–542 (1974).
Canut, B. et al. High energy heavy ion irradiation effects in α-Al2O3. Nucl. Intstrum. Methods B. 80, 1114–1118 (1993).
Schwartz, K., Trautmann, C. & Neumann, R. Electronic excitations and heavy-ion-induced processes in ionic crystals. Nucl. Intstrum. Methods B. 209, 73–84 (2003).
Lushchik, A. et al. Defect creation caused by the decay of cation excitons and hot electron-hole recombination in wide-gap dielectrics. Nucl. Intstrum. Methods B. 250, 330–336 (2006).
Lushchik, A. et al. Some aspects of radiation resistance of wide-gap metal oxides. Radiat. Meas. 42, 792–797 (2007).
Itoh, N., Duffy, D. M., Khakshouri, S. & Stoneham, A. M. Making tracks: electronic excitation roles in forming swift heavy ion tracks. J. Phys.: Condens. Matter. 21, 474205 (2009).
Lushchik, A. et al. Electronic excitations and defect creation in wide-gap MgO and Lu3Al5O12 crystals irradiated with swift heavy ions. Nucl. Intstrum. Methods B. 286, 200–208 (2012).
Lushchik, A. et al. On the mechanisms of radiation damage and prospects of their suppression in complex metal oxides, Phys. Status Solidi B. 250, 261–270 (2013).
Lushchik, A. et al. Influence of complex impurity centres on radiation damage in wide-gap metal oxides. Nucl. Intstrum. Methods B. 374, 90–96 (2016).
Lushchik, C., Lushchik, A. Evolution of anion and cation excitons in alkali halide crystals. Fiz. Tverd. Tela 60, 1478–1494 [Phys. Solid State 60, 1487-1505(2018)]. https://doi.org/10.1134/S1063783418080164 (2018).
Prieditis, G. et al. Luminescence characteristics of magnesium aluminate spinel crystals of different stoichiometry. IOP Conf. Ser.: Mater. Sci. Eng. 503, 012021 (2019).
Feldbach, E. et al. Optical characteristics of virgin and proton-irradiated ceramics of magnesium aluminate spinel. Opt. Mater. 96, 109308, https://doi.org/10.1016/j.optmat.2019.109308 (2019).
Kotomin, E., Kuzovkov, V., Popov, A. I. & Vila, R. Kinetics of F center annealing and colloid formation in Al2O3. Nucl. Intstrum. Methods B. 374, 107–110 (2016).
Kuzovkov, V. N., et al Theoretical analysis of the kinetics of low-temperature defect recombination in alkali halide crystals, Fiz. Nizk. Temp. 42 748–755. [Low Temp. Phys. 42 (2016) 588-593] https://doi.org/10.1063/1.4959018 (2016).
Kotomin, E., Kuzovkov, V., Popov, A. I., Maier, J. & Vila, R. Anomalous kinetics of diffusion-controlled defect annealing in irradiated ionic solids. J. Phys. Chem. A 122, 28–32 (2018).
Kuzovkov, V. N., Kotomin, E. A. & Popov, A. I. Kinetics of dimer F2 type center annealing in MgF2 crystals. Nucl. Intstrum. Methods B. 435, 79–82 (2018).
Kuzovkov, V. N., Kotomin, E. A. & Popov, A. I. Kinetics of the electronic center annealing in Al2O3 crystals. J. Nucl. Mater. 502, 295–300 (2018).
Popov, A. I. et al. Comparison of the F-type center thermal annealing in heavy-ion and neutron irradiated Al2O3 single crystals. Nucl. Intstrum. Methods B. 433, 93–97 (2018).
Ball, J. A. et al. Predicting lattice parameter as a function of cation disorder in MgAl2O4 spinel. J. Phys.: Condens. Matter. 17, 7621–7631 (2005).
Zeigler, J. F., Biersack, J. P., & Littmark, U. The Stopping and Ranges of Ions in Solids. Pergamon Press, New York 1985 (www.srim.org).
Baubekova, G. et al. Thermal annealing of radiation damage produced by swift 132Xe ions in MgO single crystals. Nucl. Intstrum. Methods B. 462, 163–168 (2200).
Meyer, W. & Neldel, H. Concerning the relationship between the energy constant epsilon and the quantum constant alpha in the conduction-temperature formula in oxydising semi-conductors. Phys. Z. 38, 1014–1019 (1937).
Jones, A. G. Compensation of the Meyer-Neldel compensation law for H diffusion in minerals. Geochem. Geophys. Geosyst. 15, 2616–2631 (2014).
Dyre, J. C. A phenomenological model for the Meyer-Neldel rule. J. Phys. C: Solid State Phys. 19, 5655–5664 (1986).
Platonenko, A., Gryaznov, D., Zhukovskii, Y. F. & Kotomin, E. A. Ab initio simulations on charged interstitial oxygen migration in corundum. Nucl. Intstrum. Methods B. 435, 74–78 (2018).
Brudevoll, T., Kotomin, E. A. & Christensen, N. E. Interstitial oxygen atom diffusion in MgO. Phys. Rev. B. 53, 7731–7735 (1996).
Frenkel, Y. I. Kinetic Theory of Liquids; Clarendon Press: Oxford, 1946.
Faber, T. E. An Introduction to the Theory of Liquid Metals; Cambridge University Press: Cambridge, 1972.
Acknowledgements
This work has been performed within the framework of the EUROfusion Enabling Research project: ENR-MFE19.ISSP-UL-02 “Advanced experimental and theoretical analysis of defect evolution and structural disordering in optical and dielectric materials for fusion application”. The views and opinions expressed herein do not necessarily reflect those of the European Commission. Research of A.L, E.F.,, V.S and E.S has been partly supported by the Estonian Research Council grant (PUT PRG619); has been also carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under grant agreement No 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
Author information
Authors and Affiliations
Contributions
E.F., I.K. and E.S. performed all optical absorption measurements, thermal annealing of the samples as well as processed the data; V.S. – E.P.R. measurements, while E.A.K., V.N.K. and A.I.P. performed theoretical modeling of thermal annealing kinetics. A.L., E.A.K., V.N.K. and A.I.P. wrote the main manuscript text; A.L. and A.I.P. supervised and coordinated this research; A.L., E.A.K., V.N.K. and A.I.P. contributed to the to the research planning and scientific discussions. All authors reviewed and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lushchik, A., Feldbach, E., Kotomin, E.A. et al. Distinctive features of diffusion-controlled radiation defect recombination in stoichiometric magnesium aluminate spinel single crystals and transparent polycrystalline ceramics. Sci Rep 10, 7810 (2020). https://doi.org/10.1038/s41598-020-64778-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-64778-8
This article is cited by
-
Morphological and Photophysical Tempering in Spinel MgAl2O4 Synthesized by a Novel Citrate Route Via a Suitable Annealing Scheme
Journal of Electronic Materials (2023)
-
Investigations of most versatile MAl2O4 (M=Zn, Mg, Ca) nanopowder advantageous as inexpensive, efficient photocatalyst against methyl blue dye
Applied Nanoscience (2023)
-
Evidence for the formation of two types of oxygen interstitials in neutron-irradiated α-Al2O3 single crystals
Scientific Reports (2021)
-
Study of radiation resistance to helium swelling of AlN ceramics in case of irradiation with low-energy He2+ ions with energy of 40 keV
Journal of Materials Science: Materials in Electronics (2021)
-
Atomic, electronic and magnetic structure of an oxygen interstitial in neutron-irradiated Al2O3 single crystals
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.