Abstract
Bimetallic clusters have aroused increased attention because of the ability to tune their own properties by changing size, shape, and doping. In present work, a structural search of the global minimum for divalent bimetal Be2Mgn (n = 1–20) clusters are performed by utilizing CALYPSO structural searching method with subsequent DFT optimization. We investigate the evolution of geometries, electronic properties, and nature of bonding from small to medium-sized clusters. It is found that the structural transition from hollow 3D structures to filled cage-like frameworks emerges at n = 10 for Be2Mgn clusters, which is obviously earlier than that of Mgn clusters. The Be atoms prefer the surface sites in small cluster size, then one Be atom tend to embed itself inside the magnesium motif. At the number of Mg larger than eighteen, two Be atoms have been completely encapsulated by caged magnesium frameworks. In all Be2Mgn clusters, the partial charge transfer from Mg to Be takes place. An increase in the occupations of the Be-2p and Mg-3p orbitals reveals the increasing metallic behavior of Be2Mgn clusters. The analysis of stability shows that the cluster stability can be enhanced by Be atoms doping and the Be2Mg8 cluster possesses robust stability across the cluster size range of n = 1–20. There is s-p hybridization between the Be and Mg atoms leading to stronger Be-Mg bonds in Be2Mg8 cluster. This finding is supported by the multi-center bonds and Mayer bond order analysis.
Similar content being viewed by others
Introduction
Metallic clusters, in particular, have attracted a great deal of attention in recent years due to not only their unique properties of electronic, magnetic, optical, and mechanical but also the wide applications in nanomaterials, hydrogen storage, catalyst, biomedicine, and spintronics1,2,3,4,5,6,7. The typical metallic clusters include alkali metal clusters of Lin8,9 and Nan10,11, noble metal clusters of Aun12,13,14, Agn15,16 and Cun17,18, along with magnetic transition metal clusters of Fen19,20, Con21,22, Nin23,24,25 and so on. Based on previous studies, one can draw the following conclusion that these clusters usually exhibit superior properties compared to metals in terms of activity, selectivity, stability, bonding character, and charge transfer. In addition, their superior properties sensitively depend on clusters size, element components, and dopants.
As a divalent metal, magnesium clusters have been extensively studied by both experimental and theoretical fields26,27,28,29,30,31. In previous works, one main focus of the studies is on size-induced nonmetal-to-metal transition of magnesium clusters. It is well known that the atom of divalent metal Mg has s2 closed-shell electron configuration as helium. So the bonding of the magnesium dimer is expected to be van der Waals-like32. As the number of atoms grows, the electronic properties of clusters transfer from van der Waals to covalent, then to metallic behavior. For example, Kaplan et al.33 point out that the binding in alkaline-earth trimers (Be3 and Mg3) has a mixed of physical (van der Walls) and chemical (nonadditive exchange) nature, which is different from their dimers. Gong et al.34 performed a detailed investigations in terms of the nearest neighbor bond length and s-p hybridization of the magnesium clusters. By measuring the photoelectron spectra (PES) of Mgn‾ (n = 2–22) clusters, Thomas and co-workers35 observed the s-p band gap of magnesium cluster anions to close at n = 18, signaling the onset of metallic behavior. Then the metallic behavior of Mgn‾ clusters was well explained by Jellinek and Acioli36,37 through an analysis of charged distribution characteristics of 3p orbital. In neutral Mgn clusters, this nonmetal-to-metal transition has been reported to occur around n = 2038. Another main thrust of the studies is a systematic discussion on structural and energetic properties of magnesium clusters along with their magic number. Note that the Jellium model has been most successful for explaning the magic number of the simple alkali metal clusters, even for confirming the magic number of the noble metal Aun clusters. For Mgn clusters, the ab initio calculations indicate the magic number N = 4, 10, and 20 for small sized clusters30,39,40,41, which is in agreement with simple Jellium model. However, the finding of new experiment reveals the most intensive peaks in the mass spectra at N = 5, 10, 15, 18, and 2031. Thus one can find that the stability of the Mgn clusters is not only related to their electronic shell configuration but also affected by geometric structures.
Despite a number of investigations have been carried out on the pure Mgn clusters, however, little work has been done so far on the exploration of the divalent bimetal clusters. Beryllium, as one of the lightest divalent metal, has s2 valence electronic configuration. Therefore, the properties of the beryllium clusters are very similar to magnesium clusters. The small beryllium clusters also show van der Waals character bonding and the transition from nonmetal to metal occurs around Be1342. The theoretical studies indicate more stability of small sized beryllium clusters with magic number N = 4, 10, 17, and 2043,44. So it seems a systematic study is necessary to probe the structural evolution and bonding characters of Be-doped magnesium clusters. The starting point of this work can be summarized as follows: (1) We can find the most stable structures and elucidate the structural evolution process of Be2Mgn (n = 1–20) clusters. (2) By discussing the bonding and electronic nature, we can gain a deeper understanding of the microscopic mechanisms of these bivalent bimetal clusters (3) It might provide some theoretical guidance for the development of the magnesium-based materials and their applications in catalyst, hydrogen storage, and corrosion-resistant.
Results and discussions
Geometric structure
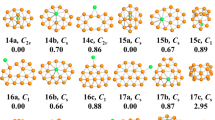
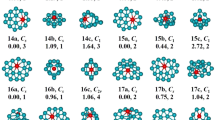
In light of their total energies of the low energetic and stable cluster candidates, the most stable isomers Be2Mgn clusters in the size range of n = 1–20 are confirmed and presented in Fig. 1. Moreover, the typical low-lying isomers, together with their relative energies and symmetries of the Be2Mgn clusters are shown in Figs. S1 and S2. (Supplementary Information). It can be noted that our theoretical dissociation energy (0.073 eV) for the Mg2 dimer agrees well with experimental result of 0.049 eV36. We can get the error in the calculation of the energy around 0.024 eV. It is clearly lower than the relative energies of the low-lying isomers. To discuss the effect of dopants on the geometries and properties of magnesium clusters, the most stable structures of pure Mgn clusters are also displayed in Fig. 1. Note that the isomers of Mgn reported by earlier works29,30,36,37,38,39,40,41 are reproduced by utilizing CALYPSO structural searching method. The most stable structures of the Mgn clusters obtained in our searches are consistent with previous results. This suggests the current method is capable of correctly identifying the lowest energy structure of magnesium and magnesium-based clusters. We list the electronic states and point group symmetries of the most stable isomers of Mgn and Be2Mgn in Table 1.
Let us compare geometries of Be2Mgn to those of pure magnesium clusters. We can find several attractive results. (1) The transition point from 2D to 3D structures is n = 2 for Be2Mgn clusters, which is consistent with that of pure Mgn+2 clusters. However, the configurations transition from hollow 3D structures to filled cage-like frameworks emerges at n = 10 for Be2Mgn clusters, which is obviously earlier than that of n = 14 for Mgn+2 clusters. (2) The Be2Mgn clusters keep the original shapes of the corresponding Mgn+2 clusters at n = 1–3, 5–8 and 16. Namely, the most stable isomers of the Be2Mg1–3,5–8,15 clusters are viewed as the substituted structures of corresponding Mg3–5,7–10,17 clusters, in which two Mg atoms are replaced by Be atoms. Due to the difference of atomic radius of Mg and Be atoms, these doped structures occur with some degree of distortion. Conversely, the remaining Be2Mgn clusters show different geometries in contrast to pure Mgn+2 clusters. It implies that the dopants might produce major influence on the frameworks of magnesium clusters in these case. (3) The Be impurity atoms prefer the convex capped sites in the size range of n = 1–4, then trend to the surface sites of the skeleton in clusters size of n = 5–9. As the number of Mg increases, stating from n–10, a different trend emerges. One of the Be atoms still localizes at the surface site, while the other tend to embed itself inside the magnesium motif. In Be2Mg16–18 clusters, the Be atom is back at the surface sites of the skeleton. At the number of Mg larger than eighteen, the Be impurity atoms have been completely encapsulated by caged magnesium framework and made more Be-Mg bonds together with surrounding Mg atoms. (4) It is worth mentioning that the most stable isomer of Mg17 cluster displays a fascinating cage structure with high D4d symmetry. Although the Be2Mg15 cluster remains this cage structure, the symmetry turns to Cs from D4d owing to effect of dopants. As shown in Fig. S2, we have predicted a high symmetric Be2Mg15 cluster (D5h symmetry) with a pentagram-shaped structure, however, it is 0.16 eV higher in total energy than the most stable isomer of Be2Mg15 cluster. In fact, for Be2Mg16–18 clusters, we also have generated some low-lying structures with two Be atoms being completely encapsulated. Further energy calculation show that these structures are less stable than the corresponding most stable isomers. Similarly, some low-lying structures with two Be atoms localizing at the surface site have been yielded for Be2Mg19–20 clusters. The present results suggest that the isomers are all less stable.
Size dependence of relative stability
Studies of the average binding energy (\({E}_{b}\)) can, therefore, shed light on the size-induced inherent stability of the Mgn+2 and Be2Mgn (n = 1–20) clusters. For mentioned clusters, \({E}_{b}\) values are calculated as
where \(E\) denote the total energy of the corresponding clusters or atoms. Figure 2(a) shows how the \({E}_{b}\) values of the Mgn+2 and Be2Mgn clusters evolve with increasing cluster size. The features of the curves are easily explained, as are the local maximum of the shapes corresponding to those clusters with robust stabilities. In the size range studied here, the \({E}_{b}\) values of doped species are always much higher than those of pure clusters. It suggests that the stabilities of the pure magnesium clusters can be enhanced by means of Be atoms doping. As cluster size increases, the averaged binding energies of doped clusters approach gradually those of pure magnesium clusters because the contributing proportion of Be atoms decreases in larger size doped clusters. The graphics of \({E}_{b}\) for both Mgn+2 and Be2Mgn clusters show the similar pattern, namely generally growing behavior with increase of cluster size and common local maximum at n = 2, 8, and 18. For large clusters, n ≥ 19, the values of \({E}_{b}\) decrease somewhat. The appearance of the maximum indicates that Be2Mg2,8,18 and Mg4,10,20 clusters have relatively strong energetic stabilities. This finding can be interpreted by spherical Jellium model, in which the spherical magic clusters with 8, 20, 40 valence electrons corresponding to the closed electronic subshells turn out to be relatively stable.
Another manifestation of the size-induced variation in cluster stability is exhibited in Fig. 2(b), which depicts the dependence of the second-order energy difference (\({\varDelta }^{2}E\)) on cluster size. For mentioned clusters, \({\varDelta }^{2}E\) values are calculated as
As shown in the graphics, for both the Mgn+2 and Be2Mgn clusters, the \({\varDelta }^{2}E\) display the similar odd-even oscillating behaviors in the range of n = 10 − 16. There are several obvious peaks at n = 5, 8, 11, 13, 15, and 18. It can reflect more relative stabilities of the Be2Mgn and Mgn+2 (n = 5, 8, 11, 13, 15, and 18) clusters. Specially, the Be2Mg8 cluster has the largest \({\varDelta }^{2}E\) value of 1.17 eV.
Let us now regard the highest occupied and the lowest unoccupied molecular orbitals energy gaps (HOMO–LUMO gaps) of the mentioned clusters. According to the energies of the frontier molecular orbitals, gaps \({E}_{g}\) of the most stable isomers of the Mgn+2 and Be2Mgn (n = 1–20) cluster are calculated and listed in Table 1. Meanwhile, the change of \({E}_{g}\) versus the number of Mg atoms are shown in Fig. 2(c). One can find that the values of \({E}_{g}\) for them exhibits a slowly but rather nonmonotonously decreasing tendency, indicating the more enhancive metallicities for the larger-sized Mgn+2 and Be2Mgn clusters. It is worth noting that tendency of gaps for pure magnesium clusters agree well with previous findings by Kuang et al.30, Acioli et al.36,37, and Lyalin et al.38. For Be2Mgn (n = 1–20) clusters, the local peaks in the curve of \({E}_{g}\) at n = 2, 8, 11, 15, and 18 accord with above analysis based on \({E}_{b}\) and \({\varDelta }^{2}E\). It signifies that these clusters possess dramatically enhanced chemical stability. Furthermore, we come to conclusion that the effect of doping Be atoms on the gaps of the Mgn clusters is slight in the range of n = 1 − 20. The reason may be that there is similar valence electron structure for Be and Mg atoms.
Ionization potential, electron affinity, chemical hardness, and charge transfer
It is well known that the vertical ionization potential (VIP), vertical electron affinity (VEA), and chemical hardness is very sensitive to the electronic structure of clusters. The correctness of our calculation is supported by the good agreement between experimental and theoretical VIP for the Mg atom (7.646 eV36 vs 7.542 eV). In Table 2, we summarize the VIP, VEA, and chemical hardness (η) of the Mgn+2 and Be2Mgn (n = 1–20) clusters. The size-dependent behavior of the VIP is shown in the Fig. 3(a). As the cluster size increases, the curves of VIP for both Mgn+2 and Be2Mgn clusters exhibit decreasing tendency in general, which means that it is easier for the larger-sized clusters to lose an electron than the smaller sized ones. On the whole curve of Be2Mgn clusters, we can clearly see some pronounced local peaks at n = 2, 8, 11, 15, and 18, indicating their high chemical stability. Indeed this finding is supported by the results of the chemical hardness. As shown in Fig. 3(b), one can also find the identical local peaks of chemical hardness for Be2Mg2,8,11,15,18 clusters. It is worth pointing that local maxima of VIP and η agree well with the results of the HOMO–LUMO gaps. In addition, the values of η for both Mgn+2 and Be2Mgn clusters tend to decrease with the growing of the number of Mg atoms for the given size.
With the aid of the natural population analysis (NPA), we can obtain the charges on Be atoms of the Be2Mgn (n = 1–20) clusters, as listed in Table 1. The results show that the Be atoms in all doped clusters act as the electron acceptors owing to the negative values of charges on them. Since the Be atom (1.59) is much more in electronegativity than the Mg atom (1.31), the partial charge transfer from Mg to Be takes place in Be2Mgn clusters. In Fig. 4, we depict the size dependence of total charge on Be atoms of the Be2Mgn clusters. The results show that charge transfer, in general, increases with the increasing cluster size. Two visible maximum of charge transfer occur at n = 5 and 13. To extract more charge transfer information, the natural electronic configuration (NEC) of the Be2Mgn (n = 1–20) clusters are listed in Table S1 of supplementary information. From the table, it is found that there is a large donation of electrons from the Be-2s and Mg-3s orbitals. Meanwhile, in corresponding clusters, the unfilled Be-2p orbitals accept 0.63–3.76 electrons, while Mg-3p orbitals accept 0.10–2.09 electrons, which illustrates the charge transfers occur in intramural s and p orbitals of the clusters. As the cluster size increases, the occupations of the Be-2s and Mg-3s orbitals decease while their 2p and 3p orbitals occupations increase. Previous works on Mgn clusters36,37 have proposed that the occupations of p orbital in Mgn clusters is an evident character of metallic bonding. Therefore, an increase in the occupations of the Be-2p and Mg-3p orbitals is a marker of the increasing metallic behavior of Be2Mgn clusters.
Bonding Characters
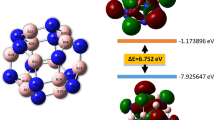
It would be interesting to shed light on the chemical bonding properties of the Be2Mgn clusters. Due to the outstanding stability, we select Be2Mg8 to be a acceptable candidate for probing the bonding feature. In Fig. 5, we analyzed its molecular orbitals and the corresponding energy levels. Because the Be2Mg8 cluster has a shell-closed electronic structure, the HOMO is doubly occupied and the LUMO is 1.99 eV higher in energy than the HOMO. Based on natural bond orbital (NBO) analysis, the components of the given molecular orbital can be obtained by Multiwfn program. For Be2Mg8 cluster, the components of LUMO contain the 13.4% of p atomic orbital (AO) of two Be atoms as well as 37.5% of s AO and 49.1% of p AO from Mg atoms. The HOMO is generated by 21.6% of Be-s AO and 25.2% of Be-p AO along with 53.2% Mg-s and Mg-p AO. For other occupied MOs, the s orbitals of the Be atoms have 6.4% contribution to the HOMO-1, while s and p AO of Mg atoms have 93.6% contribution to it. The px and py orbitals of Be atoms as well as the Mg-s, Mg-px, and Mg-py, are mainly included in HOMO-2 and HOMO-6. The HOMO-3 and HOMO-5 mostly originate from Be-p, Mg-s, and Mg-p AOs. There are 37% of Be-pz, 42.9% of Mg-s, and 20% Mg-p AO in HOMO-4. With regard to HOMO-7, the molecular orbital is mainly formed by equivalent contributions (about 23%) of Be-s and Be-p together with 33% Mg-s and 21% Mg-pz AOs. It is remarkable that the s-p hybridization between the Be and Mg atoms might lead to strong Be-Mg bonds in Be2Mg8 cluster.
To further understanding the bonding characters, we analyze the multi-center bonds and corresponding bond orders. Based on the AdNDP method, a systemic search of n-center two-electron (nc-2e) bonds is performed. It is a localized bond when n = 1 and 2, whereas it is delocalized bond when n ≥ 3. The most stable Be2Mg8 cluster is to be a suitable candidate. To give a clear insight of the distribution of the multi-center bonds, we first provide a structural diagram with all atomic labels in Fig. 6(a). Then the Fig. 6(b) displays the multi-center bonds and their occupation numbers (ONs) of Be2Mg8 cluster. Below each multi-center bonds images, the structural units generated these multi-center bonds and their bond orders are exhibited. The theoretical results reveal that non localized bond, however, eleven delocalized bonds are included in Be2Mg8 cluster. In detail, one 3c-2e σ-type bond with ON = 1.83 |e| is formed by trigonal Be(1)-Be(2)-Mg(3) unit. The multi-center bond order is 0.418. Four delocalized bonds are all 3c-2e σ-type bonds (ON = 1.78–1.71 |e|) with contributions of each planar BeMg2 units. Because of different Be-Mg bond lengths in different units, it is found that the multi-center bond orders are the highest value of 0.453 for BeMg2 units including atom labels of 1–5–8 and 2–7–8, whereas they are 0.445 for 2–6–9 and 1–4–9 of BeMg2 units. There are two 5c-2e σ-type bonds with ON = 1.83 |e|, which is derived from two BeMg4 units of 1-4-5-6-10 and 2-4-6-7-10. Their multi-center bond orders are 0.285 and 0.213, respectively. Two 7c-2e with ON = 1.91–1.78 |e| (two different Be2Mg5 units) and two 8c-2e with ON = 1.84 |e| show π-type bonding character. Their multi-center bond orders are 0.272, 0.149, 0.212, and 0.179, respectively. In order to deeply examine the nature of bonding, the Mayer bond orders for each bonds of the most stable Be2Mg8 cluster are listed in Table S2. From the table, we can find that the Be atoms have formed some strong Be-Mg bonds together with their adjacent Mg atoms because the Mayer bond orders of these Mg-Be bonds are bigger than those of Be-Be bond and the most Mg-Mg bonds in Be2Mg8 cluster.
Conclusions
In a summary, for the most stable Be2Mgn clusters, the transition point from 2D to 3D structures is n = 2 and configurations transition from hollow 3D structures to filled cage-like frameworks emerges at n = 10. In small sized, two Be atoms prefer surface capped positions. Then one Be atom tends to embed itself inside the magnesium motif with increasing cluster size. When n ≥ 19, two Be atoms have been completely encapsulated by caged magnesium framework. It is found that the charges transfer from Mg to Be atoms in all Be2Mgn clusters. As the cluster size grows, the occupations of the Be-2p and Mg-3p orbitals increase, indicating the increasing metallic behavior of Be2Mgn clusters. The investigation of the clusters stability reveal that the stabilities of Mgn clusters can be enhanced by means of Be atoms doping and Be2Mg8 cluster is very stable in studied cluster range. There are obvious s-p hybridization of the Be and Mg atoms in Be2Mg8 cluster, which might induce stronger Be-Mg bonds. It is supported by the multi-center bonds and Mayer bond order analysis.
Computational methods
To achieve the the most stable isomers of Mgn+2 and Be2Mgn clusters, it is necessary to utilize an efficient algorithm of global optimization for searching the global minima of the different sized clusters. Here we rely on the CALYPSO code45,46,47, which can quickly search the most stable structures of the clusters on the bases of the particle swarm optimization algorithm. The validity of this method for clusters structure predicting has been demonstrated by its successful application of various clusters48,49,50,51,52,53,54,55. In detail, trial structures of the clusters are ordered in generations in the process of searching. Each generation contains 50 structures, 60% of which are produced by PSO algorithm, whereas the rest is generated randomly. We performed 30 generations to produce 1000–1500 structurally different isomers for each clusters. The underlying geometric optimizations and energy computations for these isomers are performed at B3PW91/6–31 G level56,57,58. Among them, the isomers whose total energies fell into the 3 eV interval comparison with the lowest energy are reoptimized along with frequency calculation at B3PW91/6–311 G(d, p) level58, as implemented in the Gaussian 09 program package59. The effect of spin multiplicity (up to septet) is taken into account in optimized procedure. It is worth pointing out the most stable isomers are found to prefer the singlet spin state, except for Mg18 cluster (triplet spin state). Based on Multiwfn program60, the chemical bonding characters of the Be2Mgn clusters have been analyzed by utilizing the adaptive natural density partitioning (AdNDP) method61.
References
Jena, P. & Sun, Q. Super atomic clusters: Design rules and potential for building blocks of materials. Chem. Rev. 118, 5755–5870 (2018).
Ferrando, R., Jellinek, J. & Johnston, R. L. Nanoalloys: from theory to applications of alloy clusters and nanoparticles. Chem. Rev. 108, 845–910 (2008).
Vines, F., Gomes, J. R. B. & Illas, F. Understanding the reactivity of metallic nanoparticles: beyond the extended surface model for catalysis. Chem. Soc. Rev. 43, 4922–4939 (2014).
Weng, B., Lu, K. Q., Tang, Z. C., Chen, H. M. & Xu, Y. J. Stabilizing ultrasmall Au clusters for enhanced photoredox catalysis. Nat. Commun. 9, 1543 (2018).
Xing, X. D. et al. Insight into the geometries, electronic and magnetic properties of neutral and charged palladium clusters. Sci. Rep. 6, 19656 (2016).
Gao, W. et al. Design principles of inert substractes for exploiting gold clusters’ intrinsic catalytic reactivity. Sci. Rep. 5, 15095 (2015).
Pereiro, M. et al. Biomedical applications of small silver clusters. J. Appl. Phys. 103, 07A315 (2008).
Fournier, R., Cheng, J. B. Y. & Wong, Y. Theoretical study of the structure of lithium clusters. J. Chem. Phys. 119, 9444 (2003).
Jovan Jose, K. V. & Gadre, S. R. Electrostatic guidelines and molecular tailoring for density functional investigation of structures and energetic of (Li)n clusters. J. Chem. Phys. 129, 164314 (2008).
Sun, W. G. et al. Evolution of the structural and electronic properties of medium-sized sodium clusters: a honeycomb-like Na20 cluster. Inorg. Chem. 56, 1241–1248 (2017).
Kostko, O., Huber, B., Moseler, M. & von Issendorff, B. Structure determination of medium-sized sodium clusters. Phys. Rev. Lett. 98, 043401 (2007).
Huang, W. & Wang, L. S. Probing the 2D to 3D structural transition in gold cluster anions using argon tagging. Phys. Rev. Lett. 102, 153401 (2007).
Pei, Y. & Zeng, X. C. Investigating the structural evolution of thiolate protected gold clusters from first-principles. Nanoscale 4, 4054–4072 (2012).
Shao, N. et al. Structural evolution of medium-sized gold clusters Aun ‾ (n=36, 37, 38): appearance of bulk-like face centered cubic fragment. J. Phys. Chem. C 118, 6887–6892 (2014).
Alamanova, D., Grigoryan, V. G. & Springborg, M. Theoretical study of the structure and energetics of silver clusters. J. Phys. Chem. C 111, 12577–12587 (2007).
Baishya, K. et al. Optical absorption spectra of intermediate-size silver clusters from first principle. Phys. Rev. B 78, 075439 (2008).
Die, D., Zheng, B. X., Zhao, L. Q., Zhu, Q. W. & Zhao, Z. Q. Insight into the structural, electronic and magnetic properties of V-doped copper clusters: comparison with pure copper clusters. Sci. Rep. 6, 31978 (2016).
Lecoultre, S. et al. Optical absorption of small copper clusters in neon: Cun (n=1–9). J. Chem. Phys. 134, 074303 (2011).
Niemeyer, M. et al. Spin coupling and orbital angular momentum quenching in free iron clusters. Phys. Rev. Lett. 108, 057201 (2012).
Alonso, J. A. Electronic and atomic structure, and magnetism of transition-metal clusters. Chem. Rev. 100, 637–678 (2000).
Datta., S. et al. Structure, bonding, and magnetism of cobalt clusters from first-principles calculations. Phys. Rev. B 76, 014429 (2007).
Meyer, J. et al. The spin and orbital contributions to the total magnetic moments of free Fe, Co, and Ni clusters. J. Chem. Phys. 143, 104302 (2015).
Song, W., Lu, W. C., Wang, C. Z. & Ho, K. M. Magnetic and electronic properties of the nickel clusters Nin (n≤30). Comput. Theor. Chem. 978, 41–46 (2011).
Xie, Z., Ma, Q. M., Liu, Y. & Li, Y. C. First-principle study of stability and Jahn-Teller distortion of nickel clusters. Phys. Lett. A 342, 459–467 (2005).
Grigoyan, V. G. & Springborg, M. Structural and energetic properties of nickel clusters: 2≤n≤150. Phys. Rev. B 70, 205415 (2004).
Balfour, W. J. & Douglas, A. E. Absorption spectrum of the Mg2 molecule. Can. J. Phys. 48, 901–914 (1970).
Miller, J. C. & Andrew, L. Laser photoluminescence spectra of diatomic magnesium (24Mg2 and 26Mg2) in solid argon at 12 K. J. Am. Soc. Chem. 100, 2966–2970 (1978).
Kooi, B. J., Palasantzas, G., De Hosson, J. & Th, M. Gas-phase synthesis of magnesium nanoparticles: A high-resolution transmission electron microscopy study. Appl. Phys. Lett. 89, 161914 (2006).
Duanmu, K. et al. Geometries, Binding energies, ionization potentials, and electron affinities of metal clusters: Mgn 0,±1, n=1–7. J. Phys. Chem. C 120, 13275–13286 (2016).
Xia, X. X. et al. Deciphering the structural evolution and electron and electronic properties of magnesium clusters: An aromatic homonuclear metal Mg17 cluster. J. Phys. Chem. A 120, 7947–7954 (2016).
Diederich, T., Döppner, T., Braune, J., Tiggeabaunker, J. & Meiwes-Broer, K.-H. Electron depocalization in magnesium clusters grown in supercold helium droplets. Phys. Rev. Lett. 86, 4807 (2001).
Li, P., Xie, W. & Tang, T. The van der Waals potential of the magnesium dimer. J. Chem. Phys. 133, 084308 (2010).
Kaplan, I. G. & Díaz, C. C. Comparative study of the electron affinities of beryllium and magnesium dimers and trimers. Int. J. Quantum. Chem. 104, 468–474 (2005).
Gong, X. G., Zheng, Q. Q. & He, Y. Z. Electronic structures of magnesium clusters. Phys. Lett. A 181, 459–464 (1993).
Thomas, O. C., Zheng, W. J., Xu, S. J. & Bowen, K. H. Jr. Onset of metallic in magnesium clusters. Phys. Rev. Lett. 89, 213403 (2002).
Jellinek, J. & Acioli, P. H. Magnesium clusters: structural and electronic properties and the size-induced nonmetal-to-metal transition. J. Phys. Chem. A 106, 10919–10925 (2002).
Acioli, P. H. & Jellinek, J. Electron binding energies of anionic magnesium clusters and the nonmetal-to-metal transition. Phys. Rev. Lett. 89, 213402 (2002).
Lyalin, A., Solovyov, I., Solovyov, A. V. & Greiner, W. Evolution the electronic and ionic structure of Mg clusters with increase in cluster size. Phys. Rev. A 67, 063203 (2003).
Akola, P., Rytkonen, K. & Manninen, M. Metallic evolution of small magnesium clusters. Eur. Phys. J. D 16, 21–24 (2001).
Janecek, S., Krotscheck, E., Liebrecht, M. & Wahl, R. Structure of Mgn and Mgn + clusters up to n=30. Eur. Phys. J. D 63, 377–390 (2011).
Zhang, J. M., Duan, Y. N., Xu, K. W., Ji, V. & Man, Z. Y. Ab initio calculation of neutral and singly charged Mgn (n≤11) clusters. Phys. B 403, 3119–3124 (2008).
Kawai, R. & Weare, J. H. From van der Waals to metallic bonding: the growth of Be clusters. Phys. Rev. Lett. 65, 80 (1990).
Wang, J. L., Wang, G. H. & Zhao, J. J. Density functional study of beryllium clusters, with gradient correction. J. Phys.: Condens. Matter. 13, L753 (2001).
Cerowski, V., Rao, B. K., Khanna, S. N. & Jena, P. Evolution of the electronic structure of Be clusters. J. Chem. Phys. 123, 074329 (2005).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. Crystal structure prediction via particle swarm optimization. Phys. Rev. B: Condens. Matter Mater. Phys. 82, 094116 (2010).
Wang, Y. C., Lv, J., Zhu, L. & Ma, Y. M. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Lv, J., Wang, Y. C., Zhu, L. & Ma, Y. M. Particle swarm structure prediction on clusters. J. Chem. Phys. 137, 084104 (2012).
Li, C. G. et al. Structures, stabilities and electronic properties of boron-doped silicon clusters B3Sin (n=1–17) and their anions. Mol. Phys. 117, 382–394 (2019).
Li, C. G. et al. Insights into the structures and electronic properties of Cun+1 μ and CunSμ (n=1–12; μ=0, ±1) clusters. Sci. Rep. 7, 1345 (2017).
Li, C. G. et al. First-principle study of structural, electronic and magnetic properties of (FeC)n (n=1–8) and (FeC)8TM (TM=V, Cr, Mn and Co) clusters. Sci. Rep-uk. 7, 17516 (2017).
Xia, X. X. et al. Study of structural and electronic properties of neutral and charged niobium-doped silicon clusters: niobium encapsulated in silicon cages. J. Phys. Chem. C 120, 677–684 (2016).
Zhu, B. et al. Insights into the structural, electronic and magnetic properties of Ni-doped gold clusters: Comparison with pure gold clusters. J. Alloy Compd. 696, 402–412 (2017).
Zhao, Y. R. et al. Probing the structural and electronic properties of neutral and anionic lanthanum-doped silicon clusters. J. Phys. Chem. C 123, 28561–28568 (2019).
Jin, Y. Y. et al. Probing the structural evolution of ruthenium doped germanium clusters: Photoelectron spectroscopy and density functional theory calculations. Sci. Rep. 6, 30116 (2016).
Shao, P. et al. Prediction of hypervalent molecules: investigation on M nC (M=Li, Na, K, Rb and Cs; n=1-8) clusters. Phys. Chem. Chem. Phys. 19, 25289–25297 (2017).
Becke, A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648 (1993).
Perdew, J. P. & Wang, Y. Pair-distribution function and its coupling-constant average for the spin-polarized electron gas. Phys. Rev. B: Condens. Matter Mater. Phys. 46, 12947 (1992).
Feller, D. The Role of Databases in Support of Computational Chemistry Calculations. J. Comp. Chem. 17, 1571–1586 (1996).
Frisch, M. J. et al. Gaussian 09 (Revision C.01), Gaussian, Inc., Wallingford, CT, (2009).
Lu, T. & Chen, F. W. Multiwfn: A multifunctional wavefunction analyzer. Comput. Phys. Commun. 33, 580–592 (2012).
Zubarev, D. Y. & Boldyrev, A. I. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys. Chem. Chem. Phys. 10, 5207–5217 (2008).
Acknowledgements
This work was supported by the Natural Science Foundation of China (Grant No. 11404008), the China Postdoctoral Science Foundation funded project (Grant No. 2017M623310XB), the Education Department of Sichuan province (Grant Nos. 17ZA0278, 18ZA0340), the Artificial Intelligence Key Laboratory of Sichuan Province (Nos. 2018RYJ07), the Innovation and Training Program for College Students of Sichuan University of Science and Engineering (Grant Nos. cx2019005), the Innovation Training Program for College Students of Shaanxi province (Grant Nos. S201910721061), and the Innovation Training Program for College Students of Baoji University of Arts and Sciences (Grant Nos. 20191XJ087).
Author information
Authors and Affiliations
Contributions
Yanfei Hu and Yaru Zhao conceived the idea. Feige Zhang, Hairong Zhang, and Wang Xin performed the calculations. Feige Zhang, Peng Chen, and Xiaoyi Zhang wrote the manuscript and all authors contributed to revision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, F., Zhang, H., Xin, W. et al. Probing the structural evolution and electronic properties of divalent metal Be2Mgn clusters from small to medium-size. Sci Rep 10, 6052 (2020). https://doi.org/10.1038/s41598-020-63237-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-63237-8
This article is cited by
-
Probing the Structural Evolution, Stabilities and Properties of LiBn (n = 2–12) Clusters
Journal of Cluster Science (2023)
-
Structures, electronic and magnetic properties of the FexNy (x = 1–4, y = 1–4) adsorbed graphene
Research on Chemical Intermediates (2022)
-
Studies on the structural and electronic characteristics of alkaline-earth metal Mgn+1 and BaMgn (n = 2–10) clusters and their anions
Theoretical Chemistry Accounts (2022)
-
Structures and electronic properties of the MgnN and Mgn-1N2 (n = 1–6) clusters
Theoretical Chemistry Accounts (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.