Abstract
The pristine graphene described with massless Dirac fermion could bear topological insulator state and ferromagnetism via the band structure engineering with various adatoms and proximity effects from heterostructures. In particular, topological Anderson insulator state was theoretically predicted in tight-binding honeycomb lattice with Anderson disorder term. Here, we introduced physi-absorbed Fe-clusters/adatoms on graphene to impose exchange interaction and random lattice disorder, and we observed Anderson insulator state accompanying with Kondo effect and field-induced conducting state upon applying the magnetic field at around a charge neutral point. Furthermore, the emergence of the double peak of resistivity at ν = 0 state indicates spin-splitted edge state with high effective exchange field (>70 T). These phenomena suggest the appearance of topological Anderson insulator state triggered by the induced exchange field and disorder.
Similar content being viewed by others
Introduction
Two-dimensional(2D) topological insulator has helical edge boundary due to spin-orbit coupling (SOC) and time reversal symmetry leading to quantum spin Hall (QSH) phase1. This nontrivial topological phase could be also emerged when disorder is added to a trivial band structure2,3,4,5,6,7. This disorder-driven topological state, i.e. topological Anderson insulator (TAI), was first predicted in metallic 2D quantum wall2,3. The theoretical studies have shown that the TAI phenomena could be generic for disordered systems and both topology and disorder have rich combined influences on the quantum transport2,3,4,5. Yet, its experimental demonstration was recently achieved only in precisely controlled optical lattice6,7.
Electron band structure of pristine graphene has been extensively studied over the last decade because of its unusual transport properties8,9, and it has been shown that physical properties of graphene can be strongly modified when it is functionalized with various adatoms10,11,12,13,14,15,16,17,18,19,20,21,22,23, or proximity effect from heterostructures24,25,26,27,28,29,30. Disordered graphene by heavy adatoms could exhibit diverse condensed matter phenomena such as spin Hall effect and QSH state (topological insulator state) due to the instilled spin-orbit coupling and honeycomb lattice distortion. For example, chemically or physically decorated adatom in graphene could exhibit spin-charge conversion known as spin Hall effect due to induced strong spin-orbit coupling21,22,23. Also, it was theoretically predicted that dilute heavy adatoms, such as platinum, indium and thallium, could lead to a robust QSH state in graphene, with a band gap exceeding that of pure graphene by many orders of magnitude14. Even the pristine graphene was predicted to exhibit a QSH phase and have a nontrivial topological order with an energy gap generated by the intrinsic spin-orbit coupling at ultra-low temperature31.
When graphene is laminated on the ferromagnetic insulator, it could acquire local moment and/or experience magnetic exchange field27,28,29,30, as evidenced through the Zeeman Hall effect28,29 or the anomalous Hall27 effect in graphene/magnetic insulator heterostructures. In particular, p-wave nature of hybridization between conduction electrons and localized state makes induced local moment highly stable32. The intense exchange field lifts the ground-state degeneracy of graphene in the quantum Hall state, leading to spin-polarized v (filling factor of Landau level) = 0 state similar to the quantum spin Hall state or the quantum Hall metal state28,29,30. Exchange field and spin polarized density of state can be also induced by magnetic adatoms, such as Co and Fe15,33. Moreover, random distribution of magnetic adatoms accompanies disorder leading to Anderson localization34 in the vicinity of the Dirac point18. Here, the presence of the exchange coupling between the itinerant and local spins can further enhance Anderson localization above Kondo temperature18. Anderson metal insulator transition (MIT) upon changing carrier density was also predicted when adatoms is on the center of the honeycomb hexagon forming impurity plaquette11,16.
In this study, we employed magnetic impurities of Fe clusters/adatoms on graphene to induce strain and exchange field simultaneously. Results showed that the magnetic field induced conducting state, which suggests the emergence of spin-polarized Anderson state in the graphene. Near the charge neutral point (CNP) of graphene, the Anderson insulator state appeared in company with Kondo effect and it can be transited into a metallic state with a spin-splitted edge state under the high magnetic field, similar to a TAI state.
Results and Discussions
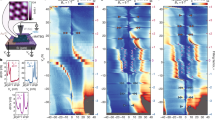
Figure 1(a) illustrates studied graphene Hall-bar device with Fe clusters (see Materials and Methods for details). The geometry of Hall-bar device has a channel width (w) of ~ 2 μm and lengths (Ls) of ~ 6 μm. Fe was physically deposited by e-beam evaporation (~0.5 nm), which forms random distribution of clusters/adatoms on the surface of graphene. Then 20 nm of Al2O3 was deposited for capping layer. Random distribution of Fe clusters can be clearly observed in transmission electron microscopy image shown in Fig. 1(b). Edge of Fe clusters on graphene is displayed in the inset of Fig. 1(b). Raman spectra of Fe-clusters graphene displays shift and broadening of 2D peak suggesting that Fe clusters and Al2O3 capping layer induced significant strain in underlying graphene35 (see Supplementary Information (SI) Fig. S1). It was theoretically reported15 that the adsorption of the adatoms on graphene can generate significant in-plane and vertical distortion in lattice of graphene, And this random strain by the adatoms can give rise to Anderson localization in the vicinity of the CNP11.
Figure 2(a) displays gate dependent ρxx upon varying temperature. The estimated mobility, μ = 1/e × dσ/dn, is about 600 cm2/V∙s at 2 K. This value of mobility is significantly lower than that of the pristine graphene, which can be attributed to the strain induced disorder by Fe particle plaquette as shown in Raman spectra (see Supplementary Information (SI) Fig. S1). The temperature dependent ρxx exhibits two different regimes. At around CNP, ρxx(T) shows insulating behavior, while it exhibits metallic behavior at high carrier density. The resistance of graphene on SiO2/Si substrate generally decreases with decreasing temperature in accordance with its semi-metallic band structure36. But it displays insulating behavior at around CNP in high magnetic field due to quantum phase transition induced by strong localization of electrons37. The MIT upon varying carrier density has been also observed on ultraclean graphene having high mobility (~200,000 cm2/V∙s) in the absence of magnetic field (e.g. suspended graphene38, graphene on h-BN39, etc). In suspended graphene, the insulator state near CNP is a result of a strongly reduced charge inhomogeneity38. In the case of graphene on h-BN, broken valley symmetry can give rise to insulating behavior39. However, disordered graphene such as hydrogenated graphene and graphene exposed to ozone, only exhibits insulating state regardless of carrier density and external magnetic field due to bandgap opening13,17. In our study, although Fe-clusters graphene device exhibits low mobility and diffusive transport by disorder, the MIT by changing gate voltage appear in the absence of magnetic field, similar to the case of ultraclean graphene38,39 or to the case of graphene on SiO2 under high magnetic field37. In disordered graphene, this MIT by changing gate voltage can be attributed to the presence of mobility edge which separates Anderson localized state near CNP from metallic state at high carrier density11.
Characteristics of charge transport in graphene with Fe clusters. (a) Resistivity as a function of gate voltage (carrier density n) measured at various temperature. Inset exhibits optical image of the fabricated device. Scale bar is 5 μm. Temperature dependent resistivity measured at VG − VD = +20 V (b) and at CNP (c) in the absence of magnetic field. Red solid line is a fitting curve with Eq. (1). Red dashed line indicates RK(T/TK) of Kondo model. Purple dash-dotted line shows variable-range hopping model. (d) Temperature dependent resistivity at CNP in the presence of the applied magnetic field 9 T, indicating metallic state.
Figure 2(b) displays low temperature variation of resistivity in the metallic regime. Result shows strong upturn in ρxx below 50 K. And ρxx was nearly saturated with decreasing temperature further. This behavior could be attributed to the Kondo effect due to the strong correlation between itinerant electrons and magnetic impurity. The Kondo effect on graphene due to magnetic adatoms12,40,41,42 and/or defect-induced moments43,44 was theoretically predicted. The temperature dependent resistivity of the conventional Kondo model can be described as follows45,46.
where R0 represents the resistance from sample disorder. T2 and T5 terms are the electron-electron and electro-phonon interaction, respectively. TK indicates Kondo temperature. The RK(T/TK) is a function representing the universal behavior of Kondo effect, i.e. logarithmic increase of resistivity below TK and its saturation at very low T. Here, \({{T}^{{\rm{{\prime} }}}}_{{\rm{K}}}={T}_{K}/({2}^{1/s}-1{)}^{1/2}\) and s = 0.22 ± 0.01 obtained by renormalization group46. We fixed s = 0.21 for fitting. The overall behavior of ρxx(T) at VG − VD = +20 V can be well fitted to the Eq. (1) as shown in Fig. 2(b). The ρxx (T) at higher carrier density also follows well to the universal behavior of Kondo effect (see Supplementary Information (SI) Fig. S2). Figure 2(c) displays measured ρxx(T) at CNP, where overall T dependence shows insulating behavior. For the disorder graphene showing insulating behavior, the temperature dependence of resistance can be described by either variable-range hopping (VRH)13,17 or the universal function of the Kondo model47. The VRH in two-dimension has a characteristic temperature dependence of \(\,\rho =\,{\rho }_{o}{e}^{{({T}_{0}/T)}^{1/3}}\), indicating divergence of resistance at low temperature. As shown in Fig. 2(c), the observed low temperature dependence of resistance at CNP is saturated and well fitted with simple Kondo model than VRH. Here, the T2 and T5 terms are nearly negligible at CNP while R0 shows peak at CNP47. The Kondo temperature at CNP and VG − VD = +20 V is 95 K and 69 K, respectively. The estimated Kondo temperatures are in order of several 10 K (see Supplementary Information (SI) Fig. S2 for Kondo temperature with various gate voltage). These values are in general much higher than that of s-wave Kondo system because hybridization of conduction electrons with localized states in graphene lead to p-wave hybridization, which typically results in higher Kondo temperature as discussed in S. A. Jafari et al.42. In addition, excitation of spin-1 boson due to inter-band particle-hole processes in graphene could further enhance the Kondo effect48,49.
Figure 2(d) displays temperature dependent ρxx at CNP in the presence of the high magnetic field 9 T. Results shows that the applied high magnetic field convert the system into conducting state at CNP. This behavior is also in agreement with Anderson localized state at CNP predicted in ref. 11. The observed field-induced conducting state can be observed only in the presence of Fe clusters/adatoms on graphene, (see Supplementary Information (SI) Fig. S3), which we will discuss later in detail.
We then performed the magnetoresistance measurement to investigate localization behavior further. Figure 3 shows measured magnetoresistance upon applying perpendicular magnetic field at various gate voltage. In all cases, the magnetoresistances were negative, and the Shubnikov-de Hass oscillations were observed at high carrier density. To find the influence of quantum interference near the CNP, we fit our data according to a localization theory developed for graphene50, where the correction to the semiclassical resistivity is given by
where ψ is digamma function, D is the diffusion coefficient, \({\tau }_{{\rm{inter}}}^{-1}\) is intervalley scattering rate, \({\tau }_{{\rm{intra}}}^{-1}\) is intravalley scattering rate, and \({\tau }_{\varphi }^{-1}\) is dephasing rate. The fit to Eq. (2) is shown in Fig. 3(a). Here, we plot \(\Delta \rho =\rho (0)-\rho (B)\) from experimental data. The dotted blue line is fitting curve for low-field magnetoresistance of weak localization behavior (\({\tau }_{\varphi }=0.3\,{\rm{ps}},\,{\tau }_{{\rm{inter}}}\,=\,0.14\,{\rm{ps}},\,{\tau }_{{\rm{intra}}}=\,0.05\,{\rm{ps}}\)). The suppression of resistivity at intermediate field can be obtained by increasing both inter- and intra- valley scattering times (\({\tau }_{\varphi }=\,0.3\,{\rm{ps}},\,{\tau }_{{\rm{inter}}}\,=\,0.01\,{\rm{ps}},\,{\tau }_{{\rm{intra}}}=\,0.014\,{\rm{ps}})\,\,\)without changing phase coherence time (\({\tau }_{\varphi })\) (dotted red line in the Fig. 3(a). Here, \({\tau }_{\varphi }\) mainly affect low-field magnetoresistance and nearly insensitive to the magnetoresistance at higher field. Note, that this upper limit of phase coherence time is much shorter than that estimated in pristine graphene (\({\tau }_{\varphi } \sim 10\,{\rm{ps}})\)51, which is possibly due to strong magnetic dephasing mechanism as discussed in Lundeberg et al.52. The fitting to low field region allows us to extract a value for phase coherence length \({L}_{\varphi }=\sqrt{{\tau }_{\varphi }D}\) with the diffusion coefficient (D) ~ 0.01. The obtained phase coherence length at around CNP was ~ 57 nm. The localization length is given by13,17
where, Le is the elastic length from Le = \({\sigma }_{D}h/2{e}^{2}{(\pi n)}^{1/2}\), σD is Drude conductivity, and n is charge carrier density. The estimated localization length at around CNP is ~3.2 nm (~160 nm at VG − VD = −10 V and ~50 μm at VG − VD = −42.5 V). The estimated localization length at CNP in pristine graphene is typically in order of 100 nm53. The observed short localization in our studied system can be attributed to the presence of random strain induced from Fe clusters/adatoms. Because the phase coherence length is much larger than localization length, this indicates the system is in the strong localization (called Anderson localization) regime. Based on the localization length scale near CNP, the Fermi velocity was estimated to be ~2 × 105 m/s, whose energy is in order of ~100 meV. This energy scale in the vicinity of CNP corresponds to the mobility edge reported in previous theoretical study11. Note that the strong suppression in magnetoresistance under high magnetic-field in Fig. 3a,b reflects that the system is in Quantum Hall regime.
Magnetoresistance upon applying perpendicular magnetic field at 2 K. Magnetoresistance curve measured at CNP (a), VG − VD = −10 V (b), and VG − VD = −42.5 V (c). The dotted line indicates fitting curve from Eq. (2). The dotted blue line shows the weak localization fitting for the low-field magnetoresistance behavior. The dotted red line is a fitting curve by increasing valley scattering without changing phase coherence time.
The original description of Kondo effect is closely related to Anderson impurity model. A low energy features of Anderson Hamiltonian is equivalent to those of Kondo Hamiltonian with exchange interaction54,55,56. As previously mentioned, it was theoretically predicted18 that magnetic adatoms (Co, Fe) on graphene can enhance Anderson localization with spin-polarized density of state in the vicinity of Dirac point. Thus, our observation of both Kondo effect and Anderson localization is consistent with previous theoretical studies.
The solution of Anderson Hamiltonian gives the mobility edges that separate localized and extended state. Anderson insulator state appears when a fermi energy lies in the localized state. Thus, transition into metallic state under high magnetic field as shown in Fig. 2(d) reflects that a conducting channel is developed due to either delocalization57 or edge state28. In order to investigate further about the conducting state under high magnetic field, we measured gate-dependent resistivity with varying applied magnetic field. As shown in Fig. 4(a), the CNP was initially located at 3.5 V in the absence of magnetic field. With increasing external magnetic field, the resistivity at around CNP develops double-peak features (at 7.5 V and 2.5 V), as shown in Fig. 4(a). Besides, further increase of magnetic field reduced the magnitude of peak at 2.5 V. Finally, the peak observed at 2.5 V was strongly suppressed at 9 T. In short, the CNP shift from 3.5 V to 7.5 V upon increasing applied magnetic field. The shift of CNP can be also clearly observed in the plot of conductance G vs Vg (see Supplementary Information (SI) Fig. S4), which exhibits base conductance of 2(e2/h).
The splitting of zeroth Landau level in Fe- clusters graphene device. (a) The resistivity as a function of gate voltage measured at 2 K with various applied magnetic field of 0 T, 5 T, 7 T, and 9 T. The splitting at around CNP was observed and the resistance peak was shifted from 3.5 V to 7.5 V with increases magnetic field. The ρxx (VG) curves are shifted vertically for clarity. (b) Schematic illustration of valley polarized state with bulk gap. In this quantum insulator state, the spin splitting is weak. (c) Schematic illustration of spin-polarized state by Zeeman splitting. A counter-propagating edge state with opposite spin polarization exist at around Dirac point similar to quantum spin Hall effect. Blue line (red line) indicates spin-up state (spin-down state). Solid line and + (dashed lines and −) represent k valley (−k valley).
Previous theoretical and experimental reports provided that the ν = 0 state could be a spin-polarized state with gapless chiral edge mode, a valley-polarized state without gapless chiral edge mode or the intermediate state between spin and valley polarized28,30,58. The valley-polarized state should lead to increasing longitudinal resistivity with increasing magnetic field, while, in the case of spin-polarized state, metallic behavior appear due to edge state28, as illustrated in Fig. 4b,c. Here, the strong interfacial magnetic exchange field can generate the spin-polarized edge transport at ν = 0 state originating from Zeeman splitting, and this edge transport will appear as the double peak of longitudinal resistivity near the Dirac point indicating the presence of counter-propagating edge channels like the quantum spin Hall effect28,30. In our sample, we observed that the double peak of longitudinal resistivity near CNP as shown Fig. 4(a) and that the resistivity with increasing magnetic field was reduced, indicating spin-polarized edge transport at ν = 0 state. For the applied magnetic field of 9 T, the magnetic length of graphene is about \(\,26/\sqrt{B}\) nm ~ 8.8 nm. The estimated localization length is ~3.2 nm at around CNP. In general, the magnetic length should be shorter than localization length to induce phase transition (from Anderson insulator to quantum metallic state)57,59. In this study, although localization length is shorter than magnetic length, the quantum metallic state with spin-polarized edge exists at around CNP. The graphene π-orbitals can have strong hybridization with the Fe 3d orbitals, and the first-principle calculation predicted a proximity-induced exchange field up to ~ 1100 T60. Experimentally, it was shown that the graphene on BiFeO3 substrate has effective exchange field about 280 T29. In our study, effective exchange field should be higher than 70 T to generate quantum phase transition as shown in Figs. 2(d) and 4(a). In addition, Wu et al., predicted61 the shift of Dirac point with spin-polarization for strained graphene with effective exchange field by using low-energy effective Hamiltonian. It was also reported that the combined play of exchange field and spin-orbit interaction could cause asymmetric spin splitting of Dirac state in the graphene20. So, we attribute double-peak and shift of CNP shown in Fig. 4 to the effective exchange field and the strain induced by Fe- clusters/adatoms.
Recently, it has been theoretically proposed that the topological Anderson insulator state is a more universal phenomenon and can appear in Kane-Mele model on a honeycomb lattice with Anderson disorder contribution2,4. The primary difference from conventional topological insulator is that Fermi energy lies within mobility gap in place of real band gap. The gapless edge states are between two extended state (mobility gap). In the strong disorder limit, topological Anderson state will eventually disappear and become trivial band structure because all states are localized without extended state62.
Physical absorption of other magnetic adatoms could also induce similar effect. Xiaojie Liu et al. predicted15 the reduced magnetic moments for the magnetic adatoms (Fe, Co, Ni) on graphene and compared magnetic moments of the corresponding isolated atoms. According to this study, the net magnetic moments for Fe, Co, Ni can be reduced from 4.0, 3.0, and 2.0 μB (for isolated atoms) to 2.0, 1.0, 0 μB in adatoms/graphene systems, respectively, due to electrons transfer. Thus, the Kondo effect or spin polarized state in Ni/graphene system could not be observed as the net magnetic moment in Ni/graphene system is zero.
Conclusions
We showed that magnetic impurities of Fe clusters/adatoms on graphene can effectively induce strain and exchange field simultaneously. The induced strain and exchange field (>70 T) by Fe particles lead to Anderson localization with Kondo effect at around CNP. In addition to Anderson localization, spin polarized edge state and the shift of CNP were emerged by applying a high magnetic field. These results provide importance insights for spin-polarized Anderson transition in two-dimensional honeycomb lattice. Our study showed that graphene with random distribution of magnetic clusters/adatoms is a good test-bed for the investigation of TAI.
Materials and Methods
Synthesis and transfer of graphene
A monolayer graphene was grown on a polycrystalline Cu foil using a chemical vapor deposition method demonstrated elsewhere23. 25 μm copper foil (Alfa Aesar, 99.8% purity) was electropolished in phosphoric acid for 15 min and rinsed with distilled water followed by isopropyl alcohol (IPA). The copper foil was loaded into a quartz tube 3-zone furnace and the temperature was increased to 1050 °C in the H2 environment for removal of native oxides in the copper with surface reconstruction. Monolayer graphene was synthesized by introducing CH4 gas under H2 gas insertion with a ratio of 10:5 (sccm) for 15 min, and transferred onto the Si/SiO2 (300 nm) subatrate using a polymethyl methacrylate (PMMA) wet transfer process. To remove possible resist residues, samples were annealed in low vacuum at 300 °C.
Fabrication of Fe-clusters/adatoms graphene Hall bar device
The pattern for Hall bar and Au electrode was fabricated by electron beam lithography. Hall bar geometry of graphene was defined via oxygen plasma etching. Thermally deposited Au (60 nm)/ Cr (3 nm) was used for electrode. Ultrathin Fe layer (~0.5 nm) was deposited by e-beam evaporation with a deposition rate of 0.05 Å/s. Finally, 20 nm of Al2O3 layer was deposited via e-beam evaporation to protect from unwanted oxidation and contamination.
Characterization of Fe-clusters/adatoms graphene
The Raman spectroscopy was performed by Alpha 300 R spectrometer (WITec) with a 532 nm laser source. The spot size of laser source was ~ 1 μm in diameter and the laser power was ~1 mW. High resolution transmission electron microscopy (HRTEM) images were acquired using an aberration-corrected Titan cube G2 operated at 80 kV
Electrical measurement
Electrical measurements were performed in a Quantum Design Physical Property Measurement System (PPMS) with the Keithley source meter (K2636) and a nano-voltmeter (K2182). The indium (In) with copper wire was used for the electrical contacts to Au pads of the device. The samples are loaded to a vacuum chamber of PPMS which can control a variable temperature (2 K~300 K) and magnetic field (−9 T~+9 T). The sample was annealed in vacuum chamber of PPMS at about 100 °C to remove moisture on graphene before electrical measurement. The 500 nA (dc) was applied for electrical transport.
References
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Li, J., Chu, R.-L., Jain, J. K. & Shen, S.-Q. Topological Anderson Insulator. Phys. Rev. Lett. 102, 136806 (2009).
Groth, C. W., Wimmer, M., Akhmerov, A. R., Tworzydło, J. & Beenakker, C. W. J. Theory of the Topological Anderson Insulator. Phys. Rev. Lett. 103, 196805 (2009).
Orth, C. P., Sekera, T., Bruder, C. & Schmidt, T. L. The topological Anderson insulator phase in the Kane-Mele model. Sci. Rep. 6, 24007 (2016).
Liu, C., Gao, W., Yang, B. & Zhang, S. Disorder-Induced Topological State Transition in Photonic Metamaterials. Phys. Rev. Lett. 119, 183901 (2017).
Stützer, S. et al. Photonic topological Anderson insulators. Nature 560, 461–465 (2018).
Meier, E. J. et al. Observation of the topological Anderson insulator in disordered atomic wires. Science 362, 929 (2018).
Castro Neto, A. H., Guinea, F., Peres, N. M. R., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev, Mod. Phys. 81, 109–162 (2009).
Young, A. F. et al. Spin and valley quantum Hall ferromagnetism in graphene. Nat. Phys. 8, 550–556 (2012).
Castro Neto, A. H. & Guinea, F. Impurity-Induced Spin-Orbit Coupling in Graphene. Phys. Rev. Lett. 103, 026804 (2009).
Amini, M., Jafari, S. A. & Shahbazi, F. Anderson transition in disordered graphene. Europhys. Lett. 87, 37002 (2009).
Wehling, T. O., Balatsky, A. V., Katsnelson, M. I., Lichtenstein, A. I. & Rosch, A. Orbitally controlled Kondo effect of Co adatoms on graphene. Phys. Rev. B 81, 115427 (2010).
Moser, J. et al. Magnetotransport in disordered graphene exposed to ozone: From weak to strong localization. Phys. Rev. B 81, 205445 (2010).
Weeks, C., Hu, J., Alicea, J., Franz, M. & Wu, R. Engineering a Robust Quantum Spin Hall State in Graphene via Adatom Deposition. Phys. Rev. X 1, 021001 (2011).
Liu, X. et al. Bonding and charge transfer by metal adatom adsorption on graphene. Phys. Rev. B 83, 235411 (2011).
Song, Y., Song, H. & Feng, S. The effects of disorder and interactions on the Anderson transition in doped graphene. J. Phys.: Condens. Matter 23, 205501 (2011).
Matis, B. R., Bulat, F. A., Friedman, A. L., Houston, B. H. & Baldwin, J. W. Giant negative magnetoresistance and a transition from strong to weak localization in hydrogenated graphene. Phys. Rev. B 85, 195437 (2012).
García, J. H., Uchoa, B., Covaci, L. & Rappoport, T. G. Adatoms and Anderson localization in graphene. Phys. Rev. B 90, 085425 (2014).
Van Tuan, D. et al. Spin Hall Effect and Origins of Nonlocal Resistance in Adatom-Decorated Graphene. Phys. Rev. Lett. 117, 176602 (2016).
Rybkin, A. G. et al. Magneto-Spin–Orbit Graphene: Interplay between Exchange and Spin–Orbit Couplings. Nano Lett. 18, 1564–1574 (2018).
Balakrishnan, J., Koon, G. K. W., Jaiswal, M., Neto, A. H. C. & Ozyilmaz, B. Colossal enhancement of spin-orbit coupling in weakly hydrogenated graphene. Nat. Phys. 9, 284–287 (2013).
Balakrishnan, J. et al. Giant spin Hall effect in graphene grown by chemical vapour deposition. Nat. Commun. 5, 4748 (2014).
Park, J. et al. Gate-dependent spin Hall induced nonlocal resistance and the symmetry of spin-orbit scattering in Au-clustered graphene. Phys. Rev. B 95, 245414 (2017).
Hong, X. et al. Unusual resistance hysteresis in n-layer graphene field effect transistors fabricated on ferroelectric Pb(Zr0.2Ti0.8)O3. Appl. Phys. Lett. 97, 033114 (2010).
Wang, Z. et al. Strong interface-induced spin–orbit interaction in graphene on WS2. Nat. Commun. 6, 8339 (2015).
Lee, S. & Lee, Y. Graphene/lead-zirconate-titanate ferroelectric memory devices with tenacious retention characteristics. Carbon 126, 176–182 (2018).
Wang, Z., Tang, C., Sachs, R., Barlas, Y. & Shi, J. Proximity-Induced Ferromagnetism in Graphene Revealed by the Anomalous Hall Effect. Phys. Rev. Lett. 114, 016603 (2015).
Wei, P. et al. Strong interfacial exchange field in the graphene/EuS heterostructure. Nat. Mater. 15, 711–716 (2016).
Wu, Y.-F. et al. Magnetic proximity effect in graphene coupled to a BiFeO3 nanoplate. Phys. Rev. B 95, 195426 (2017).
Song, H.-D. et al. Asymmetric Modulation on Exchange Field in a Graphene/BiFeO3 Heterostructure by External Magnetic Field. Nano Lett. 18, 2435–2441 (2018).
Kane, C. L. & Mele, E. J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 95, 226801 (2005).
Mashkoori, M. & Jafari, S. A. Stable local moments of vacancies, substitutional and hollow site impurities in graphene. J. Phys.: Condens. Matter 27, 156001 (2015).
Cao, C., Wu, M., Jiang, J. & Cheng, H.-P. Transition metal adatom and dimer adsorbed on graphene: Induced magnetization and electronic structures. Phys. Rev. B 81, 205424 (2010).
Anderson, P. W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 109, 1492–1505 (1958).
He, R. et al. Large Physisorption Strain in Chemical Vapor Deposition of Graphene on Copper Substrates. Nano Lett. 12, 2408–2413 (2012).
Chen, J.-H., Jang, C., Xiao, S., Ishigami, M. & Fuhrer, M. S. Intrinsic and extrinsic performance limits of graphene devices on SiO2. Nat. Nanotechnol. 3, 206–209 (2008).
Zhang, L., Zhang, Y., Khodas, M., Valla, T. & Zaliznyak, I. A. Metal to Insulator Transition on the N=0 Landau Level in Graphene. Phys. Rev. Lett. 105, 046804 (2010).
Bolotin, K. I., Sikes, K. J., Hone, J., Stormer, H. L. & Kim, P. Temperature-Dependent Transport in Suspended Graphene. Phys. Rev. Lett. 101, 096802 (2008).
Amet, F., Williams, J. R., Watanabe, K., Taniguchi, T. & Goldhaber-Gordon, D. Insulating Behavior at the Neutrality Point in Single-Layer Graphene. Phys. Rev. Lett. 110, 216601 (2013).
Rudenko, A. N., Keil, F. J., Katsnelson, M. I. & Lichtenstein, A. I. Adsorption of cobalt on graphene: Electron correlation effects from a quantum chemical perspective. Phys. Rev. B 86, 075422 (2012).
Wehling, T. O., Lichtenstein, A. I. & Katsnelson, M. I. Transition-metal adatoms on graphene: Influence of local Coulomb interactions on chemical bonding and magnetic moments. Phys. Rev. B 84, 235110 (2011).
Jafari, S. A. & Tohyama, T. Kondo resonance from p-wave hybridization in graphene. J. Phys.: Condens. Matter 26, 415601 (2014).
Fritz, L. & Vojta, M. The physics of Kondo impurities in graphene. Rep. Prog. Phys. 76, 032501 (2013).
Mitchell, A. K. & Fritz, L. Kondo effect with diverging hybridization: Possible realization in graphene with vacancies. Phys. Rev. B 88, 075104 (2013).
Lee, M., Williams, J. R., Zhang, S., Frisbie, C. D. & Goldhaber-Gordon, D. Electrolyte Gate-Controlled Kondo Effect in SrTiO3. Phys. Rev. Lett. 107, 256601 (2011).
Goldhaber-Gordon, D. et al. From the Kondo Regime to the Mixed-Valence Regime in a Single-Electron Transistor. Phys. Rev. Lett. 81, 5225–5228 (1998).
Chen, J.-H., Li, L., Cullen, W. G., Williams, E. D. & Fuhrer, M. S. Tunable Kondo effect in graphene with defects. Nat. Phys. 7, 535–538 (2011).
Baskaran, G. & Jafari, S. A. Gapless Spin-1 Neutral Collective Mode Branch for Graphite. Phys. Rev. Lett. 89, 016402 (2002).
Jafari, S. A. & Baskaran, G. Equations-of-motion method for triplet excitation operators in graphene. J. Phys.: Condens. Matter 24, 095601 (2012).
McCann, E. et al. Weak-Localization Magnetoresistance and Valley Symmetry in Graphene. Phys. Rev. Lett. 97, 146805 (2006).
Tikhonenko, F. V., Kozikov, A. A., Savchenko, A. K. & Gorbachev, R. V. Transition between Electron Localization and Antilocalization in Graphene. Phys. Rev. Lett. 103, 226801 (2009).
Lundeberg, M. B., Yang, R., Renard, J. & Folk, J. A. Defect-Mediated Spin Relaxation and Dephasing in Graphene. Phys. Rev. Lett. 110, 156601 (2013).
Mathieu Massicotte, E. W. & Victor, Yu Weak Localization in Graphene: Theory. Simulations, and Experiments. Sci. World. J. 2014, 1–8 (2014).
Anderson, P. W. Localized Magnetic States in Metals. Phys. Rev. 124, 41–53 (1961).
Schrieffer, J. R. & Wolff, P. A. Relation between the Anderson and Kondo Hamiltonians. Phys. Rev. 149, 491–492 (1966).
Bulla, R., Costi, T. A. & Pruschke, T. Numerical renormalization group method for quantum impurity systems. Rev. Mod. Phys. 80, 395–450 (2008).
Jiang, H. W., Johnson, C. E., Wang, K. L. & Hannahs, S. T. Observation of magnetic-field-induced delocalization: Transition from Anderson insulator to quantum Hall conductor. Phys. Rev. Lett. 71, 1439–1442 (1993).
Abanin, D. A. et al. Dissipative Quantum Hall Effect in Graphene near the Dirac Point. Phys. Rev. Lett. 98, 196806 (2007).
Lerner, I. V. & Imry, Y. Magnetic-Field Dependence of the Localization Length in Anderson Insulators. Europhys. Lett. 29, 49–54 (1995).
Qiao, Z. et al. Quantum Anomalous Hall Effect in Graphene Proximity Coupled to an Antiferromagnetic Insulator. Phys. Rev. Lett. 112, 116404 (2014).
Wu, Q.-P., Liu, Z.-F., Chen, A.-X., Xiao, X.-B. & Miao, G.-X. Tunable Dirac points and high spin polarization in ferromagnetic-strain graphene superlattices. Sci. Rep. 7, 14636 (2017).
Zhang, Y.-Y., Chu, R.-L., Zhang, F.-C. & Shen, S.-Q. Localization and mobility gap in the topological Anderson insulator. Phys. Rev. B 85, 035107 (2012).
Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (2017R1A2B4008286 and 2017M3A7B4049172). This research was also supported by National Research Council of Science & Technology (NST) grant (No. CAP-16-01-KIST) by the Korean government (MSIP).
Author information
Authors and Affiliations
Contributions
J.P. and J.-W.Y. designed the research. J.P. worked on device fabrication, characterization, and analysis. I.O. and M.-J.J. assisted device fabrication. J.J. and D.C. assisted device characterization and analysis. H.D.Y. and S.-Y.K. grown the CVD graphene. S.W.L. and Z.L. performed TEM analysis. H.J. and S.B.C. assisted data analysis and interpretation. J.P. and J.-W.Y. wrote the manuscript. All authors discussed about the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Park, J., Oh, I., Jin, MJ. et al. Observation of spin-polarized Anderson state around charge neutral point in graphene with Fe-clusters. Sci Rep 10, 4784 (2020). https://doi.org/10.1038/s41598-020-61481-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-61481-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.