Abstract
Humans respond to mechanical perturbations that affect their gait by changing their motor control strategy. Previous work indicates that adaptation during gait is context dependent, and perturbations altering long-term stability are compensated for even at the cost of higher energy expenditure. However, it is unclear if gait adaptation is driven by unilateral or bilateral mechanisms, and what the roles of feedback and feedforward control are in the generation of compensatory responses. Here, we used a robot-based adaptation paradigm to investigate if feedback/feedforward and unilateral/bilateral contributions to locomotor adaptation are also context dependent in healthy adults. A robot was used to induce two opposite unilateral mechanical perturbations affecting the step length over multiple gait cycles. Electromyographic signals were collected and analyzed to determine how muscle synergies change in response to perturbations. The results unraveled different unilateral modulation dynamics of the muscle-synergy activations during adaptation, characterized by the combination of a slow-progressive feedforward process and a fast-reactive feedback-driven process. The relative unilateral contributions of the two processes to motor-output adjustments, however, depended on which perturbation was delivered. Overall, these observations provide evidence that, in humans, both descending and afferent drives project onto the same spinal interneuronal networks that encode locomotor muscle synergies.
Similar content being viewed by others
Introduction
Humans have the ability to modify their motor plan in response to changes in the walking environment, a phenomenon referred to as locomotor adaptation1. The study of locomotor adaption has been pursued to improve our understanding of the organization of human locomotor circuits, given the inapplicability, in humans, of the invasive techniques employed in animal models. As a case in point, studies in the lamprey, frog, turtle and cat have consistently shown that locomotor control is accomplished by rhythmic activations of lower-level spinal circuits that regulate the activities of fixed neuromuscular modules2,3,4,5,6. It has been debated if such modules exist in humans7, and if they encode the relative levels of activation across muscles8, the temporal relations among the activations of muscle groups9, or involve more complex structures10,11. A study on adaptation during forward/backward walking on a split-belt treadmill has provided evidence that human locomotion is controlled by leg-specific and forward/backward-specific independent networks12. These observations are compatible with a two-level organization of spinal central pattern generator (CPG) circuits where the higher level regulates the timing of activation of different muscle groups, while the lower level encodes the relative contribution of the different muscles to the task.
Despite the insights generated by the above-mentioned studies, our understanding of the neural mechanisms underlying locomotor adaptation is still limited. Specifically, how behavioral, functional and physiological processes work in concert to achieve adaptation during locomotion has remained elusive to date. In fact, there has long been uncertainty about which are the variables that drive adaptation during locomotion. Previous studies have suggested them to be related to gait stability13, energy expenditure14,15, and gait symmetry16. Recent studies have questioned the role of symmetry in gait adaptations, by showing asymmetric adaptive patterns that are more metabolically efficient17 or that better fit the kinetic requirements of the task18. Recent work by our group suggests a hierarchical organization of these variables with gait stability as the primary task-relevant variable19. Because of this hierarchy, we found that behavioral responses to perturbation are context-dependent, meaning that the presence and extent of the adaptation to a gait perturbation depends on the way in which the perturbation alters the biomechanical demands of the gait task within the environment. In previous work, we found that perturbations that alter gait stability are compensated for even at the cost of increasing energy expenditure, but perturbations that do not challenge gait stability are ignored if the necessary adjustments would lead to an increase in energy expenditure19. Gait symmetry is maintained if it is needed to preserve gait stability and/or minimize energy expenditure.
At the functional level, herein intended as the set of possible control strategies employed by the CNS, locomotor adaptation is generated by feedforward mechanisms20, although the response to the perturbation that causes the adaptive response may be marked also by feedback strategies16,21,22 that may depend on changes in task demands23,24. Feedforward, predictive, mechanisms are associated with a gradual response as the CNS generates a model of the effect of the perturbation. Feedback mechanisms are associated with reactive, faster responses24. How these mechanisms are triggered and combined during gait is yet a source of debate. At the neurophysiological level, adaptation has been argued to be controlled via either leg-independent12 or bilaterally-linked25 mechanisms. It is reasonable to expect that, as observed at the behavioral level, predictive/adaptive (i.e., feedforward) and reactive (i.e., feedback) responses manifested at the functional and neurophysiological levels would also be context-dependent. Understanding how these processes contribute differently to generating responses to perturbations is particularly relevant to robot-assisted gait rehabilitation, in which robot-driven forces or modifications in the walking environment are used to trigger responses aimed to achieve a physiological gait pattern. From this perspective, a dissection of how the feedforward and feedback components of automatic responses to perturbations are triggered and combined could inform the best use of devices for gait rehabilitation. As feedforward and feedback control strategies have been observed to contribute simultaneously to locomotor adaptation21,22, their relative input can be ideally dissected by comparing the response processes to perturbations that are expected to yield different contributions from these two mechanisms. This can be done by testing perturbations that have different biomechanical effects but that are introduced in the same general experimental paradigm.
In line with this overall objective, the aim of this study is to shed light on the mechanisms, at the functional and neurophysiological levels, of locomotor adaptation to robot-induced forces altering the gait pattern of humans. We used a robot-based adaptation paradigm19 and the analysis of muscle synergies26 to investigate the relative contributions of predictive/adaptive (i.e., feedforward) vs. reactive (i.e., feedback) locomotor control strategies. We also investigated the modular organization of the muscle synergies and assessed if their control during locomotor adaptation is unilateral or bilaterally-linked25. We performed two motor adaptation experiments in healthy individuals by introducing a unilateral mechanical perturbation that resulted in either an increase (X experiment) or a decrease (Xinv experiment) in step length. We previously observed that both perturbations trigger an adaptive response19. However, given the opposite biomechanical effects of the perturbations, the two related adaptation processes are expected to be obtained through different contributions of the feedforward and feedback control mechanisms. The analyses performed in this study allowed us to separate the feedforward and feedback contributions to the adaptation to both perturbations, as, respectively, slow and progressive or fast and reactive modifications in the neuromuscular controls.
The results showed, conclusively, that not only feedforward and feedback contributions can be achieved through simultaneous access to the same muscle synergies22, but also that they contribute to adaptation together and differently depending on the biomechanical context. Adding to the rich literature analyzing the characteristics of muscle synergies during locomotion27, our results provide the strongest demonstration to date that the neuromuscular adaptive control of human locomotion can be effectively described as a context-dependent sum of feedback and feedforward strategies that simultaneously shape the activation of invariant motor primitives. These results strongly suggest the presence, in humans, of a defined population of spinal interneurons regulating muscle coordination that can be accessed by both cortical and afferent drives, as observed in animal models28. The observations derived from this work could be used to develop new approaches to the design of robot-assisted gait rehabilitation procedures targeting specific descending- and/or afferent-driven responses in muscle synergies29.
Results
Subjects walked with the lower limbs strapped to the robotic legs of a system for gait rehabilitation (Lokomat by Hocoma AG, Fig. 1A). The system was used to implement motor adaptation experiments based on a unilateral perturbation to the subjects’ right leg resulting in either an increase (X experiment) or a decrease (Xinv experiment) in step length19. Figure 1D shows a schematic representation of the experiments. Each experiment consisted of 420 gait cycles. The experiment started with a habituation phase (consisting of 180 gait cycles) followed by the Baseline (BL), Perturbation (Pert) and After-Effect (AE) phases of the experiment, each consisting of 80 gait cycles. During the habituation phase, the system was programmed to be transparent to the subject (Back-Driven Mode - BDM) except for 9 randomly-selected gait cycles during which the subject experienced a perturbation (Force-Field Mode - FFM). During the BL and AE phases, the robot was also programmed in BDM. During the Pert phase, the system was programmed in FFM and produced one of the two types of perturbation (i.e., X or Xinv) for all the gait cycles.
Experimental setup. (A) Robotic system (Lokomat, Hocoma, Switzerland) used in the experiments and graphical representation of the effects of the two perturbations on the foot trajectory. The orange, red, and light-yellow lines represent the baseline foot trajectory pattern, the effect of the X perturbation, and the effect of the Xinv perturbation, respectively. The robot is attached to the leg via two cuffs located roughly in the middle of the thigh and shank. (B) Schematic representation of the position of the EMG electrodes used during the experiments. The grey rectangles represent the positions of the cuffs linking the leg with the robotic system. (C) Schematic representation of the foot trajectory during the experiment (continuous line) and portion of the cycle during which the robot produced a perturbation (i.e., mid-to-terminal swing phase of the gait cycle marked by the orange bold-dashed line). (D) Phases of the experiment. During the habituation period (first 180 gait cycles), the system was operated in Back-Driven Mode (BDM) except for 9 Force-Field Mode (FFM) single-step perturbations randomly distributed in time. The rest of the experiment consisted of 80 BDM gait cycles (baseline - BL), 80 FFM gait cycles (perturbation - Pert) and 80 BDM gait cycles (after effect - AE).
Lower-limb adaptation to two opposite perturbations
At the onset of the X perturbation, all subjects showed an immediate step-length increase in the right, perturbed, side of 25.9 ± 6.7% (mean ± standard error) that was statistically significant (Friedman test followed by post-hoc Minimum Significance Test) (Figs. 2A and S1A). As we previously observed19, this change was followed by an adaptive response to the perturbation as indicated by a gradual restoration of BL step length in the perturbed side with a residual positive deviation (at the end of the Pert phase) of 5.5 ± 4.8%. This residual deviation from BL step length was statistically different from the deviation observed at the beginning of the Pert phase, but not significantly different from the BL step length, indicating that subjects were able to restore their baseline step length. Full adaptation to the X perturbation, estimated as 3 times the time constant of the exponential function fitting the average step-length time-course, was found to require 13.8 gait cycles (with the 95% confidence interval ranging from 10.6 to 19.9 gait cycles). At the beginning of the AE phase, when the perturbation was removed, a significant aftereffect, manifested as a 29.4 ± 6.7% decrease in step length in the perturbed side, was observed. All subjects then gradually returned to their BL step length.
Group analysis of adaptation in step length. Percentage changes in normalized step length during the BL, Pert and AE phases for the left (L) unperturbed (blue/light blue) and the right (R) perturbed (orange/yellow) legs. The data is shown for (A) the X and (B) the Xinv experiments. Each plot represents mean and standard error of the data across subjects. The bold lines shown for the right foot plots represent the exponentials (see Eq. 3, Materials and Methods) fitting the group data for the Pert and AE phases of the experiments. Lines were plotted for the BL phase of the experiments, at values equivalent to 100% step length. The horizontal plane corresponds to the 100% step length value, while the two vertical planes represent, respectively, the beginning and end of the Pert phase of the experiments. For the X perturbation (A) we observed a ~30% increase in step length of the perturbed leg at the beginning of the Pert phase. The corresponding plot shows an exponential adaptation. At the beginning of the AE phase, we observed a decrease in step length and a rapid return to BL step length. No significant changes were observed on the contralateral side. A mirrored behavior was observed in response to the Xinv perturbation (B).
Similar results were observed during the Xinv experiments, but opposite in the direction of step-length change (Figs. 2B and S1B). The initial response to the Xinv perturbation was marked by a significant decrease in step length in the perturbed side (41.2 ± 3.8%). At the end of the Pert phase, a residual step-length decrease of 9.7 ± 3.7% was observed in the perturbed side that was statistically different from the step length at the beginning of the Pert phase, but not from the BL step length, indicating, again, a return to the baseline step length. Full adaptation was achieved in 9.3 gait cycles (with the 95% confidence interval ranging from 7.2 to 13.3 gait cycles). A significant step-length increase in the perturbed side (28.2 ± 3.8%) was observed upon removal of the perturbation. All subjects were then able to return to their BL step length. No significant change was observed in the step length of the unperturbed left leg during both experiments (Figs. 2A,B and S1A,B). The time-course of adaptation for both experiments was in line with what we observed in previous experiments based on the same setup and perturbations19.
Four muscle synergies reconstructed baseline electromyographic data
Muscle synergies were extracted both unilaterally (i.e., using data collected from one leg at the time) and bilaterally (i.e., using data collected from both legs). The bilateral analysis was employed to highlight the presence or absence of adaptation processes that are bilaterally-linked.
Four muscle synergies were sufficient to reconstruct the amplitude modulation of the electromyographic (EMG) data during the BL phase with a R2 > 0.75 in both the unilateral and bilateral analyses (R2 = 0.80 ± 0.02 for the bilateral analysis; R2 = 0.86 ± 0.06 for the unilateral left leg analysis; R2 = 0.79 ± 0.04 for the unilateral right leg analysis). The muscle synergies and their corresponding activation patterns identified from the EMG recordings collected during the BL phase of both experiments (Fig. 3) were used as the reference synergy patterns for the X and Xinv experiments, and are herein referred to as REFsynX and REFsynXinv, respectively. The results of the unilateral analyses (Fig. 3A) are consistent in their muscular compositions with those previously reported for a similar set of muscles8,25. The rectus femoris (RF) and vastus medialis (VM) muscles are the main contributors to synergy #1 (S1). This synergy is primarily active during early stance and provides stability during the loading response phase of the gait cycle. The soleus (SOL) and gastrocnemius (medial head) (MG) muscles are the main contributors to synergy #2 (S2). This synergy provides propulsion during terminal stance. The tensor fasciae latae (TFL), RF, gluteus maximus (GM), and tibialis anterior (TA) muscles are the main contributors to synergy #3 (S3). During initial swing, this synergy provides ankle dorsiflexion and hip flexion. Finally, the TA and biceps femoris (BF) muscles are the main contributors to synergy #4 (S4), which is primarily active during terminal swing and is responsible for foot landing negotiation and deceleration. In the bilateral analysis (Fig. 3B), S1 of each leg combined with S3 of the contralateral leg, while S2 combined with S4. This is due to the temporal association among the phases of the gait cycles of the two legs.
Reference synergies extracted during BL. Four unilateral synergies were extracted for both the left and right legs (A). Weights for each synergy are represented as average and standard deviation across the two experiments of all the subjects. The activation patterns are represented both individually (thin lines) and as an average across the two experiments of all subjects (bold line). Shaded areas represent the swing phase of the left (green) and right (grey) gait cycles, respectively. Four muscle synergies were also extracted in the bilateral analysis (B) that appeared to result from the combination of the unilateral synergies.
No additional muscle synergy recruited during motor adaptation
At the level of muscle synergies, we expect adaptation to occur through one of the following mechanisms:
- a.
Through recruitment of ≥1 additional task-specific synergies30,31.
- b.
Through modification of the activation patterns of a fixed set of muscle synergies22,32.
- c.
Through modification of the weights of select muscles in some or all the muscle synergies33.
- d.
Through a combination of a, b and/or c30.
Herein, we systematically assess which of the above mechanisms may be at work during adaptation to the perturbations tested in the study (see Materials and Methods). We first analyzed if adaptation is associated with mechanism a by examining whether adaptation leads to a change in the number of synergies composing the EMG data. This was achieved by finding the dimensionality of the subspace shared between the 4 BL synergies (REFsynX and REFsynXinv) and sets of 4 or 5 synergies for the unilateral analyses and 4, 5 or 6 synergies for the bilateral analysis that were extracted from the EMG data recorded during the last 10 gait cycles of the Pert phase (herein referred to as the late-Pert phase) when full adaptation had been attained. We reasoned that if a new synergy emerged after adaptation without altering the pre-existing four, the dimensionality of the subspace shared between the BL synergy set and the late-Pert set would increase as the number of synergies composing the latter increased. This is because the original 4 BL synergies can be clearly identified as shared subspace dimensions only when the new additional synergies during the late-Pert phase, if any, are properly accommodated for as extra dimensions. It is worth pointing out that we tested 4, 5 and 6 synergies for the bilateral analysis (but only 4 and 5 synergies for the unilateral analyses) to account for the possibility that two distinct unilateral synergies could emerge from the analysis of the late-Pert data that would not merge in a single bilateral synergy (contrary to what was observed for the BL phase of the experiment).
We found that for both legs, during both the X and Xinv experiments, the shared subspace dimensionality between BL and late-Pert synergies remained at 3, regardless of whether 4, 5, or 6 synergies were extracted from the late-Pert EMG data, and whether unilateral or bilateral synergy subspaces were compared (Fig. 4A). Indeed, if there were, say, 1 additional synergy activated at the end of the Pert phase, one would expect the 4-synergy BL space and the 5-synergy late-Pert space to share a 4-D, instead of a 3-D, subspace. We concluded that motor adaptation during both the X and Xinv experiments did not occur by recruiting a new muscle synergy while preserving the BL muscle synergies. It should be emphasized that, in this type of analysis, the values of the cosine of the principal angles do not matter. What matters is whether the patterns shown in Fig. 4A change as we increase the number of synergies used to model the EMG data collected during the late-Pert phase.
Analysis of the dimensionality of the synergy subspaces. (A) Bar plots of the average - across subjects - cosines of the matched principal angles between the reference synergies (extracted from the gait cycles of the BL phase) and the synergies extracted unilaterally for both legs during the late-Pert phase (extracted from the last 5 segments, i.e., 10 gait cycles). Results obtained by comparing 4 and 5 unilateral (top plots) and 4, 5 and 6 bilateral synergies (bottom plots). The dotted line represents the threshold value obtained through surrogate data analysis (see Materials and Methods). For all the analyses, we observed a consistent shared subspace size. (B) Average and standard error - across subjects - of the R2 derived for the last 10 epochs of the BL phase and the first and last 10 epochs of Pert phase using the NMFFixedW and NMFFixedC algorithms. Results are shown for the unilaterally (top plots) and the bilaterally (bottom plots) extracted synergies. The p-values of Friedman’s ANOVA tests (significance level α = 0.1) are presented in each plot. Minimum Significance Difference tests showed significant differences across pairs (see Materials and Methods) as highlighted by the * symbol and the horizontal lines.
Another argument that supports the exclusion of mechanism a comes from the analysis of the R2 of the EMG data reconstruction. If adaptation happened to be associated with the recruitment of an additional 5th muscle synergy, reconstructing the EMG activity during the late-Pert phase using 4 synergies would result in a decrease in the quality of the reconstruction as reflected by smaller R2 values. We, on the other end, showed that 4 synergies could represent equally well muscular activities during both the BL phase and the late-Pert phase of the experiment (Fig. S2).
No modification of the weights of baseline muscle synergies during motor adaptation
We then tested if adaptation is achieved via modification of the activation patterns of a fixed set of muscle synergies (mechanism b) or via modification of the weights of select muscles in one of the 4 BL synergies (mechanism c). To test these hypotheses we determined how well the EMG data of the BL and Pert phases could be reconstructed by the reference BL muscle synergies while fixing either the BL muscle-synergy vectors (i.e., the W matrix of the Non-negative Matrix Factorization -NMF) (NMFFixedW), or the BL activation patterns of the synergies (i.e., the C matrix of the NMF algorithm) (NMFFixedC), (see Materials and Methods). A significant decrease in reconstruction quality in one of these analyses would indicate that either the same reference W (for NMFFixedW), or the same reference C (for NMFFixedC), was not sufficient to capture EMG changes associated with adaptation, thus implicating mechanism c in the former, or mechanism b in the latter, assuming that either W or C would be primarily modified for adaptation.
The bilateral analysis was primarily employed to highlight if mechanisms b and c, if present, are employed independently by the two legs or in a bilaterally-linked way. In the bilateral analysis (Fig. 4B), we observed that fixing either the muscle synergies or the activation patterns to their reference values led to a decrease in the reconstruction quality from the BL to the Pert EMG data irrespective of whether we considered the beginning (Early Pert) or the end (Late Pert) portions of the Pert phase. Thus, if the muscles from both sides are analyzed together, it is not possible to differentiate whether mechanisms b or c may better characterize adaptation drives. Indeed, for bilateral synergies, changes in the EMG characteristics from the BL phase to the Pert phase could only be captured if both W and C were left free to be updated in the NMF algorithm (Fig. S2).
In the unilateral analysis, implementing NMFFixedC, but not NMFFixedW, led to a drop in the reconstruction quality from the BL to Pert EMG data in both legs of both perturbation experiments (Fig. 4B). Thus, in both the X and Xinv experiments, the Pert data could not be modeled by just modulating the weights of the BL muscle synergies while keeping the temporal activations constant. However, adaptation could be modelled by modulating the muscle synergy activation patterns while leaving the composition of the muscle synergies unchanged. These results are consistent with mechanism b (fixed muscle synergies) and not with mechanism c (altered synergies post-adaptation). Furthermore, the concurrent observation that mechanism b was independently present in the muscle synergies of both legs in our unilateral, but not bilateral, analysis suggests that adaptation to the two perturbations is driven by unilateral mechanisms. It is worth pointing out that both legs could display changes in the temporal activations of the muscle synergies that would however be leg-specific. This latter point explains the inconsistency between the bilateral and unilateral results, and, more specifically, why mechanism b is not observed in the bilateral analysis. In fact, our results in the unilateral analysis suggest that left and right synergies that are linked in the bilateral analysis adapt their activation patterns independently, with different behaviors and time constants (as better explained later). Thus, when the synergies are bilaterally linked in the analysis, the changes in the resulting activation pattern cannot capture the different dynamics of the unilateral synergies.
The X and Xinv perturbations elicited two distinct behaviors in the synergy activations
The above-summarized analyses indicate that step-length adaptation during the X and Xinv experiments can be modelled by modulating the temporal activations of the muscle synergies that mark unperturbed walking. We next focused on assessing how the activation of each synergy changed during the adaptation experiments. The dynamics of this change was evaluated by measuring the similarity between the temporal activation of 2-step epochs, during the BL, Pert and AE phases, and that of the corresponding reference synergy extracted from the whole BL data. This analysis resulted in similarity value time series (Fig. 5) charting the extent to which the synergy activations deviated from the reference patterns during the experiment. To determine if the activation of each muscle synergy displayed an adaptive behavior, we fit an exponential function (Eq. 3, Materials and Methods) to the corresponding similarity value time series derived for the Pert and AE phases, respectively. The behavior was defined to be adaptive if the cumulative R2 of this fit was >0.75.
Adaptation in the unilateral activation patterns of the synergies. Results obtained using the NMFFixedW algorithm on all the EMG epochs in the two experiments, (A) for X and (B) for Xinv. For each panel, each row shows the data for a different synergy (S#L for left side synergies, S#R for right side synergies). For each synergy, the plots (from left to right) show: (1) the average - across subjects - synergy reference modules; (2) the average - across epochs - temporal activation pattern during the last 10 gait cycles of Pert phase (thin colored lines), and the average - across segments and subjects - reference temporal activation pattern (bold black line), with a black bold line at the bottom of each set of plots representing the time interval when the force-field was active; and (3) the similarity (i.e., Pearson’s linear correlation coefficient) between the activation pattern of each epoch of the experiment and the reference activation pattern (that is the average of the epochs extracted during BL); the vertical grey lines represent the beginning and the end of the Pert phase. Black lines represent the exponential best fitting of the Pert and AE data. For the BL phase, the black lines represent the average similarity during BL. Exponential fitting was added only for the synergies for which it was possible to fit two exponential functions for the Pert and AE phases with a cumulative R2 > 0.75.
Over the Pert phase of the X experiments, we observed both a modest step-wise (i.e., feedback) behavior and an adaptive (feedforward) behavior marked by a gradual change in the temporal activation similarity value time series. The adaptive behavior was detected in 3 out of 4 synergies on the left (unperturbed) side, and in all 4 synergies on the right (perturbed) side (Fig. 5A). The adaptive behavior was characterized by a decay in the similarity value time series until a stable value was reached after a few gait cycles. The time constants of this decay ranged from 9.6 (S3L) to 64.4 (S1L) gait cycles (Table S1). After removal of the perturbation, the similarity was gradually restored to its BL level. This AE phase presented time constants ranging from 2.3 (S3L) to 37.4 (S1L) gait cycles. When we examined the temporal activations of the synergies during late Pert (Figs. 5A and S3), we noticed that adaptation was largely driven by an increase in the activation amplitudes of S1L and S4R. Both were active during the portion of the gait cycle when the perturbation was produced by the robot (Fig. 5A, black bold line). Also, adaptation was associated with increased activations of S3L and S1R. It is worth noticing that the adaptation time constants of this bilaterally-linked synergy pair (S3L + S1R) were different, despite the similar modulation observed in late-Pert (Table S1 shows all the time constants and associated 95% confidence intervals), further suggesting that full adaptation is achieved via unilateral mechanisms.
In the Xinv experiment, we also observed both a step-wise (i.e., feedback) behavior and an adaptive (feedforward) behavior marked by a gradual change in the temporal activation similarity value time series. However, unlike the X experiment, the time series of the temporal activation similarity values for the muscle synergies of the right (perturbed) leg showed a dramatic change at the onset of Pert for several synergies. After this step-wise (i.e., feedback) behavior, the temporal activation similarity value time series showed a gradual return to a level close to the BL value. On the left (unperturbed) leg, even though S1L, S3L and S4L showed an initial step-like deviation from the BL value, the similarity value time series did not satisfy the set criterion of adaptation. On the perturbed right side, adaptation was visible in S1R, S2R and S4R. While all 3 synergies presented an abrupt degradation in similarity at the beginning of the Pert phase, S4R and S1R converged to levels more deviated from the average BL similarities at the end of Pert while S2R returned to its BL value. The time constants of adaptation ranged from 7.6 (S1R) to 15.8 (S2R) gait cycles in the Pert phase, and from 9.0 (S1R) to 21.2 gait cycles (S2R) in the AE phase (Table S1). Full adaptation to Xinv at the end of the Pert phase was characterized mainly by an increase in the activation of the synergies of the right leg (Fig. 5B). Changes in the temporal activations are shown in Fig. S3.
Finally, we analyzed if the two perturbations led to similar patterns of adaptation. We observed that, although the reference modules and activation patterns extracted during the BL phases of the two experiments were consistent, the activation patterns at the end of the Pert phase for the two perturbations were different (Fig. S4).
Discussion
Our results show that the activity of lower-limb muscles during locomotor adaptation to the perturbations tested in the study can be modelled by modulating the muscle synergy activation patterns observed during the BL phase of the experiment (i.e., in the absence of any perturbation) while leaving the composition of the muscle synergies unchanged. Furthermore, the study provided evidence that the response to perturbations that cause locomotor adaptation is not associated with a single response strategy, but instead, by dynamically mixing multiple response mechanisms in a context-dependent manner. Specifically, our study unravels concurrent actions of unilateral feedforward- and feedback-driven mechanisms that affect the muscle synergies of the two legs and that are a function of the biomechanical effect of the perturbation. These results provide a clear demonstration of the invariance to mechanical perturbations of the human locomotor muscle synergies and show that their temporal activations are under both feedforward and feedback control in a context-dependent fashion.
Separating feedforward- and feedback-driven EMG changes during locomotor adaptation
Motor behaviors associated with feedback (i.e., reactive) and feedforward (i.e., adaptive) mechanisms were previously observed during adaptation experiments relying on applying unilateral resistive perturbations to the hip and knee21, moving platforms acting on the stance leg22, split-belt treadmill16,20,24 and asymmetric cycling23. Feedforward-controlled behaviors are marked by error-driven, progressive modifications of motor commands - based on an internal model of the perturbation - that converge toward an adapted state. They are associated with an aftereffect once the perturbation is removed14,16. This type of control has been attributed to the cerebellum, whose role in updating the internal representation of the dynamics of the limb through sensory prediction error has been observed in both the upper34,35 and lower limbs24,36. On the other hand, motor behaviors that are the result of purely feedback mechanisms are marked by abrupt changes in response to the perturbation and are not associated with an aftereffect when the perturbation is removed. Feedback mechanisms are primarily driven by spinal circuits37.
The presence of feedforward and feedback adaptations in the EMGs has been investigated in the past by examining, in a setup similar to ours, the presence or absence of changes in the muscular activations during catch trials interspersed in the perturbed conditions21 or, more recently in the split-belt treadmill experiment, by comparing the aftereffect of a long exposure to the perturbation with the initial response to a perturbation of opposite direction20. Here, we show that these components of adaptation can also be characterized at the muscle-synergy level, and that this analysis provides valuable information on how groups of muscles adapt and/or react in concert during prolonged perturbations. The synergy activation changes that we observed during both the X and Xinv experiments can, in fact, be explained as the summation of feedback- and feedforward-driven responses (Figs. 6A, S9 and S10). The feedback-driven component observed at the onset of the Pert phase of the experiments is triggered by the initial deviation from the gait plan that marks the BL phase. This component accounts for the abrupt changes observed at the beginning of the Pert phase. Such step-like responses were observed in the X experiment (e.g., S1L and S2R, Figs. 5A and S10) but were particularly prominent in the Xinv perturbation (S1R, S2R and S4R, Figs. 5B and S10). The feedforward response, on the other hand, drives the adaptation from the initial feedback-mediated response towards the final adapted state and is marked by an exponential time-course.
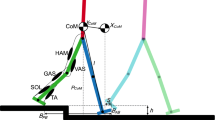
Theoretical and physiological model of the neuromuscular adaptation process as a sum of feedback and feedforward components. The adaptation behaviors that we observed in the similarity plots of Fig. 6 can be explained as the weighted sum of an exponential feedforward (FF) adaptation and a step-like feedback response (FB) (A). By modifying the relative weights of these two components, it is possible to explain all the behaviors we observed in the muscle synergies (a characterization of this model and its fitting on our data are presented in Figs. S9 and S10). At the physiological level (B) our results suggest a direct or indirect (through the rhythm generation parts of the CPGs) activity of both descending corticospinal drive and muscular afferents on the networks of interneurons encoding the muscle synergies in the spinal cord.
By analyzing the muscle synergies during the adaptation process, we successfully disentangled the feedback-driven EMG changes from those mediated by feedforward descending drives. Importantly, this separation allowed us to determine the role of the different feedback and feedforward mechanisms, operating on distinct muscle synergies with different time-courses, in response to different perturbations. The results also show how feedback and feedforward mechanisms affect simultaneously the activation patterns of multiple lower-limb muscles. The results we found on the presence of feedback and feedforward components of adaptation for the Xinv are consistent with those found by Lam and colleagues on a similar setup21.
Context-dependent locomotor adaptation
Previous studies have provided conflicting results in regard to whether locomotor adaptation is driven by unilateral or bilateral control. For instance, Choi and Bastian12 provided evidence of independent high-level neural control of the two legs, whereas Houldin et al.38 showed inter-limb transfer of learning during force-field adaptation, and Maclellan et al.25 suggested that bilaterally-linked unilateral modulations of CPG activities of the two legs takes place during split-belt adaptation.
The results of our study show that the response to perturbations that cause locomotor adaptation is context-dependent. Analysis of the results of the X experiment showed a modest feedback response and a dominant feedforward response in both legs, though the response observed in the data recorded from the right (perturbed) leg followed a different time-course of neuromuscular adjustment from the left (unperturbed) leg. In contrast, the results of the Xinv experiment showed a predominantly unilateral response affecting the right (perturbed) leg. The data collected from the left (unperturbed) leg showed only modest changes consistent with small feedback adjustments. The data from the right (perturbed) leg showed large feedback adjustments and a clear adaptation response in three out of four muscle synergies. Taken together, these results show that the relative contributions to locomotor adaptation of the two legs are context-dependent.
But why did we observe different contributions of feedback- and feedforward-mediated responses to the two perturbations? In previous work19, we showed that the primary task-relevant factor driving the response to the X and Xinv perturbations is the need for preserving long-term gait stability. As both perturbations triggered a response to preserve the same long-term gait stability plan, one would think that the discrepancy in strategy that we observed at the neuromuscular level in response to the two perturbations is due to the different effects the perturbations have on the subject’s dynamic stability.
Specifically, we argue that the larger feedback component observed during the Xinv vs. the X experiment is likely due to the more immediate balance threat induced by the Xinv perturbation compared to the X perturbation. The Xinv perturbation causes a mechanical effect that is similar to hitting an obstacle during the swing phase of the gait cycle. This is expected to bring the projection of the center of mass close to its stability boundaries in the antero-posterior direction. Hence, it is not surprising that we observed a change in the activations of the knee extensors during swing (S1R) and of the ankle plantar-flexor muscles during stance (S2R) - a response that is modulated over time to achieve an increase in the activation of the synergies (Fig. S3). In fact, previous studies have shown short- and medium-latency reflex responses in multiple muscles that appeared to be mediated by Ia and II afferents, respectively, likely caused by the overall jar that the stumbling causes on the perturbed leg39.
Unlike the Xinv perturbation, the X perturbation has an effect that is similar to delaying foot landing. A study by van der Linden et al.40 showed that unexpected delayed foot landing triggers a reflex response on multiple muscles after heel-strike, consistent with the activation adjustment we found in synergy S2R. Nevertheless, in our experiment the sensory feedback provided by the X perturbation acting on the leg likely prompted the subject to anticipate the forthcoming missteps, thus making the effects of the feedforward control to be dominant over those of the feedback response. We argue that, at the biomechanical level, the effects of the X perturbation are less immediately threatening the control of balance, but may lead, over time, to an unstable gait pattern, thus triggering a feedforward adjustment of the motor plan19.
All in all, our results demonstrate that the neural strategy underlying the response to perturbations that cause locomotor adaptation is context-dependent12. Interestingly, the complexity of the mechanisms underlying the response to these perturbations is not apparent when one examines simple aspects of the biomechanics of gait19, but it is clearly shown by examining the characteristics of the muscle synergies derived from the EMG data collected during the experiments23.
The same muscle synergies modulated by feedback- and feedforward-based mechanisms
In contrast to the changes in the activation of muscle synergies, changes in the EMG data of individual muscles in response to the perturbations were more subtle (Fig. S5). In fact, similarity plots derived from data recorded from individual muscles showed adaptation (though not as clearly as the muscle synergies) only in a few cases (Figs. S6 and S7).
Our results provide strong evidence that in humans, both descending (feedforward) and afferent (feedback) drives project, either directly or indirectly, onto the same spinal interneuronal networks that encode locomotor muscle synergies (Fig. 6B). While a modular organization of the control of muscles has been demonstrated for descending motor signals in both animal models41,42 and humans9,25,26,30, the mechanisms controlling synergistic reflexes are still poorly understood. It is known that several reflex pathways project to second and third order interneurons and are able to modulate the activation of the CPGs43. Recent studies on animal models have hypothesized a two-level organization of the CPGs44,45, with the upper-level neural oscillators commanding the lower-level pattern formation interneuronal networks.
In a previous rodent optogenetic study, Levine and colleagues28 identified a molecularly defined population of spinal interneurons that encode the coordination of multiple muscles and are simultaneously activated by both cortical and afferent drives. These networks appear to be the building blocks enabling complex feedforward- and feedback-driven behaviors and could correspond to the hypothesized pattern-formation networks at the lower level of the CPG. In humans, the possibility that sensory afferents could directly act on muscle synergies has been suggested26,30,31,46 but shown only by Chvatal and Ting22, who observed anticipatory and reactive modulations of muscle synergies in response to single-step platform perturbations of the stance leg. The results herein presented extend such observations to motor adaptation and provide further evidence that sensory afferents have a direct effect on muscle synergies by altering their recruitment together with efferent commands during continuous exposure to forces.
As a final remark, the results of the study show that the neuromuscular response of a user to the forces exerted by an exoskeleton during gait does not necessarily lead to a modification of the descending drive to the muscles, which is a primary goal of robot-assisted gait training. Being able to discern whether the neuromuscular responses to the robot-induced forces are reactive or proactive could provide the foundations for new approaches to the design of robot-assisted gait rehabilitation procedures29,47. This could be done, for example, by designing assistive or perturbing forces that trigger descending responses in the activation of selected synergies. Another, similar, approach could be based on analyzing in quasi-real time the neuromuscular adaptation to the forces that the robot is administering during the therapy and use this information for tuning the robotic assistance so as to promote proactive responses or curb reactive ones.
Materials and Methods
Study design
Nine healthy adults (3 women; age = 27.8 ± 3.5; height = 177.7 ± 6.9 cm; mass = 72.4 ± 10.6 kg) participated in the study. This was a sample of convenience. Exclusion criteria for the study were the presence of orthopedic or neurological conditions with a potential effect on the performance or outcome of the experiments. Three of the subjects had experienced the motor perturbations used in the study in a previous experiment. All data collections were performed at Spaulding Rehabilitation Hospital, Boston MA. Subjects completed all the experimental procedures in a single day. The experimental protocol was approved by the Spaulding Rehabilitation Hospital Institutional Review Board. Subjects signed an informed consent form prior to participating in the study. All study procedures were carried out in accordance with all relevant guidelines and regulations.
Generating perturbations using a robotic system
Device settings
Subjects walked with the lower limbs strapped to the robotic legs of a system designed for use in robot-assisted gait therapy (Lokomat by Hocoma AG, Switzerland)48. The robotic system (Fig. 1A) allows for both flexion and extension control of the hip and knee joints via linear actuators. Potentiometers are used to track the joint angles at the hip and knee. Force transducers are used to monitor the torques generated at the joints. The Path Control49 was used in the study. This control modality allowed subjects to naturally control the timing of their gait. The controller estimated, at every instant, the position in the gait cycle via comparison of the actual hip and knee joint angular displacement and angular velocity with template patterns. The comparison used a norm-distance minimization algorithm50. The Generalized Elasticities method51 was implemented to make the system as transparent as possible to the subjects during walking. The Body Weight Support capability of the system was not utilized in the study.
Perturbations
During the experiments, the robot was used in one of two modes of operations: Back-Driven Mode (BDM) and Force Field Mode (FFM) (Fig. 1D). In the BDM, the robot’s apparent impedance was set to zero to minimize the effect of the robot on the walking patterns (i.e., the system was as “transparent” as possible to the subjects). In the FFM, a perturbation was applied to the right leg during the swing phase of the gait cycle. The perturbation force was generated by the robot according to the following equation:
where Fx and Fy represent the antero-posterior (x) and vertical (y) components of the perturbing force acting on the foot, and Vx and Vy represent the x- and y-components of the foot velocity as reconstructed using the following Jacobian:
where lFemur is the length of the femur, lTibia is the length of the tibia, and θ is the vector of the joint angles θh at the hip and θk at the knee.
Subjects experienced two different perturbations produced by different values of the gains A and B shown in Eq. 1. The first perturbation, denoted by X, was achieved by setting \(A=0.115\,\left(\frac{N\cdot s}{Kg\cdot m}\right)\cdot SubjMass\) and B = 0, where SubjMass is the subject’s body mass in Kg. The second perturbation, denoted by Xinv, was achieved by setting \(A=0.092\,\left(\frac{N\cdot s}{Kg\cdot m}\right)\cdot SubjMass\) and \(B=-0.058\,\left(\frac{N\cdot s}{Kg\cdot m}\right)\cdot SubjMass\). These values of A and B were previously determined as suitable to induce modifications in step length (~30% of baseline length) in the forward (X perturbation) and backward (Xinv perturbation) directions, respectively, without concurrently affecting step height19.
Study procedures
Footswitches were attached to the soles of the subject’s shoes in positions corresponding to the calcaneous bone and the first metatarsophalangeal joint, respectively. Subjects were strapped to the system using the cuffs of the robotic legs. Then surface electromyographic (EMG) electrodes were placed on the following 16 muscles (8 per leg): tensor fascia latae (TFL), vastus medialis (VM), rectus femoris (RF), biceps femoris (BF), medial head of the gastroecnemius (MG), tibialis anterior (TA), soleus (SOL) and gluteus maximus (GM). Electrodes were positioned as close as possible to the cusp of the muscle belly following the SENIAM guidelines52 but avoiding contact with the cuffs of the robotic legs, which would have caused artifacts in the EMG recordings (Fig. 1B). The EMG and footswitch signals were digitized using 12 bits with a sampling rate of 3 kHz. Data collected from the robotic system was synchronously recorded at 1 kHz.
Six of the nine subjects who participated in the study had no previous experience with walking using the robotic system. In these subjects, we performed a 5-minute habituation trial using the system in BDM.
Motor adaptation paradigm
During all the experimental trials, the treadmill speed was set at 3 km/h. Subjects’ cadence was paced using a metronome set at 84 beats per minute. Subjects were instructed to pace their heel strikes with the beats of the metronome. No further instructions were given to the subjects. The metronome was used, as in our previous work19, to stabilize the pace, and consequently the speed of the foot. This was done to make sure that subjects experienced consistent perturbation magnitudes across different steps. We have shown in our previous work that the metronome does affect the adaptation process19.
A total of 4 trials were performed as follows: (1) a 90-s trial, for estimating the parameters of the Generalized Elasticities method; (2) a 120-s trial performed with the optimized controller, for estimating the subject’s baseline walking pattern that was used as a reference during the experiment; (3) a 10-min trial to test the effects of the X (or Xinv) perturbation; and (4) a 10-min trial to test the effects of the Xinv (or X) perturbation experiment. The order in which the X and Xinv perturbations were tested was randomized across subjects. A 5-minute break was allowed between the X and Xinv experiments. In each of the X or Xinv trials, subjects performed 420 gait cycles. The trials consisted of four phases.
- (i)
The habituation phase consisting of 180 gait cycles during which the system was set in BDM. 9 gait cycles during which the system was set in FFM were randomly selected after the first 40 cycles, so that there were at least 8 and no more than 18 BDM gait cycles between any two FFM gait cycles. The FFM gait cycles, named single step perturbations, were used to estimate each subject’s response to a single-cycle perturbation.
- (ii)
The baseline phase (BL) consisting of 80 consecutive BDM gait cycles.
- (iii)
The perturbation phase (Pert) consisting of 80 consecutive FFM gait cycles.
- (iv)
The aftereffect phase (AE) consisting of 80 consecutive BDM gait cycles.
Biomechanical analysis of adaptation
Step length was defined, consistently with our previous work19, as the foremost position of the foot during swing. It is important to notice that, in our set up, the reference coordinate system used to determine step length is aligned with the center of rotation of the hip. Hence, if foot contact had occurred with the ankle aligned with the hip, the estimated step length would have been equal to zero. For each subject, the step length values were normalized to the average step length recorded during the BL phase. After normalization, for each of the X and Xinv experiments, the data was averaged across subjects to determine the aggregate adaptation behavior. The time series of the step length estimates derived from the data collected during the Pert and AE phases of the experiment were modelled using exponential functions:
where α represents the response to the perturbation (for the Pert phase) or removal of the perturbation (for the AE phase) observed at the beginning of the Pert or AE phases, β is the time constant of the adaptation, and γ the asymptotic step length value observed when full adaptation has been achieved. In this analysis, similarly to what we did in previous work19, α was estimated by averaging - across all subjects - the step length values observed during the 9 single step perturbations during the habituation phase of the experiment, and β and γ were estimated using a least-squares algorithm.
EMG Pre-processing and segmentation
The EMG data was visually inspected to ensure that high-quality data was then processed. The trials and channels showing significant movement artifacts were excluded from the analysis. This process led to selecting data from 7 out of 9 subjects who participated in the study. The EMG data was first band-pass filtered (50 to 450 Hz) using a 7th-order elliptic filter. The filtered signals were then full-wave rectified and low-pass filtered (cut-off of 5 Hz) using a 7th-order elliptic filter, thus deriving the EMG envelopes. The heel-strike and toe-off times were extracted from the footswitch data of each foot. These events were used to segment the EMG data so that each segment corresponded to 2 steps. The length of each segment was normalized, and the data was re-sampled so that each segment consisted of 200 data points. The amplitude of the EMG data collected during all experimental phases was normalized to the median, across all BL segments, of the maximum values derived for each segment.
EMG analysis
Extraction of the muscle synergies
The non-negative matrix factorization (NMF) algorithm was used to estimate the muscle synergies from the normalized EMG envelopes. This algorithm models the muscular activity MA as a linear combination of muscle synergies, W, whose activity is modulated over time by a set of activation patterns, C:
To derive W and C, we used the NMF algorithm, which is based on the assumption that the EMG envelopes are corrupted by an uncorrelated Gaussian noise53. Muscle synergies were extracted unilaterally (i.e., the EMG data collected from the left leg and the right leg was analyzed separately) as well as bilaterally (i.e., the data collected using all 16 channels was analyzed together). For the BL, Pert and AE phases of each experiment and each subject, we extracted synergies from each 2-step epoch so that a total of (420 − 180)/2 = 120 synergy sets were obtained. A validation of this approach to extracting muscle synergies is shown in Fig. S8. In addition, reference muscle synergies (REFsynX for the X experiment, and REFsynXinv for the Xinv experiment) were extracted, unilaterally as well as bilaterally, from the whole BL data (80 gait cycles) of both experiments without data segmentation. Subsequently, an average activation pattern for the reference synergies was calculated by averaging - across step cycles - the reference C, segmented in time before averaging using the same method utilized to segment the EMG envelopes.
Number of muscle synergies
The R2 derived using the reconstructed EMG data (based on the muscle synergies) and the original EMG data was utilized to select the number of synergies suitable to model the EMG data. Specifically, we selected the number of muscle synergies that would yield a R2 > 0.75 both in the unilateral and bilateral analyses for all subjects. This criterion was met by selecting 4 synergies (R2 = 0.80 ± 0.02 for the bilateral analysis; R2 = 0.86 ± 0.06 for the unilateral analysis of the left leg EMG data; R2 = 0.79 ± 0.04 for the unilateral analysis of the right leg EMG data). This result is consistent with previous studies8.
Changes in muscle synergies in response to the perturbation
To investigate the possible recruitment of additional synergies during motor adaptation, we also extracted 5 unilateral synergies and 5 and 6 bilateral synergies (Figs. 4A,B and S2). We then quantified the similarity between the subspaces spanned by the reference W and the epochal W across the experimental phases. The reference W was obtained by using all the segments of data collected during the BL phase. The epochal W was derived for each segment of the data collected during all experimental phases. The cosine of the principal angles54 between the subspaces spanned by the muscle-synergy sets was then derived to quantify the similarity between the above-defined subspaces. High values of the cosines of the principal angles (i.e., close to 1) indicate that the subspaces spanned by the two synergy sets intersect over a shared subspace of n dimensions, where n is the number of cosine values above threshold. The threshold value was derived - as previously proposed by Cheung et al.55 – via the following surrogate analysis. We calculated, for each subject, the cosines of the principal angles between the reference synergy set (REFsynX or REFsynXinv) and 1,000 Gaussian noise-corrupted (μ = 0; σ = 0.1) versions of each of the 40 BL (two-step) segments. For each of these segments, we estimated the 95th percentile value of the distribution of the cosines of the principal angles obtained for each of the 1,000 Gaussian noise-corrupted versions of the BL segments. Finally, the median of this percentile value across the 40 BL epochs was computed and selected to be the threshold for determining the dimensionality of the shared subspace n for each subject. This procedure allowed us to account for the variability of the epochal muscle synergies expected from chance when determining the threshold.
We also extracted C or W from every epoch by either fitting fixed BL synergies, W (NMFFixedW), or fixed BL activation patterns, C (NMFFixedC), to the epoch data. Through all iterations of the NMF algorithm, the W (for NMFFixedW) or C (for NMFFixedC) matrix was fixed at its reference value, thus allowing for updating only the C (for NMFFixedW) or W (for NMFFixedC) matrix. Using this approach, the variability of the original data set was described only by the updated parameter (i.e., C if W was fixed or W if C was fixed).
How the muscle-synergy activation coefficients C evolved over the course of adaptation was characterized by evaluating the similarity between C of each epoch and the reference C obtained from the BL data, quantified using the Pearson’s linear correlation coefficient. For each epoch, a similarity value was obtained, thus resulting in a time series of similarity values across the BL, Pert and AE phases. To facilitate subsequent modeling of the adaptation dynamics, this time series of similarity values was smoothed using an 8-point moving average filter, that was applied separately to the values from the three phases of the experiments. We fitted the exponential function in Eq. 3 to the similarity value time-series derived for the Pert and AE phases. All three parameters α, β and γ were estimated using a least-squares algorithm. The behavior was defined to be adaptive if the cumulative R2 was >0.75.
We analyzed the data to identify changes in muscle synergies between the two experiments. In this analysis we calculated the similarity between the average weights for the EMG data collected during the BL phase of the X and Xinv experiments. We also calculated the similarity between the temporal activation patterns during the BL and the late-Pert phases across the two experiments. The similarity between the weights was calculated using the normalized dot product. The similarity between the temporal activations was calculated using Pearson coefficients.
Statistical analysis
Several statistical analyses were performed on the data recorded during the experiments. A statistical analysis was performed to test for significant differences in step length on the perturbed side during the different phases of the experiment (Fig. S1). We compared the average normalized step length during the BL phase and the step length for the first and last gait cycles of Pert and AE phases. The analysis was based on Friedman’s ANOVA test (p-values are presented in Fig. S1). The Minimum Significance Difference (MSD)56 test was used for pairwise comparisons of the values of step length between specific phases of the experiments. Similarly to what we did in19, we compared: (1) average step-length during late (last 5 cycles) BL versus first step of Pert, to test if the perturbation induced a significant change; (2) step-length values for the first step versus the last step of Pert, to test if subjects showed an adaptation to the perturbation force vector; (3) step-length values for late BL versus last step of Pert, to test if subjects fully compensated for the robot-induced changes in step-length, (4) step-length values for late BL versus first step of AE, to test for the presence of a significant aftereffect; (5) step-length values for the first step of Pert versus the first step of AE, to test if the aftereffect mirrored, in magnitude, the robot-induced change in step length; (6) step-length values for the first step versus the last step of AE, to test if subjects demonstrated changes in step length during this phase; and (7) step-length values for late BL versus the last step of AE, to test if subjects returned to baseline values of step length at the end of the aftereffect phase. The z-value for the MSD test was set to obtain an overall α of 0.05 for the seven comparisons considered, for an effective error rate per comparison equal to 0.001256.
We extracted synergies (unilaterally and bilaterally) by either using the standard NMF algorithm, or by fixing W or C (Eq. 3) to their baseline values. The R2 values extracted in the different phases of both experiments were statistically compared for all these analyses using a Friedman ANOVA test (α = 0.1). Specifically, we compared values of R2 obtained unilaterally and bilaterally using the unconstrained and constrained NMFs between the BL, early Pert and late-Pert phases. The resultant p-values for these analyses are presented in Figs. S2 and 4B. The Minimum Significance Difference test was used to perform pairwise comparisons. The z-value for the MSD test was set to obtain an overall α of 0.05 for the three comparisons considered (baseline vs. early adaptation, baseline vs. late adaptation and early adaptation vs. late adaptation), for an effective error rate per comparison equal to 0.008356. Finally, a statistical analysis based on the Wilcoxon’s signed rank test (α = 0.05) was used to test for statistically significant changes in the similarity of the activation patterns observed during the BL and late-Pert phases (Fig. S04).
Data availability
The data collected in the study is available on PhysioNet https://physionet.org/.
Code availability
The code developed for the analysis of data collected during the study is available upon request to be sent to the corresponding author.
References
Torres-Oviedo, G., Vasudevan, E., Malone, L. & Bastian, A. J. Locomotor adaptation. Prog. Brain Res. 191, 65–74, https://doi.org/10.1016/B978-0-444-53752-2.00013-8 (2011).
Grillner, S. et al. Neural networks that co-ordinate locomotion and body orientation in lamprey. Trends Neurosci. 18, 270–279 (1995).
Saltiel, P., Wyler-Duda, K., D’Avella, A., Tresch, M. C. & Bizzi, E. Muscle synergies encoded within the spinal cord: evidence from focal intraspinal NMDA iontophoresis in the frog. J. Neurophysiol. 85, 605–619 (2001).
Stein, P. S. Motor pattern deletions and modular organization of turtle spinal cord. Brain Res. Rev. 57, 118–124, https://doi.org/10.1016/j.brainresrev.2007.07.008 (2008).
Krouchev, N., Kalaska, J. F. & Drew, T. Sequential activation of muscle synergies during locomotion in the intact cat as revealed by cluster analysis and direct decomposition. J. Neurophysiol. 96, 1991–2010, https://doi.org/10.1152/jn.00241.2006 (2006).
Kargo, W. J. & Giszter, S. F. Rapid correction of aimed movements by summation of force-field primitives. J. Neurosci. 20, 409–426 (2000).
Zelik, K. E., La Scaleia, V., Ivanenko, Y. P. & Lacquaniti, F. Can modular strategies simplify neural control of multidirectional human locomotion? J. Neurophysiol. 111, 1686–1702, https://doi.org/10.1152/jn.00776.2013 (2014).
Neptune, R. R., Clark, D. J. & Kautz, S. A. Modular control of human walking: a simulation study. J. Biomech. 42, 1282–1287, https://doi.org/10.1016/j.jbiomech.2009.03.009 (2009).
Ivanenko, Y. P., Poppele, R. E. & Lacquaniti, F. Five basic muscle activation patterns account for muscle activity during human locomotion. J. Physiol. 556, 267–282, https://doi.org/10.1113/jphysiol.2003.057174 (2004).
d’Avella, A., Saltiel, P. & Bizzi, E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat. Neurosci. 6, 300–308, https://doi.org/10.1038/nn1010 (2003).
Delis, I., Panzeri, S., Pozzo, T. & Berret, B. A unifying model of concurrent spatial and temporal modularity in muscle activity. J. Neurophysiol. 111, 675–693, https://doi.org/10.1152/jn.00245.2013 (2014).
Choi, J. T. & Bastian, A. J. Adaptation reveals independent control networks for human walking. Nat. Neurosci. 10, 1055–1062, https://doi.org/10.1038/nn1930 (2007).
Prokop, T., Berger, W., Zijlstra, W. & Dietz, V. Adaptational and learning processes during human split-belt locomotion: interaction between central mechanisms and afferent input. Exp. Brain Res. 106, 449–456 (1995).
Emken, J. L., Benitez, R., Sideris, A., Bobrow, J. E. & Reinkensmeyer, D. J. Motor adaptation as a greedy optimization of error and effort. J. Neurophysiol. 97, 3997–4006, https://doi.org/10.1152/jn.01095.2006 (2007).
Finley, J. M., Bastian, A. J. & Gottschall, J. S. Learning to be economical: the energy cost of walking tracks motor adaptation. J. Physiol. 591, 1081–1095, https://doi.org/10.1113/jphysiol.2012.245506 (2013).
Reisman, D. S., Block, H. J. & Bastian, A. J. Interlimb coordination during locomotion: what can be adapted and stored? J. Neurophysiol. 94, 2403–2415, https://doi.org/10.1152/jn.00089.2005 (2005).
Sanchez, N., Park, S. & Finley, J. M. Evidence of Energetic Optimization during Adaptation Differs for Metabolic, Mechanical, and Perceptual Estimates of Energetic Cost. Sci. Rep. 7, 7682, https://doi.org/10.1038/s41598-017-08147-y (2017).
Sombric, C. J., Calvert, J. S. & Torres-Oviedo, G. Large Propulsion Demands Increase Locomotor Adaptation at the Expense of Step Length Symmetry. Front. Physiol. 10, 60, https://doi.org/10.3389/fphys.2019.00060 (2019).
Cajigas, I., Koenig, A., Severini, G., Smith, M. & Bonato, P. Robot-induced perturbations of human walking reveal a selective generation of motor adaptation. Science Robotics 2, https://doi.org/10.1126/scirobotics.aam7749 (2017).
Iturralde, P. A. & Torres-Oviedo, G. Corrective Muscle Activity Reveals Subject-Specific Sensorimotor Recalibration. eNeuro 6, https://doi.org/10.1523/ENEURO.0358-18.2019 (2019).
Lam, T., Anderschitz, M. & Dietz, V. Contribution of feedback and feedforward strategies to locomotor adaptations. J. Neurophysiol. 95, 766–773, https://doi.org/10.1152/jn.00473.2005 (2006).
Chvatal, S. A. & Ting, L. H. Voluntary and reactive recruitment of locomotor muscle synergies during perturbed walking. J. Neurosci. 32, 12237–12250, https://doi.org/10.1523/JNEUROSCI.6344-11.2012 (2012).
Zych, M., Rankin, I., Holland, D. & Severini, G. Temporal and spatial asymmetries during stationary cycling cause different feedforward and feedback modifications in the muscular control of the lower limbs. J. Neurophysiol. 121, 163–176, https://doi.org/10.1152/jn.00482.2018 (2019).
Morton, S. M. & Bastian, A. J. Cerebellar contributions to locomotor adaptations during splitbelt treadmill walking. J. Neurosci. 26, 9107–9116, https://doi.org/10.1523/JNEUROSCI.2622-06.2006 (2006).
Maclellan, M. J. et al. Muscle activation patterns are bilaterally linked during split-belt treadmill walking in humans. J. Neurophysiol. 111, 1541–1552, https://doi.org/10.1152/jn.00437.2013 (2014).
Bizzi, E. & Cheung, V. C. The neural origin of muscle synergies. Front. Comput. Neurosci. 7, 51, https://doi.org/10.3389/fncom.2013.00051 (2013).
Cheung, V. C. K. et al. A novel FES strategy for poststroke rehabilitation based on the natural organization of neuromuscular control. IEEE Rev. Biomed. Eng. 12, 154–167 (2019).
Levine, A. J. et al. Identification of a cellular node for motor control pathways. Nat. Neurosci. 17, 586–593, https://doi.org/10.1038/nn.3675 (2014).
Cheung, V. C. et al. Muscle synergy patterns as physiological markers of motor cortical damage. Proc. Natl Acad. Sci. USA 109, 14652–14656, https://doi.org/10.1073/pnas.1212056109 (2012).
Torres-Oviedo, G. & Ting, L. H. Subject-specific muscle synergies in human balance control are consistent across different biomechanical contexts. J. Neurophysiol. 103, 3084–3098, https://doi.org/10.1152/jn.00960.2009 (2010).
Torres-Oviedo, G. & Ting, L. H. Muscle synergies characterizing human postural responses. J. Neurophysiol. 98, 2144–2156, https://doi.org/10.1152/jn.01360.2006 (2007).
Cheung, V. C., d’Avella, A. & Bizzi, E. Adjustments of motor pattern for load compensation via modulated activations of muscle synergies during natural behaviors. J. Neurophysiol. 101, 1235–1257, https://doi.org/10.1152/jn.01387.2007 (2009).
Ranganathan, R., Krishnan, C., Dhaher, Y. Y. & Rymer, W. Z. Learning new gait patterns: Exploratory muscle activity during motor learning is not predicted by motor modules. J. Biomech. 49, 718–725, https://doi.org/10.1016/j.jbiomech.2016.02.006 (2016).
Smith, M. A. & Shadmehr, R. Intact ability to learn internal models of arm dynamics in Huntington’s disease but not cerebellar degeneration. J. Neurophysiol. 93, 2809–2821, https://doi.org/10.1152/jn.00943.2004 (2005).
Tseng, Y. W., Diedrichsen, J., Krakauer, J. W., Shadmehr, R. & Bastian, A. J. Sensory prediction errors drive cerebellum-dependent adaptation of reaching. J. Neurophysiol. 98, 54–62, https://doi.org/10.1152/jn.00266.2007 (2007).
Jayaram, G. et al. Modulating locomotor adaptation with cerebellar stimulation. J. Neurophysiol. 107, 2950–2957, https://doi.org/10.1152/jn.00645.2011 (2012).
Pearson, K. G. Generating the walking gait: role of sensory feedback. Prog. Brain Res. 143, 123–129, https://doi.org/10.1016/S0079-6123(03)43012-4 (2004).
Houldin, A., Chua, R., Carpenter, M. G. & Lam, T. Limited interlimb transfer of locomotor adaptations to a velocity-dependent force field during unipedal walking. J. Neurophysiol. 108, 943–952, https://doi.org/10.1152/jn.00670.2011 (2012).
Schillings, A. M., van Wezel, B. M., Mulder, T. & Duysens, J. Muscular responses and movement strategies during stumbling over obstacles. J. Neurophysiol. 83, 2093–2102 (2000).
van der Linden, M. H., Marigold, D. S., Gabreels, F. J. & Duysens, J. Muscle reflexes and synergies triggered by an unexpected support surface height during walking. J. Neurophysiol. 97, 3639–3650, https://doi.org/10.1152/jn.01272.2006 (2007).
Caggiano, V., Cheung, V. C. & Bizzi, E. An Optogenetic Demonstration of Motor Modularity in the Mammalian Spinal Cord. Sci. Rep. 6, 35185, https://doi.org/10.1038/srep35185 (2016).
Overduin, S. A., d’Avella, A., Carmena, J. M. & Bizzi, E. Microstimulation activates a handful of muscle synergies. Neuron 76, 1071–1077, https://doi.org/10.1016/j.neuron.2012.10.018 (2012).
Rossignol, S., Dubuc, R. & Gossard, J. P. Dynamic sensorimotor interactions in locomotion. Physiol. Rev. 86, 89–154, https://doi.org/10.1152/physrev.00028.2005 (2006).
McCrea, D. A. & Rybak, I. A. Organization of mammalian locomotor rhythm and pattern generation. Brain Res. Rev. 57, 134–146, https://doi.org/10.1016/j.brainresrev.2007.08.006 (2008).
Zhong, G., Shevtsova, N. A., Rybak, I. A. & Harris-Warrick, R. M. Neuronal activity in the isolated mouse spinal cord during spontaneous deletions in fictive locomotion: insights into locomotor central pattern generator organization. J. Physiol. 590, 4735–4759, https://doi.org/10.1113/jphysiol.2012.240895 (2012).
Duysens, J., De Groote, F. & Jonkers, I. The flexion synergy, mother of all synergies and father of new models of gait. Front. Comput. Neurosci. 7, 14, https://doi.org/10.3389/fncom.2013.00014 (2013).
Safavynia, S. A., Torres-Oviedo, G. & Ting, L. H. Muscle Synergies: Implications for Clinical Evaluation and Rehabilitation of Movement. Top. Spinal Cord. Inj. Rehabil. 17, 16–24, https://doi.org/10.1310/sci1701-16 (2011).
Jezernik, S., Colombo, G., Keller, T., Frueh, H. & Morari, M. Robotic orthosis lokomat: a rehabilitation and research tool. Neuromodulation 6, 108–115, https://doi.org/10.1046/j.1525-1403.2003.03017.x (2003).
Duschau-Wicke, A., von Zitzewitz, J., Caprez, A., Lunenburger, L. & Riener, R. Path control: a method for patient-cooperative robot-aided gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 18, 38–48, https://doi.org/10.1109/TNSRE.2009.2033061 (2010).
Aoyagi, D., Ichinose, W. E., Harkema, S. J., Reinkensmeyer, D. J. & Bobrow, J. E. A robot and control algorithm that can synchronously assist in naturalistic motion during body-weight-supported gait training following neurologic injury. IEEE Trans. Neural Syst. Rehabil. Eng. 15, 387–400, https://doi.org/10.1109/TNSRE.2007.903922 (2007).
Vallery, H., Duschau-Wicke, A. & Riener, R. Hiding robot inertia using resonance. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2010, 1271–1274, https://doi.org/10.1109/IEMBS.2010.5626416 (2010).
Hermens, H. J., Freriks, B., Disselhorst-Klug, C. & Rau, G. Development of recommendations for SEMG sensors and sensor placement procedures. J. Electromyogr. Kinesiol. 10, 361–374 (2000).
Cheung, V. C. & Tresch, M. C. Non-negative matrix factorization algorithms modeling noise distributions within the exponential family. Conf. Proc. IEEE Eng. Med. Biol. Soc. 5, 4990–4993, https://doi.org/10.1109/IEMBS.2005.1615595 (2005).
Golub, G. H. & Van Loan, C. F. Matrix computations. Vol. 3 (JHU Press, 2012).
Cheung, V. C. et al. Stability of muscle synergies for voluntary actions after cortical stroke in humans. Proc. Natl Acad. Sci. USA 106, 19563–19568, https://doi.org/10.1073/pnas.0910114106 (2009).
Portney, L. & Watkins, M. Foundations of clinical research: application to practice. Stamford, USA: Appleton & Lange (1993).
Acknowledgements
The authors would like to thank the R&D team at Hocoma AG for providing access to software algorithms utilized to control the robotic system used in the study. This project was partially supported by the Wyss Institute for Biologically-Inspired Engineering at Harvard University. Iahn Cajigas was partially supported by the National Institute of Neurological Disorders and Stroke (award # 1F31NS058275-01A2). Alexander Koenig was partially supported by the Swiss National Science Foundation (award # PBEZ3_137336). VC was supported by The CUHK Faculty of Medicine (Project FIA2016/A/04) and The Hong Kong Research Grants Council Grants 24115318 (ECS) and CUHK R4022-18 (RIF).
Author information
Authors and Affiliations
Contributions
G.S., A.K., C.A.D. and I.C. contributed to the study design, the performance of the experiments, the analysis of the results, and to writing the manuscript. V.C. and P.B. contributed to the study design, the analysis of the results, and to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests. The authors declare the following non-competing financial interests: G.S. has received grant support (as Principal Investigator) from the EU (H2020) and Enterprise Ireland. A.K. has received grant support (as Principal Investigator) from the German Federal Ministry of Research and Education, the Bavarian Ministry of Economic Affairs, the European Space Agency and the German Federal Ministry of Economic Affairs and Energy. He is founder, shareholder and CEO of Reactive Robotics GmbH (Munich, Germany). C.A.D. has no disclosures. I.C. has received grant support (as Principal Investigator) from the National Institutes of Health (NIH) and the Lemelson Foundation. He has also received grant support (as a co-Investigator) from Medtronic (Minneapolis, MN). V.C. has received grant support (as a Principal Investigator) from the Hong Kong Research Grants Council, the Chinese University of Hong Kong, the Guangdong Provincial Hospital of Traditional Chinese Medicine (Guangzhou, China), and the Golden King (Asia Pacific) Ltd. (Hong Kong). He has also received grant support (as a co-Investigator) from the Shun Hing Institute of Advanced Engineering (Hong Kong). He is also a shareholder and adviser (uncompensated) of Pureform Technology Ltd. (Hong Kong). P.B. has received grant support from the American Heart Association, the Department of Defense, the Michael J Fox Foundation, the National Institutes of Health (NIH), the National Science Foundation (NSF), and the Peabody Foundation including sub-awards on NIH and NSF SBIR grants from Barrett Technology (Newton MA), BioSensics (Watertown MA) and Veristride (Salt Lake City UT). He has also received grant support from Emerge Diagnostics (Carlsbad CA), MC10 (Lexington MA), Mitsui Chemicals (Tokyo Japan), Pfizer (New York City NY), Shimmer Research (Dublin Ireland), and SynPhNe (Singapore). The authors declare the following non-financial interests: G.S., A.K., C.A.D., I.C. and V.C. have no disclosures. P.B. serves in an advisory uncompensated role the Michael J Fox Foundation and the NIH-funded New England Pediatric Device Consortium. He also serves in an uncompensated role on the Scientific Advisory Boards of ABLE Human Motion (Barcelona, Spain), FormSense (San Diego CA, USA), Hocoma AG (Zurich, Switzerland), and Trexo (Toronto, Canada).
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Severini, G., Koenig, A., Adans-Dester, C. et al. Robot-Driven Locomotor Perturbations Reveal Synergy-Mediated, Context-Dependent Feedforward and Feedback Mechanisms of Adaptation. Sci Rep 10, 5104 (2020). https://doi.org/10.1038/s41598-020-61231-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-61231-8
This article is cited by
-
Investigation of adaptive muscle synergy modulated motor responses to grasping perturbations
Scientific Reports (2024)
-
A randomized controlled trial on the effects induced by robot-assisted and usual-care rehabilitation on upper limb muscle synergies in post-stroke subjects
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.