Abstract
The number of spots to monitor to evaluate soil respiration (Rs) is often chosen on an empirical or conventional basis. To obtain an insight into the necessary number of spots to account for Rs variability in a Mediterranean pine-dominated mixed forest, we measured Rs all year long on sixteen dates with a portable gas-analyser in 50 spots per date within an area 1/3 ha wide. Linear mixed-effects models with soil temperature and litter moisture as descriptors, were fitted to the collected data and then evaluated in a Monte Carlo simulation on a progressively decreasing number of spots to identify the minimum number required to estimate Rs with a given confidence interval. We found that monitoring less than 14 spots would have resulted in a 10% probability of not fitting the model, while monitoring 20 spots would have reduced the same probability to about 5% and was the best compromise between field efforts and quality of the results. A simple rainfall index functional to select sampling dates during the summer drought is proposed.
Similar content being viewed by others
Introduction
Soils are the main carbon (C) reservoir of terrestrial ecosystems and contain about twice as much C as the atmosphere1. As a consequence, small changes in soil respiration (Rs) – the efflux of CO2 to the atmosphere resulting from biological activity in soil – may have important consequences on climate and in fact received much attention in recent years2,3. Gathering Rs measurements from different biomes around the world is essential for obtaining a reliable estimate of soil CO2 efflux on a global scale3,4.
Reliable Rs data can only arise from direct measurement in the field, which still presents many challenges despite the fact that it has been carried out for more than a century. The early measurements of Rs were based on chemical absorption of CO2 within a closed chamber by alkali solutions and successive titration. Nowadays, an infrared gas analyser (IRGA) which measures the CO2 concentration build-up inside a dynamic chamber is generally used. Although the IRGA system is not free from artefacts and biases – which can however be minimized3,5 – it has the great advantage of allowing relatively fast measurements and, therefore, of measuring Rs in many different spots. Soil is actually a highly variable environment in terms of each of its features6,7,8. Features related to the soil biota are expected to be even more variable than the others9, both seasonally and spatially.
There is an extensive number of studies which have measured Rs in many ecosystem types (see the updated global dataset by Bond-Lambert and Thomson10); however, very few of them were concerned about how many spots should be measured in that specific environment to properly account for the intrinsic spatial variability of soil. One of these is the experiment set up by Saiz et al.11, who in a first rotation Sitka spruce chronosequence composed of four age classes in Ireland, first assessed that coefficients of variation in Rs varied largely during the year – being lowest during periods with highest Rs – then determined that on average the sampling strategy of 30 sampling spots per stand (of unspecified area) was adequate to obtain a Rs within 20% of its actual value with p = 0.05. Measuring Rs on a regular grid covering an area of 2400 m2 in a mature plantation of Cryptomeria japonica in Japan, Lee and Koizumi12 assessed that the spots required to produce a sample mean within ±10% of the full-population mean (p = 0.05) on three sampling dates were 75, 48, and 110. By random measurements, Rochette et al.13 showed that in a wheat crop the number of spots needed to estimate the Rs on one single hectare within 10% of its mean value decreased from 190 at the time of seeding to 30 at the end of the growing season.
Rodeghiero and Cescatti14 evaluated a method based on initial measurements in a number of randomly selected spots; this number was later reduced by a stratified sampling to the minimum required to adequately estimate Rs. In practice, the spots were sorted according to their average Rs in the first three sampling dates and then equally divided into as many “strata” as the number of spots the researchers actually wanted to continue working on (to be selected randomly one per group). To evaluate the effectiveness of the random and stratified samplings, the authors re-sampled the experimental dataset with a Monte Carlo (MC) approach, varying the sub-sample size at each site. The stratified sampling was found to be effective only in those two ecosystems (of the three studied), where the temporal correlation of the fluxes was high. A similar approach has been used by Knohl et al.15, who measured Rs every 2 to 6 weeks for more than two years in a temperate mixed deciduous forest in Germany. Starting from several measurement sessions during the first year on 40–50 spots, aimed at capturing spatial variability in an area with unknown extension, the authors estimated that at least 8 spots were required to stay within ±20% of the expected mean with p = 0.05 and at least 44 to stay within ±10% of the same mean.
The fact is that every type of stratification inevitably causes some loss of information. Moreover, such an approach bases on the weak assumption that the spots chosen at the beginning of the experiment are constantly ranked in the same way in terms of Rs. From papers dealing with Rs determined by the IRGA device and reporting enough information to infer the sampling density, we drew up Supplementary Tab. 1. The listed works were carried out all around the world, in various environments experiencing diverse types of climates and undergoing different land uses (mostly forests). The majority of these works were observational, i.e., performed without altering the natural conditions, while a few ones were designed, i.e., performed by modifying some climatic or physical features to account for the effects of plausible environmental changes. The spots were distributed randomly or regularly, along a line (transect-based) or on a grid (grid-based) on areas ranging from few square meters to 65 ha. Sampling density ranged from 1.29 to 12,727 spots per hectare (ha), where values over 300 spots ha−1 resulted from monitored surfaces which were objectively too small (less than 0.1 ha) to adequately capture the Rs spatial variation. Physical and biological controlling factors of CO2 efflux may in fact be different at larger scales. In most of the papers listed in Supplementary Tab. 1 the choice of the sampling density appears to be random or not adequately explained.
There are several papers dealing with Rs assessment in forests growing in areas with a Mediterranean climate, where weather seasonality and the spatial variability of vegetation structure are generally higher than in other environments16,17,18,19; nevertheless, few of them paid adequate attention to soil variability and the necessity of working on a number of spots sufficient to obtain a reliable estimate of Rs.
The aim of this work is to get insight into the uncertainty in Rs assessment due to both the number of monitored spots and the seasonal variation in a soil under a pine-dominated forest experiencing Mediterranean climate. The data gathered was thus used to answer to the question: how many spots should be measured to capture Rs variability in this environment? For this purpose, soil temperature, soil and litter moisture, and Rs were measured on 16 dates throughout one year with a portable gas-analyser at 50 spots per day within an area 1/3 ha wide, assuming that the above figures would yield a labour-expensive yet reasonable oversampling. Some linear mixed effects models describing the dependence of Rs on soil temperature and moisture were fitted to the collected dataset and a MC simulation was run for each model to check the effect of a progressive reduction of sampling density on model fitting and the associated uncertainty. A simple index based on cumulative rain was used to select beforehand the most convenient dates of sampling during summer droughts. The ultimate aim of this study is optimizing the allocation of efforts without missing the core of information of the experiment.
Results
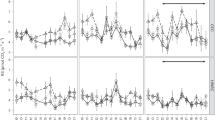
The temporal distribution of Rs values is shown in Fig. 1a, along with climatic data (Fig. 1b) and litter and soil moisture. Soil respiration was highly variable during the year and between the spots (Supplementary Tab. 1), ranging from a minimum of 0.01 g CO2 m−2 h−1 – measured in May, July, October, and August, when the highest recorded values were instead 1.15. 1.05. 0.57 and 0.48 g CO2 m−2 h−1, respectively – to a maximum of 3.58 g CO2 m−2 h−1 in April, when the lowest recorded value was 0.31 g CO2 m−2 h−1 (Supplementary Tab. 2). The time trend of Rs reflected that of litter moisture (solid and dashed lines in Fig. 1a, respectively), which supports the strong dependence of the first variable upon the second one. Only in December Rs did not rise with litter moisture, most probably because of temperatures being too low. At each date, the variability between the spots was high, with standard deviations ranging from 0.11 to 0.56 g CO2 m–2 h–1 (Supplementary Tab. 2). Boxplots in Fig. 1a show that Rs variability increased with increasing Rs
Top panel a) shows the CO2 fluxes measured at 16 dates (indicated as Julian days of 2008 on x axis) in the pine-dominated forest. Notches and dots in the boxplots are the median and the mean, respectively. The gray and white bodies indicate Moist and Dry conditions, respectively. The solid line connects the mean Rs, while the dashed and dotted lines above the boxplots indicate litter and soil moisture (% on wet weight), respectively. Bottom panel b) shows the daily precipitations (bars), the mean temperature of soil (dotted line) and air (dotted-dashed line). The gray bars highlight the 4 days before the CO2 measurements while numbers indicate the cumulative precipitation (mm).
Re-sampling strategies and Monte Carlo simulations
The relationship between the number of spots (hereafter MCspots) – i.e., 49, 48, … 6, 5 – and the converged/fitted model ratio is shown in Fig. 2. All models displayed similar behaviour as the MCspots decreased. One important outcome is that it is necessary to monitor at least 14 spots to sufficiently account for Rs variability; in fact, sampling fewer spots would imply that more than 10% of the attempted models fails to converge and this percentage would rise exponentially as the number of MCspots decreases. On the contrary, for sample sizes greater than 20 and 35 MCspots, the percentage of failed models would drop below 5% and 1%, respectively.
The ratio of converged models/fitted models (1001 converged models obtained) increases exponentially with the number of sampled spots. Vertical dotted lines are drawn at number of spots to monitor in order to have a 90, 95, and 99 ratio of converged/fitted models. RH = Relative Humidity, Moisture in the text.
The surfaces shown in Fig. 3 are the result of uncertainty in prediction (z axis, CO2 flux in original units, g m−2 h−1), based on the four models we tested as a function of both MCspots (x axis) and soil temperature (y axis). The models with the dummy variable show much lower uncertainty in prediction. This favourable feature was not evident either from the BIC values (Supplementary Tab. 3) or the shape of quantile-quantile plots (Supplementary Fig. 1). Since the models with dummy variables – log- or square root-transformed Rs – gave quite similar results both in BIC and quality of residuals, the log-transformed response is here used for the discussion. Due to the presence of the dummy variable, it is possible to show the confidence interval for the two conditions, Moist and Dry (Figs. 4 and 5). The lowest and highest uncertainties were 0.06 and 0.64 CO2 g m−2 h−1 and occurred for Moist conditions at 5 °C for a sample size of 49, and for Dry conditions at 5 °C for a sample size of 5 spots, respectively. The surface for Dry conditions rises steeply in the corner with lower sample sizes and temperatures. While the effect of sample size is obvious, the effect of temperature may be due to the fewer measurement sessions under the Dry conditions (5 sessions vs. 11). Soil respiration peaked at 18 °C and 12 °C for Moist and Dry conditions (Fig. 5), where it amounted to 0.86 and 0.40 CO2 g m−2 h−1, respectively. The fluxes at the two moisture conditions were the same at about 9 °C, where both amounted to 0.38 CO2 g m−2 h−1.
The uncertainty in prediction (l2-l1) calculated by model [1]. Two surfaces are reported, as the model has a binary dummy variable “Moisture” with Moist and Dry levels. The greater prediction intervals under Dry conditions is a direct result of both the Mediterranean climate and of the fact that the spots, when monitored, were described by Moist more often than by Dry conditions.
The fixed part of the mixed-effects model [1] described in the text. Equations were calculated from values reported in Table 2. The error bars (l2-l1, see text) cover the minimum (6 °C) and the maximum (29 °C) soil temperatures recorded in the field. The distribution of the temperature is shown as bars and split between Dry and Moist dates (bottom and top, respectively).
Discussion
Comparison of Values
The mean Rs we found lies on the higher side of the range of values shown in Supplementary Tab. 1 (min. 0.06, 1st quartile 0.26, median 0.43, mean 0.43, 3rd quartile 0.6, max 0. 99 g CO2 m−2 h−1). As regards the Mediterranean ecosystems specifically, Emran et al.20 under Pinus pinea measured an annual mean Rs of 0.69 ± 0.47 g CO2 m−2 h−1, while in two plots of a Scots pine-dominated mixed forest, Barba et al.21 measured an Rs of 0.44 g CO2 m−2 h−1 (0.04 CV, n = 97) and 0.35 (0.03 CV, n = 98) while Rey et al.17 reported a mean annual Rs of 0.46 g CO2 m−2 h−1 for a coppice of Quercus cerris L. The Mediterranean climate is characterized by the alternation of a growing wet season and a non-growing dry season, which clearly have different mean seasonal Rs22. As a consequence, every mean annual Rs to be meaningful should rely on as many as possible sampling campaigns distributed on the basis of the respective lengths of the two seasons. The mean Rs we found is thus perfectly aligned with the ones cited above. Additionally, the Rs range of values we measured is comparable with those found by Rey et al.17 (0.19 to 1.01 g CO2 m−2 h−1) and Joffre et al.18 and Asensio et al.23 in a Quercus ilex forest (0.06 to 0.80 g CO2 m−2 h−1 and 0.13 to 0.54 g CO2 m−2 h−1, respectively).
Land use is another factor of Rs variability in Mediterranean areas. In this regard, Oyonarte et al.24 in six different land uses (forest and agricultural sites) found values ranging from 0.06 g CO2 m−2 h−1 in the dry period (summer) to 0.28 g CO2 m−2 h−1 in the growing season (spring), while in a sparse Pinus halepensis forest, an olive grove, and an abandoned field, Almagro et al.19 found mean Rs of 0.33, 0.27, and 0.18 g CO2 m−2 h−1, respectively. Soils under pine woods, as the one we investigated, thus seem to release more CO2 than soils with different vegetation cover19,20.
Considerations on sampling density and allocation of resources
Supplementary Tab. 1 collates some relevant data from 38 papers including this one. The sampling densities range from 1.29 to 12,727 spots ha−1. Two aspects must be considered: the first one is that nine densities are above 288 spots ha−1 and result from designed experiments that involved areas from 0.04 to 0.006 ha. Working on so small areas of course does not allow reliably evaluating Rs variability at ecosystem level; on the other hand, such sampling densities if exported on rather large surfaces are impossible to manage. To achieve a higher density, some monitoring plans were based on the use of two or more IRGA devices or two or more days to collect data21,25,26; nevertheless, also these plans consisted of about 50 spots per day. Tedeschi et al.27 is the only exception with 100 spots per day per device, but these authors reduced the number of spots to 20 right after a first screening. A single operator can not monitor much more than 50 spots per day, therefore he must size the area to monitor on such a basis. Should the sampling campaign base on two or more devices, the instrumental error of the devices must be minimal and as similar as possible in order to work together. Furthermore, in the case of the Mediterranean climate, spreading the measurement session over two days can imply dramatic changes in weather and, thus, in Rs values, especially depending upon rains (see next section).
Considerations on temperature and moisture
As expected, temperature was a driving factor of Rs, to a varying extent depending upon Moist and Dry conditions (Table 1 and Figs. 2 and 5). The models describing the dependence of Rs on temperature are generally based on the Arrhenius equation, so exponential functions frequently occur in the literature19,28,29,30,31. Although we did not find significant differences between the log and square root transformations in our experiment, we used the log transformation because of its wider acceptance in the literature. Nevertheless, we used a parabolic equation on the right side of the models, since all our attempts to build a model in exponential form were unsatisfactory due to the bad shape of residuals and the poor significance of the model parameters. The purpose of this study was to find the relationship between Rs uncertainty and the number of sampled spots; hence, the building of the model was data-driven.
The dependence of Rs on litter and soil moisture was evident at our site, just as in other Mediterranean ecosystems17,32,33. In particular, rain pulses were able to drastically increase Rs in the dry season (June 9th and September 18th, see Fig. 1a). The infrequent rains in summer in Mediterranean climates have a substantial impact on Rs32, so much to represent actual “hot moments” throughout the year34. Almagro et al.19 meaningfully proposed as a proxy for the effect of rain pulses on Rs the “rewetting index”, RWI = P/t, where P is the mm of precipitation and t the days passed since the previous precipitation. Such a proxy actually accounted for Rs during the long lasting summer drought better than soil moisture. We based our model on an alternative proxy, the cumulative precipitation exceeding 0.5 mm of the four previous days (cp): nonetheless, we cannot exclude that in regions with different climatic conditions, other timespans may work better.
Using indexes based on climate rather than physical measurements of soil moisture, allows for better comparison between studies, since soil moisture measurements are little comparable. In fact, the various studies conduct soil moisture measurements using different 1) methods (from gravimetric to volumetric, discrete vs continuous), 2) control sections, and 3) kinds of probes/sensors, which were often not calibrated to the local conditions. Another practical advantage of a climate index is that it can be calculated a priori and off-site. While soil/litter moisture must be measured each time in the field, cp can be easily monitored remotely and when it exceeds a critical value going to perform CO2 measurements.
Considerations on alternative models
Using a model substantially reduces the number of spots to base on for measuring Rs. In fact we calculated, for each sampling date, the number of spots to monitor according to the formula proposed by Petersen and Calvin35 and used by several authors14,21,36,37
where n is the sample size, t is the t-statistic (two-way test) for a given confidence level and degrees of freedom (95% in the present case), s is the standard deviation of the full population (50 spots per date in this case), and D is the specified error limit, i.e. the width of the desired interval around the full population mean in which a smaller sample mean is expected to fall35.
The results for 1/3 ha are shown in Table 2 and are much higher than those estimated by using model 1. From a predictive point of view there is no difference between using a model that considers only the mean35 and a model that considers more variables. On the other hand, the minor effort of recording variables such as soil temperature and moisture is worthwhile, since it dramatically reduces the number of spots to monitor in terms of CO2.
Conclusion
The methodology here described – data oversampling, model building, Monte Carlo simulations – allowed reaching the principal goal of our work, i.e., to determine the number of spots necessary to capture Rs variability. This number turned out to not be less than 14 in 1/3 ha. Sampling more spots improves the precision of estimation, and 20 spots appeared to be the best compromise between field efforts and the quality of the result. In fact, in this case the probability of not finding a model dropped to less than 5%, while adding further spots does not bring any substantial benefit in terms of converged/fitted models ratio.
Another conclusion is that during the hot dry summer, a simple index based on cumulative precipitation can be used to establish the best dates to detect important CO2 pulses.
Overall, our findings encourage a more rational allocation of resources in both time and space for those aimed at measuring soil respiration in similar environments.
Materials and Methods
Study area
The study area, Pianacci (43°44′31.81″N, 11°06′14.76″E), is a forest stand located about 10 km south of Florence, Italy. The stand is dominated by maritime pine (Pinus pinaster Aiton) and, in suborder, Italian cypress (Cupressus sempervirens L.), with manna ash (Fraxinus ornus L.) and holm oak (Quercus ilex L.) as ancillary species (Supplementary Fig. 2). The climate is typically Mediterranean, with warm and dry summers and relatively cold and wet winters. Data from a weather station 3.5 km away from the study area and referring to the period 1994–2008 accounted for a mean annual precipitation of 764.3 mm, with November as rainiest month (119 mm) and July as the driest (24.4 mm), and a mean annual temperature of 14.8 °C, with January as coldest month (mean 6.5 °C) and July as the warmest (mean 24.2 °C). The terrain is located 216 to 224 m a.s.l. and has a mean slope of 5% and a west to southwest aspect. The soil formed on Oligocene sandstone chiefly composed of quartz, feldspars, and phyllosilicates and somewhere intercalated with thin siltstone layers comprising calcite, quartz, plagioclases, and phyllosilicates. It is a Brunic Arenosol of the World Reference Base for Soil Resources38 and shows an O-A-Bw-BC-C sequence of horizons. Some basic characteristics determined in a soil profile opened approximately in the centre of the stand are shown in Table 3. The very low occurrence of rock fragments in the topsoil (A and B horizons) reveals past agricultural land use.
Monitoring strategy and Rs measurements
Soil respiration was measured from February 2008 to January 2009, monthly except in April-May-June – the period of highest biological activity – when four extra measurement sessions were carried out (Fig. 1a). The CO2 efflux from soil was determined by an EGM-1 PP Systems portable gas analyser (Hitchin, UK) coupled with an SRC-1 closed air-circulation chamber 1.17 dm3 in volume. Within a 1/3 ha wide area we selected 50 spots to monitor throughout the year by a randomization procedure, excluding the outermost four-meter-wide strip of the stand to avoid any border effect. Based on the data of Supplementary Tab. 1 such a sampling density was assumed to be high enough to capture most Rs variability and to perform a Bootstrap resampling procedure aimed at finding the minimum number of spots necessary to estimate Rs with an uncertainty close to 10% of the mean of the population.
A stake was driven into the soil 10 cm north of each spot to localize it. We did not place permanent collars into the soil to prevent lateral gas leakage during measurement, as these have been shown to lead to greater underestimation of Rs due to their severing fine roots and the hyphae of mycorrhizal fungi and, possibly, modifying soil temperatures39,40,41. The Rs measurements were thus carried out by gently inserting the rimmed edge of the chamber 1 cm into the mineral soil and holding the chamber steady during the measurement, to virtually avoid uncontrolled exchanges of air to and from the chamber. At each spot, the temperature of both the atmosphere at ground level and the soil at a depth of 10 cm were recorded. All measurement sessions started at about 11:00, proceeding non-stop in an ordered sequence from spot no. 1 to spot no. 50, which was approximately measured at about 16:00; hence, spending on average about 6 minutes per spot. At each measurement session, two composite samples of both litter layer (O horizon) and top mineral soil were assembled from throughout the area to gravimetrically determine moisture by oven drying at 105 °C to constant mass.
Statistical analysis and model building
In the analysis of data, the CO2 flux (Y, response variable) was considered: 1) on the original scale; 2) after log transformation; 3) after square root transformation. Explanatory variables were: soil temperature, litter and soil moisture (water % on wet weight). Moisture variables were considered: (a) on the original quantitative scale and (b) after transformation into a binary dummy variable (more details here below). Fitting and examination of linear mixed-effect models were performed following Pinheiro and Bates42,43. In particular, within each model as in 1), 2), and 3) above-cited points, selection of linear predictors for fixed effects was performed according to BIC (Bayesian Information Criterion) values44. In the case of litter moisture, fitted models also took into consideration the above-cited (i) and (ii) alternatives about moisture. Variance heteroscedasticity was considered by introducing random effects associated to sampling dates in all models.
For each best model on the chosen scale of the response (labels 1, 2, 3, above) the analysis of residuals45 was done to look for possible evidences of violations in model assumptions. The best models resulting from the above steps were then exploited in the MC simulation.
Litter moisture was found to be a better predictor than mineral soil moisture (Supplementary Tab. 4) and no further improvements of the model came either from the insertion of a cubic parameter or the elimination of the quadratic term (Supplementary Tab. 3).
Whatever the scale for the response variable, the final model matrix X after selecting the best model refers to the following fixed effects: (i) Moisture, defined as in labels (a) and (b) above; (ii) Soil Temperature and its square; (iii) the first order interaction term: Moisture * Soil Temperature, and (iv) Moisture * Soil Temperature2.
The matrix Z for random effects has the following hierarchical structure: (i) Sampled Spot and (ii) Soil Temperature within Sampled Spot.
Thus, the expected value of the response is:
The random part of the model defines an intercept at a given date, which is randomly shifted from the value taken in the fixed part of the model. Random fluctuations of the coefficient for soil temperature are also introduced within the sampling date. Such random effects are normally distributed with null expectation. A variance parameter was introduced at each sampling date, so that the variance-covariance matrix of residuals was diagonal but not constant.
Models for transformed responses (labels 1, 2, 3) were adopted with the aim of checking the assumption of normality. A binary dummy variable (label a) was obtained by the sum of the daily precipitations of four days before the sampling date (cp, cumulative precipitation); hence, if cp was less than 0.5 mm, the dummy variable was set to Dry, otherwise it was set to Moist. The “dry” dates were identified at first on an empirical basis, i.e., as those where low values of both litter moisture and Rs were observed, namely 02–25, 05–12, 07–23, 8–29, and 10–14 (Fig. 1a). Sampling dates were those in which the cumulative precipitation was lower than 0.5 mm in the four previous days. Of course, using values other than 0.5 mm and 4 days, different “dry” dates resulted.
The combination of the CO2 flux (as such, log or square-root transformed) with the two variables (litter moisture or the dummy variable) provided six candidate models for MC simulation (Supplementary Tab. 5 and Fig. 1). The analysis of residuals showed evidence of violation in the assumptions in models with non-transformed CO2 flux as response (Supplementary Fig. 1) and did not indicate any superiority of one model over the others. Therefore, only the four models with log- or square root-transformed underwent Bootstrap re-sampling and MC simulations.
Uncertainty associated with monitoring fewer spots
The uncertainty associated with monitoring fewer spots was evaluated by Bootstrap resampling46,47. Several Bootstrap runs were performed by progressively decreasing the number of spots (MCspots) down to 5: that is 49, 48, …6, 5. In each Bootstrap run, for a given MCspots value a random sample with replacement was drawn from the complete dataset (thus forming a Bootstrap Sample dataset, BSdataset); a model was fitted on this BSdataset and, if model fitting converged, confidence intervals were recorded. The stopping rule for resampling was 1001 models successfully fitted to Bootstrap samples (without errors due to convergence, aliasing, etc.).
Two main consequences were expected from the reduction of the MCspots value: (i) the failure of convergence during model fitting and (ii) the increase of uncertainty of parameter estimates, as captured by the difference between the two endpoints of the confidence interval (95%). The R software48 and its libraries, nlme49 and lattice50, were used for data entry, model fitting, and MC simulations.
Data availability
The dataset is available at https://doi.pangaea.de/10.1594/PANGAEA.896345
References
Ussiri, D. A. N. & Lal, R. The Global Carbon Inventory. In Carbon Sequestration for Climate Change Mitigation and adaptation 77–107 (2017).
Pries, C. E. H., Castanha, C., Porras, R. C. & Torn, M. S. The whole-soil carbon flux in response to warming. Science 355, 1420–1423 (2017).
Xu, M. & Shang, H. Contribution of soil respiration to the global carbon equation. Journal of Plant Physiology 203, 16–28 (2016).
Bond-Lamberty, B. P. & Thomson, A. M. A Global Database of Soil Respiration. Data, Version 3, 0, https://doi.org/10.3334/ORNLDAAC/1235 (2014).
Davidson, E. A., Savage, K., Verchot, L. V. & Navarro, R. Minimizing artifacts and biases in chamber-based measurements of soil respiration. Agricultural and Forest Meteorology 113, 21–37 (2002).
Lin, H., Wheeler, D., Bell, J. & Wilding, L. Assessment of soil spatial variability at multiple scales. Ecological Modelling 182, 271–290 (2005).
Mzuku, M. et al. Spatial Variability of Measured Soil Properties across Site-Specific Management Zones. Soil Science Society of America Journal 69, 1572–1579 (2005).
Li, J. Sampling Soils in a Heterogeneous Research Plot. JoVE (Journal of Visualized Experiments) e58519, https://doi.org/10.3791/58519 (2019)
Speir, T. W., Ross, D. J. & Orchard, V. A. Spatial variability of biochemical properties in a taxonomically-uniform soil under grazed pasture. Soil Biology and Biochemistry 16, 153–160 (1984).
Bond-Lamberty, B. P. & Thomson, A. M. A Global Database of Soil Respiration Data, Version 3.0. ORNL DAAC, https://doi.org/10.3334/ORNLDAAC/1235 (2014)
Saiz, G. et al. Seasonal and spatial variability of soil respiration in four Sitka spruce stands. Plant Soil 287, 161–176 (2006).
Lee, N.-Y. & Koizumi, H. Estimation of the number of sampling points required for the determination of soil CO2. Efflux in two types of plantation in a temperate region. Journal of Ecology and Field Biology 32, 67–73 (2009).
Rochette, P., Desjardins, R. L. & Pattey, E. Spatial and temporal variability of soil respiration in agricultural fields. Can. J. Soil. Sci. 71, 189–196 (1991).
Rodeghiero, M. & Cescatti, A. Spatial variability and optimal sampling strategy of soil respiration. Forest Ecology and Management 255, 106–112 (2008).
Knohl, A., Søe, A. R. B., Kutsch, W. L., Göckede, M. & Buchmann, N. Representative estimates of soil and ecosystem respiration in an old beech forest. Plant Soil 302, 189–202 (2008).
Reichstein, M. et al. Severe drought effects on ecosystem CO2 and H2O fluxes at three Mediterranean evergreen sites: revision of current hypotheses? Global Change Biology 8, 999–1017 (2002).
Rey, A. et al. Annual variation in soil respiration and its components in a coppice oak forest in Central Italy. Global Change Biology 8, 851–866 (2002).
Joffre, R., Ourcival, J.-M., Rambal, S. & Rocheteau, A. The key-role of topsoil moisture on CO2 efflux from a Mediterranean Quercus ilex forest. Ann. For. Sci. 60, 519–526 (2003).
Almagro, M., López, J., Querejeta, J. & Martínez-Mena, M. Temperature dependence of soil CO2 efflux is strongly modulated by seasonal patterns of moisture availability in a Mediterranean ecosystem. Soil Biology & Biochemistry 41, 594–605 (2009).
Emran, M., Gispert, M. & Pardini, G. Comparing measurements methods of carbon dioxide fluxes in a soil sequence under land use and cover change in North Eastern Spain. Geoderma 170, 176–185 (2012).
Barba, J., Yuste, J. C., Martìnez-Vilalta, J. & Lloret, F. Drought-induced tree species replacement is reflected in the spatial variability of soil respiration in a mixed Mediterranean forest. Forest Ecology and Management 306, 79–87 (2013).
Cueva, A., Bullock, S. H., López-Reyes, E. & Vargas, R. Potential bias of daily soil CO2 efflux estimates due to sampling time. Sci Rep 7, 1–8 (2017).
Asensio, D., Penuelas, J., Llusià, J., Ogaya, R. & Filella, I. Interannual and interseasonal soil CO2 efflux and VOC exchange rates in a mediterranean holm oak forest in response to experimental drought. Soil Biology & Biochemistry 39, 2471–2484 (2007).
Oyonarte, C., Rey, A., Raimundo, J., Miralles, I. & Escribano, P. The use of soil respiration as an ecological indicator in arid ecosystems of the SE of Spain: Spatial variability and controlling factors. Ecological Indicators 14, 40–49 (2012).
Søe, A. R. B. & Buchmann, N. Spatial and Temporal Variations in Soil Respiration in Relation to Stand Structure and Soil Parameters in an Unmanaged Beech Forest. Tree physiology 25, 1427–36 (2005).
Shi, B., Gao, W., Cai, H. & Jin, G. Spatial variation of soil respiration is linked to the forest structure and soil parameters in an old-growth mixed broadleaved-Korean pine forest in northeastern China. Plant Soil 400, 263–274 (2016).
Tedeschi, V. et al. Soil respiration in a Mediterranean oak forest at different developmental stages after coppicing. Global Change Biology 12, 110–121 (2006).
Lloyd, J. & Taylor, J. On the Temperature Dependence of Soil Respiration. Functional Ecology 8, 315–323 (1994).
Zhang, L., Chen, Y., Zhao, R. & Li, W. Significance of temperature and soil water content on soil respiration in three desert ecosystems in Northwest China. Journal of Arid Environments 74, 1200–1211 (2010).
Jenkins, M. E. & Adams, M. A. Respiratory quotients and Q10 of soil respiration in sub-alpine Australia reflect influences of vegetation types. Soil Biology & Biochemistry 43, 1266–1274 (2011).
Lellei-Kovács, E. et al. Thresholds and interactive effects of soil moisture on the temperature response of soil respiration. European Journal of Soil Biology 47, 247–255 (2011).
Jarvis, P. et al. Drying and wetting of Mediterranean soils stimulates decomposition and carbon dioxide emission: the ‘Birch effect’. Tree Physiol. 27, 929–940 (2007).
Grünzweig, J. M. et al. Water limitation to soil CO2 efflux in a pine forest at the semiarid “timberline”. J. Geophys. Res. 114, G03008 (2009).
Hagedorn, F. & Bellamy, P. Hot spots and hot moments for greenhouse gas emissions from soils. In Soil Carbon in Sensitive European Ecosystems (eds. Jandl, R., Rodeghiero, M. & Olsson, ts) 13–32 (John Wiley & Sons, Ltd, 2011).
Petersen, R. G. & Calvin, L. D. Sampling. In Methods of Soil Analysis. Part 1. Physical and Mineralogical Methods. vol. 3 1–17 (Sparks D L American Society of Agronomy Inc. and Soil Science Society of America, 1996).
Adachi, M. et al. Required sample size for estimating soil respiration rates in large areas of two tropical forests and of two types of plantation in Malaysia. Forest Ecology and Management 210, 455–459 (2005).
Dore, S., Fry, D. L. & Stephens, S. L. Spatial heterogeneity of soil CO2 efflux after harvest and prescribed fire in a California mixed conifer forest. Forest Ecology and Management 319, 150–160 (2014).
IUSS Working Group WRB. World Reference Base for Soil Resources 2014, International soil classification system for naming soils and creating legends for soil maps. (2014).
Heinemeyer, A. et al. Soil respiration: implications of the plant-soil continuum and respiration chamber collar-insertion depth on measurement and modelling of soil CO2 efflux rates in three ecosystems. European Journal of Soil Science 62, 82–94 (2011).
Jovani-Sancho, A. J., Cummins, T. & Byrne, K. A. Collar insertion depth effects on soil respiration in afforested peatlands. Biol. Fertil. Soils 53, 677–689 (2017).
Wang, W. J. et al. Effect of collar insertion on soil respiration in a larch forest measured with a LI-6400 soil CO_2 flux system. Journal of Forest Research 10, 57–60 (2005).
Pinheiro, J. ́ C. & Bates, D. Fitting Linear Mixed-Effects Models. in Mixed-Effects Models in S and S-PLUS 133–196 (Springer Science & Business Media, 2000).
Pinheiro, J. ́ C. & Bates, D. Extending the basic Linear Fixed-Effects Models. in Mixed-Effects Models in S and S-PLUS 201–266 (Springer Science & Business Media, 2000).
Delattre, M., Lavielle, M. & Poursat, M.-A. A note on BIC in mixed-effects models. Electron. J. Statist. 8, 456–475 (2014).
Pinheiro, J. ́ C. & Bates, D. Examining a Fitted Model. in Mixed-Effects Models in S and S-PLUS 201–266 (Springer Science & Business Media, 2000).
Davison, A. C. & Hinkley, D. V. Bootstrap Methods and their Application, https://doi.org/10.1017/CBO9780511802843 (Cambridge University Press, 1997).
Young, G. A., Hinkley, D. V. & Davison, A. C. Recent Developments in Bootstrap Methodology. Statistical Science 18, 141–157 (2003).
R Core Team. R: A Language and Environment for Statistical Computing. (R Foundation for Statistical Computing, 2016).
Pinheiro, J., Bates, D., DebRoy, S., Sarkar, D. & R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. (2016).
Sarkar, D. Lattice: multivariate data visualization with R. (Springer, 2008).
Acknowledgements
We are indebted to Dr. Ana Rey for helpful criticism on the manuscript, and Ms. Suzanne Büecking, the owner of the forest stand, for providing us with logistic facilities.
Author information
Authors and Affiliations
Contributions
O.L. Pantani analysed and interpreted the data, performed the simulations, wrote most of the R routines, produced the graphics, drafted the work. F. Fioravanti collected data in the field and provided a clean dataset. F.M. Stefanini wrote the R routines for simulations and gave theoretical support to data analysis and interpretation, substantively revised the work. R. Berni gave theoretical support to data analysis and interpretation as well as some preliminary data analysis with mixed-effects models. G. Certini planned the experiment, collected data in the field, analysed the soil, established contacts with the owner of the forest, drafted the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pantani, OL., Fioravanti, F., Stefanini, F.M. et al. Accounting for soil respiration variability – Case study in a Mediterranean pine-dominated forest. Sci Rep 10, 1787 (2020). https://doi.org/10.1038/s41598-020-58664-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-58664-6
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.