Abstract
The study of the preparation phase of large earthquakes is essential to understand the physical processes involved, and potentially useful also to develop a future reliable short-term warning system. Here we analyse electron density and magnetic field data measured by Swarm three-satellite constellation for 4.7 years, to look for possible in-situ ionospheric precursors of large earthquakes to study the interactions between the lithosphere and the above atmosphere and ionosphere, in what is called the Lithosphere-Atmosphere-Ionosphere Coupling (LAIC). We define these anomalies statistically in the whole space-time interval of interest and use a Worldwide Statistical Correlation (WSC) analysis through a superposed epoch approach to study the possible relation with the earthquakes. We find some clear concentrations of electron density and magnetic anomalies from more than two months to some days before the earthquake occurrences. Such anomaly clustering is, in general, statistically significant with respect to homogeneous random simulations, supporting a LAIC during the preparation phase of earthquakes. By investigating different earthquake magnitude ranges, not only do we confirm the well-known Rikitake empirical law between ionospheric anomaly precursor time and earthquake magnitude, but we also give more reliability to the seismic source origin for many of the identified anomalies.
Similar content being viewed by others
Introduction
A large earthquake comes after a long-term preparation phase composed of different stages of seismicity evolution driven by the continuous but variable tectonic stress1,2. The understanding of the underlying physical processes is likely to deliver the most reliable prediction method3. As it is practically impossible to follow this process at the level of the fault (typically at least tens of km depth), an alternative is to study if the lithosphere interacts with the above atmosphere and ionosphere, i.e. assuming a Lithosphere-Atmosphere-Ionosphere Coupling (LAIC4,5,6,7,8), during this long-term phase, but with particular attention to the very last stages. Co-seismic coupling in the atmosphere is well established9, while the possible pre-earthquake coupling is more debated. A recent example is the possible ionospheric electron density enhancement before large earthquakes10.
To explain the LAIC effects, different models have been proposed in the last years. Freund5 proposed a mechanism based on the theory of p-holes (positive holes), which are produced by the stress along the fault. When p-holes reach the Earth’s surface, they could ionize the atmosphere. These charged particles could create instability in the mesosphere and on the edge of the ionosphere. The mechanisms were tested successfully in laboratory11. An alternative mechanism is proposed by Pulinets and Ouzounov6, based on gas and fluid that could rise up toward the surface in the preparatory phase of the earthquake. Another model was provided by Kuo et al.12, which relies on a numerical simulation. It takes into consideration the role of the Earth’s magnetic field, suggesting a possible mechanism of alteration of the ionosphere that improves their previous model13.
A third possible mechanism for the pre-earthquake electric field appearance is the possibility of modification of the electric field around the height of 100 km due to internal atmospheric gravity waves14.
De Santis et al.7, Pulinets and Boyarchuk15 and Hayakawa16 presented a general review about the processes that can occur in the atmosphere and ionosphere before and during an intense earthquake, and their possible correlations.
To detect the pre-earthquake ionospheric anomalies, various parameters can be monitored by ground-based equipment such as ionosondes17,18,19,20,21,22,23, Global Navigation Satellite System (GNSS) receivers24,25 and ULF magnetic field sensors26,27,28.
Parrot29 reviewed the most important results from the space investigations. The seminal satellite mission DEMETER30 was specifically designed to possibly identify a wide range of electromagnetic pre-earthquake signals31 and its statistical analyses were encouraging, pointing to LAIC above some reasonable level of randomness for 6.5 years of earthquakes32,33,34.
A promising application of the geomagnetic field monitoring by the Swarm satellite mission to the 2015 Nepal earthquake (M7.8) showed a correlation between the magnetic anomalies and earthquakes temporal pattern35. A similar approach, applied to other earthquakes provided promising results36,37,38,39,40,41.
Here we investigate the correlation of in-situ electron density and magnetic field anomalies from Swarm satellites with earthquakes. For this scope, a Worldwide Statistical Correlation (WSC) analysis based on a superposed epoch approach has been applied to Swarm data for the first time. This approach is applied in a time window around earthquakes that occurred during a period of four years and eight months since 1 January 2014.
Results
Worldwide statistical correlation analysis
We analyse the electron density (Ne) and magnetic field data from the three Swarm satellites to detect possible anomalies associated with the earthquakes from 1 January 2014 to 31 August 2018 (30 August for Ne). For the magnetic field anomalies we consider only the Y-East magnetic field component in the analysis (see Methods section for more details).
The worldwide earthquake data were extracted from the USGS (United States Geological Survey) catalogue (https://earthquake.usgs.gov), in terms of the time of occurrence, hypocenter location (geographical coordinates and depth) and magnitude. We selected the same time span of the satellite data (from 1 January 2014 to 31 August 2018) and declustered the catalogue to remove dependent earthquakes42, in order to avoid bias in superposed epoch approach. For the purpose of this study, only earthquakes with the hypocentral depth less than 50 km are considered, since deeper earthquakes are less likely to affect the ionosphere43. The final dataset of 1312 M5.5+ worldwide shallow earthquakes was the base for the statistical correlation analysis with Swarm satellite data (see Methods section for more details).
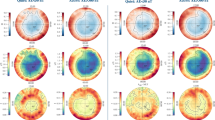
Electron density and Y magnetic component signals from all the Swarm satellites have been analysed track by track by a moving window to provide two anomaly datasets according to a universal threshold kt, one for each investigated quantity (see Methods section for algorithms description). Then we apply WSC to extract those anomalies (if any) associated in space and in time to the earthquakes and to obtain the superposed epoch diagrams (see Methods section for more details). Figures 1 and 2 show the correlation results when applied to the electron density by considering:
Worldwide Statistical Correlation (WSC) in terms of a superposed epoch approach applied to electron density Ne with threshold kt = 3.0 considering a distance of 1000 km from earthquake (EQ) epicentre; x-axis presents the days before (negative days) or after (positive days) the EQ occurrence, while y-axis shows the distance from the earthquake epicentres in degrees. The analysis has been made for all hours (H24). (a) No constraints are imposed on anomaly-EQ association (Method 1). (b) Association EQ-Anomaly is made minimizing the value of Log10(ΔT∙R), where ΔT is the precursor time and R the distance of the anomaly with respect to EQ epicentre (Method 2). (c) The same as (b) but assigning just the EQ with maximum magnitude for each anomaly (i.e. Method 3 or MaxM method). Most of the concentrations appear before and around the EQ occurrences. For the meaning of d and n, please refer to the main text. Please note the vertical extent of the bin is 3°.
The same as Fig. 1 (Ne WSC analysis) but considering the Dobrovolsky area (DbA). Please note the vertical extent of the bin is 3.4°.
1. Anomaly threshold kt = 3.0 within 1000 km from epicentres (bins of 2.4 days × 3 degrees).
2. Anomaly threshold kt = 3.0 within Dobrovolsky radius44 (bins of 2.4 days × 3.34 degrees).
Figures 3 and 4 show the correlation results when applied to the Y magnetic field data by considering:
The same as Fig. 1 but for Y magnetic field component and kt = 2.5. (a) Method 1; (b) Method 2; (c) Method 3.
The same as Fig. 3 (Y magnetic field WSC analysis) but considering the Dobrovolsky Area (DbA).
3. Anomaly threshold kt = 2.5 within 1000 km from epicentres (bins of 2.4 days × 3 degrees).
4. Anomaly threshold kt = 2.5 within Dobrovolsky radius (bins of 2.4 days × 3.34 degrees).
Although our algorithm accepts any value of the threshold kt, we applied a larger value (kt = 3.0) for Ne than Y (kt = 2.5), because the former quantity is more variable than the latter, producing usually more outliers.
Please note that Figs. 1 and 3 concern with analyses up to 1000 km from epicentres, however the diagrams extend the representation even after 1000 km (this explains the abrupt passage from colors to blue at 9°), although they do not have any physical meaning (in these cases, there are no anomaly data detected after 1000 km), only to maintain simple comparison with those of Figs. 2 and 4 that extend up to around 30°. From Figs. 1 to 4, the panels (a) include all possible anomaly-earthquake associations, i.e. anytime an anomaly falls inside the area and the time span investigated around the event a point is inserted. The advantage of this method (here also called Method 1) is to not make any hypothesis, but we know that it is extremely unlikely that an anomaly could be produced by two or even more seismic events at the same time and this case could appear too frequently when this method is applied. To overcome this unlikely situation, we propose also two other methods that are both plausible but introduce other assumptions: the first one (here also called Method 2) is shown in panels (b) where we associate the anomaly to the space-time closer earthquake by minimizing Log10 (ΔT∙R), being ΔT the time between anomaly occurrence and earthquake origin time, while R is the distance between the location of the anomaly and the epicentre. The second one (here also called Method 3) is shown in panels (c) and associates the anomaly to the largest magnitude event among all earthquakes compatible with that anomaly.
By looking at Figs. 1 and 2, large precursory concentrations of Ne anomalies fall few days (6–8 days) before the earthquakes, although some meaningful concentrations are also noticeable about 45 days and between 70 and 85 days before the events. We estimated the statistical significance of the correlation by means of two statistical parameters that indicate how much the maximum concentration is higher than a typical random maximum concentration (d parameter) and how many standard deviations σ the concentration is far from the simulated ones (n parameter) (for more details see the Methods). The statistical significance of the electron density anomalies is very low for the 1000 km analyses (d = 1.0–1.3 and n = 0.3–4.1), being comparable with typical random distributions of anomalies when Method 1 and 2 are applied, while is high for Dobrovolsky Area (DbA) analyses (d = 1.5–1.7 and n = 4.6–15.1). The 6–8 days anomaly concentration confirms previous results from DEMETER satellite34. The other longer precursory times had never been investigated so far and are the topic of the next section, where we will explain and justify this aspect in terms of the Rikitake empirical law45. It is encouraging that the methods that introduce some earthquake physical model and parameters such as Dobrovolsky strain radius as a limit of the spatial search (Fig. 2) and their maximum magnitude (Fig. 2c) show a higher statistical significance, giving empirical evidence for the seismic origin of most of these anomalies.
We notice that in the analyses performed within a radius of 1000 km from epicentres (Fig. 1a–c) some unrealistic concentrations (although not the largest ones, which always fall at the closest band to epicentres) appear at farther distances. We can interpret these features as due to anomalies actually belonging to other closer earthquake epicenters, but included in the analyses, especially for smaller earthquake magnitudes. We suspect that this feature contributes to the low statistical significance of these kinds of analyses. However, this effect disappears when analysing the data according to the Dobrovolsky area (Fig. 2a–c), for which the distance of interest for smaller magnitude earthquakes is much smaller than 1000 km.
In Fig. 3b,c, and Fig. 4b the anomalies found in the Y magnetic field component analysis maximize around 12 days before the earthquake occurrences. Figure 3a,c (and Fig. 4a,c) show concentrations at even longer time intervals (about 80 days), the same period that we found for electron density anomalies. Figure 4a presents the largest concentration around 20 days before the earthquakes, a precursor time that appears also in other analyses, although with less significance.
The Y magnetic field component analyses show larger values of d and n (d = 1.4–2.1; n = 6.0–16.6) than Ne analyses (d = 1.0–1.7; n = 0.3–15.1).
The adoption of the Dobrovolsky strain radius slightly affects the main temporal features of the WSC analysis: although the anomaly density decreases (e.g., compare Fig. 2 with Fig. 1), the periods of higher density before earthquakes are confirmed. From the spatial point of view, anomalies cluster closer to the epicentres (i.e. always within the first spatial band).
Table 1 reports the main properties of the analyses performed over the real cases as well the results on their reliability, obtained by comparison with random distributions through the d and n parameters, whose values range from 1.0 to 2.1 and from 0.3 to 16.6, respectively. Bold numbers in d and n evidence the best cases for which the real analyses are well distinct from random simulations (selected as d ≥ 1.5, because the density is equal to or larger than 50% of random distribution, or n ≥ 4, because the probability to be random is equal to or less than 0.1%). Generally the d values increase when the Dobrovolsky area and the maximum earthquake magnitude criteria are considered (this is consistent with the expectation that larger earthquakes cause greater anomalies). The best results are reported when correlation is applied to the Y component of the magnetic field. Regarding the largest anomaly concentrations, some appear in almost all analyses, in particular 7, 12, 20 and 82 days before the earthquakes. Having enlarged the temporal window of analysis with respect to previous studies allowed us to detect also high precursor times such as 86 and 82 days before the earthquakes. They look significant and appear both in Ne and in Y.
In general, one method to select the association of the anomaly with the earthquake emphasises anomalies closer to earthquake occurrences (Log(ΔT∙R), panel b), while another one tends to show also longer precursory times (earthquake magnitude, panel c). Applying all methods, however, we find signatures in electron density and Y magnetic field component anticipating the earthquakes, from a few days to around 80 days and the statistical correlation obtained makes this precursory feature compelling.
Rikitake law and its interpretation as result of a diffusion process
From what we carried out and summarized in Table 1, earthquake precursors would appear at different lead times, i.e. we would expect not only a single concentration but several concentrations at different times in advance before the earthquake occurrences, according to the range of earthquake magnitudes. A formula relating precursor time ΔT in days to magnitude M was proposed by Rikitake45: Log10(ΔT) = a + bM. To deeper investigate this concept, we extended our analysis to 500 days before the earthquake occurrences, applying Method 1, i.e. without imposing any earthquake-anomaly association, in order to not favour closer or farther anomalies with respect to earthquake occurrences. We considered both the electron density and the Y-component of the magnetic field within the Dobrovolsky area and grouped the correlations for the following individual bands of earthquake magnitude: 5.5–5.9, 6.0–6.4, 6.5–6.9, 7–7.4, 7.5+. Of course, the choice of 500 days could be critical because for a large number of events (i.e. the ones occurred in the first 500 days of 4.7 years of investigated period) not all the time domain was covered by our analysis. On the other hand, this would allow us to look at longer potential precursor times.
Figures 5a,b show the WSC results, for Ne and Y component of the magnetic field, respectively (now every single bin is 10 days × 3.34 degrees large). At a first glance, the identification of the largest group of anomalies (red ovals), taken as considering two adjacent bins of these new diagrams, is straightforward in all magnitude intervals with a few exceptions (yellow ovals). Among them, however, some can be easily excluded: the yellow ovals in the middle panel of Fig. 5a and in the top panel of Fig. 5b are actually two-bin combinations less significant than the corresponding red ovals. In addition, for the top panel of Fig. 5a, we exclude the yellow oval because is too distant from earthquake occurrence, giving more credit to the closer concentration (red oval). The results for M7.5+ are not sufficiently robust, because the number of earthquakes is rather small (16) in the 4.7 years of the study. However, to test the Rikitake law45, we included this largest range of magnitude for the electron density. We fit the same Rikitake functional law to our precursor times with respect to the central value of magnitude for each band. We estimated the error bars for the magnitude as the half width of the investigated range and for the time interval as the bin span of the anomalies concentration. Figure 5c shows the results for both Ne (black circles and thin fitting solid line) and Y (empty circles and thin fitting dash line), together with lower and upper bounds of the Rikitake law for magnetic ground precursors45 (thick lower and upper lines). It is surprising that, within the estimated errors, we find similar a,b values (a = −3.29 ± 0.76, b = 0.78 ± 0.11 for Ne and a = −3.88 ± 0.84, b = 0.92 ± 0.13 for Y) to those proposed for ground magnetic observations by Rikitake45 (see Methods section).
Worldwide Statistical Correlation (WSC) in terms of a superposed epoch approach applied to electron density with threshold kt = 3.0 (a) or Y magnetic field with threshold kt = 2.5 (b) considering the DbA around the EQ epicentre and different ranges of magnitude values. Please note that the investigated time interval is 500 days (versus 90 days before and 30 days after in the previous analyses) before the EQ occurrences and each temporal bin is of 10 days (versus 2.4 days of previous analyses). Only the closest spatial band to the EQ epicentre is shown; for convenience colour palettes are not shown, although blue stands for the lowest density (close to zero) and brown for the largest density (that differs from case to case). Red ovals indicate the larger concentrations considered for the Rikitake law; yellow ovals are not taken into account for the reason given in the main text. (c) shows the Rikitake law for electron density Ne (black circles and thin fitting solid line) and Y magnetic field (empty circles and thin fitting dash line). Also the corresponding a and b coefficients are given, together with the upper and lower bounds of the Rikitake law for ground magnetic precursors45.
Apparently the two fitting lines for Ne and Y are distinct, but both fits are within the errors. In addition, for both quantities, it appears that earthquake precursors occur within a day for events with magnitude below 4.2, although is it very unlikely that these weaker earthquakes could produce an effect in the ionosphere20.
On the other hand, the greater the earthquake magnitude, the greater the difference between the ΔT referred to Ne and Y-component: for instance, for M7.5, the Ne relation provides ΔT = 363 days, while Y relation gives ΔT around 1000 days. This could explain why we do not find a statistical significance in the M7.5+ analysis for Y magnetic component.
This result strongly supports the empirical law found by Rikitake45 for ground magnetic observations, even extended it to electron density and magnetic field satellite data, with a little adjustment of the coefficient values.
The Rikitake law is reasonable for the process of earthquake generation and coupling with the above atmosphere and ionosphere layers with simple arguments (more details are shown in Methods). Assuming a lithospheric process of stress diffusion46 across the Dobrovolsky strain radius RDb44, we obtain the relationships a = −Log(\(4\pi {\rm{D}}\,\)) and b = 2β, D is the coefficient of diffusion and β is the Dobrovolsky exponent: 0.43 (see Methods for all the passages). We can verify them by comparing the b value obtained from Rikitake (around 0.8) that, within the error, resembles the value of 0.86 deduced from Eq. 7b in Methods. From the value of a, we can even estimate D. Although a value has large uncertainty, i.e. a ≅ −2 (Rikitake), a ≅ −3.3 and a ≅ −3.9 (in our analysis of Ne and Y, respectively), we can take the central value of a ≅ −3, obtaining D ≅ 100 m2/s, which is one-two order more than a reasonable value for the crust1. However, it is really interesting that this same order of diffusivity can be found for slow earthquakes when a diffusion model is considered47. This interesting coincidence would merit more future attention, potentially opening new perspectives in seismological studies.
Conclusions
The electron density and magnetic field WSC analyses applied to about 4.7 years of Swarm satellite observations highlight that anomalies appear to occur before the earthquake occurrences, between a few days and 80 days before the earthquakes, with larger peaks at around 10, 20 and 80 days. We find that in all analysed cases considering the DbA, the largest concentration of pre-earthquake anomalies is statistically significant by a factor up to around 2 (i.e. d ∼ 2) times the simulated data, with up to 15–17 σ (i.e. n = 15–17). We note that the detected anomalies seem better correlated with earthquakes of stronger magnitude.
We confirm linear relation between the LogΔT and magnitude, and the found a, b coefficients are, within the estimated errors, close to those proposed by Rikitake45. We also provide a simple explanation of this relationship and show that the empirical expressions we found for satellite data anomalies are consistent with a stress diffusion process in the crust as that producing slow earthquakes.
The Rikitake law, confirmed by the separate analyses of Fig. 5a,b at different ranges of magnitude, supports the argument that the precursor times are related to the earthquake magnitude. Its expected effect would be to theoretically smear out eventual peaks in the analyses of all magnitude earthquakes, what we do not actually find in Figs. 1–4. However, our results are not in contradiction for two main reasons: i) The analysis limited to 90 days before and 30 days after earthquake occurrence is heavily influenced by the preponderance of low magnitude earthquakes, so concentrations are more confined within the closest times before earthquakes, while the longer time precursors, likely produced by larger earthquakes, are out of the analysed temporal interval. ii) The analyses reported in Fig. 5 are extended to 500 days before, to include longer precursor times, typical of larger magnitude earthquakes tend to appear well in advance with respect to earthquake occurrences. However, the law is an empirical law which is not “exclusive”, so an earthquake could even provide other precursors in different time.
Although this investigation would support the LAIC with clear statistical significance, another clear message emerges: not all earthquakes are in the favourable conditions to produce significant effects in the ionosphere. Only a portion of them (we estimate something around 40%; see section of Methods) generates a non-negligible electromagnetic effect that cannot be due to simple chance. Several causes can be attributed to this deficiency: insufficient satellite passes available, an inappropriate coversphere (e.g. vegetation), adverse meteorological conditions, and/or still not perfect anomaly detection strategy.
More detailed analyses, as the study of the type of earthquakes analysed, according to their occurrence in subduction zones or along strike-slip faults, in the land or under the sea, in interplate or intraplate, and the inspection of single anomalies, would help to better understand the physics behind the possible coupling phenomena. In this respect, a prolongation of the Swarm satellite mission is greatly encouraged: for example, with at least 10 years of data, longer precursor times could be investigated without loss of statistical significance. Data from other quasi-polar satellites, equipped with magnetometers and Langmuir probes (e.g. the Chinese seismo-electromagnetic satellite48), would also be useful for this scope.
A final point is clearly important here: since the ionospheric anomalies are causally related to what happens inside the Earth and at the ground-to-air interface, the corresponding parameters should be, or even must be, included in any further study. This is implicit in the Geosystemics concept8, by which we can consider the Earth system as an ensemble of cross-interacting parts. Therefore, it is mandatory to consider a multiparametric point of view to address this kind of complex phenomena, by combining seismological, atmospheric and ionospheric information8,40.
Methods
Satellite data
Swarm mission is an ESA satellite mission49 composed of three identical quasi-polar orbiting satellites, two (Alpha and Charlie satellites, also named as Swarm-A and Swarm-C, respectively) at lower orbit (around 460 km above the Earth’s surface) and the third (Bravo or Swarm-B) at the highest orbit (around 510 km). The satellites were placed in orbit on 22 November 2013 and are still orbiting around the Earth. The original configuration with Swarm-A and Swarm-B flying in parallel and Swarm-C in a higher orbit49 was changed to the present one because of early problems (from 5 November 2014) in the scalar magnetometer of Swarm-C.
The satellite payloads comprise, among others, a Langmuir probe (LP) and two magnetometers, i.e. a vector fluxgate magnetometer (VFM) and an absolute scalar magnetometer (ASM). These sensors have been here analysed systematically to detect possible pre-earthquake Lithosphere-Atmosphere-Ionosphere Coupling (LAIC) electron density and magnetic field anomalies from space.
The Ne data used in this work are measured by the LP of Swarm satellites with a sampling rate of 2 Hz. The input data have been provided by the original Swarm Advanced product called “2_Hz_Langmuir_Probe_Extended_Dataset”. This dataset is provided in Common Data Format (CDF) and freely available in the ESA Swarm FTP and HTTP Server swarm-diss.eo.esa.int (the Swarm data are also available from VIRES web platform: http://vires.services). The current release of 2 Hz Langmuir Probe Extended Dataset (Release 101) is the ESA reprocessing of all Swarm Electric Field Instrument data from the beginning of the mission to 30 August 2018.
According to ESA, the current values of electron density are up to a few 10% too high at low density (https://earth.esa.int/web/guest/missions/esa-eo-missions/swarm/data-handbook/preliminary-level-1b-plasma-dataset). This is not an issue for the purposes of our anomaly detection, as it is not based on the absolute value itself, but its derivative as reported later in the text.
We also considered scalar intensity (F) and vector X,Y,Z magnetic components. The data are at 1 Hz sampling that correspond to the low resolution magnetic data contained in the Level 1b (L1b) products. All the L1b magnetic data are provided by ESA in Common Data Format (CDF) and hosted in the ESA Swarm server.
In order to select data without evident troubles/problems during the satellite flying (https://earth.esa.int/web/guest/swarm/data-access/quality-of-swarm-l1b-l2cat2-products), we took into account the quality flags associated with both the electron density and magnetic field data.
In detail, we extracted different information from original CDF files, including the type of satellite, i.e. A for Alpha, B for Bravo, and C per Charlie, the UTC time, data quality flags, the electron density or the vector magnetic components in NEC (North, East, Centre) reference frame by the VFM instrument and the magnetic absolute intensity by ASM instrument (for A, B and C satellites; however, as ASM of C after 5 Nov. 2014 is out of work, the total intensity is calculated from the Cartesian magnetic components given by VFM instruments).
The error of the magnetic field measured by Swarm satellites can be estimated to be less than 0.3 nT, with a typical value of 0.1 nT50.
Algorithms for electromagnetic anomaly detection
The approach to identify anomalies is based on two novel algorithms, i.e. NeAD (Electron Density Anomaly Detection) and MASS (MAgnetic Swarm anomaly detection by Spline analysis), applied to the electron density Ne (2 Hz sampling) and magnetic field (components and total intensity-1Hz sampling) from Swarm satellites (A,B,C), respectively. These algorithms share the main features that we highlight below.
For each day and for all the satellites tracks (the daily number of semi-orbit for each satellite is about 32), the Local Time (LT) and the geomagnetic latitudes are evaluated, the latter based on a tilted geocentric dipole field from the last generation of the IGRF (International Geomagnetic Reference Field) global model of the geomagnetic field (IGRF-1251). Then, the first time derivatives of Ne and of the magnetic field are estimated as the first difference values divided by the time interval between two consecutive samples. Finally, a fit with cubic splines is applied to remove the long term trend.
Figures S1, S2 show an example of the output from NeAD and MASS, respectively, carried out for two different epochs and for Swarm C: April 27, 2015 (two days after the M7.8 Nepal earthquake occurred on 25 April 2015) and February 14, 2016 (almost two weeks before the M7.8 Sumatra earthquake occurred on 2 March, 2016). The track number, descending (D)/ascending (U), the corresponding local time (LT) and UTC, the geospace conditions given by the Dst and ap geomagnetic indices, areprovided. The geographical area of interest with satellite track (red), the Dobrovolsky area (yellow oval; circular on the terrestrial sphere) and the earthquake epicentre (green star) are also shown. It is worth noticing that, from Figure S2, an anomalous signal is visible especially in the East magnetic component (Y), while the total intensity does not show appreciable variability39. This could be simply explained by field aligned current processes that do not practically affect the total intensity of the magnetic field vector, but only its direction35. Accordingly, instead of analysing the whole magnetic field, we focused only on the magnetic Y component because it is less affected by external perturbations than X and Z components52 and this increases the possibility to detect Earth internal source anomalies.
To detect anomalies of interest for the WSC analysis, NeAD and MASS outputs (for the entire Swarm data set) are further analysed by overlapping sliding windows within ±50° geomagnetic latitude, to limit the effects due to the high latitude ionosphere, and under quiet magnetic conditions in terms of Dst and ap indices (|Dst| ≤ 20 nT, ap ≤ 10 nT) to limit the effects of perturbations coming from the outer space.
We consider overlapping sliding windows of 7.0° latitude length, moving by 1.4° (1/5 of window length) along the whole ±50° geomagnetic latitude range. Since the satellite speed is of about 7.6 km/s, the choice of the 7.0° sliding window allows us to include typical pre-earthquake satellite signals of some tens of seconds into a sufficiently short spatial length34,53. The approach with overlapping sliding windows provides an output matrix in which each row identifies a given window and each column contains the following quantities: the date and central time (UTC and LT) of the given window, the satellite (A,B,C), the track number, Dst, ap, the root mean square error (rms) over the samples distribution within the given window and the frequency content of the window (the latter not used in this work), together with the root mean square error (RMS) over the whole track in ±50° geomagnetic latitude.
Finally, from the output matrix, we define as anomalous those windows (i.e. the Ne and Y magnetic field component values within them) for which rms > kt∙RMS, where kt is an appropriate threshold (normally 2.5–3) and RMS is the root mean square error computed for the whole track.
Summarizing, criteria adopted by NeAD and MASS to detect anomalies are:
Swarm tracks within ±50° geomagnetic latitude;
Low magnetic activity: |Dst| ≤ 20 nT, ap ≤ 10 nT during the track acquisition time;
sliding windows of 7.0° latitude length, moving by 1.4° along the tracks;
rms (of each sliding window) > kt∙RMS (evaluated along the track).
Worldwide statistical correlation algorithm
The WSC algorithm evaluates the possible correlation in space and time of the detected anomalies by NeAD and MASS with the earthquake locations and occurrences. The earthquake catalogue was declustered first by extracting all M5+ earthquakes, then detecting and removing the dependent earthquakes, i.e. those earthquakes with magnitude M ≤ Mms−1 (Mms is the mainshock magnitude) that happen inside 10 km from the mainshock epicenter and a 10-day time window from its origin time. In the declustered catalogue, the magnitude of the mainshock is replaced by the equivalent magnitude of the seismic cluster. We then selected those shallow earthquakes with M ≥ 5.5 for which LAIC signatures are more likely to be captured as highlighted by Liu et al.20 who found a dramatic enhancement in the statistical correlation between ionospheric anomalies and earthquakes with magnitude greater than 5.4. In addition, this choice avoids problems of catalogue incompleteness54.
WSC cumulates all the anomalies of the same family (Ne or Y magnetic field component) associated with each earthquake (occurring in the time interval normally ranging between 90 days before and 30 days after the earthquakes; but we also extended the time interval up to 500 days before earthquakes to verify Rikitake law; see next dedicated section) in a unique space-time graph by a superposed epoch approach having as common origin the occurrence time and the epicentre of all investigated earthquakes along the available Swarm mission data (4.7 years). The horizontal axis of the WSC diagrams is the time lag between the anomalies and the seismic events and the vertical axis is the distance of the anomalies with respect to the epicentre (in degrees). The common time origin is represented by the white vertical line. The colour bar identifies the density level of the anomalies (number of anomalies for squared degree). A simplified flowchart of the WSC algorithm is shown in Figure S3. This method is similar to that one applied to DEMETER satellite data analysis32,33,34, apart from the use of a wider time window around the earthquakes (in Yan et al.34, for example, it was −15 to 5 days; here we normally considered −90 to 30 days). We considered a longer time window according to the empirical relationship given by Rikitake45: for a typical M5.5 earthquake, which is the most frequent in our dataset, we would expect a precursor at a mean advance time of 16 days, in a range from 2 to 144 days (see also Piscini et al.55). Therefore, extending the analysis to 90 days before the earthquake occurrence, seems to be a good compromise, avoiding border effects in time. In space, we consider either an area comprised by a fixed radius of 1000 km around the earthquake epicentre34 or the most popular Dobrovolsky’s circular area (DbA) around the earthquake epicentre, whose radius RDb in km scales with magnitude M, i.e. RDb = 100.43M, as suggested by Dobrovolsky et al.44. For our selected earthquakes, the radius of this area is between 230 km or 2.2° (M5.5) and 3700 km or 33.4° (M8.3). The DbA is considered a good empirical approximation of the preparation area of an impending earthquake56.
In addition to the adopted spatial (anomalies within 1000 km and/or within the DbA from the epicentres) and temporal (anomalies occurring from −90 days to 30 days around the earthquake occurrences) criteria, we present the analysis in three different ways.
The first method (Method 1) does not take into account any assumption, associating each anomaly to all earthquakes that fall inside the analysed space time. In the next two methods, we introduce some limitations to prevent an anomaly from being associated to more than one earthquake, which is very unlikely to happen. This can be done by:
Method 2: Referring a given anomaly to that earthquake for which Log10 (ΔT∙R) is minimum, where ΔT is the time lag between the anomaly occurrence and the earthquake (we also call it precursor time), and R is the spatial distance of the anomaly from the earthquake epicentre. This method intends to assign to the anomaly the closest earthquake in space and time. This limitation takes also into account the correlation found between Log10 (ΔT∙R) and the earthquake magnitude M when ionosphere anomalies from HF ionosondes are considered18,19,22,23.
Method 3: Referring a given anomaly to that earthquake with the greatest magnitude M (also referred as MaxM method), falling inside the analysed space-time window.
The Method 1 has the advantage to not impose any further constraints on the anomalies, but has the disadvantage to have eventually some anomalies with more than one associated earthquake.
We would underline that the selection of a particular method affects only a small percentage of the whole cases. So, all the methods have a common anomaly-earthquake association.
Therefore, we provided space-time distributions, one for each earthquake, of the anomalies (Ne and/or Y-magnetic field component) associated with it. Then we superposed all the distributions imposing a common origin that identifies the earthquake occurrence times and the epicentres. The resulting WSC distribution (one for each parameter, Ne and/or Y magnetic field component) contains all the anomalies overlapped. The density level of the anomalies (number of anomalies per squared degree) is estimated in 50 temporal bins and 10 spatial bins, so each bin of the diagram usually covers 2.4 days (120 days divided by 50 bins). The epicentral distance (vertical extent) of each bin is of 3°, i.e. about 330 km at the Earth’s surface for the 1000 km analyses (or 3.34°, i.e. about 370 km at the Earth’s surface, for the DbA analyses), up to 30° (33.4° for the DbA analyses, corresponding to the largest DbA for the largest magnitude M8.3 in the earthquake dataset). The small difference in the two full-scales is due to the different height of the bins in the two kinds of analysis. In the 1000 km analyses, it allows to complete the whole distance with three full bands, but almost preserving the possibility to compare these analyses with those made across the DbA. In any case, to maintain perfect agreement in all (1000 km and DbA) analyses the anomalies and earthquakes have been counted always in a bin of 3.34°.
The statistical significance of the WSC analysis results is based on the introduction of quality statistical quantities as follows.
To estimate how much reliable is the largest concentration of anomalies, we firstly considered the ratio between the largest concentration of the real anomalies DMAX and that of a theoretical uniform distribution (in space and time) D0 of anomalies, i.e. DMAX/D0.
D0 can be analytically defined as:
where \({N}_{an}\) is the total number of anomalies in the whole analysed region and in all times; A is the whole area of the analysis in square degrees (in this case it is the area of a tesseral zone between −50° and + 50° of geomagnetic latitude); Δt is the analysed time in days, in this study it is 1703 days, i.e. 4.7 years. Neq is the number of earthquakes associated with at least one anomaly. Thus, the units of D0 are (square degrees × days)−1.
DMAX is calculated as:
Nexan is the number of anomalies associated with earthquakes in the bin of the first row (i.e. the anomalies closest to the epicentre) with the largest concentration of anomalies; ABIN is the area of the bin (i.e. the area of the circle or of the annulus region of the first bin around the epicentre); ΔtBIN is the time width of the bin in the same unit of Δt (2.4 days if we investigate a window from 90 days before to 30 days after the earthquake occurrence).
Note, however, that DMAX/D0 is biased because the areas associated with the earthquakes could overlap, either in case of considering circles of 1000 km around the epicentres or the effective DbA. In addition, we do not analyse all the temporal periods but only those with low magnetic disturbance (i.e. |Dst| ≤ 20 nT, ap ≤ 10 nT), to roughly “filter out” those anomalies clearly depending on solar geomagnetic activity.
Then, to establish the actual statistical significance of DMAX/D0, we compare it with its analogous obtained by correlating the real earthquake dataset with a certain number (usually 100) of random distributions of anomalies (with same number of the real cases), almost homogeneous in space and time. The random anomalies are generated assigning to each of them a latitude, a longitude and an occurrence time. The latitude and longitude are selected (with homogeneous probability in space) within the analysed global area (i.e. the area with |geom. latitude| ≤50°). The occurrence time is selected among the geomagnetic quiet times with uniform probability. From the random simulations, we also calculate the average and the standard deviation σrand of the parameter [DMAX/D0]rand, to be further compared with that one corresponding to [DMAX/D0]real for the real cases.
Table S1 summarizes the main features of the random simulations, each of them referring to the different criteria adopted in the WSC real cases. For each series of 100 random simulations, we provide also the standard deviation σrand.
Then we consider the statistical parameter d defined as the ratio between [DMAX/D0]real (Table 1), estimated over the real anomaly data, and [DMAX/D0]rand, estimated over a set of simulated random anomaly data (Table S1). That is:
In this way, d would show how much the real maximum concentration is above the expected typical maximum concentration of a random anomaly distribution: the larger is the d value, the more the results of the WSC applied to real data deviate from randomness.
Finally, to increase the WSC reliability, we provide also the parameter n measuring the significance of the real statistical results with respect to the random distributions, defined as: n = ([Dmax/D0]real − [Dmax/D0]rand)/σ rand. Also in this case, the larger n, the more significant the corresponding real analysis.
Fraction of earthquakes with ionospheric effects
We can provide a rough estimate of the fraction of earthquakes that produce ionospheric effect in two ways. A way is based on the best cases of Table 1: this estimate is given by the ratio between the earthquakes with anomalies (third column) and the total number of earthquakes, i.e. 1312. Another way is based on the separate analyses of Fig. 5a,b: we can count the number of earthquakes in the largest concentrations that contribute to the Rikitake law. Both estimates point to values between 25% and 55%. Therefore, the given value of 40% is a reasonable estimation.
Rikitake law
We recall the empirical law by Rikitake45, that relates precursor time ΔT with the earthquake magnitude M:
where a = −2.08 (±1.43) and b = 0.78 (±0.23), for geomagnetic field ground observations45.
Although out of our scope, we sketch some simple reasoning on why the Rikitake law is reasonable for the process of earthquake generation and coupling with the above atmosphere and ionosphere layers. Adopting a lithospheric process of stress diffusion46 across the DbA, we can relate the spatial distance R (in km) of the anomaly from the earthquake epicentre with the time ΔT:
where D is the diffusivity. If we suppose that the first precursor can appear at the beginning of the stress evolution, then ΔT will be the precursor time.
According to Dobrovolsky et al.44 we can express RDb, as:
with β = 0.43 and M the earthquake magnitude.
If we assume R = RDb, we can replace RDb in (6) with R of the Eq. (5), so that the coefficients in Eq. (4) become:
and
From our results we could even deduce D from (7a) and verify the relationship (7b) (see Section before Conclusions).
Dedication
We would like to make a special dedication to the memory of Eigil Friis-Christensen (1944–2018), lead investigator of the Swarm satellite mission. Without him probably nothing of all published works about Swarm mission could ever have been written.
References
Scholz, C. H. The Mechanics of Earthquake and Faulting (ed. Cambridge Univ. Press) vol. xxiv., 471 (Cambridge/New York, 2002).
Olaiz, A. J. et al. European continuous active tectonic strain–stress map. Tectonophysics 474, 33–40 (2009).
Kanamori, H. Earthquake prediction: an overview in International Handbook of Earthquake and Engineering Seismology (ed. Academic Press) 1205–1216 (Amsterdam, 2003).
Hayakawa, M. & Molchanov, O. A. Seismo Electromagnetics Lithosphere-Atmosphere-Ionosphere Coupling (ed. TERRAPUB) 477 (Tokyo, 2002).
Freund, F. Pre-earthquake signals: Underlying physical processes. Journal of Asian Earth Sciences 383–400 (2011).
Pulinets, S. & Ouzounov, D. Lithosphere-Atmosphere- ionosphere coupling (LAIC) model-an unified concept for earthquake precursors validation. J. Asian Earth Sci. 41(4–5), 371–382 (2011).
De Santis, A. et al. Geospace perturbations induced by the Earth: the state of the art and future trends. Phys. & Chem. Earth 85-86, 17–33 (2015).
De Santis, A. et al. Geosystemics View of Earthquakes. Entropy 21, 412, https://doi.org/10.3390/e21040412 (2019).
Tanimoto, T., Heki, K. & Artru-Lambin, J. Interaction of Solid Earth, Atmosphere, and Ionosphere in Gerald Schubert (editor-in-chief) Treatise on Geophysics, 2nd edition (ed. Gerald Schubert), vol. 4, 421–443 (Oxford: Elsevier, 2015).
He, L. & Heki, K. Ionospheric anomalies immediately before Mw7.0– 8.0 earthquakes. J. Geophys. Res. Space Phys. 122, 8659–8678, https://doi.org/10.1002/2017JA024012 (2017).
Freund, F. T. et al. Stimulated infrared emission from rocks: assessing a stress indicator. eEarth 2, 1–10 (2007).
Kuo, C. L., Huba, J. D., Joyce, G. & Lee, L. C. Ionosphere plasma bubbles and density variations induced by pre-earthquake rock currents and associated surface charges. J. Geophys. Res. 116, A10317 (2011).
Kuo, C. L., Lee, L. C. & Huba, J. D. An improved coupling model for the lithosphere–atmosphere–ionosphere system. J. Geophys. Res. Space Phys. 119, 3189–3205 (2014).
Yang, S. S., Asano, T. & Hayakawa, M. Abnormal gravity wave activity in the stratosphere prior to the 2016 Kumamoto earthquakes. J. Geophys. Res. Space Phys. 124, https://doi.org/10.1029/2018JA026002 (2019).
Pulinets, S. & Boyarchuk, K. Ionospheric Precursors of Earthquakes (ed. Springer) (Berlin, 2004).
Hayakawa, M. Earthquake prediction with radio techniques (ed. Wiley, J. & Sons) 294 (Singapore, 2015).
Ondoh, T. & Hayakawa, M. Synthetic study of precursory phenomena of the M7.2 Hyogo-ken Nanbu earthquake. Phys. Chem. Earth 31, 378–388 (2006).
Korsunova, L. P. & Khegai, V. V. Medium-term ionospheric precursors to strong earthquakes. Int. J. Geomagn. Aeron. 6, GI3005, https://doi.org/10.1029/2005GI000122 (2006).
Korsunova, L. P. & Khegai, V. V. Analysis of seismo-ionospheric disturbances at the chain of Japanese stations for vertical sounding of the ionosphere. Geomagn. and Aeronom. 48, 392–399 (2008).
Liu, J. Y., Chen, Y. I., Chuo, Y. J. & Chen, C. S. A statistical investigation of pre-earthquake ionospheric anomaly. J. Geophys. Res. 111, A05304, https://doi.org/10.1029/2005JA011333 (2006).
Xu, T., Hu, Y. L., Wang, F. F., Chen, Z. & Wu, J. Is there any difference in local time variation in ionospheric F2 layer disturbances between earthquake induced and Q- disturbances events? Ann. Geophysicae. 33, 687–695 (2015).
Perrone, L., Korsunova, L. & Mikhailov, A. Ionospheric precursors for crustal earthquakes in Italy. Ann. Geophysicae 28, 941–950 (2010).
Perrone, L. et al. Ionospheric anomalies detected by ionosonde and possibly related to crustal earthquakes in Greece. Ann. Geophysicae 36, 361–371, https://doi.org/10.5194/angeo-36-361-2018 (2018).
Dautermann, T., Calais, E., Haase, J. & Garrison, J. Investigation of Ionospheric Electron Content Variations before Earthquakes in Southern California, 2003–2004. J. Geophys. Res. 112(B2), 1–20, https://doi.org/10.1029/2006JB004447 (2007).
Heki, K. Ionospheric Electron Enhancement Preceding the 2011 Tohoku-Oki Earthquake. Geophys. Res. Lett. 38(17), 1–5, https://doi.org/10.1029/2011GL047908 (2011).
Fraser-Smith, A. C. et al. Low-frequency magnetic field measurements near the behaviour of the Ms 7.1 Loma Prieta Earthquake. Geophys. Res. Lett. 17(9), 1465–1468, https://doi.org/10.1029/GL017i009p01465 (1990).
Hattori, K. ULF Geomagnetic Changes Associated with Large Earthquakes. TAO 15(3), 329–360 (2004).
Donner, R. V., Potirakis, S. M., Balasis, G., Eftaxias, K. & Kurths, J. Temporal correlation patterns in pre-seismic electromagnetic emissions reveal distinct complexity profiles prior to major earthquakes. Phys. Chem. Earth Parts A/B/C; https://doi.org/10.1016/j.pce.2015.03.008 (2015).
Parrot, M. Satellite observations of ionospheric perturbations related to seismic activity in Earthquake Prediction Studies: Seismo Electromagnetics (ed. Hayakawa, M.) 1–16 (TERRAPUB, Tokyo, 2013).
Lagoutte, D. et al. The DEMETER science mission centre. Planetary and Space Science 54(5), 428–440 (2006).
Parrot, M. et al. Examples of unusual ionospheric observations made by the DEMETER satellite over seismic regions. Phys. Chem. Earth 31, 486–495 (2006).
Nêmec, F., Santolik, O., Parrot, M. & Berthelier, J. J. Spacecraft observations of electromagnetic perturbations connected with seismic activity. Geophys. Res. Lett. 35, L05109, https://doi.org/10.1029/2007GL032517 (2008).
Piša, D., Nêmec, F., Santolik, O., Parrot, M. & Rycroft, M. Additional attenuation of natural VLF electromagnetic waves observed by the DEMETER spacecraft resulting from preseismic activity. J. Geophys. Res. Space Phys. 118; https://doi.org/10.1002/jgra.50469 (2013).
Yan, R., Parrot, M. & Pinçon, J.-L. Statistical study on variations of the ionospheric ion density observed by DEMETER and related to seismic activities. J. Geophys. Res. Space Phys. 122; https://doi.org/10.1002/2017JA024623 (2017).
De Santis, A. et al. Potential earthquake precursory pattern from space: the 2015 Nepal event as seen by magnetic Swarm satellites. Earth Planet. Sci. Lett. 461, 119–126 (2017).
Akhoondzadeh, M., De Santis, A., Marchetti, D., Piscini, A. & Cianchini, G. Multi precursors analysis associated with the powerful Ecuador (MW = 7.8) earthquake of 16 April 2016 using Swarm satellites data in conjunction with other multi-platform satellite and ground data. Advances in Space Research 61(1), 248–263 (2018).
Akhoondzadeh, M., De Santis, A., Marchetti, D., Piscini, A. & Jin, S. Anomalous seismo-LAI variations potentially associated with the 2017 Mw = 7.3 Sarpol-e Zahab (Iran) earthquake from Swarm satellites, GPS-TEC and climatological data. Advances in Space Research 64, 143–158 (2019).
Marchetti, D. & Akhoondzadeh, M. Analysis of Swarm satellites data showing seismo-ionospheric anomalies around the time of the strong Mexico (Mw = 8.2) earthquake of 08 September 2017. Advances in Space Research 62(3), 614–623, https://doi.org/10.1016/j.asr.2018.04.043 (2018).
Marchetti, D. et al. Magnetic field and electron density anomalies from Swarm satellites preceding the major earthquakes of the 2016-2017 Amatrice-Norcia (Central Italy) seismic sequence. Pure appl. Geophys.; https://doi.org/10.1007/s00024-019-02138-y (2019).
Marchetti, D. et al. Pre-earthquake chain processes detected from ground to satellite altitude in preparation of the 2016-2017 seismic sequence in Central Italy. Remote Sensing of Environment 229, 93–99 (2019).
De Santis, A. et al. Magnetic Field and Electron Density Data Analysis from Swarm Satellites Searching for Ionospheric Effects by Great Earthquakes: 12 Case Studies from 2014 to 2016. Atmosphere 10(7), 371, https://doi.org/10.3390/atmos10070371 (2019).
Reasenberg, P. Second-order moment of central California seismicity, 1969-82. J. Geophys. Res. 90, 5479–5495 (1985).
Molchanov, O. & Hayakawa, M. Subionospheric VLF signal perturbations possibly related to earthquakes. J. Geophys. Res. 103 (A8, 17), 489–17, 504 (1998).
Dobrovolsky, I. P., Zubkov, S. I. & Miachkin, V. I. Estimation of the Size of Earthquake Preparation Zones. Pure appl. Geophys. 117, 1025, https://doi.org/10.1007/BF00876083 (1979).
Rikitake, T. Earthquake precursors in Japan: precursor time and detectability. Tectonophysics 136, 265–282 (1987).
Shapiro, S. A., Huenges, E. & Borm, G. Estimating the crust permeability from fluid injection-induced seismic emission at the KTB site. Geophysical Journal International 131(2), 15–18 (1997).
Ide, S., Beroza, G. C., Shelly, D. R. & Uchide, T. A scaling law for slow earthquakes. Nature 447, 76–79 (2007).
Shen, X. et al. The earthquake-related disturbances in ionosphere and project of the first China seismo-electromagnetic satellite. Earthq. Sci. 24, 639–650 (2011).
Friis-Christensen, E., Luhr, H. & Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Plan. Space 58, 351–358 (2006).
Qiu, Y. et al. Combining CHAMP and Swarm Satellite Data to Invert the Lithospheric Magnetic Field in the Tibetan Plateau. Sensors 7(17), 238 (2017).
Thébault, E. et al. International geomagnetic reference field: the 12th generation. Earth Plan. and Space 67(1), 79 (2015).
Pinheiro, K. J., Jackson, A. & Finlay, C. C. Measurements and uncertainties of the occurrence time of the 1969, 1978, 1991, and 1999 geomagnetic jerks. Geochemistry, Geophysics, Geosystems 12, Q10015 (2011).
Li, M. & Parrot, M. Statistical analysis of an ionospheric parameter as a base for earthquake prediction. J. Geophys. Res. Space Phys. 118(6), 3731–3739 (2013).
Hakimhashemi, A. H. & Grünthal, G. A Statistical Method for Estimating Catalog Completeness Applicable to Long-Term Nonstationary Seismicity Data. Bull. Seismol. Soc. Am. 102(6), 2530–2546, https://doi.org/10.1785/0120110309 (2012).
Piscini, A., De Santis, A., Marchetti, D. & Cianchini, G. A multi-parametric climatological approach to study the 2016 Amatrice-Norcia (Central Italy) earthquake preparatory phase. Pure appl. Geophys. 174(10), 3673–3688 (2017).
Plastino, W., Bella, F., Catalano, P. G. & Di Giovambattista, R. Radon groundwater anomalies related to the Umbria–Marche, September 26, 1997, earthquakes. Geofis. Int. 41(4), 369–375 (2002).
Acknowledgements
This work was undertaken in the framework of the ESA-funded project SAFE (Swarm for Earthquake study; http://safe-swarm.ingv.it), and partly (in its final part) under the LIMADOU-Science, a project funded by the Italian Space Agency (ASI). We thank ESA officers and all scientists of geomagnetism community for making possible the Swarm satellite mission. We also thank the members of the scientific panel that evaluated results by SAFE project (i.e. Drs. Lj.R. Cander – chair, G. Balasis, R. Console, P. Nenovsky and M. Parrot). We finally acknowledge the comments of three anonymous referees that helped us to improve the manuscript significantly.
Author information
Authors and Affiliations
Contributions
Conceptualization, AngD.S., L.P., R.D.G. and G.D.F.; Methodology, AngD.S.; Software, F.J.P.C., D.M., L.S., G.C., M.S., S.A.C. and AnnD.S.; Validation, D.M., LuA. and L.S.; Formal Analysis, F.J.P.C., L.S. and D.M.; Investigation, AngD.S., D.M., D.S. and L.S.; Resources, AngD.S., L.P., G.D.F.; Data Curation, D.M., S.A.C., L.S., A.I. and A.P.; Writing – Original Draft Preparation, AngD.S., D.M., S.A.C.; Writing – Review & Editing, all authors; Visualization, D.M., L.S. and AnnD.S.; Supervision, AngD.S., L.P., R.D.G., C.C., R.H.; Project Administration, L.A., M.C., F.S., C.A. and D.D.; Funding Acquisition, AngD.S. and C.A.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
De Santis, A., Marchetti, D., Pavón-Carrasco, F.J. et al. Precursory worldwide signatures of earthquake occurrences on Swarm satellite data. Sci Rep 9, 20287 (2019). https://doi.org/10.1038/s41598-019-56599-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-56599-1
This article is cited by
-
Stabilization and variations to the adaptive local iterative filtering algorithm: the fast resampled iterative filtering method
Numerische Mathematik (2024)
-
Spatiotemporal analysis of OLR as a precursory signature of seismic nucleation process in Sumatra region
Environmental Earth Sciences (2024)
-
Pre-earthquake anomaly extraction from borehole strain data based on machine learning
Scientific Reports (2023)
-
Direct and indirect evidence of pre-seismic electromagnetic emissions associated with two large earthquakes in Japan
Natural Hazards (2022)
-
Earth’s gradients as the engine of plate tectonics and earthquakes
La Rivista del Nuovo Cimento (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.