Abstract
We propose mechanism for pressure-induced transitions between ferromagnetic and antiferromagnetic phases that relies on a competition between characteristic energy scales ubiquitous among d-electron metallic magnetic compounds. Principles behind the mechanism are demonstrated on the example of the minimal two-orbital p-d lattice model. We suggest that LaCrGe3, where pressure-induced ferromagnetic-to-antiferromagnetic phase transition has been recently observed, is a promising candidate to realize discussed mechanism.
Similar content being viewed by others
Introduction
Several experiments have provided evidences for magnetic groundstate switching between ferromagnetic (FM) and antiferromagnetic (AFM) orderings driven by pressure or chemical substitution in d and f electron compounds1,2,3,4,5,6. Nevertheless, there exist only few theoretical studies aiming on describing these magnetic transitions.
Recently, general expectations concerning order of transitions between FM and AFM phases have been provided within extended Landau theory7. In turn, the generic microscopic mechanisms triggering such transitions, except material specific ones8,9, are mostly unidentified. The effective action approach incorporating corrections due to quantum fluctuations10,11 constitutes a notable exception. Namely, it has been shown that in the vicinity of the ferromagnetic quantum critical point quantum fluctuations favor reconstruction of the phase diagram and the first-order transition at zero temperature or emergence of the spatially modulated magnetic phase is predicted10,11,12,13,14. Experimental observations are consistent with both scenarios2,6,15,16,17,18,19.
In this work, we propose a different mechanism for transitions between itinerant FM and AFM orders that equally applies to nominal ferromagnets as well as antiferromagnets. It relies on a common for metallic magnetic compounds low-energy electronic structure deriving from correlated orbital states hybridizing to rather uncorrelated ones (cf. Fig. 1). Such situation is indicated by ab-initio calculations for several itinerant magnets, including LaCrGe3, ZrZn2, CrAs, UGe2 and UIr20,21,22,23,24,25,26,27,28,29,30. We propose that the Fermi-liquid description of such general orbital structure can lead, exclusively in d-electron magnets, to pressure-induced transitions between FM and AFM orders.
Schematic orbital structure of the Hamiltonian (1) providing strongly localized d-orbital states (green) and delocalized p-ones (yellow). Competition between intra-d-orbital interaction (U) and, either inter-orbital hybridization (V) or direct d-orbital hopping (td), accounts for the first and the second Stoner channels, respectively. The table summarizes general necessary (not sufficient) conditions to be fulfilled by d-orbital at ambient pressure state to allow for a subsequent magnetic groundstate switch (cf. main text).
In order to demonstrate the advocated, as we call it, two-channel Stoner mechanism we analyze simple p-d model that account for a mentioned energy scales in a minimal manner. We show that both FM/AFM and AFM/FM transitions can be realized by the model in a specific regime of parameters related to the character of d-orbital such as: degree of correlations U, d-level position εd and d-orbital filling nd (cf. table of Fig. 1). It is very promising that the parametrization roughly agreeing with general energy scales and oxidation states of LaCrGe3 qualifies observed in this material pressure-induced FM to AFM transition2,3 as a potential manifestation of the two-channel Stoner physics.
Model
The p-d lattice hamiltonian
describes in a minimal manner mixing between correlated d (operators \(\hat{d}\)) and uncorrelated p (operators \(\hat{c}\)) orbital states, scenario ubiquitously present in metallic (but also insulating, e.g. Ref. 31) d-electron magnets. The stronger degree of electronic correlations among d than p states is attributed to the more localized nature of the former ones and is accounted for by the presence of the onsite Coulomb repulsion with the amplitude U in the \(\hat{d}\)-operator subspace, whereas lack thereof in the \(\hat{c}\)-operator subspace. In (1) σ ∈ {↑, ↓} is a spin index, i is a position vector of an underlying lattice of correlated orbitals, k is a momentum vector in the first Brillouin zone and \({\hat{n}}_{{\bf{i}}\sigma }^{d}\equiv {\hat{d}}_{{\bf{i}}\sigma }^{\dagger }{\hat{d}}_{{\bf{i}}\sigma }\).
The p-d Hamiltonian in a present work serves for a demonstration purposes of the principles behind two-channel Stoner mechanism rather than modeling of any realistic electronic structure. Therefore, without referring to particular orbital structure of d and p states, we assume that intra-orbital kinetic energies \({ {\mathcal E} }_{{\bf{k}}}\) and εk, of the correlated and the uncorrelated subsystems respectively, have a dispersion proportional to ξk ≡ −2(coskx + cosky), i.e., \({\varepsilon }_{{\bf{k}}}^{\alpha \in \{c,d\}}={\varepsilon }_{\alpha }+{t}_{\alpha }{\xi }_{{\bf{k}}}\) where we set εc = 0. Moreover, inter-orbital hybridization is assumed in a momentum independent form (Vk = V) and the p-p hopping is taken as the energy unit, |tc| = 1. Finally, we adopt here the condition td/tc < 0, that, unless specific geometrical reasons enter the problem, is typical case for direct bondings between orbital states differing with an angular momenta by 1. It is worth mentioning that mixed p-d quasiparticle density of states is dominated by features originating from hybridization between orbitals rather then these related to the underlying lattice. In that manner, even perfect nesting for each of the orbital subsystem in quasiparticle spectrum is inherited only at integer values of total filling. Therefore, made in our work choice of total-filling away from integer, for above assumption leads to hole- or electron-like Fermi-surfaces.
For the forthcoming discussion it is important to note that the p-d model for td = 0 reduces to the Anderson lattice model which describes mixing of localized f-states with delocalized conduction states and is frequently invoked for the description of heavy fermion systems. On the other hand for V = 0, orbital states in p-d model are not mixing and thus system of d-orbital states is described by the Hubbard model, which constitutes the simplest description of correlated electron systems, where complexity of real material is reduced just to the competition between the on-site repulsion U and hopping td.
Two-channel Stoner mechanism
Superficially one could expect that magnetism in itinerant magnets occurs by means of the usual Stoner mechanism due to a competition between the potential energy of correlated electrons and the total kinetic energy. However, such an approach overlooks in d-electron magnets such as LaCrGe3, ZrZn2 or CrAs displaying mixed correlated/uncorrelated electronic structure2,17,20,21,22,23,24,25,26,27 existence of two, qualitatively different Stoner channels.
First Stoner channel (1stSC) accounts for a competition between strong interactions among f or d states and their hybridization to the weakly correlated ligand states (U vs V, cf. Fig. 1). In turn, the second Stoner channel (2ndSC) refers to the competition between the same interactions and the kinetic energy due to a direct metallic bonding between correlated orbital states (U vs td, cf. Fig. 1). 2ndSC is usually absent in f-electron metallic magnets due to a negligible intra-f-orbital hopping28,29,30,32,33 (td ≃ 0). Contrary, it is clearly present in d-electron magnets such as LaCrGe3, ZrZn2 and CrAs20,21,22,23,24,25,26,27.
Intuition for the character of each channel separately can be gained by recalling magnetic properties of mentioned earlier, two well-established models: two-band Anderson lattice model8,32,33,34,35,36,37,38,39,40,41,42,43 (Eq. (1) with td = 0) with only 1stSC present, and single-band Hubbard model44,45,46,47,48,49 (Eq. (1) with V = 0) accounting solely for 2ndSC. Both models for moderate interactions (limit allowing to disregard local moment magnetism related either to Kondo or Mott physics) favor FM when total filling nt is away from integer. On the other hand, nt close to integer due to combined effect of nesting and stronger correlation effects yield stable AFM.
The situation in a p-d system, with both channels active, is more subtle. In such case the correlated band-filling nd is not fixed, in contrast to nt, and can notably change in a response to a modification of parameters associated with an applied pressure. Consequently, in response to a modification of nd, the character of 2ndSC possibly can change in the decisive, for a favored magnetic ordering, manner. In a following, we thoroughly explore this idea with the quantitative analysis of \( {\mathcal H} \).
Results
In this section we analyze magnetic properties of the p-d lattice model, which constitutes a minimal set-up accommodating two Stoner channels. Precisely, Hamiltonian (1) is treated within modified renormalized mean-field theory32,50,51 (see also Methods section) for a stability of three phases conveniently characterized with an average, spin and space dependent, density \(\langle {\hat{n}}_{{\bf{i}}\sigma }\rangle \): PM Fermi-liquid with \({n}_{{\bf{i}}\sigma }^{PM}\) = nt/2; uniformly polarized FM phases with \({n}_{{\bf{i}}\sigma }^{FM}\) = (nt + σmFM)/2; and spatially modulated AFM phase with \({n}_{{\bf{i}}\sigma }^{AFM}\) = (nt + \(\sigma {m}_{AF}{{\rm{e}}}^{i{\bf{Q}}{{\bf{R}}}_{{\bf{i}}}}\))/2 with usual Neél vector Q = (π, π) and mFM and mAF corresponding to uniform and staggered magnetization, respectively. Presence of the indirect hybridization gap in the spectrum allows for two FM phases, FM1 and FM2 differing with a Fermi surface topology schematically drawn in Fig. 2a32,39. We note that such a distinction provides a natural rationalization to experimentally established in several metallic ferromagnets (LaCrGe3, ZrZn2, UGe2) two different FM1 and FM2 phases in the p-T-h diagrams3,16,17,52.
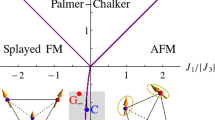
(a) Schematic picture of the spin-resolved density of states corresponding to two ferromagnetic phases, FM2 and FM1 that differ with Fermi surface topology due to spin selective gap in the former phase. (b) Magnetic phase diagram on the interaction - d-hopping, U-td plane for εd = −2, V = −0.9 and nt = 1.6. Color scale refers to the d-orbital filling, nd.
In Fig. 2b we present magnetic phase diagram on the interaction - d-hopping plane with color scale denoting d-orbital valence. Parametrization is chosen in order to demonstrate advocated scenario of two Stoner channels, and tunable character of the 2ndSC. Using the notions from the conceptual considerations in previous section, we may describe obtained magnetic phase diagram in a following manner. Total filling away from integer value fixes 1stSC to favor FM. Character of 2ndSC is in turn controlled by td and nd. In the case of non-active 2ndSC (td = 0) in Fig. 2b there is realized FM state supported by 1stSC, even when d-orbital filling is close to nd = 1. On the other hand, for substantially large |td| and when nd approaches half-filling in Fig. 2b AFM phase becomes stable. This is because in this limit, not only 2ndSC favors AFM order but also the tendency toward FM in 1stSC is overcome.
Next, we search for the parameter space of the model in a presence of active 2ndSC that could allow for the magnetic phase transitions possibly associated with applied pressure. Due to the essentially more localized nature of d than p orbital states hopping integrals in the following discussion are parametrized by |td| = |tc|/8. Effects of an applied pressure in \( {\mathcal H} \) can be reasonably captured by assuming identical increase of all kinetic amplitudes, tc, td and V, provided fixed U and εd. In the case of |tc| = 1 playing a role of an energy unit, above convention for emulating applied pressure follows decreasing ratios of U/|tc| and |εd|/|tc|, with all kinetic amplitudes unchanged.
Intriguingly, decrease of each ratio separately can influence nd, and thus 2ndSC, in an opposite manner. Namely, it is clear that change of εd/|tc| < 0 under pressure towards 0 modifies balance between orbital-resolved fillings providing lower nd. On the other hand, weakening correlations (decreasing U/|tc|), due to a reduction of the energy penalty for double occupancies, allows for its increase. The later relationship is clearly visible in Fig. 2b where decrease of U/|tc|, except FM2/FM1 transition, is accompanied with an increase of d-filling.
Shift of εd towards 0 due to an applied pressure can be of negligible importance in comparison to decreasing interactions if U/|εd| ≫ 1. Given that the ambient pressure state is characterized by \({n}_{d}\lesssim 1\), weakening correlations allow for a larger nd ≃ 1. In principle, such situation can lead to the change of the ordering favored by the 2ndSC from FM to AFM. In principle this change could be decisive for the realized state and thus pressure-driven FM/AFM transition in such scenario could be expected.
In Fig. 3a we present magnetic phase diagram on the U-V plane for the relatively shallow d-level, εd = −0.95. Indeed, we have obtained FM to AFM transitions driven by decreasing U/|tc|. As we checked, these transitions are always associated with increase of nd towards half-filling in AFM phase, in accord with the proposed two channel Stoner mechanism, suggesting in such case strengthening tendency in 2ndSC to favor AFM. In Fig. 3a we have marked with the arrow exemplary direction (V = −0.21) mirroring application of pressure encompassing triple point (TP) between FM1, FM2 and AFM phases for U ≃ 5, assuring the condition U/|εd| ≫ 1 is fulfilled. In the inset of Fig. 3a we explicitly show jump of d-orbital filling toward the half-filling at FM/AFM transition along marked arrow.
Magnetic phase diagrams (a) on the interaction - hybridization, U-V plane for εd = −0.95 and (b) on the interaction - d-level, U-εd plane for V = −0.25 (in both cases nt = 1.6). Color scale denotes total ordered magnetic moment in each phase. Arrows mark a possible directions associated with an applied pressure (cf. main text). Insets show changes of d-orbital valence along solid-line arrows encompassing, (a) FM/AFM and (b) AFM/FM, transitions.
The pressure-driven FM/AFM transition predicted by the proposed mechanism is rather fragile. This is because condensation energy of AFM state with respect to FM1 phase is small in the whole AFM stability region. In this manner, even a small Zeeman splitting due to a magnetic field would quickly decrease parameter-space area with stable AFM phase in favor of FM1 (but not FM2). Similar effect, but of different origin, has further depletion of the d-orbital filling towards nd = 0.5 by lifting d-level from εd = −0.95 (used in Fig. 3a) to εd = −0.8. It yields stable FM1 phase instead of AFM along the same direction (V = −0.21). It happens because in the diluted d-filling regime, irrespectively of the U value, the average number of double occupancies is negligible \(\langle {\hat{n}}_{\uparrow }^{d}{\hat{n}}_{\downarrow }^{d}\rangle \) ≃ 0. Consequently, decrease of the energy penalty, originating from U\(\langle {\hat{n}}_{\uparrow }^{d}{\hat{n}}_{\downarrow }^{d}\rangle \) contribution to the free energy, is not efficient enough to allow for an increase of nd triggering transition to AFM.
On the other hand, in a system which obeys U/|εd| ≃ 1, applied pressure should modify both |εd|/|tc| and U/|tc| ratios on an equal footing such that U/|εd| is fixed. In such a scenario an applied pressure is expected to decrease d-filling, due to likely leading effect of upshift of εd. Given that the ambient pressure state is characterized by nd∥1 (e.g. due to deep d-level) and favors AFM, the decrease of d-filling strengthens tendency toward FM in 2ndSC. It indicates a possibility of a pressure-driven AFM/FM transition.
In Fig. 3b we present a magnetic phase diagram on the U-εd plane for V = −0.25 which demonstrates that achieving such transition is possible. As we checked, all AFM/FM transitions along directions with fixed ratio U/|εd| are associated with decrease of nd away from half-filling, in accord with the scenario in which character of 2ndSC changes together with d-orbital filling. The solid arrow in Fig. 3b, drawn for U/|εd| = 1 determining a possible direction associated with an applied pressure, crosses AFM/FM transition. In the inset of Fig. 3b we explicitly show the evolution of the d-orbital filling along this direction.
In the table in Fig. 1 we have summarized, established by the prior analysis of \( {\mathcal H} \), conditions to be fulfilled by d-orbital at ambient pressure indicating possibility for subsequent pressure-induced FM/AFM or AFM/FM transitions supported by the two-channel Stoner mechanism.
Candidate compounds
The most promising candidate to realize magnetic phase transition due to two-channel Stoner physics is LaCrGe3. Face-sharing octahedra of Ge atoms encompassing Cr in LaCrGe3 imply that correlated 3d-states not only hybridize to p-ones of surrounding ligands but also bond between each other23, justifying a general p-d orbital structure of the model (1). In turn, parametrization of the model can be extracted from the electronic properties of LaCrGe3 (i) shallow d-level position23,24 and 3d nature of Cr valence states indicate U/|εd| ≫ 1; (ii) general agreement with (La3+)(Cr3+)(Ge2−)3 oxidation state23 pinpoints nd < 1; (iii) bonding between 3d-states twice smaller than their hybridization to p-states23 suggests 2|td| ≃ |V|.
All these features fulfill general conditions (cf. first column of table in Fig. 1) for a pressure-induced FM/AFM transition (cf. arrow in Fig. 3a) qualifying recent observation of magnetic groundstate switching in LaCrGe32,3 as a possible manifestation of the two-channel Stoner physics. The incorporation of the detailed electronic structure of this material is clearly needed to further support proposed interpretation. Nevertheless, experimental discrimination between large (Q ~ π) or small (Q ~ 0) ordering vector of the AFM state in LaCrGe3 is highly desirable. Large vector would be consistent with two-channel Stoner physics whereas small one with the mechanism based on the quantum fluctuation arguments11,13,14.
We also note that the realization of TP between FM1, FM2 and AFM phases (cf. Fig. 3a)a although constitutes very appealing rationalization of a similar FM1-FM2-AFM meeting point observed in LaCrGe3 at 2 K3, is an effect of a fine-tuning rather than a robust feature of the model. Nevertheless, field-driven increase of the stability region of FM1 phase at the expense of the AFM phase already is a generic property. It is related to the weak condensation energy of AFM phase with respect to FM1 (but not to FM2) over wide range of U values. In that manner, prediction of our simple model agrees with observations in LaCrGe3 where stability region of FM1 emerges out of AFM phase with application of pressure.Footnote 1
Second promising candidate material to realize two-channel Stoner physics is itinerant d-electron antiferromagnet CrAs. Band structure calculations for this material suggest: (i) predominant role of mixed p-d states near the Fermi level25,26,27; (ii) proximity between FM and AFM states25; (iii) weak degree of correlations due to a very wide p-band (large |tc|)25,26,27; (iv) consistency with (Cr0)(As0) oxidation state, implying occupation of 3d-orbital larger but close to half-filling26.
First two properties (i-ii) of CrAs indicate a possible importance of the two-channel Stoner mechanism to describe properties of this material. The third one (iii) suggests that due to the small ratio U/|tc|, both U and εd change under pressure on an equal footing (cf. Fig. 3b). Finally, the forth one (iv) indicates rather deep d-level such that U/|εd| < 1. Consequently, the direction possibly associated with CrAs under pressure is drawn in Fig. 3b with labeled dashed-arrow for U/|εd| = 0.5. The proximity to AFM/FM transition, present in Fig. 3b already for U/|εd| ≃ 0.6, can justify why ab-initio calculations, that are known to slightly overestimate tendency toward FM, support stable FM in CrAs under pressure25.
Finally, we note that the similar minimal model proposed for itinernat ferromagnet UGe232,33,43 not only have rationalized compound’s magnetic properties but it inspired proposal on the feasible origin of the triplet superconductivity53,54 based on the Hund’s rule induced pairing55,56,57,58. Therefore, it is tempting to ask whether our model can also shed some light on the possible origin of superconductivity in CrAs at the border of the magnetic/non-magnetic phase59. In fact, inspired by the recent experimental results in the similar class of Cr-based compounds60, we could speculate that the potential vicinity of the ferromagnetic instability in CrAs and thus ferromagnetic fluctuations can be a candidate pairing glue.
Summary
In the present work we have proposed mechanism for competing AFM and FM orders in metallic systems displaying mixed correlated d-orbital/uncorrelated ligand-orbital electronic structure in the vicinity of the Fermi level. We have analyzed magnetic instabilities of the Fermi liquid realized by a minimal two-band model in order to demonstrate properties of the mechanism. We have formulated general conditions (cf. table of Fig. 1) that relate energy scales connected with the character of d-orbital at ambient pressure with potentially realized FM/AFM or AFM/FM transitions in response to applied pressure. We found, that the character of d-orbitals in LaCrGe3 is consistent with the proposed here parametrization of the model supporting pressure induced FM/AFM transition. It is very promising result in terms of potential interpretation of recent observations of such transition in this material2, 3.
Methods
The low-energy properties of the p-d model in the T → 0 limit, i.e. the Fermi-liquid state and its magnetic instabilities, can be efficiently analyzed within the Gutzwiller approximation combined with the optimization of the Slater determinant scheme32,50,51. The technique belongs to the renormalized mean-field theory class of approaches61,62. Formally, the method accounts for the variational optimization of the average number of double occupancies \(\langle {\hat{n}}_{\uparrow }^{d}{\hat{n}}_{\downarrow }^{d}\rangle \) with the Gutzwiller correlator. In practice, it reduces to the construction of the effective single-particle mean-field Hamiltonian for each considered phase with renormalized with Gutzwiller factor qσ certain characteristics such as hybridization and d-d hoppingb.
Renormalized mean-field Hamiltonian for FM phase reads
where in above \({\Psi }^{\dagger }=\{{\hat{c}}_{{\bf{k}},\sigma }^{\dagger },{\hat{d}}_{{\bf{k}}\sigma }^{\dagger }\}\). Moreover qσ(\(\langle {\hat{n}}_{\uparrow }^{d}{\hat{n}}_{\downarrow }^{d}\rangle \), \(\langle {\hat{n}}_{\uparrow }^{d}\rangle \), \(\langle {\hat{n}}_{\downarrow }^{d}\rangle \)) is the usual Gutzwiller narrowing factor32,50 and
is a spin-resolved shift of the chemical potential, both obtained in a self-consistent manner (For technical details concerning implementation of our mean-field scheme in two-band model see Method section as well ref. 32 for FM phases and ref. 8 for AFM.). Here 〈…〉0 denotes an expectation value with the Slater determinant and 〈…〉G with the Gutzwiller wave function under the Gutzwiller approximation.
In turn renormalized mean-field Hamiltonian for the AFM phase defined in the reduced Brillouin zone (RBZ) reads
where here \({\Psi }^{\dagger }=({c}_{{\bf{k}}\sigma }^{\dagger },{c}_{{\bf{k}}+Q\sigma }^{\dagger },{f}_{{\bf{k}}\sigma }^{\dagger },{f}_{{\bf{k}}+Q\sigma }^{\dagger })\), and qσ and λσ are obtained for a one sublattice.Footnote 2
Used variational method is well suited to capture a Fermi-liquid state, even though it disregards momentum-dependence of the quasiparticle weight. One can associate the approximation imposed on the solution of the \( {\mathcal H} \) with a one concerning the d-electron self-energy
Then the Gutzwiller factor qσ can be shown to play a role of a quasiparticle weight, \({z}_{\sigma }={[{1-\frac{\partial \Re {\Sigma }_{\sigma }(\omega )}{\partial \omega }|}_{\omega \to 0}]}^{-1}\).
We note that in principle a p-d lattice model with the total-filling close to integer and in the large-U limit can support Mott or Kondo physics63,64,65,66,67,68 being responsible for magnetism of localized moments. However, for all discussed result we have assumed total filling away from integer value, nt = 1.6, providing that for small-to-moderate interaction values the exchange interactions, and thus magnetism of localized moments is not entering present considerations. For that reason it is justified to use Gutzwiller approximation that by the construction disregards exchange interactions69.
Notes
Obtained triple point is also supported at interaction - magnetic field plane due to the fact that Zeeman spliting strongly humpers AFM giving rise to FM2/FM1/AFM phase sequence.
References
Friedemann, S. et al. Quantum tricritical points in NbFe2. Nat. Phys. 14, 62, https://doi.org/10.1038/nphys4242 (2018).
Taufour, V. et al. Ferromagnetic quantum critical point avoided by the appearance of another magnetic phase in LaCrGe3 under pressure. Phys. Rev. Lett. 117, 037207, https://doi.org/10.1103/PhysRevLett.117.037207 (2016).
Kaluarachchi, U. S., Bud’ko, S. L., Canfield, P. C. & Taufour, V. Tricritical wings and modulated magnetic phases in LaCrGe3 under pressure. Nat. Comm. 8, 546, https://doi.org/10.1038/s41467-017-00699-x (2017).
Jeffries, J. R., Stillwell, R. L., Weir, S. T., Vohra, Y. K. & Butch, N. P. Emergent ferromagnetism and t-linear scattering in USb2 at high pressure. Phys. Rev. B 93, 184406, https://doi.org/10.1103/PhysRevB.93.184406 (2016).
Pospíšil, J. C. V. et al. Switching of magnetic ground states across the UIr1−xRhxGe alloy system. Phys. Rev. B 95, 155138, https://doi.org/10.1103/PhysRevB.95.155138 (2017).
Lengyel, E. et al. Avoided ferromagnetic quantum critical point in cerupo. Phys. Rev. B 91, 035130, https://doi.org/10.1103/PhysRevB.91.035130 (2015).
Belitz, D. & Kirkpatrick, T. R. Quantum triple point and quantum critical end points in metallic magnets. Phys. Rev. Lett. 119, 267202, https://doi.org/10.1103/PhysRevLett.119.267202 (2017).
Wysokiński, M. M. Microscopic mechanism for the unusual antiferromagnetic order and the pressure-induced transition to ferromagnetism in USb2. Phys. Rev. B 97, 041107, https://doi.org/10.1103/PhysRevB.97.041107 (2018).
Sandratskii, L. Magnetic phase transitions induced by pressure and magnetic field: The case of antiferromagnetic usb2. Phys. Rev. B 99, 094411, https://doi.org/10.1103/PhysRevB.99.094411 (2019).
Belitz, D., Kirkpatrick, T. R. & Vojta, T. Nonanalytic behavior of the spin susceptibility in clean Fermi systems. Phys. Rev. B 55, 9452–9462, https://doi.org/10.1103/PhysRevB.55.9452 (1997).
Green, A. G., Conduit, G. & Krüger, F. Quantum order-by-disorder in strongly correlated metals. Annu. Rev. Condens. Matter Phys. 9, 59–77, https://doi.org/10.1146/annurev-conmatphys-033117-053925 (2018).
Chubukov, A. V., Pépin, C. & Rech, J. Instability of the quantum-critical point of itinerant ferromagnets. Phys. Rev. Lett. 92, 147003, https://doi.org/10.1103/PhysRevLett.92.147003 (2004).
Conduit, G. J., Green, A. G. & Simons, B. D. Inhomogeneous phase formation on the border of itinerant ferromagnetism. Phys. Rev. Lett. 103, 207201, https://doi.org/10.1103/PhysRevLett.103.207201 (2009).
Karahasanovic, U., Krüger, F. & Green, A. G. Quantum order-by-disorder driven phase reconstruction in the vicinity of ferromagnetic quantum critical points. Phys. Rev. B 85, 165111, https://doi.org/10.1103/PhysRevB.85.165111 (2012).
Brando, M., Belitz, D., Grosche, F. M. & Kirkpatrick, T. R. Metallic quantum ferromagnets. Rev. Mod. Phys. 88, 025006, https://doi.org/10.1103/RevModPhys.88.025006 (2016).
Pfleiderer, C. & Huxley, A. D. Pressure dependence of the magnetization in the ferromagnetic superconductor UGe2. Phys. Rev. Lett. 89, 147005, https://doi.org/10.1103/PhysRevLett.89.147005 (2002).
Uhlarz, M., Pfleiderer, C. & Hayden, S. M. Quantum phase transitions in the itinerant ferromagnet ZrZn2. Phys. Rev. Lett. 93, 256404, https://doi.org/10.1103/PhysRevLett.93.256404 (2004).
Taufour, V., Aoki, D., Knebel, G. & Flouquet, J. Tricritical point and wing structure in the itinerant ferromagnet UGe2. Phys. Rev. Lett. 105, 217201, https://doi.org/10.1103/PhysRevLett.105.217201 (2010).
Kotegawa, H., Taufour, V., Aoki, D., Knebel, G. & Flouquet, J. Evolution toward quantum critical end point in UGe2. J. Phys. Soc. Jpn. 80, 083703, https://doi.org/10.1143/JPSJ.80.083703 (2011).
Jarlborg, T., Freeman, A. & Koelling, D. Self-consistent spin polarized energy band structure and magnetism in ZrZn2 and TiBe2. J. Mag. Mag. Mat. 23, 291–298, https://doi.org/10.1016/0304-8853(81)90050-0 (1981).
Santi, G., Dugdale, S. B. & Jarlborg, T. Longitudinal spin fluctuations and superconductivity in ferromagnetic ZrZn2 from ab initio calculations. Phys. Rev. Lett. 87, 247004, https://doi.org/10.1103/PhysRevLett.87.247004 (2001).
Singh, D. J. & Mazin, I. I. Competition of spin fluctuations and phonons in superconductivity of ZrZn2. Phys. Rev. Lett. 88, 187004, https://doi.org/10.1103/PhysRevLett.88.187004 (2002).
Bie, H., Zelinska, O. Y., Tkachuk, A. V. & Mar, A. Structures and physical properties of […] ReCrGe3. Chem. Mater. 19, 4613–4620 (2007).
Nguyen, M. C. et al. Using first-principles calculations to screen for fragile magnetism: Case study of LaCrGe3 and LaCrSb3. Phys. Rev. B 97, 184401, https://doi.org/10.1103/PhysRevB.97.184401 (2018).
Autieri, C. & Noce, C. First principles study of structural, magnetic and electronic properties of CrAs. Philos. Mag. 97, 3276–3295, https://doi.org/10.1080/14786435.2017.1375607 (2017).
Autieri, C., Cuono, G., Forte, F. & Noce, C. Low energy bands and transport properties of chromium arsenide. J. Physics: Condens. Matter 29, 224004 (2017).
Autieri, C., Cuono, G., Forte, F. & Noce, C. Tight-binding calculation of the magnetic moment of cras under pressure. J. Physics: Conf. Ser. 969, 012106 (2018).
Yamagami, H. et al. Electronic structure analysis of UIr using soft X-ray photoemission spectroscopy and band calculation. J. Physics: Conf. Ser. 200, 012229 (2010).
Shick, A. B. & Pickett, W. E. Magnetism, spin-orbit coupling, and superconducting pairing in UGe2. Phys. Rev. Lett. 86, 300–303, https://doi.org/10.1103/PhysRevLett.86.300 (2001).
Samsel-Czekała, M., Werwiński, M., Szajek, A., Chełkowska, G. & Troć, R. Electronic structure of UGe2 at ambient pressure: Comparison with X-ray photoemission spectra. Intermetallics 19, 1411–1419, https://doi.org/10.1016/j.intermet.2011.05.008 (2011).
Autieri, C. Antiferromagnetic and xy ferro-orbital order in insulating SrRuO3 thin films with SrO termination. J. Phys.: Condens. Matter 28, 426004, https://doi.org/10.1088/0953-8984/28/42/426004 (2016).
Wysokiński, M. M., Abram, M. & Spałek, J. Ferromagnetism in UGe2: A microscopic model. Phys. Rev. B 90, 081114(R), https://doi.org/10.1103/PhysRevB.90.081114 (2014).
Wysokiński, M. M., Abram, M. & Spałek, J. Criticalities in the itinerant ferromagnet UGe2. Phys. Rev. B 91, 081108(R), https://doi.org/10.1103/PhysRevB.91.081108 (2015).
Doradziński, R. & Spałek, J. Antiferromagnetic heavy-fermion and Kondo-insulating states with compensated magnetic moments. Phys. Rev. B 56, R14239–R14242, https://doi.org/10.1103/PhysRevB.56.R14239 (1997).
Meyer, D. & Nolting, W. Dynamical mean-field study of ferromagnetism in the periodic anderson model. Phys. Rev. B 62, 5657–5666, https://doi.org/10.1103/PhysRevB.62.5657 (2000).
Batista, C. D., Bonča, J. & Gubernatis, J. E. Segmented band mechanism for itinerant ferromagnetism. Phys. Rev. Lett. 88, 187203, https://doi.org/10.1103/PhysRevLett.88.187203 (2002).
Batista, C. D., Bonča, J. & Gubernatis, J. E. Itinerant ferromagnetism in the periodic Anderson model. Phys. Rev. B 68, 214430, https://doi.org/10.1103/PhysRevB.68.214430 (2003).
Yu, U., Byczuk, K. & Vollhardt, D. Influence of band and orbital degeneracies on ferromagnetism in the periodic Anderson model. Phys. Rev. B 78, 205118, https://doi.org/10.1103/PhysRevB.78.205118 (2008).
Kubo, K. Ferromagnetism and Fermi surface transition in the periodic Anderson model: Second-order phase transition without symmetry breaking. Phys. Rev. B 87, 195127, https://doi.org/10.1103/PhysRevB.87.195127 (2013).
Kubo, K. Lifshitz transitions in magnetic phases of the periodic Anderson model. J. Phys. Soc. Jpn. 84, 094702, https://doi.org/10.7566/JPSJ.84.094702 (2015).
Wu, W. & Tremblay, A.-M.-S. d-wave superconductivity in the frustrated two-dimensional periodic Anderson model. Phys. Rev. X 5, 011019, https://doi.org/10.1103/PhysRevX.5.011019 (2015).
Aulbach, M. W., Assaad, F. F. & Potthoff, M. Dynamical mean-field study of partial Kondo screening in the periodic Anderson model on the triangular lattice. Phys. Rev. B 92, 235131, https://doi.org/10.1103/PhysRevB.92.235131 (2015).
Abram, M., Wysokiński, M. M. & Spałek, J. Tricritical wings in UGe2: A microscopic interpretation. J. Mag. Mag. Mat. 400, 27–30, https://doi.org/10.1016/j.jmmm.2015.07.017 (2016).
Kotliar, G. & Ruckenstein, A. E. New functional integral approach to strongly correlated Fermi systems: The Gutzwiller approximation as a saddle point. Phys. Rev. Lett. 57, 1362–1365, https://doi.org/10.1103/PhysRevLett.57.1362 (1986).
Hirsch, J. E. Two-dimensional Hubbard model: Numerical simulation study. Phys. Rev. B 31, 4403–4419, https://doi.org/10.1103/PhysRevB.31.4403 (1985).
Vollhardt, D. et al. Metallic ferromagnetism: Progress in our understanding of an old strong-coupling problem. Adv. Solid State Phys. 38, 383, https://doi.org/10.1007/BFb0107631 (1999).
Lichtenstein, A. I. & Katsnelson, M. I. Antiferromagnetism and d-wave superconductivity in cuprates: A cluster dynamical mean-field theory. Phys. Rev. B 62, R9283–R9286, https://doi.org/10.1103/PhysRevB.62.R9283 (2000).
Münster, K. Z. & Bünemann, J. Gutzwiller variational wave function for multiorbital Hubbard models in finite dimensions. Phys. Rev. B 94, 045135, https://doi.org/10.1103/PhysRevB.94.045135 (2016).
Tocchio, L. F., Becca, F. & Sorella, S. Hidden Mott transition and large-U superconductivity in the two-dimensional Hubbard model. Phys. Rev. B 94, 195126, https://doi.org/10.1103/PhysRevB.94.195126 (2016).
Wysokiński, M. M. & Spałek, J. Properties of an almost localized Fermi liquid in an applied magnetic field revisited: A statistically consistent Gutzwiller approach. J. Phys.: Condens. Matter 26, 055601 (2014).
Abram, M., Zegrodnik, M. & Spałek, J. Antiferromagnetism, charge density wave, and d-wave superconductivity in the extended t-J-U model: role of intersite Coulomb interaction and a critical overview of renormalized mean field theory. J. Phys.: Condens. Mat. 29, 365602 (2017).
Kimura, N. et al. de haas–van alphen effect in zrzn2 under pressure: Crossover between two magnetic states. Phys. Rev. Lett. 92, 197002, https://doi.org/10.1103/PhysRevLett.92.197002 (2004).
Kadzielawa-Major, E., Fidrysiak, M., Kubiczek, P. & Spałek, J. Spin-triplet paired phases inside a ferromagnet induced by Hund’s rule coupling and electronic correlations: Application to uge2. Phys. Rev. B 97, 224519, https://doi.org/10.1103/PhysRevB.97.224519 (2018).
Fidrysiak, M., Goc-Jagło, D., Kadzielawa-Major, E., Kubiczek, P. & Spałek, J. Coexistent spin-triplet superconducting and ferromagnetic phases induced by hund’s rule coupling and electronic correlations: Effect of the applied magnetic field. Phys. Rev. B 99, 205106, https://doi.org/10.1103/PhysRevB.99.205106 (2019).
Spałek, J. Spin-triplet superconducting pairing due to local hund’s rule and dirac exchange. Phys. Rev. B 63, 104513, https://doi.org/10.1103/PhysRevB.63.104513 (2001).
Zegrodnik, M. & Spałek, J. Coexistence of spin-triplet superconductivity with magnetic ordering in an orbitally degenerate system: Hartree-fock-bcs approximation revisited. Phys. Rev. B 86, 014505, https://doi.org/10.1103/PhysRevB.86.014505 (2012).
Zegrodnik, M., Spałek, J. & Bnemann, J. Coexistence of spin-triplet superconductivity with magnetism within a single mechanism for orbitally degenerate correlated electrons: statistically consistent gutzwiller approximation. New J. Phys. 15, 073050, https://doi.org/10.1088/1367-2630/15/7/073050 (2013).
Zegrodnik, M., Bünemann, J. & Spałek, J. Even-parity spin-triplet pairing by purely repulsive interactions for orbitally degenerate correlated fermions. New J. Phys. 16, 033001 (2014).
Wu, W. et al. Superconductivity in the vicinity of antiferromagnetic order in CrAs. Nat. Comm. 5, 5508, https://doi.org/10.1038/ncomms6508 (2014).
Luo, J. et al. Tuning the distance to a ferromagnetic quantum critical point in a2cr3as3. arXiv:1905.06055.
Bünemann, J. & Gebhard, F. Equivalence of Gutzwiller and slave-boson mean-field theories for multiband Hubbard models. Phys. Rev. B 76, 193104, https://doi.org/10.1103/PhysRevB.76.193104 (2007).
Zhang, F. C., Gros, C., Rice, T. M. & Shiba, H. A renormalized hamiltonian approach to a resonant valence bond wavefunction. Supercond. Sci. Technol. 1, 3 (1988).
Coleman, P. New approach to the mixed-valence problem. Phys. Rev. B 29, 3035–3044, https://doi.org/10.1103/PhysRevB.29.3035 (1984).
Pruschke, T., Bulla, R. & Jarrell, M. Low-energy scale of the periodic Anderson model. Phys. Rev. B 61, 12799–12809, https://doi.org/10.1103/PhysRevB.61.12799 (2000).
De Leo, L., Civelli, M. & Kotliar, G. Cellular dynamical mean-field theory of the periodic Anderson model. Phys. Rev. B 77, 075107, https://doi.org/10.1103/PhysRevB.77.075107 (2008).
Amaricci, A., Sordi, G. & Rozenberg, M. J. Non-fermi-liquid behavior in the periodic Anderson model. Phys. Rev. Lett. 101, 146403, https://doi.org/10.1103/PhysRevLett.101.146403 (2008).
Sordi, G., Amaricci, A. & Rozenberg, M. J. Asymmetry between the electron- and hole-doped Mott transition in the periodic Anderson model. Phys. Rev. B 80, 035129, https://doi.org/10.1103/PhysRevB.80.035129 (2009).
Dong, R., Otsuki, J. & Savrasov, S. Y. Scaling between periodic Anderson and Kondo lattice models. Phys. Rev. B 87, 155106, https://doi.org/10.1103/PhysRevB.87.155106 (2013).
Wysokiński, M. M. & Fabrizio, M. Mott physics beyond the Brinkman-Rice scenario. Phys. Rev. B 95, 161106, https://doi.org/10.1103/PhysRevB.95.161106 (2017).
Acknowledgements
Author thanks T. Dietl and T. Hyart for critical reading of the manuscript as well as C. Autieri, W. Brzezicki, P. Iwanowski and V. Taufour for stimulating discussions and extremely useful comments. Author also thanks prof. A. Green for suggesting mentioned in the main text possible experimental indication that FM/AFM transition in LaCrGe3 takes place either due to proposed here mechanism or due to this relying on quantum fluctuations. The financial support from the Foundation for Polish Science under the “START” program is greatly acknowledged. The work is supported by the Foundation for Polish Science through the IRA Programme co-financed by EU within SG OP. Author acknowledges the access to the computing facilities of the Interdisciplinary Center of Modeling at the University of Warsaw, Grant No. G73-23 and G75-10.
Author information
Authors and Affiliations
Contributions
M.M.W. did all the work.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wysokiński, M.M. Mechanism for transitions between ferromagnetic and antiferromagnetic orders in d-electron metallic magnets. Sci Rep 9, 19461 (2019). https://doi.org/10.1038/s41598-019-55658-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-55658-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.