Abstract
Silicon Nitride (SiN) is emerging as a promising material for a variety of integrated photonic applications. Given its low index contrast however, a key challenge remains to design efficient couplers for the numerous platforms in SiN photonics portfolio. Using a combination of bottom reflector and a chirp generating algorithm, we propose and demonstrate high efficiency, grating couplers on two distinct SiN platforms. For a partially etched grating on 500 nm thick SiN, a calculated peak efficiency of −0.5 dB/coupler is predicted, while for a fully etched grating on 400 nm thick SiN, an efficiency of −0.4 dB/coupler is predicted. Experimentally measured coupling efficiencies are observed to be −1.17 and −1.24 dB/coupler for the partial and fully etched grating couplers respectively in the C-L band region. Furthermore, through numerical simulations, it is shown that the chirping algorithm can be implemented in eight additional combinations comprising SiN film thickness between 300–700 nm as well as alternate claddings, to achieve a per coupler loss between −0.33 to −0.65 dB.
Similar content being viewed by others
Introduction
Silicon photonics is a key technology enabler for building complex optical components for a host of applications such as high performance computing, communications as well as on-chip sensing. Moreover, the mature complementary metal-oxide semiconductor (CMOS) foundry processes provides further impetus for a scalable, low cost and high volume means to integrate electronics and photonics functionalities on a single chip1,2,3. From the materials perspective, there are primarily two CMOS compatible photonic platforms which are Silicon-on-insulator (SOI) and Silicon Nitride (SiN). The former is a widely researched platform on which a variety of active and passive devices have been implemented till date. On the other hand, a lot of interest has been brewing in the field of SiN photonics, especially as an alternative integrated platform4,5,6,7. Several reasons are attributed to this, such as SiN exhibiting a wideband spectral transparency encompassing visible to mid-infrared, having higher tolerance to fabrication imperfections owing to a moderate index contrast and its near total absence of two photon absorption. Such vast potential has paved way for the emergence of several SiN platforms that cater to applications ranging from passive wavelength division multiplexing (WDM), spectroscopy, sensing as well as integrated nonlinear photonics. The choice of SiN thickness depends largely on its targeted spectrum as well as application. Lower waveguide film thickness is generally preferred for passive WDM as well as sensing applications8,9,10,11 while thicker films are used for nonlinear photonic applications12,13,14,15.
Fiber-chip coupling is a critical aspect of any photonic integrated circuit. There are principally two ways of enabling this task, which are in-plane and out-of-plane coupling. The former typically consists of edge couplers and is known to deliver high coupling efficiency as well as a broad bandwidth. However it also requires flat cleaved, polished facets and precise alignment. The latter consists of surface diffractive features imprinted on the waveguiding layer, that is used to phase match the incoming fiber mode with that of the propagating waveguide mode.
Despite offering a comparatively lower coupling and bandwidth, surface gratings are generally preferred over edge-couplers to facilitate fiber to waveguide coupling, owing to ease of fabrication and relaxed alignment tolerances. High efficiency grating couplers on SOI have been reported using a variety of design strategies16,17,18,19,20,21,22. Achieving a similar feat on SiN is cumbersome given its moderate index-contrast. Nevertheless, several key demonstrations have been recently reported on improving efficiency of SiN gratings. Broadly speaking, the grating efficiency depends on two factors, first of which is directionality, that quantifies total power scattered upwards and the second is field overlap with the fiber mode. A generic grating suffers from poor directionality due to a substantial portion of power being leaked to the substrate. One way to improve upon the directionality is to implement a double-etched grating structure. A two level highly directional, staircase grating was reported in23 with an efficiency of −1.5 dB, on a standalone 600 nm thick SiN film. Similarly, a bi-layer, double-etched grating coupler was demonstrated in24 with an efficiency of −2.56 dB on 220 nm thick SiN. A second way to improve directionality is by hybridizing SiN with a high index platform like SOI. High bandwidth gratings have been reported on such SiN-SOI platforms, such as a composite grating of Si and SiN, demonstrated in25 on 400 nm thick SiN with a coupling of −1.3 dB and a 1 dB bandwidth of 80 nm. Likewise a deep-etched SiN-SOI grating was reported in26 with a coupling of −2.5 dB and 67 nm 1 dB bandwidth. A third way to enhance directionality is by incorporating a highly reflective bottom mirror like a Bragg stack27,28,29 or a metal layer20,21. When a bottom mirror is placed at an optimal separation from the slab, constructive interference occurs between up-scattered and downward reflected light which suppresses substrate leakage. In29, we reported enhanced efficiency of uniform SiN grating couplers, incorporated with a bottom Bragg mirror. In this work, we shall extend the scheme to non-uniform gratings. By using a combination of a bottom reflector and a chirping generator, we show a sub-dB coupling loss on two distinct platforms, which are, a 500 nm thick SiN with an air cladding and a 400 nm thick SiN on SiO2 cladding.
The total fiber to waveguide coupled output power PCE, can be determined through the following expression,
where Pdiff is the proportion of upper diffracted power (or commonly referred as directionality). \(\eta \), is the overlap integral between diffracted grating and fiber mode fields. \(\eta \) can be further evaluated from20,30 as,
where Efib is the electric field distribution of the fiber mode and Egr, that of the scattered grating field. The diffracted power profile of a uniform grating is exponentially decaying along the propagation direction, can be expressed as \(P(x)={P}_{0}{e}^{-2\alpha x}\), where α is the grating leakage parameter and x is mode propagation direction. Consequently, \(\eta \) between a exponentially varying field distribution and a Gaussian mode is limited to around 80–85%. In order to maximize \(\eta \), the leakage parameter must by engineered along the grating length so as to gradually scatter a Gaussian like profile. This variable leakage parameter α(x) can be expressed in the following form31 as,
G(x), being the Gaussian profile scattered by the grating.
Design and Simulation
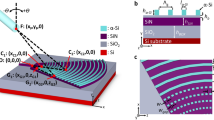
Figure 1 illustrates a schematic of proposed grating structures of the two design combinations considered. The critical parameters of relevance here are \(\Lambda \), which is the grating period, f, the fill-factor, te, the etch depth, and θ, the incidence angle of illumination. Also, tcl is the upper cladding thickness for design B, tBOX is the buried oxide thickness and tSiN is the waveguide core thickness. Out of these te is considered to be a variable quantity for design A and is fixed as tSiN for design B where all gratings are considered fully etched. tcl on the other hand, is considered to be a variable for design B. We have considered two platforms i.e. a tSiN of 500 nm for design A which is interesting for nonlinear optical applications15 and a tSiN of 400 nm for design B, which can be used for building passive photonic interconnects8. Beneath the BOX layer lies a distributed Bragg reflector (DBR) stack. The DBR stack, is composed of two cascaded layers of amorphous Silicon and Silicon dioxide (a-Si/SiO2) of thickness λ/4N each (λ is the wavelength in free-space and N is optical material index), which translates to 110/270 nm. Numerical simulations are performed in two dimensional-finite difference time domain (FDTD). The source is considered to be a Gaussian of mode field diameter 10.4 μm and is embedded a few microns above, in the air region of each grating design. A power monitor is placed in the slab waveguide, a few microns away from the grating to determine the coupling efficiency (CE). The optical indices of Si, a-Si, SiO2 and SiN are obtained from ellipsometry to be 3.46, 3.53, 1.44 and 2.015. Our goal here is to determine an optimal generator function that maximizes \(\eta \) and hence coupling to waveguide. This chirp generator algorithm can be expressed in terms of a grating constructor as,
where fs and fe are the start and end fill-factors respectively and m, the total number of grating periods. The factor \({f}_{i}\Lambda \) corresponds to the etched portion of the ith grating period. The unknown period \(\Lambda \) is assumed to be fixed in this generator algorithm. \(\Lambda \) depends on fulfilling the Bragg phase matching condition, which is,
where ncl is the top cladding index and \({N}_{gr}^{eff}\), the effective grating index. Since, the fill-factor is assumed to be a variable parameter throughout the grating length, the effective grating index of the ith period can then be expressed as,
where \({n}_{SiN}^{eff}\) and \({n}_{et}^{eff}\) are the effective modal indices of the fundamental transverse electric (TE) mode of the slab and etched portions respectively. For design B, \({n}_{et}^{eff}\) is substituted with optical index of SiO2. A rigorous optimization reveals the grating constructor in terms of the chirp generator algorithm (CGA) as,
(a) Shows a 3D illustration of a chirped fiber-waveguide focusing grating coupler with a bottom DBR mirror. (b) Shows 2D schematic of grating couplers for design A and (c) for design B, considered in this work. As indicated, no constraints on etch depth te is imposed for design A, where as only full etched gratings are considered for design B.
In effect, the grating is composed of 2 parts, i.e., a uniform section till n periods and a chirped section for m-n periods. Here fu corresponds to the uniform fill-factor and the chirped parameters \({f}_{s}^{c}\) and \({f}_{e}^{c}\) correspond to the start and end fill-factors. A parametric sweep is now conducted to find the optimal design parameters. For design A, n is found to be 3 and m-n to be 16, however in design B, n is 1 and m-n is 18. The optimal grating periods are 0.95 μm for design A and 0.99 μm for design B. All the relevant chirp parameters are provided in Table 1. In addition, optimal tcl for design B is calculated for a thickness of 2 μm.
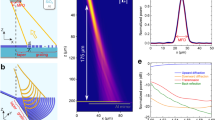
Figure 2 shows the coupling as a function of different periods and angles for the DBR aided designs. Peak CE for design A is calculated as −0.5 dB, at incident angle 3°, at 1550 nm. For design B, peak CE is calculated as −0.38 dB at 1560 nm, also at an angle of 3°. For design A, a 10 nm increase in period results in a red shift of 14 nm for peak wavelength. For design B, this red shift is observed to be slightly higher at 16 nm. The angle sweep showcases a distinctive feature of these CGA optimized gratings, which is a high coupling observed at near vertical incidence.
From the fabrication perspective, a critical parameter is the quantity \({f}_{e}^{c}\Lambda \), which determines the minimum grating trench width. At optimum coupling, the minimum trench width for design A is 142 nm and for design B is 148 nm, both of which are feasible with current state of art 193 nm immersion deep UV lithography32. In any foundry, deviations from ideal design may inevitably occur and so it is necessary to estimate tolerance of fabricated structures to such process induced imperfections. Figure 3 outlines the impact of critical design parameters on the overall device coupling performance. At first, we take a look at two process related parameters, which are, etch depth for design A and upper cladding SiO2 thickness for design B. The etch depth variation and its effect on coupling and peak wavelength is plotted in Fig. 3(a). A peak wavelength shift of only 10 nm is observed for every 20 nm change in etch depth. In addition, we also note that for a ±40 nm etch depth variation, reduction in peak coupling is only about −0.17 dB. In case of the upper cladding thickness of design B (as shown in Fig. 3(b)), a ±100 nm deviation leads to a reduction of only −0.14 dB in peak coupling with no significant change in peak wavelength. Next, we take a look at the BOX thickness variation for both designs, which is plotted in Fig. 3(c,d). For design A, tolerance to tBOX deviation is observed to be higher. For a ±100 nm variation, the change in peak coupling is only −0.15 dB. Compared to that, design B shows a lower tolerance to tBOX variation. Here, for a ±50 nm deviation, the peak coupling is observed to change by −0.26 dB. These figures are however, within the standard limitations of photonic foundry processes and underline design robustness.
Coupling dependence on critical design parameters. (a) Shows dependence of etch depth variation δte on peak coupling and wavelength for design A and (b) shows dependence of upper cladding thickness tcl on peak coupling for design B. (c) Shows the BOX thickness tBOX impact on peak coupling performance for design A and (d) shows the same for design B.
The coupling is also impacted by the number of DBR stacks. In Supplementary Fig. S1, this dependence is plotted. For design A, the difference in peak coupling between a Si substrate and a single layer DBR stack is only −0.81 dB. However for design B, this difference is significantly higher at −1.72 dB. Peak coupling between a single and double layer DBR stack differs by only −0.15 dB for design A, and by 0.35 dB for design B. For a 4 layer DBR substrate, calculated peak coupling is −0.45 dB for design A and −0.31 dB for design B. For either designs, the coupling appears to saturate beyond a 4 layer DBR.
A look at the scattered fields (as shown in Supplementary Fig. S2) shows an enhanced overlap of the fiber mode with the grating fields of both the CGA optimized designs, which would explain their high coupling performance.
Alternative Combinations
As mentioned previously, the choice of SiN core thickness or top cladding is determined by its application. Keeping that in mind, we proceeded to implement the CGA on alternative SiN slabs of low and high thickness. Essentially two types of platforms are considered i.e., a partial etched air-clad grating and a fully etched SiO2-clad grating. The SiN waveguide slab thicknesses considered are for 300, 600 and 700 nm. In addition to these, we also looked at the converse of designs A and B i.e., 400 nm slab for partially etched gratings and 500 nm slab for fully etched gratings. The coupling performance of these designs are depicted in Supplementary Figs. S3 and S4 with a summary being provided in Table 2. A key observation is that, air-clad gratings with Si substrate of a given SiN slab thickness, have a substantially higher coupling on account of strong grating contrast. However, in the case of a 2 or 4 layer DBR stack substrate, the corresponding SiO2-clad, fully etched gratings, exhibit a comparatively higher coupling and bandwidth. For either platforms, a general trend to be noticed is the bandwidth reduction with increasing slab thickness, which can be attributed to the higher effective grating index of the fundamental mode33. The difference in peak CE between a 2 and 4 layer DBR is observed to be ~0.02–0.1 dB higher, for air-clad gratings and about ~0.07–0.1 dB higher, in the case of SiO2-clad gratings with negligible change in bandwidth. Maximum coupling among all combinations for a 2 layer DBR stack is observed for 500 nm thick SiN with SiO2-clad where a peak CE of −0.33 dB is calculated. On the other hand minimum peak coupling is calculated for an air-clad grating on 300 nm SiN slab, where peak CE is observed to be −0.65 dB.
Results and Discussion
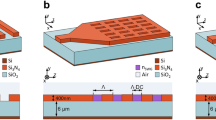
Figure 4 depicts the top view and side cross-sectional images of some of the fabricated test devices. The cross-sectional images reveal a slight under-etch for the front-end, low fill factor periods in both designs, which can be attributed to the lag effect. The results of characterization is plotted in Fig. 5. For design A, peak coupling is observed at −1.43 dB (1552 nm), −1.17 dB (1571 nm) and −1.61 dB (1580 nm) for periods of 0.960, 0.970 and 0.980 μm respectively. The corresponding 1 dB bandwidths are 45 nm, 40 nm and 43 nm. For design B, the peak coupling efficiencies are −1.83 dB (0.1561 nm), −1.24 dB (1572 nm) and −1.59 dB (1577 nm) at periods of 0.99, 1.0 and 1.01 μm with the 1 dB bandwidths being 46 nm, 39 nm and 33 nm respectively. For either designs, peak coupling is observed at 3° which also agrees with simulated data. The ripples in the measured spectrum are a consequence of reflections due to Fabry-Perot cavity effect, due to the short waveguide length. It may be mentioned that for the test devices, we chose a waveguide separation length of 700 μm. This was done to minimize contribution from propagation losses, while at the same time keeping a decent separation to avoid collision between the gonio-stage fibers at near vertical angles. The peak measured grating efficiency of the partially etched design A is observed to be slightly higher than those of design B. This is in contradiction to the simulated data which shows the fully etched gratings of design B, having a higher efficiency. Our analysis reveals that the under-etching of the front-end narrow trenches, which is more prominent in design B, to be the likely cause of this mismatch. The details of this analysis are provided in Supplementary Figs. S5 and S6. Table 3 outlines the current state of art for grating coupler demonstrations on different SiN platforms.
(a) Shows top view of some of the fabricated grating couplers. Inset shows an SEM image of one of the chirped focussing gratings. (b and c) Show side-view cross sectional SEM images of the etched grating couplers (see yellow trace) with the underneath DBR stack for (b) partial etched gratings of design A and (c) fully-etched gratings of design B prior to SiO2 cladding deposition.
Experimental characterization of test devices. (a) Shows measured spectrum for design A at different periods and (b) shows the same for design B. (c) Depicts the angle dependence at peak period for design A and (d) shows the same for design B. The thin lines are the raw data and the thick lines represent a polynomial fit.
Conclusion
In summary, we have demonstrated a novel scheme for grating couplers on SiN photonic chips. The scheme employs a chirp algorithm for gratings and a bottom Bragg reflector that can be implemented on a multitude of standalone SiN platforms. We have fabricated and characterized high efficiency chirped grating couplers on 2 distinct SiN platforms. Experimental peak efficiency for air-clad, partially etched grating on a 500 nm thick SiN is measured to be 1.17 dB/coupler at 1571 nm, with a 1 dB bandwidth of 40 nm. The corresponding efficiency for a fully etched grating on 400 nm thick SiN, with SiO2-cladding is measured to be 1.24 dB/coupler at 1572 nm, with a 1 dB bandwidth of 39 nm. The designs have minimum features that are compatible with scalable deep UV lithographic systems which have already been reported. Furthermore, we also demonstrate design robustness to significant process induced variations. Moreover, through simulations we also show that the chirping algorithm can deliver sub-dB coupler efficiency on a total of 10 different SiN chip combinations, comprising films between 300–700 nm thickness as well as surrounding claddings. These results pave way for implementing high performance gratings for a numerous applications concerning SiN platforms.
Methods
Simulation tools
All simulations were performed through a commercial FDTD solver from Lumerical Inc.
Sample preparation and Characterization
Device fabrication is described as following. A DBR stack (specifications described in section 2) is deposited on a bare Si wafer, after which a piece each of the same sample is used for designs A and B. For design A, a BOX layer of 1.92 μm is deposited followed by an SiN slab layer of 500 nm, both of which are deposited using plasma-enhanced chemical vapour deposition (PECVD). The process is repeated for design B with corresponding optimized BOX and slab values. For gratings, we implement a focussing design with the optimized periods and CGA fill factors obtained from Table 1. The length of the waveguide is chosen to be 700 μm. All patterns are written using electron beam lithography (Raith eline) with a negative resist (MaN 2403). The dimensions of rib waveguide for design A are 1.2 × 0.28 μm and of ridge waveguide for design B are 1.1 × 0.4 μm. The patterns are subsequently etched using inductively coupled reactive-ion etching (ICP-RIE, Oxford Systems) using fluorine etch chemistry. For design B, subsequent to the etching process, a top cladding layer of SiO2 of 2 μm thickness is deposited using PECVD. Further information on the fabrication process is available in29. The fabricated devices are characterized using a tunable laser source (Keysight 8146 B). SMF fibers connect the sample mounted gonio stage via polarization controllers to the laser source. The propagation loss measured through cutback method is found to be 0.5 dB/mm for design A and 0.4 dB/mm for design B. These figures are deducted from the final fiber to fiber transmission.
References
Doylend, J. K. & Knights, A. P. The evolution of silicon photonics as an enabling technology for optical interconnection. Laser Photonics Rev. 6, 504–525, https://doi.org/10.1002/lpor.201100023 (2012).
Fang, Z. & Zhao, C. Z. Recent Progress in Silicon Photonics: A Review. ISRN Opt. 2012, 1–27, https://doi.org/10.5402/2012/428690 (2012).
Thomson, D. et al. Roadmap on silicon photonics. J. Opt. (United Kingdom) 18, 1–20, https://doi.org/10.1088/2040-8978/18/7/073003 (2016).
Rahim, A. et al. Expanding the Silicon Photonics Portfolio with Silicon Nitride Photonic Integrated Circuits. J. Light. Technol. 35, 639–649, https://doi.org/10.1109/JLT.2016.2617624 (2017).
Blumenthal, D. J., Heideman, R., Geuzebroek, D., Leinse, A. & Roeloffzen, C. Silicon Nitride in Silicon Photonics. Proc. IEEE 106, 2209–2231, https://doi.org/10.1109/JPROC.2018.2861576 (2018).
Sacher, W. D. et al. Monolithically Integrated Multilayer Silicon Nitride-on-Silicon Waveguide Platforms for 3-D Photonic Circuits and Devices. Proc. IEEE 106, 2232–2245, https://doi.org/10.1109/JPROC.2018.2860994 (2018).
Baets, R. et al. Silicon Photonics: silicon nitride versus silicon-on-insulator. Opt. Fiber Commun. Conf. 2016 Th3J.1, https://doi.org/10.1364/OFC.2016.Th3J.1 (2016).
Yang, Y.-D., Li, Y., Huang, Y.-Z. & Poon, A. W. Silicon nitride three-mode division multiplexing and wavelength-division multiplexing using asymmetrical directional couplers and microring resonators. Opt. Express 22, 22172, https://doi.org/10.1364/oe.22.022172 (2014).
Tu, X. et al. Thermal independent Silicon-Nitride slot waveguide biosensor with high sensitivity. Opt. Express 20, 2640–2648, https://doi.org/10.1364/OE.20.002640 (2012).
Subramanian, A. Z. et al. Silicon and silicon nitride photonic circuits for spectroscopic sensing on-a-chip Invited. Photon. Res. 3, B47–B59, https://doi.org/10.1364/PRJ.3.000B47 (2015).
Shang, K., Pathak, S., Qin, C. & Yoo, S. J. Low-Loss Compact Silicon Nitride Arrayed Waveguide Gratings for Photonic Integrated Circuits. IEEE Photonics J. 9, https://doi.org/10.1109/JPHOT.2017.2751003 (2017).
Kim, S. et al. Dispersion engineering and frequency comb generation in thin silicon nitride concentric microresonators. Nat. Commun. 8, 372, https://doi.org/10.1038/s41467-017-00491-x (2017).
Lacava, C. et al. Si-rich Silicon Nitride for Nonlinear Signal Processing Applications. Sci. Rep. 7, 22, https://doi.org/10.1038/s41598-017-00062-6 (2017).
Levy, J. S. et al. CMOS-compatible multiple-wavelength oscillator for on-chip optical interconnects. Nat. Photonics 4, 37–40, https://doi.org/10.1038/nphoton.2009.259 (2010).
Ikeda, K., Saperstein, R. E., Alic, N. & Fainman, Y. Thermal and Kerr nonlinear properties of plasma-deposited silicon nitride/silicon dioxide waveguides. Opt. Express 16, 12987, https://doi.org/10.1364/OE.16.012987 (2008).
Vermeulen, D. et al. High-efficiency fiber-to-chip grating couplers realized using an advanced CMOS-compatible Silicon-On-Insulator platform. Opt. Express 18, 18278, https://doi.org/10.1364/OE.18.018278 (2010).
Marchetti, R. et al. High-efficiency grating-couplers: demonstration of a new design strategy. Sci. Rep. 7, 16670, https://doi.org/10.1038/s41598-017-16505-z (2017).
Watanabe, T., Ayata, M., Koch, U., Fedoryshyn, Y. & Leuthold, J. Perpendicular Grating Coupler Based on a Blazed Antiback-Reflection Structure. J. Light. Technol. 35, 4663–4669, https://doi.org/10.1109/JLT.2017.2755673 (2017).
Michaels, A. & Yablonovitch, E. Inverse design of near unity efficiency perfectly vertical grating couplers. Opt. Express 26, 4766–4779, https://doi.org/10.1364/OE.26.004766 (2018).
Zaoui, W. S. et al. Bridging the gap between optical fibers and silicon photonic integrated circuits. Opt. Express 22, 1277, https://doi.org/10.1364/OE.22.001277 (2014).
Ding, Y., Peucheret, C., Ou, H. & Yvind, K. Fully etched apodized grating coupler on the SOI platform with −0.58 dB coupling efficiency. Opt. Lett. 39, 5348–5350, https://doi.org/10.1364/OL.39.005348 (2014).
Nambiar, S. R. & Selvaraja, S. K. High-efficiency broad-bandwidth subwavelength grating-based fiber-chip coupler in silicon-on-insulator. Optical Engineering 57, 1–7–7, https://doi.org/10.1117/1.OE.57.1.017115 (2018).
Chen, Y. et al. Experimental demonstration of an apodized-imaging chip-fiber grating coupler for Si3N4 waveguides. Opt. Lett. 42, 3566–3569, https://doi.org/10.1364/OL.42.003566 (2017).
Ong, E. W., Fahrenkopf, N. M. & Coolbaugh, D. D. SiNx bilayer grating coupler for photonic systems. OSA Contin. 1, 13–25, https://doi.org/10.1364/OSAC.1.000013 (2018).
Sacher, W. D. et al. Wide bandwidth and high coupling efficiency Si3N4-on-SOI dual-level grating coupler. Opt. Express 22, 10938–10947, https://doi.org/10.1364/OE.22.010938 (2014).
Xu, P. et al. High-efficiency wideband SiNx-on-SOI grating coupler with low fabrication complexity. Opt. Lett. 42, 3391–3394, https://doi.org/10.1364/OL.42.003391 (2017).
Zhang, H. et al. Efficient silicon nitride grating coupler with distributed Bragg reflectors. Opt. Express 22, 21800–21805, https://doi.org/10.1364/OE.22.021800 (2014).
Hong, J., Spring, A. M., Qiu, F. & Yokoyama, S. A high efficiency silicon nitride waveguide grating coupler with a multilayer bottom reflector. Sci. Rep. 9, 12988, https://doi.org/10.1038/s41598-019-49324-5 (2019).
Nambiar, S., Kumar, A., Kallega, R., Ranganath, P. & Selvaraja, S. K. High-Efficiency Grating Coupler in 400 nm and 500 nm PECVD Silicon Nitride With Bottom Reflector. IEEE Photonics J. 11, 1–13, https://doi.org/10.1109/JPHOT.2019.2936430 (2019).
Schmid, B., Petrov, A. & Eich, M. Optimized grating coupler with fully etched slots. Opt. Express 17, 11066–11076, https://doi.org/10.1364/OE.17.011066 (2009).
Waldhäusl, R. et al. Efficient Coupling into Polymer Waveguides by Gratings. Appl. Opt. 36, 9383–9390, https://doi.org/10.1364/AO.36.009383 (1997).
Selvaraja, S. K. et al. 193 nm immersion lithography for high-performance silicon photonic circuits. In Proc. SPIE, vol. 9052, https://doi.org/10.1117/12.2049004 (2014).
Xiao, Z., Luan, F., Liow, T.-Y., Zhang, J. & Shum, P. Design for broadband high-efficiency grating couplers. Opt. Lett. 37, 530–532, https://doi.org/10.1364/OL.37.000530 (2012).
Zhao, X. et al. Compact Grating Coupler for 700-nm Silicon Nitride Strip Waveguides. J. Light. Technol. 34, 1322–1327, https://doi.org/10.1109/JLT.2015.2510025 (2016).
Doerr, C. R., Chen, L., Chen, Y. K. & Buhl, L. L. Wide Bandwidth Silicon Nitride Grating Coupler. IEEE Photonics Technol. Lett. 22, 1461–1463, https://doi.org/10.1109/LPT.2010.2062497 (2010).
Acknowledgements
We thank DST-SERB for funding this research. We also acknowledge funding support from MHRD through NIEIN project, from MeitY and DST through NNetRA.
Author information
Authors and Affiliations
Contributions
S.N. and S.K.S. proposed the concept. S.N. developed the CGA model and performed the numerical simulations. P.R. wrote the simulation code. S.N. conducted device fabrication and characterization. R.K. contributed substantially to device fabrication. S.K.S. supervised the project. S.N. and S.K.S. analysed the results and wrote the manuscript. All authors commented and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nambiar, S., Ranganath, P., Kallega, R. et al. High efficiency DBR assisted grating chirp generators for silicon nitride fiber-chip coupling. Sci Rep 9, 18821 (2019). https://doi.org/10.1038/s41598-019-55140-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-55140-8
This article is cited by
-
Scalable and efficient grating couplers on low-index photonic platforms enabled by cryogenic deep silicon etching
Scientific Reports (2024)
-
High-efficiency self-focusing metamaterial grating coupler in silicon nitride with amorphous silicon overlay
Scientific Reports (2024)
-
Library of single-etch silicon nitride grating couplers for low-loss and fabrication-robust fiber-chip interconnection
Scientific Reports (2023)
-
Highly efficient dual-level grating couplers for silicon nitride photonics
Scientific Reports (2022)
-
Optical meta-waveguides for integrated photonics and beyond
Light: Science & Applications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.