Abstract
The inverse sonification problem is investigated in this article in order to detect hardly capturing details in a medical image. The direct problem consists in converting the image data into sound signals by a transformation which involves three steps - data, acoustics parameters and sound representations. The inverse problem is reversing back the sound signals into image data. By using the known sonification operator, the inverse approach does not bring any gain in the sonified medical imaging. The replication of the image already known does not help the diagnosis and surgical operation. In order to bring gains in the medical imaging, a new sonification operator is advanced in this paper, by using the Burgers equation of sound propagation. The sonified medical imaging is useful in interpreting the medical imaging that, however powerful they may be, are never good enough to aid tumour surgery. The inverse approach is exercised on several medical images used to surgical operations.
Similar content being viewed by others
Introduction
A significant effort has been devoted in recent years to improve the quality of medical images used to surgery1. The Roentgen’s discovery of X-rays (1895) was followed by the computed tomography, magnetic resonance imaging, nuclear imaging, and ultrasound-positioned medical imaging used for diagnoses and surgery.
To our knowledge, we are the first to apply the sonification theory to uncover hidden details in medical images, such as vessels, organs or tumors that cannot be directly seen with the eye. The beginnings of the sonification theory are dated in 1952 when Pollack evaluates auditory displays as a visualization tool by using the information theory2,3. The International Community for Auditory Display Conference organized by Kramer in 1992 has generated great interest for this multi-disciplinary theory, from the science and technology to the arts4,5. Licht pursues the history of the sound art in 2007 by highlighting ancient art such as Sonic Youth and contemporary art that led to challenging applications, including the works of Christian Marclay, LaMonte Young, Janet Cardiff, Rodney Graham and Laurie Anderson among many others6.
The nano-guitar built at Cornell University from crystalline silicon no larger than a single human blood cell, invites bacteria inside a pacient to sing so that it can be easily detectable by a stethoscope7. The quantum whistle produces a nano-scale sound capable of detecting oscillations in the superfluid gases predicted by quantum theory8.
The sonification theory allows new perspectives in the diagnosis of diseases, such as the Alzheimers’s dementia9 and therapies in body movements, such as walking, twisting, lifting the arms or moving the legs10. The inverse problem of sonification, that is, the reversal of sound samples in new images is less studied so far, to the best of our knowledge. This is due to the fact that the known sonification operator does not bring any improvement of the medical image, because the theory behind it is the linear theory of sound motion. This article introduces a new sonification operator based on the nonlinear Burgers theory of the sound motion. The new operator has proved its ability to solve the inverse problem of sonification and to obtain essential gains in improving the medical image.
The paper is organized as follows: Section 2 is devoted to description of the direct problem of sonification. A description of the new sonification operator based on the Burgers equation of sound propagation is presented in Section 3. The methodology is described in Section 4, the applications in Section 5, while Section 6 contains the conclusions.
Direct Problem of Sonification
The direct problem of sonification, as known in the literature11,12,13,14, is based on a sonification operator S0 to transform the image point data D into sound signals Y0 as S0: D → Y0, S0: x(t) → y0(t0, x(t), p0), where x(t) is a 1D string of point data, t is the data time, t0 is the sonification time, and p0 ⊆ P0 is the set of sonification parameters.
The parameters P0 = {k0, Δ0, \({f}_{ref}^{0}\), α0, β0, ϕ0, ε0, g0, γ0, H0} include k0, the factor of time compressor on the interval T0 = T/k0, Δ0 ≥ 0, the factor of dilation, \({f}_{ref}^{0}\), the reference frequency, α0, β0 ≥ 0, the pitch scaling factors, ϕ0 ≥ 1, the power distortion factor, ε0 ≥ 0, the amplitude threshold, g0, the gain function, γ0, the decay parameter and H0, the timbral control function.
The variables of the data domain are t, ti, T. The signal x(t) can be divided into segments of different length that do not overlap, being expressed as a sequence x(n) of N = T × fs samples at the rate fs of T seconds duration. The time points ti split in time the segments xi(t). A possible division in M segments of xi(t) is
for t0 = 0 and tM = T. The duration of each segment is Ti = ti − ti−1.
Each segment xi(t) is sonified as a single event \({y}_{i}^{0}({t}^{0})\) longer or shorter than Ti
The general form for the sonified signal y0(t0) is
where xi(Δ0t0′) is the mean free segment, and xtrend(ti−1) is the trend signal at the starting point for pitch modulation. Parameter Δ0 gives the length of the event \({T}_{i}^{0}\). If Δ0 = k0 the adjacent events do not overlap but they can overlap for Δ0 ≤ k0.
To introduce control of timbre, the operator H0 acts as the sine function, so
where ai(t0) is the modulation amplitude, fref is the base frequency for the pitch range of sonification, and bi(t0) is a pitch modulator. The amplitude modulator is defined as
where φ0 is the amplitude modulator. A half-wave rectification is included for exceeding a threshold ε0 around the mean of the amplitude, a half-wave rectification is included
New Sonification Operator
We are looking for a new operator to replace (3) based on the Burgers equation of sound propagation. A digital image B is seen as a collection of N pixels. We suppose that B is subjected to external vibration force f(t) expressed as a sum of harmonic force Fp(t), and the generation sound force Fs(t). The force Fs(t) has the role to build the sonification operator. The response of B to f(t) is a new configuration b of all points P ∈ B at the time t. The vibration of B is described by Burgers equation15
where x = (x1, x2, x3) is the position vector, v = (v1, v2, v3) is the acoustic velocity vector, τ = t − x/c0 is the retarded time, t is time, c0 is the velocity of sound motion in the linear approximation, b = (b1, b2, b3) are the dissipation coefficients, ρ0 is density of medium, β = (β1, β2, β3) is nonlinearity coefficients. Details on the pulse propagation in nonlinear 1D media can be found in16,17,18,19.
Equation (7) admits the cnoidal solutions20. These solutions are localized waves that conserve their properties even after interaction among them, and then act somewhat like particles. This equation and other equations of the same kind (Schrödinger, Korteweg–de Vries equations etc.) have an infinite number of local conserved quantities, an infinite number of exact solutions expressed in terms of the Jacobi elliptic functions (cnoidal solutions) or the hyperbolic functions (solitons), and the simple formulae for nonlinear superposition of explicit solutions.
Given a known force Fp(t), we determine Fs(t) such that the acoustic power W radiated from B to be minimum. The W is written as
where v is the velocity verifying (7) and p the acoustic pressure vector, A is the area of the image, and the subscript T represents the Hermitian transpose21.
The solutions vi, i = 1, 2, 3 of (7) are expressed as
where \({{\rm{\eta }}}_{i}={k}_{1i}{x}_{1}+{k}_{2i}{x}_{2}+{k}_{3i}{x}_{3}-{{\rm{\omega }}}_{i}t+{\tilde{{\rm{\phi }}}}_{i}\), l is a finite number of degree of freedom of the cnoidal functions, 0 ≤ m ≤ 1 is the moduli of the Jacobean elliptic function, ω is frequency and \(\tilde{{\rm{\phi }}}\) the phase, k1, k2, k3 are components of the wave vector20. In the following, we stop to l = 2, and we will see that there are no sensible improvements in solutions for l > 2 The function Fs(t) is determined from
The unknown parameters \({P}_{j}=\{{m}_{j},{{\rm{\omega }}}_{j},{k}_{1j},{k}_{2j},{k}_{3j},{\tilde{{\rm{\phi }}}}_{j},{a}_{1},{b}_{1},{c}_{1},{a}_{2},{b}_{2},{c}_{2}\}\), j = 1, 2, 3, are find by a genetic algorithm which minimizes the objective function ϒ(Pj) written with respect to residuals of (7) and (10)
with
The genetic algorithm is running until it is reached a non-trivial minimizer, which will be a point at which (11) admits a global minimum.
The quality of results depends on the values of ϒ. The required precision is taken to be six places after the decimal point. The genetic parameters are assumed to be as follow: number of populations 200, ratio of reproduction 1.0, number of multi-point crossover 1, probability of mutation 0.5, and maximum number of generations 500.
Once determined the function Fs(t), the sonification operator S(D, t) is written as
where D = {d1, d2, …, dN}, di ∈ RN is the point data domain of the original image. The data matrix D is obtained from B by applying the converter C1 as C1(B) = D. The converter C1 is defined in the next Section. Data D is arranged as a matrix with arbitrarily number of elements.
In (13), \(\tilde{D}=\{{\tilde{d}}_{1},{\tilde{d}}_{2},\ldots ,{\tilde{d}}_{N}\},{\tilde{d}}_{i}\in {R}^{N}\) is the point data domain of the sonified image depending on time. If duration of the sonification procedure is T seconds, then the final sonified image is \(\tilde{D}(T)\)
This matrix D is shown in Fig. 1b. Each element of the matrix may contain color or nuances, interfaces or borders separating the colors and nuances, lines, curves and other objects (Fig. 1a).
Equation (7) is solved for sharp interface continuity conditions for both displacements and stresses. The reflections by the edges of the grids are removed by the Dirichlet and Neumann boundary conditions and a strongly attenuative buffer. The reflection coefficient is22
where j is the degree of approximation, and θ is the incidence angle. For more than one component of displacement, the Dirichlet and Neumann conditions alternate components at the boundaries. When more than one boundary is nonreflecting, more solutions are added to eliminate multiple reflections.
After sonification, the point data domain of the sonified image \(\tilde{D}=\{{\tilde{d}}_{1},{\tilde{d}}_{2},\ldots ,{\tilde{d}}_{N}\},{\tilde{d}}_{i}\in {R}^{N}\) may contain small blurred areas with cavities and white dots, due to the inaccuracies of the original images. The convertor C2 is applied to \(\tilde{D}\) in order to fill these bad zones with colors and objects by prolonging through continuity of the solutions (9) in the adjacent areas and points. The converter C2 is defined in the next Section.
Methodology
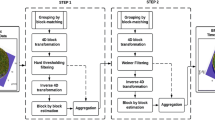
The problem to be investigated and solved in this paper can be formulated in three steps as:
- 1.
Given a digital image B, a converter C1 is applied to B to construct the data matrix D as C1(B) = D;
- 2.
The sonification operator S is apply to D to obtain the sonified image as \(S(D,t)=\tilde{D}(t)\). If duration of the sonification procedure is T seconds, then the sonified image is \(\tilde{D}=\tilde{D}(T)\).
- 3.
A converter C2 is applied to \(\tilde{D}\) to obtain the final sonified image Bfin as \({C}_{2}(\tilde{D})={B}_{fin}\).
Explanation of each path follows:
Path 1. The picture B is uniform sampled in a grid with equal size boxes B = {b1, b2, …, bN}, bi ∈ RN. The sampling must be sufficiently fine with special care devoted to eliminate (or at least to keep under control) the sources of numerical errors.
The converter C1 is applied to B to obtain the point data D = {d1, d2, …, dN}, di ∈ RN (Fig. 1b) as
where M(F) is an alphabet map containing four filters Fj, i = 1, 2, 3, 4, i.e. F1 the color and nuances filter, F2 the interfaces and borders separating the colors and nuances filter, F3 the line and curved lines filter, and F4 other objects that appears in the image filter (Fig. 1a). The filters are controlled by a code Jfil of minimizing the resolution loss and improving of the noise performance.
The filters have ability to notice fine image details be it color or line, with no connection to pixel count or pixel density. Scheme of the alphabet M(F) is presented in Fig. 2.
Each filter contains a number of sub-filters sFik, i = 1, 2, 3, 4, k = 1, 2, 3 …, K.
Filter F1 contains 39 sub-filters sF1k, k = 1, 2, 3 …, 39, for 39 color nuances. Each sub-filter captures a single color. Each color has a code αk, k = 1, 2, 3 …, 39.
Filter F2 contains \({A}_{39}^{2}\) sub-filters sF2j, j = 1, 2, …, \({A}_{39}^{2}\). Each interface has a code βk, k = 1, 2, …, \({A}_{39}^{2}\), obtained by interpolating of two codes αk, k = 1, 2, 3 …, 39.
The filter F3 contains a routine for linear, polynomial or nonlinear curve fitting along with validation of fit tests. The line or curve is introduced by points and the routine determines the most suitable equation for it.
The filter F4 identifies other objects from B. The shape Γ of the object is defined as the image of the unit n-sphere S of equation
through the affine transformation
where rij = rij(ξ, ψ, ζ) are the components of rotation which transforms the coordinate axes into the principal axes of the sphere.
An inverse problem is applied to find the set of parameters (shape parameters) that define Γ, i.e. arbitrary center coordinates xG, yG, zG, principal axes a, b, c, the principal directions defined by Euler angles ξ, ψ, ζ and the exponent n. The advantage of this model is the small number of parameters needed to represent a shape.
Each filter works across a different algorithm.
2. The sonification operator S(D, t) defined by (13) is applied to D to obtain the sonified image \(\tilde{D}\) as
where Fs(t) is the generation sound force determined from the condition of minimum acoustic power W. By setting \(\frac{\partial W}{\partial {F}_{s}}=0\), the function Fs(t) is determined as
with
In (16) \(\tilde{D}=\{{\tilde{d}}_{1},{\tilde{d}}_{2},\ldots ,{\tilde{d}}_{N}\},{\tilde{d}}_{i}\in {R}^{N}\) is the point data domain of the sonified image, and t is the sonification time.
3. After sonification, \(\tilde{D}\) may contain small blurred areas with cavities and white dots due to the inaccuracies of the original images. We term these areas as damaged zones.
The convertor C2 has the role to fill the damaged zones with color and geometric lines, through continuity of solutions (9) of adjacent areas and neighboring points.
The converter C2 is applied to \(\tilde{D}(T)=\tilde{D}\) to obtain the final sonified image Bfin = {b1fin, b2fin, …, bNfin}, bifin ∈ RN, as \({C}_{2}(\tilde{D})={B}_{fin}\)
where
measures the distance between the solution in a damaged point and the solutions in its neighboring points. In (23), δX is the solution in the damaged point, and δP is the prolonged solution through continuity of the solutions in neighboring points. \(J({\tilde{d}}_{j})\) determines the best solution in the damaged areas or points. Less spatial and color artifacts and better noise performance is assured by C2 compared with the existing schemes.
The filters are controlled by a code Jfil of minimizing the resolution loss and improving of the noise performance
where εc, εl, εI measure the relative errors for identification of colors, the lines and curves, and the moment of inertia of objects, defined as
In (24), αc, αl, αI are the associated weights.
Applications
A sample of a fictive rat liver which exhibit changes in profile by severe loss of architecture and disturbances zones (between 10 and 50 μm) at the microscopic scale23, is shown in Fig. 3a. The size of constituents is displayed in Fig. 3b.
The sonification operator (13) is exercised on fictive images of fibrotic rat liver samples inspired from an investigation of the effects of an extract of ginkgo biloba leaf against hepatic toxicity induced by methotrexate in rat23,24. The cross-sections of the rat liver are shown in Fig. 4.
For the first two applications, the simulations were performed for digital images of 1.600 × 1.200 pixels (length and width). Sonification time is 6 sec., n = 3 for the unit n-sphere S, and the weights in the code Jfil (αc, αl, αI) = (0.4, 0.4, 0.2).
The properties for the rat liver are: density ρ0 = 1.05 g/cm3, dissipation coefficients b = (b1, b2, b3) = (0.2, 0.2, 0.2) kg sec/m2, nonlinear coefficients β = (β1, β2, β3) = (0.3, 0.3, 0.3) sec.
Figure 5 visualizes the new images obtained after sonification. By comparing these images to the original ones, some differences are highlighted in yellow in the last six images. Although there appears a tendency for the replication of images already known, our results show relevant details absent in the original images.
For the next exercise, we consider the work of Salameh25 which studies the detection of nonalcoholic steatohepatitis in the fatty rat livers by magnetic resonance (MR). This study is useful in the early detection of fibrosis in the at livers26,27,28. Figure 6a shows the MR image of a liver rat with strong hepatocellular damages. Some details are purposefully hidden (red circles in Fig. 6b). We see that the inverse sonification operator recovered all initially hidden details (Fig. 6c).
Another application is related to the hepatic arterial chemotherapy29,30,31,32. The knowledge of hepatic and biliary vascular maps is absolutely necessary for planning the surgical operation. A catheter must be inserted inside the gastroduodenal artery (GDA) to distribute the chemotherapy. A possible location of the hepatic arterial infusion catheter was discussed in30 and shown in Fig. 7.
A possible location of the hepatic arterial infusion catheter30.
Figure 8a shows the CT image of the hepatic artery (CHA- common hepatic artery, LHA - left hepatic artery, RHA - right hepatic artery, SA - splenic artery, Seg IV HA - segment IV hepatic artery)30. Figure 8b shows the CT image of the left hepatic artery30.
Our intension is to obtain an image by sonification of the image shown in Fig. 8c.
For last applications, the simulations were performed for digital images of 1.600 × 1.200 pixels (length and width). Sonification time is 7 sec., n = 3 for the unit n-sphere S, and the weights in the code Jfil (αc, αl, αI) = (0.4, 0.4, 0.2).
The properties for the rat liver are: density ρ0 = 1.12 g/cm3, dissipation coefficients b = (b1, b2, b3) = (0.2, 0.2, 0.2) kg sec/m2, nonlinear coefficients β = (β1, β2, β3) = (0.3, 0.3, 0.3) sec.
Final sonified image is shown in Fig. 8d. We see that it is identically to the one shown in Fig. 7.
The last application considers the case of a tumor (pink color) located near the portal tree of the vascular territory (Fig. 9a)33,34. The vascular territory (1) and the vessel branches in the vicinity of tumor (2) are shown in Fig. 9b.
After sonification three images are obtained in Fig. 10 for the frontal, caudal and cranial views. New details on the tumor and surrounding areas are obtained and aditionally, the shape and size of the tumor is better visualized.
Conclusion
The sonification operator proposed in this paper is converting the digital data field into sounds by using the nonlinear Burgers sound equation which is solved by cnoidal method. By inverting the sound into image, the result highlights hidden details in the image seen by the sound and not seen by the eyes. To show the efficiency of the sonification procedure and to verify the correctness of the results, we intentionally hide some details in the images before the sonification. The sonification operator has a positive effect in improving the accuracy in the medical imaging by capturing and detecting hard-to-see details in original images.
The advantages of the sonification refer to: (1) there is no distinction between the data time and the sonification time; (2) reflects indirectly the relationship between the propagation of sound through tissues and the structure of these tissues; (3) discovers new hard-to-find details in original medical images; (4) demonstrates the usefulness of image-sound and sound-image conversions in exploiting the medical imaging in diagnosis and surgery.
References
Laal, M. Innovation Process in Medical Imaging. Procedia - Social and Behavioral Sciences 81, 60–64 (2013).
Pollack, I. The information of elementary auditory display. Journal of the Acoustical Society of America 24(6), 745–749 (1952).
Pollack, I. & Ficks, L. Information of elementary multidimensional auditory displays. Journal of the Acoustical Society of America 26, 155–158 (1954).
Kramer, G. An introduction to auditory display. In: Kramer, G. (eds) In auditory display, 1–79 (Addison-Wesley, Boston, MA 1994).
Kramer, G. et al. Sonification report: Status of the field and research agenda. Tech. Rep., International Community for Auditory Display (1999).
Shelley, S. et al. Interactive sonification of curve shape and curvature data. Lecture Notes in Computer Science 5763, Haptic and Audio Interaction Design, 4th International Conference, HAID2009, Dresden, Germany, Sept 10–11, 2009 (eds M. Ercan Altinsoy, Ute Jekosch, Stephen Brewster), 1–60 (2009).
Craighead, H. Silicon Guitar, http://www.npr.org/news/tech/970724.guitar.html (1997).
Davis, J. C. & Packard, R. Quantum oscillations between two weakly coupled reservoirs of superfluid He-3. Nature July 31 (1997).
Gionfrida, L. & Roginska, A. A novel sonification approach to support the diagnosis of Alzheimer’s dementia. Frontiers in Neurology 8 Article 647 (2017).
Ibrahim, A. A. & Embug, A. J. Sonification of 3D body movement using parameter mapping technique. International Conference on Information Technology and Multimedia (ICIMU) November 18–20, Putrajaya, Malaysia, 385–389 (2014).
Bonebright, T., Cook, P. & Flowers, J. H. Sonification Report: Status of the Field and Research Agenda, Faculty Publications, Department of Psychology Paper 444 (2010).
Holdrich, R. & Vogt, K. Augmented audification, ICAD 15: Proceedings of the 21st International Conference on Auditory Display, Vogt, K., Andreopoulou, A. & Goudarzi, V. (eds) Graz, Austria: Institute of Electronic Music and Acoustics (IEM), University of Music and Performing Arts Graz (KUG), 102–108 (2015).
Vickers, P. & Holdrich, R. Direct segmented sonification of characteristic features of the data domain. Department of Computer and Information Sciences, Northumbria University, Newcastle upon Tyne, UK (2017).
Rohrhuber, J. S 0- Introducing sonification variables. In Super-Collider Symposium, Berlin, 1–8 (2010).
Demin, I., Gurbatov, S., Pronchatov-Rubtsov, N., Rudenko, O. & Krainov, A. The numerical simulation of propagation of intensive acoustic noise. Acoustical Society of America, Proceedings of Meetings on Acoustics 19, 045075 (2013).
Scalerandi, M., Delsanto, P. P., Chiroiu, C. & Chiroiu, V. Numerical simulation of pulse propagation in nonlinear 1-D media. Journal of the Acoustical Society of America 106(5), 2424–2430 (1999).
Toupin, R. A. & Bernstein, B. Sound waves in deformed perfectly elastical materials. Acoustoelastic effect. Journal of the Acoustical Society of America 33, 216 (1961).
Norton, G. V. & Novarini, J. G. Including dispersion and attenuation directly in the time domain for wave propagatiom in isotropic media. Journal of the Acoustical Society of America 113, 3024–3031 (2003).
Norton, G. V. & Purrington, R. D. The Westervelt equation with viscous attenuation versus a causal propagation operator. A numerical comparison. Journal of Sound and Vibration 327, 163–172 (2009).
Munteanu, L. & Donescu, S. T. Introduction to Soliton Theory: Applications to Mechanics, Book Series Fundamental Theories of Physics, 143 (Kluwer Academic Publishers, Dordrecht, Boston, Springer Netherlands, 2004).
Lin, J. & Stuart Bolton, J. Sound power radiation from a vibrating structure in terms of structure-dependent radiation modes. Journal of Sound and Vibration 335, 245–260 (2015).
Ruffino, E. & Delsanto, P. P. Problems of accuracy and reliability in 2D LISA simulations. Computers and Mathematics with Applications 38, 89–97 (1999).
Tousson, E., Atteya, Z., EI-Atash, A. & Jeweely, O. I. Abrogation by ginkgo byloba leaf extract on hepatic and renal toxicity induced by methotrexate in rats. Journal of Cancer Research and Treatment 2(3), 44–51 (2014).
Ioan, R. et al. On the inverse sonification problem. Romanian Journal of Technical Science-Applied Mechanics 64(1), 11–19 (2019).
Salameh, N. & Larat, B. Early detection of steatohepatitis in fatty rat liver by using MR elastography. Radiology 253(1) (2009).
Munteanu, L., Chiroiu, V., Dragne, C., Rugină, C. & Bratu, P. On the sonification technique. Journal of Engineering and Innovation (JESI) 4(2), 155–167 (2019).
Chiroiu, V. et al. Using the Sonification for Hardly Detectable Details in Medical Images. International Journal of Scientific and Research Publications 9(7), 342–351 (2019).
Chiroiu, V., Munteanu, L., Dragne, C. & Stirbu, C. On the diferential dynamic logic model for hybrid systems. Acta Technica Napocensis - series: Applied Mathematics, Mechanics, and Engineering 61(4) (2018).
Chiroiu, V., Munteanu, L. & Rugină, C. On the control of a cooperatively robotic system by using a hybrid logic algorithm. Proceedings of the Romanian Academy, series A: Mathematics, Physics, technical Sciences, Information Science 19(4) (2018).
Onofrio, A. C. et al. Vascular and Biliary Variants in the Liver: Implications for Liver Surgery. Radio Graphics 28(2) (2008).
Sahani, D. et al. Preoperative hepatic vascular evaluation with CT and MR angiography: implications for surgery. Radio Graphics 24(5), 1367–1380 (2004).
Sahani, D., Saini, S. & Nichols, S. Using multidetector CT for preoperative vascular evaluation of liver neoplasms: technique and results. AJR Am. J. Roentgenol 179(1), 53–59 (2002).
Lang, H., Hindennach, M., Radtke, A. & Peitgen, H. O. Virtual liver surgery: Computer-assisted operation planning in 3D liver model. Chapter 5 In Recent Advances in liver surgery, Renzo Dionigi, Landes. Bioscience Madame Curie Bioscience Data base (2009).
Shamir, R., Tamir, I., Daboo, E., Joskowicz, L. & Shoshan, Y. A Method for Planning Safe Trajectories in Image-Guided Keyhole Neurosurgery. In: Jiang, T., Navab, N., Pluim. J. W. & Viergever, M. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2010. Lecture Notes in Computer Science. 6363, Springer Berlin Heidelberg (2010).
Acknowledgements
This work was supported by a grant of the Romanian Ministry of Research and Innovation, CCCDI – UEFISCDI, project number PN-III-P1-1.2-PCCDI-2017-0221/59PCCDI/2018 (IMPROVE), within PNCDI III. This research support includes salaries, equipment, supplies, and travel to Conferences expenses for all authors. The Romanian Ministry of Research and Innovation, CCCDI – UEFISCDI has nothing to do to the conceptualization, design, data collection, analysis, decision to publish, or preparation of this manuscript.
Author information
Authors and Affiliations
Contributions
Veturia Chiroiu, Ligia Munteanu, Rodica Ioan, Ciprian Dragne and Luciana Majercsik, authors of the paper entitled “Using the Sonification for Hardly Detectable Details in Medical Images”, declare that this article reports equal contribution of all authors in obtaining the results and the whole theory. In addition, Veturia Chiroiu and Ligia Munteanu wrote the main manuscript text, Rodica Ioan and Ciprian Dragne prepared the figures, and Luciana Majercsik helps us the reviewing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chiroiu, V., Munteanu, L., Ioan, R. et al. Using the Sonification for Hardly Detectable Details in Medical Images. Sci Rep 9, 17711 (2019). https://doi.org/10.1038/s41598-019-54080-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-54080-7
This article is cited by
-
On the flexible needle insertion into the human liver
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.