Abstract
Intense storms or earthquakes in mountains can supply large amounts of gravel to rivers. Gravel clasts then travel at different rates, with periods of storage and periods of displacement leading to their downstream dispersion over millennia. The rate of this dispersion controls the long-term downcutting rate in mountainous rivers as well as the grain-size signature of climate and tectonic variations in sedimentary basins. Yet, the millennial dispersion rates of gravel are poorly known. Here, we use 10Be concentrations measured in individual pebbles from a localized source along a 56 km-long canyon in the Central Andes to document the distribution of long-term gravel transit rates. We show that an inverse grain-size velocity relationship previously established from short-term tracer gravel in different rivers worldwide can be extrapolated to the long-term transit rates in the Aroma River, suggesting some universality of this relationship. Gravel are also dispersed by large differences in the mean transport rates independent of gravel size, highlighting that some gravel rest at the river surface over tens of thousands of years. These different transport rates imply a strong spreading of the gravel plumes, providing direct proof for the long-term river buffering of sediment signals between mountainous sources and sedimentary basins. The inferred distribution of residence times suggests the first evidence of anomalous diffusion in gravel transport over long timespans.
Similar content being viewed by others
Introduction
Gravel dispersion in rivers is inherently a stochastic process1: each gravel clast travels at its own velocity, and can be stored temporarily during different periods at depth or in lateral deposits. When gravel accumulates, the vertical erosion of bedrock river beds is reduced, whereas the impact of moving gravel can boost river incision2. Furthermore, when an initial pulse of gravel is generated in a mountain catchment through renewed tectonic activity or climate change, it spreads downstream and mixes with previously detached gravel3. Thus, different periods of large sediment supply in the mountainous source may not be recorded in distant sedimentary basins4. Moreover, if the gravel clasts are stored and recycled several times, this means that it takes a particularly long time for them to reach the basin, and then the age of the gravel deposit may be significantly younger than the climatic or tectonic change in the source, potentially biasing the dating of source variations from the stratigraphic record5,6. The lithological composition of gravel in basins is also used to infer the denudation history of mountain ranges, but this approach is significantly complicated by repeated and long periods of sediment storage and recycling7, which are difficult to quantify6,8. The downstream spreading of gravel plumes is partly taken into account by models where the downstream transport of sediment is described by a diffusion equation4,9,10, but the diffusive nature of long-term river sediment transport has never been established from the dispersion of traced particles. Furthermore, recent experimental and field data have shown that sediment transport may not follow a diffusion equation on monthly or yearly timescales11,12,13,14,15,16. Extrapolating these findings to longer timescales is uncertain because the distribution of storage periods in floodplains is unknown17. Actually, most of the uncertainty lies in the lack of data to trace the transport of sediment over millennial timescales. Uranium-series18,19, cosmogenic nuclides20,21,22 and tracer thermochronology23 have provided evidence for very long transport times of several hundreds of thousands of years for fine sediment, even in active orogens such as Taiwan19 or New Zealand23. Nevertheless, the distribution of gravel residence times in river system, which is key to characterising the gravel transport dynamics, remains unknown. Only one study has recently inferred a distribution of large minimum gravel residence times in a modern river in the Great Plains (USA) using 21Ne concentrations in individual pebbles8.
The potential for using cosmogenic nuclides to document long-term (1–100 ka) sediment transport has long been recognised24,25. Pioneer works used the downslope increase in the cosmogenic nuclide concentration in sediments to quantify their mean transport rates on hillslopes26,27,28,29, and on desert piedmonts20,21. It is theoretically possible to quantify the distribution of gravel transport rates30,31, but this requires a single source of some particular lithology within a catchment. Then, by sampling the gravel from that particular lithology at different places along the river, it is possible to obtain the distribution of the 10Be concentrations in individual gravel, from which residence times between the source and sampling point can be estimated30,31. We followed this strategy in the Aroma River in the Central Andes.
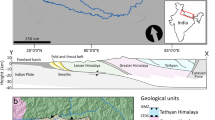
The Aroma catchment is located in Northern Chile on the western edge of the Altiplano plateau. The main river of the Aroma catchment incises into Neogene deposits forming a 56 km-long canyon ending in an alluvial fan32. Most of the rainfall comes from the catchment head during the summer months. Flash floods and debris flows occur during El Niño/La Niña events with return periods between several years to several centuries33,34. A Palaeozoic meta-sedimentary gneissic body is exhumed at the entrance of the canyon by a thrust and supplies gravel to the river via shallow landslides and detachment from the bedrock surface (Fig. 1). During this process and afterwards along the river, 10Be atoms are produced in gneissic pebbles when they reside at and near the surface (at a depth of 1 m, the 10Be production rate is ~20% of the one at the surface).
(a) Simplified geological map around the Aroma canyon (elevation data from SRTM 1 arc seconds digital elevation model88). The Palaeozoic gneiss body is exhumed in an erosion window below oligo-miocene sediment84. (b) Gravel clasts from this gneissic source were gathered downstream (cf. photos in Supplementary Fig. S1) and their 10Be concentrations were measured (analytical uncertainty smaller than the symbol size - Supplementary Table S1). The mean 10Be concentration at AromaG corresponds to an older fan surface sampled to verify the consistency of the 10Be concentration.
Our approach is to use the 10Be concentration in individual gneissic gravel clasts to infer their different residence times from their gneissic source on the hillslopes. Beginning at the location of the Palaeozoic gneiss source (AromaA), we sampled gneissic gravel clasts at seven locations (stations) along the Aroma River (AromaA to G). The last and more distal station AromaG corresponds to an alluvial surface above the more recent incised channel, and is therefore expected to be older with higher 10Be concentrations due to post-deposit exposure. Our previous theoretical study suggested that the best procedure to correct for the possible effect of pebble abrasion on the downstream 10Be concentration evolution was to sample the coarsest fraction of the river bed31. Based on this guideline, we sampled the coarsest sediment that we observed at each station, gathering gravel clasts from the river bed within a perimeter of approximately 10 m by 10 m. Although we did not measure the grain size distribution of the river bed, we observed a downstream decrease in maximum clast size, with the largest angular boulders reaching 1 m at AromaA, whereas the largest clasts corresponded to small rounded pebbles measuring several centimetres at the most distal station. Since it would be practically impossible to handle numerous whole boulders and cobbles, we collected a piece of rock (~0.5 kg and <5 cm thick) at the top surface of the cobbles (diameter D > 0.06 m - Supplementary Fig. S1). For smaller clasts (D < 0.06 cm), we took the whole clast.
In total, we sampled 478 clasts. We obtained the mean 10Be concentration of a population of clasts for seven river stations and the 10Be concentrations of 40 individual clasts (Fig. 1). To obtain the mean 10Be concentrations, we crushed the sampled rocks and mixed them by taking the same weight of material from each individual clast. The seven mean 10Be concentrations correspond to a mix of 18 angular cobble pieces at AromaA (D ∈ [0.11, 0.73] m), 20 rounded pebble pieces at AromaB (D ∈ [0.14, 0.2] m), 19 rounded pebble pieces at AromaC (D ∈ [0.11, 0.21] m), 23 rounded pebble pieces at AromaD (D ∈ [0.10, 0.24] m), 128 rounded small pebbles at AromaE (D ∈ [0.02, 0.06] m), 136 rounded small pebbles at AromaF (D ∈ [0.02, 0.06] m), and 134 rounded small pebbles at AromaG (D ∈ [0.02, 0.06] m). The 40 individual 10Be concentrations correspond to 15 clasts from AromaA, 20 from AromaC and five from AromaD (clast sizes are indicated in Supplementary Table S1 and in the same range as indicated above).
Results
Stochastic and size-dependent components of the gravel transit rates
Figure 1b shows that the mean 10Be concentrations below the first station AromaA are more than the double of the 10Be concentration at AromaA. This increase shows that more than half of the gravel 10Be concentration on average was acquired during their transit in the river. The mean 10Be concentration at AromaG (older surface) is consistently larger than the closest sample AromaF in the incised channel, demonstrating that the mean 10Be concentrations of the mixed gravel is at least qualitatively consistent with the geomorphology. Assuming that the mean 10Be concentration found in the active stream at AromaF represents a pre-deposition concentration for AromaG, the 10Be concentration at AromaG suggests a deposit that is 15 ± 2.6 ka in age, coinciding with a wetter period in the Atacama35,36. This consistency helps confirm the representativeness of these mean 10Be concentrations.
The mean 10Be concentration increases almost linearly over 43 km between AromaA and AromaD. Then, the mean 10Be concentration decreases and is nearly the same at the two following stations AromaE and AromaF. The difference between AromaD, AromaE and AromaF is ~30% whereas the 10Be concentration uncertainty is ~4%; therefore the difference is significant. The main difference between AromaD and these two stations is the size of the sampled gravel. The gravel clasts are large (10–24 cm) at AromaD, whereas they are much smaller (2–4 cm) at AromaE and AromaF. We conclude that the smaller gravel clasts were less exposed to cosmic rays on average than bigger gravel clasts. Small gravel clasts were either systematically buried at depth (smaller 10Be production rate), or they travelled faster on average. All along the river, we observed no grain size sorting up to several metres deep in some recent entrenchments. Thus we rule out the hypothesis that the smaller pebbles were systematically buried deeper than the larger ones. We conclude that the smaller mean 10Be concentration for the smaller pebbles at AromaE and AromaF means that they transited faster on average.
In addition to the downstream mean 10Be concentration increase, the variability in the 10Be concentrations in individual gravel also increases. Near the source at AromaA, the distribution of the 10Be concentrations at AromaA is positively skewed with a maximum that is approximately three times larger than the mean (Supplementary Fig. S2). This distribution reflects different residence times at different depths and elevations (different 10Be production rates) on the hillslopes. The variability in the 10Be concentrations increases sharply between AromaA and AromaC. The maximum 10Be concentration at AromaC is five times that of AromaA and the distribution at AromaC is also positively skewed with a maximum that is two times larger than the mean. At the next station, AromaD, the 10Be concentrations of the five individual pebbles analysed are either lower or slightly higher than the mean 10Be concentration of the 23 mixed pebbles, which implies that some of the 18 other pebbles in this mixture must have much higher 10Be concentrations. The smallest 10Be concentrations at AromaC and AromaD are similar to the smallest 10Be concentrations at AromaA, indicating that some pebbles were exposed at the river surface for a period of time less than several centuries, which is a minimum criterion for detectable 10Be acquisition. The large 10Be concentrations at AromaC correspond to pebbles with much longer exposure, and thus residence time. The large 10Be concentration of these slow pebbles explains the downstream increase in the station-averaged 10Be concentrations between AromaA and AromaD. The pebble size range sampled at AromaC is small (0.1–0.2 m), suggesting that a large variability in the 10Be concentrations, and therefore in the residence times, is independent of gravel size.
Distribution of gravel residence times in the river
The data show that the distribution of residence times is controlled by a component that is inversely related to gravel size, and a stochastic component that is independent of gravel size. To go further and to establish an empirical law describing the distribution of residence times downstream, we need a model to convert the 10Be concentrations into residence times. This model must account for an initial grain size distribution, for the variability in the 10Be concentrations acquired on the hillslopes, and for the downstream evolution of these concentrations at the surface of the gravel clasts during their transit. We designed such a model based on our previous work31 (Supplementary Fig. S3). We start on the hillslopes with a set of gravel of various sizes including the range of sizes sampled along the river. Gravel are enriched in 10Be during their exhumation, either by detachment from the bedrock, or within a landslide layer, with prescribed relative probabilities adjusted to fit the 10Be concentrations at AromaA (see Methods). Then in the river, each pebble is transported at the surface at a constant transit rate V and acquires 10Be. Note that V is usually called “virtual velocity” in short-term tracer gravel studies37 as it averages periods of movement and periods of rest. We impose a constant V for each pebble because their 10Be concentration is essentially a record of the time spent by gravel near the surface between two locations, regardless of the details of the gravel transit and rest periods.
To account for the stochastic component of V, we take this value from a prescribed distribution at the beginning of its transit in the river. To account for the size-dependent component of V, we multiply the value taken by a function f(D) that is inversely dependent on gravel size D. We use an empirical law based on a compilation of short-term gravel dispersion in rivers with different climatic contexts37, f(D) = (1 − log(D/Do))γ, where γ = 1.35 (±0.075) and Do is the median diameter in the original publication38. The weak dependence of f on D for D < Do is thought to result from the higher probability for small pebbles to be trapped by larger stones on the river bed38. For larger gravel, f decreases faster than linearly with D. Although we did not measure the grain size in the field, we fix Do = 0.14 m, which is the median gravel size that is also used in the hillslopes model. This size is bracketed by small gravel and larger cobbles observed in the river.
In the model, we successively run and record the displacement of 1500 gravel clasts of various sizes up to the river outlet and we trace the 10Be concentration evolution at the surface and within clasts. Once all clasts have reached the outlet, we select clasts that resided between 1 km downstream and upstream a studied river station. Their 10Be concentration distribution is compared to the distribution of the measured 10Be concentrations at this river station. The compared 10Be concentration corresponds either to a point at the surface of the cobbles (D > 0.06 m) or to the bulk 10Be concentration, just like the data. With regards to the cobbles, the 10Be concentration at their top is larger than at their bottom on the hillslopes. These two points are then traced during river transport and their 10Be concentration evolves by assuming that the clast rolls and settles in a random position at each step31. The 10Be concentration is randomly chosen between these two values, similarly to in the field where we took a piece of the large cobbles without knowing their initial positions.
We successively test three distributions of river virtual velocity V with different types of skewness, i.e. Gaussian, exponential and truncated Pareto distribution. We evaluate their consistency with the data by minimizing the misfit between the measured and predicted mean 10Be concentrations, as well as the misfit between the measured and predicted distributions of the 10Be concentrations at AromaC (see Methods).
We find that the model fits the data if the imposed distribution of the V values is a truncated Pareto distribution (Fig. 2 and Supplementary Fig. S4), with a power law tail on the form \({\rm{pdf}}(V)=\frac{\alpha +1}{{V}_{Max}^{\alpha +1}-{V}_{Min}^{\alpha +1}}{V}^{\alpha }\), with α ∈ [−1.94, −1.04], and VMin ∈ [0.4, 0.93] m a−1 for Do = 0.14 m gravel (VMax is fixed to 1 km a−1 and larger values do not change the results). In fact, a Gaussian distribution of V cannot reproduce the skewness of the 10Be concentration distribution at AromaC and the mean 10Be concentrations at the same time (Supplementary Fig. S5a). Exponential distributions of V result in 10Be concentration distributions that meet the requirements of the statistical tests (see Methods), but which systematically underestimate the frequency of small 10Be concentrations at AromaC (Supplementary Fig. S5b–d). Pareto distributions of V best reproduce the data (Fig. 2). The acceptable models fit the skewness of the 10Be concentrations well at AromaC and the other mean 10Be concentrations. This simple model fits the decreases in the 10Be concentration well for the smaller gravel at AromaE and AromaF. This decrease is due to the modelled size-dependent V relationship. Despite the large imposed variations in V for a given D, smaller pebbles go faster on average and thus their mean 10Be concentration is smaller than the coarser pebbles sampled at AromaD. Given the strong assumption that the short-term empirical law could be extrapolated over millennia, the consistency between this model and the data is remarkable. Furthermore, we tested different values of exponent γ of the velocity-size relationship and we found that the best fit is obtained with the same exponent 1.35 as determined from short-term tracers (Supplementary Fig. S6).
Results of model fit considering constant transport rates drawn from a truncated Pareto distribution \(({\rm{pdf}}(V)=\frac{\alpha +1}{{1000}^{\alpha }-{V}_{Min}^{\alpha }}{V}^{\alpha })\) and multiplied by (1 − log(D/0.14))1.35 as suggested by short-term gravel tracer studies37. (a) Distribution of AromaC 10Be concentrations and acceptable models for different values of VoMin and α. (b) Station-averaged 10Be concentrations and acceptable models. The acceptable models are those that satisfy the Komosgorov and Smirnov (KS) test with 95% confidence (p-value > 5%) for AromaC and also correspond to 99% confidence based on χ2 minimisation (see Methods). The acceptable models correspond to VMin ∈ [0.4, 0.93] m a−1 and α ∈ [−1.94, −1.04]. The best fit model (lowest χ2 and AromaC p-value > 5%) corresponds to VMin = 0.55 m a−1 and α = −1.2 (Supplementary Fig. S4).
The addition of the possibility that pebbles are temporarily buried in river sediment with an equal depth probability slightly improves the fit for the AromaC 10Be concentrations but does not change the range of acceptable exponents in the Pareto distributions (Supplementary Fig. S7). When a gravel resides at depth, the 10Be production rate is lower and thus its 10Be concentration evolves more slowly. The longer gravel residence at depth is compensated by a faster velocity when it moves to fit the observed 10Be concentrations, leading to similar ranges of inferred V distributions. Testing a smaller Do value (Do = 0.08 m) does not change our conclusions (Supplementary Fig. S8).
Last, we tested the effect of gravel size reduction via abrasion by progressively stripping off the surface of the gravel so that their size decreases exponentially with the travel distance39,40 (Supplementary Fig. S9). In the model, the attrition of a pebble accelerates its transport and slightly decreases its surface 10Be concentration, but these modifications are negligible compared to the variability in V required to fit the 10Be concentrations. As a result, gravel abrasion does not modify our outcomes. The splitting of a cobble into smaller pieces (D < 10 cm) is not taken into account by the model. The addition of these pieces to the small gravel at AromaE and AromaF would increase their mean 10Be concentrations. This would decrease the inferred difference in V values between small and large gravel. Thus, the size-dependent V evidenced from our data is robust.
Once the best-fit distribution of the virtual velocities has been established, we can use it to predict the downstream spreading of an initial mixture of 1500 gravel clasts with the same size range as at AromaA. Figure 3 shows snapshots of the gravel plume at different times. A small fraction of the gravel clasts reaches the river outlet in less than several centuries, but it then takes several tens of thousands of years to evacuate all of the gravel clasts. The resulting distribution of gravel residence times between the gneissic source and the river outlet has a power law tail (∝τ−1), indicating that a significant fraction of the gravel (6.5%) reaches the river outlet after a very long residence time (>100 ka).
Predictions of the best-fit model shown in Fig. 2 (pdf(V) = 0.23V−1.2). (a) Comparison of the predicted 10Be concentration distributions with data at the different river stations. (b) Downstream spreading of an initial population of 1500 gravel clasts in the range D ∈ [0.02, 0.72] m. Part of the gravel (including large pieces) reaches the river outlet after a couple of decades, whereas other gravel clasts are still in the river after 50 ka. The inset graph shows the resulting distribution of residence times τ (∝τ−1) in this 56 km-long river. For one specific gravel size, the predicted distribution of residence time τ is pdf(τ) = pdf(V)dV/dτ ∝ τ−α−2 ∝ τ−0.8 with α = −1.2.
Discussion
By documenting, for the first time, the distribution of the 10Be concentrations from a source to the outlet of a river, our data show that it is possible to acquire a large variability in terms of the gravel 10Be concentrations during their transit within a 56 km-long river. These data complement recent high 21Ne concentrations found in gravel from long rivers in the Great Plains (USA) which is interpreted as evidence of long residence times8. In the Aroma River, the 10Be concentrations correspond to highly variable transit rates (V > 0.4 m a−1 for 0.14 m gravel) that are larger than the mean transit rates obtained for sand in the Mojave Desert piedmont (~0.16 m a−1)20,41, probably because the transport is laterally constrained in the Aroma River case. In order to explain part of the differences in the 10Be concentration observed in some cases between sand and pebbles worldwide, it has been suggested that gravel may not accumulate detectable 10Be concentrations during their transport in channelized rivers30,42,43,44,45,46,47. The observed downstream increase in the 10Be concentration in the Aroma River demonstrates this possibility for arid environments. Such 10Be concentrations would correspond to a small inheritance that is unlikely to bias the ages of the Mio-Plio-Pleistocene alluvial surfaces in this region32,48,49. For younger deposits, however, a positively skewed distribution of pre-deposition 10Be concentrations can be expected to strongly contribute to the final distribution of 10Be concentrations used to calculate the exposure ages. These different 10Be concentrations can explain different ages for the same deposit. For example, high and variable pre-deposition 10Be concentrations were found in gravel and boulders of post-20 ka alluvial fans at the front of the Andes in Argentina50. Although the hillslopes and river contributions to this variability could not be determined in that case, our results show that the transport itself in the river can explain the high 10Be concentrations (outliers) in gravel deposited on active alluvial fans.
The variability in gravel transit rates is probably linked to different temporary storage periods and transport lengths during erosive floods. If the storage was deep (>>1 m), the increase in the 10Be concentration would be undetectable. The observed downstream 10Be concentration increase shows that the storage of highly concentrated gravel occurred mainly in the subsurface, and thus probably in bars and lateral deposits. These gravel clasts are then either reentrained or recycled by the active streams. Recycling has been identified as a major issue for interpreting the grain size and mineralogy of basins in terms of tectonics and climate, but it is difficult to prove and quantify7. Sediment recycling in an alluvial fan was recently shown to control the downstream gravel grain size variations in alluvial fans found in an arid Andean piedmont in Argentina51. Our data confirm that sediment storage and recycling occur even in this relatively short and confined river. Nevertheless, the proportion of recycled gravel in the gravel flux is difficult to estimate. In a first attempt, we can define the proportion of recycled gravel as the proportion of gravel with residence times longer than the residence time predicted in the simple case of steady gravel flux8. By multiplying the Aroma catchment area by a denudation rate of 10 m/Ma, which is characteristic for this area52,53, we estimate a sediment flux of 104 m3 a−1. The volume of the transported sediment in the river is estimated by multiplying the river length of 56 km by the mean valley width of ~100 m and by a conservative sediment mixing depth of ~10 m. Dividing the volume of transported sediment by this flux, we obtain a conservative maximum estimate of the mean gravel residence time in the river of ~5600 a. In the best-fit scenario illustrated by Fig. 3, 58% of the gravel have residence times longer than 5600 a. This is a crude estimate because gravel size should be taken into account, yet it allows us to conclude that long storage times and the recycling of sediment are processes that control the spreading of a gravel plume over long timescales in the Aroma River13.
Despite the stochasticity of gravel transit rates, our results demonstrate that small pebbles travel faster, on average, than larger ones over millennial timespans in this river. Our data fits the size-velocity relationship f(D) that was established previously from step lengths of gravel during individual floods37. This relationship arises from the size-dependent entrainment probability and transport distances37. It is likely that in our model, f(D) also reflects this behaviour of the gravel during floods54, which means that the size-dependent entrainment probability and transport distances still hold over the full range of floods over millennia. Our results thus suggest that the form of f(D) is universal.
This size-velocity relationship predicts that big gravel would have a larger probability to be buried in a subsiding basin, and would therefore imply the downstream fining of gravel. The downstream fining of gravel is observed in most basins and has been modelled experimentally9,55. From these observations, a simplified self-similar solution for the long-term substrate grain-size distribution has been proposed56 and successfully used to reconstruct subsidence rates and input flux histories in some examples57,58. A recent study has shown that this model is improved by including the lateral inputs of recycled sediments51. Our results confirm that lateral storage and recycling contributes to the downstream grain size evolution. Combined with an erosion-sedimentation mass balance equation59, the distribution of the size-dependent transit rates established in our study could be used to predict the river bed elevation and the fluxes of different gravel sizes according to grain size distributions supplied by lateral hillslopes. Such a modelling approach may complement models based on self-similarity hypothesis.
Finally, recent studies have debated on the diffusive nature of sediment transport. The diffusion equation is used to predict the long-term fluvial evolution in response to tectonic or climatic perturbations9. Small-scale river experiments60 have suggested that diffusion explains the buffering of sediment inputs. Numerical models have used diffusion theory to predict the frequency of sediment pulses that could be recorded in basins4,9,10. Yet, this theory has not been confirmed over the long term61. For the first time, our data provide some support for diffusion by evidencing the downstream spreading of a gravel plume (Fig. 3).
Yet, the parallel with diffusion is not perfect. The diffusion theory applied to an initial punctual population of gravel would predict that the distribution of residence times (“first-time passage” in diffusion theory62) is a Levy distribution. This distribution is very positively skewed and has a power law tail with a well-defined exponent −1.5. In our case, the inferred distribution of residence times in the best fit model has a power law tail with a larger exponent ~−1, i.e. a heavier tail. This value means that there is a higher probability of obtaining very large residence times. As a result, a larger proportion of slow gravel can be stored upstream for a longer time than predicted by diffusion. Consequently, our data suggest an anomalous diffusion.
This result echoes recent findings based on short-term tracer gravel in rivers and small-scale experiments that identified anomalous diffusion11,13,14,16,17,63,64,65,66. There is some consensus that anomalous diffusion arises from heavy-tailed distributions of sediment storage periods16. Such a distribution may be consistent with our inferred heavy-tailed distribution of residence times. Indeed, our data are explained by a simple model with two components, a size-dependent term and a power law distribution of mean transit rates. The first size-dependent term comes from empirical observations worldwide of gravel transport during floods. We suggest that this term has the same meaning over long timescales in Aroma, i.e. that it describes a size-selective movement of pebbles during floods in the river. Conversely, we suggest that the second component, the power law V distribution, arises from variable periods of gravel storage. In the case of Aroma River, this distribution is probably controlled by the recycling of sediment stored in the alluvial cover of the floodplain, possibly in bars and lateral deposits, which occurs over much longer periods of time than those covered by short-term tracer gravel surveys.
The origin of the anomalous diffusion evidenced in laboratory experiments on aggrading braided rivers is still unclear12. In the Aroma River, the lateral long storage of particles and their posterior recycling provide an explanation that may also hold true in laboratory experiments.
Anomalous diffusion could change our view of the landscape dynamics. When a large amount of coarse material is occasionally generated in a catchment by a landslide, this pulse of sediment will reach towns located downstream at different times and spread during different periods depending on whether diffusion or anomalous diffusion dominates. Because increased gravel flux can cause river bed aggradation and flooding67, the identification of anomalous diffusion may have implications for flooding hazard modelling at centennial timescales or even longer. Anomalous diffusion can also influence the concavity of rivers and thus the dynamics of the whole landscape. Although most models have considered that river concavity is linked to the physics of bedrock detachment and to the distribution of floods2, anomalous diffusion of the gravel cover is predicted to control the concavity and alluvial thickness distribution along mixed bedrock-alluvial rivers68. In sedimentary basins, anomalous diffusion may generate power law distributions of non-deposition or non-erosion periods. In that case, it is predicted that the reconstruction of the sedimentation and erosion rate histories over geological timescales are strongly biased69,70,71. A more in-depth long-term evaluation of anomalous diffusion as well as further investigations into its consequences on understanding the dynamics of mountain relief are needed. Meanwhile, our study provides new guidelines to document the gravel dynamics in other contexts, and new indicators for modelling the long-term sediment transport dynamics from the point of view of individual gravel clasts.
Methods
10Be concentrations
We collected samples throughout the month of May in 2010 (Supplementary Fig. S1). Then, the samples were crushed with a jaw crusher and sieved to keep the granulometric fraction between 0.5 and 1 mm. This work was carried out at GET (Géosciences Environnement Toulouse). Afterward, the chemical treatment of the samples was performed at the LN2C (Laboratoire National des Nucléides Cosmogéniques), CEREGE, Aix-en-Provence. First, magnetic minerals were separated from the bulk by a magnetic separator (Frantz LB-1). Then, the non-magnetic fractions underwent a series of acid attacks with a mixture of concentrated hydrochloric and hexafluorosilisic acids to remove all non-quartz minerals. When the quartz was extracted, meteoric 10Be was removed by three partial dissolutions with concentrated hydrofluoric acid. The decontaminated quartz was totally dissolved with concentrated hydrofluoric acid after adding of 100 μL of an home-made 9Be carrier solution72 ([9Be] = 3025 ± 9 μg/g). The resulting solutions were evaporated until dryness and the samples were recovered with hydrochloric acid. Then, the samples were precipitated with concentrated ammonia before a successive separation through an anion exchange column (Dowex 1X8) to remove the iron and a cation exchange column (Dowex 50WX8) to discard the Boron and recover the Be73. Finally, the eluted Be was precipitated to Be(OH)2 with concentrated ammonia and oxidized to BeO. After target preparation by mixing Niobium powder with the BeO oxide, the 10Be/9Be ratios were measured by Accelerator Mass Spectrometry (AMS) at the French National AMS Facility ASTER of CEREGE in Aix-en-Provence74. The measured 10Be/9Be ratios in 2012 and 2013 were directly calibrated against the National Institute of Standards and Technology Standard Reference Material 4325 NIST with an assigned value75 of (2.79 ± 0.03).10−11. The measured 10Be/9Be ratios in 2015 were calibrated against a house standard STD-11 with an assigned value76 of (1.191 ± 0.013).10−11. The analytical 1 σ uncertainties include uncertainties in the AMS counting statistics, the uncertainty in the standard 10Be/9Be, an external AMS error of 0.5%74, and a chemical blank correction. A 10Be half-life of (1.387 ± 0.01).106 years was used77,78.
Hillslope gravel model
Because the 10Be production rate depends on the elevation, which varies downstream, we need a model to convert the 10Be concentrations into transport velocities. The model31 calculates the 10Be concentration N (at g−1) at the surface of a gravel during its transport along an elevation profile (Supplementary Fig. S3). N is a solution of
where \(P={\sum }_{i=1}^{3}\frac{{P}_{i}}{\frac{\rho \varepsilon }{{\mu }_{i}}+\lambda }{e}^{\frac{-\rho z}{{\mu }_{i}}}\) is the 10Be production rate (at g−1 a−1), i stands for neutrons, fast and slow muons, Pi are the surface 10Be production rates associated with each particle79 scaled for latitude and elevation80 using a sea-level/high-latitude production rate81 of 4.0 at g−1 a−1, μi = 150, 1500 and 5400 g cm−3 are the corresponding attenuation coefficients79, ρ = 2.5 g cm−3 is the rock density, ε is the surface erosion rate, λ = 4.99 10−7 a−1 is the radioactive decay77, and z is the depth.
The elevation profile is divided into a hillslope part (gneiss elevations between 2919 and 2069 m) and the elevation profile of the main river of the aroma catchment (2069 to 1072 m). On the hillslope part, a gravel is randomly detached either from the bedrock surface or in a landslide to account for both phenomena observed on the Aroma hillslopes. If detached from the bedrock, the 10Be concentration of the gravel corresponds to the steady-state long-term balance between the 10Be lost by erosion and radioactive decay and production31 at a randomly selected elevation between 2069 and 2919 m. If the gravel is in a landslide, the landslide thickness H, the pebble elevation and its depth in this landslide are drawn according to a uniform probability distribution between 0 and H. For a landslide-derived gravel, the probability p to belong to a landslide with a thickness between H and H + dH is the relative volume of sediment produced by all landslides of that size over the long-term, or
where pdf(H) is the probability density function of landslides with a thickness H, Hmin and Hmax are the minimum and maximum landslide thicknesses and A is the landslide area. pdf(H) is determined by applying the change-of-variable technique to the frequency-area pdf of the landslides82
where A is the landslide area and β is a scaling exponent, and using a thickness-area relationship82:
This leads to
We estimate Hmax = 10 m from the observations. β and Hmin are unknown and are estimated by fitting the AromaA gravel 10Be concentrations (see below). The few data available for the gravel size distribution on hillslopes worldwide83 suggest a log-normal distribution39 in some cases. We use a log-normal distribution of log-mean 0 and log-σ 1.5 and only retain D values between 0.02 and 0.72 m corresponding to the range of the sampled gravel. The choice of σ = 1.5 ensures 95% of gravel within that range. The mean D is 0.17 m and the median is 0.14 m. Last, we observed that our conclusions are not sensitive to the initial grain size distribution (Supplementary Fig. S10). In a landslide, the gravel 10Be concentration is the sum of a steady-state 10Be concentration representing the long-term balance between gain and loss at the gravel depth and a 10Be concentration corresponding to the gravel residence time in the landslide layer31. The residence time is H/ε where ε is the long-term mean erosion rate due to landslides.
For the hillslope part of the model, we find that 30% of the clasts detached from the bedrock at a time-average rate of 0.17 mm a−1 and 70% of the clasts exported by landslides at a time-averaged erosion rate of 1 mm a−1 fit the two peaks in the 10Be concentration distribution for AromaA (Supplementary Fig. S11). These erosion rates are high in the Chilean context but consistent with the active shallow seismicity of this area84 and other 10Be pebble-derived erosion rates in northern Chile53,85,86. The landslide parameters β and Hmin are then estimated by fitting the AromaA distribution of the 10Be concentrations with the modelled 10Be concentration distributions. We generate 2500 models (1500 gravel per model) by varying β between 1.1 and 2.9 (range of the estimated values worldwide87) and Hmin between 0.1 and 1.5 m. We accept models for which the p-value of the Komolgorov-Smirnov (KS) test is larger than 5% (therefore we only accept a 5% chance of erroneously rejecting models that belong to the same 10Be concentration distribution as the data). The corresponding minimum and maximum values of β and Hmin determine the 95% confidence intervals for these parameters. At this confidence level, it turns out that we cannot reject any of the tested β and Hmin values according to the KS test (all p-values are >5% and are similar - Supplementary Fig. S11). Thus, we retain the values Hmin = 0.7 m and β = 2.3, an intermediate exponent also found in southern Peru87. Other values do not affect our results because they produce a similar distribution of the 10Be concentrations at AromaA (Supplementary Fig. S11a).
River parameters fitting
The fitting procedure for the river data assumes a time-constant distribution of the 10Be concentrations on the hillslopes. This assumption is justified by the undistinguishable distributions of the gravel 10Be concentrations measured in the Veladera River (southern Peru) and in its adjacent ~16 ka old terrace87. Assuming a Pareto distribution of V of the form given in the main text, VMin and α are determined by the following procedure. Using the best-fit β and Hmin parameters, we generate models by varying α (∈[−2.5, −0.5]) and VMin (∈[0.3, 1.5] m a−1) and calculate the p-value of the KS test. For each model, we also calculate
where yi are the modelled station-averaged 10Be concentrations, and xi and σi are the corresponding measured station-averaged 10Be concentrations and uncertainties, respectively. Both tests are carried out by selecting the simulated gravel at each river station belonging to the same size interval as the gravel collected in the field. The acceptable models finally satisfy both χ2 < χmin2 + 13.3 (13.3 is a tabulated Δχ2 cut-off value corresponding to a 99% confidence level for four degrees of freedom) and the KS test on AromaC (p-value > 0.05). The corresponding minimum and maximum values of VMin and α define the 99% confidence intervals. The best-fit model is the model with the highest p-value for the KS test applied to AromaC among the models for which χ2 < χmin2 + 13.3 (Supplementary Fig. S4). The same procedure is applied to test other distribution of V (Supplementary Fig. S5).
Data availability
An archive called COSMOBOULDER.zip contains all the codes used in this study and README file explaining how to use them.
References
Einstein, H.A. Bed load transport as a probability problem. Ph.D. thesis, ETH Zurich (1937).
Lague, D. The stream power river incision model: evidence, theory and beyond. Earth Surf. Proc. Land. 39, 38–61, https://doi.org/10.1002/esp.3462 (2014).
Allen, P. A. et al. The Qs problem: Sediment volumetric balance of proximal foreland basin systems. Sedimentol. 60, 102–130, https://doi.org/10.1111/sed.12015 (2013).
Castelltort, S. & van den Driessche, J. How plausible are high-frequency sediment supply-driven cycles in the stratigraphic record? Sedimentary Geol. 157, https://doi.org/10.1016/S0037-0738(03)00066-6 (2003).
Malatesta, L. C., Prancevic, J. P. & Avouac, J.-P. Autogenic entrenchment patterns and terraces due to coupling with lateral erosion in incising alluvial channels. J. Geophys. Res. Earth Surf. 122, 335–355, https://doi.org/10.1002/2015JF003797 (2017).
Harries, R. M. et al. Evidence for Self-Similar Bedload Transport on Andean Alluvial Fans, Iglesia Basin, South Central Argentina. J. Geophys. Res. Earth Surf. 123, 2292–2315, https://doi.org/10.1029/2017JF004501 (2018).
Weltje, G. J. Quantitative models of sediment generation and provenance: State of the art and future developments. Sedimentary Geology 280, 4–20, https://doi.org/10.1016/j.sedgeo.2012.03.010 (2012).
Sinclair, H. D., Stuart, F. M., Mudd, S. M., McCann, L. & Tao, Z. Detrital cosmogenic Ne-21 records decoupling of source-to-sink signals by sediment storage and recycling in Miocene to present rivers of the Great Plains, Nebraska, USA. Geol. 47, 3–6, https://doi.org/10.1130/G45391.1 (2019).
Paola, C., Heller, P. L. & Angevine, C. L. The large-scale dynamics of grain-size variation in alluvial basins, 1: Theory. Basin Res. 4, 73–90 (1992).
Armitage, J. J., Duller, R. A., Whittaker, A. C. & Allen, P. A. Transformation of tectonic and climatic signals from source to sedimentary archive. Nat. GeoSciences 4, 231–235, https://doi.org/10.1038/NGEO1087 (2011).
Nikora, V., Habersack, H., Huber, T. & McEwan, I. On bed particle diffusion in gravel bed flows under weak bed load transport. Wat. Resour. Res. 38, https://doi.org/10.1029/2001WR000513 (2002).
Voller, V. R. & Paola, C. Can anomalous diffusion describe depositional fluvial profiles? J. Geophys. Res. Earth Surf. 115, https://doi.org/10.1029/2009JF001278 (2010).
Bradley, D. N. & Tucker, G. E. The storage time, age, and erosion hazard of laterally accreted sediment on the floodplain of a simulated meandering river. J. Geophys. Res. Earth Surf. 118, 1308–1319, https://doi.org/10.1002/jgrf.20083 (2013).
Voepel, H., Schumer, R. & Hassan, M. A. Sediment residence time distributions: Theory and application from bed elevation measurements. J. Geophys. Res. Earth Surf. 118, 2557–2567, https://doi.org/10.1002/jgrf.20151 (2013).
Martin, R. L., Purohit, P. K. & Jerolmack, D. J. Sedimentary bed evolution as a mean-reverting random walk: Implications for tracer statistics. Geophys. Res. Lett. 41, 6152–6159, https://doi.org/10.1002/2014GL060525 (2014).
Bradley, D. N. Direct Observation of Heavy-Tailed Storage Times of Bed Load Tracer Particles Causing Anomalous Superdiffusion. Geophys. Res. Lett. 44, 12227–12235, https://doi.org/10.1002/2017GL075045 (2017).
Zhang, Y., Meerschaert, M. M. & Packman, A. I. Linking fluvial bed sediment transport across scales. Geophys. Res. Lett. 39, https://doi.org/10.1029/2012GL053476 (2012).
Chabaux, F., Granet, M., Pelt, E., France-Lanord, C. & Galy, V. 238U-234U-230Th disequilibria and timescale of sedimentary transfers in rivers: clues from the Gangetic plain rivers. Journal of Geochemical Exploration 88, 373–375 (2006).
Li, C. et al. The time scale of river sediment source-to-sink processes in East Asia. Chem. 446, 138–146, https://doi.org/10.1016/j.chemgeo.2016,06.012 (2016).
Nichols, K. K., Bierman, P. R., Hooke, R., Caffee, M. W. & Clapp, E. M. Quantifying sediment transport on desert piedmonts using 10Be and 26Al. Geomorphol. 45(2), 105–125 (2002).
Nichols, K. K., Bierman, P. R., Caffee, M. W., Finkel, R. & Larsen, J. Cosmogenically enabled sediment budgeting. Geol. 33(2), 133–136 (2005).
Reusser, L. J. & Bierman, P. R. Using meteoric Be-10 to track fluvial sand through the Waipaoa River basin, New Zealand. Geol. 38, 47–50, https://doi.org/10.1130/G30395.1 (2010).
Lang, K. A., Ehlers, T. A., Kamp, P. J. J. & Ring, U. Sediment storage in the Southern Alps of New Zealand: New observations from tracer thermochronology. Earth Planet. Sci. Lett. 493, 140–149, https://doi.org/10.1016/j.epsl.2018.04.016 (2018).
McKean, J. A., Dietrich, W. E., Finkel, R. C., Southon, J. R. & Caffee, M. W. Quantification of soil production and downslope creep rates from cosmogenic 10Be accumalations on a hillslope profile. Geol. 21, 343–346 (1993).
Bierman, P. R. & Steig, E. J. Estimating rates of denudation and sediment transport using cosmogenic isotope abundances in sediment. Earth Surf. Proc. Land. 21, 125–239 (1996).
Braucher, R. et al. African laterite dynamics using in situ-produced Be-10. Geochim. Cosmochim. Acta 62, 1501–1507, https://doi.org/10.1016/S0016-7037(98)00085-4 (1998).
Jungers, M. C. et al. Tracing hillslope sediment production and transport with in situ and meteoric Be-10. J. Geophys. Res. Earth Surf. 114, https://doi.org/10.1029/2008JF001086 (2009).
West, N. et al. Regolith production and transport at the Susquehanna Shale Hills Critical Zone Observatory, Part 2: Insights from meteoric Be-10. J. Geophys. Res. Earth Surf. 118, 1877–1896, https://doi.org/10.1002/jgrf.20121 (2013).
Struck, M. et al. Soil production and transport on postorogenic desert hillslopes quantified with Be-10 and Al-26. Geol. Soc. Am. Bull. 130, 1017–1040, https://doi.org/10.1130/B31767.1 (2018).
Carretier, S., Regard, V. & Soual, C. Theoretical cosmogenic nuclide concentration in river bedload clasts: Does it depend on clast size? Quat. Geochronol. 4, 108–123, https://doi.org/10.1016/j.quageo.2008.11.004 (2009).
Carretier, S. & Regard, V. Is it possible to quantify pebble abrasion and velocity in rivers using terrestrial cosmogenic nuclides? J. Geophys. Res. Earth Surf. 116, F04003, https://doi.org/10.1029/2011JF001968 (2011).
Evenstar, L. A. et al. Multiphase development of the Atacama Planation Surface recorded by cosmogenic He-3 exposure ages: Implications for uplift and Cenozoic climate change in western South America. Geol. 37, https://doi.org/10.1130/G25437A.1 (2009).
Houston, J. Groundwater recharge through an alluvial fan in the Atacama Desert, northern Chile: mechanisms, magnitudes and causes. hydrological Processes 16, 3019–3035, https://doi.org/10.1002/hyp.1086 (2002).
Vargas, G., Rutllant, J. & Ortlieb, L. ENSO tropical-extratropical climate teleconnections and mechanisms for Holocene debris flows along the hyperarid coast of western South America (17 degrees-24 degrees S). Earth Planet. Sci. Lett. 249, 467–483, https://doi.org/10.1016/j.epsl.2006.07.022 (2006).
Gayo, E. M. et al. Late Quaternary hydrological and ecological changes in the hyperarid core of the northern Atacama Desert (similar to 21 degrees S). Earth Sc. Rev. 113, 120–140, https://doi.org/10.1016/j.earscirev.2012.04.003 (2012).
Roperch, P. et al. Surface vitrification caused by natural fires in Late Pleistocene wetlands of the Atacama Desert. Earth Planet. Sci. Lett. 469, 15–26, https://doi.org/10.1016/j.epsl.2017.04.009 (2017).
Hassan, M. A. & Bradley, N. Geomorphic Controls on Tracer Particle Dispersion in Gravel-Bed Rivers. In Tsutsumu, D. & Laronne, J. (eds) Gravel-Bed Rivers: Process and Disasters, 167 (Wiley-Blackwell, UK, 2017).
Church, M. & Hassan, M. Size and distance of travel of unconstrained clasts on a streambed. Wat. Resour. Res. 28(1), 299–303 (1992).
Attal, M. & Lave, J. Pebble abrasion during fluvial transport: experimental results and implications for the evolution of the sediment load along rivers. J. Geophys. Res. Earth Surf. 114, F04023, https://doi.org/10.1029/2009JF001328 (2009).
Dingle, E. H., Attal, M. & Sinclair, H. D. Abrasion-set limits on Himalayan gravel flux. Nat. 544, 471+, https://doi.org/10.1038/nature22039 (2017).
Nichols, K. K., Bierman, P. R., Finkel, R. & Larsen, J. Long-term sediment generation rates for the upper Rio Chagres Basin: Implications for Panama Canal watershed management. In Harmon, R. (ed.) The Rio Chagres: A Multidisciplinary Profile of a Tropical Watershed, 297–313 (Springer, 2005b).
Belmont, P., Pazzaglia, F. & Gosse, J. Cosmogenic 10Be as a tracer for hillslope and channel sediment dynamics in the Clearwater River, western Washington State. Earth Planet. Sci. Lett. 264, 123–135, https://doi.org/10.1016/j.epsl.2007.09.013 (2007).
Codilean, A. T., Bishop, P., Hoey, T. B., Stuart, F. M. & Fabel, D. Cosmogenic Ne-21 analysis of individual detrital grains: Opportunities and limitations. Earth Surf. Proc. Land. 35, 16–27, https://doi.org/10.1002/esp.1815 (2010).
Codilean, A., Fenton, C., Fabel, D., Bishop, P. & Xu, S. Discordance between cosmogenic nuclide concentrations in amalgamated sands and individual fluvial pebbles in an arid zone catchment. Quat. Geochronol. 19, 173–80, https://doi.org/10.1016/j.quadgeo.2012.04.007 (2014).
Carretier, S. et al. Differences in 10Be concentrations between river sand, gravel and pebbles along the western side of the Central Andes. Quat. Geochronol. 27, 33–51 (2015).
Tofelde, S. et al. Effects of deep-seated versus shallow hillslope processes on cosmogenic Be-10 concentrations in fluvial sand and gravel. Earth Surf. Proc. Land. 43, 3086–3098, https://doi.org/10.1002/esp.4471 (2018).
van Dongen, R., Scherler, D., Wittmann, H. & von Blanckenburg, F. Cosmogenic Be-10 in river sediment: where grain size matters and why. Earth Surface Dynamics 7, 393–410, https://doi.org/10.5194/esurf-7-393-2019 (2019).
Ritter, B. et al. Neogene fluvial landscape evolution in the hyperarid core of the Atacama Desert. Sci. 8, https://doi.org/10.1038/s41598-018-32339-9 (2018).
Ritter, B., Binnie, S. A., Stuart, F. M., Wennrich, V. & Dunai, T. J. Evidence for multiple Plio-Pleistocene lake episodes in the hyperarid Atacama Desert. Quat. Geochronol. 44, 1–12, https://doi.org/10.1016/j.quageo.2017.11.002 (2018).
Schmidt, S., Hetzel, R., Kuhlmann, J., Mingorance, F. & Ramos, V. A note of caution on the use of boulders for exposure dating of depositional surfaces. Earth Planet. Sci. Lett. 302, 60–70, https://doi.org/10.1016/j.epsl.2010.11.039 (2011).
Harries, R. M., Kirstein, L. A., Whittaker, A. C., Attal, M. & Main, I. Impact of recycling and lateral sediment input on grain size fining trends?Implications for reconstructing tectonic and climate forcings in ancient sedimentary systems. Basin Res. 1–26, https://doi.org/10.1111/bre.12349 (2019).
Starke, J., Ehlers, T. A. & Schaller, M. Tectonic and Climatic Controls on the Spatial Distribution of Denudation Rates in Northern Chile (18 degrees S to 23 degrees S) Determined From Cosmogenic Nuclides. J. Geophys. Res. Earth Surf. 122, 1949–1971, https://doi.org/10.1002/2016JF004153 (2017).
Madella, A., Delunel, R., Akçar, N., Schlunegger, F. & Christl, M. 10Be-inferred paleo-denudation rates imply that the mid-Miocene western central Andes eroded as slowly as today. Sci. 8, 2299, https://doi.org/10.1038/s41598-018-20681-x (2018).
Phillips, C. B. & Jerolmack, D. J. Dynamics and mechanics of bed-load tracer particles. Earth Surface Dynamics 2, 513–530, https://doi.org/10.5194/esurf-2-513-2014 (2014).
Paola, C. et al. Downstream fining by selective deposition in a laboratory flume. Sci. 258, 1757–1760 (1992).
Fedele, J. J. & Paola, C. Similarity solutions for fluvial sediment fining by selective deposition. J. Geophys. Res. Earth Surf. 112, F02038, https://doi.org/10.1029/2005JF000409 (2007).
Duller, R. A. et al. From grain size to tectonics. J. Geophys. Res. Earth Surf. 115, https://doi.org/10.1029/2009JF001495 (2010).
Whittaker, A. C. et al. Decoding downstream trends in stratigraphic grain size as a function of tectonic subsidence and sediment supply. Geol. Soc. Am. Bull. 123, 1363–1382, https://doi.org/10.1130/B30351.1 (2011).
Lajeunesse, E., Devauchelle, O. & James, F. Advection and dispersion of bed load tracers. Earth Surf. Dyn. 6, 389–399, https://doi.org/10.5194/esurf-6-389-2018 (2018).
Metivier, F., Gaudemer, Y., Tapponnier, P. & Meyer, B. Northeastward growth of the Tibet plateau deduced from balanced reconstruction of two depositional area: The Qaidam and Hexi Corridor basins, China. Tectonics 17, 823–842 (1998).
Jerolmack, D. J. & Paola, C. Shredding of environmental signals by sediment transport. Geophys. Res. Lett. 37, https://doi.org/10.1029/2010GL044638 (2010).
Redner, S. In A Guide to First Passage Time Processes, 328p (Cambridge Univ. Press, New York, 2001).
Martin, R. L., Jerolmack, D. J. & Schumer, R. The physical basis for anomalous diffusion in bed load transport. J. Geophys. Res. Earth Surf. 117, https://doi.org/10.1029/2011JF002075 (2012).
Phillips, C. B., Martin, R. L. & Jerolmack, D. J. Impulse framework for unsteady flows reveals superdiffusive bed load transport. Geophys. Res. Lett. 40, https://doi.org/10.1002/grl.50323 (2013).
Fan, N., Xie, Y. & Nie, R. Bed load transport for a mixture of particle sizes: Downstream sorting rather than anomalous diffusion. J. Hydrol. 553, 26–34, https://doi.org/10.1016/j.jhydrol.2017.07.012 (2017).
Torres, M. A. et al. Model predictions of long-lived storage of organic carbon in river deposits. Earth Surf. Dyn. 5, 711–730, https://doi.org/10.5194/esurf-5-711-2017 (2017).
Chen, H. & Petley, D. The impact of landslides and debris flows triggered by Typhoon Mindulle in Taiwan. Quarterly J. Of Engineering Geology and Hydrogeology 38, 301–304, https://doi.org/10.1144/1470-9236/04-077 (2005).
Stark, C., Foufoula-Georgiou, E. & Ganti, V. A nonlocal theory of sediment buffering and bedrock channel evolution. J. Geophys. Res. 114, F01029, https://doi.org/10.1029/2008JF000981 (2009).
Schumer, R. & Jerolmack, D. J. Real and apparent changes in sediment deposition rates through time. J. Geophys. Res. Earth Surf. 114, https://doi.org/10.1029/2009JF001266 (2009).
Finnegan, N. J., Schumer, R. & Finnegan, S. A signature of transience in bedrock river incision rates over timescales of 10(4)-10(7) years. Nat. 505, 391+, https://doi.org/10.1038/nature12913 (2014).
Ganti, V. et al. Time scale bias in erosion rates of glaciated landscapes. Sci. 2, https://doi.org/10.1126/sciadv.1600204 (2016).
Merchel, S. et al. Towards more precise 10Be and 36Cl data from measurements at the 10(-14) level: Influence of sample preparation. Nucl. 266, 4921–4926, https://doi.org/10.1016/j.nimb.2008.07.031 (2008).
Merchel, S. & Herpers, U. An update on radiochemical separation techniques for the determination of long-lived radionuclides via accelerator mass spectrometry. Radiochimica Acta 84, 215–219 (1999).
Arnold, M. et al. The French accelerator mass spectrometry facility ASTER: Improved performance and developments. Nucl. 268, 1954–1959, https://doi.org/10.1016/j.nimb.2010.02.107 (2010).
Nishiizumi, K. et al. Absolute calibration of 10Be AMS standards. Nuclear Instruments and Methods. Physics. Research 258, 403–413 (2007).
Braucher, R. et al. Preparation of ASTER in-house Be-10/Be-9 standard solutions. Nucl. 361, 335–340, https://doi.org/10.1016/j.nimb.2015.06.012 (2015).
Chmeleff, J., von Blanckenburg, F., Kossert, K. & Jakob, D. Determination of the Be-10 half-life by multicollector ICP-MS and liquid scintillation counting. Nucl. 268, 192–199, https://doi.org/10.1016/j.nimb.2009.09.012 (2010).
Korschinek, G. et al. A new value for the half-life of Be-10 by Heavy-Ion Elastic Recoil Detection and liquid scintillation counting. Nucl. 268, 187–191, https://doi.org/10.1016/j.nimb.2009.09.020 (2010).
Braucher, R., Brown, E., Bourlès, D. & Colin, F. In situ produced 10Be measurements at great depths: implications for production rates by fast muons. Earth Planet. Sci. Lett. 211, 251–258, https://doi.org/10.1016/S0012-821X(03)00205-X (2003).
Stone, J. Air pressure and cosmogenic isotope production. J. Geophys. Res. 105, 23753–23759, ISI:000089895700027 (2000).
Martin, L. et al. The CREp program and the ICE-D production rate calibration database: A fully parameterizable and updated online tool to compute cosmic-ray exposure ages. Quat. Geochronol. 38, 25–49, https://doi.org/10.1016/j.quageo.2016.11.006 (2017).
Hovius, N., Stark, C. P. & Allen, P. A. Sediment flux from a mountain belt derived by landslide mapping. Geol. 25, 231–234 (1997).
Sklar, L. S. et al. The problem of predicting the size distribution of sediment supplied by hillslopes to rivers. Geomorphol. 277, 31–49, https://doi.org/10.1016/j.geomorph.2016.05.005 (2017).
Farías, M., Charrier, Comte, D., Martinod, J. & Hérail, G. Late Cenozoic deformation and uplift of the western flank of the Altiplano: Evidence from the depositional, tectonic, and geomorphologic evolution and shallow seismic activity (northern Chile at 19°30S). Tectonics 24, TC4001, https://doi.org/10.1029/2004TC001667 (2005).
Dunai, T., Lopez, G. & Juez-Larre, J. Oligocene-Miocene age of aridity in the Atacama Desert revealed by exposure dating of erosion-sensitive landforms. Geol. 33, 321–324 (2005).
Carretier, S. et al. Review of erosion dynamics along the major N-S climatic gradient in Chile and perspectives. Geomorphol. 300, 45–68, https://doi.org/10.1016/j.geomorph.2017.10.016 (2018).
McPhillips, D., Bierman, P. R. & Rood, D. H. Millennial-scale record of landslides in the Andes consistent with earthquake trigger. Nat. GeoScience 7, 925–930, https://doi.org/10.1038/NGEO2278 (2014).
Farr, T. G. et al. The shuttle radar topography mission. Rev. 45, https://doi.org/10.1029/2005RG000183 (2007).
Acknowledgements
ASTER AMS national facility (CEREGE, Aix-en-Provence) is supported by the INSU/CNRS, the ANR through the “Projets thématiques d’excellence” program for the “Equipements d’excellence” ASTER-CEREGE action, IRD. K Keddadouche and G. Aumaître are thanked for their valuable help in AMS measurements. Discussions with P. Maffre were beneficial. This study was funded by IRD (LMI COPEDIM) and INSU/CNRS (SESPEED project). We thank two reviewers and three reviewers on a previous version for their help to improve our manuscript.
Author information
Authors and Affiliations
Contributions
S.C. and V.R. designed the study and developed the model. M.F. proposed the field site, established the geology of the Aroma region and collected the samples with S.C.; V.R. and S.C. physically prepared the samples and L.L. was in charge of the chemical preparation. S.C. wrote the paper with input from all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carretier, S., Regard, V., Leanni, L. et al. Long-term dispersion of river gravel in a canyon in the Atacama Desert, Central Andes, deduced from their 10Be concentrations. Sci Rep 9, 17763 (2019). https://doi.org/10.1038/s41598-019-53806-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-53806-x
This article is cited by
-
Integration of Near-Surface Complementary Geophysical Techniques for the Study of Ancient Archaeological Areas in the Atacama Desert (Pampa Iluga, Northern Chile)
Surveys in Geophysics (2023)
-
Cosmogenic nuclide techniques
Nature Reviews Methods Primers (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.