Abstract
Transcranial magnetic stimulation combined with electroencephalography is a powerful tool to probe human cortical excitability. The EEG response to TMS stimulation is altered by drugs active in the brain, with characteristic “fingerprints” obtained for drugs of known mechanisms of action. However, the extraction of specific features related to drug effects is not always straightforward as the complex TMS-EEG induced response profile is multi-dimensional. Analytical approaches can rely on a-priori assumptions within each dimension or on the implementation of cluster-based permutations which do not require preselection of specific limits but may be problematic when several experimental conditions are tested. We here propose an alternative data-driven approach based on PARAFAC tensor decomposition, which provides a parsimonious description of the main profiles underlying the multidimensional data. We validated reliability of PARAFAC on TMS-induced oscillations before extracting the features of two common anti-epileptic drugs (levetiracetam and lamotrigine) in an integrated manner. PARAFAC revealed an effect of both drugs, significantly suppressing oscillations in the alpha range in the occipital region. Further, this effect was stronger under the intake of levetiracetam. This study demonstrates, for the first time, that PARAFAC can easily disentangle the effects of subject, drug condition, frequency, time and space in TMS-induced oscillations.
Similar content being viewed by others
Introduction
Transcranial magnetic stimulation (TMS) is a non-invasive tool to probe neurophysiological processes in the human brain. A TMS pulse depolarizes the stimulated neuronal population and remote anatomically connected regions1. The registration of TMS effects with electroencephalography (EEG) allows to quantify and characterize spread of neural activation that follows in time, spatial and frequency domains2. The summation of synaptic potentials produces a series of time-locked positive and negative deflections visible in the EEG signal, termed the TMS-evoked potentials (TEPs). TEPs are a sequence of peaks which reflect cortical reactivity and changes in their amplitude and latency reflect changes in cortical activity3. In addition, brain responses to TMS can be interrogated applying a time-frequency analysis at single trial level removing the evoked (i.e. TEPs) component from the signal. TMS-induced oscillations are the result of this analytical approach and they provide non-phase locked neural information4.
TEPs and TMS-induced oscillations are outcome measures used to characterise brain states in health, diseases and under experimental conditions such as drug manipulation5. Previous work showed that TMS-EEG is a powerful tool to investigate effects of drugs acting in the human brain6,7,8,9,10. In these studies, the effects of drugs were quantified in term of differences between conditions (or subjects) in evoked activity in specific time windows corresponding to TEPs and in specific sets of EEG electrodes. A cluster based permutation approach is the golden standard used to overcome the problem of multiple comparisons. It requires an a-priori selection of time windows or a post-hoc correction for the large number of non-independent comparisons across many tested conditions. It seems highly likely that important effects will be lost through inadvertent selection of the “wrong” time windows and/or electrodes, or through the necessarily harsh post-hoc correction for multiple non-independent comparisons.
The high dimensionality of TMS-EEG data is a challenge for analysis and interpretation, and motivates approaches to simplify the data by reducing the dimensionality. Specifically, we can hypothesise that TMS stimulation of the brain gives rise to activity in specific brain networks following stimulation, and that these networks will have a specific spatial distribution and specific spectral characteristics (i.e. the network operates in a particular frequency range) – but identifing such underlying patterns in highly multidimensional data is difficult. Here, we apply a methodology based on tensor decomposition to reveal such underlying patterns.
The term “tensor” refers to a multi-way (i.e. multidimensional) array, that is a collection of variables that can be indexed by more than two terms. Whereas the position of and element in a vector or matrix is determined, respectively, by one (e.g., i) or two indices (e.g., i, j), the values in a tensor are indexed by more than two parameters: i, j, k...11. In a similar way to how matrix decompositions (e.g., principal component analysis) can represent a two-dimensional array (a matrix) as a product of factor matrices, tensor decompositions allow us to extract from seemingly complex multidimensional data parsimonious and unique representations of underlying patterns11,12. Since the introduction of the PARAFAC algorithm, which decomposes a tensor into a sum of outer products of low-rank components13, tensor decompostions, and PARAFAC in particular, have been used in a wide range of studies of EEG activity14. Seminal studies focused on the analysis of event-related potentials15,16. Subsequent tensor decompositions of EEG data enabled the inspection of time-frequency representations of EEGs during cognitive states17. Tensor decomposition has also been used in artefact rejection and estimation of seizure onset zone18,19. Other applications include localisation of EEG sources20, connectivity estimation21, brain computer interfaces22,23, and feature extraction in clinical and psychological studies24,25,26. Tensor decomposition are also useful when fusing EEG with other datasets27,28,29. Overall, the use of tensor decompositions is advatageous over matrix factorisations when the data are naturally multdimensional like in the case of EEG, and TMS-EEG12.
In this study, we sought to apply a data-driven approach, exploting the multidimensional structure of previously collected TMS-EEG data, allowing a parsimonious dimensionality reduction that summarises effects in the high-dimensional data. We hypothesise that PARAFAC will be able to reveal underlying patterns of activity with different topographical (accounting for the spatial distribution of a brain network), temporal (indicating time period after TMS stimulation during which the network is active) and spectral (informing about the typical operating frequency of the network) profiles that will be characteristic of the effects of each type of anti-epileptic drug (AED) in the TMS-EEG data without a-priori assumptions.
Methods
Subjects
Thirteen healthy male volunteers aged 19–34 years (mean age 25.2 years, SD = ±4.62) participated in the study after written informed consent was given. All subjects were classified as right-handed according to the Edinburgh Handedness Inventory30 and underwent physical examination and screening for any contraindications to TMS or study drugs31. The College Research Ethics Committee (CREC) of King’s College London approved the research, which was performed in accordance with relevant guildlines and regulations. Informed consent was obtained from all participants. The TMS-evoked EEG potential (TEP) analyses of this sample have been published previously7,32.
Experimental design
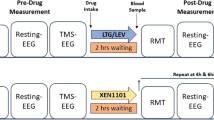
We performed a double-blind, randomized, placebo-controlled, crossover study to investigate the impact of levetiracetam (LEV, 3000 mg) and lamotrigine (LTG, 300 mg) on TMS-induced EEG oscillations. Each subject participated in three experimental sessions in total, administered lamotrigine, levetiracetam or placebo in each session in a randomized order, spaced at least one week apart to allow a washout period. At each session, we first performed baseline pre-drug TMS-EEG recording. Later, the post-drug recording was performed two hours after drug ingestion, please see the details of the experimental setting and protocol in the Supplementary Section A.1.
Data analysis
TMS-EEG data construction
TMS-induced oscillations were analysed using MATLAB® (Mathworks Ltd, USA, R2012b) (The Mathworks Inc.) and FieldTrip toolbox33. After excluding records/trials with prominent eye movements, blinks, and muscle artefacts (on the basis of visual inspection), EEG data was analyzed using an established multistep procedure34. Data was down sampled to 1 kHz, segmented 1 s before and after the pulse, and linearly interpolated for ±10 ms to remove the TMS artefact. Bad channels were removed from the EEG, and the signal was reconstructed by interpolating the surrounding electrode signals. Data was then notched filtered (50 Hz). Independent Component analysis (ICA) was applied to remove TMS-related artifacts (i.e., the cranial muscle response, the recharging of capacitors, and related exponential decay artifacts35,36,37, as well as further muscle and ocular activity. Finally, remaining data were re-referenced to the average of all electrodes, baseline corrected (from −1000 to −50 ms) and band-pass filtered (1–80 Hz).
After that, for each segment we estimated its time-frequency plot by applying a Hanning taper windowed fast Fourier transform (FFT) with frequency-dependent window length (width: 3.5 cycles per time window, time steps: 10 ms, frequency steps: 1 Hz from 4 to 45 Hz)38. TMS-induced responses were obtained by subtracting the individual time-domain average from each trial before calculating the TF of the single trials39. We performed single-trial normalization by z-transforming the TF of each trial for each frequency. The z-transformation was based on the respective mean and standard deviation derived from the full trial length. This was followed by an absolute baseline correction for each trial, by subtracting the average of the 100 to 50 ms period for each frequency to ensure z-values represented a change from pre-TMS baseline.
At the end, we had an array of 61 × 42 × 201 elements (61 channels, 4 Hz to 45 Hz with frequency resolution of 1 Hz, and data starting from −1000 to + 1000 ms with time step of 10 ms). Note that, to minimise TMS and DC shifts effects along the time (3rd dimension) and frequency (2nd dimension) axes, we selected the data starting from 40 ms after the TMS pulse to 1000 ms after the TMS pulse and frequency bins between 4 to 34 Hz resulting in a new 3D array of 61 × 31 × 98 elements. These steps were repeated for all segments and all channels.
Tensorisation of TMS-EEG data and PARAFAC modelling
The TMS-EEG data construction described in section 2.3.1 resulted in a three dimensional tensor [channel (or space) × frequency × time], representing a time varying spectrum of all channels. Tensors are multi-dimensional data arrays that extend vectors (one dimensional) and matrices (two dimensional) to more than two dimensions11,12. This three-dimensional tensor [channel (or space) × frequency × time] will be used in our subsequent tensor decomposition based analysis. Figure 1 illustrates the principle of tensor decomposition based on the PARAFAC model for our tensorised TMS-EEG data (as a 3D tensor for simplicity).
(A) Shows N decomposed components from the 3D tensor W, each component comprises three vectors (A, B and C). (B) shows an example when the technique was used to decompose the 3D (space × frequency × time) of subject#2 post LEV. In this case, the three components represent high, medium and low-frequency ranges (15–30 Hz “Beta”, 6–13 Hz “Alpha”, and 4–6 Hz “Theta”. The bottom two insets show a Space-vs-Frequency plot at 150 milliseconds after TMS pulse and its grand average across all channels.
Assuming that we have a 3D tensor W, this data array can be approximated as a sum of N rank-one tensors, which represent underlying components13,17. Each component is an outer product of three matrices (A, B and C) as:
where wijk is an element in the tensor W, which is approximated by the summation of N rank-1 components which are the outer product of \({a}_{r},{b}_{r},{c}_{r}\,\), where, for example, \({a}_{ir}\)is an element in the matrix A which contains the profiles of the extracted components along the first dimension (channel or space) in its columns ar. Likewise, B and C contains the estimated components along the second (frequency) and third (time), respectively, see Fig. 1(A,B). This data model assummes that the neural generators resulting in the scalp EEG activity are stationary during the recording period.
Selecting the optimum number of components
There is no a priori means to determine how many components will best represent the data. Explained varinace were used to help estimate an appropriate number of components in PARAFAC.
To estimate the optimal number of components, we decomposed a 5D tensor (consisting of all conditions from all subjects [61 × 31 × 98 × 13 × 6 elements]) into a different number of components ranging from one to eight (n = 1, .., 8 in Eq. 1), and estimated the explained variance in each instance. The selection of a relatively low number of components reduces the chances of overfitting and faciltiates its intepretation. More importantly, the topographical, temporal and spectral profiles of the extracted components were inspected to determine a number of PARAFAC components that would aid in the interpretation of the data. It is important to inspect the profiles of components extracted for each considered value of n since it is not guaranteed that the components extracted when computing PARAFAC with n–1 will appear again when doing so with n components13.
Besides estimating the explained varaince, we also estimated the core consistency diagnosis (CORCONDIA, see the Supplementary Section A2)40. CORCONDIA is a heuristic measure to check if the data can be modelled fully multilinearly.
Using tensor decomposition to characterise and contrast effects of AEDs and placebo
Building on the 3D tensor described above, we constructed a five dimensional tensor consisting of the three previously described dimensions (space, frequency, time) and adding two further dimensions, subject and condition (see Fig. 2), by stacking 3D tensors obtained from section 2.3.2 in order to account for all the interactions of space, time and EEG oscillation frequency with the effects of drugs on the subjects. We then tested the effects of drugs on the subjects by contrasting conditions in four different ways, and including these conditions in the 5th dimension (condition):
Model 1: We also use this model as a proof of concept to study the components obtained from PARAFAC without any effect from drug in order to validate the tensor decomposition of TMS-EEG data.
Model 2: To test the hypothesis that levetiracetam and lamotrigine have different effects, we included four conditions: pre-LEV, post-LEV, pre-LTG, post-LTG.
Model 3: To test the hypothesis that levetiracetam has a different effect than placebo, we included four conditions: pre-placebo, post-placebo, pre-LEV, post-LEV.
Model 4: To test the hypothesis that lamotrigine has a different effect than placebo, we included four conditions: pre-placebo, post-placebo, pre-LTG, post-LTG.
These four separate models allow us to first validate the application of PARAFAC to TMS-EEG data and then to compare in pairs the effect of each drug between them and versus placebo in data-driven, unsupervised way. Considering the post processed data (3D tensors) obtained from step 2.3.2, for each subject (per condition) we had a data array of 61 × 31 × 98 elements. After stacking these 3D tensors from all subjects for the specific conditions as described in each model, we obtained a 5D tensor of 61 × 31 × 98 × 13 × 4 elements. Unlike the example in Fig. 1, showing the decomposition of the 3D tensor, with the newly constructed 5D tensor we could decompose this 5D array into a sum of 5 rank-one tensors (space (or channel), frequency, time, subject, and condition).
In this study, we used the N-way toolbox version 3.3 for tensor decomposition41 (http://www.models.life.ku.dk/nwaytoolbox). Note that we applied the non-negativity constraint to all dimensions while performing decomposition. Thus every element in the decomposed arrays would be at or greater than zero14,17,42. This constraint was imposed for a ease of interpretation.
Statistics
We applied a permutation based analysis to test for significant difference between pre-vs-post drug. All steps taken are presented as follows (see the graphical representation of all the steps in the Supplementary Fig. A1). At each model, we first decomposed the 5D tensor (with 61 × 31 × 98 × 13 × 4) into three components. These components were considered as ‘master’ components (that is, the ‘true labelled’ components, in distinction to permuted components, see below). Each of these components consisted of five profiles across the five dimensions (axes). For example in model-1, at each component we obtained five rank-1 tensors with 61, 31, 98, 13, and 4 elements for space, frequency, time, subject and condition, respectively.
Then we permuted this 5D tensor for 1,000 iterations. At each iteration, we permuted the elements on the 4th and 5th dimensions (subjects and conditions). Next, we decomposed this permuted 5D tensor while fixing all elements in the first three tensors. From this step, we obtained a new set of five rank-1 tensors, where thre first three tensors (representing space, frequency and time) were similar to the ones in the master, but the elements in the 4th and 5th tensors could be different from the master because shuffling the data along those dimensions destroys the inherent structure.
To assess the effects after drug/placebo intake, we subtracted the value on the 5th dimension of the pre drug from the value post drug. For example, considering the 2nd component of the master (true label), we subtracted the value before LEV intake from the value after LEV intake see the Supplementary Fig. A1). For the permuted data, at each iteration we estimated the level of change post drug as we did with the master. Then, we computed a histogram of these values. The level of change in master (true label) was significant if its value was less (or greater) than 2.5% of the distribution of the histogram. Note that the green square in the histogram at the bottom tight of the Supplementary Fig. A1 represents the difference between pre-vs-post LEV, where the two red vertical lines represent the upper and lower 2.5% of the histogram.
Results
Optimum number of decomposed components
We first explored our data to determine the optimal number of components. We decomposed the 5D tensor (space, frequency, time, subject, condition) build from all subjects and all six conditions into a range of number of components from one to eight. First, we showed the percentage of explained variance at different number of components in Table 1. Then, we showed the topographical, temporal and spectral profiles of the extracted components from all eight cases (see the Supplementary Figs. A2–A4).
From Table 1, a marked change was found in these parameters when increasing the number of components from one to three: i.e. ~10% increase in terms of explained variance. Above 4 components, further increasing the number of components did not significantly change either of these parameters.
In the Supplementary Fig. A2, representing the decomposed components on the 1st dimension (space), we found three typical underlying spatial patterns (highlighted in green, red and blue), which were relatively consistent (at least 6 out of 8 scenarios).
Moving on to the frequency axis (2nd dimension), if we decomposed the 5D tensor into a single component, this component would be represented primarily in the alpha range, see the Supplementary Fig. A3. When decomposing the same 5D tensor into two components, a component primrily in the theta frequency range was found in addition to the alpha component. Decomposed into three components, we observed they were distinct, primarily in theta, alpha and beta bands. After that, increasing the number of components did not add any other distinct components at other frequency bands, as most of the further decomposed components overlapped with the components found when decomposed into just three.
Finally, in the time axis unlike the first two axes it was harder to justify a number of independent components. By visual inspection, at least three distinct components were found, see the Supplementary Fig. A4.
Taking these together, we decided to decompose the 5D tensor into three components where the three distinct frequency band and three unique spatial patterns were clearly observed and the explained variance reached its plateau at about 40%.
Comparison across the four models
Figure 3 shows three components decomposed from our four different models. The 5D tensor from each model was decomposed into three components at three different frequency bands (theta, alpha, and beta, see the 2nd column in Fig. 3).
We present the three components decomposed from 5D tensor in four different models. The top row shows the decomposed components in space (topographical plots), frequency and time dimension. Three colours (blue, red and yellow) are used to indicate the three decomposed components: beta (with peak frequency between 15–30 Hz), alpha (with peak frequency between 6–13 Hz) and theta (with peak frequency between 4–6 Hz), respectively.
The model 1 is a proof of concept showing the three physiological components (beta, alpha and theta) decomposed from the TMS-EEG data without any effect from LEV or LTG.
First considering the beta components (labelled in blue) from all models, these components mostly represented frontal brain activities. On the time axis (3rd dimension), each of these beta components could be divided into 3 phases: (1) initial peak (during 40–200 milliseconds), (2) suppression (200–400 milliseconds) and (3) rebound (400 milliseconds onward). When we compared between models 3 and 4 (between LTG and LEV), one could observe less rebound of this beta component in LTG as compared to LEV.
The next component, which was predominantly observed in alpha range, showed the most variability (in terms of magnitude and spatial pattern) among the three components (theta, alpha, and beta) across all models. Whereas one could see the alpha component dominating occipital lobe in models 2 and 3, in model 4 this alpha activity can be seen everywhere (with high amplitude) except on the areas next to the earlobes.
Moving on to the last component, or theta labelled in orange, it was spatially identical across all models and represented the activities on C3. This component reached its peak around 200 milliseconds and completely suppressed starting ~400 milliseconds to the end of each recording.
Model 2: comparison of the effects of levetiracetam and lamotrigine
Figure 4 shows the three decomposed components in five dimensions, which were highlighted in blue, red and orange for 1st, 2nd and 3rd components respectively. The first component (blue) represented the brain activities (in the beta range, peak at 19 Hz) over the frontal and central areas. On the time axis (3rd dimension), this component initially peaked at ~90 milliseconds after applied TMS pulse, then suppressed between 190–400 milliseconds, and rebounded from 440 milliseconds to the end of the recording.
The second component (red) represented the activities with relatively lower frequency (at alpha band or between 6–13 Hz), which predominantly involved the occipital lobe. Initially, during 40–140 milliseconds after the TMS pulse, while the 1st component (frontal beta) was reaching its peak, this component (occipital alpha) was absent. Subsequently, during 140–340 seconds, while the 1st component was declining and eventually completely diminished, this 2nd component was on the rise and reached a plateau. Starting from 440 milliseconds until the end of the recording, these two components coexisted.
The last component (3rd, orange) was found in the theta band (4–6 Hz), centered on EEG electrode C3, which was the location where the TMS pulses were given. This component reached its peak between 90–240 milliseconds, and later was suppressed starting from 440 milliseconds until the end of recording (which was the period where both 1st and 2nd components coexisted).
Inter-subject variabilities were revealed in the 4th dimension showing the 1st, 10th and last subject being different from the others. On the 5th dimension condition (drug) effects were revealed, and we observed reduction in all components after receiving medication (both LEV and LTG). From this plot, one could see a stronger post medication effect for LEV as compared to LTG, especially in the 2nd component. At a group level, there was a significant effect of reduction of the 2nd component after LEV intake (see Fig. 5).
Each histogram shows the distribution of strength on the 5th dimension obtained from 1000 iterations of permutation. Two vertical red lines indicate the upper and lower 2.5% of the histogram. Each green square oindicates the difference between pre and post medication on the 5th dimension. In the top and bottom rows (showing the results from components 1 and 3, respectively), no significant reduction was found. For component #2 (middle row), we observed the significant reduction in terms of strength on the 5th dimension after receiving LEV.
Statistics
Figure 6 shows distributions of difference between pre-and-post medication from 1000 iterations in models 2, 3 and 4. Statistically, no significant change in either theta or beta components was found (see columns 1 and 3). Considering models 3 and 4, when we investigated the effects after drug vs after plecebo, we found significant reduction of alpha component in both post LEV (p = 0.015*) and post LTG (p = 0.021*) conditions. In model 2, when we compared the effects after drug intakes in both LEV vs LTG, the post-LEV shows a significantly stronger reduction of the alpha component than post-LTG with p = 0.01*.
Each histogram shows the distribution of difference between pre and post medication(or placebo) from 1000 iteration. The two red lines in the histograms indicate the first and last 2.5 percent. The green square represents the post vs pre difference on the 5th dimension. *Denotes significant (P < 0.025). All histograms on the top, middle and bottom rows are the distribution from model 2, 3, and 4, respectively. Note that all the p-values in this study are reported in the Supplementary Table A1.
Discussion
In this study, we introduced a tensor decomposition method to reduce multi-dimensionality of TMS-EEG data. We showed a series of components which provides a parsimonious description of neurophysiological responses underlying TMS-induced oscillations. In addition we demonstrated the utility of PARAFAC on existing data to disentangle the effect of anti-epileptic drugs on TMS-indueced oscillations. This method does not require a-priori selection of anatomical regions of interest, time periods of interest and frequency components of interest in the multi-dimensional EEG data, and without requiring potentially harsh post-hoc statistical correction for multiple comparisons. PARAFAC revealed an effect of both levetiracetam and lamotrigine, significantly suppressing oscillations in the alpha range in the occipital region, during the time period approximately 140 ms − 840 ms after the TMS pulse. Furthermore, this technique also reveals that the suppression of alpha oscillations is significantly stronger during the intake of levetiracetam than lamotrigine.
Optimum number of decomposed components and justification of PARAFAC model
From Table 1, the explained variance in the data reached its plateau when splitting into three components. This suggsests three as the optimal components. To justify our choice, we also visually inspected the decomposed profiles on space, time and frequency axes (Supplementary Figs. A2–A4). This is important as the profiles of components extracted for each considered value of n since it is not guaranteed that the components extracted when computing PARAFAC with n–1 will appear again when doing so with n components13. The fact that similar patterns appeared naturally provides further support to the interpretability of our chosen model. The inspection of the components also enabled us to grasp which physiological processes captured by the data-driven components were prominent in the TMS-EEG recordings. The results support our choice of 3 components. It was clear that along the frequency axis (Supplementary Fig. A3) regardless of the number of decomposed components we could only break down into maximum three different frequency bands (theta, alpha, and beta). Moving on to the spatial axis (the Supplementary Fig. A2), it was debatable if a maximum number of components could be either three or four. Finally, along the time axis (the Supplementary Fig. A4), the optimal number of component was unclear (it could either be any number between two to four). Looking at the CORCONDIA in the Supplementary Table A2, we found that by extracting more than one component the value of CORCONDIA drop to zero. This suggests our 5D tensor is not a fully multilinear form and also explains the non-equivalent number of optimal components along different axes40. Taking all these together, we then decided to decompose into three components, where all three unique signatures along frequency and spatially domains were found, and the explained variances reached its plateau. It is important to note that the explained variance may not increase significantly with the number of components since the multilinear PARAFAC model will not explain the noise and random variations in the data. Furthermore, increasing the number of components would lead to higher computational cost43.
Although another family of tensor decompositions (Tucker decompositon) may provide a solution to the case with a non-equivalent number of optimal components, it does not preserve one-to-one interaction33,44. Hence, the decomposed components using Tucker decomposition are harder to interpret. To sum up, we decided to decompose the TMS-EEG 5D tensor using PARAFAC, which preserves one-to-one interaction. That is each component will be entitled to a unique interpretation, for example, the TMS induced component may be seen in a particular frequncy range, anatomical distribution and time period. Future work will explore the suitability of other more flexible, but still unique models such as PARAFAC221, to improve the modelling of TMS-EEG data and reveal even more subtle interactions.
Physiological meanings behind the three components
From model 1 (without drug) we found three physiological components (theta, alpha and beta), these components are highly similar (spatially, temporally and spectrally) across four models, see Fig. 3. Given that the PARAFAC solution is unique under very mild conditions, this further reinforces that the extracted components have physiological meaning. These components (frontal-sensorimotor beta, posterior alpha and theta related to the site of stimulation) represented the hidden signature of the data for all conditions (pre/post PLA, pre/post LEV, pre/post LTG). We considered the frontal-sensorimotor beta component to represent the spreading of cortical reactivity from the stimulated site (C3) through its neighboring areas via local fibers as well as to the contralateral motor cortex via corpus callosum45. Sensorimotor rhythms, which dominate the motor cortex, are found in mu (8–13 Hz) and beta rhythms (15–30 Hz)46,47. By giving a TMS pulse, it may elicit similar effects on the cortical neurons seen as event-related (de)-synchronization (ERD/ERS) time locked to motor movement over motor cortex areas48,49,50. Since the rebound of sensorimotor rhythms (synchronization) is uniquely observed in the beta range after giving stimuli48,49, by imposing the non-negativity constraint to the 5D tensor we might limit the decomposed component at this area only in the beta band. Moving on to the posterior alpha, it is found to be a key component shown to differentiate between the two drugs, seen as the stronger reduction of alpha component after LEV compard to LTG intake, in model 2. Considering both models 3 and 4 (placebo vs each type of drug), we found the significant reduction of this component after both LEV and LTG intake (whereas no change was found post placebo). Results suggest that both types of drug cause similar effects on the generation of posterior alpha. The same observation derived from the investigation of these AEDs on TEPs, where despite the varying profile of effects and regardless of the (putative) molecular targets of the different drugs, systemically administered LEV and LTG exert similar modulation of TEPs9. In addition, the effect on alpha was stronger under LEV exposure which had the highest average concentration in blood outside the reference range, with LTG averaging toward a lower concentration for its reference range9.
Lastly, considering theta, this component represents the TMS-induced effect on the stimulation site, because its spatial pattern was centred on C3 and its temporal signature shows a peak soon after stimualtion and then subsided.
Strengths and weaknesses of this study
Unlike a conventional TMS-EEG analysis, which requires predefining time, anatomical area and frequency of interest, tensor decompositions offer a purely data-driven approach. In particular, we applied PARAFAC due to its parsimony and ease of interpretation since the interactions of the components are restricted. In our analysis, the 5D tensor for each mode had dimensions 61 × 31 × 98 × 13 × 4 (9,636,536 entries in total). Decomposing it with PARAFAC, the method was able to account for approximately 40% of the explained variance with just 3 components which include only 621 elements – i.e., 3 × (61 + 31 + 98 + 13 + 4), less than 0.01% of the total number of entries in the tensor. The results were tested under permutation-based statistics. We successfully showed that each decomposed component represents the unique signature on the spatial, spectral and temporal domains with physiological meaning. Furthermore, along the 4th dimension, one could make the inference about these hidden signatures at a single subject level. Despite the postive results provided by this innovative analysis approach of TMS-EEG data, it must be take into consideration that the TMS pulse can induce unwanted somatosensory input that have an impact on TEPs51. We purposely selected a PARAFAC model with non-negativity constraints to simplify the interpretation of the components extracted from TMS-EEG activity in this first application of tensor decompositions to this type of data. However, we acknoledge that the choice of the non-negativity constraint implies that we were not able to reveal potential patterns in negative values and that our results are also limited by the small number of participants and we advice the reader to intepret them with care.
Conclusion
To our knowledge, it is the first time tensor decomposition has been applied in TMS-EEG data. Our results show the power of tensor decompositions to reveal the profiles underlying the complex responses in TMS-EEG data associated with different AEDs in healthy subjects in a data-driven and parsimonious way. Future work will seek to develop classifiers able to predict the level of response to each AED in new subjects by projecting their TMS-EEG recordings on the “characteristic filters” associated with previously revealed tensor components in space, time and frequency26,52. We will also consider the possibility of applying tensor decompositions to TMS-EEG signals in the time domain following other previous applications of these techniques to event-related EEG activity14.
Highlights
-
TMS-EEG allows probing of human brain excitability and functionality in health and disease.
-
Tensor decomposition to identify key features of high-dimensional EEG data.
-
Using this data-driven approach, we reveal the effects of antiepileptic drugs on TMS-EEG.
Data and Code availability
Data and code are available upon request.
References
Hallett, M. Transcranial magnetic stimulation: a primer. Neuron 55, 187–199, https://doi.org/10.1016/j.neuron.2007.06.026 (2007).
Ilmoniemi, R. J. et al. Neuronal responses to magnetic stimulation reveal cortical reactivity and connectivity. Neuroreport 8, 3537–3540 (1997).
Rogasch, N. C. & Fitzgerald, P. B. Assessing cortical network properties using TMS-EEG. Hum Brain Mapp 34, 1652–1669, https://doi.org/10.1002/hbm.22016 (2013).
Rosanova, M. et al. Natural frequencies of human corticothalamic circuits. J Neurosci 29, 7679–7685, https://doi.org/10.1523/JNEUROSCI.0445-09.2009 (2009).
Tremblay, S. et al. Clinical utility and prospective of TMS–EEG. Clinical Neurophysiology. https://doi.org/10.1016/j.clinph.2019.01.001 (2019).
Darmani, G. et al. Effects of the Selective alpha5-GABAAR Antagonist S44819 on Excitability in the Human Brain: A TMS-EMG and TMS-EEG Phase I Study. J Neurosci 36, 12312–12320, https://doi.org/10.1523/JNEUROSCI.1689-16.2016 (2016).
Premoli, I., Biondi, A., Carlesso, S., Rivolta, D. & Richardson, M. P. Lamotrigine and levetiracetam exert a similar modulation of TMS-evoked EEG potentials. Epilepsia 58, 42–50, https://doi.org/10.1111/epi.13599 (2017).
Darmani, G. et al. Effects of antiepileptic drugs on cortical excitability in humans: A TMS-EMG and TMS-EEG study. Hum Brain Mapp 40, 1276–1289, https://doi.org/10.1002/hbm.24448 (2019).
Premoli, I., Biondi, A., Carlesso, S., Rivolta, D. & Richardson, M. P. Lamotrigine and levetiracetam exert a similar modulation of TMS-evoked EEG potentials. Epilepsia, https://doi.org/10.1111/epi.13599 (2016).
Premoli, I. et al. TMS-EEG signatures of GABAergic neurotransmission in the human cortex. J Neurosci 34, 5603–5612, https://doi.org/10.1523/JNEUROSCI.5089-13.2014 (2014).
T. G. Kolda, B. W. B. Tensor Decompositions and Applications. SIAM Reviews 51, 455–500 (2009).
Cichocki, A. et al. Tensor Decompositions for Signal Processing Applications. Ieee Signal Processing Magazine 32, 145–163, https://doi.org/10.1109/Msp.2013.2297439 (2015).
Harshman, R. A. Foundations of the PARAFAC procedure: Models and conditions for an —explanatory“ multimodal factor analysis. UCLA Working Papers in Phonetics 16, 1–84 (1970).
Cong, F. Y. et al. Tensor decomposition of EEG signals: A brief review. Journal of Neuroscience Methods 248, 59–69, https://doi.org/10.1016/j.jneumeth.2015.03.018 (2015).
Cole, H. W. & Ray, W. J. Eeg Correlates of Emotional Tasks Related to Attentional Demands. International Journal of Psychophysiology 3, 33–41, https://doi.org/10.1016/0167-8760(85)90017-0 (1985).
Mocks, J. Decomposing Event-Related Potentials - a New Topographic Components Model. Biological Psychology 26, 199–215, https://doi.org/10.1016/0301-0511(88)90020-8 (1988).
Miwakeichi, F. et al. Decomposing EEG data into space-time-frequency components using Parallel Factor Analysis. Neuroimage 22, 1035–1045, https://doi.org/10.1016/j.neuroimage.2004.03.039 (2004).
Acar, E., Aykut-Bingol, C., Bingol, H., Bro, R. & Yener, B. Multiway analysis of epilepsy tensors. Bioinformatics 23, i10–18, https://doi.org/10.1093/bioinformatics/btm210 (2007).
De Vos, M. et al. Canonical decomposition of ictal scalp EEG reliably detects the seizure onset zone. Neuroimage 37, 844–854, https://doi.org/10.1016/j.neuroimage.2007.04.041 (2007).
Becker, H. et al. EEG extended source localization: tensor-based vs. conventional methods. Neuroimage 96, 143–157, https://doi.org/10.1016/j.neuroimage.2014.03.043 (2014).
Spyrou, L., Parra, M. & Escudero, J. Complex Tensor Factorization With PARAFAC2 for the Estimation of Brain Connectivity From the EEG. IEEE Trans Neural Syst Rehabil Eng 27, 1–12, https://doi.org/10.1109/TNSRE.2018.2883514 (2019).
Cichocki, A. et al. Noninvasive BCIs: Multiway Signal-Processing Array Decompositions. Computer 41, 34–+, https://doi.org/10.1109/Mc.2008.431 (2008).
Zhang, Y. et al. L1-regularized Multiway canonical correlation analysis for SSVEP-based BCI. IEEE Trans Neural Syst Rehabil Eng 21, 887–896, https://doi.org/10.1109/TNSRE.2013.2279680 (2013).
Wang, J. et al. Characteristics of evoked potential multiple EEG recordings in patients with chronic pain by means of parallel factor analysis. Comput Math Methods Med 2012, 279560, https://doi.org/10.1155/2012/279560 (2012).
Cong, F. et al. Benefits of multi-domain feature of mismatch negativity extracted by non-negative tensor factorization from EEG collected by low-density array. Int J Neural Syst 22, 1250025, https://doi.org/10.1142/S0129065712500256 (2012).
Latchoumane, C. F. et al. Multiway array decomposition analysis of EEGs in Alzheimer’s disease. J Neurosci Methods 207, 41–50, https://doi.org/10.1016/j.jneumeth.2012.03.005 (2012).
Martinez-Montes, E., Valdes-Sosa, P. A., Miwakeichi, F., Goldman, R. I. & Cohen, M. S. Concurrent EEG/fMRI analysis by multiway Partial Least Squares. Neuroimage 22, 1023–1034, https://doi.org/10.1016/j.neuroimage.2004.03.038 (2004).
Kinney-Lang, E., Ebied, A., Auyeung, B., Chin, R. F. M. & Escudero, J. Introducing the Joint EEG-Development Inference (JEDI) Model: A Multi-Way, Data Fusion Approach for Estimating Paediatric Developmental Scores via EEG. IEEE Trans Neural Syst Rehabil Eng 27, 348–357, https://doi.org/10.1109/TNSRE.2019.2891827 (2019).
Karahan, E., Rojas-Lopez, P. A., Bringas-Vega, M. L. & Valdes-Hernandez, P. A. & Valdes-Sosa, P. A. Tensor Analysis and Fusion of Multimodal Brain Images. Proceedings of the Ieee 103, 1531–1559, https://doi.org/10.1109/Jproc.2015.2455028 (2015).
Oldfield, R. C. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9, 97–113 (1971).
Rossi, S., Hallett, M., Rossini, P. M. & Pascual-Leone, A. & Safety of, T. M. S. C. G. Safety, ethical considerations, and application guidelines for the use of transcranial magnetic stimulation in clinical practice and research. Clin Neurophysiol 120, 2008–2039, https://doi.org/10.1016/j.clinph.2009.08.016 (2009).
Premoli, I., Costantini, A., Rivolta, D., Biondi, A. & Richardson, M. P. The Effect of Lamotrigine and Levetiracetam on TMS-Evoked EEG Responses Depends on Stimulation Intensity. Front Neurosci 11, 585, https://doi.org/10.3389/fnins.2017.00585 (2017).
Oostenveld, R., Fries, P., Maris, E. & Schoffelen, J. M. FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput Intell Neurosci 2011, 156869, https://doi.org/10.1155/2011/156869 (2011).
Premoli, I. et al. The impact of GABAergic drugs on TMS-induced brain oscillations in human motor cortex. Neuroimage 163, 1–12, https://doi.org/10.1016/j.neuroimage.2017.09.023 (2017).
Herring, J. D., Thut, G., Jensen, O. & Bergmann, T. O. Attention Modulates TMS-Locked Alpha Oscillations in the Visual Cortex. The Journal of neuroscience: the official journal of the Society for Neuroscience 35, 14435–14447, https://doi.org/10.1523/jneurosci.1833-15.2015 (2015).
Korhonen, R. J. et al. Removal of large muscle artifacts from transcranial magnetic stimulation-evoked EEG by independent component analysis. Med Biol Eng Comput 49, 397–407, https://doi.org/10.1007/s11517-011-0748-9 (2011).
Rogasch, N. C. et al. Removing artefacts from TMS-EEG recordings using independent component analysis: importance for assessing prefrontal and motor cortex network properties. NeuroImage 101, 425–439, https://doi.org/10.1016/j.neuroimage.2014.07.037 (2014).
Delorme, A. & Makeig, S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods 134, 9–21, https://doi.org/10.1016/j.jneumeth.2003.10.009 (2004).
Cohen, M. X. & Donner, T. H. Midfrontal conflict-related theta-band power reflects neural oscillations that predict behavior. J Neurophysiol 110, 2752–2763, https://doi.org/10.1152/jn.00479.2013 (2013).
Bro, R. & Kiers, H. A. L. A new efficient method for determining the number of components in PARAFAC models. Journal of Chemometrics 17, 274–286, https://doi.org/10.1002/cem.801 (2003).
Andersson, C. A. & Bro, R. The N-way Toolbox for MATLAB. Chemometrics and Intelligent Laboratory Systems 52, 1–4, https://doi.org/10.1016/S0169-7439(00)00071-X (2000).
Comon, P., Luciani, X. & de Almeida, A. L. F. Tensor decompositions, alternating least squares and other tales. Journal of Chemometrics 23, 393–405, https://doi.org/10.1002/cem.1236 (2009).
Sidiropoulos, N. D. et al. Tensor Decomposition for Signal Processing and Machine Learning. Ieee Transactions on Signal Processing 65, 3551–3582, https://doi.org/10.1109/Tsp.2017.2690524 (2017).
Massimini, M. et al. Breakdown of cortical effective connectivity during sleep. Science 309, 2228–2232, https://doi.org/10.1126/science.1117256 (2005).
Voineskos, A. N. et al. The role of the corpus callosum in transcranial magnetic stimulation induced interhemispheric signal propagation. Biol Psychiatry 68, 825–831, https://doi.org/10.1016/j.biopsych.2010.06.021 (2010).
Lopes da Silva, F. Neural mechanisms underlying brain waves: from neural membranes to networks. Electroencephalogr Clin Neurophysiol 79, 81–93 (1991).
Neuper, C. & Pfurtscheller, G. Event-related dynamics of cortical rhythms: frequency-specific features and functional correlates. Int J Psychophysiol 43, 41–58 (2001).
Pfurtscheller, G., Graimann, B., Huggins, J. E., Levine, S. P. & Schuh, L. A. Spatiotemporal patterns of beta desynchronization and gamma synchronization in corticographic data during self-paced movement. Clin Neurophysiol 114, 1226–1236 (2003).
Pfurtscheller, G. & Lopes da Silva, F. H. Event-related EEG/MEG synchronization and desynchronization: basic principles. Clin Neurophysiol 110, 1842–1857 (1999).
Brignani, D., Manganotti, P., Rossini, P. M. & Miniussi, C. Modulation of cortical oscillatory activity during transcranial magnetic stimulation. Hum Brain Mapp 29, 603–612, https://doi.org/10.1002/hbm.20423 (2008).
Conde, V. et al. The non-transcranial TMS-evoked potential is an inherent source of ambiguity in TMS-EEG studies. Neuroimage 185, 300–312, https://doi.org/10.1016/j.neuroimage.2018.10.052 (2019).
Escudero, J., Acar, E., Fernandez, A. & Bro, R. Multiscale entropy analysis of resting-state magnetoencephalogram with tensor factorisations in Alzheimer’s disease. Brain Res Bull 119, 136–144, https://doi.org/10.1016/j.brainresbull.2015.05.001 (2015).
Acknowledgements
J.E. acknowledges support by EPSRC, UK, under Grant EP/N014421/1 and from an RS MacDonald Seedcorn Award. M.P.R. is funded by MRC Programme Grant MR/K013998/1, EPSRC Centre for Predictive Modelling in Healthcare EP/N014391/1, and by the NIHR Biomedical Research Centre and South London at Maudsley NHS Foundation Trust and King’s College London. This study represents independent research supported by the National Institute for Health Research (NIHR)-Wellcome King’s Clinical Resaerch Facility and the NIHR Biomedical Research Centre at South London and Maudsley NHS Foundation Trust and King’s College London. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health and Social Care.
Author information
Authors and Affiliations
Contributions
M.R., J.E. and R.C. designed and supervised the research. I.P. collected and preprocessed the data. C.T. and L.S. wrote the analysis scripts. C.T. analysed the data. C.T., I.P. and J.E. wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tangwiriyasakul, C., Premoli, I., Spyrou, L. et al. Tensor decomposition of TMS-induced EEG oscillations reveals data-driven profiles of antiepileptic drug effects. Sci Rep 9, 17057 (2019). https://doi.org/10.1038/s41598-019-53565-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-53565-9
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.