Abstract
The 2016 Paris agreement set a global mean surface temperature (GMST) goal of not more than 2 degrees Celsius above preindustrial. This is an ambitious goal that will require substantial decreases in emission rates of long-lived greenhouse gasses (GHG). This work provides a mathematical framework, based on current state of the art climate models, to calculate the GHG emissions consistent with prescribed GMST pathways that meet the Paris agreement goal. The unique capability of this framework, to start from a GMST timeseries and efficiently calculate the emissions required to meet that temperature pathway, makes it a powerful resource for policymakers. Our results indicate that aerosol emissions play a large role in determining the near-term allowable greenhouse gas emissions that will limit future warming to 2 °C, however in the long term, drastic GHG emissions reductions are required under any reasonable aerosol scenario. With large future aerosol emissions, similar to present day amounts, GHG emissions need to be reduced 8% by 2040 and 74% by 2100 to limit warming to 2 °C. Under a more likely low aerosol scenario, GHG emissions need to be reduced 36% and 80% by 2040 and 2100, respectively. The Paris agreement Intended Nationally Determined Contributions are insufficient to meet this goal.
Similar content being viewed by others
Introduction
A pressing question in this era of global change is how much GHG emissions need to be reduced to limit global warming. Although no human-caused climate perturbation is desirable, the 2015 Paris agreement set a GMST goal of below 2 °C compared to preindustrial levels, with an effort to limit warming to 1.5 °C. While some authors suggest that the 1.5 degree goal is still attainable1,2 many others argue that it is unlikely without immediate and drastic reductions in emissions or active carbon sequestration, i.e. negative emissions3,4. Current policy efforts in the form of INDCs are not predicted to achieve a 1.5 or even 2 °C GMST anomaly by end of century5,6,7. There are arguments that overshooting scenarios, i.e. situations in which the GMST rises above the goal temperature for some period before returning to the goal, can help achieve temperature goals by releasing energy from the Earth system to space via long wave radiation. Overshooting scenarios can have converging climate properties similar to non-over-shooting scenarios with the same cumulative CO2 emissions depending on the time horizon8. However, there is a growing consensus that overshooting scenarios for end of century temperature goals will require negative emissions4,5,9. Negative emissions scenarios are not reliable plans for global warming mitigation. Not only are they susceptible to future political will, the technology is also currently not developed or tested10. Furthermore, solar geoengineering is not a reliable offset for GHG radiative forcing. There are many potential risks to humanity associated with solar geoengineering, including; acid rain, changes to the hydrological cycle, and termination shock, i.e. a dramatic warming if solar engineering is stopped10. As such, the safest plan for limiting future warming is to limit GHG emissions.
The year that the Paris agreement was signed, 2016, saw record global warming of 1.23 °C above preindustrial, and the last decade, 2009–2018, has warmed by 0.3 °C alone11. Although some of this recent warming was likely an accelerated response to the 2000’s global warming slowdown, the current warming rate need only be maintained for a decade before we reach 1.5 °C. Thus, in this paper, we focus on the emission limits that would lead to the more attainable goal of a 2 °C above preindustrial.
Results
While most climate studies5,12,13 start with a GHG scenario and calculate the GMST response, the technique presented here does the opposite, and starts with a policy relevant temperature goal, 2 °C above preindustrial, and calculates the GHG emissions that would create that temperature. We consider two temperature pathways that approach 2 °C by 2100 and maintain 2 °C out to 2200; a logistic function that exponentially asymptotes, and an overshooting pathway (Fig. 1a,b). We extend our analysis to 2200 to ensure that the temperatures are not simply passing through the end of century goal, but are maintained. Using a novel kernel method14, based on the 5th Climate Model Intercomparison Project (CMIP5)15 GMST response to CO2 forcing, we calculate the total effective radiative forcing (ERF) that the average CMIP5 climate model would need to follow to achieve these GMST pathways. The allowed GHG ERF is calculated by subtracting an assumed aerosol scenario (Fig. 1c,d) from the total ERF. The NOAA Adjusted Greenhouse Gas Index (AGGI)16 over the last 40 years is used to calibrate the historical aerosol ERF.
(a,b) The historical GMST anomaly24,25,26,27 (blue) along with assumed future asymptotic and overshoot temperature pathways (black). (c,d) The allowed GHG effective radiative forcing (ERF) calculated from the fitted temperature time series using the CMIP5 kernels (black) and two different aerosol scenarios. Dashed lines indicate the reduced anthropogenic aerosol scenario. Grey shading indicates the range of ERF calculated from the inter 2/3 s of CMIP5 model kernels. The NOAA GHG forcing16 during the past few decades is shown in blue. (e,f) The past and future equivalent CO2 emissions (CO2e) corresponding the GHG ERF time series. Recent CO2e emission estimates from the Netherlands Environmental Assessment Agency (PBL)19 are plotted in blue for comparison. For reference, 1ppmv equals about 7.8 Pg of CO2.
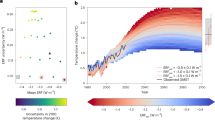
Aerosols, which scatter light back to space, negatively force the climate system and offset some of the GHG ERF. Larger future aerosol emissions would allow more GHG emissions for the same temperature change. We partition the future ERF pathway into GHG, volcanic, and anthropogenic aerosol. While future volcanic eruptions are impossible to predict, not including a volcanic term would bias the results. Thus, we assume a constant volcanic aerosol ERF equal to the global mean volcanic aerosol forcing over the historical period from 1850–2011 of −0.35 (W/m2)17. Adding variability to future volcanic forcing does not change the allowed cumulative GHG emissions. The amount of future anthropogenic aerosol assumed greatly affects the GHG emissions allowable under a 2 °C temperature pathway. We consider two future scenarios, a high aerosol scenario in which the anthropogenic aerosols offset a similar fraction of the GHG forcing as they do in 2017 and a low aerosol scenario in which the aerosol forcing is reduced to 0.4 W/m2 over the next 60 years. The latter is chosen to be consistent with the CMIP5 RCP45 projections. The aerosol radiative forcing at the end of the century in these two scenarios are 1.17 and 0.4 W/m2, respectively (Fig. 2). The low aerosol scenario is considered a more realistic scenario, as emissions of anthropogenic aerosol are expected to decrease with decreased GHG emissions and increased pollution controls. It is unlikely that GHG emissions will decrease without related reductions in aerosol emissions.
Using the analytical formulae to convert GHG ERF to CO2 concentration, and the atmospheric lifetime of CO2, we calculate the corresponding equivalent CO2 (CO2e) emissions that would result in the calculated GHG forcing (Fig. 1e,f) (see methods). Here we use a quad exponential based on empirical fits to a carbon cycle multi-model intercomparison to calculate the lifetime of CO218. The allowed GHG emissions calculated in this study are sensitive to the CO2 lifetime, and an increase in the CO2 lifetime would decrease the allowed emissions calculated using this method. However, our independent estimate of historical GHG emissions derived from the temperature and CMIP5 models compares well with a bottom up CO2e emissions estimate19 (Fig. 1e,f). GHGs have different lifetimes and thus will affect climate on different time scales. Here we use CO2e to represent GHG emissions, knowing that CO2e does not capture the complex set of scenarios that can evolve with different ratios of GHG emissions. However, CO2e is the best metric available for current predictions starting from temperature and forcing requirements and provides a robust estimate of GHG emissions that is comparable with past literature. Under the asymptotic temperature pathway and high aerosol burden, the global CO2e emissions peak at 7.0 ppmv yr−1 or 55 Gt yr−1 in 2024. Under reduced aerosols, CO2e emissions peak at 6.8 ppmv yr−1 or 53 Gt yr−1 in 2021. The overshoot temperature pathway allows for substantial increase in CO2e emissions for decades, however it also requires prolonged and unlikely negative emissions late this century.
Under either aerosol scenario, GHG emissions need to reduce drastically by the end of the century to limit warming to 2 °C (Fig. 1e,f). By 2100, the allowed CO2e emissions in the high and low aerosol scenarios are 11 and 14 Pg/yr, respectively. The assumed aerosol scenario mostly affects the near-term emissions limits, with high aerosol emissions simply buying time before GHG reductions are necessary.
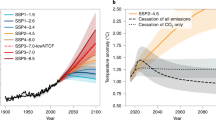
Figure 3 highlights the near-term future of the CO2e emission pathways shown on Fig. 1. The uncertainty estimates indicate the emissions required by the inter 2/3 CMIP5 models to recreate the prescribed temperature pathways. This spread reflects the range of model climate sensitivities. However, all of the models respond to increased GHG emissions with increased warming. Although this range encompasses both the current policy and INDC estimates, the uncertainty presented in Fig. 3 should not be interpreted as allowable emissions limits before mitigation. The GHG ERF and emissions derived from the median CMIP5 model response is consistent with observed GHG forcing and emissions estimates16,19. Therefore, following the median emissions pathway gives the best chance at following the prescribed temperature pathways.
Near-term allowed CO2e emissions limits for high (solid line) and low (dashed line) aerosol scenarios for each temperature pathway along with estimates of recent bottom up emissions19 (blue) and future emissions from INDCs (purple) and current policies (orange) in 2025 and 20306. Grey shading indicates the range of ERF calculated from the inter 2/3 s of CMIP5 model kernels.
To be consistent with 2 °C warming in 2100, CO2e emissions need to decrease by 8% in 2040 and 74% in 2100 assuming no reductions in aerosols (Fig. 2a, Table 1). The estimated INDC emissions in 2025 and 2030 are consistent with the median emission pathway. The current policy estimates and INDCs indicate increasing emissions between 2025 and 2030 however, which is inconsistent with a 2 °C temperature limit. CO2e emissions need to start decreasing in the near future to limit warming to 2 °C, and every year they continue to rise, that temperature goal becomes less likely. The overshoot pathway, even under the low aerosol scenario, allows for larger GHG emissions than current policy estimates. However, this scenario would require reliance on negative emissions later in the century (Fig. 2b).
If anthropogenic aerosol pollution is reduce as expected, the emissions reductions necessary to reach the 2 °C temperature goal are much greater. Under our clean air (low aerosol) scenario, which has 65% less anthropogenic aerosol forcing in 2100, CO2e emissions need to be reduced by 40% by 2040 and 82% by 2100 (Table 1). These are substantial reductions in emissions and well outside of the near term INDC estimates, however these may still be feasible. A recent study finds that phasing out the current fossil fuel infrastructure over the next 40 years might limit warming to 1.5 C; however, waiting until 2030 to start mitigation greatly reduces that likelihood2.
It is well known that the GMST is proportional to the cumulative CO2e emissions20,21, so it is not surprising that the cumulative CO2e emission for the two temperature pathways converge after 2100 (Fig. 4a). Between 2019 and 2100, allowed cumulative CO2e emissions to achieve 2 °C warming under our high aerosol scenario are 2900 (2470–3650) Pg. If the anthropogenic aerosol burden is reduced by about 65%, the cumulative allowed CO2e emissions are 1820 (1470–2440) Pg by 2100.
Cumulative CO2e (a) and ocean heat content (OHC) (b) associated with each temperature pathway (see Fig. 1). Grey shading indicates the range of OHC from the asymptotic temperature pathway and the inter 2/3 of CMIP5 kernels.
Global surface warming is not the only climate risk associated with GHG emissions. Along with surface warming comes precipitation changes, ocean acidification, and global sea level rise4. We find that the change in ocean heat content (OHC) in the overshoot temperature pathway is about 300 ZJ larger in 2100 than in the asymptotic pathway (Fig. 4b). This translates into 3 cm difference in thermosteric seal level in 2100 between the two scenarios. Consistent with our findings, the GFDL model indicated strong pathway-dependence of sea level rise in northern North American cities, with overshoot forcing producing up to 10 cm of additional thermosteric sea level rise by 2100 relative to stabilization forcing12. Furthermore, we note that although the GMST remains constant at 2 °C under these temperature pathways, the OHC and sea level show no signs of stabilization by 2200. While temperature goals are useful, it is important to be mindful of the many additional climate risks associated with elevated CO2 and other GHG concentrations.
Discussion
Future aerosol emissions play a crucial role in determining the allowable GHG emissions. However, the heterogeneity in space and time of future aerosol emissions adds a great deal of uncertainty to estimating the radiative forcing. Variability in the timing of volcanic eruptions will create variability in the ERF and climate signal from aerosols but will not affect the cumulative allowed GHG emissions to reach the 2 °C temperature target. Regional changes in the type and amount of anthropogenic aerosol emission could change the anthropogenic aerosol ERF directly through the amount of aerosol emitted and indirectly through changes in efficacy which is tied to the location and type of emitted aerosol. Recent observations suggest differing regional trends in aerosol optical depth and radiative forcing22,23. For these reasons, we consider a large range of future aerosol ERF in calculating our allowed GHG emissions.
Global GHG emissions and atmospheric concentrations are still on the rise16. Each year that we persist with the “business as usual” plan puts the Paris agreement temperature goals further out of reach. Modest GHG emission reductions, beyond the INDCs, in the near future could keep us on track to limiting warming to 2 °C, however aerosol emissions add a great deal of uncertainty about the timing and rate of GHG reductions. Cleaning up anthropogenic aerosol emissions, which is a likely scenario under GHG emissions mitigation, will require much larger reductions in GHG emissions in the near-term and slightly larger reductions in the long term to limit global warming to 2 °C above preindustrial. Regardless of the aerosol scenario, GHG emissions need to drastically reduce by 2100, with high aerosol emissions only buying a little time.
Methods
Calculating GHG effective radiative forcing from GMST
We fit Earth’s past GMST and the future pathway to 2 °C above preindustrial with a logistic function. Logistics make a very good approximation for past and current warming while constraining future warming to a goal temperature. We also include an overshoot scenario modeled as the logistic function, for consistency in past and current warming, with an added Gaussian function peaking in 2070 at 2.45 C. The functional forms of each fitted temperature pathway are as follows:
The slope (0.036) and midpoint (2014.5) of the logistic function were determined using a least-squares fit to the mean observed temperature anomaly time series from the following sources: NOAA24, GISS25, Hadcrut26, and Berkeley27.
We use the temporal kernel method14 to calculate the historical ERF from observed global mean surface temperatures based on the CMIP5 median kernel from the 4xCO2 experiments28. This method uses the response of the global mean surface temperature (T) to a radiative forcing step change experiment from the CMIP5 models to calculate a temporal kernel (t). We fit a function consisting of two exponentials to the temperature response in that step change experiments to extend our kernels out to 500 years14. Step change experiments, such as 4xCO2, in the CMIP5 simulations have constant ERF (F0). Here we use the median value from the models, F0 = 7.14 W/m2. In Eq. 3, i, is the year since the start of the simulation and j, is the year since the change in forcing. Here, Ti, is the total temperature response in year i to the scaled changes in forcing in years j = 0 to i, with ti-j, being the temperature response in year i to the change in forcing in year j. ΔFj is the change in forcing from the previous year.
Equation 4 is simply Eq. 3 written in matrix notation, where T and ΔF are one-dimensional vectors and t is a two-dimensional square matrix.
Equation 4 can be inverted to create Eq. 5, which calculates the change in forcing for a given temperature time series.
Finally, the ERF time series can be calculated as the sum of the forcing step changes.
The kernel functions (t) derived from the CMIP5 4xCO2 step change experiments for global mean surface temperature and ocean heat content are available online (https://github.com/larsonej/CMIP5_kernels). Here, the historical ERF is calculated from the observed temperature time series and is primarily the net forcing from the large positive GHG forcing and large negative forcing from volcanic and anthropogenic aerosols. There are many other forcing agents, such as ozone and land use change, that are small compared to these two.
The GHG ERF is calculated by subtracting an aerosol ERF from the total ERF calculated above from the temperature anomalies. Here we use −0.35 W/m2 of constant volcanic aerosol forcing, which is the global mean forcing between 1850 and 2011 from the IPCC AR517. Although, we cannot predict future volcanic eruptions, assuming zero future volcanic forcing would bias our results. Using the mean volcanic forcing ignores the variability associated with volcanic events, but produces an energy budget that is consistent with past volcanic activity.
Published estimates are used for the past anthropogenic aerosol from 1880–201129. Between 1980 and 2018, we used a linearly decreasing anthropogenic aerosol term to −0.93 W/m2. This is done to both smooth variability over the past four decades, extend the time series, and to create a GHG ERF that is consistent with the NOAA AGGI16 (Fig. 1b). This anthropogenic aerosol estimate is consistent in magnitude and trend with other published estimates30,31. We considered two future anthropogenic aerosol emission scenarios. In the first scenario, the aerosol burden remains at or above present-day levels into the future and is scaled to the GHG forcing. The second scenario greatly reduces the anthropogenic aerosol burden to −0.4 W/m2 by the end of the century (Fig. 2), roughly consistent with the aerosol burden in the RPC4.5 scenario.
Calculating emissions from GHG ERF
We use the logarithmic CO2 forcing equation to calculate the equivalent CO2 (CO2e) concentration, Ci, from the GHG ERF time series, Fi32. The logarithmic formula presented here is for the adjusted radiative forcing, however, we are applying it to the ERF. Previous work has also showed that the instantaneous forcing follows a logarithmic relationship33. The assumption that the CO2 effective and adjusted radiative forcings are equivalent creates some uncertainty in the estimate. Zhang and Huang find that the effective and adjusted radiative forcings are 6.4 and 7.3 W/m2, or about 15% different in the CMIP5 models they assessed34. This suggests that this method may be underestimating the allowed GHG emissions. As long as the adjustments scale linearly with the forcing, this can be overcome by using the adjusted F0 in the kernel method as opposed to the effective F0. The kernels in this method are using an F0 of 7.14 W/m2 based on the median CMIP5 y-intercept of 150-year regressions of ΔT and N, the top of atmosphere radiative imbalance. The logarithmic formula for a quadrupling of CO2 provides 7.4 W/m2 of adjusted RF, or 0.26 W/m2 different. Thus, the underestimate is expected to be about 3.5 percent. This is small compared to the substantial spread in the CMIP5 model calculated forcing, which is encompassed in the uncertainty estimates in the figures.
To convert the CO2e concentration to allowed emissions, we need to consider the lifetime of CO2 in the atmosphere. The remaining fraction of CO2e, X, is modeled as a sum of exponentials with weights (w = 0.2173, 0.224, 0.2824, 0.2763) and lifetimes (t = 394.4, 36.54, 4.304 years) from a multi-model analysis18.
The total concentration of CO2e in year i given an emission timeseries can then be written as
where Xi-j is the fraction of CO2e emitted in year j that remains in year i, and Ej, is the emission in year j. Similar to the temporal kernel method, X, can be treated as a kernel and Eq. 9 can be written in matrix form and inverted as follows,
The allowed CO2e emissions are then calculated using the inverted kernel and the concentration time series.
OHC from ERF
Ocean heat content (OHC) consistent with each temperature pathway is calculated from the historical and future ERF using the temporal kernel method14,28 described above.
References
Holden, P. B. et al. Climate–carbon cycle uncertainties and the Paris Agreement. Nat. Clim. Change 8, 609–613 (2018).
Smith, C. J. et al. Current fossil fuel infrastructure does not yet commit us to 1.5 °C warming. Nat. Commun. 10, 101 (2019).
Goodwin, P. et al. Pathways to 1.5 °C and 2 °C warming based on observational and geological constraints. Nat. Geosci. 11, 102–107 (2018).
Knutti, R., Rogelj, J., Sedláček, J. & Fischer, E. M. A scientific critique of the two-degree climate change target. Nat. Geosci. 9, 13–18 (2016).
Sanderson, B. M., O’Neill, B. C. & Tebaldi, C. What would it take to achieve the Paris temperature targets?: Achieving the paris temperature targets. Geophys. Res. Lett. 43, 7133–7142 (2016).
Schleussner, C.-F. et al. Science and policy characteristics of the Paris Agreement temperature goal. Nat. Clim. Change 6, 827–835 (2016).
Rogelj, J. et al. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 534, 631–639 (2016).
Nusbaumer, J. & Matsumoto, K. Climate and carbon cycle changes under the overshoot scenario. Glob. Planet. Change 62, 164–172 (2008).
Tanaka, K. & O’Neill, B. C. The Paris Agreement zero-emissions goal is not always consistent with the 1.5 °C and 2 °C temperature targets. Nat. Clim. Change 8, 319–324 (2018).
Lawrence, M. G. et al. Evaluating climate geoengineering proposals in the context of the Paris Agreement temperature goals. Nat. Commun. 9, 3734 (2018).
NOAA National Centers for Environmental information. Climate at a Glance: Global Time Series (2019).
Palter, J. B., Frölicher, T. L., Paynter, D. & John, J. G. Climate, ocean circulation, and sea level changes under stabilization and overshoot pathways to 1.5 K warming. Earth Syst. Dyn. 9, 817–828 (2018).
Goodwin, P., Brown, S., Haigh, I. D., Nicholls, R. J. & Matter, J. M. Adjusting Mitigation Pathways to Stabilize Climate at 1.5 °C and 2.0 °C Rise in Global Temperatures to Year 2300. Earths Future 6, 601–615 (2018).
Larson, E. J. L. & Portmann, R. W. A Temporal Kernel Method to Compute Effective Radiative Forcing in CMIP5 Transient Simulations. J. Clim. 29, 1497–1509 (2016).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012).
Hofmann, D. J. et al. The role of carbon dioxide in climate forcing from 1979 to 2004: introduction of the Annual Greenhouse Gas Index. Tellus B Chem. Phys. Meteorol. 58, 614–619 (2006).
IPCC, 2013: Annex II: Climate System Scenario Tables. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Prather, M. et al.) 1395–1445 (Cambridge University Press, 2014).
Joos, F. et al. Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: a multi-model analysis. Atmospheric Chem. Phys. 13, 2793–2825 (2013).
Olivier, J. G. J. & Peters, J. A. W. Trends in global CO 2 and total greenhouse gas emissions: 2018 report. (PBL Netherlands Environmental Assesment Agency, 2018).
Gillett, N. P., Arora, V. K., Matthews, D. & Allen, M. R. Constraining the Ratio of Global Warming to Cumulative CO2 Emissions Using CMIP5 Simulations*. J. Clim. 26, 6844–6858 (2013).
Zickfeld, K., MacDougall, A. H. & Matthews, H. D. On the proportionality between global temperature change and cumulative CO 2 emissions during periods of net negative CO 2 emissions. Environ. Res. Lett. 11, 055006 (2016).
Ningombam, S. S. et al. Long-term (1995–2018) aerosol optical depth derived using ground based AERONET and SKYNET measurements from aerosol aged-background sites. Atmospheric Pollut. Res. 10, 608–620 (2019).
Paulot, F., Paynter, D., Ginoux, P., Naik, V. & Horowitz, L. W. Changes in the aerosol direct radiative forcing from 2001 to 2015: observational constraints and regional mechanisms. Atmospheric Chem. Phys. 18, 13265–13281 (2018).
Vose, R. S. et al. NOAA’s Merged Land–Ocean Surface Temperature. Analysis. Bull. Am. Meteorol. Soc. 93, 1677–1685 (2012).
Hansen, J., Ruedy, R., Sato, M. & Lo, K. Global Surface Temperature Change. Rev. Geophys. 48, RG4004 (2010).
Morice, C. P., Kennedy, J. J., Rayner, N. A. & Jones, P. D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set: The Hadcrut4 Dataset. J. Geophys. Res. Atmospheres 117, n/a–n/a (2012).
Rohde, R., A. Muller, R., Jacobsen, R., Muller, E. & Wickham, C. A New Estimate of the Average Earth Surface Land Temperature Spanning 1753 to 2011. Geoinformatics Geostat. Overv. 01 (2013).
Larson, E. J. L., Portmann, R. W., Solomon, S. & Murphy, D. M. Decadal attribution of historic temperature and ocean heat content change to anthropogenic emissions. Preprint at https://arxiv.org/abs/1910.13651 (2019).
Meinshausen, M. et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Change 109, 213–241 (2011).
Skeie, R. B. et al. Anthropogenic radiative forcing time series from pre-industrial times until 2010. Atmospheric Chem. Phys. 11, 11827–11857 (2011).
Miller, R. L. et al. CMIP5 historical simulations (1850–2012) with GISS ModelE2. J. Adv. Model. Earth Syst. 6, 441–478 (2014).
Myhre, G. et al. Anthropogenic and Natural Radiative Forcing. in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T. F. et al. (eds)] (Cambridge University Press, 2013).
Huang, Y. & Bani Shahabadi, M. Why logarithmic? A note on the dependence of radiative forcing on gas concentration: Huang & Bani Shahabadi. J. Geophys. Res. Atmospheres 119(13), 683–13,689 (2014).
Zhang, M. & Huang, Y. Radiative Forcing of Quadrupling CO2. J. Clim. 27, 2496–2508 (2014).
Acknowledgements
We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP. We thank the climate modelling groups for producing and making available their model output, and the International Institute for Applied System Analysis for hosting the IPCC AR5 Scenario Database. For CMIP, the US Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provided coordinating support and led development of so ware infrastructure in partnership with the Global Organization for Earth System Science Portals. This study was supported in part by NOAA’s Climate Program Office.
Author information
Authors and Affiliations
Contributions
E.J.L.L. led the writing of the manuscript and carried out the analysis with significant contributions from R.W.P.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Larson, E.J.L., Portmann, R.W. Anthropogenic aerosol drives uncertainty in future climate mitigation efforts. Sci Rep 9, 16538 (2019). https://doi.org/10.1038/s41598-019-52901-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-52901-3
This article is cited by
-
CO2 conversion to synthetic fuels using flow cell reactor over Cu and Ag based cathodes
Materials for Renewable and Sustainable Energy (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.