Introduction

Generation of dissipationless spin-polarized (spin-triplet) supercurrent is the major interest of superconducting devices, which can be utilized to establish energy efficient superconducting spintronics1,2. In last two decades, rigorous works have been conducted to produce and control spin-triplet supercurrents using heterostructures of ferromagnets (Fs) and conventional spin-singlet superconductors (SSCs)3,4,5,6,7,8,9,10,11,12,13. It has been established that magnetic inhomogeneity is always required to emerge spin-triplet supercurrent at F/SSC interface, which can be achieved by e.g. using non-collinear magnetization in multilayer ferromagnets6,7,9. Complicated magnetic structure of multilayer ferromagnets makes it hard to functionalize the F/SSC devices. This issue can be settled by replacing SSC with a spin-triplet superconductor (TSC). In F/TSC heterostructures, a single F layer can effectively emerge spin-polarized supercurrents with fully conserved spin degree of freedom in the entire device. Furthermore, recent theoretical work suggested that superconducting properties of F/TSC junctions strongly depends on relative orientation of magnetization (m) of the F and d-vector of the TSC14,15,16,17,18. Interestingly, when the d-vector and m are perpendicular (i.e. when the angle between d-vector and m, θmd, = π/2) the spin-triplet correlation can induce monotonically over a long range. However, for parallel configuration, i.e. θmd = 0, the induced order parameter oscillates spatially18.

Sr2RuO4 (SRO214) is one of the best-candidates of TSCs19 with the superconducting critical temperature (Tc) of 1.5 K. Most likely, it exhibits the chiral p-wave spin-triplet state with broken time-reversal symmetry20,21,22,23,24,25,26,27,28, although there are still unresolved issues29,30,31. We should comment that the very recent nuclear magnetic resonance (NMR) study shows the reduction of Knight shift, which cannot be explained by a simple chiral-p-wave spin-striplet scenario32,33. Such a chiral-p-wave superconductivity in, SRO214 attracts interest for exploring topological superconducting phenomena originating from its orbital phase winding19,26,27,28. The superconducting order parameter of a SRO214 can be represented by a vector d = \(\hat{{\bf{z}}}\)(px ± ipy), where \(\hat{{\bf{z}}}\) is the out-of-plane (along the c-axis) basis vector, and px and py are the x and y components of the orbital order parameters, respectively19. Note that the d-vector is always perpendicular to the spin of triplet Cooper pairs. For bulk SRO214 superconductor, d-vector is aligned along the c-axis (out-of-plane) fixed by spin-orbit coupling34,35,36 but at the surface it may not be true because of surface effects. It is expected that d-vector may rotate to the in-plane direction with external magnetic field of about 20 mT applied along the out-of-plane direction37,38.

Newly, we developed F/TSC heterostructures by growing epitaxial ferromagnetic SrRuO3 (SRO113) thin films on a spin-triplet superconductor SRO214 single crystal using pulsed laser deposition39. Furthermore, long-ranged proximity effect is also observed, where even frequency p-wave spin-triplet correlation may dominate compared to odd frequency s-wave spin-triplet, as junctions were in clean limit40,41.

In this article, we present our investigations on differential conductance (dI/dV) of Au/SRO113/SRO214 junctions as a function of temperature and magnetic field applied along both in-plane (Hin) and out-of-plane (Hout) directions. We found that the induced correlation exhibits anisotropic behaviour in the response of applied field. Vortex dynamics cannot explain our results. This anisotropic effect can be attributed to the relative orientation of the d-vector of SRO214 and m of SRO113.

Results

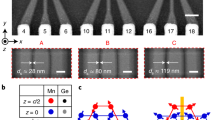
In this article, we present the results of various junctions but mainly focus on two junctions J4 and J5 that exhibit different normal-state resistance (RN) 7.83 m Ω and 198 m Ω, respectively. A schematic illustration of a junction is shown in Fig. 1(a).

Figure 1
figure 1

(a) Schematic of Au/SrRuO3/Sr2RuO4 junctions. Note that a ≈ 30-nm thick neck of SRO214 was prepared in order to separate a part of superconductor from the bulk substrate. (b) Temperature dependent resistance R(T) from 300 K down to 2 K for Junction J1 with the junction area of 20 × 20 μm2. Inset shows R(T) close to the superconducting transition. (c) R(T) of Junction J4 (5 × 5 μm2) at various applied currents. Vertical solid line indicates the bulk Tc of SRO214. Inset shows R(T) of the SRO214 substrate measured by using a four probes technique. (d) Current-voltage curves below and above Tc of Junction J4.

Full size image

Temperature dependent resistance R(T) was measured during cooling in zero field down to 300 mK. SRO214, SRO113 and Au are good metals with very low resistivity at low temperatures, except the resistivity of SRO214 along the c-axis (ρc)29. It suggests that at low temperatures resistivity of our junctions is dominated by the SRO113/SRO214 and Au/SRO113 interfaces39,40. Our present junctions exhibit RRR = 27, which that is three times larger than that of our previous junctions40. Furthermore, a sharp superconducting transition is observed that reflects good quality of the junctions (inset of Fig. 1(b)). It is also clear that, in the normal state, the resistivity data have major contributions of ρc of SRO214, as evidenced by the characteristic hump in R(T) at around 100 K. This result indicates that current is flowing along the normal of the junctions, which excludes the possibility of any direct contact between Au electrode and SRO214 superconductor.

Figure 1(c) presents R(T) at low temperatures of Junction J4 (5 × 5 μm2) measured with different applied currents (Ia in the range of 0.1 to 3 mA) that shows two superconducting regions robust and weak against Ia. At Ia = 0.1 mA the transition onset appears at Tc = 1.38 K, which is higher than Tc ≈ 1.23 K of SRO214 substrate (see the inset of Fig. 1(c)). This increase in Tc may arises due to mutual strain (pressure) between the substrate and the film close to the interface42. The R(T) behaviour with increasing Ia reveals that there are two distinct transition regions. The first transition with change in the resistance ΔR1 = 1.15 mΩ is only weakly dependent on Ia. The second transition is strongly suppressed with increasing Ia with the change in the resistance of ΔR2 = 0.45 mΩ. Multiple transitions are expected to emerge in a multi-barrier junction such as the junctions presented here: Normal-metal/F/TSC. Essentially, the same behaviour has been observed in our previous study40. These observations suggest that ΔR1 and ΔR2 correspond to resistance changes at the SRO113/SRO214 and Au/SRO113 interfaces, respectively. It means that dI/dV as a function of bias voltage should exhibit Andreev reflection (AR) features occurring at two distinct interfaces.Note that AR can occur for a bias voltage below superconducting gap (induced minigap in SRO11341) at SRO113/SRO214 (Au/SRO113) interface. To study the AR, we obtained dI/dV(V) by taking first order numerical derivative of the measured current-voltage (I-V) curves shown in Fig. 1(d). We investigate dI/dV as a function of externally applied magnetic fields both in-plane Hin and Hout directions and temperature as well.

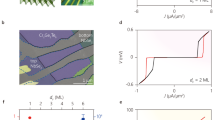
First, we present dI/dV data measured at different temperatures (see Fig. 2(a)). It shows an enhancement in dI/dV below superconducting transition temperature Tc. Below Tc, the conductance of a transparent F/SSC interface increases with opening of AR channel, which is related with spin-polarization of the ferromagnet as well. At 0.3 K and zero applied field (after zero field cooling), the conductance enhances by ≈10% below ±V3 with almost flat top. This transition yields the change in the conductance Δσ2 = 13.84 Ω−1 that corresponds to ΔR2 (second transition in R(T)). At temperatures higher than 1.1 K an additional enhancement within our applied bias voltage can be observed at ±V2. Note that there are sharp dips associated with V2 features (Fig. 2(a)), which may correspond to the destruction of superconductivity at SRO113/SRO214 interface with critical current41. However, the temperature dependence of dI/dV (Fig. 2(c)) shows that the dip persists up to the bulk Tc, which suggests that the dip can be attributed to the critical current of SRO214-neck part of the junctions, and the proximity effect at the SRO113/SRO214 interface is simultaneously switched off. The V2 transition exhibits ≈14% increase with Δσ1 = 18.04 Ω−1 consistent with ΔR1 (first transition in R(T)). It indicates that characteristic voltages of V3 and V2 are corresponding to multi AR features occurred at Au/SRO113 and SRO113/SRO214 interfaces, respectively. The data presented in Fig. 2(b) is extracted from Fig. 2(c). It shows a monotonic suppression of the AR with increase in the temperature. Similar behaviour is observed for junction J5 as well which is shown in Fig. 3(f) and discussed more at the end of the section.

Figure 2
figure 2

Temperature and field dependent differential conductance (dI/dV) of Au/SrRuO3/Sr2RuO4 Junction J4. (a) dI/dV measured at different temperatures between 1.4 K and 0.3 K. At 0.3 K a flat-top central conductance peak appears between ±V3. Note that there are additional oscillations with the minima at V1* and V2*. At temperatures above 1.1 K, another transition at ±V2 becomes visible within the range of bias voltage. (b) Temperature dependence of all characteristic voltages appeared in dI/dV data. (c) dI/dV at various temperatures. The data are shifted with a step of 10 m Ω−1 but for 1.2 K and 1.3 K are shifted with 30 m Ω−1 for clarity. dI/dV as a function of magnetic field applied along (d) the in-plane and (e) the out-of-plane (c-axis) directions. Data are shifted for clarity.

Full size image
Figure 3
figure 3

Differential conductance of Au/SrRuO3/Sr2RuO4 Junction J5. (a) Colour plot of dI/dV(V) vs temperature. The V3 is indicated with open circles. dI/dV(V) vs magnetic field applied along (b) the c-axis and (c) the in-plane directions, respectively. (d) V2 and V3 vs applied field along the c-axis normalized by the upper critical field. Inset shows R(T) at low temperatures of Junction J5. (e) All characteristic voltages V1, V2 and V3 vs in-plane applied field. V1 and V2 decrease expectedly. In contrast V3 exhibits an anisotropic behaviour with hysteresis below 200 mT. (f) Normalized V3 vs applied field along both in-plane (Hin) and out-of-plane directions Hout, as well as vs temperature plotted for comparison.

Full size image

The observations of multiple enhancements in dI/dV reveal that superconductivity penetrates into the 15-nm hick SRO113 layer and reaches at the Au/SRO113 interface as well. This is only possible with spin-triplet superconducting correlation, since spin-singlet coherence length of SRO113 is of the order of 1-nm43. Note that two additional oscillations with minima at V1* and V2* appear between V3 and V2. These oscillations are suppressed monotonically just like V3 with the increase in the temperature, see Fig. 2(b,c). These oscillations may correspond to McMillan-Rowell resonance44 resulting from interference between Andreev reflected quasiparticles at the SRO113/SRO214 interface and the quasiparticles reflected back into SRO113-layer from the Au/SRO113 interface.

The most interesting and important part of this study is voltage biased dI/dV as a function of applied field. Figure 2(d,e) shows the dI/dV(V) data obtained with the fields Hin and Hout, respectively. In case of the applied field Hin, V3 is abruptly suppressed up to 200 mT and decreases slowly with further increase in Hin. In contrast V2 is suppressed gradually, which is an expected behaviour of Cooper pair breaking under applied magnetic fields (orbital effects). For fields Hout, both V3 and V2 decreases monotonically. Thus spin-triplet proximity effect into the SRO113 layer exhibits an anisotropic response to applied field. Such an effect can be expected for anisotropic d-vector rotation with applied field, further discussions are given in the discussions section.

Junction J4 with lower RN exhibits various interesting features in the junction voltage. However, concerning to the signal to noise ratio a junction with larger RN is preferable. Indeed in Junction J5 with rather high RN = 198.2 mΩ, we observed good quality data that also exhibits AR features with multiple transitions. For Junction J5, dI/dV(V) as a function of temperature and applied field exhibit two transitions corresponding to V3 and V2. Note that we also obtained the V1 feature particularly at 0.3 K and zero field as observed in our previous junctions40. The characteristic voltage V1 most probably arises due to critical-current of SRO214 neck40. Note; in this junction the oscillations corresponding to McMillan-Rowell resonance are not observed due to its lower amplitude and higher RN. By comparing Fig. 3(b,c), a strong anisotropy in V3 is obviously reproduced. In fact, we observed this anisotropic effect in almost all our working junctions.

For Junction J5, under the effect of Hout fields, the characteristic voltage V2 shown in blue in Fig. 3(b) becomes vague at higher fields as shown in Fig. 3(d). It reflects that in junctions with higher RN (lower interface conductance) the AR features are overlapped with each other. However, all the characteristic-voltage features are obviously present for all Hin fields, see Fig. 3(e). Interestingly, V3 exhibits hysteretic effect only below 200 mT. For a comparison, we plotted normalized V3 as a function of field and temperature in Fig. 3(f).

We applied theoretical fits on temperature and field dependent V3 to analyse its behaviour. The behaviour of V3 versus temperature follows the interpolation formula, \({V}_{3}(T)={V}_{3}\mathrm{(0)}\,\tanh \,\sqrt{a({T}_{c}/T-\mathrm{1)}}\) with constant a = 1.56. We comment that the formula with the same functional form can be used to approximate the temperature dependence of the superconducting gap, with a = 1.74 for the s-wave superconductivity. Interesting, a = 1.56 is indicates unconventional superconducting proximity effect and potentially consistent with p-wave superconductivity41,45. The monotonic suppression of V3 under fields Hout can be reasonably fitted with the expression \({V}_{3}(H)={V}_{3}\mathrm{(0)}\sqrt{\mathrm{(1}-H/{H}_{c})}\). However, V3 under fields Hin is strongly suppressed at lower fields less than 200 mT and slowly decreases for higher fields. Note that the coercive field of SRO113 layer is ≈200 mT for rectangular pads of the size of tens of microns40. It indicates that there are two distinct decoherence effects on the induced spin-triplet correlation in the SRO113 layer, such as orbital effect and m rotation relative to the d-vector of SRO214 superconductor. The phenomenological fit shown in Fig. 3(f) is discussed below.

Discussion

Before starting our discussion, let us summarize our main results. We observed AR features in dI/dV with characteristic voltages V3 and V2 emerging at Au/SRO113 and SRO113/SRO214 interfaces, respectively. The V3 (V2) exhibits anisotropic (isotropic) behaviour in the response of applied magnetic field. The AR feature with V3 is suppressed strongly below 200 mT and decreases slowly with farther increase under the field Hin. However, V2 decreases monotonically with Hout and Hin as well. For the field along the c-axis V3 decreases similar to V2.

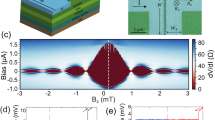
First, we discuss the subtraction of resistance contributions other than interfaces to estimate the accurate values of characteristic voltages V3 and V2. As described below, the measured resistance of our devices may contain some contributions from non-interface resistance, such as from the neck part of SRO214. To estimate accurate values of characteristic voltages specifically, V3 at 0.3 K, we subtract the contributions of estimated additional resistances. For simplicity, let us assume an ideal situation that AR probability is 100% so that the conductance of each interface is enhanced by a factor of two compared to its normal-state conductance. Under this assumption, for Junction-J4 (JunctionJ5) the total resistance of Au/SRO113 and SRO113/SRO214 interface is two times the ΔR = ΔR1 + ΔR2 = 1.55 mΩ (12.74 mΩ). At 0.3 K, additional resistance of JunctionJ4 (JunctionJ5) Ra = RN − 2ΔR = 4.73 m Ω (172.72 mΩ) that contributes additional voltage drop across the junction. We subtract a linear contribution of Ra and plotted the results in Fig. 4(a). It reveals that V3 for JunctionJ4 (junction-J5) is ≈3 μV (≈20 μV). It shows that JunctionJ5 exhibits an order higher V3 due to lower interface transparency and more drop of voltage across it.

Figure 4
figure 4

(a) Current-voltage curves at 0.3 K for Junctions J4 (red) and J5 (blue) after subtracting additional contributions. (b) R(T) at different applied fields both Hin and Hout. (c) Schematic illustration of induction of superconductivity in the junction. Explanations are given in the main text.

Full size image

It is important to discuss the vortex effect on proximity effect in Au/SRO113/SRO214 junctions, which can also be anisotropic. Of course, vortices can be induced for the fields higher than Hc1. Note that Hc1 of SRO214 is 1 mT and 70 mT along the a-axis (in-plane) and the c-axis19, respectively. Transport properties of a superconducting junction can be affected when vortices are crossing the interface because of vortex dynamics. According to the geometry of our junctions (c-axis is normal of the junction), the field induced vortices can encounter the interface only for fields Hout. However, vortices align parallel to the interface for the fields Hin. It means, AR features should exhibit additional suppression for fields Hout. In contrast, V3 is suppressed strongly for the fields Hin only.

To understand the effect of vortices in our junctions, we measured R(T) under the fields Hin and Hout. Even for the same effective field, Tc of the first transition with ΔR1 of SRO113/SRO214 interface decreases more under Hc than Hab, see Fig. 4(b). However, the second transition corresponding to Au/SRO113 interface is in contrast. It indicates that the electronic transport properties of our junctions can encounter vortices only for the fields Hout. Furthermore, it also reveals that the observed anisotropic response of V3 under applied fields does not arise due to vortex dynamics.

Effect from the spin part: spin-triplet proximity effect at F/TSC interface can be dictated by angle θdm between d-vector of SRO214 and m vector of SRO113 layer14,15,16,17,18. We applied a following phenomenological fit to V3(Hin),

$${V}_{3}(H)={V}_{3}(0)[F(H)-G({\theta }_{md})]$$
(1)

where, V3(0) is the characteristic voltage at zero temperature, \(F(H)=\sqrt{1-H/{H}_{c2}}\) and G(θmd) = A cos(θmd) with a constant A. We obtained a good fit by changing the θmd nonmonotonically; first linearly decreased until 200 mT and increased for higher fields. This model implicitly assumes that that d-vector is aligned along the in-plane direction at the interface.

In bulk SRO214 superconductor, the d-vector is aligned along the c-axis and in the result the spins of the Cooper pairs are aligned along the ab-plane. The d-vector and Cooper pair spins can be rotated with an applied magnetic field Hout of 20 mT37,38 to in-plane and to out-of-plane, respectively. In this scenario, Hin cannot rotate the d-vector. That means, proximity effect should supress more in case of Hout rather than Hin. But, our results are suggesting in contrast.

If the d-vector is perpendicular a space between perpendicular and to the c-axis particularly at the interface, V3 can be affected with rotation of θmd with Hin. It is be possible that broken inversion symmetry at the SRO113/SRO214 interface induces Rashba-type46 spin-orbit coupling with in-plane vector characterizing the spin–orbit coupling g = (ky, kx, 0) with out-of-plane effective field, which tends to align the d-vector along the in-plane direction. Additionally, out-of-plane magnetic anisotropy of SRO113 thin film is also supporting such an alignment of the d-vector. As a result, at zero applied field, spin of triplet Cooper pairs in SRO214 and m of SRO113 are parallel and thus θmd = π/2, which is a favourable configuration for proximity effect in F/TSC junctions. The angle θmd can be reduced with either rotation of m or d-vector that dictates the proximity effect in the junction accordingly18. It is most likely that the rotation of m of SRO113 is responsible for first strong suppression in V3 up to coercive field of SRO113-layer ≈200 mT40. It may also be the reason of hysteresis in V3 below 200 mT; above 200 mT, m is saturated and fully aligned along Hin. As a result θmd decreases up to coercive field and suppresses the proximity effect. On the other hand, at the same time, the applied field Hin tends to align the d-vector along the c-axis. Therefore, θmd never becomes zero and proximity effect is weakly suppressed with increasing Hin above 200 mT. In this configuration of d-vector at the interface as illustrated in Fig. 4(c), Hout cannot rotate the d-vector, as spins of Cooper pairs are aligned to the out-of-plane direction. Therefore, V3 suppresses monotonically with Hout. Of course, temperature change between 2 K and 0.3 K cannot change m or d-vector. Thus, there is no anomalous suppression in V3 as a function of temperature.

The rotation of the d-vector under the influence of an external magnetic field is well known for superfluid3 He-A phase47 analogous to the chiral p-wave spin-triplet superconductivity anticipated in SRO214. In case of the standard chiral-p-wave scenario for SRO214, the d-vector should be fixed along the c-axis because of spin-orbit coupling. Possibility of rotation of the d-vector to an in-plane direction under c-axis magnetic field is discussed in the NMR study for H||c37. However, at SRO113/SRO214 interface, broken inversion symmetry and out-of-plane exchange field of SRO113 can significantly affect the spin-orbit coupling. That may result into easier rotation of the d-vector along the in-plane direction. This scenario explains our results well. Theoretically, Annett et al.38, predicted that the d-vector rotation by magnetic field along the c-axis is accompanied by chiral to nonchiral phase transition depending on spin dependent effective pairing interaction. However, for a proximity effect in a junction based on a spin-triplet superconductor, the crucial parameter is the orientation of the d-vector18, whereas, the transition in the orbital part may not considerably modulate the proximity effect unless the junction size is of the order of the typical size of a chiral domain.

Effect from the orbital part: SRO214 exhibits multi-component (px + ipy) superconducting order parameter28. That may also explain this anisotropic behaviour of V3. The component px can be significantly suppressed compared to py when magnetic field Hin is parallel to y and vice versa48,49,50. However, the fields along the z-direction, perpendicular to the both px and py components, can simultaneously affect both components of the order parameter. In this way, the differential conductance should depend differently on the in-plane and out-of-plane applied magnetic fields. Such anisotropic effect corresponding to the order parameter of the bulk SRO214 should emerge mainly in the SRO214 side and that should result in anisotropic behaviour either only in V2 or both V2 and V3. Thus, our observed anomalous anisotropic behaviour only in V3 cannot be explained by the above mentioned non-chiral scenario. Rather, this observation supports that the spin-triplet proximity effect is controlled with the change in θmd due to the relative rotation of m and d-vector. More experimental and theoretical works are needed to understand and manipulate the rotation of θmd.

Conclusion

We studied long-range proximity effect in Au/SRO113/SRO214 double barrier junctions. Two distinct Andreev reflection features are observed in differential conduction vs bias voltage coming from two SRO113/SRO214 and Au/SRO113 interfaces with the induction of spin-triplet Cooper pairs in 15-nm thick SRO113 from SRO214. The transition of Au/SRO113 interface is suppressed anisotropically with externally applied magnetic fields. This anomalous anisotropic behaviour cannot be explained with vortex dynamics since differential conductance as a function of temperature and out-of-plane applied fields if qualitatively similar. However, conductance of SRO113/SRO214 interface suppressed faster when field is applied along the in-plane direction. Our results will stimulate the theoretical work to understand the correlation between unconventional superconductivity and ferromagnetism, p-wave proximity effect and applications to initiate the Superconducting Spintronics.

Methods

Single crystals of SRO214 were grown in Kyoto using a floating-zone method51. Some parts of the SRO214 crystals tend to contain Sr3Ru2O7, SRO113, as well as Ru-metal inclusions. These inclusions are unavoidable in order to eliminate Ru deficiencies and obtain Tc close to the intrinsic T ≈ 1.5 K. To fabricate our superconducting junctions, we carefully choose the parts of SRO214 crystals that do not contain impurities but with a slightly lower Tc ≈ 1.23 K. Ferromagnetic SRO113 thin films with thickness of 15-nm were epitaxially deposited using pulsed laser deposition on the cleaved ab-surface of the SRO214 substrates (3 × 3 × 0.5 mm3) in Seoul. The details of SRO113 thin film deposition can be found elsewhere39,40. Immediately after the growth of SRO113 film, a 5-nm thick Ti adhesive layer and a 20-nm thick Au capping layer were deposited ex-situ by dc-sputtering.

Double interface Au/SRO113/SRO214 junctions shown schematically in Fig. 1a were fabricated in RIKEN. First, 25 × 25 μm2 and 10 × 10 μm2 pads of SRO113 were prepared on flat surfaces using photolithography and Ar ion etching. Then, an insulating 300-nm thick SiOx layer was sputtered. Finally, a 600-nm thick Au top electrode was deposited by electron beam evaporation with junction areas of 20 × 20 μm2 and 5 × 5 μm2 over 25 × 25 μm2 and 10 × 10 μm2 SRO113 pads, respectively. Note, a 30-nm thick neck part of SRO214 substrate was prepared with over-etching during SRO113 layer etching to define a bottom superconducting electrode, as shown in Fig. 1(a). Detailed descriptions of these processes are given in ref.40.

Electrical transport measurements were performed using the four-point technique with two contacts (I+, V+) on the Au top electrode and the other two contacts (I−, V−) connected directly to the side of the SRO214 crystal. Transport properties were studied down to 300 mK using a3 He cryostat equipped with a vector superconducting magnet.