Abstract
Large-scale quantum communication networks are still a huge challenge due to the rate-distance limit of quantum key distribution (QKD). Recently, twin-field (TF) QKD has been proposed to overcome this limit. Here, we prove that coherent-state-based TF-QKD is a time-reversed entanglement protocol, where the entanglement generation is realized with entanglement swapping operation via an entangled coherent state measurement. We propose a coherent-state-based TF-QKD with optimal secret key rate under symmetric and asymmetric channels by using coherent state and cat state coding. Furthermore, we show that our protocol can be converted to all recent coherent-state-based TF-QKD protocols by using our security proof. By using the entanglement purification with two-way classical communication, we improve the transmission distance of all coherent-state-based TF-QKD protocols.
Similar content being viewed by others
Introduction
Since the first quantum key distribution (QKD) experiment with 32 cm free-space channel1, a lot of efforts have been devoted to achieving long-distance QKD. Recently, the maximum distance of point-to-point QKD has been pushed up to 421 km ultralow-loss fiber2. Several experiments show that quantum-limited measurement3,4 and QKD5 can be demonstrated by using satellite-to-ground downlink with more than 1000 km free-space channel. Furthermore, measurement-device-independent (MDI) QKD6 has been performed over 404 km ultralow-loss fiber7 by using the optimal four-intensity set8, which is immune to any attack on detection9 by exploiting the Bell state measurement. Further increasing the fiber-based transmission distance without quantum repeater is a difficult obstacle to overcome. In the literature, without the help of trusted relay or quantum repeater, people believe that the limit is approximately 500 km fiber10. The strong evidence comes from the secret key agreement capacity of repeaterless quantum channel11,12, where the optimal rate is linear scaling with the transmittance of two communication parties, known as the repeaterless bound12.
A breakthrough called twin-field (TF) QKD13 has been proposed to break this bound, resulting in many variants14,15,16,17,18,19,20,21,22 and experimental demonstrations23,24,25,26. However, each security proof of the coherent-state-based TF-QKD14,18,19,20, or called phase-matching QKD, is carefully tailored. Cat state, superposition of coherent states with two opposite phases, as an important resource, has been widely used for quantum information processing, including quantum computation27, quantum teleportation28, quantum repeater29,30, QKD31 and quantum metrology32. Importantly, cat states have been successfully generated and exploited to demonstrate various quantum tasks33,34,35,36,37.
Here, we point out the physics in coherent-state-based TF-QKD is exactly entanglement swapping operation via the entangled coherent state (ECS) measurement. The coherent-state-based TF-QKD is a time-reversed entanglement protocol by using ECS measurement, which is similar with the MDI-QKD by using the Bell state measurement. We propose a coherent-state-based TF-QKD protocol under symmetric and asymmetric channels by using coherent state and cat state coding. The entanglement purification with one-way38,39 and two-way40 classical communication techniques are used to prove the security of our protocol against coherent attacks in the asymptotic regime. The secret key rate of our protocol is larger than refs14,18,19. Furthermore, we show that our protocol can be converted to other coherent-state-based protocols14,18,19,20 by using our security proof, which means that all coherent-state-based TF-QKD can be unified under a single framework. We consider the TF-QKD with two-way classical communication, which significantly improves the transmission distance of all coherent-state-based TF-QKD protocols with large misalignment.
Results
ECS measurement
Generally, the symmetric beam splitter (BS) and single-photon detectors are used to implement the interference measurement of TF-QKD13. One can assume that the two inputs of BS are a and b modes while the two output modes are \(\tilde{a}=(a+b)/\sqrt{2}\) and \(\tilde{b}=(a-b)/\sqrt{2}\). The four two-mode ECS forms41,42 are \(|{\Phi }^{\pm }\rangle =(|\alpha \rangle |\alpha \rangle \pm |\,-\,\alpha \rangle |\,-\,\alpha \rangle )/\sqrt{{N}_{\pm }}\) and \(|{\Psi }^{\pm }\rangle =(|\alpha \rangle |\,-\,\alpha \rangle \pm |\,-\,\alpha \rangle |\alpha \rangle )/\sqrt{{N}_{\pm }}\), where \({N}_{\pm }=2(1\pm {e}^{-4\mu })\) are the normalization factors and \(\mu =|\,\pm \,\alpha {|}^{2}\) is the intensity of coherent states \(|\,\pm \,\alpha \rangle \). The four ECSs are sometimes called quasi-Bell states. The quantum states \(|\,\pm \,\alpha \rangle \) constitute the quasi-computational basis while the quantum states \(|{\xi }^{\pm }(\alpha )\rangle =(|\alpha \rangle \pm |\,-\,\alpha \rangle )/\sqrt{2}\) constitute the quasi-dual basis. After passing through the lossless symmetric BS, the four states become
where \(|{\rm{even}}{\rangle }_{\tilde{a}}\) (\(|{\rm{odd}}{\rangle }_{\tilde{a}}\)) means that the output mode \(\tilde{a}\) contains even (odd) photon numbers. If we consider the case of ideal photon-number-resolving detector and lossless channel, one can unambiguously discriminate the four ECSs by performing photon-number parity measurement.
For the case of lossy channel and threshold detector, one can only discriminate the case with or without detector clicks. Generally, a successful detection event in TF-QKD13 is defined that one and only one detector clicks. Therefore, we make only detector L (R) clicking represent that the result of the ECS measurement is the state \(|{\Phi }^{-}\rangle \) \((|{\Psi }^{-}\rangle )\). Due to decoherence of the cat states in lossy channel, the states \(|{\Phi }^{+}\rangle \) and \(|{\Psi }^{+}\rangle \) will always be mistakenly measured as quantum states \(|{\Phi }^{-}\rangle \) and \(|{\Psi }^{-}\rangle \), respectively. However, the corresponding probabilities can be restricted to be very low when the optical intensity is low and there is no eavesdropper’s disturbance. The post-selected joint quantum states of two legitimate users have quantum correlations, which then means that coherent-state-based TF-QKD have MDI characteristic.
TF-QKD with cat state
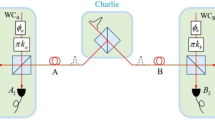
We introduce a coherent-state-based TF-QKD with coherent state and cat state coding, as shown in Fig. 1. State preparation. Alice (Bob) randomly chooses the Z and X bases with probabilities pZ and pX. For the Z basis, Alice (Bob) randomly prepares coherent state optical pulses \(|{\alpha }_{a(b)}\rangle \) and \(|\,-\,{\alpha }_{a(b)}\rangle \) with equal probabilities for the logic bits 0 and 1. For the X basis, Alice (Bob) randomly prepares cat state optical pulses \(|{\xi }^{+}({\alpha }_{a(b)})\rangle \) and \(|{\xi }^{-}({\alpha }_{a(b)})\rangle \) with equal probabilities for the logic bits 0 and 1. Entanglement measurement. Alice and Bob send the optical pulses to the untrusted Charlie through insecure quantum channel with efficiency \({\eta }_{a}\) and \({\eta }_{b}\) (with detector efficiency taken into account). Charlie is supposed to perform the ECS measurement. For example, he let the two optical pulses interfere in the symmetric BS which would be detected by two threshold detectors L and R. Announcement. Charlie publicly discloses whether he has obtained a successful measurement result and which ECS is acquired. Alice and Bob only keep the data of successful measurement and discard the rest. Reconciliation. Alice and Bob announce their bases over an authenticated classical channel. They only keep the data of the same basis and discard the rest. For the Z basis, Bob flips his key bit if Charlie announces a result with \(|{\Psi }^{-}\rangle \). For the X basis, Bob always flips his key bit. Parameter estimation. The data of the Z basis are used for constituting raw key and calculating the gain QZ and quantum bit error rate (QBER) EZ of the Z basis. The data of the X basis are all announced to calculate QBER EX of the X basis. Key distillation. Alice and Bob exploit the error correction and privacy amplification to distill secret key.
The coherent-state-based TF-QKD with coherent state and cat state coding. Alice (Bob) randomly prepares coherent states \(|\,\pm \,{\alpha }_{a(b)}\rangle \) and cat states \(|{\xi }^{\pm }({\alpha }_{a(b)})\rangle \) if choosing the Z and X bases, respectively. Alice and Bob use the insecure channels \({\eta }_{a}\) and \({\eta }_{b}\) to send the optical pulses to untrusted Charlie, who is supposed to perform the ECS measurement on the two incoming pulses. Only L (R) detector click means a successful measurement outcome \(|{\Phi }^{-}\rangle \) (\(|{\Psi }^{-}\rangle \)). The case of \({\mu }_{a}{\eta }_{a}={\mu }_{b}{\eta }_{b}\) is required to keep perfect interference in the Z basis, where intensity \({\mu }_{a(b)}=|{\alpha }_{a(b)}{|}^{2}\) and \({\eta }_{a(b)}\) is the efficiency between Alice (Bob) and Charlie.
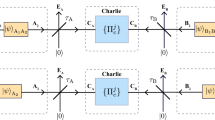
Here, we prove that coherent-state-based TF-QKD with coherent state and cat state coding is secure against coherent attacks in the asymptotic regime. Any one of two successful detections is enough for proving the security. The coherent-state-based TF-QKD can be regarded as a time-reversed entanglement protocol, where Alice and Bob prepare maximally entangled state \(|\psi {\rangle }_{a^{\prime} a}={(|+z\rangle }_{a^{\prime} }|{\alpha }_{a}{\rangle }_{a(b)}+|\,-\,z{\rangle }_{a^{\prime} }|\,-\,{\alpha }_{a}{\rangle }_{a})/\sqrt{2}\) and \(|\psi {\rangle }_{b^{\prime} b}={(|+z\rangle }_{b^{\prime} }|{\alpha }_{b}{\rangle }_{b}+|\,-\,z{\rangle }_{b^{\prime} }|\,-\,{\alpha }_{b}{\rangle }_{b})/\sqrt{2}\), respectively. \(|\,\pm \,z\rangle \) are the eigenstates of Pauli’s Z operator. Alice and Bob keep the qubit and send the optical mode to Charlie, who is supposed to perform entanglement swapping via the ECS measurement. Thereby, the bipartite states between Alice and Bob have quantum correlation through Charlie’s entanglement swapping operation. One can use the entanglement purification technique38 to distill maximally entangled state and generate the secret key. If Alice and Bob measure qubits before sending optical pulses in the virtual entanglement protocol, it will become the prepare-and-measurement protocol, i.e., coherent-state-based TF-QKD. Details can be found in Supplemental Material. The efficient QKD scheme43 can be directly applied, where we let \({p}_{Z}\approx 1\) in the asymptotic limit. The secret key rate of our coherent-state-based TF-QKD with one-way classical communication39 in the asymptotic limit is
where \(h(x)=-\,x\,{\log }_{2}\,x-(1-x)\,{\log }_{2}\,(1-x)\) is the Shannon entropy and \(f=1.16\) is the error correction efficiency. In our simulation, without Charlie’s disturbance, we have gain \({Q}_{Z}=(1-{p}_{d})[1-(1-2{p}_{d}){e}^{-2x}]\), QBERs \({E}_{Z}=(1-{p}_{d})[{e}_{{d}_{Z}}(1-{e}^{-2x})+{p}_{d}{e}^{-2x}]\) and \({E}_{X}=\frac{1}{2}\{1+{e}^{-2({\mu }_{a}+{\mu }_{b})}[1-(1-2{p}_{d}){e}^{2x}]/[1-(1-2{p}_{d}){e}^{-2x}]\}\), where \(x={\mu }_{a}{\eta }_{a}={\mu }_{b}{\eta }_{b}\), \({e}_{{d}_{Z}}\) is the misalignment rate of the Z basis and pd is the dark count rate. The misalignment of the X basis can be neglected since Bob always flips his bit.
Here, we exploit the two-way entanglement purification40 into our coherent-state-based TF-QKD protocol to increase transmission distance. Specifically, before implementing Key distillation step, Alice randomly permutes all raw key bits and divides them into two groups, Bob does the same. Alice and Bob compute a parity on raw key of two groups and compare the parities. The second group is always discarded. If their parities are the same, they keep the bit of the first group. Otherwise, they discard it. One can repeat the above operation once for each B step. After kth B step is applied, the gain, bit and phase error rates can be given by \({Q}_{Z}^{k}=\frac{1}{2}{A}^{k-1}{Q}_{Z}^{k-1}\), \({E}_{Z}^{k}={({E}_{Z}^{k-1})}^{2}/{A}^{k-1}\), and \({E}_{X}^{k}=2{E}_{X}^{k-1}(1-{E}_{Z}^{k-1}-{E}_{X}^{k-1})/{A}^{k-1}\), where we have \({A}^{k-1}={(1-{E}_{Z}^{k-1})}^{2}+{({E}_{Z}^{k-1})}^{2}\), \({Q}_{Z}^{0}={Q}_{Z}\), \({E}_{Z}^{0}={E}_{Z}\) and \({E}_{X}^{0}={E}_{X}\). The secret key rate of our coherent-state-based TF-QKD after kth B step in the asymptotic limit is
Converting to other protocols
Without loss of generality, let positive-operator valued measure \({E}_{10}\) and \({E}_{01}\) (\({E}_{s}={E}_{10}+{E}_{01}\)) denote the successful measurement results with ECSs \(|{\Phi }^{-}\rangle \) and \(|{\Psi }^{-}\rangle \); let \(\hat{{\rm{P}}}(|u,v\rangle ):\,=|u\rangle \langle u|\otimes |v\rangle \langle v|\) with \(|u,v\rangle =|u\rangle |v\rangle \). The density matrix of the Z and X bases are \({\rho }_{Z}=\frac{1}{4}[\hat{{\rm{P}}}(|{\alpha }_{a},{\alpha }_{b}\rangle )\)\(+\hat{{\rm{P}}}(|{\alpha }_{a},-\,{\alpha }_{b}\rangle )\) + \(\hat{{\rm{P}}}(|\,-\,{\alpha }_{a},{\alpha }_{b}\rangle )+\hat{{\rm{P}}}(|\,-\,{\alpha }_{a},-\,{\alpha }_{b}\rangle )]\) and \({\rho }_{X}=\frac{1}{4}[\hat{{\rm{P}}}(|{\xi }^{+}({\alpha }_{a}),{\xi }^{+}({\alpha }_{b})\rangle )+\)\(\hat{{\rm{P}}}(|{\xi }^{+}({\alpha }_{a}),{\xi }^{-}({\alpha }_{b})\rangle )\) + \(\hat{{\rm{P}}}(|{\xi }^{-}({\alpha }_{a}),{\xi }^{+}({\alpha }_{b})\rangle )+\hat{{\rm{P}}}(|{\xi }^{-}({\alpha }_{a}),{\xi }^{-}({\alpha }_{b})\rangle )]\), where we have \({\rho }_{X}\equiv {\rho }_{Z}=\rho \). For the cases of \(|{\xi }^{+}({\alpha }_{a}),{\xi }^{+}({\alpha }_{b})\rangle \) and \(|{\xi }^{-}({\alpha }_{a}),{\xi }^{-}({\alpha }_{b})\rangle \), they always generate the error gain since Bob always flips his bit, and the corresponding density matrix is \({\rho }_{X}^{E}=\frac{1}{4}[\hat{{\rm{P}}}(|{\xi }^{+}({\alpha }_{a}),{\xi }^{+}({\alpha }_{b})\rangle )+\hat{{\rm{P}}}(|{\xi }^{-}({\alpha }_{a}),{\xi }^{-}({\alpha }_{b})\rangle )]\). Let \({Q}_{X}\) and \({Q}_{X}^{E}\) represent the gain and error gain of the X basis. In the case of asymptotic limit, we always have \({Q}_{X}\equiv {Q}_{Z}={\rm{Tr}}(\rho {E}_{s})\) and \({Q}_{X}^{E}={\rm{Tr}}({\rho }_{X}^{E}{E}_{s})\). Therefore, the QBER EX (phase error rate of the Z basis) in the asymptotic limit can be given by \({E}_{X}={Q}_{X}^{E}/{Q}_{X}={Q}_{X}^{E}/{Q}_{Z}\). If one can acquire an upper bound of \({Q}_{X}^{E}\), the QBER EX can be bounded.
By using the entanglement purification with one-way38,39 and two-way40 classical communication to prove security, we only require the estimation of the QBER EX. This means that we do not need to prepare cat state if we can acquire the QBER EX through alternative method. The alternative method need to ensure that the prepared state by Alice (Bob) is linearly dependent, which cannot allow Charlie to implement unambiguous-state-discrimination attack44 before performing the entanglement swapping. Here, we show that our protocol can be converted to the coherent-state-based protocols of refs14,18,19,20 by using our security proof.
For the protocol proposed in ref.20, Alice and Bob randomly prepare coherent state \(|{e}^{i{\theta }_{a}}\sqrt{{\mu }_{a}}\rangle \) and \(|{e}^{i{\theta }_{b}}\sqrt{{\mu }_{b}}\rangle \) if they choose the X basis, where they need phases \({\theta }_{a(b)}\in [0,2\pi )\) and infinite intensities \({\mu }_{a(b)}\). As pointed out in ref.20, the operator \({\rho }_{X}^{E}\) can be approximated to arbitrary precision in the Hilbert-Schmidt norm by the discrete diagonal coherent state representation \({\rho }_{X}^{E}={\sum }_{i=1}^{\infty }\,{\lambda }_{i}\hat{{\rm{P}}}(|{\omega }_{a}^{i},{\omega }_{b}^{i}\rangle )\), where \(|{\omega }_{a}^{i},{\omega }_{b}^{i}\rangle \) is the tensor product of coherent state and λi is complex number. Thereby, the error gain \({Q}_{X}^{E}\) can be precisely obtained by using coherent states with infinite intensities. Indeed, in the ideal situation with symmetric channel, \(\mu ={\mu }_{a}={\mu }_{b}\) and \(\eta ={\eta }_{a}={\eta }_{b}\), the secret key rate of this protocol by using our security proof with one-way classical communication is given by \(R=(1-{e}^{-\mu \eta })[1-h(\frac{1-{e}^{-4\mu +2\mu \eta }}{2})]\), which is the same with the results of ref.20.
For the protocol proposed in refs18,19, Alice and Bob randomly prepare phase-randomized coherent state if they choose the X basis. As pointed out in refs18,19, by using the Cauchy-Schwarz inequality, we can bound the error gain \({Q}_{X}^{E}\) with photon-number state, i.e., \({Q}_{X}^{E}={\rm{Tr}}({\rho }_{X}^{E}{E}_{s})\) ≤ \({({\sum }_{n,m=0}^{\infty }\sqrt{{P}_{2n}^{a}{P}_{2m}^{b}{Y}_{2n,2m}})}^{2}\) + \({({\sum }_{n,m=0}^{\infty }\sqrt{{P}_{2n+1}^{a}{P}_{2m+1}^{b}{Y}_{2n+1,2m+1}})}^{2}\). \({Y}_{n,m}\) is the yield given that Alice and Bob send \(n\) and \(m\) photon states and \({P}_{n}^{a(b)}={e}^{-{\mu }_{a(b)}}{\mu }_{a(b)}^{n}/n!\). Decoy-state method45,46,47 can be used to estimate the yield \({Y}_{n,m}\), which has been realized with finite intensities18,48. Here, we use the three-intensity, \(0 < \omega < \nu \), to estimate the yield, which can be found in Methods.
For the protocol proposed in ref.14, Alice and Bob always prepare the coherent state \(|{e}^{i({\theta }_{a}+{\kappa }_{a}\pi )}\sqrt{{\mu }_{a}}\rangle \) and \(|{e}^{i({\theta }_{b}+{\kappa }_{b}\pi )}\sqrt{{\mu }_{b}}\rangle \), where \({\kappa }_{a(b)}\in \{0,1\}\) and \({\theta }_{a(b)}\in [0,2\pi )\). They keep the raw key bit only if \(|{\theta }_{a}-{\theta }_{b}|=0\) or π. As pointed out in ref.14, one can introduce a virtual trusted party who prepares a state, splits it using symmetric BS, and sends it to both Alice and Bob. We have the following observations \(\hat{{\rm{P}}}(|\alpha \rangle )+\hat{{\rm{P}}}(|\,-\,\alpha \rangle )=\hat{{\rm{P}}}(|{\xi }^{+}(\alpha )\rangle )+\hat{{\rm{P}}}(|{\xi }^{-}(\alpha )\rangle )\) and \(\hat{{\rm{P}}}(|{\xi }^{+}(\sqrt{2}\alpha ),0\rangle )+\hat{{\rm{P}}}(|0,{\xi }^{+}(\sqrt{2}\alpha )\rangle )\) \(\mathop{\longrightarrow }\limits^{{\rm{BS}}}\) \(\hat{{\rm{P}}}(|{\xi }^{+}(\alpha ),{\xi }^{+}(\alpha )\rangle )+\hat{{\rm{P}}}(|{\xi }^{-}(\alpha ),{\xi }^{-}(\alpha )\rangle )\). For the post-selected phase-matching, the error gain can be given by \({Q}_{X}^{E}={\sum }_{n=0}^{\infty }\,{e}^{-2\mu }{(2\mu )}^{2n}{Y}_{2n}/(2n)!\), where we need to assume \({\mu }_{a}={\mu }_{b}=\mu \). \({Y}_{n}\) is the yield given that the total photon number sent by Alice and Bob is n. Only even photon numbers have contribution to the phase error rate in our security proof which is only the same with the results of ref.14 in the ideal situation. Different from protocols of ours and refs18,19,20, the protocol of ref.14 seems to be only suitable for symmetric channel.
Discussion
For simulation, we use the following parameters. The inherent loss of fiber is 0.16 dB/km, the efficiency and dark count rate of threshold single-photon detector are \({\eta }_{d}=85 \% \) and \({p}_{d}={10}^{-7}\). For simplicity, we let Protocol 1 represent our coherent state and cat state coding protocol. Let Protocol 2 represent the protocol in refs18,19 with three-intensity phase-randomized coherent state. Here, we fix the intensities of phase-randomized coherent state with \(\nu =0.1\) and \(\omega =0.02\). The secret key rate of our protocol is equal to that of protocol in ref.20 since cat state can be approximated to arbitrary precision in the Hilbert-Schmidt norm by the discrete diagonal coherent state representation20. The performance of Protocols 1 and 2 under symmetric channel have been shown in Fig. 2, which assumes 1 GHz system repetition rate23. Here, we do not consider the performance of protocols in ref.14, whose secret key rate has been shown lower than protocols in refs 18,19,20. The secret key rate and transmission distance of Protocol 1 are both superior to Protocol 2. The transmission distance of Protocols 1 and 2 can both be improved by using the two-way classical communication. Especially, the advantages are very clear when the system misalignment rate is large, like \({e}_{{d}_{Z}}=10 \% \). The large system misalignment of TF-QKD is reasonable since the phase-locking and long-distance phase stabilization techniques in field are still difficult even with some experimental progresses23,24,25,26. The performance of Protocols 1 and 2 under asymmetric channel have been shown in Fig. 3. The secret key rate of Protocol 1 can still surpass the repeaterless bound when the asymmetric channel ratio is 70%. The asymmetric channel ratio is the ratio between A-C and A-B, where A-C (B) represents the distance between Alice and Charlie (Bob). Compare Fig. 2 with 3, the performance of coherent-state-based TF-QKD is the best under symmetric channel due to the single-photon-type interference.
The secret key rate under symmetric channel. (a,b) The misalignment of the Z basis is \({e}_{{d}_{Z}}=3 \% \) (10%). Protocols 1 and 2 denote our protocol and the protocol proposed in refs18,19 with three-intensity phase-randomized coherent state, respectively. We optimize the intensity of coherent state in the Z basis for each transmission loss. The repeaterless bound12 is also shown in the figure.
The secret key rate under asymmetric channel. We optimize the intensity for each transmission loss. The repeaterless bound12 is also shown in the figure.
In summary, we propose a coherent-state-based TF-QKD with optimal secret key rate by using coherent state and cat state coding. By using the ECS measurement as the entanglement swapping operation, we unify all known coherent-state-based TF-QKD protocols under a single framework. We have proved that the coherent-state-based TF-QKD is a time-reversed entanglement protocol, which means that one can use the known techniques of qubit-based QKD to further develop the coherent-state-based TF-QKD. The results show that coherent-state-based TF-QKD is suitable for building quantum communication networks within hundreds of kilometers without trusted relay or quantum repeater. We remark that cat states used for high-speed QKD will have difficulty under current experimental conditions. However, current experiments on the demonstration of various quantum tasks with cat states are very active33,34,35,36,37, implying that cat states may become a practical resource with the rapid development of technology.
Methods
Decoy-state analysis
The phase-randomized coherent state can be seen as a mixture of Fock states. Let \({Q}_{a,b}\) represent the gain when Alice and Bob send phase-randomized coherent state with intensity \(a\) and \(b\), respectively. Let \({Y}_{n,m}\) represent the yield when Alice and Bob send n-photon and m-photon. Thereby, we have \({Q}_{a,b}={\sum }_{n=0}^{\infty }\,{\sum }_{m=0}^{\infty }\,{e}^{-a-b}\frac{{a}^{n}{b}^{m}}{n!m!}{Y}_{n,m}\). Here, we exploit the decoy-state method with three-intensity to estimate the upper bound of the yield \({Y}_{n,m}\) with analytical method. The upper bound of \({Y}_{\mathrm{1,1}}\), \({Y}_{\mathrm{0,2}}\) and \({Y}_{\mathrm{2,0}}\) can be given by
and
where we have \({Y}_{0,0}={Q}_{0,0}\). The upper bound of \({Y}_{\mathrm{0,}n}\) and \({Y}_{n\mathrm{,0}}\) with \(n\ge 3\) can be written as
and
Let \({F}_{x,y}={e}^{x+y}{Q}_{x,y}-{e}^{x}{Q}_{x,0}-{e}^{y}{Q}_{0,y}+{Q}_{0,0}\), the upper bound of \({Y}_{\mathrm{1,}n}\) and \({Y}_{n\mathrm{,1}}\) with \(n\ge 2\) can be given by
and
Similarly, the upper bound of \({Y}_{n,m}\) with \(n,m\ge 2\) can be given by
References
Bennett, C. H., Bessette, F., Brassard, G., Salvail, L. & Smolin, J. Experimental quantum cryptography. Journal of Cryptology 5, 3–28 (1992).
Boaron, A. et al. Secure quantum key distribution over 421 km of optical fiber. Phys. Rev. Lett. 121, 190502 (2018).
Takenaka, H. et al. Satellite-to-ground quantum-limited communication using a 50-kg-class microsatellite. Nature Photonics 11, 502 (2017).
Günthner, K. et al. Quantum-limited measurements of optical signals from a geostationary satellite. Optica 4, 611–616 (2017).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43 (2017).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Yin, H.-L. et al. Measurement-device-independent quantum key distribution over a 404 km optical fiber. Phys. Rev. Lett. 117, 190501 (2016).
Zhou, Y.-H., Yu, Z.-W. & Wang, X.-B. Making the decoy-state measurement-device-independent quantum key distribution practically useful. Phys. Rev. A 93, 042324 (2016).
Braunstein, S. L. & Pirandola, S. Side-channel-free quantum key distribution. Phys. Rev. Lett. 108, 130502 (2012).
Gisin, N. How far can one send a photon? Frontiers of Physics 10, 100307 (2015).
Takeoka, M., Guha, S. & Wilde, M. M. Fundamental rate-loss tradeoff for optical quantum key distribution. Nature Commun. 5, 5235 (2014).
Pirandola, S., Laurenza, R., Ottaviani, C. & Banchi, L. Fundamental limits of repeaterless quantum communications. Nature Commun. 8, 15043 (2017).
Lucamarini, M., Yuan, Z., Dynes, J. F. & Shields, A. J. Overcoming the rate–distance limit of quantum key distribution without quantum repeaters. Nature 557, 400 (2018).
Ma, X., Zeng, P. & Zhou, H. Phase-matching quantum key distribution. Phys. Rev. X 8, 031043 (2018).
Tamaki, K., Lo, H.-K., Wang, W. & Lucamarini, M. Information theoretic security of quantum key distribution overcoming the repeaterless secret key capacity bound. arXiv:1805.05511 (2018).
Wang, X.-B., Yu, Z.-W. & Hu, X.-L. Twin-field quantum key distribution with large misalignment error. Phys. Rev. A 98, 062323 (2018).
Yin, H.-L. & Fu, Y. Measurement-device-independent twin-field quantum key distribution. Sci. Rep. 9, 3045 (2019).
Cui, C. et al. Twin-field quantum key distribution without phase postselection. Phys. Rev. Applied 11, 034053 (2019).
Curty, M., Azuma, K. & Lo, H.-K. Simple security proof of twin-field type quantum key distribution protocol. npj Quantum Information 5, 64 (2019).
Lin, J. & Lütkenhaus, N. Simple security analysis of phase-matching measurement-device-independent quantum key distribution. Phys. Rev. A 98, 042332 (2018).
Primaatmaja, I. W., Lavie, E., Goh, K. T., Wang, C. & Lim, C. C. W. Versatile security analysis of measurement-device-independent quantum key distribution. Phys. Rev. A 99, 062332 (2019).
Xu, H., Yu, Z.-W., Jiang, C., Hu, X.-L. & Wang, X.-B. General theory of sending-or-not-sending twin-field quantum key distribution. arXiv preprint arXiv:1904.06331 (2019).
Minder, M. et al. Experimental quantum key distribution beyond the repeaterless secret key capacity. Nature Photonics 13, 334 (2019).
Liu, Y. et al. Experimental twin-field quantum key distribution through sending-or-not-sending. Phys. Rev. Lett. 123, 100505 (2019).
Wang, S. et al. Beating the fundamental rate-distance limit in a proof-of-principle quantum key distribution system. Phys. Rev. X 9, 021046 (2019).
Zhong, X., Hu, J., Curty, M., Qian, L. & Lo, H.-K. Proof-of-principle experimental demonstration of twin-field type quantum key distribution. Phys. Rev. Lett. 123, 100506 (2019).
Lund, A. P., Ralph, T. C. & Haselgrove, H. L. Fault-tolerant linear optical quantum computing with small-amplitude coherent states. Phys. Rev. Lett. 100, 030503 (2008).
Andersen, U. L. & Ralph, T. C. High-fidelity teleportation of continuous-variable quantum states using delocalized single photons. Phys. Rev. Lett. 111, 050504 (2013).
Sangouard, N. et al. Quantum repeaters with entangled coherent states. J. Opt. Soc. Am. B 27, 137–145 (2010).
Brask, J. B., Rigas, I., Polzik, E. S., Andersen, U. L. & Sørensen, A. S. Hybrid long-distance entanglement distribution protocol. Phys. Rev. Lett. 105, 160501 (2010).
Yin, H.-L. et al. Long-distance measurement-device-independent quantum key distribution with coherent-state superpositions. Opt. Lett. 39, 5451–5454 (2014).
Joo, J., Munro, W. J. & Spiller, T. P. Quantum metrology with entangled coherent states. Phys. Rev. Lett. 107, 083601 (2011).
Ourjoumtsev, A., Tualle-Brouri, R., Laurat, J. & Grangier, P. Generating optical schrödinger kittens for quantum information processing. Science 312, 83–86 (2006).
Ourjoumtsev, A., Jeong, H., Tualle-Brouri, R. & Grangier, P. Generation of optical schrödinger cats from photon number states. Nature 448, 784 (2007).
Vlastakis, B. et al. Characterizing entanglement of an artificial atom and a cavity cat state with bells inequality. Nature Commun. 6, 8970 (2015).
Ulanov, A. E., Sychev, D., Pushkina, A. A., Fedorov, I. A. & Lvovsky, A. Quantum teleportation between discrete and continuous encodings of an optical qubit. Phys. Rev. Lett. 118, 160501 (2017).
Le Jeannic, H., Cavaillès, A., Raskop, J., Huang, K. & Laurat, J. Remote preparation of continuous-variable qubits using loss-tolerant hybrid entanglement of light. Optica 5, 1012–1015 (2018).
Lo, H.-K. & Chau, H. F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999).
Shor, P. W. & Preskill, J. Simple proof of security of the bb84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441–444 (2000).
Gottesman, D. & Lo, H.-K. Proof of security of quantum key distribution with two-way classical communications. IEEE Transactions on Information Theory 49, 457–475 (2003).
Sanders, B. C. Entangled coherent states. Phys. Rev. A 45, 6811 (1992).
Jeong, H. & Kim, M. S. Purification of entangled coherent states. Quantum Inf. Comput. 2, 208–221 (2002).
Lo, H.-K., Chau, H. F. & Ardehali, M. Efficient quantum key distribution scheme and a proof of its unconditional security. Journal of Cryptology 18, 133–165 (2005).
Tang, Y.-L. et al. Source attack of decoy-state quantum key distribution using phase information. Phys. Rev. A 88, 022308 (2013).
Hwang, W.-Y. Quantum key distribution with high loss: Toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Grasselli, F. & Curty, M. Practical decoy-state method for twin-field quantum key distribution. New J. Phys. 21, 073001 (2019).
Acknowledgements
We gratefully acknowledges support from the National Natural Science Foundation of China under Grant No. 61801420 and Nanjing University.
Author information
Authors and Affiliations
Contributions
H.-L.Y. and Z.-B.C. conceived and designed the study. H.-L.Y. performed the numerical simulation. All authors contributed extensively to the work presented in this paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yin, HL., Chen, ZB. Coherent-State-Based Twin-Field Quantum Key Distribution. Sci Rep 9, 14918 (2019). https://doi.org/10.1038/s41598-019-50429-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-50429-0
This article is cited by
-
Rotating coherent states in the dispersive regime of the generalized Jaynes–Cummings model
Optical and Quantum Electronics (2024)
-
Surpassing the repeaterless bound with a photon-number encoded measurement-device-independent quantum key distribution protocol
npj Quantum Information (2023)
-
Polarization based discrete variables quantum key distribution via conjugated homodyne detection
Scientific Reports (2022)
-
Satellite-based phase-matching quantum key distribution
Quantum Information Processing (2022)
-
Practical long-distance twin-field quantum digital signatures
Quantum Information Processing (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.