Abstract
Recently, we reported the observation of superconductivity at ~0.5 K in a La2O2M4S6-type (M: metal) layered compound La2O2Bi3AgS6, which is a layered system related to the BiS2-based superconductor system but possesses a thicker Bi3AgS6-type conducting layer. In this study, we have developed the La2O2Bi3AgS6-type materials by element substitutions to increase the transition temperature (Tc) and to induce bulk nature of superconductivity. A resistivity anomaly observed at 180 K in La2O2Bi3AgS6 was systematically suppressed by Sn substitution for the Ag site. By the Sn substitution, Tc increased, and the shielding volume fraction estimated from magnetization measurements also increased. The highest Tc (=2.3 K) and the highest shielding volume fraction (~20%) was observed for La2O2Bi3Ag0.6Sn0.4S6. The superconducting properties were further improved by Se substitutions for the S site. By the combinational substitutions of Sn and Se, bulk-superconducting phase of La2O2Bi3Ag0.6Sn0.4S5.7Se0.3 with a Tc of 3.0 K (Tconset = 3.6 K) was obtained.
Similar content being viewed by others
Introduction
Layered superconductors have been extensively studied due to observations of unconventional superconductivity and high transition temperature (Tc)1,2. In addition, the great flexibility of constituent elements and layered (stacking) structure, the studies on layered superconductor system can be widely developed. The recent discovery of BiS2-based superconductors has also created remarkable attention in the superconductivity community: the typical materials are Bi4O4S3, REO1−xFxBiS2 (RE = La, Ce, Pr, Nd, Yb), and Sr1−xRExFBiS23,4,5,6,7,8,9,10,11,12,13,14. For instance, the crystal structure of the typical system LaOBiS2 is composed of alternate stacks of a La2O2 blocking layer and two BiS2 layers. Since the parent phase (LaOBiS2) is an insulator with a band gap15, electron doping is needed to induce metallic and superconducting characteristics. Furthermore, local in-plane structure should be optimized to induce bulk superconductivity in the BiS2 layer16. Thus, the Tc of BiS2-based is sensitive to physical pressure4,17,18,19,20,21 and chemical pressure22,23,24 effects and reaches 11 K in LaO0.5F0.5BiS2. Therefore, an increase in the highest record of Tc in the BiS2-based superconductor family can be expected by further material development and tuning of structural and electrical properties14.
Very recently, we reported on the superconductivity in oxychalcogenide La2O2Bi3AgS6 with Tc of 0.5 K25. The crystal structure of La2O2Bi3AgS6 is similar to the typical BiS2-based superconductor LaOBiS2, but the conducting layer thickness is thicker than that of LaOBiS2. The crystal structure of the system can be described as La2O2M4S6, in which the M site can be Pb, Bi, and Ag26,27,28. There are two different metal sites [M1 and M2 displayed in Fig. 1(c)] in the M4S6-type conducting layer. For the outer layers with the M1 site, Bi selectively occupies, and the layers can be regarded as the BiS2-type layers. For the inner layer with the M2 site, NaCl-type (Bi,Ag)S2 layers are inserted in between the BiS2-type layers.
Crystal structure and composition analyses results for La2O2Bi3Ag1−xSnxS6 (x = 0–0.5). (a) Room-temperature XRD pattern for x = 0–0.5. The impurity peaks of La2Sn2O7 are indicated by asterisks (*). (b) XRD pattern near the 103 (Miller index) peak of the tetragonal phase of La2O2Bi3AgS6. (c) A schematic image of the crystal structure of La2O2M4S6 (two M sites, M1 and M2, are occupied by Bi, Ag, and Sn in the present system). (d,e) Lattice parameters of a and c obtained from Rietveld refinements. (f,g) Nominal composition dependences of compositions (x and y) analyzed by EDX, where x and y are defined as La2O2Bi3+y(Ag1−xSnx)1−yS6.
Interestingly, an anomalous transport property was observed in the temperature dependence of resistivity in La2O2Bi3AgS625, which is similar to the charge-density-wave (CDW) transition in EuFBiS229. In this study, we have investigated the Sn substitution effect for the Ag site in La2O2Bi3Ag1−xSnxS6 and found that the resistivity anomaly was suppressed by Sn substitutions. Tc reached 2.3 K for x = 0.4 (La2O2Bi3Ag0.6Sn0.4S6). Furthermore, by Se substitutions for the S site in La2O2Bi3Ag0.6Sn0.4S5.7Se0.3, the Tc further increased to 3.5 K, and bulk nature of superconductivity was confirmed from magnetic shielding volume fraction.
Results
Sn substitution effect on structural and physical properties in La2O2Bi3Ag1−xSnxS6
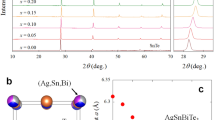
Figure 1a displays the room temperature XRD patterns for La2O2Bi3Ag1−xSnxS6 (x = 0–0.5). All the La2O2Bi3Ag1−xSnxS6 samples are crystallized in the tetragonal structure with the space group of P4/nmm. An impurity phase of La2Sn2O7 was observed for x = 0.2–0.5. Figure 1b shows the shift in the 103 peak position, which slightly shifts towards the low angle side for x = 0.1. As the Sn concentration increases from x = 0.2 to 0.5, the 103 peak shifts towards the higher angle side. The schematic image of the crystal structure of La2O2M4S6 is shown in Fig. 1c. For the La2O2Bi3Ag1−xSnxS6 phase, Bi selectively occupies the M1 site, and Sn is expected to substituted for Ag at the M2 site, which was qualitatively confirmed by Rietveld refinements. The evolutions of the lattice parameters by the Sn substitution are shown in Fig. 1d,e. The lattice parameters are a = 4.061(1) Å and c = 19.445(1) Å for x = 0 and a = 4.0648(1) Å and c = 19.48(1) Å for x = 0.1. The lattice parameter c tends to decrease by Sn substitution for x = 0–0.2, and then, it continuously increases with increasing x for x = 0.2–0.5. The lattice parameter a increases for the x = 0.1, but it tends to decrease with increasing x for higher x. However, the changes in those lattice parameters are small. On the basis of the lattice parameter evolutions, we consider that the Sn substitution does not largely affect the lattice volume, which may be due to smaller ionic radius of Sn2+ (93 pm) than that of Ag+ (113 pm). The La2O2Bi3AgS6-type structure can be considered as the stacking of a La2O2 layer, two BiS2 layers, and an NaCl-type AgBiS2 layer. In such a layered structure, the unit cell is almost determined by the hardest layer due to the different ionic bonding nature. In this structure, La2O2 layer structure is the hardest.
The actual ratio of the metals in the conducting layer (Bi, Ag, and Sn) in the La2O2Bi3Ag1−xSnxS6 (x = 0–0.5) samples were examined by EDX. The nominal and analyzed values of x are plotted in the Fig. 1f. Although there is slight deviation from the nominal values, the analyzed values of xEDX linearly increases with increasing nominal x. We found that Bi is slightly excess for x = 0.1–0.3. Therefore, y parameter with a formula of La2O2Bi3+y(Ag1−xSnx)1−yS6 was introduced to analyze the Bi concentration. The analyzed values of yEDX are plotted in Fig. 1g. yEDX is higher for x = 0.1–0.3 but almost zero for x = 0, 0.4, and 0.5. Therefore, we consider that the Bi excess can be ignored in the discussion on the Sn substitution (and Se substitution) effect, and we use the formula La2O2Bi3Ag1−xSnxS6 in this paper.
Figure 2a–c show the temperature dependences of magnetic susceptibility (4πχ-T) under an applied magnetic field of 10 Oe for La2O2Bi3Ag1−xSnxS6 (x = 0.3–0.5). The diamagnetic signals in the 4πχ curve were observed below 2.2, 2.8, and 2.6 K for x = 0.3, 0.4, and 0.5, respectively. A large diamagnetic signal was observed below 2.8 K in the ZFC curve for x = 0.4. The shielding value fractions estimated from 4πχ (ZFC) at 1.9 K is nearly 20% [See Fig. 2(d).] while it is still not saturated. From the susceptibility results, we consider that Sn substitution is effective to improve the superconducting properties of La2O2Bi3AgS6 but not sufficient to induce bulk superconductivity.
Superconducting properties examined from magnetic susceptibility for La2O2Bi3Ag1−xSnxS6 (x = 0.3–0.5). (a–c) Temperature (T) dependences of magnetic susceptibility (4πχ) for x = 0.3–0.5 measured in the ZFC and FC modes with an applied magnetic field of 10 Oe. (d) Sn concentration dependence of the shielding volume fraction estimated using the ZFC data at 1.9 K.
Figure 3 shows the temperature dependences of electrical resistivity from 300 to 0.1 K for La2O2Bi3Ag1−xSnxS6 (x = 0–0.5). The electrical resistivity at 300 K decreases with increasing Sn concentration up to x = 0.3 and increases again for x = 0.4 and 0.5. The normal-state resistivity of the Sn-doped samples changes remarkably. For example, the pure sample (x = 0) shows a linear decrease in resistivity on cooling below the anomaly temperature T* = 180 K. A similar behavior was observed up to x = 0.2. The resistivity anomaly at T* appears for x ≤ 0.2, and the T* shifts towards the lower temperature side with increasing x. In contrast, the normal-state ρ(T) for x = 0.3–0.5 shows an upturn below ~50 K. The anomaly disappears for x ≥ 0.3. Figure 3g shows the zoomed view of the Figs. 3a–f near the superconducting transition. The Tc clearly increases with increasing Sn concentration in La2O2Bi3Ag1−xSnxS6. The highest Tc was achieved for x = 0.4, and Tc decreases for a higher substitution with x = 0.5.
The room-temperature Seebeck coefficient (S) for La2O2Bi3Ag1−xSnxS6 (x = 0–0.5) are shown in Fig. 4. The Seebeck coefficient is a good scale for the carrier concentration in BiS2-based compounds30. We observed a slight change in S by Sn substitution. The S in x = 0.2–0.4 are almost the same, but that for x = 0 and 0.5 are slightly large. This suggests that the carrier concentrations for x = 0.2–0.4 are higher than those for x = 0 and 0.5. This seems to be related to the evolution of Tc. However, the large change in Tc from 0.6 to 2.3 K between x = 0.1 and 0.4 cannot be simply understood by the carrier concentration only.
Figure 5 shows the superconductivity phase diagram of La2O2Bi3Ag1−xSnxS6, which shows the interplay between the resistivity anomaly temperature (T*) and the superconducting transition temperature (Tczero). The T* is suppressed by the Sn substitution, and it disappears at x = 0.3. The Tc gradually increases with increasing x in La2O2Bi3Ag1−xSnxS6. The highest Tczero = 2.3 K is achieved for x = 0.4. A lower Tczero = 1.9 K is observed for the highest (solubility-limit) Sn concentration of x = 0.5.
Here, we discuss about the possible influence of the presence of the La2Sn2O7 impurity to the composition. Due to the change in the impurity amount for x = 0–0.5, the actual compositions may deviate from the nominal compositions. Although the Sn concentration to that of Ag was checked by EDX (Fig. 1f), oxygen deficiency in the blocking layer was not checked in this study. However, we consider that oxygen deficiency was not introduced because it is expected to make the structure unstable even if it has been introduced in the La2O2Bi3AgS6-type structure. We have tried to dope electrons by oxygen deficiency or fluorine substitution for the La2O2Bi3AgS6-type structure. However, in the La2O2Bi3AgS6 system, such trials of fluorine substitutions (or oxygen deficiency) resulted in decomposing of the La2O2Bi3AgS6-type structure into LaO1−xFxBiS2. This indicates that an electron-doped composition with the La2O2Bi3AgS6-type structure cannot be obtained easily due to the competition to the high stability of the REO1−xFxBiS2-type phase. In addition, oxygen deficiency has not been observed in the REOBiS2 systems.
Superconducting properties of Se-doped La2O2Bi3Ag0.6Sn0.4S5.7Se0.3
As shown above, the Sn substitution improved the superconducting properties in La2O2Bi3Ag1−xSnxS6, and the highest Tc and shielding volume fraction were obtained for x = 0.4. In the BiS2-based compounds, partial Se substitutions for the S site of the superconducting BiS2 layers have significantly improved the superconducting properties and the bulk characteristics of superconductivity. Therefore, we tried to substitute the S site by Se for the x = 0.4 sample. The 5%-Se sample La2O2Bi3Ag0.6Sn0.4S5.7Se0.3 was successfully synthesized, but samples with higher Se concentration contained selenide impurity phases. The solubility limit of Se for the S site is around 5%. The composition estimated from the EDX analyses for Bi, Ag, Sn, S, Se elements was La2O2Bi3.09Ag0.65Sn0.26S5.73Se0.27. Since the obtained composition is close to the nominal formula, we call the sample with the nominal value below.
Figure 6 shows the XRD pattern and the Rietveld refinement result for La2O2Bi3Ag0.6Sn0.4S5.7Se0.3. Although two peaks related to the La2Sn2O7 impurity phase were observed, other peaks could be refined using the tetragonal (P4/nmm) model with a reliability factor Rwp of 13.4%. In the refinement, Se was assumed to be substituted for the S1 site. The lattice parameters were a = 4.0759(2) Å and 19.4824(11) Å, which are clearly larger than those of La2O2Bi3Ag1−xSnxS6 due to the presence of Se.
X-ray diffraction analysis for La2O2Bi3Ag0.6Sn0.4S5.7Se0.3. XRD pattern and the Rietveld refinement result are shown. The arrows indicate the peaks for the impurity phase La2Sn2O7. The inset image shows the crystal structure depicted using the structural parameters obtained from the Rietveld refinement.
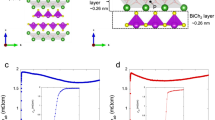
Figure 7 displays the superconducting properties of La2O2Bi3Ag0.6Sn0.4S5.7Se0.3. As shown in Fig. 7a, a large shielding volume fraction close to 100% was observed. From the resistivity measurements (Fig. 7b), zero resistivity was observed at 3.0 K, and the onset temperature (Tconset) was 3.5 K; we estimated the temperature where the resistivity becomes almost 90% of normal-state resistivity. Although superconductivity was observed, the ρ(T) curve still shows a semiconducting-like localization at low temperatures. We have measured ρ(T) under magnetic fields up to 9 T. The obtained Tconset and Tczero were plotted in Fig. 7d to evaluate the upper critical field Hc2 and the irreversible field Hirr. The Hc2(0) was estimated as 2.15 T using the WHH model (Werthamer-Helfand-Hohenberg model)31. In addition, from rough estimation with a linear fitting of Hirr, the Hirr(0) was estimated as 1.0 T.
Superconducting properties for La2O2Bi3Ag0.6Sn0.4S5.7Se0.3. (a) Temperature dependence of magnetic susceptibility. (b) Temperature dependence of electrical resistivity [ρ(T)]. (c) Low-temperature ρ(T) under magnetic fields up to 9T. (d) Temperature-magnetic field phase diagram with the upper critical field (Hc2) and the irreversible field (Hirr).
Discussion
Suppression of resistivity anomaly by the Sn substitution
Here, we discuss the possible origin of the increase in Tc by the Sn substitution. As revealed in the crystal structure part, the lattice parameters were not largely affected by the Sn substitution. Therefore, in-plane chemical pressure amplitude in the Bi-S superconducting plane, which has been revealed as the essential parameter for the emergence of superconductivity in BiS2-based compounds24, should not be significantly changed. Therefore, we consider that the in-plane chemical pressure effect is not the origin for the increase in Tc by the Sn substitution. On carrier concentration, the absolute value of the Seebeck coefficient slightly decreases by Sn substitution for x = 0.1–0.4, which can be corresponding to the slight increase in electron carriers by Sn substitution. However, the large increase in Tc for x = 0.4 may not be understood from the increase in carrier concentration only because the difference in carrier concentration between x = 0.1 (Tc = 0.6 K) and x = 0.4 (Tc = 2.3 K) is expected to be quite small. On the basis of these facts, we briefly mention about the possible relation to the CDW ordering and the possible scenario of the suppression of CDW by Sn substitution in this system. In the ρ-T plots, an anomaly was observed in the La2O2Bi3Ag1−xSnxS6 system. A similar feature in the normal-state resistivity has been observed in the EuFBiS2 superconductor (Tc = 0.3 K). The origin of the hump was proposed as a CDW transition29. We assume that the suppression of the CDW ordering is the origin for the increased Tc in La2O2Bi3Ag1−xSnxS6. In addition, the anomaly temperature T* was shifted to a lower temperature by Sn substitution, and the anomaly disappeared at x = 0.3. At around x = 0.3 and 0.4, Tc is the maximum. These facts imply that Tc increased by the suppression of T*. Although we have no evidence for the CDW states in the La2O2Bi3Ag1−xSnxS6 system and the suppression mechanism by the Sn substitution, introduction of randomness at the M2 site may be effective to suppress the charge ordering states.
Bulk superconductivity in La2O2Bi3Ag0.6Sn0.4S5.7Se0.3
As shown in the Result part, a partial Se substitution for S induced bulk superconductivity in La2O2Bi3Ag0.6Sn0.4S5.7Se0.3. Although the solubility limit of Se for the S site is very low (5%), the lattice parameters clearly changed by the partial Se substitution, and the superconducting properties were significantly improved. Although we refined three models with different Se site (assuming the substitution at the S1, S2, or S3 sites), we could not find the site selectivity of doped Se. However, we expect that the doped Se occupies the Ch1 site in the inset of Fig. 6. In previous reports on the Se substitution in BiS2-based compounds, the site selectivity of Se at the in-plane site was observed24,32,33. According to the relationship between in-plane disorder at the chalcogen site and superconductivity in BiS2-based systems16,24, we assume that Se substitution reduced the in-plane disorder at the S1 site and induced bulk superconductivity. Furthermore, the room-temperature Seebeck coefficient for the La2O2Bi3Ag0.6Sn0.4S5.7Se0.3 sample was similar to those shown in Fig. 4 (S = −25 μV/K). This also suggests that the bulk nature of superconductivity was induced by local structural optimization but not due to changes in carrier concentration.
Since the phases contain Sn in their structure, we have to exclude the possibility of superconductivity of elemental Sn in the examined samples. From XRD, no peaks of Sn was observed. However, amorphous Sn may exist and show superconducting transition. We cannot directly exclude this possibility, but we consider that the bulk superconductivity observed here is not originated from elemental Sn. We have investigated similar Sn substitution effects in the La2O2Bi2Pb2−xSnxS6 system. La2O2Bi2Pb2S6 (LaOBiPbS3) shows an insulating transport property26,27. The insulating behavior was not suppressed by Sn substitution, and superconducting transition was not observed for all the examined samples of La2O2Bi2Pb2−xSnxS6. This fact may indirectly suggest that the bulk superconductivity observed in the La2O2Bi3Ag0.6Sn0.4S5.7Se0.3 sample is not caused by Sn amorphous impurities.
In conclusion, we have reported the emergence of bulk superconductivity in La2O2M4S6-type (four-layer-type) layered oxychalcogenide La2O2Bi3Ag0.6Sn0.4S5.7Se0.3. According to the material design strategy shown here, we can further develop related four-layer-type Bi-based layered superconductors. Recently, a new superconductor Bi3O2S2Cl with the one-layer-type Bi-Cl-S superconducting layer was discovered by Ruan et al.34. In Fig. 8, schematic images of typical one-layer-type (Fig. 8a), two-layer-type (Fig. 8b), and four-layer-type (Fig. 8c) are displayed for comparison. All the materials have the similar RE2O2 or Bi2O2 blocking layer. By changing the constituent elements in the superconducting layers, the thickness can be changed in this superconductor family. On the basis of these facts, we will be able to design various types of Bi-based layered superconductors with a higher Tc as developed with various Cu-oxide layers in the cuprate family. With such material development with a different type of conducting layer, remarkable changes in superconducting properties can be expected.
Comparison of crystal structure of typical Bi-based layered compounds with different thickness of superconducting layer. (a) Schematic image of the crystal structure of Bi3O2S2Cl, which was recently discovered by Ruan et al.34. In this material, the conducting layer can be regarded as the one-layer-type BiS2Cl. (b) Schematic image of the crystal structure of the typical BiS2-based superconductor RE(O,F)BiS2. In the series, the conducting layer can be regarded as the two-layer-type Bi2S4 bilayer. (c) Schematic image of the crystal structure of La2O2Bi3AgS6-type (La2O2M4S6-type) materials whose conducting layer can be regarded as the four-layer-type M4S6 layer.
Methods
The polycrystalline samples of La2O2Bi3Ag1−xSnxS6 with x = 0, 0.1, 0.2, 0.3, 0.4, and 0.5 were prepared by a solid-state reaction method. The polycrystalline samples of Se-substituted La2O2Bi3Ag0.6Sn0.4S6−zSez with z = 0.3 and 0.6 were also prepared by a solid-state reaction method. Powders (or grains) of Bi2O3 (99.9%), La2S3 (99.9%), Sn (99.99%), and AgO (99.9%) and grains of Bi (99.999%), S (99.99%), and Se (99.99%) with a nominal composition of La2O2Bi3Ag1−xSnxS6−zSez were mixed in a pestle and mortar, pelletized, sealed in an evacuated quartz tube, and heated in an electric furnace. The heat treatment condition was 725 °C for 15 h for both samples. However, for La2O2Bi3Ag0.6Sn0.4S6−zSez, heating the sample to 725 °C in 1 h was needed to suppress the generation of impurity phases. The obtained samples were reground for homogeneity, pelletized, and heated in the same procedure. The phase purity of the prepared samples and the optimal annealing conditions were examined using X-ray diffraction (XRD) with a Cu-Kα radiation. The lattice parameters were determined using the Rietveld method with RIETAN-FP35. Schematic image of the crystal structure was drawn using VESTA36. The actual composition was analyzed by energy-dispersive X-ray spectroscopy (EDX) on scanning electron microscope TM3030 (Hitachi). The magnetic susceptibility measurements were carried out using a superconducting quantum interference device (SQUID) magnetometer (MPMS-3, Quantum Design). The susceptibility data were taken after both zero-field cooling (ZFC) and field cooling (FC). The temperature dependence of electrical resistivity [ρ(T)] was measured by four-terminal method on the Physical Property measurement system (PPMS, Quantum Design). The resistivity measurement down to 0.4 K was measured using a 3He probe platform of PPMS. The ADR system on PPMS was used for resistivity measurements down to 0.1 K. For clarity, we labeled the examined samples with the nominal compositions. The Seebeck coefficient was measured by a four-probe method on ZEM-3 (Advance RIKO) at 300 K.
Data Availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
References
Bednorz, J. G. & Müller, K. A. Possible high T c superconductivity in the Ba-La-Cu-O system. Z. Physik B Condensed Matter 64, 189–193 (1986).
Kamihara, Y. et al. Iron-Based Layered Superconductor La[O1−xFx]FeAs (x = 0.05−0.12) with T c = 26 K. J. Am. Chem. Soc. 130, 3296–3297 (2008).
Mizuguchi, Y. et al. BiS2-based layered superconductor Bi4O4S3. Phys. Rev. B 86(1–5), 220510 (2012).
Mizuguchi, Y. et al. Superconductivity in Novel BiS2-Based Layered Superconductor LaO1−xFxBiS2. J. Phys. Soc. Jpn. 81(1–5), 114725 (2012).
Singh, S. K. et al. Bulk Superconductivity in Bismuth Oxysulfide Bi4O4S3. J. Am. Chem. Soc. 134, 16504–16507 (2012).
Demura, S. et al. BiS2-based superconductivity in F-substituted NdOBiS2. J. Phys. Soc. Jpn. 82(1–3), 033708 (2013).
Jha, R. et al. Synthesis and superconductivity of new BiS2 based superconductor PrO0.5F0.5BiS2. J. Supercond. Nov. Magn. 26, 499–502 (2013).
Jha, R. et al. Superconductivity at 5 K in NdO0.5F0.5BiS2. J. Appl. Phys. 113(1–3), 056102 (2013).
Xing, J. et al. Superconductivity Appears in the Vicinity of an Insulating-Like Behavior in CeO1−xFxBiS2. Phys. Rev. B 86(1–5), 214518 (2012).
Yazici, D. et al. Superconductivity of F-substituted LnOBiS2 (Ln = La, Ce, Pr, Nd, Yb) compounds. Philos. Mag. 93(1–8), 673 (2012).
Yazici, D. et al. Superconductivity induced by electron doping in La1-xMxOBiS2 (M = Ti, Zr, Hf, Th). Phys. Rev. B 87(1–8), 174512 (2013).
Lin, X. et al. Superconductivity induced by La doping in Sr1−xLaxFBiS2. Phys. Rev. B 87(1–4), 020504 (2013).
Mizuguchi, Y. Review of superconductivity in BiS2-based layered materials. J. Phys. Chem. Solids 84, 34–48 (2015).
Mizuguchi, Y. Material Development and Physical Properties of BiS2-Based Layered Compounds. J. Phys. Soc. Jpn. 88(1–17), 041001 (2019).
Usui, H., Suzuki, K. & Kuroki, K. Minimal electronic models for superconducting BiS2 layers. Phys. Rev. B 86(1–5), 220501 (2012).
Mizuguchi, Y. et al. Evolution of Anisotropic Displacement Parameters and Superconductivity with Chemical Pressure in BiS2-Based REO0.5F0.5BiS2 (RE = La, Ce, Pr, and Nd). J. Phys. Soc. Jpn. 87, 023704 (2018).
Kotegawa, H. et al. Pressure Study of BiS2-Based Superconductors Bi4O4S3 and La(O,F)BiS2. J. Phys. Soc. Jpn. 81(1–4), 103702 (2012).
Mizuguchi, Y. et al. Stabilization of High-T c Phase of BiS2-Based Superconductor LaO0.5F0.5BiS2 Using High-Pressure Synthesis. J. Phys. Soc. Jpn. 83(1–4), 053704 (2014).
Wolowiec, C. T. et al. Enhancement of superconductivity near the pressure-induced semiconductor–metal transition in the BiS2-based superconductors LnO0.5F0.5BiS2 (Ln = La, Ce, Pr, Nd). J. Phys.: Condens. Matter 25(1–6), 422201 (2013).
Jha, R., Tiwari, B. & Awana, V. P. S. Impact of Hydrostatic Pressure on Superconductivity of Sr0.5La0.5FBiS2. J. Phys. Soc. Jpn. 83(1–4), 063707 (2014).
Jha, R., Tiwari, B. & Awana, V. P. S. Appearance of bulk superconductivity under hydrostatic pressure in Sr0.5RE0.5FBiS2 (RE = Ce, Nd, Pr, and Sm) compounds. J. Appl. Phys. 117(1–7), 013901 (2015).
Kajitani, J. et al. Chemical pressure effect on superconductivity of BiS2-based Ce1−xNdxO1−yFyBiS2 and Nd1−zSmzO1−yFyBiS2. J. Phys. Soc. Jpn. 84(1–6), 044712 (2015).
Hiroi, T. et al. Evolution of superconductivity in BiS2-based superconductor LaO0.5F0.5Bi(S1−xSex)2. J. Phys. Soc. Jpn. 84(1–4), 024723 (2015).
Mizuguchi, Y. et al. In-plane chemical pressure essential for superconductivity in BiCh2-based (Ch: S, Se) layered structure. Sci. Rep. 5(1–8), 14968 (2015).
Jha, R. et al. Superconductivity in Layered Oxychalcogenide La2O2Bi3AgS6. J. Phys. Soc. Jpn. 87(1–3), 083704 (2018).
Sun, Y. L. et al. Design and Synthesis of a New Layered Thermoelectric Material LaPbBiS3O. Inorg. Chem. 53, 11125–11129 (2014).
Mizuguchi, Y. et al. Crystal structure, site selectivity, and electronic structure of layered chalcogenide LaOBiPbS3. EPL 119(p1–p5), 26002 (2017).
Hijikata, Y. et al. Synthesis, Crystal Structure, and Physical Properties of New Layered Oxychalcogenide La2O2Bi3AgS6. J. Phys. Soc. Jpn. 86(1–4), 124802 (2017).
Zhai, H. F. et al. Possible Charge-density wave, superconductivity and f-electron valence instability in EuBiS2F. Phys. Rev. B 90(1–9), 064518 (2014).
Mizuguchi, Y., Nishida, A., Omachi, A. & Miura, O. Thermoelectric properties of new Bi-chalcogenide layered compounds. Cogent Phys. 3(1–14), 1156281 (2016).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects. Phys. Rev. 147, 295–302 (1966).
Tanaka, M. et al. Site selectivity on chalcogen atoms in superconducting La(O,F)BiSSe. Appl. Phys. Lett. 106(1–5), 112601 (2015).
Jinno, G. et al. Bulk Superconductivity Induced by In-plane Chemical Pressure Effect in Eu0.5La0.5FBiS2−xSex. J. Phys. Soc. Jpn. 85(1–6), 124708 (2016).
Ruan, B. B. et al. Superconductivity in Bi3O2S2Cl with Bi-Cl Planar Layers. J. Am. Chem. Soc. 141, 3404–3408 (2019).
Izumi, F. & Momma. Three-Dimensional Visualization in Powder Diffraction. Solid State Phenom. 130, 15–20 (2007).
Momma, K. & Izumi, F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658 (2008).
Acknowledgements
We gratefully appreciate O. Miura of Tokyo Metropolitan University for his technical support. This work was financially supported by grants in Aid for Scientific Research (KAKENHI) (Grant Nos 15H05886, 15H05884, 16H04493, 17K19058, 16K05454, and 15H03693) and Advanced Research Program under the Human Resources Funds of Tokyo.
Author information
Authors and Affiliations
Contributions
R.J. synthesized the examined samples. R.J. and Y.M. evaluated the sample qualities and analyzed the crystal structure. R.J., T.D.M., Y.A., M.N. and I.T. measured electrical resistivity and analyzed the data. R.J. and Y.G. measured magnetic susceptibility and Seebeck coefficient. R.J. and Y.M. wrote the manuscript. Y.M. designed the research project.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jha, R., Goto, Y., Matsuda, T.D. et al. Bulk superconductivity in a four-layer-type Bi-based compound La2O2Bi3Ag0.6Sn0.4S5.7Se0.3. Sci Rep 9, 13346 (2019). https://doi.org/10.1038/s41598-019-49934-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-49934-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.