Abstract
Nitrogen-vacancy (NV) centres in diamond hold promise in quantum sensing applications. A major interest in them is an enhancement of their sensitivity by the extension of the coherence time (T2). In this report, we experimentally generated more than four dressed states in a single NV centre in diamond based on Autler-Townes splitting (ATS). We also observed the extension of the coherence time to T2 ~ 1.5 ms which is more than two orders of magnitude longer than that of the undressed states. As an example of a quantum application using these results we propose a protocol of quantum sensing, which shows more than an order of magnitude enhancement in the sensitivity.
Similar content being viewed by others
Introduction
A single spin of a nitrogen-vacancy (NV) centre in diamond has a long coherence time (T2) under ambient conditions, and hence it is a promising candidate for classical- and quantum-sensing applications1,2,3,4,5,6,7,8,9,10,11,12,13. Various approaches to enhance the sensitivity of the NV based sensors have been experimentally demonstrated so far. For example, hybrid quantum sensors, which are inspired by quantum memory effects12,13, are of great concern. They use nuclear spins of carbon or nitrogen around the NV centre as quantum memories. If paramagnetic impurities such as substitutional nitrogen (P1) centres and 13C nuclear spins are sufficiently suppressed14, we can keep T2 long and the sensitivity can be enhanced15. While, when we consider the situation to increase the number of nearby nuclear spins as quantum memories to enhance the sensitivity more, T2 of both the electron and nuclear spins become shorter16. Here, we focus on the microwave (MW) dressed state based on Autler-Townes splitting (ATS)17,18,19,20,21,22. Using ATS, a large number of the dressed states can be generated17. It has also been reported that T2 of the MW dressed states is longer than that of undressed states17.
In this report, we experimentally demonstrate the generation of the MW dressed states in the single NV centre in diamond by ATS at ambient conditions in order to analyse fundamental phenomena. Next, we show the extension of T2 under the generation of the dressed states. Finally, we propose a protocol for the quantum sensing with the dressed states for AC-field sensing and numerically estimate the sensitivity as functions of the number of the dressed states and T2.
Mechanism of Autler-Townes Splitting
Dressed states based on the ATS are experimentally generated using the single NV centre in diamond by irradiation of an MW drive field. Figure 1(a) shows the energy level of the NV electron spin coupled with the 14N nuclear spin of the NV centre, where \(|{m}_{s},{m}_{I}\rangle \) is defined as the electron and the 14N nuclear spin of the NV centre, respectively. After laser illumination, the NV centre is equally polarised in \(|0,0\rangle \), \(|0,1\rangle \), and \(|0,-1\rangle \) depicted by the open circles under the application of a static magnetic field (B0). Figure 1(a) also depicts the irradiation of an unperturbed drive field whose frequency is close to a resonant frequency of a transition between \(|0,1\rangle \) and \(|-1,1\rangle \). When the drive field is considered as a classical mw mode, the NV centre can be coupled to the mode of the drive field. Then, each \(|0,1\rangle \) and \(|-1,1\rangle \) is split into two levels described in Fig. 1(b). It should be noted that Fig. 1(b) depicts the minimum number of dressed states by the ATS as an example. Thus, Fig. 1(b) depicts the generation of four dressed states of \(|0,1\rangle |1\rangle \), \(|-1,1\rangle |0\rangle \), \(|0,1\rangle |2\rangle \), and \(|-1,1\rangle |1\rangle \) in the presence of coupling between the NV centre (\(|0,1\rangle \) and \(|-1,1\rangle \)) and the mode of the drive field (\(|0\rangle \), \(|1\rangle \), and \(|2\rangle \)). This phenomenon is called (weak) ATS. Figure 1(b) also shows the energy levels of the dressed states which are characterised by the Rabi frequency of an NV electron spin (Ω) and frequency of the drive field (ω), and its spectrum is given by the following equation23:
where ν is the incident probe-frequency. κ is the inverse of the dephasing time. ∆ω = ω0 − ω. Here ω0 means the resonant frequency of an NV electron spin. The first term of Eq. (1) shows the resonant frequency depends on just ω and the second and third terms of Eq. (1) show the resonant frequencies depend on not only ω but also Ω. Thus, Eq. (1) is described as a Mollow-triplet spectrum. In the case of ∆ω = 0, the resonant frequency of the central peak, which is described by the first term in Eq. (1), does not depend on the Ω, while the side peaks, which are described by the second and third terms in Eq. (1), have linear dependences on Ω. In the case of \(\Delta \omega \ne 0\), the resonant frequency of the central peak depends on ∆ω according to the following relation24: \(\Omega =\sqrt{{{\Omega }_{0}}^{2}+{(\Delta {\rm{\omega }})}^{2}}\), where Ω0 is the Rabi frequency in the on-resonance condition. On the other hand, the changes in the resonant frequencies of the side peaks satisfy the following relation24: \(\Omega ={\Omega }_{0}\pm \sqrt{{{\Omega }_{0}}^{2}+{(\Delta {\rm{\omega }})}^{2}}\).
Results and Discussion
The information of our sample and experimental setup
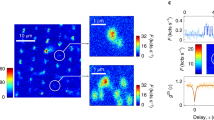
Figure 2(a) shows our experimental setup (See Methods). The sample is a high-temperature high-pressure (HTHP) type IIa (111) diamond. The second-order autocorrelation function, g(2)(τ), was measured using the Hanbury-Brown-Twiss (HBT) setup25 to confirm whether NV centre indicated by the circle depicted in Fig. 2(b) is a single centre or not. The power of the 532-nm laser is 100 µW. Figure 2(c) shows the measured g(2)(0) is ∼0.1. Therefore, this NV centre is a single centre.
In our experiment, we chose an NV centre that is weakly coupled to other nuclear spins (e.g., 13C nuclear spin). We measured the optically detected magnetic resonance (ODMR) spectrum with a 1-µs pulsed laser by sweeping the frequency of a 5.5-µs pulsed probe MW (Pmw) pulse (π pulse) depicted top of Fig. 3. In Fig. 3(a), the ODMR spectrum has three dips with 2.1 MHz splitting, which corresponds to the hyperfine splitting of the 14N nuclear spin of the NV centre26.
(a) ODMR spectrum without any drive fields. (b) Resonant frequencies as a function of the strength of the drive field (Bdrive). Black, red, and blue plots show the changes in resonant frequencies under the irradiation of Dmw frequencies of 2834.75 MHz (Dmw 1), 2837.05 MHz (Dmw 2), and 2839.18 MHz (Dmw 3), respectively. Solid lines are fitted for each resonant frequency. (c) ODMR spectrum under a Dmw at a frequency of 2834.75 MHz and a Dmw power of 33 µT. We can observe the Mollow triplet, which we call ATS.
Experimental generation of dressed states by ATS
First, we measured the change in the dressed-state resonant frequencies by changing the power of continuous drive MW (Dmw) with pulse sequence depicted in the top of Fig. 3. These experiments use the three Dmw frequencies of 2834.75 MHz (Dmw1), 2837.05 MHz (Dmw2), and 2839.18 MHz (Dmw3) to generate dressed states. The results are shown in Fig. 3(b). The signals for each Dmw frequency split into three above ∼10 µT.
Here we focus on the 2834.75 MHz of Dmw1. It should be noted that all three Dmw frequencies have the same dependences on the power of the continuous Dmw. The ODMR spectrum under continuous irradiation at Dmw1 with the power of 33 µT is shown in Fig. 3(c). It shows the increase of PL intensity was observed around 2835 MHz with continuous irradiation of Dmw1 (Fig. 3(c)) while the decrease of PL intensity was observed around 2835 MHz without continuous irradiation of Dmw1 (see Fig. 3(a)). The peaks are inverted, and the reason may come from the pulse sequence depicted in the top of Fig. 3. It shows the pulsed laser and the continuous Dmw field are simultaneously applied to the NV centre in the initialisation process. When the NV centre can be initialised into \(|-1\rangle \) by the pulsed laser and continuous Dmw field, the increase of PL intensity may be observed at magnetic resonance conditions of the NV electron spin as discussed in ref.27. In addition, Fig. 3(c) shows the ODMR spectrum at ∼2834.75 MHz splits into three peaks under the irradiation of the Dmw. Figure 3(b) shows that the resonant frequencies of the dressed states as a function of Bdrive. The solid lines show the linear fitting for each observed data. The absolute values of these slopes in Fig. 3(b) agree well with the gyromagnetic ratio of the NV electron spin (γNV)28, so that means the resonant frequencies of side peaks are linearly proportional to the Rabi frequencies of the NV electron spin. This result is in agreement with the theory of the change of resonant frequencies according to the second and third terms in Eq. (1) with Ω = γBdrive.
Next, we measured the change in the resonant frequencies of the dressed states by changing the continuous Dmw frequency while fixing the Dmw power at 33 µT with the pulse sequence depicted in the top of Fig. 4. The Dmw frequency was changed by the step of 0.2 MHz. The result is shown in Fig. 4(a). It shows that the dressed states are generated when the Dmw frequencies are close to resonant frequencies of the NV electron spin.
(a) ∆PL/PL intensity plots as functions of the Dmw vs Pmw frequencies. (b) Resonant frequencies of dressed states as a function of the Dmw frequencies. The black line shows a linear fitting with \(\Omega =\sqrt{{{\Omega }_{0}}^{2}+\,{(\Delta \omega )}^{2}}\). Red and blue solid lines show fittings with \(\Omega ={\Omega }_{0}\pm \sqrt{{{\Omega }_{0}}^{2}+\,{(\Delta \omega )}^{2}}\).
Figure 4(b) illustrates the dressed-state resonant frequencies as a function of the Dmw frequency around the centre of 2835 MHz to understand more details of the results depicted in Fig. 4(a). The black squares in Fig. 4(b) show the change of resonant frequencies of the centre peaks as a function of Dmw frequency. The dependence can be fitted by a linear function shown in solid black line in Fig. 4(b), and hence this is in good agreement with the theoretical prediction of \(\Omega =\sqrt{{{\Omega }_{0}}^{2}+\,{(\Delta \omega )}^{2}}\) described in Eq. (1). The red circles and the blue triangles in Fig. 4(b) also show the resonant frequencies of low- and high-resonant frequencies of the side peaks, respectively. Their resonant frequencies can be fitted by using the relation of the \(\Omega ={\Omega }_{0}\pm \sqrt{{{\Omega }_{0}}^{2}+{(\Delta \omega )}^{2}}\)24. Thus, all results are consistent with the theoretical prediction in ATS, demonstrating the generation of more than four dressed states by the ATS.
Coherence time of dressed states
First, we show whether the magnetic moment of the dressed states is the same with that of the undressed NV electron spin or not, since the dressed states were generated due to the coupling between the NV electron spins and mode of the Dmw. In order to investigate the magnetic moments of the dressed and undressed states, we measured Rabi oscillations of the dressed states and the NV electron spin with the pulse sequence depicted in the top of Fig. 5. It noted that while the Rabi oscillation of the dressed state was measured with continuous Dmw, the Rabi oscillation of the NV electron spin was measured without continuous Dmw. Moreover, we kept the pulse sequence time (Tseq) constant adjusting interval between the pulsed Pmw and the readout laser pulse depicted in Fig. 5, in order to perform the initialisation of the dressed states by the simultaneous irradiation of the pulse laser and the continuous Dmw in the Rabi measurements. The bottom of Fig. 5 shows the results of the Rabi measurements, and it indicates the Rabi frequency of the dressed spin states is the same with that of undressed spin states. Consequently, the magnetic moment of the NV electron spin and the dressed states are the same with each other.
(Top) Pulse sequence to observe Rabi oscillations of the dressed state and undressed NV electron spin. (Bottom) Black and red plots show the results of the Rabi oscillations of the dressed state and the undressed NV electron spin, respectively. They are fitted by sinusoidal curve described by black and red solid lines.
Next, we experimentally measured coherence time of the dressed states (T2ρ) and coherence time of a single NV centre (T2) in a 12C enriched diamond, since a coherent oscillation due to 13C nuclear spins on echo measurements29 can be suppressed using the NV centre in 12C enriched diamond. The top of Fig. 6 shows the pulse sequence for the T2ρ and T2 measurements. It is noted that while T2ρ was measured with the continuous Dmw irradiation, T2 was measured without continuous Dmw irradiation. Since the pulsed laser and continuous Dmw were simultaneously irradiated to the NV centre during the T2ρ measurements, we kept the pulse sequence time (Tseq) constant adjusting interval between the final π/2 Pmw pulse and the readout laser pulse depicted in Fig. 6. Then, the dressed spin states can be initialised by simultaneous irradiation of the pulse laser and the continuous Dmw in the T2ρ measurements. Additionally, a phase cycling technique was applied to T2ρ measurements in order to remove common-mode noise from laser fluctuations30. It is noted that the phase of the last π/2 Pmw pulse is indicated by ± signs depicted in the top of Fig. 6. In the case of a Pmw and Dmw strength of ~0.43 MHz and ~1.2 MHz, respectively, the result of T2ρ (black plots) and T2 (red plots) measurements fitted with exponential decay curves are shown in Fig. 6. The results show that we observed a coherence time of T2ρ ~ 1.5 ms of the dressed states, which is more than two orders of magnitude longer than T2 ~ 4.2 μs of the undressed states. While such an extension can also be demonstrated by a dynamical decoupling technique, e.g., a Carr-Purcell-Meiboom-Gill (CPMG) sequence in the NV centres6,31,32,33,34, an extension of two orders of magnitude by the ATS is much larger than the extension of about one order of T2 in the dynamical decoupling techniques6,30,31,32,33. The extended T2 by the ATS is also close to the longest T2 of a single NV centre in a 12C enriched diamond15.
Estimation of the sensitivity of the quantum sensing with dressed states
We propose a quantum sensing protocol with the MW dressed states for AC magnetic field sensing and discuss the numerical estimation of the sensitivity for this sensing under a simple and ideal case. First, we shortly explain how to generate an arbitrary number of MW dressed states. Here we consider the NV centre is coupled with the mode of a strong Dmw, as illustrated in Fig. 7. The first energy is ħω/2, and the other states are separated by ħω, where ħ and ω are the reduced Planck constant and the frequency of Dmw, respectively. If such a mode of the Dmw (\(|n\rangle \)) is coupled with two states of the NV centre of \(|1\rangle \) and \(|2\rangle \), dressed states of \(|{(D(n)\rangle }_{\pm }\) appear. The \(|D\,(n){\rangle }_{\pm }\) and their energies (E±(n)) are described by the following equations18,35:
respectively. c1 and c2 are the coefficients, which satisfy \({|{c}_{1}|}^{2}\) + \({|{c}_{2}|}^{2}\) = 1. Since a number of photons is large in the classical mw field mode17, a large number of dressed states can be generated. Then, we discuss the sensitivity of the AC magnetic field sensing using the arbitrary number of dressed states. The detections of the AC magnetic field using the undressed states and the dressed states discussed in Supplementary Informaiton are demonstrated based on a magnetic resonance technique. Thus, the sensitivity of the dressed states can be proportional to \(1/\sqrt{M{T}_{2{\rm{\rho }}}}\), where 2M corresponds to the number of dressed states (Details are disucssed in Supplementary Information). In addition, our experimental demonstrations show the magnetic moments of dressed states are the same with that of undressed states and the coherence time of the dressed states is more than two orders of magnitude longer that of the undressed states. Based on the above discussion, the ratio of the sensitivities with and without the dressed states is taken by \(\sqrt{M{T}_{2\rho }/{T}_{2}}\). In the case of T2ρ ~ 1.5 ms and T2 ~ 4.2 μs, the sensitivity is approximately enhanced 27 times with M = 2. Thus, the sensitivity can be effectively enhanced by using the dressed states. In particular, our protocol is very useful for an ensemble system which has very short T2, because of two effects: ‘the extension of T2’ and ‘the addition of the sensing information measured by generated dressed states’. Although we, here, do not consider the number of operations of the integration is limited by T2, our proposal opens up a new way for higher sensitivity on NV based AC magnetic field sensing.
Conclusion
In conclusion, we have experimentally demonstrated the generation of more than four dressed states of an NV centre in diamond with irradiating the continuous Dmw based on ATS. Our experimental results were good agreement with the theoretical prediction. Additionally, we have proposed a new quantum sensing protocol with the dressed states for AC magnetic fields sensing. Numerical estimations show the sensitivity of the quantum sensing with the dressed states can be enhanced at least one-order of magnitude with experimentally observed T2ρ and T2. Thus, we believe that the quantum sensing with the dressed states can be applicable for improving the sensitivity of a quantum sensing.
Note: Recently, we have become aware of related works on quantum sensing with a one-time measurement based on a combination of the Mollow triplet and dynamical decoupling under sensing of a weak AC field with GHz frequencies36,37. Our work has three differences: 1) the frequency range for the sensing target, 2) the effect of integration of dressed states for a higher sensitivity, and 3) robustness against environmental noises (extension of T2). Our work can realise sensing of a weak low-frequency AC field by dressed states generated by ATS.
Methods
Sample preparation
To generate dressed states by ATS, we used high-temperature and high-pressure (HTHP) type IIa (111) diamond. After the nitrogen (14N) was implanted into the diamond with a 30-keV accelerating energy, the sample was annealed at 750 °C for 30 min for the generation of NV centres in diamond. To measure T2 and T2ρ, we used a single NV centre in a CVD-grown 12C enriched diamond layer on a type Ib (111) diamond substrate. The NV centres were generated during the growth of the diamond layer.
Home-made confocal microscope with an electromagnetic field irradiation system
All experiments were performed by a homemade confocal microscope with an electromagnetic field (emf) irradiation system at room temperature depicted in Fig. 2(a). A 532-nm laser focused by an objective lens illuminates an NV centre in diamond. The detection system is composed of a 50:50 beam splitter (BS) and two avalanche photodiodes (APDs) in order to detect the photoluminescence and measure g(2)(τ). Two high frequencies with ~2.8 GHz irradiate to the NV centre by a by a thin copper wire with a diameter of 10 µm to manipulate the electron spin of an NV centre under the application of a static magnetic field generated by a neodymium magnet.
Data Availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Taylor, J. M. et al. M. D. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 4, 810 (2008).
Maurer, P. C. et al. Far-field optical imaging and manipulation of individual spins with nanoscale resolution. Nat. Phys. 6, 912 (2010).
McGuinness, L. P. et al. Quantum measurement and orientation tracking of fluorescent nanodiamonds inside living cells. Nat. Nanotech. 6, 358 (2011).
Kucsko, G. et al. Nanometre-scale thermometry in a living cell. Nature 500, 54 (2013).
Sage, D. L. et al. R. L. Optical magnetic imaging of living cells. Nature 496, 486 (2013).
Shi, F. et al. Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 10, 21 (2014).
Ajoy, A., Bissbort, U., Lukin, M. D., Walsworth, R. L. & Cappellaro, P. Atomic-Scale Nuclear Spin Imaging Using Quantum-Assisted Sensors in Diamond. Phys. Rev. X 5, 011001 (2015).
Zhu, X. et al. Coherent coupling of a superconducting flux-qubit to an electron spin ensemble in diamond. Nature 482, 221 (2011).
Kubo, Y. et al. Hybrid Quantum Circuit with a Superconducting Qubit Coupled to a Spin Ensemble. Phys. Rev. Lett. 107, 220501 (2011).
Matsuzaki, Y. et al. Improving the coherence time of a quantum system via a coupling with an unstable system. Phys. Rev. Lett. 114, 120501 (2015).
Unden, T. et al. Quantum Metrology Enhanced by Repetitive Quantum Error Correction. Phys. Rev. Lett. 116, 230502 (2016).
Zaiser, S. et al. Enhancing quantum sensing sensitivity by a quantum memory. Nat. Commun. 7, 12279, https://doi.org/10.1038/ncomms12279 (2016).
Matsuzaki, Y. et al. Hybrid quantum magnetic field sensor with an electron spin and a nuclear spin in diamond. Phys. Rev. A 94, 052330 (2016).
Wang, Z.-H. & Takahashi, S. Spin decoherence and electron spin bath noise of a nitrogen-vacancy center in diamond. Phys. Rev. B 87, 115122 (2013).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater. 8, 383 (2009).
Mizuochi, N. et al. Coherence of single spins coupled to a nuclear spin bath of varying density. Phys. Rev. B 80, 041201(R) (2009).
Laucht, A. et al. A dressed spin qubit in silicon. Nat. Nanotech. 12, 61 (2017).
Autler, S. & Townes, C. Stark Effect in Rapidly Varying Fields. Phys. Rev. 100, 703 (1955).
Cohen-Tannoudji, C., Dupont-Roc, J. & Grynberg, G. Atom-photon interactions basic processes and applications, vol. 6 (Wiley, J. New York, 1992).
He, X., Fisk, P. T. H. & Manson, N. B. Autler–Townes effect of the photoexcited diamond nitrogen-vacancy center in its triplet ground state. J. Appl. Phys. 72, 211 (1992).
Manson, N. B., Rogers, L. J., Wilson, E. A. & Wei, C. Hole burning—EIT studies of the NV centre in diamond. J. Lumin. 130, 1959 (2010).
Yan, F. et al. Rotating-frame relaxation as a noise spectrum analyser of a superconducting qubit undergoing driven evolution. Nat. Commun. 4, 2337, https://doi.org/10.1038/ncomms3337 (2013).
Mollow, B. R. Power Spectrum of Light Scattered by Two-Level Systems. Phys. Rev. 188, 188 (1969).
Wei, C. & Manson, N. B. Experimental investigations of the absorption and dispersion profiles of a strongly driven transition: Two-level system with a weak probe. Phys. Rev. A 49, 4751 (1994).
Berthel, M. et al. Photophysics of single nitrogen-vacancy centers in diamond nanocrystals. Phys. Rev. B 91, 035308 (2015).
Steiner, M., Neumann, P., Beck, J., Jelezko, F. & Wrachtrup, J. Universal enhancement of the optical readout fidelity of single electron spins at nitrogen-vacancy centers in diamond. Phys. Rev. B 81, 035205 (2010).
Kehayias, P. et al. Microwave saturation spectroscopy of nitrogen-vacancy ensembles in diamond. Phys. Rev. B 89, 245202 (2014).
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1 (2013).
Childress, L. et al. Dynamics of Coupled Electron and Nuclear Spin Qubits in Diamond. Science 314, 281 (2006).
Pham, L. M. et al. NMR technique for determining the depth of shallow nitrogen-vacancy centers in diamond. Phys. Rev. B 93, 045425 (2016).
Lange, G., de, Wang, Z. H., Ristè, D., Dobrovitski, V. V. & Hanson, R. Universal Dynamical Decoupling of a Single Solid-State Spin from a Spin Bath. Science 330, 60 (2010).
Naydenov, B. et al. Dynamical decoupling of a single-electron spin at room temperature. Phys. Rev. B 83, 081201(R) (2011).
Pham, L. M. et al. Enhanced solid-state multispin metrology using dynamical decoupling. Phys. Rev. B 86, 045214 (2012).
Farfurnik, D. et al. Optimizing a dynamical decoupling protocol for solid-state electronic spin ensembles in diamond. Phys. Rev. B 92, 060301(R) (2015).
Rand, S. C. Lectures on Light Nonlinear and Quantum Optics using the Density Matrix, vol. 6 (OXFORD University Press, New York, 2010).
Joas, T., Waeber, A. M., Braunbeck, G. & Reinhard, F. Quantum sensing of weak radiofrequency signals by pulsed Mollow absorption spectroscopy. Nat. Commun. 8, 694, https://doi.org/10.1038/s41467-017-01158-3 (2017).
Stark, A. et al. Narrow-bandwidth sensing of high-frequency fields with continuous dynamical decoupling. Nat. Commun. 8, 1150, https://doi.org/10.1038/s41467-017-01159-2 (2017).
Acknowledgements
This work is supported by KAKENHI (No. 15H05868, 16H02088) and the Collaborative Research Program of ICR, Kyoto University (Grant # 2018-90). HM is supported by a Grant-in-Aid for Young Scientists (B), Grant No. 16K17484 and by the Future Development Funding Program of Kyoto University Research Coordination Alliance.
Author information
Authors and Affiliations
Contributions
H.M., T.T. and D.M. performed the measurements and the data analysis. H.K. synthesised the 12C-enriched diamond layers. All the authors (H.M., T.T., D.M., H.K., T.M., S.Y., M.F. and N.M.) contributed to the data analysis, discussion, and manuscript preparation.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41598_2019_49683_MOESM1_ESM.pdf
Supplementary Information: Extension of the Coherence Time by Generating MW Dressed States in a Single NV Centre in Diamond
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morishita, H., Tashima, T., Mima, D. et al. Extension of the Coherence Time by Generating MW Dressed States in a Single NV Centre in Diamond. Sci Rep 9, 13318 (2019). https://doi.org/10.1038/s41598-019-49683-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-49683-z
This article is cited by
-
Relaxation of a dense ensemble of spins in diamond under a continuous microwave driving field
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.