Abstract
Radiative nanomaterial thermal behavior within a permeable closed zone with elliptic hot source is simulated. Darcy law is selected for simulating permeable media in existence of magnetic forces. Contour plots for various buoyancy, Hartmann numbers and radiation parameter were illustrated. Carrier fluid is Al2O3-water with different shapes. Outputs prove that conduction mode augments with enhance of Ha. Nu augments with considering radiation source term.
Similar content being viewed by others
Introduction
Transport processes of nanofluid through medium with porosity have been a challenging study in recent times because of its immense applications in geothermal operations, thermal insulations, food processing, and other petrochemical applications. Modeling of nanomaterial flow with imposing Lorentz forces was scrutinized by Yadav et al.1 and buoyancy force was involved in governing PDEs. A survey present in the literature has shown that thermal properties of nanofluids are better than the usual fluids. Results available have shown that heating properties of solid is larger than liquid. The thermal conductivity engine oil and H2 O are thousand times lower than that of copper (Cu). Some preliminary experiments on Cu−water suspended nanoparticles are performed by Eastman et al.2. In the augmentation of heat transmission, Khanafer et al.3 obtained some interesting results by utilizing nanofluids. The problem studied by Qiang4 studied experimentally for copper based water nanofluid and obtained some interesting results. More detail on the investigation of heat transmission with nanofluids can be found in5,6,7,8,9,10. CuO-water based nanofluid inside absorptive medium in the actuality of magnetic force with Brownian motion is performed by Sheikholeslami11. MHD fluid flow was portrayed by Raju et al.12 over a cone. Kolsi et al.13 employed moved fin to control nanofluid migration through a channel. Different applications of Fe3O4-water nanofluid were categorized by Sheikholeslami and Rokni14. Haq et al.15 utilized carbon nanotubes with slip flow to improve convective heat transfer.
Nanomaterial flow has received considerable attention from many scientists due to its large uses in engineering16,17,18. Plasma studies and aerodynamics are some practical examples of such flows of radiation mechanism. Radiation is often encountered in frequent engineering problems. Keeping in view its applications Sheikholeslami et al.19,20,21,22,23 presented the application of nanomaterial in various domains. Some recent publications about heat transfer can be found in24,25,26,27,28,29,30,31,32. To preserve the conduction of about fluid low, nano liquids have been recommended in past ages. Influence electric field on ferrofluid inside a tank with dual adaptable surfaces was demonstrated by Sheikholeslami et al.33. The investigation of nanofluid with magnetic forces with physical effects and applications can studied from34,35,36. Turbulator effect on swirling nanofluid flow was examined by Sheikholeslami et al.37. Utilizing such tools make the flow more complex. New model was introduced by Yadav et al.38 for thermal instability. Furthermore, instability of thermal treatment of nanomaterial within a penetrable zone was exemplified by Yadav et al.39. They considered variation of nanomaterial viscosity in their simulation. Viscous heating effect on nanomaterial radiative behavior in existence of electric field was scrutinized by Daniel et al.40. In addition, they considered double stratification with magnetic field. Nanomaterial free convection with double-diffusive was scrutinized by Yadav et al.41 involving rotation system. Permeable plate with considering radiative impact was modeled by Daniel et al.42. They imposed Lorentz forces and utilized HAM to solve the problem. Nanomaterial exergy loss with implementation of innovative approach was established by Sheikholeslami43. He is expert in this field and shows the approach applications in appearance of magnetic field. Entropy production during transient nanomaterial MHD flow was demonstrated by Daniel et al.44. They derived governing equations with considering electric field effect. Developments on numerical approach for simulating treatment of nanomaterial were presented in different publications45,46,47,48,49,50,51.
In current study, effects magnetic force and radiation on migration of nanofluid inside a porous medium was illustrated. CVFEM is considered as tool for showing roles of Rd, Ra, & Ha on performance.
Problem Explanation
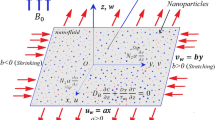
The shape of enclosure and its boundary conditions have been demonstrated in Fig. 1. Furthermore, example element was demonstrated. Uniform q″ was imposed on inner wall. Unchanging magnetic field impact on nanomaterial flow style is surveyed. Porous domain has been full of H2O based nanofluid.
Governing equations and CVFEM
Free convection and radiation impacts on migration of nanofluid inside a penetrable media were pretend under the effect of Lorentz forces. Considering Darcy model, final formulations can be written as:
Characteristics of nanofluid have following formulas:
μnf & knf are represented the Brownian motion forces functions and function of shape factor as mentioned in52:
To get the properties of carrier fluid, we utilized alike model used in52. To estimate temperature dependent properties, Rokni et al.53,54 provide new formulation.
The following non dimensional variables by using of the stream function and, can be gained:
Thus, the last equations are:
Important variables can be introduced as:
Inner and outer surfaces have following conditions:
Nuave and Nuloc have been calculated as:
Simulation technique, grid and verification
Combine of two influential approaches has been assembled in CVFEM. As explained in ref.33 and shown in Fig. 1(b), such grid is applied in CVFEM. Final equations have attainment to values of θ, Ψ by using of Gauss-Seidel technique. Table 1 exhibits the sample for grid management. This procedure should be done because last result should be immaterial of grid size. Verifications of current code for nanofluid convective flow are displayed in Fig. 2 3. These observations show nice accuracy of CVFEM code.
Verification with Khanafer et al.3 for ϕ = 0.1, Gr = 104 and \(\Pr =6.2(Cu-Water)\).
Outcome and Discussion
Radiative nanofluid heat transmission through a penetrable enclosure by means of Darcy law was displayed. Effects of Brownian motion and shape factor on nanomaterial behavior were examined. CVFEM was applied to display the variations of Rayleigh number (R a = 100 to 600), radiation (Rd = 0 → 0.08), Concentration of Alumina (ϕ = 0 to 0.04) and magnetic forces (Ha = 0 to 20). Deviations of Nu respect to m are represented in Table 2. Higher value of Nu is described for Platelet shape. Thus, it is designated for more simulations. Role of scattering Al2O3 in H2O have exemplified in Fig. 3. It is observed that \(|{\psi }_{\max }|\) and Nu enhances by diffusing Al2O3. Since Lorentz force acting, the impact of ϕ on isotherms is not important. Impacts of substantial parameters on isotherms and streamlines are displayed in Figs 4, 5 and 6. \(|{\psi }_{\max }|\) rises with increase of buoyancy effect while it diminishes with escalation of Ha. Simulations for higher Ra leads to complex shape of isotherm with imposing greater buoyancy forces and thermal plume appears. Imposing Lorentz forces make suppress the plume and isotherms force to being parallel to each other’s. For better description, below formula was derived and Fig. 7 was displayed.
Greater values of radiation parameter and Ra lead to thinner boundary layer which indicates greater Nuave. Slender thickness of boundary layer was seen with reduce of Hartmann number which proves reduction effect of Hartmann number on Nuave.
Conclusions
Imposing Lorenz forces influence on nanomaterial flow by means of Darcy law inside a porous enclosure is reported. Shape factor role was involved to predict nanomaterial properties as well as Brownian motion. CVFEM modeling was done to find the variations of Lorentz and buoyancy forces and radiation parameter on nanofluid thermal characteristic were demonstrated. The concluded points are given as
-
Outputs depict that Nu improves with improve of buoyancy force but it decrease with augment of Ha.
-
Higher value of Nu is described for Platelet shape.
-
Nu augments with considering radiation source term.
-
As Ha enhances, the velocity of working fluid decreases.
References
Yadav, D., Wang, J., Bhargava, R., Lee, J. & Cho, H. H. Numerical investigation of the effect of magnetic field on the onset of nanofluid convection. Applied Thermal Engineering. 103, 1441–1449 (2016).
Eastman, J. A. et al. Novel thermal properties of nanostructured materials. J. Metastable Nanocryst. Mater. 2, 629–637 (1999).
Khanafer, K., Vafai, K. & Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 46, 3639–3653 (2003).
Qiang, L. & Yimin, X. Convective heat transfer and flow characteristics of Cu-water nanofluid. Sci. China Ser. E 45, 408–416 (2002).
Sheikholeslami, M., Haq, R.-u., Shafee, A. & Li, Z. Heat transfer behavior of Nanoparticle enhanced PCM solidification through an enclosure with V shaped fins. International Journal of Heat and Mass Transfer 130, 1322–1342 (2019).
Shah, Z., Islam, S., Ayaz, H. & Khan, S. Radiative Heat And Mass Transfer Analysis Of Micropolar Nanofluid Flow Of Casson Fluid Between Two Rotating Parallel Plates With Effects Of Hall Current. ASME Journal of Heat Transfer, https://doi.org/10.1115/1.4040415 (2018).
Shah, Z., Islam, S., Gul, T., Bonyah, E. & Khan, M. A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 9, 1201–1214, https://doi.org/10.1016/j.rinp.2018.01.064 (2018).
Shah, Z., Dawar, A., Kumam, P., Khan, W. & Islam, S. Impact of Nonlinear Thermal Radiation on MHD Nanofluid Thin Film Flow over a Horizontally Rotating Disk. Appl. Sci. 9, 1533 (2019).
Shah, Z., Dawar, A., Islam, S., Khan, I. & Ching, D. L. C. Darcy-Forchheimer Flow of Radiative Carbon Nanotubes with Microstructure and Inertial Characteristics in the Rotating Frame. Case Studies in Thermal Engineering. 12, 823–832 (2018).
Daniel, Y. S., Aziz, Z.A, Ismail, Z., Salah, F. Entropy Analysis of Unsteady Magnetohydrodynamic Nanofluid over Stretching Sheet with Electric Field. International Journal for Multiscale Computational Engineering. 15(6) (2017)
Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. Journal of Molecular Liquids 249, 921–929 (2018).
Raju, C. S. K., Sandeep, N. & Malvandi, A. Free convective heat and mass transfer of MHD non-Newtonian nanofluids over a cone in the presence of non-uniform heat source/sink. Journal of Molecular Liquids 221, 108–115 (2016).
Kolsi, L. et al. Control of Heat Transfer and Fluid Flow via Moved Fin in a Triangular Enclosure Filled with Nanofluid, Heat Transfer Research, https://doi.org/10.1615/HeatTransRes.2018019485 (2019).
Sheikholeslami, M. & Rokni, H. B. Simulation of nanofluid heat transfer in presence of magnetic field: A review. International Journal of Heat and Mass Transfer 115, 1203–1233 (2017).
Haq, U. R., Nadeem, S., Khan, Z. H. & Noor, N. F. M. Convective heat transfer in MHD slip flow over a stretching surface in the presence of carbon nanotubes. Physica B: Condensed Matter 457(15), 40–47 (2015).
Khan, A. S. et al. Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Appl. Sci. 8, 2244 (2018).
Khan, A. et al. Darcy–Forchheimer flow of micropolar nanofluid between two plates in the rotating frame with non-uniform heat generation/absorption. Adv. Mech. Eng. 10, 1–16 (2018).
Li, Z. et al. Time dependent heat transfer in a finned triplex tube during phase changing of nanoparticle enhanced PCM. The European Physical Journal Plus (EPJP). 134, 173, https://doi.org/10.1140/epjp/i2019-12627-9 (2019).
Sheikholeslami, M., Shah, Z., shafi, A., khan, I. & Itili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle, Scientific report, https://doi.org/10.1038/s41598-018-37964-y (2019).
Shah, Z., Bonyah, E., Islam, S., Gul, T. Impact of thermal radiation on electrical mhd rotating flow of carbon nanotubes over a stretching sheet, AIP Advances 9, 015115 https://doi.org/10.1063/1.5048078 (2019).
Sheikholeslami, M., Jafaryar, M., Hedayat, M., Shafee, A. & Li, Z. Truong Khang Nguyen, Mohsen Bakouri, Heat transfer and turbulent simulation of nanomaterial due to compound turbulator including irreversibility analysis. International Journal of Heat and Mass Transfer 137, 1290–1300 (2019).
Ramzan, M., Sheikholeslami, M., Saeed, M. & Chung, J. D. On the convective heat and zero nanoparticle mass flux conditions in the flow of 3D MHD Couple Stress nanofluid over an exponentially stretched surface. Scientific Reports 9, 562, https://doi.org/10.1038/s41598-018-37267-2 (2019).
Sheikholeslami, M., Khan, I. & Tlili, I. Non-equilibrium model for nanofluid free convection inside a porous cavity considering Lorentz forces. Scientific Reports, https://doi.org/10.1038/s41598-018-33079-6(2018).
Nasir, S. et al. Three dimensional Darcy-Forchheimer radiated flow of single and multiwall carbon nanotubes over a rotating stretchable disk with convective heat generation and absorption. AIP Advances 9, 035031 (2019).
Sheikholeslami, M. et al. Heat transfer simulation during charging of nanoparticle enhanced PCM within a channel. Physica A: Statistical Mechanics and its Applications 525, 557–565 (2019).
Kumam, P., Shah, S., Dawar, A., Rasheed,H. & Islam, S. Entropy Generation in MHD Radiative Flow of CNTs Casson Nanofluid in Rotating Channels with Heat Source/Sink, Mathematical Problems in Engineering, 2019, https://doi.org/10.1155/2019/9158093 (2019).
Khan, A. S., Nie, Y. & Shah, Z. Impact of Thermal Radiation and Heat Source/Sink on MHD Time-Dependent Thin-Film Flow of Oldroyed-B, Maxwell, and Jeffry Fluids over a Stretching Surface. Processes 7, 191 (2019).
Ishaq, M. et al. Nanofluid Film Flow of Eyring Powell Fluid with Magneto Hydrodynamic Effect on Unsteady Porous Stretching Sheet. Punjab University Journal of Mathematics 51(2), 131–153 (2019).
Muhammad, S., Ali, G., Shah, Z., Islam, S. & Hussain, S. A. The Rotating Flow of Magneto Hydrodynamic Carbon Nanotubes over a Stretching Sheet with the Impact of Non-Linear Thermal Radiation and Heat Generation/Absorption. Appl. Sci. 8, 482 (2018).
Saeed, A. et al. Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction. Symmetry 11, 439 (2019).
Jawad, M. et al. Impact of Nonlinear Thermal Radiation and the Viscous Dissipation Effect on the Unsteady Three-Dimensional Rotating Flow of Single-Wall Carbon Nanotubes with Aqueous Suspensions. Symmetry 11, 207 (2019).
Sheikholeslami, M. et al. Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger. International Journal of Heat and Mass Transfer 135, 470–478 (2019).
Sheikholeslami, M. Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method, Computer Methods in Applied Mechanics and Engineering, 344 306–318.
Haq, R., Rashid, I. & Khan, Z. H. Effects of aligned magnetic field and CNTs in two different base fluids over a moving slip surface. J. Mol. Liq. 243, 682–688 (2017).
Bhatti, M. M., Zeeshan, A. & Ellahi, R. Simultaneous effects of coagulation and variable magneticfield on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc. Res. 11, 32–42 (2017).
Marina, S. et al. MHD natural convection and entropy generation of ferrofluid in an open trapezoidal cavity partially filled with a porous medium. Int. J. Mech. Sci. 136, 493–502 (2018).
Sheikholeslami, M., Jafaryar, M., Shafee, A., Li, Z. & Haq, R. Heat transfer of nanoparticles employing innovative turbulator considering entropy generation. International Journal of Heat and Mass Transfer 136, 1233–1240 (2019).
Yadav, D., Agrawal, G. S. & Lee, J. Thermal instability in a rotating nanofluid layer: A revised model. Ain Shams Engineering Journal 7, 431–440 (2016).
Yadav, D. et al. Linear and nonlinear analysis of thermal instability in a rotating porous layer saturated by a non-Newtonian nanofluid with thermal conductivity and viscosity variation. Microfluidics and Nanofluidics 16, 425–440 (2014).
Yadav, D., Aziz, Z. A., Ismail, Z. & Salah, F. Effects of thermal radiation, viscous and Joule heating on electrical MHD nanofluid with double stratification. Chinese Journal of Physics. B(3), 630–51 (2017).
Yadav, D., Lee, D., Cho, H. H. & Lee, J. The onset of double-diffusive nanofluid convection in a rotating porous medium layer with thermal conductivity and viscosity variation: A revised model. Journal of Porous Media 19, 1–16 (2016).
Yadav, D. & Daniel, S. K. Effects of buoyancy and thermal radiation on MHD flow over a stretching porous sheet using homotopy analysis method. Alexandria Engineering Journal. 54(3), 705–12 (2015).
Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Computer Methods in Applied Mechanics and Engineering 344, 319–333 (2019).
Daniel, Y. S., Aziz, Z. A., Ismail, Z. & Salah, F. Numerical study of Entropy analysis for electrical unsteady natural magnetohydrodynamic flow of nanofluid and heat transfer. Chinese Journal of Physics 55(5), 1821–48 (2017).
Sheikholeslami, M., Jafaryar, M., Shafee, A. & Li, Z. Simulation of nanoparticles application for expediting melting of PCM inside a finned enclosure. Physica A: Statistical Mechanics and its Applications 523, 544–556 (2019).
Yadav, D., Lee, J. & Cho, H. H. Brinkman convection induced by purely internal heating in a rotating porous medium layer saturated by a nanofluid. Powder Technology 286, 592–601 (2015).
Daniel, Y. S., Aziz, Z. A., Ismail, Z. & Salah, F. Slip Effects on Electrical Unsteady MHD Natural Convection Flow of Nanofluid over a Permeable Shrinking Sheet with Thermal Radiation. Engineering Letters. 26(1) (2018).
Zheng, S., Juntai, S., Keliu, W. & Xiangfang, L. Gas Flow Behavior through Inorganic Nanopores in Shale Considering Confinement Effect and Moisture Content. Industrial & Engineering Chemistry Research 57, 3430–3440 (2018).
Zheng, S. et al. An analytical model for gas transport through elliptical nanopores. Chemical Engineering Science 199, 286–293 (2019).
Zheng, S. et al. An analytical model for transport capacity of water confined in nanopores. International Journal of Heat and Mass Transfer 138, 620–630 (2019).
Shah, Z., Bonyah, E., Islam, S. & Gul, T. Impact of thermal radiation on electrical mhd rotating flow of carbon nanotubes over a stretching sheet. AIP Advances 9, 015115, https://doi.org/10.1063/1.5048078 (2019).
Sheikholeslami, M., Shehzad, S. A., Li, Z. & Shafee, A. Numerical modeling for Alumina nanofluid magnetohydrodynamic convective heat transfer in a permeable medium using Darcy law. International Journal of Heat and Mass Transfer. 127, 614–622 (2018).
Rokni, H. B., Moore, J. D., Gupta, A., McHugh, M. A. & Gavaises, M. Entropy scaling based viscosity predictions for hydrocarbon mixtures and diesel fuels up to extreme conditions. Fuel 241, 1203–1213 (2019).
Rokni, H. B. et al. Purely predictive method for density, compressibility, and expansivity for hydrocarbon mixtures and diesel and jet fuels up to high temperatures and pressures. Fuel 236, 1377–1390 (2019).
Acknowledgements
This project was supported by the Theoretical and Computational Science (TaCS) Center under Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT. This research was funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
Author information
Authors and Affiliations
Contributions
M.S. and Z.S. modeled and solved the problem. Z.S. and T.T.N. wrote the manuscript. P.K. contributed in the numerical compuattuions and plotting the graphical results. T.T.N. and A.S. edited the manuscript grammatically and thoroughly checked the mathematical modeling and English corrections. All the corresponding authors finalized the manuscript after its internal evaluation.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nguyen-Thoi, T., Sheikholeslami, M., Shah, Z. et al. Magnetohydrodynamic nanofluid radiative thermal behavior by means of Darcy law inside a porous media. Sci Rep 9, 12765 (2019). https://doi.org/10.1038/s41598-019-49269-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-49269-9
This article is cited by
-
Integrated intelligent computing application for effectiveness of Au nanoparticles coated over MWCNTs with velocity slip in curved channel peristaltic flow
Scientific Reports (2021)
-
Wall properties and convective conditions in MHD radiative peristalsis flow of Eyring–Powell nanofluid
Journal of Thermal Analysis and Calorimetry (2021)
-
On the Thermal Performance of a Fractal Microchannel Subjected to Water and Kerosene Carbon Nanotube Nanofluid
Scientific Reports (2020)
-
Peristaltic channel flow and heat transfer of Carreau magneto hybrid nanofluid in the presence of homogeneous/heterogeneous reactions
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.