Abstract
Myocardial tracking and strain estimation can non-invasively assess cardiac functioning using subject-specific MRI. As the left-ventricle does not have a uniform shape and functioning from base to apex, the development of 3D MRI has provided opportunities for simultaneous 3D tracking, and 3D strain estimation. We have extended a Local Weighted Mean (LWM) transformation function for 3D, and incorporated in a Hierarchical Template Matching model to solve 3D myocardial tracking and strain estimation problem. The LWM does not need to solve a large system of equations, provides smooth displacement of myocardial points, and adapt local geometric differences in images. Hence, 3D myocardial tracking can be performed with 1.49 mm median error, and without large error outliers. The maximum error of tracking is up to 24% reduced compared to benchmark methods. Moreover, the estimated strain can be insightful to improve 3D imaging protocols, and the computer code of LWM could also be useful for geo-spatial and manufacturing image analysis researchers.
Similar content being viewed by others
Introduction
Cardiovascular Disease (CVD) is an important burden on the global population. It accounts for almost 31% of the mortality1. CVD covers a spectrum of diseases but mainly dysfunction of the heart muscles, from various aetiologies, and heart rhythm. The heart can be investigated and assessed using invasive and increasingly more non-invasive techniques2. Magnetic resonance imaging (MRI) with 3D imaging capabilities is gaining more support and applications2,3. The assessment of myocardium (heart wall muscles) provides clinical experts with the details of CVD diagnosis, prognosis and therapeutic interventions2,4,5. The details such as left ventricular (LV) myocardial tracking and strain (shortening or lengthening of the myocardium muscles) could objectively quantify myocardial health, providing a better understanding of cardiac diseases such as cardiomyopathy, myocardial infarction, arrhythmia, and valvular diseases2,6.
Heart muscles shrink, expand, rotate and create torsion simultaneously during a cardiac cycle and a common complication that arises in left ventricular (LV) myocardial tracking is the consideration of longitudinal heart movement. As a conventional or common practice, multiple 2D short-axis and 2D long-axis images are used to construct 3D myocardial motion and strain7,8,9. However, the approach is prone to 2D slice misregistration, patient cooperation, and dependent on radiographer (subjective)10, because the acquisition of 2D long-axis and 2D short-axis images happen at a different time while scanning a patient. As a result, 3D tagging is emerged as a promising method to allow reconstruction of 3D myocardial strain from single image volume rather than multiple different 2D images10,11,12. However, methods such as HARmonic Phase (HARP), Strain Encoding (SENC) are natively 1D or 2D, and merged with other methods or multiple 2D long- and short-axis images to calculate 3D myocardial strain11,13,14. However, a limited number of long-axis images could affect the accuracy of such tracking11. This fact motivates the use of 3D MRI instead of 2D short- and long-axis images, making it crucial to perform accurate 3D myocardial tracking. Medical image analysis researchers have contributed algorithms using direct detection-based methods15, Fourier-based methods13,14,16, tracking-based methods17,18,19,20,21,22, and block-matching-based methods17,23,24,25. Direct detection-based methods detect and track tag intersection points which could avoid image artefacts but too sparse tag points could limit the accuracy of myocardial tracking12,26. Fourier-based methods (for example HARP14) exploit the correspondence property of a local shift in the spatial domain and a phase shift in the Fourier domain but the method is limited to use tagged MRI12. Tracking-based methods optimize similarity between frame intensities and estimates transformation model, however, they can be dependent on a spatial regularization which could limit the accuracy12.
The block-matching approach has provided promising results using 3D ultrasound images17, and 2D MRI25. The standard myocardial tracking technique uses 3D speckle tracking through ultrasound images2,17. The method tracks an inherent pattern (speckle) of ultrasound imaging using a matching kernel (block or volume-of-interest), and the sum of absolute difference as a block-matching criterion. However, the accuracy of such a method is highly dependent on the size of the kernel, as too large or too small kernels could lead to incorrect tracking17. Such technical limitation could be overcome by using a hierarchy of matchings, which can provide a promising correlation up to the smallest level of the matching25,27. The hierarchical matching using 2D MRI is reported with promising accuracy in the literature25, however, 3D myocardial tracking using 3D MRI has received less attention in the literature12. Therefore, in this article, we have extended the standard block-matching technique by incorporating a hierarchical matching for 3D myocardial tracking.
Myocardial tracking algorithms use a transformation function to establish a point-to-point correspondence between two images28. Spline-based functions are commonly used as they can efficiently handle image deformations11,20,29,30. However, researchers have reported that the spline functions can generate large errors when the spacing between points is irregular28. It is also reported that the Cartesian coordinate B-spline model can generate errors due to ill-conditioned and ill-posed polynomials30. To address this issue, other approaches are suggested such as cylindrical coordinate B-spline model30 (as LV is roughly cylindrical), explicit regularization29 and local weighted-mean transformation function25,28,31,32. The cylindrical coordinate system and regularisation function with B-spline function could lead to detailed and complicated design and planning of myocardial tracking, whereas, Local Weighted Mean (LWM) function is proposed in the literature to overcome the elaborated procedure of spline interpolation33. The function is reported advantageous over the thin-plate spline and multi quadratics as the LWM function does not need a solution of a very large system of equations28. LWM functions can provide up to sub-pixel smoothness and accuracy in the displacement gradient28. Moreover, the averaging procedure of the LWM smoothes the noise in correspondences28. The function is adapted by researchers for 2D image registration of geo-spatial images28,32,34 and reviewed for medical imaging31. Previously, we show the promising results of 2D LWM function for 2D cardiac image registration25. In this work, we propose an extension of the standard 2D LWM function to 3D and use it to perform 3D myocardial tracking.
In this article, we extend a Hierarchical Template Matching (HTM)25 method for 3D myocardial tracking and strain estimation. The 3D LWM function is introduced and adapted for 3D myocardial tracking pipeline. The objective is to improve numerical stability in myocardial tracking by reducing maximum error and outliers. The 3D myocardial tracking and strain calculation is performed using state-of-the-art tagged MRI dataset12 of 15 healthy patients. The method is validated using four different strategies which include tracking of known LV points, calculating displacement, strain values and eigenvalues analysis in a cardiac cycle.
Methods and Material
Proposed method
The objective of the proposed method is to track 3D myocardial points, and calculate strain values. The overall flow of the method is divided into three steps: (i) Segmentation of 3D volumes of LV, (ii) Hierarchical block-matching and calculation of LWM function, (iii) Myocardial point tracking and strain calculation. The Biomedical and Scientific Research Ethics Committee (BSREC) approval to conduct the research is obtained from the University of Warwick (REGO-2016-1865). The study involves anonymised data of healthy volunteers which are downloaded from publicly available data repository12. The data was previously collected, anonymized, and made publicly available by the authors of the literature12. We have not recruited any participants for our study. We have developed and tested our algorithm using this anonymised and publicly available dataset.
Segmentation of 3D volume of LV
The entire cardiac cycle is covered with multiple 3D MRI volumes. These volumes are collected as mentioned in the dataset section (see Section 1.2.1). The segmented LV for each patient is also collected from the same dataset. In each patient, the segmentation of end-diastolic LV volume is collected. The segmented LV is obtained from steady-state free precision images at end-diastole (as mentioned by dataset providers12). As shown in Fig. 1, the registration of segmented LV mesh and MRI volume at end-diastole is performed using the dicom file header information as per dataset guidelines. The registered LV mesh is tracked in all the frames of a cardiac cycle for myocardial tracking.
Hierarchical matching and calculation of LWM function
Figure 2 depicts the proposed hierarchical matching approach for a pair of reference and moving images. The reference image is the end-diastolic image, while the moving image is a current frame of the cardiac cycle. The method is inspired by existing box-matching-based tracking17 and landmark-based non-rigid image registration28,31 algorithms. We propose a three steps method with the following stages: (a) Generating control points in moving image that will be interpreted as landmarks, (b) matching corresponding control points in the reference image, and (c) calculating a dense transformation function from the sparsely matched landmarks.
Generating control points in moving image: We generate a set of regular moving image points (also referred in this work as landmarks or control points) by dividing the moving image into multiple blocks of size t × t × t, which are defined as templates (see Fig. 3). Each template is further divided into segments of size t/2 × t/2 × t/2. Each segment is divided into t/4 × t/4 × t/4 size chunks, and each chunk is divided into t/8 × t/8 × t/8 size windows. It should be noted that throughout this article we will use the word ‘block’ to describe template, segment, chunk or window interchangeably. We define the first point of each window as its representative point (or landmark). The set of all representative points in the moving image is therefore defined as \({P}_{moving}=\{{m}_{1},{m}_{2},\ldots ,{m}_{n}|n=total\,number\,of\,Windows\}\).
The template size t × t × t pixels is determined considering literature3,17,25 and small in-house analysis. Previous work on speckle tracking has mentioned that template size 8 could perform myocardial tracking in ultrasound images17. The MRI feature tracking researchers have mentioned that the larger template size is required to capture large muscular deformations3, and a hierarchy of templates could improve matching25. Therefore, we have selected template size as 16 × 16 × 16 pixels with a hierarchy of segments of 8 × 8 × 8 pixels, chunks of 4 × 4 × 4 pixels, and windows of 2 × 2 × 2 pixels.
Matching corresponding control points in the reference image: The matching of moving image landmarks is performed using 3D Normalized Cross-Correlation (NCC)27,35,36. As mentioned in Equation (1), the NCC returns the value of a correlation coefficient (CC) at each point of the image, which ranges from -1.0 to + 1.0. The maximum value of the CC matrix leads to the matching location. The correlation coefficient λ is defined in Equation (1).
In Equation (1), b represents 3D moving image block and \(\overline{b}\) is the mean intensity value, f represents the reference image and \(\overline{f}\) is the mean intensity of reference image which is covered under the block b.
Each template of the moving image is slid over the reference image, and CC at each location of the reference image is calculated using Equation (1). The maximum value of CC leads to the location of the matching template of the reference image. After that, each moving template is divided into four segments. Each segment is slid over the reference template, and CC is calculated. The maximum CC value leads to the location of the corresponding segment of the reference image. Similarly, each moving segment is divided into four chunks. Each moving chunk is matched with reference image chunk using CC. Finally, each moving chunk is divided into four windows. Each moving window is matched with reference image window using CC. The pictorial representation of the process is shown in Fig. 4. The matching procedure gives the correspondence between a moving image block, and a reference image block. The set of first points of each reference image window creates a reference point set. \({P}_{reference}=\{{r}_{1},{r}_{2},\ldots ,{r}_{n}|n=total\,number\,of\,Windows\}\).
The matching process discussed in the previous paragraph could result in incorrect point correspondences. To update these incorrect point correspondences, the pyramidal approach is used as overlapping blocks. An overlapping block is defined as a surrounding block of a Segment. Each Segment is surrounded by three overlapped blocks of different sizes, creating a pyramid structure. If a Segment and its overlapped blocks match in the same hierarchy within the corresponding Template then the matching Segment is considered as a true matching Segment. Similarly, each Chunk is surrounded by an overlapped block. If a Chunk and its overlapped block match in the same hierarchy within the corresponding Segment then the matching Chunk is considered as a true match. If the match is not a true match then the point is set as a non-displaced point.
Calculating Transformation Function – LWM: A radial basis local weighted mean (LWM) function calculates transformation between a moving image and a reference image using a set of control points (as derived in section 1.1.2.a and 1.1.2.b). The calculated LWM function is used to map every point from the moving image to the reference image. It is desired to estimate a dense LWM transformation function between a moving image and a reference image, given that the sparse correspondences between the moving and reference image are known. We formulate the problem as follows.
As a first step, the sets of corresponding matched control points of the moving and reference image \(\{({x}_{i},{y}_{i},{z}_{i}),\,({X}_{i},{Y}_{i},{Z}_{i}):i=1,\ldots ,N\}\), are organized as \(\{({x}_{i},{y}_{i},{z}_{i},{X}_{i}):i=1,\ldots ,N\}\), \(\{({x}_{i},{y}_{i},{z}_{i},{Y}_{i}):i=1,\ldots ,N\}\), \(\{({x}_{i},{y}_{i},{z}_{i},{Z}_{i}):i=1,\ldots ,N\}\). After that, we determine polynomials \(Pol{y}_{i,x}\), \(Pol{y}_{i,y}\) and \(Pol{y}_{i,z}\) that fit ith control point and its (n − 1) nearest neighbour control points. The polynomials are second order polynomials with ten coefficients. \(Pol{y}_{i,x}\) is used to calculate X-component of the transformed point, \(Pol{y}_{i,y}\) is used to calculate Y-component of the transformed point, and \(Pol{y}_{i,z}\) is used to calculate Z-component of the transformed point.
A random point p = (x, y, z) can be transformed using the weighted mean of all polynomials passing over p. The transformed X-component, Y-component and Z-component of a transformed point can be calculated as defined in Equation (2).
where Rn represents the distance of point p from its (n − 1)th nearest control point, and W is defined as follows in Equation (3) and Equation (4):
The definition of W ensures that the polynomials \(Pol{y}_{i,x}\),\(\,Pol{y}_{i,y}\), and \(Pol{y}_{i,z}\) will affect only those points whose distance from a control point \(({x}_{i},{y}_{i},{z}_{i})\) in the reference image is lower than Rn. Hence, it ensures local transformation. Moreover, as mentioned in Equation (5), the first derivative of the weight function with respect to R is 0 for the values R = 0 and R = 1. Therefore, the smoothness and continuity of the weighted sum is maintained for all image points even when the point is beyond the reach of the polynomial influence.
The transformation functions among all the image pairs of a cardiac cycle are calculated with respect to the reference frame. The calculated transformation function is further used for myocardial point tracking. The local deformation of the mesh is ensured by selecting n local control points to calculate transformation in local areas. The value of n is determined considering literature28,31,32 and small in-house analysis. A grid search over a selected range of values (10, 20, 30, …, 350) of n is performed. The smaller values of n increase tracking error, very large values may not be able to calculate local deformations of the image. Therefore, we choose n = 100 since it resulted in minimum myocardial tracking error.
Myocardial point trhacking and strain calculation
Myocardial point tracking and strain calculation steps are followed from continuum mechanics literature37,38. We consider the segmented LV myocardium points of the first frame as reference points, and track them using the estimated LWM transformation function. The tracking is performed in a forward tracking fashion from the first frame to the final frame of a cardiac cycle. The spatial location of the myocardial point \(p(x,y,z)\) at time t is defined as \({[x,y,z]}^{T}={f}_{Deformation}(p,t)\). The spatial displacement vector at time t is calculated as a difference in spatial locations with respect to reference frame points \(u(x,t)={[{u}_{x},{u}_{y},{u}_{z}]}^{T}\). The displacement gradient tensor \(U(x,t)=\bigtriangledown u(x,t)\) is defined as follows (Equation (6)).
The displacement gradient tensor U is used to calculate deformation gradient tensor37 \(F(x,t)\), which is mentioned in Equation (7). The computer code is adapted from MATLAB39 and updated with Lagranje strain definition.
As mentioned in Equation (8), the 3D Lagrange strain tensor38 \(E(x,t)\,\,\)can now be calculated using \(F(x,t)\).
After computing the global frame X, Y, Z we calculate longitudinal strain (EL), circumferential strain (EC), and radial strain (ER) using a local co-ordinate system. Global strain E is projected in a specific direction using the equation \({E}_{p}={p}^{T}\cdot E\cdot p\) where p represents a given direction (circumferential, radial, longitudinal). The longitudinal direction (L) is defined by drawing a line from apex to the mitral valve. The radial direction (R) is computed using a normal (M) at each node and longitudinal direction. \(R=M-(M\cdot L)L\). Hence, the radial direction is at right angles to the epicardial border, and outwards. Circumferential direction (C) is calculated as a cross product of L and R. Hence, the direction of C is parallel to the epicardial border in the short-axis plane and counter-clockwise when observed from the base. We have adopted the definition of projecting strain in circumferential, longitudinal and radial direction from the benchmark framework12.
Dataset and validation
The study involves a publicly available dataset of 3D tagged MRI volumes12. We used fifteen volumes, each one having a pixel size of 0.96 millimetre. The patient-specific imaging details such as a total number of slices, end-systolic frame number, and the total number of cardiac phases are different for each patient (see Table 1 for a complete report). Moreover, the patient-specific characteristics such as body surface area, age, and sex are also reported in Table 1.
We validated the proposed method using four strategies: (i) calculating the tracking error of ground truth landmarks, (ii) visualizing myocardial points displacement, (iii) performing strain calculation, and (iv) analysing eigenvalue curve. The last frame of the cardiac cycle is referred to as a final frame in each patient. The validation results are reported in the Results and Validation section.
Results and Validation
Tracking of ground truth landmarks
The first validation strategy of tracking ground truth landmarks was performed with the manually tracked landmarks by two different observers. The landmark details were obtained from the dataset provider12, and summarized as follows. The total number of landmarks per observer is 12, which are distributed all over the myocardial wall. One landmark per each anterior, septal, posterior, and lateral wall at each level basal, apical, and mid-ventricular is placed. The inter-observer variability by comparing relative positions of the landmarks was computed to include the landmark for validation. If the final position and initial position of the landmark in each individual observer are relatively close, and the final position of the landmark is relatively close in both observers then the landmark is considered as the ground truth landmark. The position is referred to as relatively close if the distance is less than the 75th percentile of all measured distances.
The landmarks are tracked over all the cardiac frames using 3D TAG patients dataset. As mentioned in Fig. 5(a), the tracking error is reported at all frames together, at end-systolic frames and at final frames. The median error using the proposed method at all frames is 1.49 mm, at final frames are 1.73 mm, and at end-systolic frames is 2.88 mm.
The errors are compared with benchmark methods MEVIS (Fraunhofer MEVIS, Bremen, Germany), IUCL (Imperial College London – University College London, UK), UPF (Universitat Pompeu Fabra, Barcelona, Spain), and INRIA (Inria-Asclepios project, France). As mentioned in Fig. 5(b), the median error using the same 3DTAG dataset are MEVIS = 1.33 mm, IUCL = 1.52 mm, UPF = 1.09 mm, INRIA = 1.32 mm, and HTM(proposed method) = 1.49 mm. The results show that the proposed method has a similar median error to one of the benchmark methods, and half a millimetre higher error compared to other benchmark method.
Moreover, as shown in Fig. 5(c), the maximum error (considering all the frames) is MEVIS=14.4 mm, IUCL=11 mm, UPF = 10 mm, INRIA = 12.1 mm, and the proposed method HTM = 10.9 mm. The HTM has reduced 24.3% maximum error compared to MEVIS, 0.9% compared to IUCL, −9% compraed to UPF, and 9.9% compared to INRIA. The highest maximum error is reported with MEVIS method, and the lowest is reported with UPF method. The proposed method has a higher error than lowest. However, as mentioned in Fig. 5(c), the proposed method has the lowest error at the end-systolic frame and final frame compared to other benchmark methods. At final frames, the highest error is reported by MEVIS (13.8 mm) and the lowest error is reported by the proposed method (HTM = 3.97 mm). At end-systolic frames, the highest error is reported by MEVIS (12 mm) and the lowest error is reported by the proposed method (HTM = 7.8 mm).
Displacement of myocardial points
The second validation strategy is to observe displacement at the end-systolic frame and the final frame with respect to the reference frame. The end-systolic frame should have a higher displacement. The myocardium points of the segmented LV were tracked in all the frames of a cardiac cycle and the displacement is visualized for the end-systolic and final frame. The displacement of myocardial points was measured as the point-to-surface distance in millimetre. The point-to-surface distance is defined as the distance of a point from the end-diastolic surface.
The end-systolic frame has average 8 mm to 18 mm of point-to-surface distance, and the final frame has 0 to 6 mm point-to-surface distance over the LV wall. We have divided the original dataset into three categories as per the quality of images: (i) average images, (ii) good images, (iii) excellent images. In Fig. 6, we have chosen an example from each category. As shown in Fig. 6, the displacement of myocardial points at end-systole is higher compared to the final frame. The end-systolic frame of patient V6 has a higher displacement in basal, mid-ventricular, and some of the apical area compared to the final frame. The patient V10 has a higher displacement in basal, mid-ventricular, apical, and some of the apex area compared to the final frame. The patient V16 has a higher displacement in the mid-ventricular area compared to the final frame. The similar point-to-surface distance is observed in the literature12.
Strain analysis
The third validation strategy is the analysis of strain values. The myocardial strain for each frame was computed by estimating the displacement with respect to the end-diastolic frame. The strain tensor is computed as described in the Methods section. In order to validate the results, the strain values in all the cardiac frames are plotted. The peak strain values are compared with literature40. Moreover, the pattern of myocardial strain values in healthy patients is also analysed with physiological ground truth function of LV.
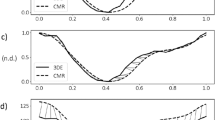
Figure 7 shows the strain curves in longitudinal, circumferential, and radial directions using all LV points. Strain in four patients V4, V1, V2, and V14 is shown. Two patients have excellent quality images, one has good quality images, and one has average quality images. The longitudinal and circumferential strain have negative values. Moreover, the end-systolic frame has a peak value of strain. The strain is increased at the beginning of a cardiac cycle, and decreased during the latter part. The radial strain is reported almost zero. The similar observation is mentioned in the literature using the same dataset12.
Eigenvalue analysis
The fourth validation strategy is based on eigenvalue analysis. The strategy is adopted from a protocol in bio-mechanics literature41,42,43. The entire LV wall is considered as a finite collection of points, and, at each point, a Lagrange strain tensor is calculated (as mentioned in Equation 8). The eigenvalues of each strain tensor are calculated, and each strain tensor returned three eigenvalues. After that, threes sets of eigenvalues are prepared, and a median of each set is evaluated. This step provided us with a median eigenvalue in one frame of a cardiac cycle. A similar process is repeated for all the frames of a cardiac cycle to generate an eigenvalue curve during a cardiac cycle. The eigenvalue curve of subject V8, which has good quality images, is shown in Fig. 8. An additional analysis of longitudinal, circumferential and radial strain is also reported for the same subject.
As shown in Fig. 8(a), the eigenvalue curve has increased values at the beginning and decreased values in the latter part of the cardiac cycle. The peak eigenvalues and peak strain values are reported at the same end-systolic frame. Eigenvalue 1, eigenvalue 2, longitudinal strain and circumferential strain are reported with mostly negative values. Eigenvalue 3 and radial strain are reported with values closer to zero. The discussion of the results is reported in the Discussion section.
Discussion
The article has contributed a 3D myocardial tracking and strain calculation methodology to reduce myocardial tracking error. The novel aspects of the article are as follows:
-
Myocardium tracking can be performed with 1.49 mm median error and a very few outliers (numerically stable).
-
Maximum myocardial tracking error is reduced up to 24% compared to the benchmark methods.
-
Extension of the previously published 2D method25 for 3D, which can provide simultaneous 3D myocardial strain.
-
To the best of authors’ knowledge, the introduction and adaptation of LWM function in 3D myocardial tracking pipeline.
The circumferential and longitudinal strain curves could provide insights into cardiac MRI-based diagnosis. As the 3D TAG MRI data which is used in the article is an emerging imaging technology for research, the standardization of 3D TAG MRI protocol is necessary before using it for real-world applications. In the future, the proposed methodology could potentially aid the diagnosis of myocardial infarction patients to locate akinetic segments and understand ventricular remodelling2,44, diagnosis of cardiac resynchronization therapy patients to locate dyskinetic segments2,5 valvular disease patients2. The strain values calculated from this method could be used in 3D finite element model to predict in-vivo myocardial properties45, and subsequently, estimate the ventricular wall stress for healthy46,47 and diseased patient48 for improved understanding of cardiac biomechanics. The 3D LWM function is written in C/C++ for reusability, which is an extension of the MATLAB function and source code for 2D images49. Then LWM is used with MATLAB code for the remaining methodology. The discussion of results is mentioned in the further sub-sections. The results, validation, and discussion are using healthy patients. However, a similar approach can be extended for diseased patients.
Tracking of ground truth landmarks
As mentioned in Fig. 5, the proposed method has a similar median error to one of the benchmark methods, and half a millimetre higher error compared to other benchmark methods. However, the tracking error at all frames, final frames, and end-systolic frames do not have large outliers. As mentioned in Section 2.1, the maximum error is up to 24% reduced in the proposed method compared to the benchmark methods. The reason is the technical advantages of LWM transformation function. LWM functions do not require to solve a very large system of linear equations, and local polynomials can be efficiently solved with a small system of equations, which helps to avoid ill-conditioned polynomials. As a result, tracking errors are more consistent and do not have large outliers. Moreover, LWM function can adapt the local geometrical shape and different density of points, and as a result, landmark tracking does not require a specific type of coordinate systems such as mentioned in the literature30 which also helps to avoid ill-conditioned polynomials and large error outliers. In addition, a large number of control points with relatively uniform distance is available, and the averaging process of the transformation function may help to smooth any noise in corresponding landmarks as suggested in the literature28, which may help to improve tracking when tag points of MRI suffer from fading issues. The time complexity of 3D LWM transformation for a U × U × U size 3D image is O(NTU3), where N refers to the number of linear equations while solving a system of equations (same as local control points n) and T refers to the number of co-efficients in a polynomial. The proposed method has used second order polynomials with ten coefficients.
Displacement of myocardial points
As mentioned in the dataset section, all the scans are from healthy patients. Therefore, the LV muscles should have a higher contraction at end-systolic frame compared to other cardiac frames. Our results support the fact that the end-systolic frame of a healthy patient should have a higher displacement compared to the displacement at the final frame, hence follow the expected physiological pattern. The values of point-to-surface distance are smooth over LV which shows that the LWM function provides a smooth transformation (mathematical characteristic of smoothness is mentioned in equation (5)).
Strain analysis
As per the physiology of the healthy human heart, LV contracts in longitudinal and circumferential directions and expands in the radial direction during systole. Therefore, circumferential and longitudinal strain values are expected to be negative with an increased strain in the beginning and reduced strain in the later part of a cardiac cycle. This fact is highlighted in our results of Fig. 7, which follows the expected physiological pattern. However, the average peak strain is expected to be −20% in the circumferential direction, −16% in the longitudinal direction, and +45% in the radial direction40. The reported peak strain is reduced compared to the literature40, which shows that the methodology and dataset need further advancements before using it for real-world applications. It is indicated in the literature12 that the 3D TAG MRI protocols are under research, therefore, the derived strain values using different methodology are reduced. However, this may provide insights to further improve 3D imaging sequences which ultimately could improve dataset and strain calculation.
Eigenvalue analysis
It is expected that the eigenvalue curve, similar to the strain curve, follow a physiological pattern of LV contraction and expansion. The results of eigenvalue 1 and eigenvalue 2 are decreased in the beginning and increased in the later part of the cardiac cycle which is expected. In addition, peak eigenvalues and strain values are reported at the end-systolic frame, which is expected. However, our observation shows that the eigenvalue which is less than zero is corresponding to the LV contraction. In literature41, it is observed that the eigenvalue less than one corresponds to the LV contraction. This difference is due to the different definitions of the strain tensor in both literature12,41. It is observed that both researchers have reported a similar shape in the eigenvalue curve. It is observed that the eigenvalues 3 are closer to zero and the range of eigenvalues (between maximum and minimum) is reduced in our results compared to the literature41. The potential reason is the use of a different subject and different imaging modalities as they have used echocardiography images whereas our model is based on 3D TAG MRI. This observation could be insightful to further improve 3D TAG MRI acquisition protocol. A similar observation with strain values is made by the researchers who worked on the same dataset12.
In eigenvalue analysis, the derived three eigenvalues correspond to three principal strains, and a corresponding eigenvector designates a principal direction of associated with a principal strain. Principal strains (maximum and minimum normal strain), are diagonal elements of a strain tensor when off-diagonal (shear strain) is zero. Therefore, eigenvalue analysis provides principal strain (maximum and minimum normal strains) when shear strain is zero. However, longitudinal, circumferential, and radial strain are easier to interpret and communicate with clinical experts as they are common in clinical practise although they do not convey maximum/minimum normal strain and includes shear strain. Therefore, considering a technical and a clinical scenario, both analyses are crucial.
Limitations and future work
The results are derived using a benchmarking dataset of 3D + time MRI to evaluate the proposed methodology and technical contributions. It should be noted that our results can not be directly used as a clinical measure. Before concluding any generalised clinically interpretable results, the proposed methodology has to be tested with a large number of data samples. We consider collecting a large number of 3D + time data as future work. The proposed method has difficulty in capturing radial strain, which is reported by other researchers as well12. As a possible solution and future work of this article, we are considering to merge different modalities such as 3D steady-state free precision to improve the calculation of radial strain using the proposed method.
It should be noted that our contribution is not limited to only cardiac 3D MRI analysis. The transformation function, which is extended in this article for 3D, can be used with other application areas where 3D imaging has already established standards. For example, finding defects in industrially manufactured parts could be possible with 3D computed tomography image analysis50. Such image analysis of registration-based methodology could use the contributed 3D transformation function. Similarly, the exploration of natural resources could be possible with landmark-based geo-spatial image registration32,34. Such methodologies can utilize the contributed 3D transformation function. Moreover, 3D speckle tracking methods17 with 3D ultrasound images can utilize the contributed transformation function. Such applications are considered as future applications of this article.
Conclusion
In this article, we proposed a 3D myocardial tracking and strain calculation method. The novel aspect of this method is the adaptation of LWM function for 3D myocardial tracking problem. The function is extended for 3D, and adapted for 3D myocardial tracking and strain calculation. The proposed method can perform myocardial tracking without using a specific type of coordinate system and elaborated spline process which can help to avoid ill-conditioned polynomials and large errors. As a result, the myocardium tracking is numerically stable with 1.49 mm median error, and the maximum error of tracking is reduced up to 24% compared to benchmark methods. The protocol of eigenvalues and derived strain values can provide insights to the researchers working on 3D TAG MRI imaging sequences. Moreover, the article could be insightful for the 3D image analysis in manufacturing, and geoinformatics. The contributed computer code of the transformation function can be directly utilized for landmark-based image registration techniques of 3D images. In the future, after the development and standardization of 3D TAG MRI, the article could be useful for real-world applications of cardiac MRI-based diagnosis.
Data Availability
The computer code of the method is available from the corresponding author on a reasonable request. The original MRI scans with user guidelines can be accessible as mentioned in the literature12.
References
WHO. WHO Cardiovascular Diseases (CVDs). Available at: http://www.who.int/mediacentre/factsheets/fs317/en/ (2017).
Smiseth, O. A., Torp, H., Opdahl, A., Haugaa, K. H. & Urheim, S. Myocardial strain imaging: How useful is it in clinical decision making? Eur. Heart J. 37, 1196–1207b (2016).
Pedrizzetti, G., Claus, P., Kilner, P. J. & Nagel, E. Principles of cardiovascular magnetic resonance feature tracking and echocardiographic speckle tracking for informed clinical use. J. Cardiovasc. Magn. Reson. 18, 1–12 (2016).
Cerqueira, M. D. et al. Standardized Myocardial Segmentation and Nomenclature for Tomographic Imaging of the Heart: A Statement for Healthcare Professionals From the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. J. Am. Soc. Echocardiogr. 15, 463–467 (2002).
Haugaa, K. H. et al. Mechanical Dispersion Assessed by Myocardial Strain in Patients After Myocardial Infarction for Risk Prediction of Ventricular Arrhythmia. JACC Cardiovasc. Imaging 3, 247–256 (2010).
Gorcsan, J. & Tanaka, H. Echocardiographic assessment of myocardial strain. J. Am. Coll. Cardiol. 58, 1401–1413 (2011).
Kuijer, J. P. A., Marcus, J. T., Götte, M. J. W., van Rossum, A. C. & Heethaar, R. M. Three-dimensional myocardial strain analysis based on short- and long-axis magnetic resonance tagged images using a 1D displacement field. Magn. Reson. Imaging 18, 553–564 (2000).
van Dockum, W. G. et al. Septal ablation in hypertrophic obstructive cardiomyopathy improves systolic myocardial function in the lateral (free) wall: a follow-up study using CMR tissue tagging and 3D strain analysis. Eur. Heart J. 27, 2833–2839 (2006).
Young, A. A., Cowan, B. R., Occleshaw, C. J., Oxenham, H. C. & Gentles, T. L. Temporal evolution of left ventricular strain late after repair of coarctation of the aorta using 3D MR tissue tagging. J. Cardiovasc. Magn. Reson. 4, 233–243 (2002).
Rutz, A. K., Ryf, S., Plein, S., Boesiger, P. & Kozerke, S. Accelerated Whole-Heart 3D CSPAMM for Myocardial Motion Quantification. Magn. Reson. Med. 59, 755–763 (2008).
Shi, W. et al. A comprehensive cardiac motion estimation framework using both untagged and 3-D tagged MR images based on nonrigid registration. IEEE Trans. Med. Imaging 31, 1263–1275 (2012).
Tobon-gomez, C. et al. Benchmarking framework for myocardial tracking and deformation algorithms: An open access database. Med. Image Anal. 17, 632–648 (2013).
Wang, H. & Amini, A. A. Cardiac motion and deformation recovery from MRI: A review. IEEE Trans. Med. Imaging 31, 487–503 (2012).
Pan, L., Prince, J. L., Lima, J. A. C. & Osman, N. F. Fast tracking of cardiac motion using 3D-HARP. IEEE Trans. Biomed. Eng. 52, 1425–1435 (2005).
Chen, T., Wang, X., Chung, S., Metaxas, D. & Axel, L. Automated 3D motion tracking using gabor filter bank, robust point matching, and deformable models. IEEE Trans. Med. Imaging 29, 1–11 (2010).
Arts, T. et al. Mapping displacement and deformation of the heart with local sine-wave modeling. IEEE Trans. Med. Imaging 29, 1114–1123 (2010).
Crosby, J. et al. 3-D Speckle Tracking for Assessment of Regional Left Ventricular Function. Ultrasound Med. Biol. 35, 458–471 (2009).
Chandrashekara, R., Mohiaddin, R. H. & Rueckert, D. Analysis of 3-D myocardial motion in tagged MR images using nonrigid image registration. IEEE Trans. Med. Imaging 23, 1245–1250 (2004).
Schnabel, J. A. et al. A generic framework for non-rigid registration based on non-uniform multi-level free-form deformations. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes. Bioinformatics) 2208, 573–581 (2001).
Rueckert, D. et al. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Trans. Med. Imaging 18, 712–21 (1999).
De Craene, M. et al. Temporal diffeomorphic free-form deformation: Application to motion and strain estimation from 3D echocardiography. Med. Image Anal. 16, 427–450 (2012).
Phatak, N. S. et al. Strain measurement in the left ventricle during systole with deformable image registration. Med. Image Anal. 13, 354–361 (2009).
Krücker, J. F., Lecarpentier, G. L., Fowlkes, J. B. & Carson, P. L. Rapid Elastic Image Registration for 3-D Ultrasound. IEEE Trans Med Imaging 21, 1384–1394 (2002).
Linguraru, M. G. et al. Fast Block Flow Tracking of Atrial Septal Defects in 4D Echocardiography. Image (Rochester, N.Y.) 12, 397–412 (2008).
Bhalodiya, J. M. et al. A Novel Hierarchical Template Matching Model for Cardiac Motion Estimation. Sci. Rep. 8, 4475 (2018).
Smal, I., Niessen, W. & Meijering, E. Particle filtering methods for motion analysis in tagged MRI. In ISBI 488–491 (2010).
Taylor, C. C. Measures of Similarity between Two Images Author. Spat. Stat. Imaging 20, 382–391 (1991).
Zagorchev, L. & Goshtasby, A. A comparative study of transformation functions for nonrigid image registration. IEEE Trans. Image Process. 15, 529–538 (2006).
Radeva, P., Amini, A. A. & Huang, J. Deformable B-Solids and Implicit Snakes for 3D Localization and Tracking of SPAMM MRI Data. Comput. Vis. Image Underst. 66, 163–178 (1997).
Deng, X. & Denney, T. S. Three-Dimensional Myocardial Strain Reconstruction Model. IEEE Trans. Med. Imaging 23, 861–867 (2004).
Holden, M. A review of geometric transformation for nonrigid body registration. IEEE Trans. Med. Imaging 27, 111–128 (2008).
Goshtasby, A. Image registration by local approx methods. Image Vis. Comput. 6, 255–261 (1988).
Maude, A. D. Interpolation-mainly for graph plotters. Comput. J. (1971).
Goshtasby, A. A. Image Registration: Principles, Tools and Methods, https://doi.org/10.1007/978-1-4471-2458-0 (Springer, 2012).
Lewis, J. P. Fast Normalized Cross Correlation. Ind. Light Magic 10, 120–123 (1995).
Haralick, R. M. & Shapiro, L. G. Computer and Robot Vision Vol. 2. (Addison-Wesley, 1993).
Abd-elmoniem, K. Z., Stuber, M. & Prince, J. L. Direct three-dimensional myocardial strain tensor quantification and tracking using z HARP. Med. Image Anal. 12, 778–786 (2008).
Lai, W. M., Rubin, D. & Krempl, E. Introduction to continuum mechanics, Chapter 3. (Butterworth-Heinemann/Elsevier, 2010).
Kroon, D.-J. MATLAB File Exchange. Available at: https://www.mathworks.com/matlabcentral/mlc-downloads/downloads/submissions/21451/versions/12/previews/functions/strain.m/index.html.
Moore, C. C., Lugo-Olivieri, C. H., McVeigh, E. R. & Zerhouni, E. A. Three-dimensional Systolic Strain Patterns in the Normal Human Left Ventricle: Characterization with Tagged MR Imaging. Radiology 214, 453–466 (2000).
Gabriele, S., Nardinocchi, P. & Varano, V. Evaluation of the strain-line patterns in a human left ventricle: a simulation study. Comput. Methods Biomech. Biomed. Engin. 18, 790–798 (2015).
Evangelista, A. et al. Non-invasive assessment of functional strain lines in the real human left ventricle via speckle tracking echocardiography. J. Biomech. 48, 465–471 (2015).
Evangelista, A. et al. A comparative analysis of the strain-line pattern in the human left ventricle: experiments vs modelling. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 4, 164–173 (2016).
Ran, H. et al. Assessment of Left Ventricular Myocardial Viability by 3-Dimensional Speckle-Tracking Echocardiography in. J Ultrasound Med 35 (2016).
Palit, A., Bhudia, S. K., Arvanitis, T. N., Turley, G. A. & Williams, M. A. In vivo estimation of passive biomechanical properties of human myocardium. Med. Biol. Eng. Comput. 56, 1615–1631 (2018).
Palit, A., Bhudia, S. K., Arvanitis, T. N., Turley, G. A. & Williams, M. A. Computational modelling of left-ventricular diastolic mechanics: Effect of fibre orientation and right-ventricle topology. J. Biomech. 48, 604–612 (2015).
Palit, A. et al. Passive diastolic modelling of human ventricles: Effects of base movement and geometrical heterogeneity. J. Biomech. 52, 95–105 (2017).
Lee, L. C. et al. Analysis of patient-specific surgical ventricular restoration: importance of an ellipsoidal left ventricular geometry for diastolic and systolic function. J. Appl. Physiol. 115, 136–144 (2013).
MATLAB. Fitgeotrans. Available at, https://uk.mathworks.com/help/images/ref/fitgeotrans.html.
Viot, P. & Bernard, D. Three-dimensional image correlation from X-ray computed tomography of solid foam. 39, 1253–1265 (2008).
Acknowledgements
We would like to acknowledge the Health Data Research (HDR) UK grant funding support for the University of Warwick. HDR UK is funded by the UK Medical Research Council, Engineering and Physical Sciences Research Council, Economic and Social Research Council, Department of Health and Social Care (England), Chief Scientist Office of the Scottish Government Health and Social Care Directorates, Health and Social Care Research and Development Division (Welsh Government), Public Health Agency (Northern Ireland), British Heart Foundation and Wellcome Trust. Enzo Ferrante is beneficiary of an AXA Research Fund fellowship.
Author information
Authors and Affiliations
Contributions
J.M.B. and A.P. have developed a model, implemented algorithm, and written manuscript. M.K.T., T.N.A. and M.A.W. have provided technical feedback for designing algorithm and analysing results. E.F. and S.K.B. have provided writing corrections. All the authors have reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bhalodiya, J.M., Palit, A., Ferrante, E. et al. Hierarchical Template Matching for 3D Myocardial Tracking and Cardiac Strain Estimation. Sci Rep 9, 12450 (2019). https://doi.org/10.1038/s41598-019-48927-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-48927-2
This article is cited by
-
Functional and Metabolic Imaging in Heart Failure with Preserved Ejection Fraction: Promises, Challenges, and Clinical Utility
Cardiovascular Drugs and Therapy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.