Abstract
The signal amplification by reversible exchange (SABRE) technique is a very promising method for increasing magnetic resonance (MR) signals. SABRE can play a particularly large role in studies with a low or ultralow magnetic field because they suffer from a low signal-to-noise ratio. In this work, we conducted real-time superconducting quantum interference device (SQUID)-based nuclear magnetic resonance (NMR)/magnetic resonance imaging (MRI) studies in a microtesla-range magnetic field using the SABRE technique after designing a bubble-separated phantom. A maximum enhancement of 2658 for 1H was obtained for pyridine in the SABRE-NMR experiment. A clear SABRE-enhanced MR image of the bubble-separated phantom, in which the para-hydrogen gas was bubbling at only the margin, was successfully obtained at 34.3 μT. The results show that SABRE can be successfully incorporated into an ultralow-field MRI system, which enables new SQUID-based MRI applications. SABRE can shorten the MRI operation time by more than 6 orders of magnitude and establish a firm basis for future low-field MRI applications.
Similar content being viewed by others
Introduction
Magnetic resonance imaging (MRI) is usually carried out in a strong magnetic field because of the Zeeman effect. Because the signal intensity depends on the population difference between nuclei in the upper and lower energy states, which is proportional to the strength of the applied magnetic field, the magnetic resonance (MR) signal intensities will be considerably higher on instruments with more powerful magnets. However, maintaining a stable strong magnetic field with a strong magnet requires great effort and cost. The magnitude of the MR signal can be enhanced by the so-called hyperpolarization process, in which a considerable number of magnetic nuclei are induced into an identical spin state. This process results in a considerable increase in the level of available signal strength due to the much greater population inequality across energy levels. Many hyperpolarization methods have been widely studied: spin-exchange optical pumping of a noble gas1,2, optical pumping in semiconductors3, chemically induced dynamic polarization4, and photoexcited triplet states5. The most common hyperpolarization technique, already in clinical trials, transfers polarization from electron polarization to neighbouring nuclei, which is known as dynamic nuclear polarization (DNP)6. Recently, refined dissolution DNP was optimized by hyperpolarizing electron spin and its transfer to the nuclei to adapt to high-field MRI7,8. However, its transfer from nuclear magnetic resonance (NMR) to MRI applications necessitates overcoming several obstacles, such as the long T1 time (i.e., the polarization sustaining time), efficiency, and purification of the substrate from the catalyst. In addition, the DNP method is expensive and loses a significant degree of polarization when the sample is thawed and heated to room temperature.
Alternatively, one of the most promising methods for enhancing the NMR signal strength was proposed by Bowers and Weitekamp in 19869. They suggested that the addition of H2 molecules enriched in the para-state can result in the enhancement in NMR signals. This method was initially called para-hydrogen and synthesis allows dramatically enhanced nuclear alignment (PASADENA) and was later named para-hydrogen induced polarization (PHIP)10. Another hyperpolarization technique, called signal amplification by reversible exchange (SABRE), which was developed recently, is considered a significant extension of PHIP11. The SABRE hyperpolarization technique is relatively fast, cheap, and effective and can be successfully used to achieve a non-Boltzmann state necessary to improve the MR signal strength.
On the other hand, low-field and microtesla MRI are promising tools in several fields that can surpass the merits of high-field MRI. These techniques can avoid the potential risk of high-field MRI, and the greater relaxation contrast in low-field MRI than in high-field MRI has been proposed for the detection of tumour cells12,13,14,15,16,17. Furthermore, the simultaneous detection of various MRI-active nuclei18 is a powerful tool for obtaining important information in a short time. In addition, microtesla MRI can change the magnetic field in a short time and harness magnetic field-dependent MRI information19. However, the magnetic signal caused by the Zeeman effect in a microtesla-range magnetic field is extremely low. Therefore, highly sensitive sensors, such as a superconducting quantum interference device (SQUID)20 or an optical atomic magnetometer21, are required to detect the NMR/MRI signals. Because the MR signal obtained by these sensors does not have an inductive detection loss depending on frequency, one may reduce the signal loss at the ultralow field by replacing the conventional inductive coil with these sensors. In addition, to obtain a good MR image in SQUID-based microtesla MRI, a pre-polarization field (Bp) is required before the MR signal from the sample is detected. Therefore, some attempts17,22,23 were made to obtain a strong Bp, including optimizing the Bp coils and cooling these coils to reduce noise. Increasing Bp using a coil also yielded critical effects: the generation of eddy currents on the walls of a magnetically shielded room (MSR)24,25 and flux trapping in a pickup coil26. These side effects can hamper the development of microtesla MRI in the future.
The hyperpolarization technique can solve this pre-polarization problem to enable the polarization of materials with an extremely high order of magnitude. There have been several recent reports18,22,27,28,29,30 on this strategy. The most well-known way of achieved hyperpolarization, DNP, which is used to transfer polarization from electrons to nuclei, was harnessed to obtain a high-contrast microtesla MR image18,22. Alternatively, SABRE, which induces hyperpolarization on a variety of substrates via low-cost, high-throughput hyperpolarization without complex devices under normal conditions, utilizes para-hydrogen (p-H2) by forming a metal complex with some target substrates and transfers hyperpolarization from a polarized proton to a weakly bound substrate31,32,33. Polarization transfer is carried out by matching the scalar coupling/chemical shift and Zeeman energy of active nuclei in a complex structure. Because the ligands in the complex are weakly bound, the exchange of ligands continuously builds up a pool of hyperpolarization in the solution. Several MR studies with SABRE were performed at low field (47.5 mT)34,35 and earth’s magnetic field36. Moreover, Buckenmaier et al. reported the detection of a hyperpolarized NMR signal using SQUID-based NMR with SABRE29. However, despite its great potential, technically controlled investigations under low-magnetic-field conditions, especially those under ultralow-magnetic-field conditions, are lacking.
Using the above information, we matched the condition for the highest SABRE polarization and designed a SABRE-based MRI phantom. This phantom can be used to obtain a real-time accumulated MR signal from a hyperpolarized proton signal of a small concentration of pyridine by continuously bubbling (Fig. 1). Therefore, in this study, we report the first SQUID-based microtesla MR image based on the para-hydrogen SABRE system. An enhancement factor of more than 2650 and a clear SABRE-derived 1H MR image of the phantom were obtained with 8 mT Bp at 34.3 µT.
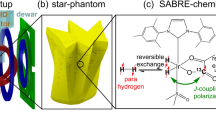
Experimental equipment for the microtesla para-hydrogen (p-H2) NMR/MRI experiments. (a) Schematic diagram of the p-H2 generator. Approximately 50% p-H2 was generated through a liquid-nitrogen (LN2) chamber including an iron oxide-based catalyst. (b) Schematic diagram of a 3D phantom containing a methanol solution in which pyridine as a substrate and an Ir catalyst were dissolved. The p-H2 gas entered the 3D phantom through the p-H2 inlet and many holes in the bottom and generated bubbles. A mesh was attached to prevent the generation of bubbles in the imaging region. (c) Experimental apparatus for the microtesla MRI experiment. As a Bp coil, a silicon-oil-cooled pancake-type coil mounted inside a Bp Dewar was used. A double Helmholtz coil was used as the Bm coil. Two pairs of square-type Helmholtz coils, aligned mutually orthogonally, and the remaining coils were used as the B1 coil and three-axis gradient coils, respectively.
Results
Magnetic field-dependent phase changes for ortho-, meta-, and para-hydrogen on pyridine
SABRE polarization is sensitive to an external field, which induces hyperpolarization in a weak magnetic field. Furthermore, quantum mechanically, p-H2 gives only the singlet state, which is an anti-aligned hyperpolarized spin state of the proton, when it induces polarization transfer; therefore, its phase in polarization may depend on the external magnetic field due to the polarization transfer mechanism, which is related to the chemical shift and scalar coupling of the active SABRE complex37,38,39. The polarized nuclear spin states from p-H2 are more complex than those from polarization at thermal equilibrium. Both of the above factors present a challenge in obtaining polarization in a low field. The challenge arises from the fact that p-H2-derived 1H NMR signals often have an anti-phase character, which results in significant signal cancellation if resonances are not resolved. Therefore, we observed magnetic field-dependent phase changes for ortho-, meta-, and para-hydrogen on pyridine (Fig. 2) and optimized the external field for the most efficient in-phase polarization transfer on all protons in pyridine. As suggested in other reports37,40, polarization of the protons in all positions (ortho-, meta-, and para-) on pyridine was maximized in the range from 5 to 9 mT (Fig. 2(b,c)). The phase changes are due to the mismatch between the Zeeman effect and the J-coupling when SABRE chemical exchange is conducted in a lower magnetic field, e.g., earth’s magnetic field of approximately 50 µT, as proposed in previous studies37,38,39.
SABRE-enhanced 1H NMR results, measured at 1.4 T. (a) Structure of pyridine with labeled protons. (b) NMR intensity of each attached proton versus the applied magnetic field for hyperpolarization. (c) Merged NMR intensity as a function of the applied magnetic field. The data were obtained by summing three types of hydrogen peaks on pyridine in each magnetic field. The dashed line is for visual guidance.
Dependence of the enhancement factor on the B p strength and the B p time
The microtesla NMR experiment was performed to investigate the effect of the SABRE-enhanced 1H NMR signal (i.e., the pyridine signal) on the external field and the application time of this field. The dependence of the NMR signal on Bp is displayed in Fig. 3(a). Because the chemical shifts of the ortho-, meta-, and para-hydrogen on pyridine, including the methanol peak, cannot be distinguished in the microtesla range, all peaks are mixed in the presence of a p-H2 gas stream. On the other hand, when the p-H2 flux is absent, the NMR signal of methanol is the main contributor to the measurable proton signal because the proton population difference after the addition of pyridine is relatively small. Since the phase of the SABRE-enhanced NMR signal, compared to that of the reference signal, was inverted, as shown in the inset of Fig. 3(a), the SABRE-enhanced NMR signal intensity (closed circles) and the reference signal intensity (open circles) increase in the negative and positive direction, respectively, as Bp increases. The inset shows the FFT spectra with (dashed line) and without (solid line) p-H2 flowing at 8 mT Bp. Therefore, the enhancement factor (ESABRE) can be defined as follows:
where SSABRE is the SABRE-enhanced NMR signal, S is the reference NMR signal of all protons when there is no p-H2 gas flow, and α (=99) and β (=4/5) are the volume and nuclear spin ratios of the pyridine and methanol, respectively. The dependence of ESABRE on Bp is shown in Fig. 3(b). ESABRE increases with increasing Bp and then reaches a maximum value around a Bp of 7 ~ 9 mT. The overall trend in ESABRE is quite consistent with the result for the high-field experiment shown in Fig. 2(c). The ESABRE was also obtained as a function of Bp time (tBp) at 8 mT Bp (Fig. 3(c)). In our experiments, ESABRE began to converge to a maximum value for a Bp time above 30 s and increased up to approximately 2658 for tBp = 60 s.
SABRE-enhanced 1H NMR results. (a) NMR intensity as a function of the Bp strength obtained with a fixed time (tBp = 10 s). The inset shows the FFT spectra with (dashed line) and without (solid line) p-H2 flowing at 8 mT Bp. (b) Enhancement factor versus Bp. (c) Enhancement factor as a function of the Bp time (tBp) obtained at 8 mT Bp. All data were measured four times at each point. Error bars represent the standard error of repeated measurements. NMR intensities were obtained with a real spectrum area and phase correction at each data point. The enhancement factors were calculated with the additional considerations of the volume and nuclear spin ratios of pyridine and methanol.
SABRE-enhanced 1H MR image
The SABRE-derived 1H MR image, obtained with 8 mT Bp at 34.3 µT, is displayed in Fig. 4. As more methanol evaporated with increasing total imaging time, the MR experiment was performed while accounting for the total imaging time and image resolution. The following experimental parameters were used: tBp = 13 s, tpe = 0.12 s, tacq = 0.3 s, \({G}_{{\rm{x}}}=|\pm {G}_{{\rm{z}},{\rm{\max }}}|=0.6\)µT/cm, 49 phase encoding steps (ΔGz = 0.025 µT/cm), and 4 iterations. Therefore, the resolution, estimated from the experimental parameters, was approximately 1.6 × 1.6 mm2. On the other hand, the enhancement factor in the MR experiment was more than 1800 at a given tBp(=13 s), which was estimated by interpolation of the data in Fig. 3(c). Because the MR signal obtained by the SQUID sensor is proportional to the magnetic field, including the measurement field (Bm) and Bp, it is possible to predict a polarization enhancement of approximately 420,000-fold by comparison with the thermal polarization at 34.3 µT Bm. In the MR image, the outside regions, denoted as the “mesh” in Fig. 1(b), were only faintly visible because of the bubbles of p-H2 gas. In contrast, the inside regions were reasonably clearly imaged. Among the nine rectangular blocks located on the right side of the phantom, the three rectangular blocks located in the middle could not be distinguished from each other individually on the MR image because these patterns were smaller than the imaging resolution.
Discussion
We performed high-field NMR and microtesla NMR/MRI experiments. From the high-field NMR results, it was confirmed that all protons of pyridine had in-phase polarization in an external field greater than approximately 3 mT. An enhancement factor exceeding 2650, compared with the NMR intensity of the methanol solution, was obtained with 8 mT Bp at 34.3 µT. An enhanced MR image of the bubble-separated phantom was obtained using the SABRE technique in the ultralow field. In that phantom, the bubbles are formed at only the margin, and the hyperpolarized pyridine from the bubbling region is diffused into the imaging region. The advantage of the experimental approach introduced in this study is that the relaxation time is negligible because hyperpolarization generation and MR imaging can be performed at the same place at the same time. One of the breakthroughs that must be made in conventional MRI is a shortening of the operation time, which is usually lengthened by increasing the scan time to obtain a sufficient amount of signal-to-noise41,42,43. An enhancement factor on the order of a few thousands in real-time NMR/MRI was achieved in the ultralow field, even though the actual level of polarization was on the order of 0.00007%; this value was estimated from the equation ESABRE × tanh(γħBp/2kBT), in which γ is the gyromagnetic ratio of a proton, T is the temperature, and ℏ and kB are Planck’s constant and the Boltzmann constant, respectively. This result means that it is possible to shorten the scan time by more than 6 orders of magnitude. After induction of hyperpolarization on biomaterials near MRI devices under normal conditions, the introduction of a hyperpolarized material into the patient would enable a short-time MRI operation. Until now, however, in vivo imaging by the SABRE-hyperpolarization technique has not been reported. Furthermore, additional sensitivity enhancement would be possible with, for example, more hyperpolarized para-hydrogen, deuterated substances, or polarization transfer to 13C or 15N with a long-lived nuclear spin state44,45,46. Our result, based on this concept, may open up a new field of application of low-field MRI. This work showed the possibility of obtaining a hyperpolarized SQUID-based microtesla MR image based on the SABRE system, which means that any imaging studies using the SABRE system are extended to further advanced studies, especially low-field hyperpolarized MRI. Furthermore, this method led to polarization enhancement by more than 420,000-fold in hyperpolarized proton MRI. This study has established a firm basis for a future low-field MRI system, which holds many advantages over a high-field MRI system. Furthermore, detailed and large-scale research on the development of new SABRE systems and hyperpolarization in biomaterials, such as SABRE-Relay47 and SABRE in shield enables alignment transfer to heteronuclei (SABRE-SHEATH)48, would reduce the time required for the actual application of SQUID-based microtesla MRI in human and magnetic resonance spectroscopy. These ongoing integrated studies will open up a new area of MRI applications that will allow the detection of many useful materials, tumours, and even pathogens in humans by microtesla MR imaging.
Methods
Chemistry
All chemicals were purchased from Sigma-Aldrich and used without further purification unless otherwise indicated. All SABRE experiments were performed with the Ir catalyst [Ir(COD)(IMes)(Cl)] (2 mM) in methanol (approximately 20 mL for SQUID and 0.7 mL for high-field NMR) without degassing49. A pyridine solution of approximately 124 mM (10 µL in 1 mL of methanol) was hyperpolarized by polarization transfer.
Para-hydrogen
Approximately 50% p-H2 was generated by the catalytic conversion at liquid-nitrogen temperature using a home-built p-H2 generator (Fig. 1(a)). Hydrogen gas (a mixture of spin isomers of hydrogen, i.e., ortho-hydrogen and para-hydrogen) was passed through a heat exchanger filled with a FeO(OH) catalyst in a liquid-nitrogen Dewar.
High-field NMR
A Spinsolve Ultra (Magritek) spectrometer operating at 60 MHz was used to obtain hyperpolarized 1H NMR spectra of pyridine. The instrument was shimmed on 5% D2O using an automated algorithm, and the NMR signals were tested with pyridine in benzene. A mixture of pyridine (10 µL) and methanol (1 mL) was added to a 5 mm NMR tube after lowering the oxygen level in the solution by bubbling pure nitrogen gas for approximately 2 min. A home-built solenoid coil was set up to induce the designed magnetic field. Each designed magnetic field was formed to study the magnetic field-dependent phase change. In each magnetic field, the generated p-H2 was bubbled into a 5 mm NMR tube for 30 s at 23 °C and 1 atm and transferred into the spectrometer (<1 s). Spectra were obtained at 60 MHz and 23 °C in one scan using a π/2 proton pulse. The NMR data were processed and analysed using Mnova software (Mestrelab Research, S.L.).
Experimental setup for microtesla NMR/MRI
Figure 1(b) shows the 3D-printed p-H2 phantom with inner dimensions of 50 (L) × 50 (W) × 21.3 (H) mm3. The p-H2 phantom contained pyridine and an Ir catalyst dissolved in a methanol solution. The thickness of the character “K” was approximately 5 mm. Nine rectangular blocks were placed on the right side of the phantom: (top) three blocks with dimensions of 5 (L) × 3 (W) mm2 and 2 mm spacing, (middle) three blocks with dimensions of 5 (L) × 1 (W) mm2 and 1 mm spacing, and (bottom) three blocks with dimensions of 5 (L) × 2 (W) mm2 and 2 mm spacing. Because the p-H2 gas entered the 3D phantom through a p-H2 inlet and many holes in the bottom and generated bubbles, a mesh was attached to prevent the generation of bubbles in the imaging region.
Figure 1(c) shows the experimental setup for SQUID-based NMR/MRI experiments installed inside the MSR. A dc-SQUID connected with a second-order gradiometric pickup coil placed inside a liquid-helium SQUID Dewar was used to detect the NMR/MRI signal. Bm and Bp were generated using a double Helmholtz coil and a pancake-type coil cooled with silicon oil that was mounted inside the Bp Dewar, respectively. A circularly polarized nutation pulse (B1)50 was used to avoid the Bloch-Siegert effect in the microtesla region. Two pairs of square-type Helmholtz coils, aligned orthogonally to each other, were used to create a circularly polarized π/2 B1. Three-axis gradient fields (Gx, Gy, and Gz) were generated using the rest coil sets. Because the p-H2 generator shown in Fig. 1(a) was placed outside the MSR, the 3D phantom, mounted between the SQUID and Bp Dewars, and the p-H2 generator were connected using an 8.5 m tube. During the NMR and MRI experiments, p-H2 gas flowed continuously at a rate of 70 mL/min and bubbled into the reaction mixture inside the 3D phantom at room temperature.
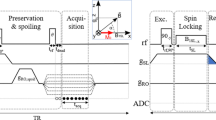
Pulse sequence for microtesla NMR/MRI
Figure 5 shows the NMR and MRI pulse sequences used in this study. Because an external field on the order of millitesla is necessary to create SABRE polarization, Bp was applied during the time tBp. In this study, the variable range of the Bp strength, measured at the centre of the top plate of the Bp Dewar, was approximately 2.1 to 10 mT. Because the axes of the coils Bp and Bm are perpendicular to each other, the nuclear spins were initially aligned parallel to the direction of Bp. To rotate the spins in the direction of Bm, an adiabatic pulse23 (i.e., an adiabatic change in Bp and Bm followed by a non-adiabatic change in Bm) was applied for 35 ms. Bm strengths of 106.6 and 34.3 µT were used to satisfy the adiabatic condition and detect the NMR/MRI signal, respectively. After the application of circularly polarized π/2 B1, the NMR signal or the MRI signal following the additional gradient echo pulse can be measured using the SQUID sensor. During the MRI experiments, Gx and Gz were used as the frequency- and phase-encoding gradients, respectively.
Data Availability
The relevant data supporting the findings of this study are available within the paper or are available from the corresponding author, K.K., upon reasonable request.
References
Walker, T. G. & Happer, W. Spin-exchange optical pumping of noble-gas nuclei. Rev. Mod. Phys. 69, 629–642 (1997).
Jeong, K. et al. Investigation of DOTA–Metal chelation effects on the chemical shift of 129Xe. Chem Phys Chem 16, 3573–3577 (2015).
Hayes, S. E., Mui, S. & Ramaswamy, K. Optically pumped nuclear magnetic resonance of semiconductors. J. Chem. Phys. 128, 052203 (2008).
Goez, M. An introduction to chemically induced dynamic nuclear polarization. Concepts Magn. Reson. 7, 69–86 (1995).
Lee, J. H., Sekhar, A. & Cavagnero, S. 1H-detected 13C photo-CIDNP as a sensitivity enhancement tool in solution NMR. J. Am. Chem. Soc. 133, 8062–8065 (2011).
Overhauser, A. W. Polarization of nuclei in metals. Phys. Rev. 92, 411–415 (1953).
Denysenkov, V. et al. Continuous-flow DNP polarizer for MRI applications at 1.5 T. Sci. Rep. 7, 44010 (2017).
Guglielmetti, C. et al. Hyperpolarized 13C MR metabolic imaging can detect neuroinflammation in vivo in a multiple sclerosis murine model. Proc. Natl. Acad. Sci. USA 114, E6982–E6991 (2017).
Bowers, C. R. & Weitekamp, D. P. Transformation of symmetrization order to nuclear-spin magnetization by chemical reaction and nuclear magnetic resonance. Phys. Rev. Lett. 57, 2645–2648 (1986).
Eisenschmid, T. C. et al. Para hydrogen induced polarization in hydrogenation reactions. J. Am. Chem. Soc. 109, 8089–8091 (1987).
Adams, R. W. et al. Reversible interactions with para-hydrogen enhance NMR sensitivity by polarization transfer. Science 323, 1708–1711 (2009).
Gupta, R. K. NMR spectroscopy of cells and organisms. Volume II (CRC Press Inc, Boca Raton, FL (USA), 1987).
Lee, S. K. et al. SQUID-detected MRI at 132 μT with T1-weighted contrast established at 10 μT–300 mT. Magn. Reson. Med. 53, 9–14 (2005).
Yasui, H. et al. Low-field magnetic resonance imaging to visualize chronic and cycling hypoxia in tumor-bearing mice. Cancer Res. 70, 6427–6436 (2010).
Busch, S. et al. Measurements of T1-relaxation in ex vivo prostate tissue at 132 μT. Magn. Reson. Med. 67, 1138–1145 (2012).
Lee, S. J. et al. T1 relaxation measurement of ex-vivo breast cancer tissues at ultralow magnetic fields. BioMed Res. Int. 2015, 385428 (2015).
Körber, R. et al. SQUIDs in biomagnetism: a roadmap towards improved healthcare. Supercond. Sci. Technol. 29, 113001 (2016).
Zotev, V. S. et al. Microtesla MRI with dynamic nuclear polarization. J. Magn. Reson. 207, 78–88 (2010).
He, Y. et al. Simultaneous acquisition of multi-nuclei enhanced NMR/MRI by solution-state dynamic nuclear polarization. Sci. China Chem. 59, 830–835 (2016).
McDermott, R. et al. Liquid-state NMR and scalar couplings in microtesla magnetic fields. Science 295, 2247–2249 (2002).
Theis, T. et al. Zero-field NMR enhanced by parahydrogen in reversible exchange. J. Am. Chem. Soc. 134, 3987–3990 (2012).
Lee, S. J., Shim, J. H., Kim, K., Yu, K. K. & Hwang, S. M. Magnetic resonance imaging without field cycling at less than earth’s magnetic field. Appl. Phys. Lett. 106, 103702 (2015).
Lee, S. J. et al. Toward a magnetic resonance electrical impedance tomography in ultra-low field: a direct magnetic resonance imaging method by an external alternating current. Appl. Phys. Lett. 112, 153703 (2018).
Hwang, S. M., Kim, K., Kang, C. S., Lee, S. J. & Lee, Y. H. Effective cancellation of residual magnetic interference induced from a shielded environment for precision magnetic measurements. Appl. Phys. Lett. 99, 132506 (2011).
Nieminen, J. O. et al. Avoiding eddy-current problems in ultra-low-field MRI with self-shielded polarizing coils. J. Magn. Reson. 212, 154–160 (2011).
Hwang, S. M. et al. Type-I superconductor pick-up coil in superconducting quantum interference device-based ultra-low field nuclear magnetic resonance. Appl. Phys. Lett. 104, 062602 (2014).
Lee, S. J., Kim, K., Kang, C. S., Hwang, S. M. & Lee, Y. H. Pre-polarization enhancement by dynamic nuclear polarization in SQUID-based ultra-low-field nuclear magnetic resonance. Supercond. Sci. Technol. 23, 115008 (2010).
Lee, S. J., Shim, J. H., Kim, K., Yu, K. K. & Hwang, S. M. Dynamic nuclear polarization in the hyperfine-field-dominant region. J. Magn. Reson. 255, 114–121 (2015).
Buckenmaier, K. et al. SQUID-based detection of ultra-low-field multinuclear NMR of substances hyperpolarized using signal amplification by reversible exchange. Sci. Rep. 7, 13431 (2017).
Lee, H. J., Lee, S. J., Shim, J. H., Moon, H. S. & Kim, K. In-situ Overhauser-enhanced nuclear magnetic resonance at less than 1 µT using an atomic magnetometer. J. Magn. Reson. 300, 149–152 (2019).
Roy, S. S., Rayner, P. J., Norcott, P., Green, G. G. R. & Duckett, S. B. Long-lived states to sustain SABRE hyperpolarised magnetisation. Phys. Chem. Chem. Phys. 18, 24905–24911 (2016).
Rayner, P. J. & Duckett, S. B. Signal amplification by reversible exchange (SABRE): from discovery to diagnosis. Angew. Chem. Int. Edit. 57, 6742–6753 (2018).
Shchepin, R. V., Jaigirdar, L. & Chekmenev, E. Y. Spin-lattice relaxation of hyperpolarized metronidazole in signal amplification by reversible exchange in micro-tesla fields. J. Phys. Chem. C 122, 4984–4996 (2018).
Coffey, A. M. et al. High-resolution low-field molecular magnetic resonance imaging of hyperpolarized liquids. Anal. Chem. 86, 9042–9049 (2014).
Barskiy, D. A. et al. In situ and ex situ low-field NMR spectroscopy and MRI endowed by SABRE hyperpolarization. Chem Phys Chem 15, 4100–4107 (2014).
Hövener, J. B. et al. A hyperpolarized equilibrium for magnetic resonance. Nat. Commun. 4, 2946 (2013).
Pravdivtsev, A. N. et al. Spin polarization transfer mechanisms of SABRE: a magnetic field dependent study. J. Magn. Reson. 261, 73–82 (2015).
Shchepin, R. V., Barskiy, D. A., Coffey, A. M., Goodson, B. M. & Chekmenev, E. Y. NMR signal amplification by reversible exchange of sulfur-heterocyclic compounds found in petroleum. Chemistry Select 1, 2552–2555 (2016).
Olaru, A. M. et al. Extending the scope of 19F hyperpolarization through signal amplification by reversible exchange in MRI and NMR spectroscopy. Chemistry Open 7, 97–105 (2018).
Richardson, P. M. et al. Quantification of hyperpolarisation efficiency in SABRE and SABRE-Relay enhanced NMR spectroscopy. Phys. Chem. Chem. Phys. 20, 26362–26371 (2018).
Fischer, M. C. et al. Single-acquisition sequence for the measurement of oxygen partial pressure by hyperpolarized gas MRI. Magn. Reson. Med. 52, 766–773 (2004).
Ajraoui, S. et al. Compressed sensing in hyperpolarized 3He lung MRI. Magn. Reson. Med. 63, 1059–1069 (2010).
Saloner, D., Liu, J. & Haraldsson, H. MR physics in practice: how to optimize acquisition quality and time for cardiac MRI. Magn. Reson. Imaging Clin. N. Am. 23, 1–6 (2015).
Norton, V. A. & Weitekamp, D. P. Communication: partial polarization transfer for single-scan spectroscopy and imaging. J. Chem. Phys. 135, 141107 (2011).
Theis, T. et al. Direct and cost-efficient hyperpolarization of long-lived nuclear spin states on universal 15N2-diazirine molecular tags. Sci. Adv. 2, e1501438 (2016).
Shchepin, R. V. et al. Hyperpolarizing concentrated metronidazole 15NO2 group over six chemical bonds with more than 15% polarization and 20 minute lifetime. Chem. Eur. J. 25, 8829–8836 (2019).
Iali, W., Rayner, P. J. & Duckett, S. B. Using parahydrogen to hyperpolarize amines, amides, carboxylic acids, alcohols, phosphates, and carbonates. Sci. Adv. 4, eaa06250 (2018).
Theis, T. et al. Microtesla SABRE enables 10% nitrogen-15 nuclear spin polarization. J. Am. Chem. Soc. 137, 1404–1407 (2015).
Cowley, M. J. et al. Iridium N-heterocyclic carbene complexes as efficient catalysts for magnetization transfer from para-hydrogen. J. Am. Chem. Soc. 133, 6134–6137 (2011).
Shim, J. H., Lee, S. J., Yu, K. K., Hwang, S. M. & Kim, K. Strong pulsed excitations using circularly polarized fields for ultra-low field NMR. J. Magn. Reson. 239, 87–90 (2014).
Acknowledgements
This work was supported by Development of Next-generation Measurement Technology for Biomagnetic Resonance (KRISS-2018-GP2018-0021) and the Development of Core Technology for Advanced Scientific Instrument (KRISS-2019-GP2019-0018) funded by Korea Research Institute of Standards and Science.
Author information
Authors and Affiliations
Contributions
S.J.L. and K.J. contributed equally to this work. K.K. and K.J. conceived the project. S.J.L. and K.J. mainly prepared the manuscript after discussing the results with other authors. S.J.L. and K.J. mainly conducted the ULF NMR/MRI and HF NMR experiments, respectively. K.J. performed the sample preparation and synthesis with the help of S.M., S.M.C. and S.K.N. S.J.L. designed and manufactured the 3D phantom. K.J., J.H.S., H.J.L. and K.K. assisted with the ULF NMR/MRI experiment and the design and manufacture of the 3D phantom. All authors reviewed the manuscript. K.K. supervised the project.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lee, SJ., Jeong, K., Shim, J.H. et al. SQUID-based ultralow-field MRI of a hyperpolarized material using signal amplification by reversible exchange. Sci Rep 9, 12422 (2019). https://doi.org/10.1038/s41598-019-48827-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-48827-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.