Abstract
An anisotropic coding metasurface (CM) is proposed for achieving circular-to-linear polarization conversion and beam deflection. Different phase coding consequences were independently achieved for two orthogonal linear polarized (LP) waves. Thus by elaborately designing coding sequences of the metasurfaces, different functions can be achieved, respectively for waves polarized along two orthogonal directions. More importantly, for circularly polarized (CP) wave, anisotropic CM can achieve circular-to-linear polarization conversion and beam deflection simultaneously. As a proof, a 1-bit anisotropic CM with 0101…/0101… and 0000…/1111… coding sequences respectively for two orthogonal LP waves was designed. The simulation results indicated that the incident CP wave is deflected into two x-polarized waves in x-o-z plane and two y-polarized waves in y-o-z plane. Both the simulation and experimental results verify the circular-to-linear polarization conversion performance of the anisotropic coding metasurfaces. The proposed anisotropic coding metasurfaces have the potential for the applications of multifunctional devices.
Similar content being viewed by others
Introduction
Since Yu et al. put forth the generalized Snell’s laws1, artificial metasurfaces composed of subwavelength structures have proven to be very effective for controlling electromagnetic (EM) waves2,3,4,5,6,7. Due to its low loss and thin thickness, metasurfaces is widely employed in the microwave8,9,10, terahertz3,11 and visible frequencies12, and its applications in many fields have resulted in quite good effects, such as stealth technology13,14,15,16 antenna technology17,18,19 and holographic technology20,21.
In recently year, coding metasurface (CM) was proposed22, which offers a new developing direction for metasurface. According to this concept, the design of metasurface is effectively combined with the binary codes. By designing different coding sequences, a variety of functions can be realized like anomalous reflection7,23, generation of orbital angular momentum24 and diffusion scattering25,26 of EM waves. This concept can be extended to higher bits for more flexible control of EM waves.
Not long ago, the concept of anisotropic CM has been proposed27,28,29, which can achieve two separate responses for orthogonal polarization EM waves. Because of special function of anisotropic CM, it is widely used in the development of dual-functional devices30,31,32. In addition, the anisotropic CM can not only realize anomalous reflections but also linear-to-circular polarization conversion. However, there are few studies on circular-to-linear polarization conversion and beam deflection by anisotropic CM. In this paper, we demonstrate the ability of anisotropic metasurfaces to transform circularly polarized (CP) waves into linear polarized (LP) waves and achieve beam deflection simultaneously. As an example, a 1-bit anisotropic CM with different coding sequences for x- and y-polarized incidence waves was designed. Both the simulation and experimental results support our prediction and demonstrate the circular-to-linear polarization conversion function of the anisotropic CMs.
Results
Operating principle and theoretical analysis
In order to clarify multifunctionality of anisotropic CMs and their ability to transform CP waves into LP waves, we expound the principle by a simple 1-bit anisotropic CM. For the 1-bit anisotropic CM, coding sequences are composed of four basic encodings [0/0, 0/1, 1/0, 1/1]. The digit code before ‘/’ represents the phase state of the unit cell under x-polarization, while the digit code after ‘/’ represents the phase state of the unit cell under y-polarization. For a CM which is encoded with coding sequence [0,1;0,1], the incident x-polarization wave is reflected into two equal waves along x direction (Fig. 1(a)). Similarly, if the CM is encoded with coding sequence [0,0;1,1], the incident y-polarization wave is reflected into two equal waves along y direction (Fig. 1(b)). As it is known to all, a CP wave can be decomposed into two orthogonal LP waves with same amplitude and phase difference is 90°. Therefore, when anisotropic CM is illuminated by CP wave, the CP wave is transformed into LP wave and achieving beam deflection simultaneously, as shown in Fig. 1(c).
Schematics of the proposed anisotropic CM illuminated by different polarized wave. (a) The incident x-polarization wave is reflected into two equal waves along x direction. (b) The incident y-polarization wave is reflected into two equal waves along y direction. (c) The incident CP wave is split into four symmetrical waves.
To mathematically describe the anisotropic CM, a tensor \({\overline{{\rm{R}}}}_{mn}\) is used to express the reflection coefficient of a unit cell indicated below:
where \({R}_{mn}^{x}\) and \({R}_{mn}^{y}\) denote reflection coefficients under x- and y-polarizations, respectively. For isotropic unit cells, \({R}_{mn}^{x}\) = \({R}_{mn}^{y}\); for anisotropic unit cells, the two reflection coefficients are different.
The anomalous reflection angle (θ, φ) can be obtained from theory of beam superposition of array antenna22, and the formulas is as follows:
where 𝜆 is the wavelength of the free-space, and the lengths of one period of gradient phase distribution along x- and y- directions are marked by Dx and Dy.
Numerical simulation
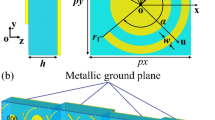
Two types of unit cells, an anisotropic ‘split ring’-shaped and an isotropic ‘Crusades’-shaped metallic pattern are designed for anisotropic CM. Both unit cells have the same period a = 5.2 mm and thickness d = 3 mm.
The ‘split ring’ pattern is used as anisotropic unit cell (Fig. 2). The top is metal ‘split ring’, and then dielectric substrates (εr = 2.65, tan δ = 0.001), the below is metal backboard. The other geometrical parameters are r = 2.3 mm, wr = 0.1 mm, s = 2 mm, l = 1.48 mm, wl = 0.2 mm. The reflected phases and amplitudes of the ‘split ring’ pattern under incident x-polarized and y-polarized wave are shown in Fig. 2(c). The phase difference between the two is about 180°, and the reflective amplitudes are more than 98%. Therefore, it is treated as ‘1’ and ‘0’ numeric state under x- and y-polarizations respectively.
The ‘Crusades’ pattern is used as isotropic unit cell (Fig. 3). The top is metal ‘Crusades’, the other two layers are the same as the anisotropic unit cell. By optimizing design, the ‘Crusades’-shaped metallic pattern with b = 0.5 mm and b = 2.16 mm are treated as ‘1’ and ‘0’ numeric state respectively and the corresponding reflection phases and amplitudes are shown in Fig. 3(c). The four basic structures of 1-bit anisotropic CM are shown in the Fig. 4.
In this paper, two different coding sequences are presented to demonstrate the special ability of anisotropic metasurface. The first coding sequence is composed of a periodic coding matrix C1:
The completed view of the anisotropic CM with matrix C1 is show in Fig. 5(a). The three-dimensional (3D) and two-dimensional (2D) far-field scattering patterns of anisotropic CM with matrix C1 under incident x-polarized wave at 14 GHz are show in Fig. 6(a,d) respectively. The simulated results show that the incident x-polarized wave is reflected into two symmetrical waves in φ = 0° cutting plane, and θ = 31.5°. The theoretical deviation angle is calculated as 31°, which is consistent with the numerical simulation. For the y-polarization, the incident wave is reflected into two symmetrical waves in φ = 90° plane, and the deviation angle θ = 31.5°, as shown in Fig. 6(b,e). So far we have proved the anisotropic properties of the designed CM. For the left-handed circularly polarized (LCP) incident wave, the wave is deflected to four symmetrical waves (φ = 0°, 90°, 180°, 270°, θ = 31°), as shown in Fig. 6(c,f). The simulated results indicates that the reflection characteristics of the anisotropic CM under CP wave incidence simultaneously possesses the both reflection characteristics under two orthogonal LP waves. To further verify the polarization characteristics of reflected beam, the axial ratio are analyzed. As shown in Fig. (7), two cutting planes φ = 0°, 90° are selected, and the axial ratio of the reflected waves (θ = ±31°) exceed 18 dB. Therefore the CP incident wave is converted to LP wave as expected.
To test this further, a periodic coding matrix C2 is designed:
The completed view of the anisotropic CM with matrix C2 is show in Fig. 5(b). The 3D and 2D far-field scattering patterns of anisotropic CM with matrix C2 under incident x-, y-polarized and LCP wave at 14 GHz are show in Fig. 8. For the x-polarization (Fig. 8(a,d)), the incident wave is deflected to two symmetrical waves in φ = 0° cutting plane (θ = 31°). For the y-polarization (Fig. 8(b,e)), the incident wave is deflected into four waves in diagonal direction (φ = 45°, 135°, 225°, 315°, θ = 46.75°). Whereas for LCP wave, the wave is split into six directions as anticipated. Similarly, the axial ratio of reflected waves are analyzed, two cutting planes φ = 0°, −45° are selected, and the axial ratio of the reflected waves (φ = 0°, θ = ±31°; φ = −45°, θ = ±46.75°) are all above 20 dB, as shown in Fig. 9.
The results of these simulations are consistent with the theoretic analysis, it indicates that anisotropic CMs can convert the CP wave into LP wave and achieve beam deflection simultaneously.
Experiment
To validate the performance of the designed anisotropic CMs, one sample (as shown in Fig. 10(a)) is fabricated, which corresponds to the coding matrix C1. The measurement was carried out in a microwave anechoic chamber, and the sketch maps of the test setup is given in Fig. 10(b). The measured 2D far-field scattering patterns of the anisotropic CM with matrix C1 at 14 GHz are show in Fig. 10. The results show that the measured deviation angle is accordance with the simulated result roughly, which demonstrates that anisotropic CMs can convert CP incident wave into LP wave and achieve beam deflection simultaneously.
Conclusions
In conclusion, we have proposed an anisotropic CM, which can achieve circular-to-linear polarization conversion and beam deflection simultaneously. Due to the characteristic of anisotropic, the coding sequences depend on the EM wave’s states of polarization, and the manipulation of EM waves becomes more flexible. In other word, the same metasurfaces can achieve different functions under the different polarized incident waves. Moreover, by analyzing the axial ratio of reflected EM waves, it is found that the anisotropic CMs can convert CP wave into LP wave. Both the simulated and measured results indicate that anisotropic CM can achieve circular-to-linear polarization conversion and beam deflection simultaneously. The proposed anisotropic CMs have the potential for the applications of multifunctional devices.
Methods
Simulations
EM simulations were simulated with CST Microwave Studio. The reflected amplitudes and phases of unit cells were simulated using the Frequency domain solver. The unit cell boundary was set for both the x and y directions, and the open at space boundary for the z directions. The full model was calculated using the Time domain solver with open boundary conditions along all directions.
Measurements
The measurement was made in a microwavechamber. A CP horn antenna served as transmitter, and maintained 2 m distance from the sample. Both the sample and the CP horn were bolted to the revolving stage, which could rotate 360°. In addition, a LP horn antenna was used as the receiving antenna to receive the scattering fields.
References
Yu, N. F. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011).
Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin Hall effect at metasurfaces. Science 339, 1405–1407 (2013).
Gao, L. H. et al. Broadband diffusion of terahertz waves by multi-bit coding metasurfaces. Light Sci. Appl. 4, e324 (2015).
Li, Y. F. et al. Wideband Polarization Conversion with the Synergy of Waveguide and Spoof Surface Plasmon Polariton Modes. Phys. Rev. Appl. 10, 064002 (2018).
Holloway, C. L. et al. An overview of the theory and applications of metasurfaces: the two-dimensional equivalents of metamaterials. IEEE Antennas Propag. Mag. 54, 10–35 (2012).
Li, Y. F. et al. Achieving wide-band linear-to-circular polarization conversion using ultra-thin bi-layered metasurfaces. J. Appl. Phys. 117, 044501 (2015).
Zhu, H. & Semperlotti, F. Anomalous refraction of acoustic guided waves in solids with geometrically tapered metasurfaces. Phys. Rev. Lett. 117, 034302 (2016).
Zheng, Q. Q. et al. Wideband, wide-angle coding phase gradient metasurfaces based on Pancharatnam-Berry phase. Sci. Rep. 7, 43543 (2017).
Wu, H. T. et al. Controlling Energy Radiations of Electromagnetic Waves via Frequency Coding Metamaterials. Adv. Sci. 4, 1700098 (2017).
Feng, M. C. et al. Wide-angle flat metasurface corner reflector. Appl. Phys. Lett. 113, 143504 (2018).
Zhao, J., Cheng, Q., Wang, T. Q., Yuan, W. & Cui, T. J. Fast design of broadband terahertz diffusion metasurfaces. Opt. Express 25, 1050–1061 (2017).
Ni, X. J., Wong, Z. J., Mrejen, M., Wang, Y. & Zhang, X. An ultrathin invisibility skin cloak for visible light. Science 349, 1310–1314 (2015).
Sui, S. et al. Absorptive coding metasurface for further radar cross section reduction. J. Phys. D: Appl. Phys. 51 (2018).
Li, Y. F. et al. Wideband radar cross section reduction using two-dimensional phase gradient metasurfaces. Appl. Phys. Lett. 104, 221110 (2014).
Feng, M. C. et al. Two-dimensional coding phase gradient metasurface for RCS reduction. J. Phys. D: Appl. Phys. 51, 375103 (2018).
Xiang, N. et al. Bifunctional metasurface for electromagnetic cloaking and illusion. Appl. Phys. Express 8, 092601 (2015).
Xu, H. X., Wang, G. M., Liang, J. G., Qi, M. Q. & Gao, X. Compact circularly polarized antennas combining meta-surfaces and strong space-filling meta-resonators. IEEE Trans. Antennas Propag. 61, 3442–3450 (2013).
Han, Y. J. et al. Miniaturized-Element Offset-Feed Planar Reflector Antennas Based on Metasurfaces. IEEE Antennas. Wireless Propag. Lett. 16, 282–285 (2017).
Minatti, G., Maci, S., Vita, P. D., Freni, A. & Sabbad, M. A circularly-polarized isoflux antenna based on anisotropic metasurface. IEEE Trans. Antennas Propag. 60, 4998–5009 (2012).
Wang, B. et al. Polarization-controlled color-tunable holograms with dielectric metasurfaces. Optica. 4, 1368–1371 (2017).
Zhang, K., Yu, H., Ding, X. & Wu, Q. Experimental validation of active holographic metasurface for electrically beam steering. Opt. Express 26, 6316–6324 (2018).
Cui, T. J., Qi, M. Q., Wan, X., Zhao, J. & Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci. Appl. 3, e218 (2014).
Liang, L. J. et al. Anomalous terahertz reflection and scattering by flexible and conformal coding metamaterials. Adv. Opt. Mater. 3, 1374–1380 (2015).
Zhang, K. et al. Phase-engineered metalenses to generate converging and non-diffractive vortex beam carrying orbital angular momentum in microwave region. Opt. Express 26, 1351–1360 (2018).
Jing, Y. et al. Full-space-manipulated multifunctional coding metasurface based on “Fabry-Pérot-like” cavity. Opt. Express 27, 21520–21531 (2019).
Jing, Y. et al. Fast coding method of metasurfaces based on 1D coding in orthogonal directions. J. Phys. D: Appl. Phys. 51, 475103 (2018).
Liu, S. et al. Anisotropic coding metamaterials and their powerful manipulation of differently polarized terahertz waves. Light Sci. Appl. 5, e16076 (2016).
Zhuang, Y. Q., Wang, G. M., Cai, T. & Zhang, Q. F. Design of bifunctional metasurface based on independent control of transmission and reflection. Opt. Express 26, 3594–3603 (2018).
Zhang, L. et al. Transmission-Reflection-Integrated Multifunctional Coding Metasurface for Full-Space Controls of Electromagnetic Waves. Adv. Fun. Mater. 1802205 (2018).
Cai, T. et al. Bifunctional Pancharatnam-Berry Metasurface with High-Efficiency Helicity-Dependent Transmissions and Reflections. Annalen der Physik 530, 1700321 (2018).
Liu, S. et al. Full-state controls of terahertz waves using tensor coding metasurfaces. ACS Appl. Mater. Interfaces 9, 21503–21514 (2017).
Liu, S. & Cui, T. J. Concepts, working principles, and applications of coding and programmable metamaterials. Adv. Opt. Mater. 5, 1700624 (2017).
Author information
Authors and Affiliations
Contributions
Y.J. and Y.L. conceived the idea and did the numerical simulations. Y.J., M.F., T.Q., H.W. and Y.H., fabricated the samples and conducted the measurements. Y.J., Y.L., J.Z., J.W., H.Ma. and S.Q. completed the theoretical analysis. Y.J. and Y.L. co-wrote the manuscript, and all authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jing, Y., Li, Y., Zhang, J. et al. Achieving circular-to-linear polarization conversion and beam deflection simultaneously using anisotropic coding metasurfaces. Sci Rep 9, 12264 (2019). https://doi.org/10.1038/s41598-019-48812-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-48812-y
This article is cited by
-
Simultaneous realization of polarization conversion for reflected and transmitted waves with bi-functional metasurface
Scientific Reports (2022)
-
Dual-band linear-to-circular and circular-to-linear polarization converter based on reflective metasurface
Applied Physics A (2022)
-
Ultra-wideband Linear-to-Circular and Circular-to-Linear Polarization Conversion Realized by Anisotropic Metasurface
Plasmonics (2022)
-
Frequency coding all-dielectric metasurface for flexible control of electromagnetic radiation
Applied Physics A (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.