Abstract
InN superconductivity is very special among III–V semiconductors, as other III–V semiconductors (such as GaAs, GaN, InP, InAs, etc.) usually lack strong covalent bonding and thus seldom show superconductivity at low temperatures. Here, we probe the different superconducting phase transitions in InN highlighted by its microstructure. Those chemical-unstable phase-separated inclusions, such as metallic indium or In2O3, are intentionally removed by HCl acid etching. The quasi-two-dimensional vortex liquid-glass transition is observed in the sample with a large InN grain size. In contrast, the superconducting properties of InN with a small grain size are sensitive to acid etching, showing a transition into a nonzero resistance state when the temperature approaches zero. Since the value of ξ0 (the zero-temperature-limit superconducting coherence length) is close to the grain size, it is suggested that individual InN grains and intergrain coupling should be responsible for the sample-dependent InN superconducting phase transition. Our work establishes a guideline for engineering superconductivity in III-nitride.
Similar content being viewed by others
Introduction
Group-III nitrides are no doubt the typical semiconductors considered in optoelectronic applications1,2,3. Therefore, it is surprising that one of its members, InN (indium nitride), can be a superconductor at low temperatures4,5. Since the first report by Inushima et al.6, InN superconductivity and related physics are still not well resolved. It is known that a typical III–V semiconductor (e.g., GaAs, InAs, GaN, etc., except for BN, whose B and N atoms are bound by strong covalent bonds) is usually not easily made superconducting7,8. In contrast, IV semiconductors (e.g., Si, diamond, SiC, etc.) can become superconducting by heavy doping9. The reason is explained under the framework of the BCS mechanism: the IV semiconductor has strong directional covalent bonds, but the III–V semiconductor has weak covalent bonds. Therefore, the III–V semiconductor does not have a sufficiently large phonon energy and strong electron-phonon coupling. Additionally, the enhanced spin-orbit coupling in III–V tends to break the Copper pairing under the BCS mechanism. Along this line of thinking, GaN (which has a more covalent character) would more easily exhibit superconductivity than would InN. However, experimental evidence for GaN superconductivity is still lacking7. The traditional IV semiconductor superconductivity mechanism, which is driven by phonons strongly coupled to holes at the Γ point and requires the material to be p-type10, is not straightforwardly applicable in InN (the superconductivity of which is observed in n-type samples but not in p-type samples)11,12,13.
Although InN superconductivity seems to be “unreasonable” within the framework of current superconductivity theory for semiconductors, the major controversy against InN superconductivity does not stem from this point but from another simpler speculation: InN can have two phase-separated superconducting inclusions, i.e., indium metal (In) and indium oxide (In2O3), the superconductivity of which may “contaminate” InN. However, this naive In/In2O3 speculation faces strong challenges. Concerning In, its upper critical field Hc2 (~0.03 T) is much smaller than that of InN (~1 T). Although a small In nanoparticle was theoretically proposed to increase Hc214, this proposal is not reliable because the small size effect has been experimentally proven to suppress the superconductivity in In15. Furthermore, another similar III-nitride, GaN, has been made superconducting by it containing a heavy amount of Ga but has a similar Hc to that of Ga7,16. Thus, it is less persuasive to assume that the metal nanoparticle superconductivity effect is present only in InN and not in other III-nitrides. Concerning In2O3, the attribution of the 33° XRD peak to In2O3 is not well recognized17, as metallic indium, amorphous InN, InN(10–11), and cubic InN can also produce similar XRD reflections12. Additionally, achieving In2O3 superconductivity is not easy and requires low disorder18. It is difficult to believe that the unintentionally introduced In2O3 in InN can meet such requirements.
In addition to its importance in superconductivity physics, InN superconductivity is of technical interest. For example, an InN superconductor can be used to fabricate a superconducting single-photon detector (SSPD) with the following justifications. First, compared with NbN, which is the most successful material in an SSPD19,20, InN shares many similar and attractive properties, namely, high chemical stability, good mechanical performance, etc. Second, InN has a suitable transition temperature Tc (~3 K). In contrast, high-Tc superconducting material is not suitable for SSPD applications, as its large superconducting gap energy will reduce the sensitivity to photons of a given energy (especially at longer wavelengths)20. On the other hand, too low Tc requires a large cooling power, so it is less convenient. Finally, the application of InN in the superconducting industry is favored because it can be integrated with the III–V semiconductor technology, allowing an easy combination of semiconductor and superconductor function within one material system, i.e., III-nitride.
In this work, we remove the In/In2O3 inclusions (which are highly reactive) in InN by acid etching and check the InN superconductivity. This experiment is not yet available in the literature. This work is also useful for future applications of InN in an SSPD, where chemical stability is preferred.
Experimental Method
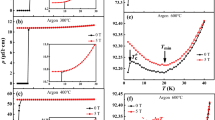
Two n-type InN samples (sample A and sample B) were grown by metalorganic vapor phase epitaxy (MOVPE) on insulative GaN/sapphire (0001) templates at the University of Fukui. A varying growth-temperature strategy21 is adopted to control the grain size of the InN crystal. The growth temperature is 520 °C (480 °C) for sample A (B). The detailed growth conditions and crystal structure characterizations can be found elsewhere21. The thickness of sample A (B) is measured to be ~850 nm (~950 nm) by cross-section SEM.
The room temperature electron mobility and concentration of sample A (B) is 505 cm2/Vs (280 cm2/Vs) and 1.2 × 1019 cm−3 (2.2 × 1019 cm−3). Figure 1(c,d) are the X-ray diffraction (XRD) results of samples A and B, respectively. In addition to the InN(0002) reflection at 31.36°, both samples have a small peak at ~33.0°, which can be removed by HCl acid etching. Therefore, it is attributed to In(101) (2θ = 32.95°)22 or (110) reflection of a rhombohedral phase In2O3 (2θ = 32.92°).
Each sample was cut into small pieces (with a size of ~1 mm × 10 mm) and subjected to HCl etching to remove the possible In/In2O3 inclusions. Figure 1(a,b) show the surface morphologies (SEM images) of the HCl etched samples. As seen in the figure, sample B shows more voids after HCl etching than does sample A, indicating more significant phase separation in sample B. Transport measurements were performed at the Shanghai Institute of Technical Physics with a dilution refrigerator down to a temperature of ~30 mK and a cryogen-free low-temperature system with 1.5 K as the lowest temperature. A magnetic field was applied vertical to the sample surface, i.e., along the InN c[0001] axis. The ohmic contacts were made from metal indium or silver pastes.
Results and Discussions
Demonstration of the chemical-stable InN superconductivity
Figure 2(a,b) display the normalized resistance R/Rn (Rn is the normal state resistance) as a function of temperature T (R-T) and magnetic field H (R-H) of sample A. Because the superconductivity is observed both in the as-grown and etched sample A, the superconductivity in InN is proven to be able to survive acid etching. The critical temperature and magnetic field are not changed significantly by etching. This indicates that the effect of those chemical unstable inclusions (e.g., large-sized In/In2O3) on InN superconductivity is very limited.
(a) R-T transitions and (b) R-H transitions for as-grown and etched sample A. (c) Normalized resistance as a function of temperature T under different magnetic fields H for as-grown sample A. (d) The upper critical field (Hc2) as a function of temperature T for as-grown and etched sample A. In (a–d), the resistance is measured with a current of 1 μA.
Figure 2(c) displays the R-T curves of the as-grown sample A under different magnetic fields (H). With increasing H, the superconducting transition broadens and shifts to lower temperatures. From these curves, we can deduce the upper critical field (Hc2), which is defined as the H field when R/Rn = 10%. Figure 2(d) gives the deduced Hc2 as a function of temperature T. From Fig. 2(d), we can calculate the dirty-limit coherence length (ξ0,dirty) of sample A by the dirty-limit (in the case of the mean free path l ≪ ξ0) relation23:
where mean-field Tc(H) at different H is determined from R-T scans, in which R/Rn = 10% is met. Eq. (1) gives the ξ0,dirty value for the as-grown/etched sample A as 76 nm/71 nm, respectively. The clean-limit (Pippard) coherence length ξ0,clean of sample A is estimated by24,25,26:
where 2Δ = Eg is the superconducting energy gap, VF is the fermi velocity, and Tc = 2.4 K is the transition temperature where R/Rn = 10% occurs. It reaches ξ0,clean ≈ 710 nm.
In a conventional superconductor, the coherence length ξ(T) will approach ξ0 in the limit of T → 0. Meanwhile, near Tc, ξ(T) diverges as (Tc-T)−1/2. ξ0 is equal to ξ0,clean if the sample is “clean” and to ξ0,dirty if it is “dirty” (i.e., when the mean free path l ≪ ξ0)26. By the Hall measurements and InN effective electron mass me*/m0 = 0.075, we reach l ≈ 25 nm for sample A. Therefore, the dirty limit requirement l ≪ ξ0,dirty is not met well23, and ξ0 will be close to ξ0,clean. Considering the fact that l < ξ0,dirty < ξ0 < ξ0,clean here, ξ0 is believed to lie in the range of 100–1000 nm.
Note that this InN ξ0 range (i.e., 100–1000 nm) deduced above is consistent with the previous magnetic susceptibility measurements on the MOVPE InN sample (also from Fukui and with l ~ 38 nm) in ref.12. From ref.12, where the “Hc2” (~4 mT) and “Tc”(~1.7 K) values are reached by the magnetic susceptibility results, the following results hold: ξ0,dirty ~ 290 nm and ξ0,clean ~ 820 nm, which sets the ξ0 range to 290 nm–820 nm in ref.12. Therefore, the InN ξ0 values measured by different methods are not far from each other and lie mainly in the range of 100–1000 nm.
Previously, the largest grain size of our MOVPE InN was observed to be ~500 nm21, which agrees with the morphology in Fig. 1(a). Therefore, ξ0 is now close to the grain size21 of MOVPE InN and will make difference in the superconducting properties of InN. Since ξ0 is the characteristic size that permits the occurrence of superconductivity15,25, an InN sample with a smaller grain size will be more sensitive to microstructure details with respect to superconductivity, which we will discuss later.
The basic features of the InN superconducting phase transition: quasi-two-dimensional vortex liquid-glass transition
Although zero resistance is the major characteristic of a superconductor, an understanding of the superconductor’s vortex dynamics (which causes dissipation and thus resistivity) and the resulting superconducting phase transition is necessary. Among various experimental methods, the current-voltage (I–V) measurements at different temperatures and magnetic fields can provide important information on the phase transition. On the other hand, the nonlinear and scaled I–V curves (see below) can further support the idea that InN is truly a superconductor rather than a normal metal with very low resistivity.
For the etched sample A, Fig. 3(a) shows the I–V curves under different temperatures T, with a small magnetic field μ0H = 5 mT (for introducing the vortex). Figure 3(c) displays the I–V curves under different magnetic fields H, with a temperature of 0.5 K (≪Tc). The I–V curves show a smooth evolution in the curvature from convex to linear with increasing T and H. These phenomena agree well with the vortex-glass (VG) theory, where the vortex comes from the self-field due to a persistent current and the applied magnetic field is pinned at small T/H (which results in the “convex” I–V) and then depinned at large T/H (which results in the linear I–V).
In VG theory, with the decrease in T, the mobile vortex (i.e., vortex-liquid state) will finally be pinned by the randomly distributed pinning centers, reaching the superconducting state (i.e., vortex-glass state). Therefore, the I–V curves at different temperatures near the liquid-glass phase transition temperature (Tg) can be scaled into two different branches by the scaling law27,28,29:
where v is the exponent of the vortex-glass correlation length ξg and ξg diverges at Tg as:
z is the dynamical critical exponent, D is the number of dimensions, and f± are the scaling functions above and below Tg. Above Tg, being in the vortex-liquid phase, there is a finite linear resistance for a low current limit I → 027:
and the I–V curve becomes nonlinear for large I. At Tg, the I–V curve satisfies the relationship:
Below Tg, being in the vortex-glass regime, the double-logarithmic I–V curves have downward curvatures corresponding to a vanishing linear resistance. The scaling results are shown in Fig. 3(b). The I–V curves are nicely scaled into two branches, which touch each other at the T = 1 K−1.2 K scaling curves. This agrees well with the fitting Tg value Tg = 1.1 K.
Figure 3(a) can be fully explained within the framework of VG theory. When temperature T < Tg, the sample is in the vortex-glass state. Thus, the resistance falls rapidly with decreasing current and is zero below the critical current. At T > Tg, the sample is in the vortex-liquid state, the I–V curves exhibit ohmic behavior and the resistance remains constant even at small current I. Previous theoretical and experimental studies show that z = 4~7 and ν = 1~2 are reasonable values for the VG phase transition27. To obtain a good scaling performance, we have D = 2, ν = 1.9, and z = 4.2.
Since the magnetic field and temperature exhibit analogous effects in suppressing superconductivity and generating quasi-particles in conventional superconductors, the I–V relations under different magnetic fields, which are shown in Fig. 3(c), are qualitatively similar to the I–V curves at different temperatures in Fig. 3(a). After scaling, these I–V curves are separated into two branches by a particular magnetic field (μ0Hg). We can modify Eq. (3) by replacing Tg with Hg, based on VG theory27. Then, those IV curves can also be scaled into two branches, with μ0Hg = 10 mT and D = 2.
D = 2 means that the VG transition in Fig. 3 is quasi-two-dimensional (quasi-2D)29,30. This is further supported by two behaviors in I–V. First, as shown in Fig. 3(a), for temperatures in the range 1.5 K-2 K (i.e. the vortex-liquid region), the I–V curves exhibit a crossover from linear behavior at small current I to nonlinear behavior at high I. This crossover is anticipated in the quasi-2D VG model: at low I, the vortex dynamics at length scales larger than ξg (ξg is on the order of ξ) is considered, where the system will behave like a vortex liquid with a linear resistance; at high I, the excitations involve length scales smaller than ξg, and the associated glassy dynamics yields a nonlinear I–V relation29. Second, a Berezinskii-Kosterlitz-Thouless (BKT) transition30,31,32, which is a characteristic phase transition in a 2D superconductor, was found at a specific temperature TBKT = 1.5 K in Fig. 3(a) by the occurrence of V ∝ I3 30. Below TBKT, the vortex/antivortex pairs generated by topological excitations will be bound, leading to a zero linear resistivity. At TBKT, V ∝ I3, which is a sign of the BKT transition. The observed VG transition agrees with previous reports that InN is a type-II superconductor12. The quasi-2D VG character indicates that the thickness of sample A, i.e., ~900 nm, is comparable or smaller than the ξ0 and the corresponding ξg.
The modified InN superconducting phase transition
Different from sample A, sample B is sensitive to acid etching. Figure 4(a) displays the R-T curves of the etched sample B. Compared with the as-grown sample B, the superconducting transition is greatly broadened after etching. In addition, the resistance of the etched sample B is not zero even at the lowest temperature T ≈ 35 mK. The R-H measurements in Fig. 4(b) show that the “critical” magnetic field of etched sample B is also significantly reduced.
(a) R-T transitions and (b) R-H transitions for as-grown and etched sample B. (c) The linear resistance Rlin at I → 0 [deduced from the I–V curves in Fig. 4(d)] as a function of temperature for etched sample B. (d) I–V curves measured at magnetic field μ0H = 0 T for etched sample B. (e) Scaling of the I–V curves in (d).
Figure 4(d) shows the I–V curves of etched sample B at different temperatures. With increased temperature, the I–V curves show an evolution from convex curvature to linear dependence, which indicates that the superconducting vortex-glass state does not exist even at the lowest temperature, i.e., ~35 mK. The trend toward the BKT transition with V ∝ I3 is observed under reduced temperature. The resistance goes to a finite value as the current I approaches zero, i.e., V ∝ I at I → 0. In Fig. 4(e), we try to scale the I–V curves, but the attempt fails, and the two-branch characteristic in the VG transition cannot be produced. The fitting parameters also cannot be adjusted to the reasonable range, e.g., z = 1.17 is outside the z = 4~7 range.
The failed scaling is mainly due to the appearance of a nonzero resistance state (NZRS) at the limit of T → 033. As shown in Fig. 4(c), the NZRS is not a vortex-liquid state with Tg = 0 K, as the deduced I → 0 linear resistance Rlin is not linear to log(T), as required by Eq. (5)30. This NZRS is also inconsistent with other mechanisms that can suppress the superconductivity, such as phase slip (PS), in which the phase of the superconducting condensate wave-function jumps irreversibly, leading to the nonzero resistance. These phase slips represent activation processes that can be triggered either thermally (i.e., thermally activated phase slip, TAPS) or through quantum tunneling (quantum phase slip, QPS)33. However, a TAPS requires a temperature dependence of the resistance as33:
where U is the activation energy. However, NZRS does not follow Eq. (7) at T → 0, as shown in Fig. 4(c, inset). On the other hand, the QPS explanation requires that the sample sheet resistance Rs in the normal state is larger than the quantum resistance RQ = h/4e2 = 6.45 kΩ 34, while the Rs of our InN sample is too small (~10 Ω).
According to the phase transition theory, the scaling behavior is attributed to the existence of a characteristic length that diverges at the transition temperature10, as in Eq. (4). Therefore, we propose that there should be a special size that limits the expansion of the vortex-glass correlation length ξg in the etched sample B even at T → 0 K. We believe that the InN grain size can be such a special size, where the intergrain boundary can destroy the correlation among the vortex in nearby grains. On the other hand, since NZRS is not observed in the as-grown sample B, as shown in Fig. 4(a), the In/In2O3 inclusion seems to “suppress” the NZRS.
Figure 5(a) gives our theoretical picture regarding the NZRS. In this picture, we suggest that two factors in the microstructures are highlighted in InN superconductivity. First, the grain size L makes a difference. If L is comparable to or smaller than the coherence length ξ0 (e.g., ~700 nm or less), the magnitude fluctuations of the superconducting order parameter will destroy the superconductivity15. Consequently, this grain will no longer be superconducting. Second, the intergrain coupling can recover the superconductivity in InN. In this case, the diffusion of electron pairs from the superconductor grain into the normal material (known as the proximity effect) and then into the neighboring superconductor grain gives rise to global superconductivity.
(a) Schematics of the intergrain superconducting coupling in InN(0001) film. The presence of intergrain inclusion can enhance the intergrain coupling J. If these inclusions are removed, the grain boundary can serve only as a weak link of small J. (b) Schematic phase diagram of InN superconductor with the presence of a vortex (under a small magnetic field or with the persistent current’s self-field) as a function of J and temperature T.
Figure 5(b) gives the schematic phase diagram describing InN superconductivity with the presence of vortex as a function of intergrain coupling J and temperature T. Since superconductivity in an individual grain is fragile owing to its small size L < ξ0 or L ~ ξ0, nonsuperconducting T = 0 states are presented as the NZRS. The appearance of the NZRS signifies the existence of a mesoscopic energy scale on each grain (e.g., an effective “charging energy” or the electronic level spacing on a grain, etc.)15,32. Therefore, a minimum interisland coupling Jm must be overcome to obtain the global superconductivity15.
Discussion on the sample-dependent superconducting phase transition in InN
With the phase diagram in Fig. 5(b), which is based on the grain size and intergrain coupling J, we can consistently understand the various sample-dependent superconductivity results for InN. For those small grain size InN films (e.g., sample B), since the superconductivity in each grain is fragile or even not present, the sample’s global superconductivity heavily relies on the intergrain coupling, which is realized by the intergrain inclusion In/In2O3. Previous reports22 also clearly demonstrated that indium metal prefers to reside on the (11–20) planes of InN, which is the intergrain interface of InN. Acid etching can remove such inclusions and reduce the intergrain coupling J. Consequently, a broadened superconducting transition does result not only simply from a spread in Tc of the individual grains but also from an inhomogeneous distribution of J. The NZRS will then appear due to J < Jm. For an InN film with a large grain size (e.g., sample A), its individual grains have a robust superconductivity with a rather uniform Tc, and its intergrain coupling is already strong (because of the large area of the intergrain directly touching the interface without the presence of In/In2O3 inclusions). Therefore, acid etching has no obvious influence. The morphology observed in Fig. 1(c,d) and in previous reports21 agrees with the grain-size attribution above.
On the roles of In/In2O3 in InN superconductivity, we believe that they can enhance the superconductivity by filling the gaps between InN grains. However, if In or In2O3 alone wants to establish global superconductivity, it must (a) continuously distribute from the source to the drain and undergo exposure there and (b) have a grain size > ~30 nm for an In/In-oxide composite film35 or >4 nm for pure metal In15. However, items (a) and (b) will make In/In2O3 easy to etch away by acid, thus removing the superconductivity. Kadir et al. claimed that In2O3 alone contributes to the superconductivity in InN via a thermal annealing experiment17. However, their annealing temperature was too high (530–650 °C) compared with the growth temperature. The grain size and intergrain coupling were certainly modified there.
Summary
We prove that InN superconductivity can be chemically stable, which supports InN as an intrinsic superconductor. This paves the way for the future field of semiconductor-superconductor integrated electronics (or optoelectronics) within only one material family (i.e., III-nitride). For example, the InN superconducting single-photon detector (SSPD) can be equipped with an on-wafer amplifying circuit made by a GaN/AlGaN HEMT (high electron mobility transistor). InN is obviously more suitable for semiconductor-superconductor integration than the previously suggested NbN superconductor36. On the other hand, we show that the InN superconductivity property can be a function of its grain size and the intergrain inclusions. If the intergrain inclusions play an important role in coupling the superconductivity between nearby InN grains, their removal can greatly modify the superconducting behaviors of InN. This provides a novel method for controlling the superconductivity properties of III-nitride by engineering the crystal’s microstructures.
References
Akasaki, I. Nobel Lecture: Fascinated journeys into blue light. Rev. Mod. Phys. 87, 1119 (2015).
Amano, H. Nobel Lecture: Growth of GaN on sapphire via low-temperature deposited buffer layer and realization of p-type GaN by Mg doping followed by low-energy electron beam irradiation. Rev. Mod. Phys. 87, 1133 (2015).
Nakamura, S. Nobel Lecture: Background story of the invention of efficient blue InGaN light emitting diodes. Rev. Mod. Phys. 87, 1139 (2015).
Bhuiyan, A. G., Hashimoto, A. & Yamamoto, A. Indium nitride (InN): A review on growth, characterization, and properties. J. Appl. Phys. 94, 2779 (2003).
Wu, J. When group-III nitrides go infrared: New properties and perspectives. J. Appl. Phys. 106, 011101 (2009).
Inushima, T. et al. Physical properties of InN with the band gap energy of 1.1 eV. J. Cryst. Growth 227, 481 (2001).
Iakoubovskii, K. Recent advances in superconductivity of covalent superconductors. Physica C 469, 675 (2009).
Bustarret, E. Superconductivity in doped semiconductors. Physica C. 514, 36 (2015).
Blase, X., Bustarret, E., Chapelier, C., Klein, T. & Marcenat, C. Superconducting group-IV semiconductors. Nature material 8, 375 (2009).
Bustarret, E. et al. Superconductivity in doped cubic silicon. Nature 444, 465 (2006).
Xie, W. et al. Transport properties for Zn+ ion implanted InN films at low temperature. Materials Letters 208, 23 (2017).
Inushima, T. et al. Superconducting Properties of InN with Low Carrier Density near the Mott Transition. J. Phys. Soc. Jpn. 81, 044704 (2012).
Tiras, E., Gunes, M., Balkan, N., Airey, R. & Schaff, W. J. Superconductivity in heavily compensated Mg-doped InN. Appl. Phys. Lett. 94, 142108 (2009).
Komissarova, T. A., Parfeniev, R. V. & Ivanov, S. V. Comment on “Superconductivity in heavily compensated Mg-doped InN”. Appl.Phys. Lett. 95, 086101 (2009).
Jaeger, H. M., Haviland, D. B., Orr, B. G. & Goldman, A. M. Onset of superconductivity in ultrathin granular metal films. Phys. Rev. B 40, 182 (1989).
Alekseevskii, N. E., Samsonov, G. V. & Shulishova, O. I. Superconductivity of Gallium Nitride. Sov. Phys. JETP 17, 950 (1963).
Kadir, A. et al. Non-intrinsic superconductivity in InN epilayers: Role of Indium Oxide. Solid State Commun. 146, 361 (2008).
Shahar, D. & Ovadyahu, Z. Superconductivity near the mobility edge. Phys. Rev. B 46, 10917 (1992).
Hadfield, R. H. Single-photon detectors for optical quantum information applications. Nature Photonics 3, 696 (2009).
Natarajan, C. M., Tanner, M. G. & Hadfield, R. H. Superconducting nanowire single-photon detectors: physics and applications. Supercond. Sci. Technol. 25, 063001 (2012).
Yamamoto, A., Kodama, K., Shigekawa, N., Matsuoka, T. & Kuzuhara, M. Low-temperature (≥400 °C) growth of InN by metalorganic vapor phase epitaxy using an NH3 decomposition catalyst. Jpn. J. Appl. Phys. 55, 05FD04 (2016).
Kang, T.-T. et al. InN nanoflowers grown by metal organic chemical vapor deposition. Appl. Phys. Lett. 89, 071113 (2006).
Chockalingam, S. P. et al. Superconducting properties and Hall effect of epitaxial NbN thin films. Phys. Rev. B 77, 214503 (2008).
Poole, C. P., Jr., Farach, H. A., Creswick, R. J. & Prozorov, R., Superconductivity, 2nd ed. P149 (Academic Press, 2007).
Bezryadin, A. Superconductivity in Nanowires: Fabrication and Quantum Transport, 2nd ed (Wiley-VCH, Weinheim, 2013).
Tinkham, M. Introduction to superconductivity, 2nd ed. (McGraw-Hill, NewYork, 1996).
Sun, Y. et al. Voltage-current properties of superconducting amorphous tungsten nanostrips. Sci. Rep. 3, 2307, https://doi.org/10.1038/srep02307 (2013).
Huse, D. A., Fisher, M. P. A. & Fisher, D. S. Are superconductors really superconducting? Nature 358, 553–559 (1992).
Dekker, C., Wöltgens, P. J. M., Koch, R. H., Hussey, B. W. & Gupta, A. Absence of a finite-temperature vortex-glass phase transition in two-dimensional YBa2Cu3O7−δ films. Phys. Rev. Lett. 69, 2717 (1992).
Yang, H. et al. I–V characteristics of the vortex state in MgB2 thin films. Phys. Rev. B 76, 134513 (2007).
Resnick, D. J., Garland, J. C., Boyd, J. T., Shoemaker, S. & Newrock, R. S. Kosterlitz-Thouless Transition in Proximity-Coupled Superconducting Arrays. Phys. Rev. Lett. 47, 1542 (1981).
Eley, S., Gopalakrishnan, S., Goldbart, P. M. & Mason, N. Approaching zero-temperature metallic states in mesoscopic superconductor–normal–superconductor arrays. Nature Phys 8, 59 (2012).
Baumans, X. D. A. et al. Thermal and quantum depletion of superconductivity in narrow junctions created by controlled electromigration. Nat. Commun. 7, 10560, https://doi.org/10.1038/ncomms10560 (2016).
Fisher, M. P. A. Quantum Phase Slips and Superconductivity in Granular Films. Phys. Rev. Lett. 57, 885 (1986).
Fiory, A. T., Hebard, A. F. & Glaberson, W. I. Superconducting phase transitions in indium/indium-oxide thin-film composites. Phys. Rev. B 28, 5075 (1983).
Yan, R. et al. GaN/NbN epitaxial semiconductor/superconductor heterostructures. Nature 555, 183–189 (2018).
Acknowledgements
The work was supported by the National Natural Science Foundation of China (NSFC) 11204334, 61475178, 61574150, 61376015, and 91321311 and the Shanghai Science and Technology Foundation 14JC1406600 and 18JC1420401 (2018–2021). T.K. especially thanks the “Hundred Talent program” of the Chinese Academy of Sciences for the funds given to establish the low-temperature transport lab.
Author information
Authors and Affiliations
Contributions
T.K. initiated and supervised this research. Z.S. performed the measurements. Z.S. and T.K. analyzed the data. T.K. wrote the manuscript. P.C. provided the InN samples for the early stage of this research. A.Y. provided the InN samples used in this research. L.S., Z.H. and J.C. kindly provided support to T.K. for conducting this work. All requests for materials should be addressed to T.K.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Song, ZY., Shang, L., Hu, Z. et al. InN superconducting phase transition. Sci Rep 9, 12309 (2019). https://doi.org/10.1038/s41598-019-48783-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-48783-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.