Abstract
The captivating attributes of carbon nanotubes (CNT) comprising chemical and mechanical steadiness, outstanding electrical and thermal conductivities, featherweight, and physiochemical consistency make them coveted materials in the manufacturing of electrochemical devices. Keeping in view such exciting features of carbon nanotubes, our objective in the present study is to examine the flow of aqueous based nanofluid comprising single and multi-wall carbon nanotubes (CNTs) past a vertical cone encapsulated in a permeable medium with convective heat and solutal stratification. The impacts of heat generation/absorption, gyrotactic-microorganism, thermal radiation, and Joule heating with chemical reaction are added features towards the novelty of the erected model. The coupled differential equations are attained from the partial differential equations by exercising the local similarity transformation technique. The set of conservation equations supported by the associated boundary conditions are worked out numerically by employing bvp4c MATLAB function. The sway of numerous appearing parameters in the analysis on the allied distributions is scrutinized and the fallouts are portrayed graphically. The physical quantities of interest including Skin friction coefficient, the rate of heat and mass transfers are assessed versus essential parameters and their outcomes are demonstrated in tabulated form. It is witnessed that the velocity of the fluid decreases for boosting values of the magnetic and suction parameters in case of both nanotubes. Moreover, the density of motile microorganism is decreased versus larger estimates of bio-convection constant. A notable highlight of the presented model is the endorsement of the results by matching them to an already published material in the literature. A venerable harmony in this regard is achieved.
Similar content being viewed by others
Introduction
The topic of nanofluid flow has earned exceptional consideration in the last two decades due to its standing in copious industrial and engineering applications. The scientists and researchers have not only explored the surprising thermal characteristics of nanofluids but also suggested the reasons for the enhancement of thermal conductivity of nanofluids. Because of surprising features of nanofluids, these are being considered as future coolants for computers and obviously the reliable coolants for nuclear reactors. An amalgamation of nanofluids and biotechnological mechanisms may offer promising applications in biological sensors, pharmaceuticals and agricultural. In the field of biotechnology, numerous nanomaterials like nanofibers, nanoparticles, nanostructures, and nanowires are in practice. The Nano biotechnological has a potential market and one can foresee that the future of such products is very bright. Likewise, in the area of biomedical devices and procedures, the importance of nano and micro-fluidics can’t be denied. The magnetic nanofluids own both magnetic and liquid characteristics and have applications in varied fields like optical switches, tunable optical fiber filters, modulators, and optical gratings. The magnetic nanoparticles have an imperative role in medicine, cancer therapy, loudspeakers, and sink-float separation. The concept of renewable energy generation is the core subject of today’s era across the world. Solar energy is the prime source of renewable energy with minimal ecological pollution. One can obtain energy, electricity, and water from the solar source directly. Researchers are of the opinion that solar collection processes can be triggered by the insertion of nanoparticles in the fluids. In several industrial processes, such as power transportation and manufacturing, cooling and heating of fluids is the prime requirement. Improvement in the cooling process in high energy devices is the need of the day. But ordinary heat transfer liquids like water, engine oil, and ethylene glycol possess poor heat transfer characteristics and do not meet the cooling requirements of the industry. Instead, if we talk about the thermal conductivities of the metals which are relatively much higher than those of conventional aforementioned fluids. Thus, a combination of both ingredients to form an excellent heat transfer medium that performs as fluid can be comprehended. Choi1 ground-breaking idea of nanofluid by addition of metallic nanoparticles (with size less than 100 nm in diameter) into the conventional fluids like water for the enhancement of the thermal conductivity has revolutionized the engineering and industrial world. Then Buongiorno2 deliberated the characteristics of nanofluid keeping in view the Brownian motion and thermophoresis. The flow of nanofluid with H2O as base fluid over a convectively heated surface is studied by Makinde and Aziz3. The nanofluid flow in an enclosure with impacts of non-isothermal temperature distribution and natural convection was studied by Oztop et al.4. Turkyilmazoglu5 found an exact analytical solution of hydro-magnetic viscous fluid flow past a spongy surface with thermal slip condition. The flow of nanofluids, with water base fluid in a lid-driven cavity with crimped surfaces in attendance of mixed convection, was studied by Cho et al.6. Sheikholeslami and Ganji7 discussed the analytical solution of copper-water nanofluid squeezing flow amid two parallel plates using Homotopy perturbation method. The flow of non-Newtonian fluid flow with the amalgamation of Sodium alginate and Titanium oxide past two coaxial cylinders in a spongy medium was discussed by Hatami and Ganji8. The flow of time-dependent nanofluid by a vertical surface in the attendance of mixed convection and thermal radiation was discussed by Turkyilmazoglu and Pop9. Sheikholeslami et al.10 deliberated analytical solution of nanofluid flow past a spongy channel with effects of magnetohydrodynamics. Ibrahim and Makinde11 inspected the flow of nanofluid by a vertical plate influenced by thermal and solutal stratification. Turkyilmazoglu12 examined the flows of some nanofluids with numerous nanoparticles like copper, silver, copper oxide, titanium oxide and alumina with water as base fluid with two types of temperature boundary conditions. The flow of nanofluid past a penetrable rotating disk in attendance of the magnetohydrodynamics with the impact of entropy generation was conducted by Rashidi et al.13. Lin et al.14 deliberated the flow of pseudo-plastic nanofluid with Marangoni convection flow, variable thermal conductivity and thermal radiation. Hussain et al.15 described the series solutions of the flow of the Casson nanofluid flow with convective heat and mass boundary conditions over an exponentially stretching surface. The flow of 3D viscoelastic nanofluid under the influences of chemical reaction and magnetohydrodynamics was analyzed by Ramzan and Bilal16. Lu et al.17 debated numerically the flow of three-dimensional nanofluid with the binary chemical reaction, gyrotactic microorganism, activation energy and anisotropic slip along with a moving plate. The flow of viscous nanofluid with impacts of motile gyrotactic micro-organisms and nonlinear thermal radiation is deliberated by Ramzan et al.18. Additional effects of chemical reaction with Joule heating and slip boundary condition are also considered. Fewer recent investigations highlighting nanofluids may be found in19,20,21,22,23,24,25.
The movement of an electrically charged fluid owing to a magnetic field is characterized as magnetohydrodynamics (MHD). The idea of MHD got the attention in 1918 as stated by Rossow26, after the coined work of an electromagnetic pump that leads to the definition of Hartmann number. Alfven27 described that an electric current will be produced by an electromotive force (e.m.f.) which is generated by the fluid that is under the influence of a constant magnetic field. Because of this e.m.f., a kind of electric current is induced while the other generates the Lorentz force. Because of the magnetic field, these electric currents produce mechanical forces that alter the fluid’s state of motion and eventually electromagnetic-hydrodynamic wave is produced. Since that time, scientists and researchers have worked on many applications of MHD like MHD generators, metallurgy, MHD pumps’ designs and dispersion of metals, etc. Geophysics does possess the physiognomies of MHD owing to the association of magnetic field and conducting fluid. In the area of planetary and stellar, the problem of MHD convection has vital significance. The flow of Micropolar nanofluid under the influence of MHD, Buoyancy forces, and activation energy with binary chemical reaction accompanied by double stratification is examined by Ramzan et al.28. Lu et al.29 analyzed the flow of MHD 3D Oldroyd-B fluid associated with the impacts of nonlinear thermal radiation, variable thermal conductivity, and homogeneous-heterogeneous reactions analytically. The flow of Jeffrey MHD nanofluid flow with nonlinear radiative heat flux is studied by Ijaz et al.30. Recently, Zhang et al.31 found numerical solution Fractional Oldroyd-B nanofluid between two concentric cylinders using Finite difference technique amalgamated with L1-algorithm and many therein32,33,34,35.
Carbon nanotubes (CNTs) are cylindrical shaped tubes with irreplaceable characteristics like good thermal conductivity, and tremendous potency makes them highly desirable materials in varied applications like microwave amplifier, optics, drug delivery, nanotubes transistors, and prostheses and many other areas36,37,38,39. CNTs are available in the form of single-wall carbon nanotubes (SWCNTs) and multi-wall carbon nanotubes (MWCNTs). Iijima introduced MWCNTs in 1991. Then in 1993, Donald Bethune gave the idea of SWCNTs. Ramasubramaniam et al.40 in his exploration examined that SWCNTs are quite helpful in electrical conductivity applications. Xue41 identifies that composite nanotubes are essential to improve thermal conductivity. The flow of peristaltic nanofluid comprising of SWCNTs and blood is discussed by Nadeem et al.42. The influence of h-h reactions in a 3D flow of CNTs is deliberated by Hayat et al.43. Shah et al.44 inspected the rotating flow of carbon nanotubes under the influence of heat generation/absorption and nonlinear thermal radiation past a linearly stretching surface. Recent studies highlighting nanofluids impacts in various scenarios may be found in33,45,46,47,48,49,50,51,52,53,54.
The literature quoted above reveals that numerous articles are available pertaining to nanofluids with varied geometries but less literature exists relating to nanofluid flows with CNTs over a cone. Further, this exploration becomes unique when above-mentioned characteristics are supported with Joule heating, entropy generation, chemical reaction, Heat generation/absorption, and solutal stratification boundary condition. The solution of the erected model is obtained numerically via bvp4c MATLAB built-in function.
Mathematical Modeling
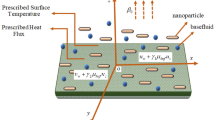
We assume a water based nanofluid flow with CNTs over a vertical cone in a permeable medium. The additional effects accompanied the model are Heat generation/absorption, solutal stratification, Joule heating, chemical reaction with entropy generation. The flow is induced along the x–axis and a magnetic field is applied along the y–axis as shown in Fig. 1. The equations resulting from the above assumptions are modeled as55:
with the corresponding boundary conditions
Here, (μnf, μf), (\({\rho }_{CNT}\), \({\rho }_{f}\)), (β, β*), γ1, B0, αnf, qr, Q0, \({(\rho {c}_{p})}_{nf}\), and \({(\rho {c}_{p})}_{f}\), Dm, Kr, Wc, Dn, (kf, knf, k), hf, (d, e), and V0 represent dynamic viscosity, density, thermal and solutal expansion coefficients, cone half-angle, magnetic field of strength, modified thermal diffusivity, thermal radiation coefficient, Dimensional heat generation/absorption parameter, heat capacities, Brownian diffusion coefficient, rate of chemical reaction, maximum cell swimming speed, diffusivity of microorganisms, thermal conductivity, convective parameter, reference temperature and concentration dimensionless constants and suction/injection parameter respectively.
Table 1 is erected to depict the characteristics of water and CNTs of both types.
Thermal conductivity and effective density of the nanofluid are given by:
The similarity transformations are defined as
Equation (1) is satisfied and equations (3) to (8) take the form
The parameters in non-dimensional form are stated as:
Here, Pr, k1, M, Nr, Rb, Rd, Ec, γ, Sc, Cr, Lb, Pe, δ, B1, and n characterize Prandtl number, Porous parameter, magnetic parameter, buoyancy ratio parameter, Bio-convection Rayleigh number, Radiation parameter, heat generation/absorption parameter, Schmidt number, Chemical reaction parameter, bio-convection Lewis number, Bio-convection constant, Boit number and solutal stratification respectively.
The physical quantities like drag coefficient, local Nusselt and Sherwood numbers, and local density of motile microorganisms are given by:
In dimensionless form, the above physical quantities are evaluated as:
Table 2 shows the resemblance of the present results with Khan et al.56 for numerous estimates of \(\varphi \) in limiting case. An exception concurrence between both results is found.
Entropy Generation
The model representing the entropy generation is given by:
In Eq. (17), entropy is consisting of three terms viz. i) I (heat transfer irreversibility) ii) II (fluid friction irreversibility) and iii) III (diffusion irreversibility). The entropy generation NG is given by:
Here, \({S\prime\prime\prime }_{gen}\) is entropy generation rate and \({S\prime\prime\prime }_{0}\) the characteristic entropy generation rate represented by:
where
Here, Rax, Br, λ, ζ, and α represent Reynold number, Brinkman number, diffusive constant parameter, concentration difference parameter, and temperature difference parameter respectively.
Results and Discussion
This section is dedicated to discuss and anticipate the impacts of various parameters \(0.01\le \varphi \le 0.03\), \(0.4\le M\le 1.0\), \(0.1\le {k}_{1}\le 0.7\), \(0.1\le {{\boldsymbol{v}}}_{{\boldsymbol{0}}}\le 0.3\), \(0.2\le {N}_{r}\le 1.5\), \(0.1\le {R}_{b}\le 0.3\), \(0.5\le {B}_{1}\le 1.5\), \(0.1\le {R}_{d}\le 0.7\), \(0.5\le {S}_{c}\le 1.5\), \(0.1\le n\le 0.5\), \(0.1\le {C}_{r}\le 0.9\), \(0.5\le {P}_{e}\le 0.9\), \(0.5\le {L}_{b}\le 0.7\), \(0.1\le \delta \le 0.5\), \(0.1\le {\alpha }_{c}\le 0.3\), \(0.1\le \lambda \le 0.5\), \(1.0\le {R}_{x}\le 3.0\), \(0.1\le \xi \le 0.5\), on involved distributions. The numerical values of parameters are fixed as given below: \(\varphi =0.01\), \({S}_{c}={B}_{1}=1.0=M={V}_{0}\), \({N}_{r}={P}_{e}={k}_{1}=0.5={L}_{b}\), \({R}_{b}=n={R}_{d}=0.1={C}_{r}=\delta \) and \(\Pr =6.2\) unless stated separately. Figure 2 demonstrates the action of solid volume fraction \(\varphi \) of nanoparticle on axial velocity. The velocity field enhances for augmenting values of the solid volume fraction \(\varphi \) for both nanoparticles. It is also understood that the velocity distribution upsurge rapidly for SWCNT in comparison to MWCNT. Figure 3 is portrayed to depict the impact of the magnetic parameter M on the velocity field. The velocity of the fluid lessens for boosting values of M. It is because the strong Lorentz force that presents resistance to the fluid’s movement that eventually lowers the fluid’s movement. In Fig. 4, the consequence of porous parameter k1 on velocity profile is sketched. It is comprehended that the velocity is a lessening function of k1. Further, the momentum boundary layer for both nanoparticles declines while increasing k1. The influence of suction parameter v0 on axial velocity is shown in Fig. 5. It is perceived that the velocity profile diminishes for boosting estimations of the suction parameter v0. Also, the momentum boundary layer declines for cumulative values of v0 for both SWCNTs and MWCNTs. The buoyancy ratio parameter Nr and bio-convection Rayleigh number Rb effects on axial velocity are examined in Figs 6 and 7. The velocity profile declines with increasing values of Nr and Rb. It is also found that the velocity profile for MWCNT decreases more rapidly than SWCNT in both cases. Figure 8 is illustrated to depict the impact of Biot number B1 on temperature field. An upsurge in temperature of the fluid is visualized for larger estimates of B1 for both types of CNTs. Higher thermal resistance in comparison to the boundary layer inside the cone is witnessed. As a result, temperature of the fluid in the vicinity of the boundary layer is seen. The thermal radiation parameter Rd effect on the temperature distribution is shown in Fig. 9. More heat is generated with the rise in values of Rd. That is why rise in temperature of the fluid is perceived. The outcome of Schmidt number Sc on concentration field is visualized in Fig. 10. The weak concentration of the fluid is seen for higher values of Sc. As the Schmidt number is the quotient of kinematic viscosity to molecular diffusion coefficient small values of molecular diffusion coefficient results in large estimates of Sc that lowers the concentration. Figures 11 and 12 are graphed to comprehend the effect of solutal stratification n and chemical reaction parameter Cr on the concentration of the fluid. It is witnessed that concentration of the fluid is on decline for higher estimates of n and Cr in case of both types of CNTs. Figures 13, 14 and 15 are portrayed to see the impression of bio-convection constant δ, bio-convection Peclet number Pe and bio-convection Lewis number Lb on the density of motile microorganism respectively. It is observed that density of motile microorganism is on decline for all three parameters for both types of nanoparticles. Figures 16 to 19 illustrate the impression of different physical parameters versus the entropy generation number NG. From Fig. 16, it is seen that increasing the temperature difference parameter α, the entropy generation number NG decreases for both nanoparticles. Figures 17 and 18 demonstrate the effects of concentration difference ζ and Reynold number Rax on the entropy generation number. The entropy generation profile enhances with enhancing the value of Rax and ζ for both nanoparticles. The local entropy generation increases for growing estimates of the diffusive constant parameter λ for both SWCNT and MWCNT which is displayed in Fig. 19.
Table 3 is erected for Skin friction coefficient versus numerous estimates of the arising parameters in the defined mathematical model. It is comprehended that Skin friction parameter rises versus suction parameter and solid volume fraction. Likewise, it decreases for the values of the magnetic parameter, bio-convection Rayleigh number, and porous medium. The values of Nusselt number for various values of involved parameters are given in Table 4. It is witnessed that Nusselt number is decreasing function of magnetic parameter and it enhances for radiation parameter, Biot number, and solid volume fraction. Table 5 is erected to witness the behavior of parameters versus the Sherwood number. For the growing estimates of the buoyancy ratio parameter and concentration stratification, Sherwood number is on the decline and grows versus numerical values of the Schmidt number and chemical reaction parameter. To see the impact of certain parameters on Motile density number, Table 6 is formed. It is witnessed that Motile density number escalates for the values of microorganism concentration difference parameter and Peclet number. Whereas it deteriorates for increasing estimates of Rayleigh number.
Concluding Remarks
The aqueous base nanofluid flow with both types of CNTs (SWCNT and MWCNT) over a vertical cone accompanied by impacts of a gyrotactic microorganism containing motile organisms and solutal stratification in a porous medium is deliberated numerically here. The analysis is performed in the presence of heat generation/absorption, Joule heating, and chemical reaction. An additional effect of Entropy generation is also taken into account. The salient characteristics of the modeled problem are:
-
With an increase in estimates of Peclet number, Motile density number enhances.
-
For both CNTs, the velocity of the fluid escalates versus growing values of suction and magnetic parameters.
-
The fluid’s temperature is on the rise for the estimates of the buoyancy ratio parameter.
-
For both types of CNTs, the concentration of the fluid is on the decrease in the values of solutal stratification.
-
For the growth estimates of the buoyancy ratio parameter, Sherwood number is on the decline and grows versus numerical values of chemical reaction parameter.
-
Skin friction parameter rises for solid volume fraction.
-
Nusselt number is decreasing the function of the magnetic parameter.
References
Choi, S. U. S. Enhancing thermal conductivity of fluids with nanoparticles. ASME MD 231, FED, 66, 99–105 (1995).
Buongiorno, J. Convective transport in nanofluids. ASME J. Heat Transfer 128, 240–250 (2006).
Makinde, O. D. & Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 50, 1326–1332 (2011).
Oztop, H. F., Abu-Nada, E., Varol, Y. & Al-Salem, K. Computational analysis of non-isothermal temperature distribution on natural convection in nanofluid filled enclosures. Superlattice. Microst. 49, 453–467 (2011).
Turkyilmazoglu, M. Exact analytical solutions for heat and mass transfer of MHD slip flow in nanofluids. Chem. Eng. Sci. 84, 182–187 (2012).
Cho, C. C., Chen, C. L. & Chen, C. K. Mixed convection heat transfer performance of water-based nanofluids inlid-driven cavity with wavy surfaces. Int. J. Therm. Sci. 68(6), 181–190 (2013).
Sheikholeslami, M. & Ganji, D. D. Heat transfer of Cu–water nanofluid flow between parallel plates. Powder Technol. 235, 873–879 (2013).
Hatami, M. & Ganji, D. D. Heat transfer and flow analysis for SA-TiO2 non-Newtonian nanofluid passing through the porous media between two coaxial cylinders. J. Mol. Liq. 188, 155–161 (2013).
Turkyilmazoglu, M. & Pop, I. Heat and mass transfer of unsteady natural convection flow of some nanofluids past a vertical infinite flat plate with radiation effect. Int. J. Heat Mass Transf. 59, 167–171 (2013).
Sheikholeslami, M., Hatami, M. & Ganji, D. D. Analytical investigation of MHD nanofluid flow in a semi-porous channel. Powder Technol. 246, 327–336 (2013).
Ibrahim, W. & Makinde, O. D. The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate. Comput. Fluids. 86, 433–441 (2013).
Turkyilmazoglu, M. Unsteady convection flow of some nanofluids past a moving vertical flat plate with heat transfer. ASME J. Heat Transfer. 136, 031704 (2013).
Rashidi, M. M., Abelman, S. & Mehr, N. F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 62, 515–525 (2013).
Lin, Y., Zheng, L. & Zhang, X. Radiation effects on Marangoni convection flow and heat transfer in pseudo-plastic non-Newtonian nanofluids with variable thermal conductivity. Int. J. Heat Mass Transf. 77, 708–716 (2014).
Hussain, T., Shehzad, S. A., Alsaedi, A., Hayat, T. & Ramzan Flow of Casson nanofluid with viscous dissipation and convective conditions: a mathematical model. J. Cent. South Uni. 22(3), 1132–1140 (2015).
Ramzan, M. & Bilal, M. Three-dimensional flow of an elastico-viscous nanofluid with chemical reaction and magnetic field effects. J. Mol. Liq. 215, 212–220 (2016).
Lu, D., Ramzan, M., Ullah, N., Chung, J. D. & Farooq, U. A numerical treatment of radiative nanofluid 3D flow containing gyrotactic microorganism with anisotropic slip, binary chemical reaction and activation energy. Sci. Rep. 7(1), 17008 (2017).
Ramzan, M., Chung, J. D. & Ullah, N. Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int. J. Mech. Sci. 130, 31–40 (2017).
Ramzan, M., Sheikholeslami, M., Saeed, M. & Chung, J. D. On the convective heat and zero nanoparticle mass flux conditions in the flow of 3D MHD Couple Stress nanofluid over an exponentially stretched surface. Sci. Rep. 9(1), 562 (2019).
Li, Z., Shafee, A., Ramzan, M., Rokni, H. B. & Al-Mdallal, Q. M. Simulation of natural convection of Fe 3 O 4-water ferrofluid in a circular porous cavity in the presence of a magnetic field. Eur. Phys. J. Plus. 134(2), 77 (2019).
Suleman, M. et al. A numerical simulation of Silver–Water nanofluid flow with impacts of Newtonian heating and homogeneous–heterogeneous reactions past a nonlinear stretched cylinder. Symmetry 11(2), 295 (2019).
Li, Z. et al. Influence of adding nanoparticles on solidification in a heat storage system considering radiation effect. J. Mol. Liq. 273, 589–605 (2019).
Suleman, M. et al. Entropy Analysis of 3D non-Newtonian MHD nanofluid flow with nonlinear thermal radiation past over exponential stretched surface. Entropy. 20(12), 930 (2018).
Lu, D. M., Ramzan, S., Ahmad, A. & Shafee, M. Suleman, Impact of nonlinear thermal Radiation and Entropy Optimization Coatings with Hybrid Nanoliquid Flow Past a curved stretched surface. Coatings. 8(12), 430 (2018).
Li, Z. et al. Numerical approach for nanofluid transportation due to electric force in a porous enclosure. Microsyst Technol. 1–14 (2018).
Rossow, V. J. On flow of electrically conducting fluids over a flat plate in the presence of a transverse magnetic field. Tech. Report Arch. & Image Lib. (1958).
Alfvén, H. Existence of electromagnetic-hydrodynamic waves. Nature. 150(3805), 405 (1942).
Ramzan, M., Ullah, N., Chung, J. D., Lu, D. & Farooq, U. Buoyancy effects on the radiative magneto Micropolar nanofluid flow with double stratification, activation energy and binary chemical reaction. Sci. Rep. 7(1), 12901 (2017).
Lu, D. et al. On three-dimensional MHD Oldroyd-B fluid flow with nonlinear thermal radiation and homogeneous–heterogeneous reaction. J. Braz. Soc. Mech. Sci. & Eng. 40(8), 387 (2018).
Khan, M. I., Hayat, T., Waqas, M., Alsaedi, A. & Khan, M. I. Effectiveness of radiative heat flux in MHD flow of Jeffrey-nanofluid subject to Brownian and thermophoresis diffusions. J. Hydro. 1–8 (2019).
Yan, Z., Jiang, J. & Bai, Y. MHD flow and heat transfer analysis of fractional Oldroyd-B nanofluid between two coaxial cylinders. Compt. & Math. Appl. (2019).
Li, Z., Shafee, A., Ramzan, M., Rokni, H. B. & Al-Mdallal, Q. M. Simulation of natural convection of Fe3O4-water ferrofluid in a circular porous cavity in the presence of a magnetic field. Eur. Phys. J. Plus 134(2), 77 (2019).
Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comp. Meth. Appl. Mech. Eng. 344, 319–333 (2019).
Turkyilmazoglu, M. MHD natural convection in saturated porous media with heat generation/absorption and thermal radiation: closed-form solutions. Arch. Mech. 70(1) (2019).
Turkyilmazoglu, M. A note on the induced flow and heat transfer due to a deforming cone rotating in a quiescent fluid. J. Heat Trans. 140(12), 124502 (2018).
Khan, U., Ahmed, N. & Mohyud-Din, S. T. Numerical investigation for three dimensional squeezing flow of nanofluid in a rotating channel with lower stretching wall suspended by carbon nanotubes. Appl. Therm. Eng. 113, 1107–1117 (2017).
Hayat, T., Haider, F., Muhammad, T. & Alsaedi, A. On Darcy-Forchheimer flow of carbon nanotubes due to a rotating disk. Int. J. Heat Mass Transfer. 112, 248–254 (2017).
Rahmati, A. R. & Reiszadeh, M. An experimental study on the effects of the use of multi-walled carbon nanotubes in ethylene glycol/water-based fluid with indirect heaters in gas pressure reducing stations. Appl. Therm. Eng. 134, 107–117 (2018).
Shahzadi, I., Sadaf, H., Nadeem, S. & Saleem, A. Bio-mathematical analysis for the peristaltic flow of single wall carbon nanotubes under the impact of variable viscosity and wall properties. Comput. Meth. Prog. Bio. 139, 137–147 (2017).
Ramasubramaniam, R., Chen, J. & Liu, H. Homogeneous carbon nanotube/polymer composites for electrical applications. Appl. Phys. 83, 2928–2930 (2003).
Xue, Q. Z. Model for thermal conductivity of carbon nanotube-based composites. Phys. B. 368, 302–307 (2005).
Nadeem, S. Single wall carbon nanotube (SWCNT) analysis on peristaltic flow in an inclined tube with permeable walls. Int. J. Heat Mass Transfer. 97, 794–802 (2016).
Hayat, T., Ahmed, S., Muhammad, T., Alsaedi, A. & Ayub, M. Computational modeling for homogeneous-heterogeneous reactions in three-dimensional flow of carbon nanotubes. Results. Phys. 7, 2651–2657 (2017).
Muhammad, S., Ali, G., Shah, Z., Islam, S. & Hussain, S. The rotating flow of magneto hydrodynamic carbon nanotubes over a stretching sheet with the impact of non-linear thermal radiation and heat generation/absorption. Appl. Sci. 8(4), 482 (2018).
Sheikholeslami, M. Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method. Compt. Meth. Appl. Mech. Eng. 344, 306–318 (2019).
Sheikholeslami, M., Barnegat., M., Gerdroodbary, R. M., Shafee, A. & Zhixiong, L. Application of Neural Network for estimation of heat transfer treatment of Al2O3-H2O nanofluid through a channel. Compt. Meth. Appl. Mech. Eng. 344, 1–12 (2019).
Sheikholeslami, M. & Mahian, O. Enhancement of PCM solidification using inorganic nanoparticles and an external magnetic field with application in energy storage systems. J. Clean. Prod. 215, 963–977 (2019).
Sheikholeslami, M., Shafee, A., Zareei, A., Haq, R. U. & Li, Z. Heat transfer of magnetic nanoparticles through porous media including exergy analysis. J. Mol. Liq. 279, 719–732 (2019).
Sheikholeslami, M., Jafaryar, M., Shafee, A. & Li, Z. Simulation of nanoparticles application for expediting melting of PCM inside a finned enclosure. Phys. A: Stat. Mech. Appl. 523, 544–556 (2019).
Sheikholeslami, M. & Sadoughi, M. K. Simulation of CuO-water nanofluid heat transfer enhancement in presence of melting surface. Int. J. Heat and Mass Trans. 116, 909–919 (2018).
Sheikholeslami, M. & Shehzad, S. A. Simulation of water based nanofluid convective flow inside a porous enclosure via non-equilibrium model. Int. J. Heat Mass Trans. 120, 1200–1212 (2018).
Sheikholeslami, M. & Zeeshan, A. Analysis of flow and heat transfer in water based nanofluid due to magnetic field in a porous enclosure with constant heat flux using CVFEM. Compt. Meth. Appl. Mech. Eng. 320, 68–81 (2017).
Sheikholeslami, M., Shafee, A., Ramzan, M. & Li, Z. Investigation of Lorentz forces and radiation impacts on nanofluid treatment in a porous semi annulus via Darcy law. J. Mol. Liq. 272, 8–14 (2018).
Sheikholeslami, M. & Rokni, H. B. Numerical simulation for impact of Coulomb force on nanofluid heat transfer in a porous enclosure in presence of thermal radiation. Int. J. Heat Mass Trans. 118, 823–831 (2018).
Sreedevi, P., Reddy, P. S. & Chamkha, A. J. Magneto-hydrodynamics heat and mass transfer analysis of single and multi-wall carbon nanotubes over vertical cone with convective boundary condition. Int. J. Mech. Sci. 135, 646–655 (2018).
Khan, W. A., Khan, Z. H. & Rahi, M. Fluid flow and heat transfer of carbon nanotubes along a flat plate with Navier slip boundary. Appl Nanosci. 4(5), 633–641 (2014).
Acknowledgements
This research was funded by Zayed University research fund, Abu Dhabi, UAE. The funder has no role in the conceptualization, design, data collection, analysis, decision to publish, or preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
M.R. wrote the main manuscript text, M.M. simulate the problem and F.H. prepared all figures and tables.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ramzan, M., Mohammad, M. & Howari, F. Magnetized suspended carbon nanotubes based nanofluid flow with bio-convection and entropy generation past a vertical cone. Sci Rep 9, 12225 (2019). https://doi.org/10.1038/s41598-019-48645-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-48645-9
This article is cited by
-
Effects of surface roughness and thermal radiation on mixed convective (GO–MoS2/H2O–C2H6O2) hybrid nanofluid flow past a permeable cone
Indian Journal of Physics (2022)
-
Upshot of heterogeneous catalysis in a nanofluid flow over a rotating disk with slip effects and Entropy optimization analysis
Scientific Reports (2021)
-
Irreversibility minimization analysis of ferromagnetic Oldroyd-B nanofluid flow under the influence of a magnetic dipole
Scientific Reports (2021)
-
Thermal and Fluid Dynamics Performance of MWCNT-Water Nanofluid Based on Thermophysical Properties: An Experimental and Theoretical Study
Scientific Reports (2020)
-
Heat transfer exaggeration and entropy analysis in magneto-hybrid nanofluid flow over a vertical cone: a numerical study
Journal of Thermal Analysis and Calorimetry (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.