Abstract
TiO2 anatase is considered to play a significant importance in energy and environmental research. However, for developing artificial photosynthesis with TiO2, the major drawback is its large bandgap of 3.2 eV. Several non-metals have been used experimentally for extending the TiO2 photo-absorption to the visible region of the spectrum. It’s therefore of paramount importance to provide theoretical guidance to experiment about the kind of defects that are thermodynamically stable at a realistic condition (e.g. Temperature (T), oxygen partial pressure (\({{\boldsymbol{p}}}_{{{\bf{O}}}_{{\bf{2}}}}\)), doping). However, disentangling the relative stability of different types of defects (viz. substitution, interstitial, etc.) as a function of charge state and realistic T, \({{\boldsymbol{p}}}_{{{\bf{O}}}_{{\bf{2}}}}\) is quite challenging. We report here using state-of-the-art first-principles based methodologies, the stability and meta-stability of different non-metal dopants X (X = N, C, S, Se) at various charge states and realistic conditions. The ground state electronic structure is very accurately calculated via density functional theory with hybrid functionals, whereas the finite T and \({{\boldsymbol{p}}}_{{{\bf{O}}}_{{\bf{2}}}}\) effects are captured by ab initio atomistic thermodynamics under harmonic approximations. On comparing the defect formation energies at a given T and \({{\boldsymbol{p}}}_{{{\bf{O}}}_{{\bf{2}}}}\) (relevant to the experiment), we have found that Se interstitial defect (with two hole trapped) is energetically most favored in the p-type region, whereas N substitution (with one electron trapped) is the most abundant defect in the n-type region to provide visible region photo-absorption in TiO2. Our finding validates that the most stable defects in X doped TiO2 are not the neutral defects but the charged defects. The extra stability of \({({\bf{S}}{\bf{e}}{\bf{O}})}_{{\bf{O}}}^{+{\bf{2}}}\) is carefully analyzed by comparing the individual effect of bond-making/breaking and the charge carrier trapping energies.
Similar content being viewed by others
Introduction
TiO2 has attracted worldwide research sensation in the past few decades because of its unique properties and potential applications as a photo-catalyst1,2,3,4,5,6. Anatase is the technologically most relevant polymorph of TiO27,8,9,10. However, owing to its large bandgap (~3.2 eV), it absorbs only ultra-violet light (λ < 400 nm) and shows almost no response to visible and near infra-red light (i.e. 400 ≤ λ ≤ 1400 nm). Hence, reducing the band gap of TiO2 to coincide with the visible spectrum is an active area of research.
Doping-mediated modulation of the band gap is one of the most pragmatic approaches adopted in the pursuit to improve photo-absorption of TiO2 in the visible region11. Various dopants viz. transition metals12,13,14,15, noble metals16,17, charge-compensated and uncompensated co-doped elements18,19 have been reported in the past. However, these metal dopants often act as recombination centre due to their capacity to induce trapping levels in the band gap and reduce a significant amount of photo-excited carriers9.
To avoid such additional trapping levels inside the band gap region, non-metal doping is suggested as an alternative strategy to improve visible-light absorption5,20,21,22,23,24,25,26. Various non-metal dopants viz. N27,28,29,30, C31,32, S26,33,34, Se35,36 have already been experimentally reported. However, despite significant amount of research are done both experimentally and theoretically on this system, there exists a lot of controversy relating to most preferred defect site31,32. Moreover, it’s still an open question concerning the stability of various types of defects as a function of charge state at realistic conditions (e.g. Temperature (T), oxygen partial pressure (\({p}_{{{\rm{O}}}_{2}}\)) and doping (doping is considered as means of fixing the chemical potential of the electrons (μe))). Note that the formation energy of one isolated defect can be reduced significantly by several eVs, when the charge carriers (holes or electrons) are available in the material. Moreover, charge-carrier doping (either accidental or intentional) can strongly influence the material’s surface properties37. Thus, disentangling the relative stability of different types of charged defects in enhancing photo-catalytic action is quite challenging. It’s therefore of profound importance to provide theoretical guidance to experiment to address the stability of charges. However, until date, theoretical calculations are limited to neutral defects only in TiO2 and do not address clearly the case of charged defects.
This motivates us to revisit the bulk anatase form of TiO2 to elucidate the role of non-metal dopants as a function of charge at a realistic condition. We have used state-of-the-art density functional theory (DFT) with hybrid functionals combined with ab initio atomistic thermodynamics approach38,39. We have modeled non-metal (X) doped TiO2, assuming various types of defect possibilities: (i) the non-metal X can replace O atom making a substitutional defect (X)O, (ii) the non-metal X can form interstitial defects (XO)O defect, and (iii) combination of both (i) and (ii) i.e. one X is replacing one O forming substitutional defect, while at the same time one additional X is present as an interstitial at the same site. The latter is denoted as (X2)O defect (see Fig. 1). The experimental evidences of the stability and existence of some of the configurations (X)O, (XO)O, (X2)O are confirmed via XPS studies34,40,41,42,43,44. It is also noted that, we have considered the case, where we have taken substitution at O-site only. However, S and Se non-metal dopants also have a possibility to substitute at Ti-site. The substitution at Ti site is already studied well45, due to which we have limited our study to O-site only. In this article we, therefore, provide an exhaustive study on the relative stability of different types of charged X-related defects (vide infra, [(X)O]q, [(XO)O]q and [(X2)O]q with X = N, C, S, Se; q = −2, −1, 0, +1, +2, etc.) in TiO2 anatase at various realistic conditions. However, this theoretical work aims on the thermodynamic stability of dopants under realistic temperatures and oxygen partial pressures, while the experimental results sometimes rely on kinetic stability under practical growth conditions, such as the heating rate, holding time and experimental atmosphere. The latter study is beyond the scope of the present paper. Nevertheless, providing a phase diagram by accurate estimation of free energy of formation is very useful for the experimentalists in many instances. Seeing such phase diagram one can get a qualitative information regarding the possible relevant defect states of that concerned material at a given temperature and pressure even if the stability might get changed over time by considering the kinetic effect. Further, we have also given a quantitative analysis to address the underlying reason for extra stability of a specific defect at a given environmental condition by comparing the contribution of bond-making/breaking and charge carrier trapping energies.
Results and Discussion
Most stable defect configurations
We have determined the energetically most favorable geometric configurations (X)O, (XO)O and (X2)O defects optimized at various charge states \(q=-\,2,-\,1,0,+\,1,+\,2\) for various non-metal dopants (X = N, C, S, Se) in the Ti16O32 framework. In our supercell of Ti16O32 the geometric configurations XTi16O31□1, XTi16O32 and X2Ti16O31□1 represent respectively (X)O, (XO)O and (X2)O. For this purpose, we have adopted an iterative strategy46: starting with the Ti16O32 supercell, we first identified the most favorable sites for the O-□ by scanning over all possible sites. We find that, since they belong to the same symmetry point, all the atomic sites are equivalent. Hence, we can substitute non-metal dopants at any O-site in the system. For interstitial and complex interstitial configurations, we simply consider one oxygen atom in the Ti16O32 framework and scan its all surrounding positions. The configuration having minimum energy is taken as a final structure for studying defects. Note that for all geometry relaxations we have used PBE functional as the difference in geometry optimized by PBE and HSE06 are insignificant. Therefore, on top of the final relaxed geometry, we have performed HSE06 calculations to determine the correct energetics associated with those optimized structures.
Validation of DFT functionals
To ensure that our findings are not an artifact of the chosen treatment of the xc-functional, we have first thoroughly benchmarked the xc-functionals. Note that using PBE, the band gap of TiO2 is quite underestimated from the experimental value [PBE (2.12 eV), Expt. (3.2 eV)]. On varying the “Hubbard parameter U” one can reproduce the experimental band gap with PBE + U approach. With U = 6.3 eV, we could reproduce the band gap to be 3.2 eV. However, the energetics of PBE + U to estimate defect formation energy of a single oxygen vacancy at various charge states doesn’t match with respect to advanced hybrid xc-functional HSE06 (see Supplementary Information; Figs S1 and S2). Note that, the default α = 0.25 value of HSE06 is unable to reproduce the exact experimental band gap. We find that a proportion of 22% Hartree Fock exchange with 78% PBE exchange produces the experimental band-gap (3.2 eV) for HSE06. In view of this, the accuracy of HSE06 with α = 0.22 needs also to be validated. We thus further validate HSE06 xc-functional (with α = 0.22) with respect to experimentally observed optical transition of various (X)O (X = N, C, S, Se) (i.e. X substituted at oxygen vacancy defects) in TiO2. The optical transitions associated with the process \({{\rm{X}}}_{{\rm{O}}}^{0}+{\rm{h}}\nu \to {{\rm{X}}}_{{\rm{O}}}^{+}+{{\rm{e}}}^{-}\) are shown in (Fig. 2) by forming a configuration co-ordinate diagram. To do this, we have taken 3 different geometries of XO (optimized for charges = 0, +1, +2). Then, we have taken intermediate structure between geometry 1 and geometry 2 (simply by averaging the atomic positions of the geometry 1 and 2). The same is then repeated for the geometry 2 and geometry 3. In this way, we have achieved the 5 intermediate relaxed structure. We then linearly interpolate the relaxed structures in the ground and the constrained state by using five intermediate structures and calculate the formation energies using HSE06 xc-functional (with α = 0.22). A parabolic fit of the formation energies of these five intermediate geometries is thus obtained. The same is then repeated for the other charge states (+2 is not shown here). Now the possible transitions are illustrated as shown in Fig. 2. Knowing the optical transitions, the corresponding optical spectra can thus be computed. The details of this state-of-the-art theoretical spectroscopy techniques are explained by Rinke et al.47. The process involved absorption of photon and emission of electron. The Peak positions are determined by assuming that the atoms in the vicinity of the defect do not have time to relax during the transition from charge state q to charge state q′ = q ± 1(Franck-Condon principle). Thus, the difference in formation energies in charge states q and q′ gives the absorption and emission energy. The difference in the value of absorption and emission peaks arises due to difference in geometry relaxation for both the charge states q and q′. The amount of energy lost during relaxation to the new equilibrium position is the Franck-Condon shift. We have found that XO leads to sub-bandgap optical transitions centred at 2.8 eV (442 nm) for N, 2.04 eV (607 nm) for C, 2.32 eV (534 nm) for S and 1.92 eV (645 nm) for Se respectively. These results are in good agreement with the experimental observations in which sizeable absorption occurs at visible region (400–700 nm)48,49,50,51. Note that, we have also tried the same for Phosphorous substitution at O-site in TiO2 anatase. Unfortunately, we have got the response in infra-red region (1.48 eV) (see Supplementary Information; Fig. S6). In view of this, we have not considered it for further study. Therefore, this validates that our HSE06 xc-functional with (α = 0.22) is sufficiently accurate to ensure correct energetics at various charge defects in TiO2.
Formation energy of charged defects
We have now considered three types of defects viz. (X)O, (XO)O and (X2)O with X = N, C, S, Se to understand the most stable defect with specific charge state q at a given T and \({p}_{{{\rm{O}}}_{2}}\). The explicit dependence on T and \({p}_{{{\rm{O}}}_{2}}\) is introduced by employing the concept of ab initio atomistic thermodynamics39. We address the stability of the substitutional and interstitial configurations of N, C, S, and Se dopants in TiO2 by computing formation energies as a function of chemical potentials of the respective species viz. μO, μN, μC, μS, μSe as discussed in the following sections. Here the doping is considered as varying the chemical potential of electrons μe. In the following sections, we will use \({{\rm{E}}}_{{\rm{f}}}[({\rm{X}}{)}_{{\rm{O}}}^{q}]\), \({{\rm{E}}}_{{\rm{f}}}[({\rm{XO}}{)}_{{\rm{O}}}^{q}]\), \({{\rm{E}}}_{{\rm{f}}}[{({{\rm{X}}}_{2})}_{{\rm{O}}}^{q}]\) as the formation energies of (X)O, (XO)O and (X2)O related defects at a charge state q for X = N, C, S, Se. Similarly, E[XTi16O31]q, E[XTi16O32]q and E[X2Ti16O31]q are the total DFT energies (HSE06) at a charge state q of the respective supercells. E[Ti16O32]0 represents the total DFT energy (HSE06) of the pristine supercell at neutral charge state. E[N2] and E[O2] are the total DFT (HSE06) energies of N2 and O2 molecules respectively.
N-related dopant
The formation energy of (N)O in charge state q is given by:
where, μe is the chemical potential of the electron referenced to the valence-band maximum (VBM) of pristine neutral supercell. ΔV accounts for the core level alignment between (Ti16O31)q and (Ti16O32)0.
Therefore, ΔμO can be written as a function of \((T,{p}_{{{\rm{O}}}_{2}})\) [see details of this methodology in ref.52].
where m is the mass, \( {\mathcal M} \) is the spin multiplicity, and σ is the symmetry number.
The formation energy for interstitial N i.e., (NO)O is given by:
As explained above, here ΔV represents the core level alignment between (NTi16O32)q and (Ti16O32)0. Similarly, formation energy for N complex in which interstitial N sharing a lattice site with (N)O i.e., (N2)O is given by:
where ΔV is core level alignment between (N2Ti16O31)q and (Ti16O32)0. The calculated formation energies of charged and neutral defects depend on the selected values for μTi and μO. The chemical potential of O and Ti must satisfy the stable growth condition for TiO2.
where ΔHf(TiO2) is the enthalpy of formation for TiO2 and its value is −9.73 eV53. Next, we present results of the formation energies for O-poor, O-intermediate and O-rich conditions. The O-rich condition corresponds to ΔμO = 0, ΔμTi = −9.73 eV (obtained from Eq. 6). Under extreme O-poor condition (Ti-rich condition) the growth of Ti2O3 becomes favorable. As a result, ΔμTi is estimated by the formation of Ti2O3.
where ΔHf(Ti2O3) is the enthalpy of formation for Ti2O3 and its value is −15.35 eV53. From above two equations (Eqs 6 and 7) we can write ΔμTi = 2ΔHf(Ti2O3) − 3ΔHf(TiO2) and ΔμO = −ΔHf(Ti2O3) + 2ΔHf(TiO2). Solving this we get, under O-poor condition ΔμTi = −1.51 eV and ΔμO = −4.11 eV. Defect formation energy depends on the chemical potential of Ti, O and the doped impurities. Note that to avoid the precipitation of the host elements, the chemical potential μX must have a constraint that ΔμX ≤ 0. We find that under O-poor conditions (i.e. Ti-rich) ΔμX = 0 and ΔμO = −4.1 eV. Under O-rich conditions ΔμO = 0 and μN is estimated by the formation of N2 molecule, i.e., ΔμN = 0; while the limit of the other impurities X (excluding N) (X = C, S, Se) are determined by the formation of the corresponding oxides i.e.,
The chemical potentials ΔμX for X = C, S, Se are, therefore, determined by formation enthalpy of CO2 (ΔHf = −4.07 eV), SO3 (ΔHf = −4.101 eV) and SeO2 (ΔHf = −2.336 eV) respectively54. Note that we have chosen only those oxides which are used as precursor in experiments. With this background, we report now the most stable charged impurities for various non-metals X.
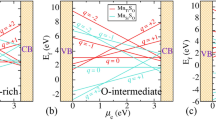
Formation energy is shown as a function of μe for (N)O, (NO)O, (N2)O at various charge states for O-poor, O-rich and O-intermediate limit as shown in Fig. 3. As we have explained, O-poor (Fig. 3a) and O-rich (Fig. 3b) represent two of the extreme possible limit of oxygen concentration (Since ΔμO is a function of T and \({p}_{{{\rm{O}}}_{2}}\), at a given T = 300 K, O-poor and O-rich conditions respectively correspond to a pressure \({p}_{{{\rm{O}}}_{2}}={10}^{-129}\) and 109 atm), while the O-intermediate (see Fig. 3c) represents an experimental condition.
Formation energy for N-related defects in anatase Ti16O32 (a) O-poor limit ΔμO = −4.1 eV and ΔμN = 0 eV. (b) O-rich limit ΔμO = 0 eV and ΔμN = 0 eV. (c) O-intermediate (Experimental growth condition) ΔμO = −1.5 eV. (d) Phase diagram for N-related defects (N)O, (NO)O, (N2)O. Here, on x-axis ΔμO is varied in accordance with the corresponding T and \({p}_{{{\rm{O}}}_{2}}\). On y-axis μe is varied from valence band maximum to conduction band minimum of the TiO2. On z-axis the negative \({{\rm{E}}}_{{\rm{f}}}(T,{p}_{{{\rm{O}}}_{2}})\) values are plotted so that only the most stable phases are visible from the top. The region within the rectangular red lines represents the experimentally relevant conditions at T = 848 K with a realistic \({p}_{{{\rm{O}}}_{2}}\) range.
The intersection of the formation energies [e.g. 0/−1, +1/−1, +2/−1 etc.] for the different charge states correspond to the thermodynamic transition levels. Note that N has one electron less than O in the valence shell. Therefore, (N)O in TiO2 is expected to act as an acceptor level. It can be stable either in \({({\rm{N}})}_{{\rm{O}}}^{0}\) or \({({\rm{N}})}_{{\rm{O}}}^{-}\) charge states. At a lower μe i.e., near valence band maximum (VBM) \({({\rm{N}})}_{{\rm{O}}}^{0}\) is stable and for a larger value of μe (i.e., in the upper part near the conduction band minimum (CBm)) \({({\rm{N}})}_{{\rm{O}}}^{-}\) is stable (see Fig. 3). Since, Nitrogen will act as an electron acceptor because it has one electron less than oxygen, it is more feasible at higher values of μe i.e., n-type doping. Our key conclusion from calculated formation energies indicate that (N)O is the prevalent defect for μe values near CBm for the O-poor and O-intermediate condition. The thermodynamic transition level (0/−1) is located at μe = 1.50 eV above the VBM, which indicates that (N)O is a deep acceptor. The formation energies of (N)O under O-poor condition is rather high and it is even higher under O-intermediate and O-rich condition. Therefore (N)O is not suitable for p-type doping in TiO2. This result is similar to the behavior of (N)O in ZnO55 and SrTiO356, indicating that (N)O cannot give p-type conductivity in TiO2. To mimic the experimental growth condition, i.e. \({p}_{{{\rm{O}}}_{2}}=2\times {10}^{5}\,{\rm{Torr}}\) and T = 575 °C, we have obtained the corresponding value of ΔμO = −1.5 eV using Eq. 2. The stability of (N)O at this value of ΔμO (see Fig. 3c) is well in agreement with previous findings28 of Verley et al.
In (NO)O defect, N forms a strong bond with a O atom in the TiO2 lattice so that in the relaxed configuration interstitial N shares the same site as that of O atom. (NO)O introduces a state in the band gap that is partially occupied with one electron. According to the Pauli’s exclusion principle, maximum two electrons can be filled in one state. Hence, there are possibilities of removal and addition of electrons, resulting in \({({\rm{NO}})}_{{\rm{O}}}^{+}\) and \({({\rm{NO}})}_{{\rm{O}}}^{-}\) charge states. \({({\rm{NO}})}_{{\rm{O}}}^{+}\) is stable for a smaller value of μe near VBM (p-type doping) and \({({\rm{NO}})}_{{\rm{O}}}^{-}\) is more significant for a larger value of μe near CBm (n-type doping).
We also find that interstitial N can form a complex with (N)O in the form of (N2)O split interstitial. (N2)O has a deficiency of one electron than (NO)O, so (N2)O should be stable as \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{+2}\) or \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{0}\). \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{+2}\) is energetically preferable for the lower part of the band gap near VBM and \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{0}\) is preferable for the upper part of the band gap near CBm.
Now, we can summarize the whole information from a phase diagram where negative z-axis corresponds to formation energy as shown in Fig. 3d. Since we are visualizing from the top, we are limited to see only the most negative values i.e., we see only the most stable phases. On x-axis, we have ΔμO varied from O-poor to O-rich conditions. On y-axis, we have μe referenced to VBM. Among all the three possible configurations, we observed from Fig. 3d, \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{+2}\) is the most stable defect state near VBM (p-type doping). In n-type doping, \({({\rm{N}})}_{{\rm{O}}}^{-1}\) is the most stable defect state near CBm under both O-poor and O-intermediate while under O-rich \({({\rm{NO}})}_{{\rm{O}}}^{-1}\) is stable. The rectangular box is showing the experimentally feasible region at T = 848 K with a viable pressure range.
C-related dopant
Similarly for Carbon (C) related defects, we have considered three configurations: Carbon substituted oxygen (C)O, Carbon as interstitial (CO)O, Interstitial carbon sharing a lattice site with (C)O forming (C2)O. The formation energy can be calculated in a similar way for all the three configurations using either C or CO2 as a precursor. In either case we have checked that the results are same. To use CO2 as the precursor, we have used the following formula to estimate E[C]:
The same can be calculated directly from DFT total energy from a supercell of C8. The equations related to the formation energy of C related defects in charge state q are given in Supplementary Information. In Fig. 4 we have shown the variation of formation energy as a function of μe for (C)O, (CO)O, (C2)O at various charge states under O-poor, O-rich and O-intermediate conditions. We know from the electronic configuration of C that it has two electrons less than O in the valence shell. Therefore, (C)O in TiO2 is expected to act as an acceptor and be stable in either the \({({\rm{C}})}_{{\rm{O}}}^{0}\), \({({\rm{C}})}_{{\rm{O}}}^{-1}\) and \({({\rm{C}})}_{{\rm{O}}}^{-2}\) charge states. In (C)O defect, at a lower values of μe i.e., near VBM \({({\rm{C}})}_{{\rm{O}}}^{0}\) is stable and for larger values of μe (i.e., in the upper part near the CBm) \({({\rm{C}})}_{{\rm{O}}}^{-2}\) is stable (see Fig. 4) for all the three conditions. Our main concern is near CBm as it is an acceptor dopant.
Formation energy for C-related defects in anatase Ti16O32 (a) O-poor limit ΔμO = −4.1 eV and ΔμC = 0 eV. (b) O-rich limit ΔμO = 0 eV and ΔμC = −4.07 eV. (c) O-intermediate (Experimental growth condition) ΔμO = −1.5 eV. (d) Phase diagram for C-related defects (C)O, (CO)O, (C2)O. The region within the rectangular red lines represents the experimentally relevant conditions at T = 848 K with a realistic \({p}_{{{\rm{O}}}_{2}}\) range.
Note that for interstitial C in TiO2 i.e., (CO)O induces several localized occupied states in the band gap. Hence it is stable either in neutral charge state \({({\rm{CO}})}_{{\rm{O}}}^{0}\) or in +2 charge state \({({\rm{CO}})}_{{\rm{O}}}^{+2}\). From Fig. 4, it is clear that \({({\rm{CO}})}_{{\rm{O}}}^{+2}\) is stable for all values of μe for all the three conditions. Interstitial C can form a complex with (C)O in the form of (C2)O. (C2)O has two electrons fewer than (CO)O, and we thus find it to be stable as \({({{\rm{C}}}_{2})}_{{\rm{O}}}^{+2}\). In this way we have chosen the favorable charges for our calculations that can be expected on the basis of fundamental chemical intuition. DFT energetics further validate the same. \({({{\rm{C}}}_{2})}_{{\rm{O}}}^{+2}\) is energetically preferable for lower part of the band gap and \({({{\rm{C}}}_{2})}_{{\rm{O}}}^{0}\) is preferable for upper part of the band gap. Our key conclusion from calculated formation energies indicate that at O-poor condition, (C)O is the prevalent defect for μe values near CBm while for O-rich and O-intermediate conditions, C has predominant preference for occupying the interstitial site (CO)O. The result regarding stability of configuration (either substitutional or interstitial) is in agreement with previous finding of Ghosh et al.11 but with charge state −2 and +2 respectively (see the phase diagram as in Fig. 4d). From this phase diagram, under O-poor condition \({({\rm{CO}})}_{{\rm{O}}}^{+2}\) is energetically preferable in lower part of the band gap (p-type doping) and \({({\rm{C}})}_{{\rm{O}}}^{-2}\) is predominant near CBm (n-type doping), while under O-rich condition \({({\rm{CO}})}_{{\rm{O}}}^{+2}\) is preferable for all values of μe. The rectangular box is showing the experimentally feasible region at T = 848 K with a realistic oxygen partial pressure \({p}_{{{\rm{O}}}_{2}}\) range.
S-related dopant
Next, we have addressed Sulfur (S) related defects, where we have considered the same three configurations: Sulfur substituted oxygen (S)O, Sulfur as interstitial (SO)O, and interstitial Sulfur sharing a lattice site with (S)O forming (S2)O. The formation energy can be calculated in a similar way for all the three configurations using either S or SO3 as a precursor. In either case we have verified that the results are same. To use SO3 as a precursor, we have used the following formula to estimate E(S):
The same can also be calculated directly from DFT total energy from a supercell of S8 (see equations in Supplementary Information). In Fig. 5, the formation energy is shown as a function of μe for (S)O, (SO)O, (S2)O at various charge states (viz. 0/+1/+2/−1/−2) for O-poor, O-rich and O-intermediate limits. (S)O has the same number of electrons in the outermost shell as oxygen. Insertion of S into the TiO2 lattice is difficult to achieve due to its larger ionic radius. However, Periyat et al. have reported S-doped TiO2 through modification of titanium isopropoxide with sulphuric acid57. Note that the insertion of cationic sulfur (positive charge) is chemically favorable over the anionic sulfur (negative charge)58. Our findings are quite in agreement with this observation. We have found that positive charges (viz. 0/+1/+2) are more favorable than negative charges. Hence, it will act as an electron donor dopant, which is more feasible at lower values of μe i.e., p-type doping. In (S)O defect, at a lower values of μe i.e., near VBM \({({\rm{S}})}_{{\rm{O}}}^{+2}\) is stable and for larger values of μe (i.e., in the upper part near CBm) \({({\rm{S}})}_{{\rm{O}}}^{0}\) is stable (see Fig. 5) for all the three conditions. In (SO)O defect, it is clear from Fig. 5 that \({({\rm{SO}})}_{{\rm{O}}}^{+2}\) is stable for lower values of μe and \({({\rm{SO}})}_{{\rm{O}}}^{0}\) is stable for higher values of μe. Interstitial S complex (S2)O has same number of electrons as (SO)O. Consequently, (S2)O preferred the same charge state as that by (SO)O. From Fig. 5 \({({{\rm{S}}}_{2})}_{{\rm{O}}}^{+2}\) is energetically preferable for lower part of the band gap and \({({{\rm{S}}}_{2})}_{{\rm{O}}}^{0}\) is preferable for upper part of the band gap. We can summarize them all into a phase diagram as shown in Fig. 5d. Under O-poor condition, \({({\rm{S}})}_{{\rm{O}}}^{+2}\) is energetically favorable for lower values of μe and \({({\rm{S}})}_{{\rm{O}}}^{0}\) is preferable for upper values of μe i.e., near CBm. Under O-rich condition, \({({\rm{SO}})}_{{\rm{O}}}^{+2}\) is energetically preferable for lower part of the band gap and \({({\rm{SO}})}_{{\rm{O}}}^{0}\) becomes prominent for upper part of the band gap. These findings indicate that the synthesis of substitutional S (S)O may be easier than that of interstitial S (SO)O under the O-poor condition because of low formation energy. On the contrary, under the O-rich condition (less Ti atoms), the calculated formation energy shows that interstitial S (SO)O is more prevalent defect than other configurations.
Formation energy for S-related defects in anatase Ti16O32 (a) O-poor limit ΔμO = −4.1 eV and ΔμS = 0 eV. (b) O-rich limit ΔμO = 0 eV and ΔμS = −4.101 eV. (c) O-intermediate (Experimental growth condition) ΔμO = −1.5 eV. (d) Phase diagram for S-related defects (S)O, (SO)O, (S2)O. The region within the rectangular red lines represents the experimentally relevant conditions at T = 848 K with a realistic \({p}_{{{\rm{O}}}_{2}}\) range.
Se-related dopant
The formation energy formula for Selenium related defects for all the three configurations using SeO2 as a precursor is given in Supplementary Information. The calculated Formation energy is shown in Fig. 6 as a function of μe for (Se)O, (SeO)O, (Se2)O at various charge states for O-poor, O-rich and O-intermediate limits.
Formation energy for Se-related defects in anatase Ti16O32 (a) O-poor limit ΔμO = −4.1 eV and ΔμSe = 0 eV. (b) O-rich limit ΔμO = 0 eV and ΔμSe = −2.336 eV. (c) O-intermediate (Experimental growth condition) ΔμO = −1.5 eV. (d) Phase diagram for Se-related defects (Se)O, (SeO)O, (Se2)O. The region within the rectangular red lines represents the experimentally relevant conditions at T = 848 K with a realistic \({p}_{{{\rm{O}}}_{2}}\) range.
Like S, Se has same number of electrons in the outermost shell as that of oxygen. Selenium possessing both cationic and anionic doping behavior. Thus, it can potentially provide electron trapping centers, which results in inhibition of their recombination with photo-generated holes. Hence, it can act as an electron donor as well as an electron acceptor dopant. From the calculated formation energies we have found that positive charges (viz. 0/+1/+2) are more favorable than negative charges. Hence, it will act as electron donor dopant, which is more feasible at lower values of μe i.e., p-type doping. In (Se)O defect, at lower values of μe i.e., near VBM \({({\rm{Se}})}_{{\rm{O}}}^{+2}\) is stable and for larger values of μe (i.e., in the upper part near the CBm) \({({\rm{Se}})}_{{\rm{O}}}^{0}\) is stable (see Fig. 6) under any equilibrium growth condition. In (SeO)O defect, it is clear from Fig. 6 that \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) is stable for all values of μe for all the three conditions. Interstitial S complex (Se2)O has same number of electrons as (SeO)O. Consequently, (Se2)O preferred the same charge state as preferred by (SeO)O. \({({{\rm{Se}}}_{2})}_{{\rm{O}}}^{+2}\) is energetically preferable for lower part of the band gap and \({({{\rm{Se}}}_{2})}_{{\rm{O}}}^{+1}\) is preferable for upper part of the band gap. Phase diagram shown in Fig. 6(d) summarize the whole information briefly. It states that under O-poor condition, \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) is energetically favorable for lower part of band gap and \({({\rm{Se}})}_{{\rm{O}}}^{0}\) is preferable for upper part i.e near CBm. Under O-rich condition, \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) is energetically preferable for all values of μe throughout the band gap.
Note that, from all the above explanation it is cleared that, in order to stabilize the system in case of doping, we need to supply external charges into the system. This means if we assume of having reservoir of electrons (from where the dopant can trap one electron), the dopant will be stabilized at the defect site. This is as good as claiming the presence of having several oxygen vacancies in the lattice with uncompensated electrons and those electrons can be trapped by the external dopant. Thus we can adapt either of the approaches i.e. (1) addition of external charge to the dopant or (2) explicit presence of oxygen vacancy for the neutral dopants. In the literatures, people have adopted the methodology in which charge compensation are done to the (neutral) dopant by creating O-vacancies24,25,59,60,61,62. However, here we have adopted a different approach, where the charge compensation are performed by adding or removing the extra electrons/holes to the dopant (charged defects). Both the approaches yield to the same conclusion as they are doing effectively the same charge compensation at the defect site and therefore our results are well in agreement with the previous findings of the Pacchioni’s group24,25,59,60,61,62. For further details see Supplementary Information; (Figs S3 and S4).
Underlying reasons for extra stability of a specific charged defects
In order to determine the most abundant non-metal dopants in TiO2, we have compared the thermodynamic stability of all the most stable individual non-metal defects cases (viz. N, C, S, Se at various charge states as obtained from respective 3-D phase diagrams) at O-intermediate conditions (see Fig. 7). We see the most relevant defects are \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\), \({({\rm{CO}})}_{{\rm{O}}}^{+2}\), \({({\rm{SO}})}_{{\rm{O}}}^{+2}\), \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{+2}\), \({({\rm{S}})}_{{\rm{O}}}^{0}\) and \({({\rm{N}})}_{{\rm{O}}}^{-1}\). It is shown in Fig. 7 that at O-intermediate condition, \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) is the most stable defect at the lower value of μe, whereas \({({\rm{N}})}_{{\rm{O}}}^{-1}\) is the only stable defect at the higher value of μe. A similar study at O-rich and O-poor condition is given in (see Supplementary Information; Fig. S5).
It’s interesting to understand the underlying reason for this enhanced stability of \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) over \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{+2}\), \({({\rm{CO}})}_{{\rm{O}}}^{+2}\), \({({\rm{SO}})}_{{\rm{O}}}^{+2}\) in pristine TiO2 in the p-type doping condition. Therefore, the enhanced stability of \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) is carefully further analyzed quantitatively. For this purpose, we have decomposed the overall defect formation energy into two parts: (i) bond-making/breaking energy (Δ\(\varepsilon \)) and (ii) charge carrier trapping energy (Δ\(\zeta \)). The combined effect of these two competing factors decides which defect configurations will get more stabilized over other configurations. Now Δ\(\varepsilon \) is given by:
Note that μe is varied from VBM (i.e. highest possible p-type doping) to the CBm (i.e. highest possible n-type doping). Here to understand the stability at a given μe, we have fixed our μe at VBM of pristine TiO2 at charge state 0. The VBM of pristine Ti16O32 is taken as a reference for calculating charge carrier trapping energy. Therefore, the charge carrier trapping energy i.e., Δ\(\zeta \) is given by (see Fig. 8):
It should be mentioned here that Eq. 12 is explicitly for p-type doping. Note that, for n-type doping one needs to set a different μe as reference level in the n-type region (viz. CBm(TiO2)0). From Table 1, we see that Δ\(\varepsilon \) is of comparable order for \({({{\rm{N}}}_{2})}_{{\rm{O}}}^{+2}\), \({({\rm{SO}})}_{{\rm{O}}}^{+2}\) and \({({\rm{CO}})}_{{\rm{O}}}^{+2}\), whereas this is quite low for \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\). However a favourable Δ\(\zeta \) further stabilizes \({({\rm{CO}})}_{{\rm{O}}}^{+2}\) and \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) defects in O-intermediate condition. While comparing these two defects viz. \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) and \({({\rm{CO}})}_{{\rm{O}}}^{+2}\), we see that the former has more negative Δ\(\varepsilon \) value than the latter, whereas the trend is slightly reversed for Δ\(\zeta \). However, the sum of Δ\(\zeta \) and Δ\(\varepsilon \) results a more negative value for \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) as compared to other stable configurations in O-intermediate region with p-type doping condition. Therefore, this concludes that both the bond-making/breaking energy and charge carrier trapping energy play an important role in providing enhanced stability to \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) defect configuration in TiO2. For n-type region only one stable defect is present, which is \({({\rm{N}})}_{{\rm{O}}}^{-1}\). A similar explanation can also be drawn for the stable compositions at other environmental conditions viz. O-poor and O-rich as shown in (see Supplementary Information; Fig. S5).
Conclusion
In summary, we have presented an exhaustive study to understand the most stable non-metal related defect in bulk form of anatase TiO2 as a function of charge at a realistic condition. As a first step, we have validated our DFT functionals, where we find that involvement of hybrid functional HSE06 is essential and semi-local functional and its improved variants are not sufficient even to address this problem qualitatively. We further notice that the α parameter of HSE06 needs to be adjusted to 0.22 so as to correctly predict the experimental bandgap of 3.2 eV and the optical transitions as found in experiments for different (X)O related defects (X = N, C, S, Se). Depending on the oxygen-concentration, we have analyzed the stability of different configurations at three different environmental conditions at a given T and \({p}_{{{\rm{O}}}_{2}}\) i.e. O-rich, O-poor and O-intermediate to mimic all possible experimental growth conditions. Three different defect configurations are considered viz. X substituted O (X)O, X as interstitial (XO)O and X as interstitial sharing a lattice site with XO, (X2)O. We have found that substitutional NO and (N2)O are energetically favorable in TiO2 under most of the equilibrium growth conditions when the material is n-type and p-type doped, respectively. On the other hand, for C-related defects, C has a predominant preference for occupying the interstitial site (CO)O. For S-related defects, S substitutional (SO) is dominant under the O-poor condition, whereas under O-rich condition, S interstitial (SO)O becomes more stable. And finally, for Se-related defects Se interstitial (SeO)O is prevalent defect under most of the doping conditions, in contrast to Se substitution (Se)O, which is slightly favored only at the n-type doped condition under O-poor condition. Finally, we have provided a comparative stability analysis of all the individual stable doped configurations in TiO2 at O-intermediate conditions. We conclude that for p-type doping \({({\rm{SeO}})}_{{\rm{O}}}^{+2}\) is the most abundant defect, whereas for n-type doping it’s \({({\rm{N}})}_{{\rm{O}}}^{-1}\). The enhanced stability is also carefully analyzed quantitatively by including the individual effect of bond-making/breaking and the charge carrier trapping energies.
Computational Details
We have performed the DFT calculations with PAW pseudopotential method63 as implemented in Vienna ab initio simulation package (VASP)64. The supercell, consisting 48 atoms, is constructed by 2 × 2 × 1 replication of the tetragonal TiO2 unit cell (space group number:141, I41/amd). The supercell size ensures enough spatial separation between the periodic images of the doped impurities under periodic boundary conditions. We have explicitly checked this by making a single O-vacancy to be fully localized inside the cell. To ensure the supercell size convergence, test calculations using 96-atom supercell have also been performed for the case of O-vacancy. The results are consistent with that obtained from a 48-atom supercell. However, a drawback of limited system sizes is that the dopant concentrations are artificially higher (perhaps two to three times) than the experimental case11. In order to ensure that our findings are not just an artifact of DFT functionals, we have used a number of exchange and correlation (xc) functionals viz. generalized gradient approximation (GGA) with PBE65, GGA + U66 (where U is Hubbard parameter) and hybrid functional HSE0667,68. The results given here are from HSE06 xc-functional. The performance of the other xc-functionals are discussed in detail in Supplementary Information; Figs S1 and S2. All the structures are fully relaxed (atomic position) upto 0.001 eV/Å force minimization using conjugate gradient minimization with 4 × 4 × 2 K-mesh. For electronic structure energy calculations, the brillouin zone is sampled with a 8 × 8 × 4 Monkhorst-Pack69 K-mesh with 0.01 meV energy tolerance. In all our calculations, the plane wave energy cut-off is set to 600 eV.
References
Fujishima, A., Rao, T. N. & Tryk, D. A. Titanium dioxide photocatalysis. Journal of Photochemistry and Photobiology C: Photochemistry Reviews 1, 1–21 (2000).
Fujishima, A. & Honda, K. Electrochemical photolysis of water at a semiconductor electrode. Nature 238, 37–38 (1972).
Grätzel, M. Photoelectrochemical cells. Nature 414, 338–344 (2001).
Sivula, K. & Van De Krol, R. Semiconducting materials for photoelectrochemical energy conversion. Nature Reviews Materials 1, 15010 (2016).
Asahi, R., Morikawa, T., Ohwaki, T., Aoki, K. & Taga, Y. Visible-light photocatalysis in nitrogen-doped titanium oxides. Science 293, 269–271 (2001).
Nasirian, M. & Mehrvar, M. Modification of TiO2 to enhance photocatalytic degradation of organics in aqueous solutions. Journal of Environmental Chemical Engineering 4, 4072–4082 (2016).
Gai, Y., Li, J., Li, S.-S., Xia, J. B. & Wei, S.-H. Design of narrow-gap TiO2: a passivated codoping approach for enhanced photoelectrochemical activity. Physical Review Letters 102, 036402 (2009).
Park, N.-G., Van de Lagemaat, J. & Frank, A. J. Comparison of dye-sensitized rutile-and anatase-based TiO2 solar cells. The Journal of Physical Chemistry B 104, 8989–8994 (2000).
Pelaez, M. et al. A review on the visible light active titanium dioxide photocatalysts for environmental applications. Applied Catalysis B: Environmental 125, 331–349 (2012).
Kawahara, T. et al. A patterned TiO (anatase)/TiO (rutile) bilayer-type photocatalyst: effect of the anatase/rutile junction on the photocatalytic activity. Angewandte Chemie 114, 2935–2937 (2002).
Ghosh, S. & English, N. J. Ab initio study on optoelectronic properties of interstitially versus substitutionally doped titania. Physical Review B 86, 235203 (2012).
Kim, S. K., Kim, W.-D., Kim, K.-M., Hwang, C. S. & Jeong, J. High dielectric constant TiO thin films on a Ru electrode grown at 250 °C by atomic-layer deposition. Applied Physics Letters 85, 4112–4114 (2004).
Liu, B. et al. Large-scale synthesis of transition-metal-doped TiO2 nanowires with controllable overpotential. Journal of the American Chemical Society 135, 9995–9998 (2013).
Wang, Y., Zhang, R., Li, J., Li, L. & Lin, S. First-principles study on transition metal-doped anatase TiO2. Nanoscale Research Letters 9, 46 (2014).
Janisch, R., Gopal, P. & Spaldin, N. A. Transition metal-doped TiO2 and ZnO-present status of the field. Journal of Physics: Condensed Matter 17, R657 (2005).
Ribao, P., Rivero, M. J. & Ortiz, I. TiO2 structures doped with noble metals and/or graphene oxide to improve the photocatalytic degradation of dichloroacetic acid. Environmental Science and Pollution Research 24, 12628–12637 (2017).
Ma, X., Dai, Y., Yu, L. & Huang, B. Noble-metal-free plasmonic photocatalyst: hydrogen doped semiconductors. Scientific Reports 4 (2014).
Zhu, W. et al. Band gap narrowing of titanium oxide semiconductors by noncompensated anion-cation codoping for enhanced visible-light photoactivity. Physical Review Letters 103, 226401 (2009).
Wang, J., Sun, H., Huang, J., Li, Q. & Yang, J. Band structure tuning of TiO2 for enhanced photoelectrochemical water splitting. The Journal of Physical Chemistry C 118, 7451–7457 (2014).
Irie, H., Watanabe, Y. & Hashimoto, K. Nitrogen-concentration dependence on photocatalytic activity of TiO2−xNx powders. The Journal of Physical Chemistry B 107, 5483–5486 (2003).
Irie, H., Watanabe, Y. & Hashimoto, K. Carbon-doped anatase TiO2 powders as a visible-light sensitive photocatalyst. Chemistry Letters 32, 772–773 (2003).
Li, Y., Hwang, D.-S., Lee, N. H. & Kim, S.-J. Synthesis and characterization of carbon-doped titania as an artificial solar light sensitive photocatalyst. Chemical Physics Letters 404, 25–29 (2005).
Chen, X. & Burda, C. Photoelectron spectroscopic investigation of nitrogen-doped titania nanoparticles. The Journal of Physical Chemistry B 108, 15446–15449 (2004).
Di Valentin, C. & Pacchioni, G. Trends in non-metal doping of anatase TiO2: B, C, N and F. Catalysis Today 206, 12–18 (2013).
Di Valentin, C., Pacchioni, G. & Selloni, A. Theory of carbon doping of titanium dioxide. Chemistry of Materials 17, 6656–6665 (2005).
Ohno, T., Mitsui, T. & Matsumura, M. Photocatalytic activity of S-doped TiO2 photocatalyst under visible light. Chemistry Letters 32, 364–365 (2003).
Jin, Y. J. et al. Defect evolution enhanced visible-light photocatalytic activity in nitrogen-doped anatase TiO2 thin films. The Journal of Physical Chemistry C 122, 16600–16606 (2018).
Varley, J., Janotti, A. & Van de Walle, C. Mechanism of visible-light photocatalysis in nitrogen-doped TiO2. Advanced Materials 23, 2343–2347 (2011).
Liu, G. et al. Synergistic effects of B/N doping on the visible-light photocatalytic activity of mesoporous TiO2. Angewandte Chemie International Edition 47, 4516–4520 (2008).
Ansari, S. A., Khan, M. M., Ansari, M. O. & Cho, M. H. Nitrogen-doped titanium dioxide (N-doped TiO2) for visible light photocatalysis. New Journal of Chemistry 40, 3000–3009 (2016).
Wang, H., Wu, Z. & Liu, Y. A simple two-step template approach for preparing carbon-doped mesoporous TiO hollow microspheres. The Journal of Physical Chemistry C 113, 13317–13324 (2009).
Ohno, T., Tsubota, T., Nishijima, K. & Miyamoto, Z. Degradation of methylene blue on carbonate species-doped TiO2 photocatalysts under visible light. Chemistry Letters 33, 750–751 (2004).
Liu, G. et al. Sulfur doped anatase TiO2 single crystals with a high percentage of {001} facets. Journal of Colloid and Interface Science 349, 477–483 (2010).
Umebayashi, T., Yamaki, T., Itoh, H. & Asai, K. Band gap narrowing of titanium dioxide by sulfur doping. Applied Physics Letters 81, 454–456 (2002).
Rockafellow, E. M., Haywood, J. M., Witte, T., Houk, R. S. & Jenks, W. S. Selenium-modified TiO2 and its impact on photocatalysis. Langmuir 26, 19052–19059 (2010).
Nasirian, M., Lin, Y., Bustillo-Lecompte, C. & Mehrvar, M. Enhancement of photocatalytic activity of titanium dioxide using non-metal doping methods under visible light: A review. International Journal of Environmental Science and Technology 15, 2009–2032 (2018).
Linsebigler, A. L., Lu, G. & Yates, J. T. Jr. Photocatalysis on TiO2 surfaces: principles, mechanisms, and selected results. Chemical Reviews 95, 735–758 (1995).
Bhattacharya, S., Berger, D., Reuter, K., Ghiringhelli, L. M. & Levchenko, S. V. Theoretical evidence for unexpected O-rich phases at corners of MgO surfaces. Physical Review. Materials 1, 071601 (2017).
Reuter, K., Stampf, C. & Scheffler, M. Ab initio atomistic thermodynamics and statistical mechanics of surface properties and functions. Handbook of Materials Modeling, 149–194 (Springer, 2005).
Fujishima, A., Zhang, X. & Tryk, D. A. TiO2 photocatalysis and related surface phenomena. Surface Science Reports 63, 515–582 (2008).
Zhang, L., Tse, M. S., Tan, O. K., Wang, Y. X. & Han, M. Facile fabrication and characterization of multi-type carbon-doped TiO2 for visible light-activated photocatalytic mineralization of gaseous toluene. Journal of Materials Chemistry A 1, 4497–4507 (2013).
Shi, J. W. et al. Carbon-doped titania hollow spheres with tunable hierarchical macroporous channels and enhanced visible light-induced photocatalytic activity. ChemCatChem 4, 488–491 (2012).
Parangi, T. & Mishra, M. K. Titania nanoparticles as modified photocatalysts: A review on design and development. Comments on Inorganic Chemistry 1–37 (2019).
Sun, Y.-Y. & Zhang, S. Kinetics stabilized doping: computational optimization of carbon-doped anatase TiO for visible-light driven water splitting. Physical Chemistry Chemical Physics 18, 2776–2783 (2016).
Xie, W., Li, R. & Xu, Q. Enhanced photocatalytic activity of Se-doped TiO2 under visible light irradiation. Scientific Reports 8 (2018).
Bhattacharya, A. & Bhattacharya, S. Unraveling the role of vacancies in the potentially promising thermoelectric clathrates Ba8ZnxGe46-x-y. Physical Review B 94, 094305 (2016).
Rinke, P. et al. First-principles optical spectra for F centers in MgO. Physical Review Letters 108, 126404 (2012).
Darzi, S. J., Mahjoub, A. & Sarfi, S. Visible-light-active nitrogen doped TiO2 nanoparticles prepared by sol–gel acid catalyzed reaction. Iranian Journal of Materials Science & Engineering 9, 17–23 (2012).
Lin, X., Rong, F., Ji, X. & Fu, D. Carbon-doped mesoporous TiO2 film and its photocatalytic activity. Microporous and Mesoporous Materials 142, 276–281 (2011).
Li, H., Zhang, X., Huo, Y. & Zhu, J. Supercritical preparation of a highly active S-doped TiO2 photocatalyst for methylene blue mineralization. Environmental Science & Technology 41, 4410–4414 (2007).
Preethi, L., Antony, R. P., Mathews, T., Walczak, L. & Gopinath, C. S. A study on doped heterojunctions in TiO2 nanotubes: an efficient photocatalyst for solar water splitting. Scientific Reports 7, 14314 (2017).
Bhattacharya, S., Levchenko, S. V., Ghiringhelli, L. M. & Scheffler, M. Efficient ab initio schemes for finding thermodynamically stable and metastable atomic structures: Benchmark of cascade genetic algorithms. New Journal of Physics 16, 123016 (2014).
Matsubara, M., Saniz, R., Partoens, B. & Lamoen, D. Doping anatase TiO2 with group Vb and VI-b transition metal atoms: a hybrid functional first-principles study. Physical Chemistry Chemical Physics 19, 1945–1952 (2017).
Lide, D. R. Standard thermodynamic properties of chemical substances. CRC Handbook of Chemistry and Physics 5 (2007).
Lyons, J. L., Janotti, A. & Van de Walle, C. G. Why nitrogen cannot lead to p-type conductivity in ZnO. Applied Physics Letters 95, 252105 (2009).
Reunchan, P. et al. Energetics and optical properties of nitrogen impurities in SrTiO3 from hybrid density-functional calculations. Physical Review B 95, 205204 (2017).
Periyat, P., Pillai, S. C., McCormack, D. E., Colreavy, J. & Hinder, S. J. Improved high-temperature stability and sun-light-driven photocatalytic activity of Sulfur-doped anatase TiO2. The Journal of Physical Chemistry C 112, 7644–7652 (2008).
Periyat, P., McCormack, D. E., Hinder, S. J. & Pillai, S. C. One-pot synthesis of anionic (nitrogen) and cationic (sulfur) codoped high-temperature stable, visible light active, anatase photocatalysts. The Journal of Physical Chemistry C 113, 3246–3253 (2009).
Di Valentin, C., Pacchioni, G. & Selloni, A. Origin of the different photoactivity of N-doped anatase and rutile TiO2. Physical Review B 70, 085116 (2004).
Di Valentin, C. et al. N-doped TiO2: Theory and experiment. Chemical Physics 339, 44–56 (2007).
Livraghi, S. et al. Origin of photoactivity of nitrogen-doped titanium dioxide under visible light. Journal of the American Chemical Society 128, 15666–15671 (2006).
Di Valentin, C., Pacchioni, G. & Selloni, A. Reduced and n-type doped TiO2: nature of Ti3+ species. The Journal of Physical Chemistry C 113, 20543–20552 (2009).
Blöchl, P. E. Projector augmented-wave method. Physical Review B 50, 17953 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B 54, 11169 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Physical Review Letters 77, 3865 (1996).
Kulik, H. J., Cococcioni, M., Scherlis, D. A. & Marzari, N. Density functional theory in transition-metal chemistry: A self-consistent hubbard U approach. Physical Review Letters 97, 103001 (2006).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. The Journal of Chemical Physics 118, 8207–8215 (2003).
Krukau, A. V., Scuseria, G. E., Perdew, J. P. & Savin, A. Hybrid functionals with local range separation. The Journal of Chemical Physics 129, 124103 (2008).
Monkhorst, H. J. & Pack, J. D. Special points for brillouin-zone integrations. Physical Review B 13, 5188 (1976).
Acknowledgements
P.B. acknowledges UGC, India, for the senior research fellowship [grant no. 20/12/2015 (ii) EUV]. S.S. acknowledges CSIR, India, for the senior research fellowship [grant no. 09/086 (1231) 2015-EMR-I]. M.K. acknowledges CSIR, India, for the junior research fellowship [grant no. 09/086(1292)2017-EMR-I]. S.B. and E.A. acknowledge the financial support from YSS-SERB research grant, SERB India (grant no. YSS/2015/001209). S.B. acknowledges Amrita Bhattacharya for many helpful discussions and Bryan R. Goldsmith for reading the manuscript. We acknowledge the High Performance Computing (HPC) facility at IIT Delhi for computational resources.
Author information
Authors and Affiliations
Contributions
S.B. and P.B. conceived the project. S.B. supervised overall. P.B. performed all the calculations. P.B., S.S., E.A., A.S. and M.K. got involved in various discussion to analyze the data. All authors took part in finalizing the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Basera, P., Saini, S., Arora, E. et al. Stability of non-metal dopants to tune the photo-absorption of TiO2 at realistic temperatures and oxygen partial pressures: A hybrid DFT study. Sci Rep 9, 11427 (2019). https://doi.org/10.1038/s41598-019-47710-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-47710-7
This article is cited by
-
Role of Main Group Nonmetal Dopants on the Electronic Properties of the TcS2 Monolayer Revealed by Density Functional Theory
Journal of Electronic Materials (2023)
-
Theoretical insights of codoping to modulate electronic structure of \(\hbox {TiO}_2\) and \(\hbox {SrTiO}_3\) for enhanced photocatalytic efficiency
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.