Abstract
Perturbation-based exercise interventions challenge balance and improve reactive motor control. Our purpose was to investigate the modular organisation during a standing balance task in both stable and unstable conditions to provide new insights into the neuromuscular control mechanisms needed to cope with perturbations. Fifteen participants performed 54 cycles of a specific task (i.e. pass from a double- to a single-leg standing) on stable ground and an unstable oscillating platform (Posturomed). Muscle synergies were extracted from the electromyographic activity of thirteen lower limb muscles. The maximum Lyapunov exponents of different body segments were calculated using kinematic data. We found two synergies functionally associated with the single- and double-leg stance in both stable and unstable conditions. Nonetheless, in the unstable condition participants needed an extra muscle synergy also functionally related to the single stance. Although a simple organisation of the neuromuscular system was sufficient to maintain the postural control in both conditions, the increased challenge in the oscillating platform was solved by adding one extra synergy. The addition of a new synergy with complementary function highlighted an increased motor output’s robustness (i.e. ability to cope with errors) in the presence of perturbations.
Similar content being viewed by others
Introduction
For humans, maintaining balance is a necessary requirement not only during locomotion1 but in many other motor tasks as well2,3,4,5. Daily-life activities involve perturbations which challenge the neuromuscular system to modify its control strategies6,7,8. Challenging balance conditions and perturbations have been proposed as an effective exercise intervention to reduce fall risk in older adults9,10,11. Training programmes using unexpected or continuous perturbations to exercise the mechanisms of dynamic stability have the potential to enhance muscle strength as well as sensory information processing within the motor system12. Furthermore, perturbation-based interventions improve reactive balance control in post-stroke13,14 and Parkinson’s disease patients15. The reaction to a perturbation is related to the type of perturbation, whilst a large perturbation may require a recovery movement a small perturbation will not necesarlly modify the motor behaviour16. Both abilities, cooping with large and small perturbations are key components for a stable motor output17. The sensitivity of any system to small perturbations is normally referred as “local stability”18 and is crucial for the execution of a task uninterruptedly in dynamic conditions19,20. The maximum Lyapunov exponent (MLE) is a measure of the local dynamic stability and is considered to reflect the ability of dynamical systems -such as humans during gait- to withstand perturbations17,18,21,22. The theoretical concept of the MLE suggests that although the entire dynamic of the system can be approximated by measuring only one site23,24, assessing different components of the system may also provide specific information about the sub-system being evaluated21.
There is little information about how muscle activations are organized to control the body in the presence of perturbations. Nonetheless, challenging motor control strategies through perturbations is an effective way to investigate the neuromuscular responses to unstable conditions7 and could highlight possible neuromuscular mechanisms responsible for the positive effects of perturbation-based interventions.
A generally accepted idea is that the central nervous system (CNS) might simplify the production of movement by activating muscles in common patterns called synergies25,26,27. Instead of activating each muscle individually, the CNS might create a motor output by combining small sets of time-dependent commands (motor primitives) and time-independent weights (motor modules) that create patterns in muscles26,27,28. It has been proposed that synergies may be specific to each task29. This task-related control could allow for fast reconfigurations when the task demands change30,31. During walking and running, although the general modular organisation remains unaltered in the presence of perturbations, a modification of the temporal components of the muscle synergies, characterized by a widening of the motor primitives, has been reported7,32. This widening increases the overlap of chronologically adjacent synergies and has been interpreted as a motor control strategy that is used to increase the robustness of the neuromuscular system’s output while performing a task7,16,33. Kitano proposed that a biological system is evolutionally robust when its characteristics can withstand perturbations or uncertainty34. In a similar manner, robustness can be defined as the ability of the CNS to cope with perturbations or with errors of execution7. Therefore, using perturbations offers advantages to study the neuromuscular responses that might be providing robustness to the neuromuscular system’s output, and be, consequently, related to the effectiveness of fall prevention programs. Hence, the purpose of the current study was to investigate the modular organisation in healthy young adults during a standing balance task on a stable and an unstable platform in order to improve our understanding of the neuromuscular control mechanisms in the presence of external perturbations. We hypothesized an increased robustness of the motor output in the unstable compared to the stable condition, achieved through a reorganisation of the time-dependent activation coefficients (motor primitives) of muscle synergies.
Methods
Experimental protocol
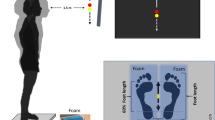
We recruited 15 healthy adults (11 males, 4 females, height 1.75 ± 0.10 m, body mass 67 ± 11 kg, age 28 ± 5 years). The sample size was a priori calculated based on the aforementioned motor primitive’s modification in the presence of perturbation during locomotion7. All participants were regularly active and had no history of neuromuscular or musculoskeletal impairments, nor any injury at the time of the measurements or in the previous six months. The Ethics Committee of the Humboldt-Universität zu Berlin reviewed and approved the study design (HU-KSBF-EK_2018_0013). All the participants gave written informed consent for the experimental procedure, in accordance with the Declaration of Helsinki. Kinematics data were recorded through a ten infrared-camera motion capture system (Vicon, Oxford, U.K.) operating at 250 Hz. The activity of 13 ipsilateral muscles was recorded using a 16-channel wireless electromyography (EMG) system (Myon m320, Myon AG, Schwarzenberg, Switzerland), with a sampling frequency of 1 kHz.
The participants were asked to pass from an initial double- to a single-leg standing on the right foot (DLS and SLS, respectively), maintain the SLS position for 3 s and return to the DLS. The whole cycle, defined as the time between two consecutive foot lift-offs, lasted for 6 s and the task was then immediately repeated (Fig. 1). A metronome aided with timing the task. The participants performed 54 cycles, on two different surfaces: hard uniform stable ground (SG) and damped oscillating unstable platform (Unstable Ground – UG, Posturomed Haider GmbH, Germany). The platform consisted of a 60 * 60 cm plate suspended by a double swinging mechanism that responded to any force application with a maximum damped displacement of 50 mm to the sides and 80 mm in the anteroposterior direction with an oscillation frequency between 1.0 and 3.2 Hz. (Fig. 2). The order of conditions was randomized.
Cycle assessment
Sixteen reflective markers were placed bilaterally on the following anatomic landmarks: greater trochanter, lateral and medial epicondyle of the femur, Achilles tendon insertion on the calcaneus, lateral malleolus, tip of the first toe, dorsal margin of the fifth and first metatarsal heads. The second, seventh and tenth thoracic and the second lumbar vertebrae were marked as well. The cycle breakdown was obtained from the kinematics of the foot (calcaneus, toe tip, fifth and first metatarsal). This data was low-pass filtered using a 4th order IIR Butterworth zero-phase filter with cut-off frequency of 50 Hz35. Touchdown was estimated using the modified foot contact algorithm developed by Maiwald et al.7,35. For assessing lift-off, we used the foot acceleration and jerk algorithm7. The algorithm searches for the vertical acceleration’s global maximum of the fifth metatarsal between two consecutive touchdown events to estimate the lift-off (LOe, where the “e” stays for “estimated”). To get closer to the “real” lift-off timing, a characteristic minimum in the vertical acceleration (i.e. when the jerk equals zero) of the fifth metatarsal marker is identified in a reasonably small neighbourhood of the LOe. We found [LOe − 50 ms, LOe + 200 ms] to be the sufficiently narrow intervals needed to make the initial lift-off estimation. Since all participants, in the SG condition, stepped with the left foot onto a force plate (AMTI BP600, Advanced Mechanical Technology, Inc., Watertown, MA, USA) we assessed the performance of both approaches in this condition against true values assessed from kinetic data. True errors were of 9 ± 6 ms for the estimation of touchdown and 13 ± 9 ms for the estimation of lift-off. To avoid inaccuracies, the first and last two cycles were removed from each data set and the central 50 cycles were kept for further analysis.
EMG recording and processing
The activity of the following 13 ipsilateral (right side) muscles was recorded: gluteus medius (ME), gluteus maximus (MA), tensor fasciae latae (FL), rectus femoris (RF), vastus medialis (VM), vastus lateralis (VL), semitendinosus (ST), biceps femoris (long head, BF), tibialis anterior (TA), peroneus longus (PL), gastrocnemius medialis (GM), gastrocnemius lateralis (GL) and soleus (SO). The EMG signals were high-pass filtered and then full-wave rectified and low-pass filtered using a 4th order IIR Butterworth zero-phase filter with cut-off frequencies of 50 Hz (high-pass) and 20 Hz (low-pass), respectively7,36 using R v3.4.4 (R Found. for Stat. Comp.). After subtracting the minimum, the amplitude was normalised to the maximum activation recorded in each trial37. Each cycle was time-normalised to a length of 1200 points through resampling the data. To approximately maintain the ratio between the SLS and DLS timing, we assigned 800 points to the SLS and 400 points to the DLS.
Muscle synergies assessment
The classical Gaussian non-negative matrix factorisation (NMF) algorithm7,38 was used for the extraction of muscle synergies from EMG data through a custom script39 (R v3.4.4, R Found. for Stat. Comp.). The time-dependent muscle activity vectors were grouped in an m × n matrix V, where m = 13 (number of muscles) and n = number of normalised time points. This matrix was factorised such that V ≈ VR = WH. The new reconstructed matrix VR approximates the original matrix V. H represents the motor primitives matrix36,40 containing the time-dependent coefficients of the factorisation with dimensions r × n, where r represents the number of synergies necessary to sufficiently reconstruct the EMG signals. The m × r motor modules matrix W36,41, contained the time-invariant muscle weightings. H and W described the synergies necessary to accomplish a movement. The update rules for H and W are presented in Eqs 1.1 and 1.2.
The limit of convergence was reached when a change in the calculated R2 between V and VR was smaller than the 0.01% in the last 20 iterations7,36,42, meaning that, with that amount of synergies, the signal could not be reconstructed any better. This operation was first completed by setting the number of synergies to 1. Then, it was repeated by increasing the number of synergies each time, until a maximum of 10 synergies. The number 10 was chosen to be lower than the number of muscles, since extracting a number of synergies equal to the number of measured EMG activities would not reduce the dimensionality of the data. Specifically, 10 is the rounded 75% of 13, which is the number of considered muscles. The computation was repeated 10 times for each synergy, each time creating new randomised initial matrices H and W, in order to avoid local minima7,43. The solution with the highest R2 was then selected for each of the 10 synergies.
The minimum number of synergies required to represent the original signals was chosen fitting the curve of R2 values versus synergies using a simple linear regression model for all the synergies. The mean squared error was then repeatedly calculated, each time removing the lower synergy point, until only two points were left or until the mean squared error fell below 10−5 7,36. The extracted synergies were classified based on the timing of motor primitives’ global maxima. Following previous definitions7,36 only fundamental primitives (i.e. showing a single activation peak) were considered. When two or more fundamental synergies are blended into one, a combined synergy appears. Combined synergies usually constitute, in our data, 10 to 20% of the total extracted synergies. Due to the lack of consent in the literature on how to interpret them, we excluded the combined synergies from the analysis.
Metrics for comparison of curves
In order to compare the motor primitives of both conditions, we evaluated the centre of activity (CoA) and full width at half maximum (FWHM). The CoA was defined as the angle of the vector (in polar coordinates) that points to the centre of mass of that circular distribution7,44. The polar direction represented the cycle’s phase, with angle 0 ≤ θt ≤ 2π. The following equations define the CoA:
where p is the number of points of each cycle (p = 1200) and P is the activation vector. The FWHM was calculated as the number of points exceeding each cycle’s half maximum, after subtracting the cycle’s minimum7,44.
Local dynamic stability assessment
We calculated the point-by-point Euclidean norm of the vectors containing the 3D-coordinates of the reflective markers, thus converting the three components (xi, yi, zi) to a single value \({n}_{2}=\sqrt{{x}_{i}^{2}+{y}_{i}^{2}+{z}_{i}^{2}}\). The resulting data was filtered with a 4th order IIR Butterworth zero-phase filter with a low-pass cut-off frequency of 20 Hz. The anatomical regions of interest were then represented by the respective markers: spine (the 2nd, 7th, 10th thoracic and 2nd lumbar vertebrae), pelvis (greater trochanter), knee (lateral and medial epicondyle of the femur) and foot (lateral malleolus). When two or more markers were related to a region (i.e. spine and knee), a point-by-point average was calculated for each marker group after filtering. The resulting single-vector time series for each right lower limb’s region and spine were used for further analysis and calculation of the Maximum Lyapunov Exponent. To avoid dependencies, we used the maximum number of shared cycles (50) for all trials and participants21,45, and excluded the first and last cycle (analysing a total of 48 cycles per participant), one participant was excluded from the analysis due to missing data. The coordinates of the data segments corresponding to the exact number of cycles were then extracted and normalised to a uniform length. The high number of analysed cycles ensured the reliability of the measurements based on our previous studies on locomotion21,46. Moreover during our pilot tests we noticed that after the designated number of repetitions fatigue began to set in.
State space reconstruction was achieved through delay coordinate embedding47,48, for each point of the time series and its time-delayed copies as follows:
with S(t) being the m-dimensional reconstructed state vector, z(t) the input 1D coordinate series, τ the time delay and m the embedding dimension. Time delays were calculated for each time series from the first minimum of the mutual-information curve, based on the Average Mutual Information function49.
Different values of τ and m can yield very different state-space reconstructions50,51,52. It is therefore suggested that optimised values of τ and m are necessary to best represent a dynamical system21,53. In the current study dimension of 3 was sufficient21,54 and time delays were individually chosen for each participant and each analysed segment53. Time delays were approximately 0.33 of the cycle length which is common in human movement studies21,54. Following the reconstruction of the times series, the Rosenstein algorithm was used to compute the average exponential rate of divergence of the trajectories in the state space, by calculating the linear distance of each point’s trajectory divergence to its closest trajectory18,23. The MLE were then calculated from the slope of the linear fit in the resulting divergence curves from 0 to 0.25 of a whole cycle. Analysis of the data was performed on MATLAB 2014b (Mathworks Inc., Natick, United States). Higher values in MLE indicate increased instability of the system.
Statistics
To compare CoA and FWHM, we used a two-way analysis of variance (ANOVA) with repeated measures, using standing synergy (SLS, DLS) and condition (SG, UG) as within-subjects factor followed by a Tukey post-hoc analysis with false discovery rate p-value adjustment. To compare modules between conditions we adopted the same procedure using muscle (number of muscles) and condition as within-subjects factor. A two-way ANOVA for repeated measures was performed with anatomical region (spine, pelvis, knee, foot) and condition (SG, UG) as within-subjects factor on the MLE. A Bonferroni-corrected post-hoc analysis was conducted in the case of a significant time effect or interaction of the factors anatomical region and condition. All the significance levels were set to α = 0.05 and analyses were conducted on R v3.4.4.
Results
Cycle parameters
The duration of the cycles (lift-off to lift-off) did not differ when switching from SG to UG (6.035 ± 0.109 s and 6.013 ± 0.073 s for SG and UG, respectively, p = 0.522). The average duration of the SLS did not show differences between conditions either (stable = 3.684 ± 0.509 s, unstable = 3.512 ± 0.534 s, p = 0.374). Nonetheless, participants in the unstable condition showed an increased variability expressed in a significant larger variance (stable = 0.137 ± 0.069 s, unstable = 0.307 ± 0.270 s, paired t-test p = 0.012).
Local dynamic stability
The MLE was significantly higher at the ankle compared to proximal segments (F (3,39) = 15.909, p = 0.001, η2 = 0.550) regardless the ground condition. Furthermore, there was an interaction between anatomical region and condition group (F (3,39) = 6.866, p = 0.02, η2 = 0.346). The MLE was significantly lower at the spine on the unstable ground (p = 0.006, 95% C.I = 86.7:97.7 for the SG and 75.7:86.6 for UG, Table 1). There were no differences for the pelvis (p = 0.444) nor the knee (p = 0.754) or foot among conditions (Table 1).
Modular organisation
For all the trials, a minimum of two synergies and a maximum of four were sufficient to satisfactorily reconstruct the measured EMG activity (median = 2 and 3 for SG and UG respectively). More synergies were needed to reconstruct the trials of the unstable (mean = 3.2 ± 0.5) compared to the stable condition (mean 2.5 ± 0.7, paired t-test p = 0.029, Fig. 3). In both conditions, the fundamental activation patterns were associated with temporally different phases of the task (Fig. 4). The first synergy was shared between conditions and functionally referred to the SLS (peak at ~9% and ~16% of the cycle for stable and unstable, respectively) and showed a major involvement of hip abductors, hip extensors and plantar flexors. The second synergy, which was also shared among conditions, described the DLS (peak at ~90% and ~89% of the cycle for stable and unstable, respectively) and showed a main contribution of knee extensors and flexors and hip extensors. The extra synergy for the unstable ground condition was functionally related to the SLS (peak at ~21%) and was mainly characterized by the involvement of mediolateral stabilizers of the lower leg. For this reason, from now on it will be referred to as SLS mediolateral synergy. Since this synergy was only present in the UG condition, comparisons between SG and UG conditions were performed for the SLS and DLS synergies exclusively.
Frequency distribution of the minimum number of synergies necessary to sufficiently reconstruct the EMG signals recorded from all participants on stable and unstable ground. Significant differences were observed for the mean (2.5 ± 0.7 for the stable and 3.2 ± 0.5 for the unstable condition, p = 0.029) and median values (2 for the stable and 3 for the unstable condition, p = 0.035).
Average motor modules and motor primitives of the fundamental synergies needed to perform the postural task on stable and unstable ground. The motor modules are presented on a normalised y-axis base. For the motor primitives, the x-axis full scale represents one cycle (lift-off to lift-off, time-normalised to the same amount of points, the vertical line indicates the touchdown, i.e. the beginning of the double leg stance) and the y-axis the normalised amplitude. SLS = single leg stance, DSL = double leg stance, ME = gluteus medius, MA = gluteus maximus, FL = tensor fasciae latae, RF = rectus femoris, VM = vastus medialis, VL = vastus lateralis, ST = semitendinosus, BF = biceps femoris (long head), TA = tibialis anterior, PL = peroneus longus, GM = gastrocnemius medialis, GL = gastrocnemius lateralis and SO = soleus.
There were no differences for the shared motor primitives of the SLS and DLS in either the FWHM or the CoA between SG and UG (F (1,14) = 8.16, p = 0.201, Table 2). Similarly, the motor modules in any of the shared synergies (SLS and DLS) did not differ between conditions (F (12, 364) = 0.28, p = 0.972 for the SLS and p = 0.267 for the DLS).
Discussion
In the present study, we investigated the modular organisation of a standing balance task on stable and unstable ground in order to improve our understanding of the neuromuscular control mechanisms adopted by the CNS to maintain motor task functionality during external perturbations. Our results show that a very simple organisation of the neuromuscular system is sufficient to maintain the postural control in DLS and SLS on both SG and UG. In the SG condition, two synergies were sufficient to describe the modular organisation of the task, one for each stance, and achieve the functional goal of keeping the upright posture. In the UG condition, the increased challenge of postural stability was solved by adding one extra synergy during the SLS.
Stability increased (lower MLE) from the distal (foot) to the proximal (spine) anatomical regions in both SG and UG. Remarkably, this phenomenon was more pronounced in the unstable condition. The lower MLE from the spine in UG compared to SG suggest that the neuromuscular system increased the stability of the trunk in relation to the foot to a higher extent in presence of distal perturbations. Previous studies reported a stability prioritization of proximal over distal segments during balancing and walking55,56,57,58. Our results show that this phenomenon (i.e. priority of proximal segment stability) is facilitated in the perturbed condition. It has been shown that stability of the head is critical to obtain visual and vestibular references that are crucial for dynamic postural control59,60,61. In balance-challenging conditions, the integration of visual and vestibular information for effective postural control may be more relevant than in less challenging tasks, thus requiring higher trunk-head stability. Furthermore, our data indicate that the preservation of the task functionality in the presence of perturbations was achieved at the expense of accuracy: the variability of the cycle duration was twice as high (p = 0.012) in UG compared to SG.
It is well known that muscle activity is organized to control the displacement of the centre of mass by controlling the centre of pressure during upright posture58,62,63. The SLS synergy modules showed a main contribution of ankle (PL, GM, GL and SO) and hip muscles (MA, FL, ME), whilst in the DLS synergy, the main contribution was provided from rectus femoris and gluteus maximus. These two synergies remained unaffected by the change of ground condition (stable or unstable) in their spatial (i.e. motor modules) and their temporal (i.e. motor primitives) structure. In the UG condition, the displacement of the base of support amplified the need to compromise between keeping balance and maintaining the upright posture2. For this reason, any attempt to control the centre of mass necessarily results in a displacement of the base of support. From a mechanical point of view, these reciprocal constraints change the behaviour of the body from an inverted pendulum to a balancing pole64,65. As stated above, the incremented postural stability challenge was solved by adding one extra synergy during the SLS. This new synergy was present in most of the participants (73.3%) and was characterised by a dominant contribution of the shank muscles, especially the peroneus longus. It has been reported that distal muscles are more sensitive to perturbations than proximal muscles66. This could be due to specific morphological and anatomical properties (i.e. short fascicles, long tendons, and large pennation angles) that allow these muscles to be particularly sensitive to perturbations happening at low levels of force67.
Based on previous results from our group, we expected a conservation of the modular organisation of the system (i.e. same number of synergies) with a modification of its time coefficients (widening of motor primitives) leading to an increased motor output’s robustness7. A “robust adaptation” in response to perturbations is observed when (a) the state of the system is modified and the system is able to return to its original attractor or (b) the system moves to a new attractor that is able to respond adequately to perturbations maintaining its functionality34. The ability to maintain specific functionalities by changing the modes of operation in a flexible way is a characteristic of robust adaptation34. Considering the observed addition in the number of synergies as a modification of the state of the system and the fact that all participants managed to perform the task in face of perturbations, we can assume that functionality was maintained, despite an alteration of the modular organisation when comparing SG and UG tasks. Modularity is often presented as a biological design principle that allows robust responses34,68. Muscles synergies represent neural sets of task-specific modules that can be selected and combined for the production of different movement patterns69,70. The performed task was partially mechanically constrained by maintaining the upright standing position on one and two legs and on stable and unstable ground. Considering that a task-specific mechanical goal is likely to be reflected in a task-specific muscle synergy43,71, our results support the idea that for the induced perturbations, the control system increased its robustness by adding a new synergy with different muscle organisation, but complementary target function. In other words, while the shared SLS synergy is likely responsible for keeping the upright posture, the added synergy might be responsible for controlling the perturbations imposed by the displacement of the base of support. During the DLS, despite the presence of the same kind of perturbations (i.e moving ground), there was no necessity for an extra synergy. This might be due to the bigger base of support that provided larger boundaries of stability60,72,73.
Recent studies reported that perturbation-based training programmes using continuously variable and partly unpredictable disturbances can improve the neuromuscular control of the motor system and increase its stability during sudden balance recovering tasks12,74. Furthermore, it has been proposed that exercise including small continuous and unpredictable perturbations may introduce a more robust response to large perturbations by improving the modular organisation of the control system16. In highly challenging conditions, humans increase the fuzziness of the temporal boundaries in the modular organisation of walking and running and create a “buffer” of motor control enhancing the robustness needed to cope with external perturbations7. In this notion and considering our results, we interpret the addition of a new independent synergy as a “safety buffer” created by the neuromuscular system to minimize the effects of perturbations on the motor output.
Feedback-based control is crucial for robust locomotion75 and one of the main balance recovery mechanisms when perturbations are large or unexpected76. During bipedal balance tasks, in which distal segments are the first to move after a perturbation, proprioceptive pathways provide extremely fast feedback information77. However, large corrective responses undergo bigger time delays before being detectable65,77. These delays might be overcome by adaptive control strategies able to make up for the temporary lack of feedback65,78. Given the fundamental role of proprioception for feedback-based responses33,77,79, we reasoned that the additional synergy, mainly involving lower leg muscles, could promote the adaptive control of posture. This might happen by allowing the control of the base of support after perturbation with the smallest possible latency77.
Our results support the idea that the CNS takes advantage of sensorimotor integration to ensure robust control65,80 and that a modular organisation facilitates robustness7,34. Furthermore, the increased control’s robustness in the presence of external perturbations might be one important neural mechanism contributing to stability performance and could be of special interest for training and rehabilitation designs. For the latter, the aforementioned sensitivity of lower leg muscles to perturbations might explain why perturbation-based training programmes promote strength increase in these muscles12. However, perturbations must be challenging enough to engage or trigger the additional response to having a training effect12.
In conclusion, our results support the idea that the addition of a new synergy was a strategy to increase the robustness (i.e. ability to cope with errors) of the system’s motor output to perturbations. The new synergy was characterised by a major contribution of the lower leg muscles and had a temporal profile that was similar to the one of the SLS synergy. Such temporally co-existing synergies are likely to have different but complementary goals, in this case keeping the upright posture and controlling the displacement of the base of support. Moreover, modularity in the neuromuscular system might be an important feature to ensure robustness by providing a source to adaptive control strategies depending on the task characteristics.
Data Availability
The datasets generated and analysed during the current study are available from the corresponding author on reasonable request.
References
Toebes, M. J. P., Hoozemans, M. J. M., Furrer, R., Dekker, J. & van Dieën, J. H. Local dynamic stability and variability of gait are associated with fall history in elderly subjects. Gait Posture 36, 527–531 (2012).
Berrigan, F., Simoneau, M., Martin, O. & Teasdale, N. Coordination between posture and movement: Interaction between postural and accuracy constraints. Exp. Brain Res. 170, 255–264 (2006).
St George, R. J., Gurfinkel, V., Kraakevik, J., Nutt, J. & Horak, F. Case Studies in Neuroscience: A dissociation of balance and posture demonstrated by camptocormia. J. Neurophysiol. 119, 33–38 (2018).
Hof, A. L., Vermerris, S. M. & Gjaltema, W. A. Balance responses to lateral perturbations in human treadmill walking. J. Exp. Biol. 213, 2655–2664 (2010).
Shumway-cook, A. & Woollacott, M. H. Motor Control. (Lippincott Williams & Wilkins, 2016).
Jacobs, J. V. & Horak, F. External postural perturbations induce multiple anticipatory postural adjustments when subjects cannot pre-select their stepping foot. Exp. Brain Res. 179, 29–42 (2007).
Santuz, A., Ekizos, A., Eckardt, N., Kibele, A. & Arampatzis, A. Challenging human locomotion: stability and modular organisation in unsteady conditions. Sci. Rep. 8, 2740 (2018).
Oliveira, A. S., Gizzi, L., Kersting, U. G. & Farina, D. Modular organization of balance control following perturbations during walking. J. Neurophysiol. 108, 1895–1906 (2012).
Hamed, A., Bohm, S., Mersmann, F. & Arampatzis, A. Follow-up efficacy of physical exercise interventions on fall incidence and fall risk in healthy older adults: a systematic review and meta-analysis. Sport. Med. - Open 4, 56 (2018).
Okubo, Y., Schoene, D. & Lord, S. R. Step training improves reaction time, gait and balance and reduces falls in older people: A systematic review and meta-analysis. Br. J. Sports Med. 51, 586–593 (2017).
Kurz, I. et al. Unexpected perturbations training improves balance control and voluntary stepping times in older adults - A double blind randomized control trial. BMC Geriatr, https://doi.org/10.1186/s12877-016-0223-4 (2016).
Hamed, A., Bohm, S., Mersmann, F. & Arampatzis, A. Exercises of dynamic stability under unstable conditions increase muscle strength and balance ability in the elderly. Scand. J. Med. Sci. Sports 28, 961–971 (2018).
Handelzalts, S. et al. Effects of Perturbation-Based Balance Training in Subacute Persons With Stroke: A Randomized Controlled Trial. Neurorehabil. Neural Repair 154596831982945, https://doi.org/10.1177/1545968319829453 (2019).
Mansfield, A. et al. Does perturbation-based balance training prevent falls among individuals with chronic stroke? A randomised controlled trial. BMJ Open 8, e021510 (2018).
Jöbges, M. et al. Repetitive training of compensatory steps: A therapeutic approach for postural instability in Parkinson’s disease. J. Neurol. Neurosurg. Psychiatry 75, 1682–1687 (2004).
Van Hooren, B., Meijer, K. & McCrum, C. Attractive Gait Training: Applying Dynamical Systems Theory to the Improvement of Locomotor Performance Across the Lifespan. Front. Physiol. 9, 1934 (2019).
Bruijn, S. M., Meijer, O. G., Beek, P. J. & van Dieën, J. H. Assessing the stability of human locomotion: a review of current measures. J. R. Soc. Interface 10, 20120999–20120999 (2013).
Dingwell, J. B. & Cusumano, J. P. Nonlinear time series analysis of normal and pathological human walking. Chaos An Interdiscip. J. Nonlinear Sci. 10, 848 (2000).
Patla, A. E. Strategies for dynamic stability during adaptive human locomotion. IEEE Eng. Med. Biol. Mag. 22, 48–52 (2003).
Bohm, S., Mademli, L., Mersmann, F. & Arampatzis, A. Predictive and Reactive Locomotor Adaptability in Healthy Elderly: A Systematic Review and Meta-Analysis. Sport. Med. 45, 1759–1777 (2015).
Ekizos, A., Santuz, A., Schroll, A. & Arampatzis, A. The maximum Lyapunov exponent during walking and running: Reliability assessment of different marker-sets. Front. Physiol. 9, 1–11 (2018).
Raffalt, P. C., Guul, M. K., Nielsen, A. N., Puthusserypady, S. & Alkjær, T. Economy, Movement Dynamics and Muscle Activity of Human Walking at Different Speeds. Sci. Rep. 7, 43986 (2017).
Rosenstein, M. T., Collins, J. J. & De Luca, C. J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 65, 117–134 (1993).
Dingwell, J. B., Cusumano, J. P., Sternad, D. & Cavanagh, P. R. Slower speeds in patients with diabetic neuropathy lead to improved local dynamic stability of continuous overground walking. J. Biomech. 33, 1269–1277 (2000).
Bernstein, N. A. Coordination and Regulation of Movements. (1967).
Mussa-Ivaldi, F. A., Giszter, S. F. & Bizzi, E. Linear combinations of primitives in vertebrate motor control. Proc. Natl. Acad. Sci. USA 91, 7534–7538 (1994).
Bizzi, E., Cheung, V. C. & d’Avella, A. Combining modules for movement. Brain Res. … 57, 125–133 (2008).
Bizzi, E. & Cheung, V. C. The neural origin of muscle synergies. Front. Comput. Neurosci. 7, 51 (2013).
Torres-Oviedo, G. & Ting, L. H. Subject-Specific Muscle Synergies in Human Balance Control Are Consistent Across Different Biomechanical Contexts. J. Neurophysiol. 103, 3084–3098 (2010).
Fiete, I. R., Hahnloser, R. H. R., Fee, M. S. & Seung, H. S. Temporal Sparseness of the Premotor Drive Is Important for Rapid Learning in a Neural Network Model of Birdsong. J. Neurophysiol. 92, 2274–2282 (2004).
McKay, J. L., Burkholder, T. J. & Ting, L. H. Biomechanical capabilities influence postural control strategies in the cat hindlimb. J. Biomech. 40, 2254–2260 (2007).
Martino, G. et al. Neuromuscular adjustments of gait associated with unstable conditions. J. Neurophysiol. 114, 2867–2882 (2015).
Santuz, A. et al. Modular organization of murine locomotor pattern in the presence and absence of sensory feedback from muscle spindles. J. Physiol. 597, 3147–3165 (2019).
Kitano, H. Biological robustness. Nature Reviews Genetics 5, 826–837 (2004).
Maiwald, C., Sterzing, T., Mayer, T. A. & Milani, T. L. Detecting foot-to-ground contact from kinematic data in running. Footwear Sci. 1, 111–118 (2009).
Santuz, A., Ekizos, A., Janshen, L., Baltzopoulos, V. & Arampatzis, A. On the Methodological Implications of Extracting Muscle Synergies from Human Locomotion. Int. J. Neural Syst. 27, 1750007 (2017).
Torres-Oviedo, G. & Ting, L. H. Muscle synergies characterizing human postural responses. J. Neurophysiol. 98, 2144–56 (2007).
Lee, D. D. & Seung, H. S. Learning the parts of objects by non-negative matrix factorization. Nature 401, 788–791 (1999).
Santuz, A. et al. Modular control of human movement during running: An open access data set. Front. Physiol. 9, 1–11 (2018).
Dominici, N. et al. Locomotor Primitives in Newborn Babies and Their Development. Science (80-.). 334, 997–999 (2011).
Gizzi, L., Nielsen, J. F., Felici, F., Ivanenko, Y. P. & Farina, D. Impulses of activation but not motor modules are preserved in the locomotion of subacute stroke patients. J. Neurophysiol. 106, 202–210 (2011).
Cheung, V. C. Central and Sensory Contributions to the Activation and Organization of Muscle Synergies during Natural Motor Behaviors. J. Neurosci. 25, 6419–6434 (2005).
d’Avella, A. & Bizzi, E. Shared and specific muscle synergies in natural motor behaviors. PNAS 102, 3076–3081 (2005).
Cappellini, G. et al. Immature Spinal Locomotor Output in Children with Cerebral Palsy. Front. Physiol. 7, 1–21 (2016).
Bruijn, S. M., van Dieën, J. H., Meijer, O. G. & Beek, P. J. Statistical precision and sensitivity of measures of dynamic gait stability. J. Neurosci. Methods 178, 327–333 (2009).
Kang, H. G. & Dingwell, J. B. Intra-session reliability of local dynamic stability of walking. Gait Posture 24, 386–390 (2006).
Packard, N. H., Crutchfield, J. P., Farmer, J. D. & Shaw, R. S. Geometry from a time series. Physical Review Letters 45, 712–716 (1980).
Takens, F. Detecting strange attractors in turbulence. in Dynamical Systems and Turbulence, Warwick 1980 (eds Rand, D. & Young, L.-S.) 366–381, 10.1007/BFb0091924 (Springer, 1981).
Fraser, A. M. & Swinney, H. L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 33, 1134–1140 (1986).
Bradley, E. & Kantz, H. Nonlinear time-series analysis revisited. Chaos An Interdiscip. J. Nonlinear Sci. 25, 097610 (2015).
Kantz, H. & Schreiber, T. Nonlinear Time Series Analysis. 7, (Cambridge University Press, 2004).
Kugiumtzis, D. State space reconstruction parameters in the analysis of chaotic time series — the role of the time window length. Phys. D Nonlinear Phenom. 95, 13–28 (1996).
Ekizos, A., Santuz, A. & Arampatzis, A. Transition from shod to barefoot alters dynamic stability during running. Gait Posture 56, 31–36 (2017).
Ekizos, A., Santuz, A. & Arampatzis, A. Short- and long-term effects of altered point of ground reaction force application on human running energetics. J. Exp. Biol. 221, jeb176719 (2018).
Pozzo, T. & Levik, Y. Head and trunk movements in the frontal plane during complex dynamic equilibrium tasks in humans. 327–338, https://doi.org/10.1007/bf00241128 (1995).
Mazzà, C., Iosa, M., Pecoraro, F. & Cappozzo, A. Control of the upper body accelerations in young and elderly women during level walking. J. Neuroeng. Rehabil. 5, 30 (2008).
Latt, M. D., Menz, H. B., Fung, V. S. & Lord, S. R. Walking speed, cadence and step length are selected to optimize the stability of head and pelvis accelerations. Exp. Brain Res. 184, 201–209 (2008).
Hughey, L. K. & Fung, J. Postural responses triggered by multidirectional leg lifts and surface tilts. Exp. Brain Res. 165, 152–166 (2005).
Willigenburg, N. W., Kingma, I. & van Dieën, J. H. How is precision regulated in maintaining trunk posture? Exp. Brain Res. 203, 39–49 (2010).
Horak, F. Postural orientation and equilibrium: what do we need to know about neural control of balance to prevent falls? Age Ageing 35, ii7–ii11 (2006).
Peterka, R. J. & Loughlin, P. J. Dynamic regulation of sensorimotor integration in human postural control. J. Neurophysiol. 91, 410–423 (2004).
Horak, F. & Nashner, L. M. Central programming of postural movements: adaptation to altered support-surface configurations. J. Neurophysiol. 55, 1369–1381 (1986).
Winter, D. A., Prince, F., Frank, J. S., Powell, C. & Zabjek, K. F. Unified theory regarding A/P and M/L balance in quiet stance. J. Neurophysiol. 75, 2334–2343 (1996).
Reeves, N. P., Narendra, K. S. & Cholewicki, J. Spine stability: Lessons from balancing a stick. Clin. Biomech. 26, 325–330 (2011).
Milton, J. et al. The time-delayed inverted pendulum: Implications for human balance control. Chaos 19 (2009).
Biewener, A. A. & Daley, M. A. Unsteady locomotion: integrating muscle function with whole body dynamics and neuromuscular control. J. Exp. Biol. 210, 2949–2960 (2007).
Azizi, E. & Brainerd, E. Variable gearing in pennate muscles. Proc. 105, 3–8 (2008).
Hartwell, L. H., Hopfield, J. J., Leibler, S. & Murray, A. W. From molecular to modular cell biology. Nature 402, C47–C52 (1999).
d’Avella, A., Saltiel, P. & Bizzi, E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat. Neurosci. 6, 300–308 (2003).
Ting, L. H. & Macpherson, J. M. A limited set of muscle synergies for force control during a postural task. J. Neurophysiol. 93, 609–13 (2005).
Torres-Oviedo, G., Macpherson, J. M. & Ting, L. H. Muscle synergy organization is robust across a variety of postural perturbations. J. Neurophysiol. 96, 1530–1546 (2006).
Hof, A. L., Gazendam, M. G. J. & Sinke, W. E. The condition for dynamic stability. J. Biomech. 38, 1–8 (2005).
Karamanidis, K., Arampatzis, A. & Mademli, L. Age-related deficit in dynamic stability control after forward falls is affected by muscle strength and tendon stiffness. J. Electromyogr. Kinesiol. 18, 980–9 (2008).
Arampatzis, A. et al. A random-perturbation therapy in chronic non-specific low-back pain patients: a randomised controlled trial. Eur. J. Appl. Physiol. 117, 2547–2560 (2017).
Dickinson, M. H. How Animals Move: An Integrative View. Science (80-.). 288, 100–106 (2000).
Santos, M. J., Kanekar, N. & Aruin, A. S. The role of anticipatory postural adjustments in compensatory control of posture: 1. Electromyographic analysis. J. Electromyogr. Kinesiol. 20, 388–97 (2010).
Le Goic, M. et al. An Initial Passive Phase That Limits the Time to Recover and Emphasizes the Role of Proprioceptive Information. Front. Neurol. 9, 1–15 (2018).
Insperger, T. Act-and-wait concept for continuous-time control systems with feedback delay. IEEE Trans. Control Syst. Technol. 14, 974–977 (2006).
Akay, T., Tourtellotte, W. G., Arber, S. & Jessell, T. M. Degradation of mouse locomotor pattern in the absence of proprioceptive sensory feedback. Proc. Natl. Acad. Sci. 111 (2014).
Lockhart, D. B. & Ting, L. H. Optimal sensorimotor transformations for balance. Nat. Neurosci. 10, 1329–1336 (2007).
Acknowledgements
Victor Munoz-Martel is a scholarship holder of the German Academic Exchange Service (D.A.A.D.). The authors acknowledge support by the German Research Foundation (DFG) and the Open Access Publication Fund of Humboldt-Universität zu Berlin.
Author information
Authors and Affiliations
Contributions
V.M.-M. and A.A. design the experiment. V.M.-M. conducted the experiment. V.M.-M. analysed the data and A.S., A.E. and A.A. substantially contributed to data analysis; V.M.-M., A.S., A.E. and A.A. interpreted the data; V.M.-M., A.S. and A.A. drafted the manuscript and A.E. made important intellectual contributions during revision. All authors approved the final version of the manuscript and agree to be accountable for the content of the work.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Munoz-Martel, V., Santuz, A., Ekizos, A. et al. Neuromuscular organisation and robustness of postural control in the presence of perturbations. Sci Rep 9, 12273 (2019). https://doi.org/10.1038/s41598-019-47613-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-47613-7
This article is cited by
-
The ability to increase the base of support and recover stability is limited in its generalisation for different balance perturbation tasks
European Review of Aging and Physical Activity (2021)
-
Muscle synergies for the control of single-limb stance with and without visual information in young individuals
BMC Sports Science, Medicine and Rehabilitation (2021)
-
Standing on unstable surface challenges postural control of tracking tasks and modulates neuromuscular adjustments specific to task complexity
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.