Abstract
Dynamic optical imaging (e.g. time delay integration imaging) is troubled by the motion blur fundamentally arising from mismatching between photo-induced charge transfer and optical image movements. Motion aberrations from the forward dynamic imaging link impede the acquiring of high-quality images. Here, we propose a high-resolution dynamic inversion imaging method based on optical flow neural learning networks. Optical flow is reconstructed via a multilayer neural learning network. The optical flow is able to construct the motion spread function that enables computational reconstruction of captured images with a single digital filter. This works construct the complete dynamic imaging link, involving the backward and forward imaging link, and demonstrates the capability of the back-ward imaging by reducing motion aberrations.
Similar content being viewed by others
Introduction
Dynamic optical imaging is able to acquire images in the motion condition either a moving camera observes a stationary scene, or a stationary camera observes a moving scene, or a moving camera observes a moving scene. Dynamic optical imaging has been widely used in many fields, especially in low-light-level imaging based on time delay integration (TDI) technology of Charge Coupled Device (CCD) or Complementary Metal–Oxide–Semiconductor (CMOS)1,2,3,4,5,6. Dynamic optical imaging fundamentally involves two movements: photo-induced charge transfer and optical image movements. Figure 1 shows a typical dynamic imaging principle with time-delay integration.
Optical images are formed when lights of objects pass through the optical system of a camera. In the dynamic condition, Optical images gradually move on the photoreception. In the meanwhile, the photo-induced charge is gradually transferred and accumulated from the previous stage to the current stage. The current photo-induced charge is the sum of the previous stages with the current stage. After the integration period of the last stage, the photo-induced charge packet accumulated by the multiple integration stages is transferred a horizontal register and then is output and processed by an analog-digital converter to form a line image. The relative movement between photo-induced charges and optical images inevitably appear motion aberrations in the dynamic imaging process.
To remove motion aberrations (i.e. compensation for the motion blur) in the dynamic imaging process, two forward imaging approaches (i.e. forward active imaging approaches and forward passive imaging approaches) have been developed. The forward active imaging approaches aim at the matching between the photo-induced charge transfer speed and direction and the optical image motion velocity and direction to obtain high-quality images. Any mismatching of movement vectors (i.e. speed and direction) between the photo-induced charge transfer and optical image movement in dynamic processing would produce motion aberrations and the corresponding image is blurred. Forward active imaging approaches firstly calculate the motion vector of optical images based on the geometric imaging relationships7,8,9,10,11,12 between cameras and objects. The motion vector calculation needs to use auxiliary information from multi-sensory measurements, involving position and attitude sensors13 in conjunction with the imaging equations of the camera14. The forward active imaging approach enables matching between the image motion vector and photogenic charges transfer to compensate for motion blur. The speed component of motion vectors is used as the reference to control the integration time15 and the direction component adjusts the image sensor direction by means of mechanical structures (i.e. angle drift mechanism)16. However, the motion vector is not completely accurate because of motion vector model errors and the measurement errors of sensors17. Moreover, the measurement frequency of current attitude sensors is far lower than the photogenic charges line-transfer frequency. Optical image movements are achieved by angle drift mechanisms in conjunction with electronic controlling, where a lot of errors (e.g. controlling errors, mechanical errors, assembly errors, measurement errors, etc.) exist. Therefore, residual motion aberrations of the forward active imaging method disturb dynamic imaging and residual motion blur still exist in acquired images.
Forward passive imaging methods firstly introduce a high-speed motion sensor in the optical camera to measure images18,19,20. After that, optical correlators are utilized to calculate the relative motion between the photo-induced charge and the optical image, enabling compensation for image motion blur. Optical correlators are able to be achieved by block-matching methods21,22,23 to measure image motion to avoid the active imaging problem arising from multisensory measurement errors, controlling errors, complex imaging model errors, etc. However, forward passive imaging methods need to transform the motion information of the high-speed motion sensor to the camera. The transform errors inevitably exist because of position measurement errors and assembly errors of motion sensors. Therefore, forward passive imaging methods inevitably involve the mismatching (either motion speed, direction, or both) between the photo-induced charge transfer and optical image movement, which means motion aberrations appear in the dynamic imaging process.
To remove the motion aberrations from the forward imaging, backward inversion imaging methods are very interesting. Wang et al. proposed an active optical flow method to remove the residual high-frequency motion aberration of the forward active imaging approaches24. However, the optical flow has low inversion accuracy because auxiliary parameters used in optical flow inversion, such as the attitude and position information from the multiple sensory, has a lot of measurement errors. Computational imaging methods including blind deconvolution (BD) approach25,26,27,28,29 and modulate transfer function compensation (MTFC) method30,31,32 are able to be used in the backward inversion imaging. Unfortunately, the BD-based methods suffer from high computational complexity because it doesn’t utilize any prior knowledge of dynamic imaging. The MTFC-based methods are suitable to compensate for the total degraded factors including a camera optical system, image sensor, atmospheric, electronic circuits, atmosphere, temperature, etc.
Here, we demonstrate an efficient dynamic backward inversion imaging method with optical flow deep learning to remove motion aberrations. The proposed method uses deep learning networks33,34,35 to construct optical flow which enables reconstruction of the motion point spread function that is used to recover the observed image in dynamic forward imaging link.
Proposed Method
Forward imaging model
The image motion velocity vector (denoted by Ф) of the optical image formed by lights passing optical systems can be characterized by amplitude-phase form as
where vp is the amplitude of the image motion velocity vector, β is the phase (i.e. drift angle) of the image motion velocity vector, (vpx, vpy) are vertical and horizontal components, K is the coordinate transform matrix between the motion sensor and image sensor of the camera in the forward passive imaging. In the forward active imaging, K = [1 0; 0 1]. The drift angle β represents the direction of motion velocity vector of optical images on the focal plane, while the velocity vp represents the motion velocity in the current direction β. To match between image motion vector and photogenic charges transfer, the forward active imaging method utilizes a drift adjusting mechanism rotate the optical focal plane (integrated image sensors) to ensure the same motion direction of both movements. Under the same motion direction, the transfer speed of photo-induced charges in each stage is controlled by the line-transfer signal of photoreceptions to synchronously move with the optical image due to the camera moving. Here, a TDI stage is a row of photo-sensitive elements (See Fig. 1). The line-transfer period of photo-induced charges, matching with the moving time required for the optical line-to-line image, can be expressed as
where f is the focal length of the remote sensing camera, a is the pixel size of the photoreception, H is the distance between the observed objective and the camera, and vp is the image velocity of optical images. In theory, the drift adjustment mechanism can completely implement the motion direction matching between photo-induced charges and the optical image. However, current drift adjustment mechanisms are physically limited due to a lot of errors, such as control errors, mechanical errors, assembly errors, etc. The optical image direction controlled by the drift adjustment mechanisms couldn’t completely match with the transfer direction of photo-induced charges. On the other hand, the transfer speed of photo-induced charges is determined by H, vP, and f. The velocity vector (vp, β) is calculated using an imaging equation in conjunction with coordinate transformation approaches12,36, (vp, β) needs all kinds of auxiliary parameters, involving camera positions and attitude parameters from attitude sensors (e.g. gyroscope and GPS). However, these auxiliary parameters for the calculating (vp, β) include a lot of errors due to the measurement errors of sensors. In particular, the measurement frequency of current attitude sensors is far lower than the photogenic charges line-transfer frequency, which means mismatching between optical image movements and photogenic charge transferring exists within the period of the integration time. Therefore, motion aberrations disturb dynamic imaging and motion blur exist in acquired images. The dynamic imaging process with an integration time T is modeled as37:
where (x, y) is the sampling grid of the scene B, Ksensor is an amplification factor of image sensors, \(u(x,y)\) is a image term, and \(\eta (x,y)\) is a noise term. The \(u(x,y)\) and \(\eta (x,y)\) are independent random variables. The \(u(x,y)\) and \(\eta (x,y)\) follow respectively the Poisson and Gaussian distributions as:
where λ is the quantum efficiency of the image sensor, the function f (·) is the original image. (sx(·), sy(·)) is the motion trajectory of the apparent motion between the scene and image sensors during the integration time. The motion blur is modeled by a linear and shift-invariant operator since (sx(·), sy(·)) is the same for the whole image. The following equation can be expressed as:
where \(\delta (\,\cdot \,)\) is the Dirac delta function at \(({s}_{x}(t),{s}_{y}(t))\), h(x, y) is the motion PSF (MPSF), which can be expressed as
with
where Ω = R2 the two dimensions real coordinate space. Here, we use optical flow neural learning networks to invert motion point spread function to enable computational reconstruction of captured images in conjunction with single digital filters.
Inversion imaging
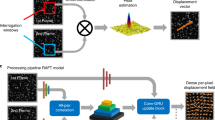
The dynamic inversion imaging adopts deep learning optical flows to reconstruct the motion point spread function, enabling removing sub-pixel level motion aberrations. Figure 2 shows the dynamic inversion imaging principle. First, the motion spread function is reconstructed by neural learning networks of optical flow. Two adjacent frame images are used as the input of the motion information extraction. In these two frames, the overlap area is from the same ground objects. Firstly, an image block with the size is N × N is selected in an overlapped area from the Frame 1, where the selected block area, denoted by f(x, y), is called a registration reference template. Then, block registration algorithms38,39,40 are able to apply to the reference template (f(x, y)) and Frame 2 to determine the matched block in Frame 2. Here, the matched block in Frame 2 is denoted by f ′(x, y). The image motion (denoted by (Δx, Δy)) between the f(x, y) and f ′(x, y) can be calculated. The calculated (Δx, Δy) is the pixel-level shifts of the whole block area. Therefore, the block matching method is a coarse motion evaluation and the (Δx, Δy) reflect the integer pixel motion evaluation. Here, we use deep learning optical flow to extract the sub-pixel-level shift.
Dynamic inversion imaging using deep learning optical flow. First, the sub-pixel level motion is inverted by deep learning neural networks with motion coarse evaluation of block-matching algorithms. Second, the sub-pixel motion is used to construct the motion PSF with probability density function49,50,51. Third, the motion PSF enables computational reconstruction of captured images with a single digital filter, such as the Wiener filter52,53.
To extract sub-pixel level movements, we utilize the coarse evaluation of motion (Δx, Δy) calculated by the block registration method. The reference block f(x, y) is firstly shifted by (Δx, Δy) along x- and y-direction, respectively. A new reference block, denoted by g(x, y), is obtained. The original and new reference block have a relationship of g(x, y) = f(x + Δx, y + Δy). Let the displacements between g(x, y) and f ′(x, y) be (dx, dy), where the (dx, dy) is the sub-pixel movement. Thus, the final motion is (Δx + dx, Δy + dy). The sub-pixel movement (dx, dy) is adjusted on a pixel-by-pixel basis. In this paper, we use learning optical flow to evaluate the (dx, dy). The new reference block g(x, y) and the matched block f ′(x, y) satisfy the following relationship:
Based on the optical flow theory, the f ′(x, y) is expanded into a Taylor series as:
with
where R is the higher order terms. The optimal movements (dx, dy) can be evaluated to minimize the cost function as:
The deep neural network (DNN) with the back-propagating algorithm can be established to calculate the optimal shift (dx, dy). In the DNN, the input stimulus is g, g′x, g′y; the weights are (dx, dy); and the output response is f′. We use supervised learning41,42 to invert sub-pixel-level motion information (dx, dy) that is considered as the synaptic weights of the deep neural network with multiplayer perceptron. We use weights w to express the motion information, i.e. w = (dx, dy). We use P with K elements to express the input stimulus of the DNN as
The desired-response is expressed as d = f′. Let the training learning task has J training examples. The training example set can be expressed as
Figure 3 shows the deep neural network for reconstructing optical flow. In the DNN, adjustments to synaptic weights, wjk, of the multilayer perception are performed on an example-by-example basis Sj. The training examples are arranged in the order S1, S2, …, SJ, where J is the training example number. Each training example has K input stimulus. The first example basis S1 is presented to the DNN, and the weight adjustments are performed with a back-propagation algorithm43,44. Then the second example S2 is presented to the DNN, where the weights are adjusted further. This procedure is continued until the last example SJ is performed.
The DNN with multilayer perceptron is achieved by means of two propagating passes, i.e. the forward pass and the backward pass. In the forward pass, the local fields and function (output) signals of the neurons are computed by proceeding forward through the network, layer by layer. It is important to note that the synaptic weights remain unaltered throughout the network, and the function signals of the network are computed on a neuron-by-neuron basis in the forward pass. The backward pass computation starts at the output layer by passing the error signals leftward through the network, layer by layer, and recursively computing the local gradient signals for each neuron. In these two propagating passes, the neurons located on the output and hidden layers have different weight updating and the local gradient forms. Figure 4(a) shows that the neuron l is located at the output layer and the hidden layer. When the neuron l is a hidden node, the neuron l is fed by a set of function (out) signals produced by a hidden layer of neurons to its left in the forward propagating pass. the local filed βl(j) of the neuron l is calculated with the input of the activation function related to the neuron l, which is expressed as:
where m is the total number of inputs applied to the neuron l. In the output layer, the function signal xl(j) produced at the output of neuron l by the stimulus input S(j) is
In the backward propagating pass, the corresponding error signal produced at the output of neuron l is expressed as:
The instantaneous error energy of neuron j is expressed as:
The total instantaneous error energy of the whole network is
where the set C consists of all the neurons in the output layer. In the backward propagating pass, the correction weights of the neuron l are calculated as:
where \({\tau }_{l}(j)\) is the local gradient of the neuron l, which can be expressed as:
When the neuron l is a hidden node, the specified desired response for this neuron doesn’t exist. In the backward propagating pass, the error signal for a hidden neuron is determined recursively and working backward in terms of the error signals of all the neurons to which that hidden neuron is directly connected. Figure 4(b) shows the neuron l as a hidden node of the DNN. The instantaneous error energy of neuron j is expressed as:
In the backward propagating pass, the local gradient \({\tau }_{l}(j)\) for hidden neuron l is expressed as:
The partial derivative \(\partial A(j)/\partial {x}_{l}(j)\) is calculated backward. The local gradient of the neuron l can be expressed as
The whole DNN for optical flow reconstruction is summarized into the Algorithm 1.
Experimental Results
To verify the proposed method, we use self-generated images to simulate dynamic inversion imaging. The simulation demonstrates the capability of the proposed method to reconstruct PSF accurately from different motion blurred images. Teapot images are produced in 3ds Max. The self-generated teapot image is blurred with the different motion PSFs (See Fig. 5). The corresponding motion PSFs are directly upper left their blurred images in Fig. 5. Random noise with different noise level (P) is added to the blurred images. To verify the proposed method, we use the method with deep learning optical flow and the block matching (without deep learning optical flow) to reconstruct the motion PSF from blurred images. Figure 6 shows the measured motion PSFs using the two methods. The measured results show that the proposed method has more accurate the motion PSF than the case without deep learning optical flow.
We experimentally demonstrate the proposed method to reconstruct the motion PSF of the camera and to remove motion aberrations. A sketch of the dynamic imaging setup is shown in Fig. 7(a). We use a dynamic coarse integration holography45 to produce a dynamic 3D objects. A 5 mW point laser with the wavelength of 635 nm is used as the optical source. The laser beam is collimated and expanded by two lenses. The collimated beam is reflected by a mirror and then passes through a spatial light modulator (SLM). After that, the beam is diffracted by the SLM. To implement the dynamic forward imaging, a 2D scanner, and a galvanometric scanner (QS-30) provided by Nutfield Technology, is used to implement the movement of an optical image. The QS-30 has 30 mm and 45 mm aperture mirrors and could handle inertias in the 0.6 to 80 g-cm2 range. We use 3ds Max to design a 3D and 2D object model. A layer-based CGH algorithm is used to calculate holograms. The calculated holograms are displayed through the SLM and scanning system. A camera with the focal length of 55 mm, a maximum aperture of f/5.6, and pixel size of 4.77um observes the 3D and 2D holographic image. The image sensor of the camera is a CMOS detector; the spectral range is 400-1000 nm. Our method is geared to meet the requirements of the TDI push-broom imaging mode. In our experiments, we use the shutter mode of the CMOS detector to implement the TDI push-broom imaging mode, enabling the same results as a TDI sensor. Figure 7(b,e) show the captured images by the camera. Figure 7(c,f) show the reconstructed image. Figure 7(d,g) show the reconstructed motion PSF. From the inversion imaging results, the proposed method gains the better image quality than the results of the forward imaging.
We also used the remote sensing image to demonstrate the capability of the inversion imaging. The motion PSF is a platform vibration function with a sin function as its basis, which is the motion model widely used in satellite motion. The platform vibration function can be expressed as
where A is peak value, \({T}_{0}\) is period, \({\alpha }_{0}\) is an original phase, and \(N(t)\) is Gauss noise. The motion PSF is constructed based on the proposed method (See Fig. 8(a,g,k)). The measured PSF is used to recover images (See Fig. 8(b,f,j)). After the deconvolution using the motion PSF, the original images can be recovered. The reconstructed images indicate the proposed method has the good results for removing the motion. We also use a mean structural similarity (MSSIM)46, peak signal noise ratio (PSNR)47, and visual information fidelity (VIF)48 to evaluate image performance, which is shown in the Fig. 8(d,h,l). From the measured results, the proposed method gains the better-reconstructed results than the use of the block-matching method without optical flow.
Finally, we use four images from Satellites to analyze the reconstructed performance. The directly observed images have motion-effects because mismatching of the drift and velocity can result in blurred images. Using the proposed method to remove the motion aberrations, the high-quality image is obtained. We also adopted the blind method and MTF-based method to reconstruct images. We use an MSSIM, VIF and PSNR to evaluate image performance. Figure 9 shows the reconstructed performance of three methods. In Fig. 9, the variance is the different motion deviation from the best motion estimation. In comparing the results, the proposed method has a higher value in PSNR, VIF and MSSIM, which means the proposed has a better-reconstructed result than the other two methods. The proposed method can significantly improve the image quality and remove motion aberrations.
Conclusion
The motion aberration limits the imaging performance at dynamic conditions due to the mismatching between the image field motion and the photo-induced charge transferring in the forward imaging. This paper reports a novel backward inversion imaging method using deep learning networks of optical flow. First, the optical flow is inverted using deep learning network. Second, the motion point spread function is constructed based on the measured optical flow information. Finally, the motion point spread function computationally reconstructs captured images in conjunction with a single digital filter. This method is experimentally confirmed. This work is a backward and forward imaging link that enables reducing motion aberrations arising from the forward dynamic imaging.
References
Holdsworth, D. W., Gerson, R. K. & Fenster, A. A time-delay integration charge-coupled device camera for slot-scanned digital radiography. Medical physics 17, 876–886 (1990).
Haghshenas, J. Onboard TDI stage estimation and calibration using SNR analysis. Paper presented at Proceedings of SPIE Conference on Sensors, Systems, and Next-Generation Satellites XXI, Warsaw, Poland, vol.10423. (2017 Sept. 11-24).
Li, Y. H., Wang, X. D., Liu, W. G. & Wang, Z. Analysis and reduction of the TDI CCD charge transfer image shift. Applied optics 56, 9233–9240 (2017).
Wang, D., Zhang, T. & Kuang, H. Clocking smear analysis and reduction for multi phase TDI CCD in remote sensing system. Optics Express 19, 4868–4880 (2011).
Lan, T., Xue, X., Li, J., Han, C. & Long, K. A high-dynamic-range optical remote sensing imaging method for digital TDI CMOS. Applied Sciences 7, 1089 (2017).
Ren, H. et al. An Improved Electronic Image Motion Compensation (IMC) Method of Aerial Full-Frame-Type Area Array CCD Camera Based on the CCD Multiphase Structure and Hardware Implementation. Sensors 18, 2632 (2018).
Hochman, G. et al. Restoration of images captured by a staggered time delay and integration camera in the presence of mechanical vibrations. Applied Optics 43, 4345–4354 (2004).
Wang, J., Yu, P., Yan, C., Ren, J. & He, B. Space optical remote sensor image motion velocity vector computational modeling, error budget and synthesis. Chinese Optics Letters 3, 414–417 (2005).
Wu, J. et al. An active-optics image-motion compensation technology application for high-speed searching and infrared detection system. Paper presented at Proceedings of SPIE Young Scientists Forum, Shanghai, China, 10710. (2017 Nov. 24-26).
Zhong, W., Deng, H., Sun, Z. & Wu, X. Computation model of image motion velocity for space optical remote cameras. Paper presented at Proceedings of IEEE International Conference on Mechatronics and Automation, Changchun, China, 588–592. (2009 Aug. 09-12).
Wang, D., Li, W., Yao, Y., Huang, H. & Wang, Y. A fine image motion compensation method for the panoramic TDI CCD camera in remote sensing applications. Optics Communications 298, 79–82 (2013).
Li, Y., Lu, P., Jin, L., Li, G. & Wu, Y. Image Motion Compensation of Off-Axis TMA Three-Line Array Aerospace Mapping Cameras. Journal of Harbin Institute of Technology 6, 013 (2016).
Li, S., Zhong, M. & Zhao, Y. Estimation and compensation of unknown disturbance in three-axis gyro-stabilized camera mount. Transactions of the Institute of Measurement and Control 37, 732–745 (2015).
Li, J., Xing, F. & You, Z. Space high-accuracy intelligence payload system with integrated attitude and position determination. Instrument 2, 3–16 (2015).
Heo, H. P. & Ra, S. W. Reducing Motion Blur by Adjusting Integration Time for Scanning Camera with TDI CMOS. International Journal of Signal Processing Systems 3, 172–176 (2015).
Ren, S., Fan, X., Zhang, F. & Su, Z. Analysis of Drift Adjustment by Space Optical Camera Platform. Paper presented at Conference of Spacecraft TT&C Technology in China, Beijing, China, 391-399. (2016 Nov. 8-10).
Li, J., Liu, Z. & Liu, S. Suppressing the image smear of the vibration modulation transfer function for remote-sensing optical cameras. Applied optics 56, 1616–1624 (2017).
Janschek, K. & Tchernykh, V. Optical correlator for image motion compensation in the focal plane of a satellite camera. Space Technology 21, 127–132 (2001).
Janschek, K., Tchernykh, V., Dyblenko, S. & Harnisch, B. Compensation of the attitude instability effect on the imaging payload performance with optical correlators. Acta Astronautica 52, 965–974 (2003).
Janschek, K., Tchernykh, V. & Dyblenko, S. Performance analysis of opto-mechatronic image stabilization for a compact space camera. Control Engineering Practice 15, 333–347 (2007).
Barjatya, A. Block matching algorithms for motion estimation. IEEE Transactions Evolution Computation 8, 225–239 (2004).
Yaakob, R., Aryanfar, A., Halin, A. A. & Sulaiman, N. A comparison of different block matching algorithms for motion estimation. Procedia Technology 11, 199–205 (2013).
Cheng, S. C. & Hang, H. M. A comparison of block-matching algorithms mapped to systolic-array implementation. IEEE Transactions on Circuits and Systems for Video Technology 7, 741–757 (1997).
Wang, C. et al. Optical flow inversion for remote sensing image dense registration and sensor’s attitude motion high-accurate measurement. Mathematical Problems in Engineering 432613, 1–16 (2014).
Ayers, G. R. & Dainty, J. C. Iterative blind deconvolution method and its applications. Optics Letters 13, 547–549 (1988).
Liang, J., Xu, T. & Ni, G. Compensation with multi motion models for images from TDI-CCD aerial camera. Paper presented at Proceedings of IEEE 2010 Symposium on Photonics and Optoelectronics, Chengdu, China, 1–5. (2010 Jun. 19-21).
Levin, A., Weiss, Y., Durand, F. & Freeman, W. T. Understanding blind deconvolution algorithms. IEEE transactions on pattern analysis and machine intelligence 33, 2354–2367 (2011).
Fish, D. A., Brinicombe, A. M., Pike, E. R. & Walker, J. G. Blind deconvolution by means of the Richardson–Lucy algorithm. JOSA A 12, 58–65 (1995).
Chan, T. F. & Wong, C. K. Total variation blind deconvolution. IEEE transactions on Image Processing 7, 370–375 (1998).
Li, J. & Liu, Z. Image quality enhancement method for on-orbit remote sensing cameras using invariable modulation transfer function. Optics Express 25, 17134–17149 (2017).
Li, J., Xing, F., Sun, T. & You, Z. Efficient assessment method of on-board modulation transfer function of optical remote sensing sensors. Optics Express 23, 6187–6208 (2015).
Li, J., Liu, Z. & Liu, F. Using sub-resolution features for self-compensation of the modulation transfer function in remote sensing. Optics Express 25, 4018–4037 (2017).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436 (2015).
Schmidhuber, J. Deep learning in neural networks: An overview. Neural networks 61, 85–117 (2015).
Deng, L. & Yu, D. Deep learning: methods and applications. Foundations and Trends® in Signal Processing 7, 197–387 (2014).
Lee, J. & Shin, S. Y. A coordinate-invariant approach to multiresolution motion analysis. Graphical Models 63, 87–105 (2001).
Boracchi, G. & Foi, A. Modeling the performance of image restoration from motion blur. IEEE Trans. Image Processing 21, 3502–3517 (2012).
Yousef, A., Li, J. & Karim, M. High-speed image registration algorithm with subpixel accuracy. IEEE Signal Processing Letters 22, 1796–1800 (2015).
Aboutajdine, D. & Essannouni, F. Fast block matching algorithms using frequency domain. Paper presented at Proceedings of IEEE 2011 International Conference on Multimedia Computing and Systems, Ouarzazate, Morocco, 1-6. (2011 Apr. 7-9).
Reddy, B. S. & Chatterji, B. N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE transactions on image processing 5, 1266–1271 (1996).
Caruana, R. & Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. Paper presented at Proceedings of ICML ‘06 Proceedings of the 23rd international conference on Machine learning, New York, NY, USA, 161-168. (2006 Jun. 25-29).
Møller, M. F. A scaled conjugate gradient algorithm for fast supervised learning. Neural networks 6, 525–533 (1993).
Hirose, Y., Yamashita, K. & Hijiya, S. Back-propagation algorithm which varies the number of hidden units. Neural Networks 4, 61–66 (1991).
Van Ooyen, A. & Nienhuis, B. Improving the convergence of the back-propagation algorithm. Neural networks 5, 465–471 (1992).
Li, J., Smithwick, Q. & Chu, D. Full bandwidth dynamic coarse integral holographic displays with large field of view using a large resonant scanner and a galvanometer scanner. Optics Express 26, 17459–17476 (2018).
Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing 13, 600–612 (2004).
Kumar, M. N. N. & Ramakrishna, S. An Impressive Method to Get Better Peak Signal Noise Ratio (PSNR), Mean Square Error (MSE) Values Using Stationary Wavelet Transform (SWT). Global Journal of Computer Science and Technology 12, 1–7 (2012).
Sheikh, H. R. & Bovik, A. C. Image information and visual quality. Paper presented at Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, Que., Canada, iii-709. (2004 May 17-21).
Stern, A. & Kopeika, N. S. Analytical method to calculate optical transfer functions for image motion and vibrations using moments. JOSA A 14, 388–396 (1997).
Tico, M. & Vehvilainen, M. Estimation of motion blur point spread function from differently exposed image frames. Paper presented at Proceedings of IEEE 14th European Signal Processing Conference, Florence, Italy, 1-4. (2006 Sept. 4-8).
Jian, Y., Yao, R., Mulnix, T., Jin, X. & Carson, R. E. Applications of the line-of-response probability density function resolution model in PET list mode reconstruction. Physics in Medicine & Biology 60, 253 (2014).
Khireddine, A., Benmahammed, K. & Puech, W. Digital image restoration by Wiener filter in 2D case. Advances in Engineering Software 38, 513–516 (2007).
Kondo, K., Ichioka, Y. & Suzuki, T. Image restoration by Wiener filtering in the presence of signal-dependent noise. Applied Optics 16, 2554–2558 (1977).
Acknowledgements
National Natural Science Foundation of China (NSFC) under Grant 61875180; the National Key Research and Development Plan of China under Grant 2017YFF0205103.
Author information
Authors and Affiliations
Contributions
J.L. designed initial experimental scheme. Z.L. performed the simulations. J.L. and Z.L. analyzed the experiments data and wrote the manuscript. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, J., Liu, Z. High-resolution dynamic inversion imaging with motion-aberrations-free using optical flow learning networks. Sci Rep 9, 11319 (2019). https://doi.org/10.1038/s41598-019-47564-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-47564-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.