Abstract
We develop an effective theory approach to investigate the phase properties of globular proteins. Instead of interactions between individual atoms or localized interaction centers, the approach builds directly on the tertiary structure of a protein. As an example we construct the phase diagram of (apo)myoglobin with temperature (T) and acidity (pH) as the thermodynamical variables. We describe how myoglobin unfolds from the native folded state to a random coil when temperature and acidity increase. We confirm the presence of two molten globule folding intermediates, and we predict an abrupt transition between the two when acidity changes. When temperature further increases we find that the abrupt transition line between the two molten globule states terminates at a tricritical point, where the helical structures fade away. Our results also suggest that the ligand entry and exit is driven by large scale collective motions that destabilize the myoglobin F-helix.
Similar content being viewed by others
Introduction
In the description of a complex system such as a protein, it is often impractical, if not impossible, to accurately model physical phenomena with a “fundamental” level precision. For example, practical chemistry, including even precision first-principles quantum chemistry, is never concerned with the detailed structure of the atomic nucleus. Instead, one focuses on a few key variables and constructs an effective theory for those. In many circumstances and in particular when the system admits either symmetries or a separation of scales, the reduced set of variables can then be treated on its own right.
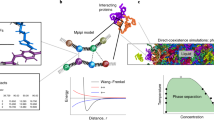
In the case of proteins, the great success of structural classification schemes such as SCOP1 and CATH2 and many others3, demonstrates that folded proteins are built in a modular fashion, and from a relatively small number of components that are made of several amino acids. Here we exploit this modularity of protein structures to construct the phase diagram of globular proteins, with temperature (T) and acidity (pH) as the thermodynamical variables. The methodology that we develop is very general and applicable to most globular proteins4, even though we here develop it using myoglobin (Mg)5,6,7 as a concrete example: Our approach is based on the Landau-Ginsburg-Wilson (LGW) paradigm8,9 which is a systematic way to construct effective theories that model the properties of different phases in a material system, and transitions between them. Instead of individual atoms or other highly localized interaction centers and their mutual interactions, our effective theory description employs the entire tertiary structure of a protein as the fundamental constituent: We describe the protein backbone as a single multi-soliton10,11. This multi-soliton acts as an attractor in the energy landscape, it is a minimum free energy state towards which other conformations become funneled. Indeed, a multi-soliton solution to a non-linear difference (differential) equation is the paradigm structural self-organizing principle in many physical scenarios. Here it emerges as a stable solution to a variational equation that we obtain from the LGW free energy, and it governs the mutual interactions between the individual solitons that model the super-secondary structures (helix-loop-helix etc.) of the protein.
The advantage of the LGW formalism in combination with the soliton-concept is computational efficiency, over any other approach to protein dynamics that we are aware of; the method enables us to perform numerical simulations and analyses with very high efficiency. Similar approaches have proven highly successful in many complex scenarios with extended filament-like objects, from the description of interacting superconducting vortex lines to complex knotted fluxtubes12,13. Indeed, the evaluation of a T−pH phase diagram of any protein using e.g. molecular dynamics would be unthinkable, with presently available computers.
Myoglobin is a stable, relatively simple globular protein that is the paradigm example in protein folding and unfolding studies14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30. It plays an important role in biological processes such as electron transfer, oxygen delivery, catalysis and signaling. In particular, myoglobin can bind small non-polar ligands such as O2, CO, and NO in its interior, where they become attached to the iron atom of the heme. The native folded state (N) of myoglobin is very compact, and supports eight α-helices (labelled A to H). Since there is no apparent static channel for the ligands to enter and exit, myoglobin must undergo conformational deformations for the ligands to pass5,6,7,31,32,33,34,35,36. These deformations are regulated by changes in physiological conditions in particular by variations in temperature and/or acidity. Several experiments have been performed to investigate (un)folding pattern of myoglobin as a function of pH, mostly at room temperature. These experiments reveal that the (un)folding proceeds reversibly and sequentially, according to a four-state scheme: At low pH values near or below around pH~2 the structure resembles a random coil (U). In the vicinity of the regime \({\rm{2}}\lesssim pH\lesssim 4\) two folding intermediates Ia and Ib can be found18,19, both akin a molten globule37,38 with a structure that changes with varying pH. When pH reaches values that are above 4–4.5 (apo)Mg starts entering its native folded state. Overall, the transitions seems to proceed according to the scheme N ↔ Ib ↔ Ia ↔ U as the acidity changes18. Variable-T experiments are less common, but the results are quite similar27,28,29: At very low temperatures and near neutral pH, the structure of Mg is in the folded native state N; the F-helix of apoMg is disordered, even at relatively low temperatures. Below T~340 K and close to neutral pH the structure remains in the vicinity of its native state. When T increases further Mg becomes a molten globule, and when T becomes even higher the helical content starts to decrease: The first to unfold is helix F followed by helices B,C,D and E. Then the helices A, G and H loose their stability. At very high temperatures the structure resembles a random coil.
Methods
Our effective theory approach describes the (virtual) Cα protein backbone in terms of the (virtual) bond (θ) and torsion (ϕ) angles. To evaluate these coordinates, we frame the Cα backbone by the mutually orthonormal backbone tangent (ti), binormal (bi) and normal (ni) vectors
where ri (i = 1,..., n) are the Cα coordinates. These vectors are subject to the discrete (Frenet) equation39
Here T2 and T3 generate three dimensional rotations, with (Ti)jk = εijk. From (1), (2) we can determine (θi, ϕi) in terms of the Cα coordinates ri. Conversely, when θi and ϕi are all known we can reconstruct the ri by solving (2) (for details see Supplementary Material) when we assume that the distance between neighboring Cα atoms remains close to the average value ~3.8 Å: A good quality all-atom approximation of the entire heavy atom structure of a protein can always be reconstructed from the knowledge of the (θ, ϕ) coordinates3,40,41,42,43. In particular, we may employ (θi, ϕi) as the variables in a free energy that models the protein backbone.
Previously, a number of effective energy functions for the Cα backbone have been constructed using the coordinates (θi, ϕi). Familiar examples include the fully flexible chain model and its extensions44,45,46, that are widely used in studies of biological macromolecules and other filament-like objects.
Here we introduce a free energy description that is designed to model folded proteins and their properties at the level of the tertiary structures39,47,48,49,50,51. The structure of the energy landscape is determined by the following free energy (for details see Supplementary Material)
In the first sum of (3) we recognize the structure of the energy function of the discretized non-linear Schrödinger (DNLS) equation in the Hasimoto representation10. The second sum of (3) then extends the DNLS energy function so that it model folded proteins: The first two terms in the second sum are both among the conserved charges in the DNLS hierarchy, they are called the momentum and the helicity respectively. Both of these terms are odd in torsion angles, thus they break parity which makes the backbone (right-handed) chiral. The third term of the second sum is the Proca mass, together with the second term in the first sum it comprises the original Kirchhoff energy of an elastic rod45. Finally, the last term is a hard-core Pauli repulsion with a step-wise profile, it ensures that the distance between any two Cα atoms is at least 3.8 Å (for detailed analysis of V(r) see51).
Note that there is no need to introduce any long distance contribution to V(r). The long distance interactions are already accounted for by the properties of the solution to the extended DNLS equation: The DNLS equation is the prototype integrable difference equation that supports solitons as its classical solutions. Solitons are the paradigm examples of extended self-organized objects in a physical system11. For appropriate parameter values the DNLS free energy (3) models the entire tertiary structure of a given folded protein backbone, as a single stable minimum energy multi-soliton solution to the variational equations
The multi-soliton profile then describes the various super-secondary structures such as helix-loop-helix (regular-loop-regular) as mutually interacting individual solitons52,53. Over a single soliton profile the parameter values in (3) are uniform, and since a soliton extends over several amino acids the number of parameters is generically much smaller than the number of amino acids. In the case of a myoglobin, we use the Protein Data Bank (PDB) structure 1ABS (sperm whale)33 as a decoy to construct the parameters. This structure has been measured at the very low liquid helium temperature value of around 20 Kelvin and as a consequence the thermal B-factors are very small. We identify ten individual DNLS solitons profiles along the 154 residue 1ABS backbone that become combined into a single multi-soliton solution of the DNLS equations (4), (5) with ~0.8 Å Cα root-mean-square-distance (RMSD) precision47 (see also Supplementary Material).
We construct the T-pH phase diagram by computing the grand canonical ensemble of statistical physics, and evaluate the observables \({\mathscr{O}}(\theta ,\phi )\) by averaging them over all possible tertiary structures, weighted by the grand canonical distribution with free energy (3):
Here \({\mathscr{Z}}\) is a normalization factor, β is the inverse temperature factor and μN is a chemical potential contribution to be specified. Since the trace extends over all possible tertiary structures, the entropy contribution relates to the number of all possible tertiary structures. We evaluate (6) numerically, using the Glauber algorithm with acceptance ratio determined by the probability distribution51,54,55
Here \(\Delta ( {\mathcal F} -\mu N)\) is the variation of \( {\mathcal F} -\mu N\) between consecutive Monte Carlo steps. We note that Glauber algorithm models pure relaxation dynamics, and for simple systems it reproduces Arrhenius law. At the same time it has been found that small proteins fold according to Arrhenius law56. We also note that the (inverse of the) Glauber temperature factor β does not coincide with physical temperature factor kT where k is the Boltzmann constant and T is measured in Kelvin’s, instead the relation is determined by renormalisation group techniques47,57.
We determine the chemical potential contribution in (6), by recalling the Henderson-Hasselbalch equation58 that relates the concentrations of protonated and non-protonated amino acids to the difference between pH and acid dissociation constant pKa. On the other hand, Gibbs free energy is commonly taken to vary with acidity as follows,
where \({{\mathscr{P}}}_{H}^{a}\) is the protonation probability of a particular amino acid. Histidine with pKa~6.0 is the only amino acid in the genetic code that has strong reactivity to pH variations in the physiologically important range from pH~8 down to pH~4. For lower pH both glutamic acid (pKa~4.2) and aspartic acid (pKa~3.9) need to be accounted for. For simplicity, here we only aim to model the phase diagram for pH above ~4 and up to neutral value so that we only need to account to the contribution of the \({N}_{H}^{his}=12\) histidines in 1ABS. Then
and to leading order
We recognize in (9) the format of the Glauber transition probability (7). Moreover, since the DNLS hierarchy admits a unique conserved number operator N~θ2 10 we propose that in the LGW approach
where the summation extends over the histidines of 1ABS. As a consequence, to leading order in the LGW approximation μ depends linearly on pH. We also note that for 1ABS pH = 9.0. Accordingly we normalize μ = 0 at that value, to ensure that the ensuing multi-soliton profile models the 1ABS backbone.
As order parameters a.k.a. reaction coordinates we use the radius of gyration Rg and the α-helical content \({{\mathscr{Q}}}_{\alpha }\). We compute their (T, μ) dependence numerically from (6). We take a Cα atom to be in an α-helical posture when for (θi, ϕi) both |θi−θ0| ≤ 0.14 (rad) and |ϕi−ϕ0| < 0.3 (rad) where θ0 = 1.55 and ϕ0 = 0.9 are the PDB average values of the α-helical bond and torsion angle. The \({{\mathscr{Q}}}_{\alpha }\) counts the relative number of residues in α-helical posture as a function of T and pH; most PDB myoglobins have a \({{\mathscr{Q}}}_{\alpha }\) value 72–78%, and for 1ABS \({{\mathscr{Q}}}_{\alpha }=72 \% \).
We have simulated 5.000 independent heating and cooling (unfolding and folding) trajectories using the Glauber algorithm, obtained by varying the (inverse) temperature factor β; the trajectories are equally distributed between 50 values of μ ∈ [0, 0.05]. Along each trajectory we first increase temperature (i.e. decrease β) at an adiabatically slow rate, so that the system remains very close to a thermal equilibrium for all β. The value of β is also kept at its high temperature value for a large number of simulation steps, for full thermalization. Finally, the system is brought back to the low temperature value, by reversal of the heating procedure: We have been extremely careful to always thermalize the ensemble before we evaluate any observable51.
Results
In Fig. 1 we compare the μ = 0 temperature dependence of the observable \({{\mathscr{Q}}}_{\alpha }\) to experimentally measured α-helicity of (horse heart) myoglobin during thermal denaturation. The experimental data is adapted from28. We use this Figure to relate the Glauber temperature TG to Celsius scale. Accordingly, our simulations cover the range 0 °C–120 °C at each μ value. The Figs 2–5 summarizes our findings:
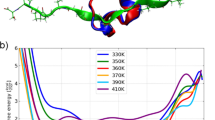
Fig. 2 shows the helix (dis)ordering during a heating and cooling simulation cycle, as a function of temperature at μ = 0 and in terms of the average value of torsion angles ϕ; we recall that for an α-helix ϕ ≈ 1 (rad).
We observe that F-helix starts to disorder soon after T = 20 °C and becomes fully randomized slightly above T = 40 °C. The next to disorder are the helices B, C, D and E; this occurs near T = 90 °C. This is followed by disordering of the helices H and A, and the helix G is last to disorder. Slightly above T = 100 °C the entire chain is fully randomized; according to Fig. 1, at these temperature values \({{\mathscr{Q}}}_{\alpha }\) also reaches its high temperature asymptotic value. All these simulation results are fully in line with experimental observations24.
Fig. 3 identifies the simulated phase structure on the (T, μ) plane in terms of radius of gyration Rg. For μ ≈ 0 we confirm the findings of the Figs 1 and 2: The native state (N) is a region with low temperature (T < 30 °C) and very small values μ < 0.003. Beyond this there is a region where the F-helix (dis)orders (F), it extends to around T ≈ 40 °C and to μ-values up to μ ≈ 0.01. When T and μ increase further, we identify a phase that we denote Ib and identify as a molten globule intermediate; the radius of gyration values are above 20 Å but below 28 Å in this region, depending on values of T and μ.
We propose that the high sensitivity of the F-helix that we observe, when either temperature or acidity increases from their low values, controls the ligand entry and exit: The F-helix contains the proximal histidine that is connected to the heme. Thus disordering of the F-helix may expose the heme, for ligand transport.
At μ ≈ 0.027 and for values T < 80 °C we observe a rapid transition: The radius of gyration decreases in a jump-like fashion, by around 4–6 Å depending on T. We interpret this to be a transition between two molten globule intermediates so that for μ > 0.027 we have the second molten globule Ia18,19.
Most notably, we observe the presence of an apparent tricritical point, in conjuction with the two molten globule states: The transition line between Ia and Ib terminates at around T ≈ 80 °C when both molten globules simultaneously enter the random coil phase.
The different regions of the phase diagram in Fig. 3 can be scrutinized using the detailed Rg values. In Fig. 4 we show how Rg varies as a function of μ, at T = 0 °C. We observe a clear change in the derivate of Rg w.r.t. μ at around μ ≈ 0.003 and also around μ ≈ 0.01. These correspond to the transitions between the N and F, and between the F and Ib regions in the phase diagram on Fig. 2. Note that the Rg value of the molten globule Ib is very close to the experimentally reported value Rg~23.6 Å16,21,24.
We also have a jump-like (discontinuous) transition in Rg values at around μ = 0.027, between the two molten globules Ib and Ia.
Finally, in Fig. 5 we display the values of \({{\mathscr{Q}}}_{\alpha }\) that counts the relative number of residues in α-helical posture, for T < 40 °C. We observe that there is only a weak dependence on μ, even though we do note a slight change in the overall stability of helix-F even at relatively small μ values. We conclude that at low temperatures the increase of μ appears to have a stronger influence on loops than on helices. In particular, the ligand transport mechanism if indeed associated with instability in helix-F, appears to engage the adjacent loop structures as well.
Comparison between simulated (sperm whale) value \({{\mathscr{Q}}}_{\alpha }\) that counts the relative number of residues in α-helical posture, and experimentally determined (horse heart) α-helical content during thermal denaturation. Experimental data is adapted from28.
The results in Fig. 5 are consistent with room temperature CD helicity measurements that report only minor signal variations for pH values above ~4.523: Acidity does not have a strong effect on the hydrogen bonds that stabilize the helical structures. In the Figure we identify the transition between Ib and Ia, in terms of a region with (slightly) decreased value of \({{\mathscr{Q}}}_{\alpha }\). It is also notable that right prior to the transition, there is region in Ib with an enhanced \({{\mathscr{Q}}}_{\alpha }\) values.
Discussion
In summary, we have proposed to model protein thermodynamics directly at the tertiary level of structures, in terms of the multi-soliton solution of the DNLS equation. We have numerically evaluated the ensuing grand canonical partition function at finite temperature and chemical potential, with the latter identified by comparison with the Henderson-Hasselbalch equation. As an example we have constructed the (T, pH) phase diagram of myoglobin. All our results are in a good agreement with experimental observations. In particular, the ordering of helix stabilization and the emergence of two molten globules are qualitatively in full agreement with experimental observations. Furthermore, we observe that the F-helix with its proximal histidine, is the first to loose stability as either temperature or acidity increase from neutral values. This supports that the destabilization of the F-helix region might have a pivotal role for ligand entry and exit. We have also made predictions for future experiments, in particular we have proposed that at high temperatures near T = 80 °C there is an apparent tricritical point where the two molten globules come together with the random coil phase. Our results show that effective theories that model protein structure directly at the tertiary structure level, can provide a viable computational approach to investigate the phase structure of complex globular proteins.
References
Murzin, A. G., Brenner, S. E., Hubbard, T. & Chothia, C. Scop: a structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 247, 536 (1995).
Dawson, N. L. et al. Cath: an expanded resource to predict protein function through structure and sequence. Nucleic Acids Res. 45, D289–D295 (2017).
Holm, L. & Sander, C. Database algorithm for generating protein backbone and side-chain coordinates from a cα trace: Application to model building and detection of coordinate errors. Journ. Mol. Biol. 218, 183–194 (1991).
Peng, X., He, J. & Niemi, A. J. Clustering and percolation in protein loop structures. BMC Struc. Biol. 15, 22 (2015).
Kendrew, J. C. et al. A three-dimensional model of the myoglobin molecule obtained by x-ray analysis. Nat. 181, 662 (1958).
Perutz, M. et al. Structure of haemoglobin: a three-dimensional fourier synthesis at 5.5-å resolution, obtained by x-ray analysis. Nat. 185, 416 (1960).
Kendrew, J. et al. Structure of myoglobin: A three-dimensional fourier synthesis at 2 å resolution. Nat. 185, 422 (1960).
Wilson, K. G. & Kogut, J. The renormalization group and the ε expansion. Phys. Repts. 12, 75 (1974).
Goldenfeld, N. Lectures on phase transitions and the renormalization group (Addison-Wesley, Reading, 1992).
Takhtadzhyan, L. A. & Faddeev, L. D. Hamiltonian approach to soliton theory (Springer, Berlin, 1987).
Manton, N. & Sutcliffe, P. Topological Solitons (Cambridge University Press, Cambridge, 2004).
Svistunov, B. V., Babaev, E. S. & Prokof’ev, N. Superfluid States of Matter (CRCPress, Boca Raton, 2015).
Battye, R. & Sutcliffe, P. M. Solitons, links and knots. Proc. Royal Soc. A455, 4305–4331 (1999).
Griko, Y. V., Privalov, P. L., Venyaminov, S. Y. & Kutyshenko, V. P. Thermodynamic study of the apomyoglobin structure. Journ. Mol. Biol. 202, 127–138 (1988).
Jennings, P. A. & Wright, P. E. Formation of a molten globule intermediate early in the kinetic folding pathway of apomyoglobin. Sci. 262, 892–896 (1993).
Eliezer, D. et al. The radius of gyration of an apomyoglobin folding intermediate. Sci. 270, 487–488 (1995).
Eliezer, D. & Wright, P. E. Is apomyoglobin a molten globule? structural characterization by nmr. Journ. Mol. Biol. 263, 531–538 (1996).
Jamin, M. & Baldwin, R. L. Two forms of the ph 4 folding intermediate of apomyoglobin. Journ. Mol. Biol. 276, 491–504 (1998).
Jamin, M., Yeh, S. R., Rousseau, D. L. & Baldwin, R. L. Submillisecond unfolding kinetics of apomyoglobin and its ph 4 intermediate. Journ. Mol. Biol. 292, 731–740 (1999).
Uzawa, T. et al. Collapse and search dynamics of apomyoglobin folding revealed by submillisecond observations of (alpha)-helical content and compactness. PNAS (USA) 101, 1171–1176 (2004).
Nishimura, C., Dyson, H. J. & Wright, P. E. Identification of native and non-native structure in kinetic folding intermediates of apomyoglobin. Journ. Mol. Biol. 355, 139–156 (2006).
Uzawa, T. et al. Hierarchical folding mechanism of apomyoglobin revealed by ultra-fast h/d exchange coupled with 2d nmr. PNAS (USA) 105, 13859 (2008).
Aoto, P. C., Nishimura, C., Dyson, H. J. & Wright, P. E. Microsecond folding dynamics of apomyoglobin at acidic ph. Biochem. 53, 3767 (2014).
Dyson, H. J. & Wright, P. E. Microsecond folding dynamics of apomyoglobin at acidic ph. Acc. Chem. Res. 50, 105 (2017).
Hargrove, M. S. & Olson, J. S. The stability of holomyoglobin is determined by heme affinity. Biochem. 35, 11310–11318 (1996).
Culbertson, D. S. & Olson, J. S. Microsecond folding dynamics of apomyoglobin at acidic ph. Biochem. 49, 6052–6063 (2010).
Ochiai, Y. et al. Thermal denaturation profiles of tuna myoglobin. Biosci. Biotech. Biochem. 74, 1673–1679 (2010).
Moriyama, Y. & Takeda, K. Critical temperature of secondary structural change of myoglobin in thermal denaturation up to 130 oc and effect of sodium dodecyl sulfate on the change. J. Phys. Chem. B114, 2430–2434 (2010).
Ochiai, Y. Temperature-dependent structural perturbation of tuna myoglobin. World Acad. Sci. Eng. Technol. 5, 2–24 (2011).
Xu, M., Beresneva, O., Rosario, R. & Roder, H. Microsecond folding dynamics of apomyoglobin at acidic ph. J. Phys. Chem. B116, 7014–7025 (2012).
Elber, R. & Karplus, M. Enhanced sampling in molecular dynamics: use of the time-dependent hartree approximation for a simulation of carbon monoxide diffusion through myoglobin. J. Am. Chem. Soc. 112, 9161 (1990).
Huang, X. & Boxer, S. G. Discovery of new ligand binding pathways in myoglobin by random mutagenesis. Nat. Struct. Biol. 1, 226 (1994).
Schlichting, I., Berendzen, J., Phillips, G. N. & Sweet, R. M. Crystal structure of photolysed carbonmonoxy-myoglobin. Nat. 371, 808 (1994).
Teng, T. Y., Schildkamp, W., Dolmer, P. & Moffat, K. Two open-flow cryostats for macromolecular crystallography. J. Appl. Crystallogr. 27, 133 (1994).
Tilton, R. F., Kuntz, I. D. & Petsko, G. A. Cavities in proteins: structure of a metmyoglobin xenon complex solved to 1.9. ang. Biochem. 23, 2849 (1984).
Krokhotin, A., Niemi, A. J. & Peng, X. On the role of thermal backbone fluctuations in myoglobin ligand gate dynamics. Journ. Chem. Phys. 13, 175101 (2013).
Ohgushi, M. & Wada, A. Molten globule state: a compact form of globular proteins with mobile side chains. FEBS Lett. 164, 21–24 (1983).
Ptitsyn, O. B., Pain, R. H., Semisotnov, G. V., Zerovnik, E. & Razgulyaev, O. I. Evidence for a molten globule state as a general intermediate in protein folding. FEBS Lett. 262, 20–24 (1990).
Hu, S., Lundgren, M. & Niemi, A. J. Discrete frenet frame, inflection point solitons, and curve visualization with applications to folded proteins. Phys. Rev. E83, 061908 (2011).
DePristo, M. A., Bakker, P. I. W., Shetty, R. P. & Blundell, T. L. Discrete restraint-based protein modeling and the cα-trace problem. Prot. Sci. 12, 12032–2046 (2003).
Lovell, S. C. et al. Structure validation by cα geometry. Proteins 50, 437–450 (2003).
Rotkiewicz, P. & Skolnick, J. Fast procedure for reconstruction of full-atom protein models from reduced representations. Journ. Comp. Chem. 29, 1460–1465 (2008).
Li, Y. & Zhang, Y. Remo: A new protocol to refine full atomic protein models from c-alpha traces by optimizing hydrogen-bonding networks. Proteins 76, 665–676 (2009).
Kratky, O. & Porod, G. Röntgenuntersuchung gelöster fadenmoleküle. Rec. Trav. Chim. Pays-Bas. 68, 1106–1123 (1949).
Marko, J. F. & Siggia, E. D. Bending and twisting elasticity of dna. Macromol. 27, 981–988 (1994).
Bergou, M., Wardetzky, M., Robinson, S., Audoly, B. & Grinspun, E. Discrete elastic rods. ACM Trans. Graph. (SIGGRAPH) 27, 1 (2008).
Peng, X., Sieradzan, A. K. & Niemi, A. J. Thermal unfolding of myoglobin in the landau-ginzburg-wilson approach. Phys. Rev. E94, 062405 (2016).
Niemi, A. J. Phases of bosonic strings and two dimensional gauge theories. Phys. Rev. D67, 106004 (2003).
Danielsson, U. H., Lundgren, M. & Niemi, A. J. Gauge field theory of chirally folded homopolymers with applications to folded proteins. Phys. Rev. E82, 021910 (2010).
Niemi, A. J. What is life - sub-cellular physics of live matter. In Chamon, C., Goerbig, M. O., Moessner, R. & Cugliandolo, L. F. (eds) Topological Aspects of Condensed Matter Physics: Lecture Notes of the Les Houches Summer School (Oxford University Press, Oxford, 2017).
Sinelnikova, A., Niemi, A. J. & Ulybyshev, M. Phase diagram and the pseudogap state in a linear chiral homopolymer model. Phys. Rev. E92, 032602 (2015).
Chernodub, M., Hu, S. & Niemi, A. J. Topological solitons and folded proteins. Phys. Rev. E82, 011916 (2010).
Molkenthin, N., Hu, S. & Niemi, A. J. Discrete nonlinear schrödinger equation and polygonal solitons with applications to collapsed proteins. Phys. Rev. Lett. 106, 078102 (2011).
Glauber, R. Time-dependent statistics of the ising model. Journ. Math. Phys. 4, 294 (1963).
Berg, B. A. Markov Chain Monte Carlo Simulations And Their Statistical Analysis (World Scientific, Singapore, 2014).
Scalley, M. L. & Baker, D. Protein folding kinetics exhibit an arrhenius temperature dependence when corrected for the temperature dependence of protein stability. PNAS (USA) 94, 10636 (1997).
Krokhotin, A., Lundgren, M., Niemi, A. J. & Peng, X. Soliton driven relaxation dynamics and protein collapse in the villin headpiece. J. Phys.: Cond. Mat. 25, 325103 (2013).
Po, H. N. & Senozan, N. M. The henderson-hasselbalch equation: its history and limitations. J. Chem. Educ. 78, 1499 (2001).
Acknowledgements
The research was carried out within the state assignment of the Ministry of Science and Education of Russia (Grant No. 3.6261.2017/8.9). The research by A.N. was supported by a grant from VR, and by Qian Ren grant at BIT. Open access funding provided by Stockholm University.
Author information
Authors and Affiliations
Contributions
A.M. and A.N. conceived the study. A.B. and A.M. performed the simulations. All authors contributed to analysis. A.N. wrote the article. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Begun, A., Molochkov, A. & Niemi, A.J. Protein tertiary structure and the myoglobin phase diagram. Sci Rep 9, 10819 (2019). https://doi.org/10.1038/s41598-019-47317-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-47317-y
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.