Abstract
An investigation of simultaneous dynamic mass and length change measurement for wood is presented. In contrast to the equilibrium in moisture content and swelling and shrinking, where extensive data exists for different wood species, less information is available for the dynamics of moisture changes in direct comparison to the related dimensional changes during the sorption process. This is due to a lack of methods. A gravimetric sorption system, equipped with a high resolution camera and an automated image evaluation, is used to examine simultaneous effects of water vapour sorption dynamics and dimensional change. This method proves a strong correlation between mass and dimensional change, which is in contrast to other investigations. Equilibrium moisture content as well as swelling and shrinking data is in good agreement with literature and manual measurements. The method enables the possibility to determine swelling and shrinking values in-situ without disturbing the targeted climatic conditions. The system is applicable for the investigation of natural wood, modified wood, wood composites or other lignocellulosic materials.
Similar content being viewed by others
Introduction
All wood and other lignocellulosic materials contain a certain amount of water in their service conditions. This water exerts an important impact on many properties of the material.
Wood as hydrophilic material structure is influenced by water sorption. Depending on the surrounding conditions, wood can uptake (absorption) or release water (desorption). Within this process, swelling and shrinking take place below fibre saturation in all anatomical directions1,2.
In the last decades a wide range of studies have been carried out to determine wood-water-interactions and several reviews have been done1,3,4. Reliable data for mass and dimensional changes caused by sorption phenomena are important for the mathematical modelling of water sorption processes5,6. Newer studies showed that sorption data from the Forest Products Laboratory, Wood Handbook Chapter 47, used for a wide range of publications and calculations, seem not to be reliable enough for scientific purposes8,9. Therefore, accurate sorption data are of great interest for engineering and research purposes.
The moisture content as well as swelling and shrinking values between different equilibriums are well known for different wood species10. Less information is available for the speed of moisture change and the related dimensional change within the sorption process. This is due to a lack of available methods, which are needed for these investigations. For this purpose, a balance with high resolution placed in a defined and controlled environment with a combined method to measure the sample dimensions is needed.
Existing methods for measuring swelling and shrinking are usually based on equilibrium state values. The dynamic determination of sample dimensions in varying climate conditions is an important technique to characterize wood, composites, modified wood or other hygroscopic materials. This information can be used to improve the basic understanding of structure and behaviour of lignocellulosic materials.
Sorption isotherms based on equilibrium moisture content (EMC) can be determined by dynamic vapour sorption (DVS) systems11,12,13,14. These systems often allow only one or two samples to be measured at the same time. A system to study the sorption isotherms with 100 samples in parallel at the same time was recently developed by Zelinka et al.15. More samples measured in same conditions in one experiment offer a better comparability between the results. These methods are not able to determine the sample dimensions.
Measuring systems differ depending on the level of resolution. On microscopic level, swelling was investigated by phase-contrast X-ray tomography16 and neutron imaging17. As these methods require expensive and rarely available equipment another option are macroscopic measurements. At this scale, laser displacement sensors can be used18. Redman et al.19 used a microbalance and scanning laser micrometres to investigate dimensional changes. Ma et al.20 investigated wood samples with an electronic balance and recorded the radial and tangential dimensional changes via CCD laser displacement sensors. One main result found by the authors was a slower moisture change compared to the dimensional change. Dimensional changes were typically recorded by laser sensors or determined by algorithms that consider the area or the width in one direction. Consequently, more advanced algorithm need to be developed, where the preliminary study of Rosner et al.17 serve as a basis. In this respect, cameras with CCD sensors for imaging combined with sensible balance systems are promising equipments21. With these systems, the dimensional change can be observed in several directions within one measurement leading to more reliable data.
Based on existing literature the dimensional change within the sorption process can be described in the following way. Generally, values of swelling and shrinking depend on the species22. When focusing on the anatomical direction of one species the dimensional change in the longitudinal direction is lower than in radial or tangential direction1,16. Longitudinal length change is below 1% in the hygroscopic range23. These dimensional changes show a linear behaviour between a moisture content of 5 and 20%24,25. Compared to sorption isotherms hysteresis is only shown when the dimensional change is plotted over relative humidity (r.h.)26. When swelling and shrinking are plotted over moisture content hysteresis disappears27,28.
For comparison of sorption data, the applied handling procedure is important. Only when starting with fully saturated samples a sorption isotherm can be collected, otherwise the measured data will present a scanning isotherm29,30. Therefore, sample preparation with water saturation is important for reliable results29.
The present study presents a new approach for a combined determination of mass and dimensions during a dynamic change of the environmental conditions. The method offers the investigation of water vapour sorption in combination with in-situ measuring dimensional change in two directions with multiple samples. The general use and possible deviations of the system are presented.
Results
Swelling and shrinking
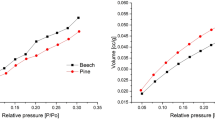
The method is able to record a precise mass change over relative humidity. Standard sorption isotherms for different materials in equilibrium can be measured (Fig. 1, left). With the additional setup, an in-situ observation of swelling and shrinking is possible in high resolution. In Fig. 1 (right) the EMC values of swelling and shrinking in dependence to relative humidity for beech and pine are shown. The change in radial direction is approximately half compared to the tangential direction. A hysteresis between absorption and desorption is clearly observable.
Figure 2 displays the equilibrium state after swelling or shrinking over moisture content. The absorption and desorption curves follow the same line and hysteresis disappears. At lower moisture contents (zero to five %) absorption and desorption show a slightly non-linear behaviour. The desorption is slightly different for beech at higher moisture contents compared to pine. A slight crossing of desorption and absorption lines can be observed for beech.
Additionally to the evaluation of moisture and dimension at equilibrium, the dynamics of the sorption above and below fibre saturation can be analysed. The sorption dynamics of drying from fully water soaked condition to 0% and remoistening to 85% relative humidity are shown in Fig. 3. Drying does not cause a shrinking up to 40% moisture content for beech and 30% for pine, respectively. The transition between drying without shrinking and a linear relation between moisture content and shrinking is very abrupt for pine (between 32% and 28% moisture content) in contrast to beech, where transition starts at approx. 40% and ends at 20% moisture content.
Using the maximal and minimal measured dimensions of the samples, the maximum and differential swelling was calculated. Table 1 depicts the values compared to literature31 and manually measured samples prepared in a climate chamber. The differential swelling from the developed method is in good agreement with the compared data (Table 1) and the manual measurement.
Figure 4 displays a comparison between data sets gained from the developed measurement system and manual measurements made from the identical raw material. The results show that the swelling and shrinking values of the developed measurement system are in good agreement with the manual measurements.
Sorption dynamics
The simultaneous measurement of sample size and moisture content without disturbing the environment offers the opportunity to compare the dynamics of both processes. This analysis is shown in Fig. 5 for pine as example between 80% and 85% relative humidity. The values gained from the experiment for swelling (range from min 3.02% to 3.38% radial; 5.30% to 6.00% tangential) and moisture content (range from min 16.88% to max 18.44%) were normalized, plotted and a linear curve fitting was applied. There is a strong linear correlation between moisture content and swelling (R² from 0.98 to 0.99) showing that water uptake and volume change in wood occur at the same rate within the given range of relative humidity. This proves that the absorbed water causes a direct change in the sample size. In total, no significant difference between the processes of water sorption and swelling or shrinking can be seen.
Wood samples with the square area of 20 mm × 20 mm and different thicknesses in longitudinal direction (1, 3, 5, 10, 20 mm) were measured by the developed measurement system for determining the ideal sample thickness prior to the final measurements. Desorption took place from fully saturated samples to 0% relative humidity. Afterwards, absorption was measured starting from 0% to 80% relative humidity. As an example, Fig. 6 displays the moisture content of pine during desorption over time.
Depending on the measurements with different sample thicknesses, an approximate equilibrium was calculated for the absorption and desorption speed (Table 2). Here, the original values were rounded to three decimal places. Then the first point where the difference to its successor was zero was used. After comparing this time between the different samples, the smallest sample size of 1 mm would be ideal for the measurements. A sample size of 1.5 mm thickness was chosen based on a trade-off between a fast sorption rate (i.e. for an effective measurement time) while still having a representative biological structure (i.e. cell wall geometry) of the samples.
The measurement system showed a low long-term variability over a period of 250 h, tested for one sorption step (Fig. 7). Between 50 h and 250 h, the moisture content of pine samples showed a range (max-min) of 0.30%, the swelling in radial direction a range (max-min) of 0.65% and the swelling in tangential direction a range (max-min) of 0.43%.
Discussion
Gravimetric data measured was reliable and highly correlates with existing literature32,33,34,35. Swelling and shrinking of specimens could be determined in-situ without disturbing the surrounding climatic conditions, which leads to more precise results. With the shown resolution, EMC points for isotherms can be determined and dynamic measurements can be realized. The results of swelling and shrinking are in agreement with literature values as well as manual measurements in a climate chamber. Dynamic data evaluation features a strong correlation between mass and length change, which is in opposite to the findings of Ma et al.20.
Holding times of water vapour sorption measurements are under critical debate36,37. Our equilibrium settings of mass change lower than 0.01% within 60 minutes calculated by linear regression of the last five measurement points would correspond to 0.00016% min−1. This value is in good agreement with the findings of Glass et al.37 who recommend the usage of 0.0003% min−1 as EMC criteria. This is supported by long-term measurements, where the difference between the used EMC criteria and longer sorption time is negligible (Fig. 7).
Although the presented values for absolute and differential swelling and shrinking are in good agreement with literature, several aspects need to be addressed. The beech samples probably warped with different moisture contents, which might cause an increased variation of results. On the other hand, the crossing of absorption and desorption of beech samples was also seen by Chauhan and Aggarwal38. A non-linear curve shape at the beginning or at the end of the isotherm was also seen for beech by Hartley & Avramidis24, for tropical hardwoods by Hernández39 and for eucalyptus by Kelsey40.
The non-linear curve of desorption from fibre saturation to 20% moisture content for beech could not be clarified by now (Fig. 3, right). One reason could be that some small cells within the wood are filled with water but are not cut from the outside compared to bigger cells as it was seen in magnetic resonance microimaging41,42. Therefore, water still needs to be transported in these regions while in other regions the cell wall is already shrinking. This would also mean that no equilibrium state has been reached within the first desorption step. Furthermore, it is possible that beech, due to more complex anatomy, causes warping or in plane movement of the sample, which disturbs the current image evaluation process. Another explanation stated by Redman et al.19 could be a cell collapse due to the fast drying process within several hours from moisture content high above fibre saturation of 20% moisture content, which was observed for eucalyptus. Additionally, pine has more homogenous pores compared to beech. Further investigations via pressure plate technique can be made to investigate this behaviour43. The loss of bound water at 41% moisture content inducing shrinking was also observed for birch by Almeida & Hernández2. In this case, the observed non-linear curve could be attributed to a species specific property.
Samples were cut from one tree to see deviations in the measuring method. In future, an investigation of several individual trees with various wood characteristics is needed to derive comprehensive knowledge for specific wood species. In the present study, technically dried timber was used for the measurements as it is mainly used in the industry. For a better fundamental knowledge, also undried wood needs to be investigated.
For the length measurements using image analysis, the definition of the threshold for CIELAB images is crucial. To avoid the influence of colour and brightness of samples, the background of the image was used to define the threshold. Additional geometrical parameters such as bending or crowning of wood samples might provide even deeper insights into anisotropic sorption processes in wood and will be included in future research, e.g. by digital image correlation.
When comparing the setup to other sorption systems, the possibility of measuring up to 11 samples at the same time is an important advantage. Additionally, with DVS systems the measurement of length changes is not feasible until today37,44. Alternatively, determining the volume change in a climate chamber followed by manual measuring would disturb the ambient conditions and would not allow for dynamic investigations38,45. The presented system overcomes these limitations.
Conclusions
A new investigation of simultaneous dynamic mass and length change for wood is presented. High correlations between mass and dimensional change indicate a direct connection between the sorption process and swelling and shrinking. The sample size was selected based on an optimum between stable equilibrium conditions and minimum durations of single sorption steps. The method was critically evaluated for possible uncertainties. However, no significant drawbacks could be observed. Generated data is in good agreement with literature and manual measurements. It is now possible to determine swelling and shrinking values in-situ without disturbing the surrounding climatic conditions of the experiment. In future, image evaluation will be extended to detect annual ring deformation, bending or crown. The system can be used to investigate various wood species, modified samples, wood composites or other lignocellulosic materials.
Material and Methods
Measurement system and sample preparation
Sorption isotherm and kinetics measurements where performed on a Sorption Test System (SPS) “SPSx-1µ-High-Load” by ProUmid, Germany. The resolution of the build in high resolution balance is 1 µg with a repeatability of +/−5 µg. Temperature and relative humidity are measured by a “HC2A-S Ambient Air Probe from ROTRONIC. It was equipped with a Large Objects Sample Tray (ProUmid). Eleven samples can be measured simultaneously in one experiment. An attached CCD camera (BASLER acA2040-25gc - setup by ProUmid) was used to collect individual images at every mass measurement time. A specialized sample holder for the wood specimens was developed (Fig. 8) to expose a maximum surface area of the specimens to the ambient conditions.
Technically dried wood of European beech (Fagus sylvatica) and Scots pine (Pinus sylvestris) was used for the measurements. The total setup is shown in (Fig. 9). Samples were cut from one individual board within the adult wood (beech) and sapwood (pine) region to obtain samples with year rings parallel to one edge of the sample. In especially, wood samples with the dimension 30 × 30 × 1.5 mm (tangential, radial, longitudinal direction) were cut using a bench saw. The samples were shaped with a wood shaper to the final dimensions of 20 × 20 × 1.5 mm. Afterwards a 2 mm hole was drilled into the middle of the sample. Samples at 0% relative humidity have mean weight of 306 mg for pine and 394 mg for beech with a mean density of 0.392 g/cm³ (pine) and 0.554 g/cm³ (beech) respectively. The mean ratio between earlywood and latewood is 9.1 ± 3.6 for beech and 2.3 ± 0.6 for pine. Prior to the measurement, the samples were immersed into distillated water for one week.
The measurements were performed at 20 °C. The relative air humidity varied in steps of 5% or 10% between 85% and 0% (Table 3).
The duration of one single conditioning step varied depending on the equilibrium time. Relative humidity was changed when the change in mass was less than 0.01% over a 60 minutes period with weighing cycles every 15 minutes. In total, minimum 5 weighing points were used to calculate the equilibrium criteria in percent as slope of a linear regression within the software automatically. Additionally a minimum cycle time of 36 h was set and the maximum time was set to 48 h. For each species, 10 samples were measured.
The moisture content m of the samples was calculated according to
were, mu represents the current mass of the sample and m0 represents the mass of the dry sample at 0% relative humidity. Equilibrium moisture content are mean values for the whole sample determined in an “equilibrium condition”, which was defined as a mass change lower than 0.01% within 60 min.
For the measurement with different sample thicknesses, wood pieces with 20 × 20 mm in square and different longitudinal length (1, 3, 5, 10 and 20 mm) were cut with a bench saw. Afterwards the samples were immersed in water prior to the measurement in the sorption chamber.
Manual measurements of beech and pine samples (20 × 20 × 10 mm; 20 pieces each) were performed with a caliper. The samples were conditioned in Binder KBF 720 climate chamber. The duration for each step was set to a minimum of 10 days prior to the measurement at different relative humidity steps according to an in-house handling procedure (detail information can be found in the supplementary material). Radial, tangential and longitudinal values were collected for both species based on the same material as the digital evaluated samples. The measurements of mass and length change were performed outside of the climate chamber directly after removal from climate zone. For the dry state - drying was performed within a drying oven Heraeus T6120 at 103° for 2 days. Sample mass was recorded with a Balance Sartorius LP3200D (Resolution 0.001 g, Reproducibility +/−0.001 g) and dimensions were recorded with a Caliper Mitutoyo 293-521-30 Micrometer (resolution of 0,001 mm).
Image analysis
Image pre-processing
Depending on the total duration of the measurement, up to 3,329 images were taken for each sample. Images (RGB) had a size of 2,046 × 2,046 pixels and a resolution of 0.018 mm/pixel. According to the Nyquist–Shannon sampling theorem, the maximum detectable accuracy of objects within the image is 0.036 mm. As relative dimensional changes are of main interest in the present study, the focus was laid on a high reproducibility of the imaging with regard to exposure, camera settings, focus area as well as sample preparation and mounting.
For the analysis of images, scripts were developed using MATLAB R2017b and the inbuilt image processing toolbox. Images were chronologically sorted and imported into MATLAB. Then RGB images were converted into CIELAB colour space. To detect the edges of the samples, images were binarized using the threshold L = 1.821/17.536, a = −2.656/7.803, b = −11.501/3.916, to subtract the background within the image. “Artefacts” (connected objects with a maximum size of 7,000 pixels) outside of the edges of the sample were removed and “holes” (background pixels within the edges of the sample) within the sample were filled. Afterwards images were rotated to align the sample parallel to the edge of the image using a rotation matrix. Additionally, the tangential direction of all samples was aligned horizontally.
Calculation of geometrical parameters
Parameters were calculated using matrices of the binary or grayscale images. Figure 10 shows an exemplified grayscale image of a pine sample with lines indicating the positions of measurements. The width of the sample in radial direction w(cr) was measured by summing up nonzero entries of the binary matrix I that indicate the sample across the centre of the sample using the arithmetic mean of a set of f columns, consisting of 81-neighbored columns (1.473 mm) by
where c indicates the central column of the sample, m the number of rows in I and h about half of the set of columns f by
Analogous, w(ct) was calculated in tangential direction by
where r indicates the central row of the sample and n the number of columns in I.
The differential swelling and shrinking values where calculated by dividing the maximum length change in percent in the middle of the sample in each direction by the maximum mass when the sample began to shrink (in percent). In especially, this point in time was taken from the plot of length change versus moisture content (Fig. 3), whereas samples of beech began to shrink at 40% moisture content and samples of pine began to shrink at 30% moisture content.
For comparing swelling and shrinking against the moisture content for each sorption step, the values were normalized. In especially, the maximum differential swelling value of one sorption step was set to one and the lowest differential swelling value was set to zero.
Data Availability
Data generated during this study are included in Supplementary Information files.
References
Skaar, C. Wood-water relations (Springer-Verlag, Berlin, New York, 1988).
Almeida, G. & Hernández, R. E. Changes in Physical Properties of Yellow Birch Below and Above the Fiber Saturation Point. Wood And Fiber Science 38, 74–83 (2007).
Siau, J. F. Transport Processes in Wood (SPRINGER, Berlin, Heidelberg, 1984).
Engelund, E. T., Thygesen, L. G., Svensson, S. & Hill, C. S. A critical discussion of the physics of wood–water interactions. Wood Science and Technology 47, 141–161, https://doi.org/10.1007/s00226-012-0514-7 (2013).
Krabbenhøft, K., Damkilde, L. & Hoffmeyer, P. Moisture transport in wood: A study of physical-mathematical models and their numerical implementation (Technical University of Denmark, 2003).
Hozjan, T. & Svensson, S. Theoretical analysis of moisture transport in wood as an open porous hygroscopic material. Holzforschung 65, 97–102, https://doi.org/10.1515/hf.2010.122 (2011).
Ross, R. J. Wood handbook. Wood as an engineering material (U.S. Department of Agriculture, Forest Service, Forest Products Laboratory, Madison, Wisconsin, 2010).
Glass, S. V., Zelinka, S. L. & Johnson, J. A. Investigation of Historic Equilibrium Moisture Content Data from the Forest Products Laboratory. USDA Forest Service, Forest Products Laboratory, General Technical Report, FPL-GTR-229, 2014, 37 p 229, 1–37 (2014).
Zelinka, S. L., Glass, S. V. & Thybring, E. E. Myth versus reality. Do parabolic sorption isotherm models reflect actual wood–water thermodynamics? Wood Science and Technology 52, 1701–1706, https://doi.org/10.1007/s00226-018-1035-9 (2018).
Rijsdijk, J. F. & Laming, P. B. Physical and Related Properties of 145 Timbers (Springer Netherlands, Dordrecht, 1994).
Olsson, A.-M. & Salmen, L. The association of water to cellulose and hemicellulose in paper examined by FTIR spectroscopy. Carbohydrate Research 339, 813–818, https://doi.org/10.1016/j.carres.2004.01.005 (2004).
Hill, C. A. S., Norton, A. J. & Newman, G. The water vapour sorption properties of Sitka spruce determined using a dynamic vapour sorption apparatus. Wood Science and Technology 44, 497–514, https://doi.org/10.1007/s00226-010-0305-y (2010).
Rautkari, L., Hill, C., Curling, S., Jalaludin, Z. & Ormondroyd, G. What is the role of the accessibility of wood hydroxyl groups in controlling moisture content? Journal of Materials Science 48, 6352–6356 (2013).
Simón, C. et al. Comparison of the saturated salt and dynamic vapor sorption methods in obtaining the sorption properties of Pinus pinea L. Eur. J. Wood Prod, 1–8; https://doi.org/10.1007/s00107-016-1155-6 (2016).
Zelinka, S. L. et al. Apparatus for gravimetric measurement of moisture sorption isotherms for 1-100 g samples in parallel. Wood and fiber science 50, 244–253 (2018).
Derome, D., Griffa, M., Koebel, M. & Carmeliet, J. Hysteretic swelling of wood at cellular scale probed by phase-contrast X-ray tomography. Journal Of Structural Biology 173, 180–190, https://doi.org/10.1016/j.jsb.2010.08.011 (2011).
Rosner, S. et al. Within-ring movement of free water in dehydrating Norway spruce sapwood visualized by neutron radiography. Holzforschung 66, https://doi.org/10.1515/hf-2011-0234 (2012).
Yang, T., Wang, J., Sheng, N. & Ma, E. Comparison of dynamic sorption and hygroexpansion of wood by different cyclic hygrothermal changing effects II. Journal Of Building Physics 41, 360–376, https://doi.org/10.1177/1744259117708353 (2018).
Redman, A. L., Bailleres, H., Turner, I. & Perré, P. Characterisation of wood-water relationships and transverse anatomy and their relationship to drying degrade. Wood Science and Technology 50, 739–757, https://doi.org/10.1007/s00226-016-0818-0 (2016).
Ma, E., Nakao, T., Zhao, G., Ohata, H. & Kawamura, S. Relation Between Moisture Sorption and Hygroexpansion of Sitka Spruce During Adsorption Processes. Wood And Fiber Science 42, 304–309 (2010).
Hansmann, C., Konnerth, J. & Rosner, S. Digital image analysis of radial shrinkage of fresh spruce (Picea abies L.) wood. Wood Material Science & Engineering 6, 2–6, https://doi.org/10.1080/17480272.2010.515032 (2011).
Mantanis, G. I., Young, R. A. & Rowell, R. M. Swelling of wood. Part I. Swelling in water. Wood Science and Technology 28, 119–134, https://doi.org/10.1007/BF00192691 (1994).
Seifert, J. von. Zur Sorption und Quellung von Holz und Holzwerkstoffen—Zweite Mitteilung. Das Quellungsverhalten von Holz und Holzwerkstoffen. Holz als Roh- und Werkstoff 30, 294–303, https://doi.org/10.1007/BF02615203 (1972).
Hartley, I. D. & Avramidis, S. Static dimensional changes of Sitka spruce and western hemlock influenced by sorption conditions. Journal of the Institute of Wood Science (United Kingdom) 14, 83–88 (1996).
Murata, K. & Masuda, M. Microscopic observation of transverse swelling of latewood tracheid. Effect of macroscopic/mesoscopic structure. Journal of Wood Science 52, 283–289, https://doi.org/10.1007/s10086-005-0760-5 (2006).
Zhang, M. et al. Dimensional Changes of Tracheids during Drying of Radiata Pine (Pinus radiata D. Don) Compression Woods. A Study Using Variable-Pressure Scanning Electron Microscopy (VP-SEM). Plants (Basel, Switzerland) 7, https://doi.org/10.3390/plants7010014 (2018).
Lanvermann, C. Sorption and swelling within growth rings of norway spruce and implications on the macroscopic scale (ETH Zurich, Zurich, 2014).
Patera, A., van den Bulcke, J., Boone, M. N., Derome, D. & Carmeliet, J. Swelling interactions of earlywood and latewood across a growth ring. Global and local deformations. Wood Sci.Technol. 52, 91–114, https://doi.org/10.1007/s00226-017-0960-3 (2018).
Fredriksson, M. & Thybring, E. E. Scanning or desorption isotherms? Characterising sorption hysteresis of wood. Cellulose 25, 4477–4485, https://doi.org/10.1007/s10570-018-1898-9 (2018).
Thybring, E. E., Thygesen, L. G. & Burgert, I. Hydroxyl accessibility in wood cell walls as affected by drying and re-wetting procedures. Cellulose, 1–10; https://doi.org/10.1007/s10570-017-1278-x (2017).
DIN 68100. Toleranzsystem für Holzbe- und -verarbeitung - Begriffe, Toleranzreihen, Schwind- und Quellmaße (Beuth Verlag GmbH, 2010).
Zelinka, S. L., Glass, S. V., Boardman, C. R. & Derome, D. Moisture storage and transport properties of preservative treated and untreated southern pine wood. Wood Material Science & Engineering 11, 228–238, https://doi.org/10.1080/17480272.2014.973443 (2015).
Chirkova, J., Andersons, B. & Andersone, I. Study of the Structure of Wood-Related Biopolymers by Sorption Methods. Bioresources 4, 1044–1057, https://doi.org/10.15376/biores.4.3.1044-1057 (2009).
Hering, S. Charakterisierung und Modellierung der Materialeigenschaften von Rotbuchenholz zur Simulation von Holzverklebungen (ETH Zurich, Zurich, 2011).
Strømdahl, K. Water Sorption in Wood and Plant Fibres (Technical University of Denmark (DTU), Lyngby, 2000).
Glass, S. V., Boardman, C. R. & Zelinka, S. L. Short hold times in dynamic vapor sorption measurements mischaracterize the equilibrium moisture content of wood. Wood Science and Technology, 1–18; https://doi.org/10.1007/s00226-016-0883-4 (2016).
Glass, S. V., Boardman, C. R., Thybring, E. E. & Zelinka, S. L. Quantifying and reducing errors in equilibrium moisture content measurements with dynamic vapor sorption (DVS) experiments. Wood Sci Technol, 1–19, https://doi.org/10.1007/s00226-018-1007-0 (2018).
Chauhan, S. S. & Aggarwal, P. Effect of moisture sorption state on transverse dimensional changes in wood. Holz als Roh- und Werkstoff 62, 50–55, https://doi.org/10.1007/s00107-003-0437-y (2004).
Hernández, R. E. Influence of moisture sorption history on the swelling of sugar maple wood and some tropical hardwoods. Wood Science and Technology 27, 337–345, https://doi.org/10.1007/BF00192220 (1993).
Kelsey, K. E. The shrinkage intersection point. Its significance and the method of its determination. Forest Prod. J 6, 411–417 (1956).
Passarini, L., Malveau, C. & Hernández, R. E. Distribution of the equilibrium moisture content in four hardwoods below fiber saturation point with magnetic resonance microimaging. Wood Science and Technology 49, 1251–1268, https://doi.org/10.1007/s00226-015-0751-7 (2015).
Hernández, R. & Caceres, C. Magnetic resonance microimaging of liquid water distribution in sugar maple wood below fiber saturation point. Wood and Fiber Science 42 (2010).
Fredriksson, M. & Johansson, P. A Method for Determination of Absorption Isotherms at High Relative Humidity Levels: Measurements on Lime-Silica Brick and Norway Spruce (Picea abies (L.) Karst.). Drying Technology 34, 132–141, https://doi.org/10.1080/07373937.2015.1041035 (2016).
Hill, C. A. S., Norton, A. & Newman, G. Analysis of the water vapour sorption behaviour of Sitka spruce [Picea sitchensis (Bongard) Carr.] based on the parallel exponential kinetics model. Holzforschung 64, 469, https://doi.org/10.1515/hf.2010.059 (2010).
Arévalo, R. & Hernández, R. E. Influence of Moisture Sorption on Swelling of Mahogany (Swietenia macrophylla King) Wood. Holzforschung 55, 197, https://doi.org/10.1515/HF.2001.096 (2001).
Acknowledgements
The authors would like to thank Carina Rößler (Wood K plus) for supporting data evaluation and image analysis. We would like to thank the “Gesellschaft der Förderer und Freunde der Holzwissenschaft in HAMBURG e.V”. for their financial support.
Author information
Authors and Affiliations
Contributions
M.N. and M.R. wrote the main manuscript text. M.R. developed the image evaluation. M.N. prepared the figures. M.N. developed the sample holder and the technical setup. A.K. and C.H. contributed to the total method development and data evaluation. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41598_2019_46381_MOESM1_ESM.docx
Supplementary data - Simultaneous change of wood mass and dimension caused by moisture dynamics – Nopens Riegler Hansmann Krause
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nopens, M., Riegler, M., Hansmann, C. et al. Simultaneous change of wood mass and dimension caused by moisture dynamics. Sci Rep 9, 10309 (2019). https://doi.org/10.1038/s41598-019-46381-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-46381-8
This article is cited by
-
Effects of surface perforation on the drying characteristics and sound absorption coefficients of Russian poplar board
European Journal of Wood and Wood Products (2023)
-
Hydrogen bonding and other non-covalent interactions at the surfaces of cellulose microfibrils
Cellulose (2023)
-
Limits in reaching the anhydrous state of wood and cellulose
Cellulose (2023)
-
Water vapour sorption and moisture transport in and across fibre direction of wood
Cellulose (2022)
-
Drying of green veneer hollow tubes monitored using stereo digital images correlation
European Journal of Wood and Wood Products (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.