Abstract
In this work, a high thermoelectric figure of merit, zT of 1.9 at 740 K is achieved in Ge1−xBixTe crystals through the concurrent of Seebeck coefficient enhancement and thermal conductivity reduction with Bi dopants. The substitution of Bi for Ge not only compensates the superfluous hole carriers in pristine GeTe but also shifts the Fermi level (EF) to an eligible region. Experimentally, with moderate 6–10% Bi dopants, the carrier concentration is drastically decreased from 8.7 × 1020 cm−3 to 3–5 × 1020 cm−3 and the Seebeck coefficient is boosted three times to 75 μVK−1. In the meantime, based on the density functional theory (DFT) calculation, the Fermi level EF starts to intersect with the pudding mold band at L point, where the band effective mass is enhanced. The enhanced Seebeck coefficient effectively compensates the decrease of electrical conductivity and thus successfully maintain the power factor as large as or even superior than that of the pristine GeTe. In addition, the Bi doping significantly reduces both thermal conductivities of carriers and lattices to an extremely low limit of 1.57 W m−1K−1 at 740 K with 10% Bi dopants, which is an about 63% reduction as compared with that of pristine GeTe. The elevated figure of merit observed in Ge1−xBixTe specimens is therefore realized by synergistically optimizing the power factor and downgrading the thermal conductivity of alloying effect and lattice anharmonicity caused by Bi doping.
Similar content being viewed by others
Introduction
Thermoelectric (TE) materials enable the direct energy conversion between heat and electricity that are of great interest in the field of waste heat recovery and solid-state cooling according Seebeck and Peltier effects, respectively. The conversion efficiency is mainly determined by the dimensionless figure of merit zT = σ S2T/κ, in which σ, S, T, κ and σ S2 are the electrical conductivity, Seebeck coefficient, absolute temperature, thermal conductivity, and power factor (PF), respectively. These parameters are strongly coupled with each other, leading to the difficulty in manipulation of zT enhancement1. To achieve a high zT value, band engineering approaches including band convergence2, dimensionality reduction3, resonant levels4, low band effective mass5, minority carrier energy filtering6, dislocations7, 2-dimensional electron gas8, have been proposed to improve the performance of electronic contribution, while nanostructuring9, multi-scale microstructuring10, lattice anharmonicity11,12, rattling atoms13, liquid phonons14, lattice disorder15, and interstitial point defects16,17 are strategies commonly used for minimizing thermal conductivity of lattice contribution.
To date, group-IV monochalcogenides-based compounds are considered to be the leading TE materials in intermediate temperature range (600–923 K)18,19. Among them, GeTe is a heavily p-type semiconductor with an inherent high carrier concentration of ~1021 cm−3. It stabilizes in a non-centrosymmetric rhombohedral structure with an space group R3m (No. 160) at room temperature, which undergoes a second-order ferroelectric phase transition to a cubic structure (Fm \(\bar{3}\) m) at 600–700 K, accompanied by an angle distortion of the unit cell from ~57.5° to 60°. The transition temperature depends on the sample stoichiometry and carrier concentration20. Its maximum zT is close to 1.0 near 700 K. Recently, several pseudobinary system have been found to exhibit zT > 1.75 between 600–800 K21,22,23,24. Besides Sb and Pb, Bi is also a good dopant in this system, i.e., zT = 1.3 for Ge0.94Bi0.06Te melt ingot at 700 K25. However, in some cases polycrystalline or single crystals show much better thermoelectric properties as compared to that of the melt ingots. The innovation of this work is that we applied the Bridgman method to grow Ge1−xBixTe crystalline samples, and found an extraordinary high zT of 1.9 (700~740 K) in the Bridgman-grown Ge0.9Bi0.1Te crystal.
Results and Discussion
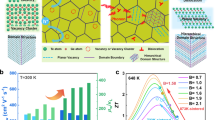
The image of as grown Ge1−xBixTe ingots are shown in Fig. 1(a). These samples are ~40 g in weight with 13 mm in diameter. They have a rhombohedral lattice at room temperature (the inset in Fig. 1(d)) and are free from secondary phases, as confirmed by the powder X-ray diffraction (XRD) patterns (Fig. 1(b)). With increasing Bi content, the XRD peaks between 42°–44° merge that signifies the increasing cubic nature of Ge1−xBixTe structure. From XRD Rietveld refinement, as x increases, the lattice parameters of a and b increase while the lattice parameter c decreases monotonically (Fig. 1(c)). Though the ionic radius of Bi is larger than that of Ge, the volume of Ge1−xBixTe unit cell is nearly invariant with x. This causes the increase of crystal density from ~6.14 g cm−3 to 6.58 g cm−3, as shown in Fig. 1(d). The thermal stability of samples can also be examined by x-ray diffraction in thermal cycles. Here we carried out the temperature dependence of XRD to check the thermal stability of the Bi doped GeTe samples, for example of Ge0.9Bi0.1Te (Supplementary Fig. S1), as the sample was heated to 700 K, the diffraction peaks remained the same, thus confirmed the thermal stability of Ge0.9Bi0.1Te.
For pristine GeTe, the inherently high carrier concentration of nH~8.7 × 1020 cm−3 makes the Fermi level (EF) falls deeply into the valence band, as shown by the black line in Fig. 2(a), where we show the DFT calculated band structure for the pristine GeTe. The intersections of EF with L and Σ create hole pockets with large Fermi surfaces that leads to its metallic nature. When the Bi content x increases from 0 to 0.12, the nH reduces from 8.7 × 1020 cm−3 to 0.7 × 1020 cm−3 due to the carrier compensation given by the excess electrons from Bi. For a metallic system, Seebeck coefficient at temperature T can be described by Mott’s relation26:
where kB, q and N(E) are Boltzmann constant, elementary charge, and energy dependent density of state (DOS) near EF, respectively. Certainly, a large Seebeck coefficient can be brought by a low N(E) coupled with a steep slope of ∂N(E)/∂E near EF. Note that as the EF intersects with the “pudding mold valley” at L point when nH~3–5 × 1020 cm−3 (the cyan region in Fig. 2(a))27,28,29, the Seebeck coefficient becomes extremely large and effectively compensates the degradation of electrical conductivity and thus successfully maintains the power factor as large as or even superior than that of the pristine GeTe. The calculated Seebeck coefficients (the orange dashed line in the Fig. 2(b)) were obtained based on the pristine GeTe electronic structure with the BoltzTraP code using rigid-band and constant-relaxation-time approximations30. It can be found that the trend of the calculated Seebeck coefficients are consistent with the experimental values. Besides the energy dependent density of state N(E), the effective mass is another factor that has an important influence on the Seebeck coefficient. Hence, the relationship between the carrier concentration and Seebeck coefficient of Ge1−xBixTe was plotted in Fig. 2(b), and the fitting results derived from the single parabolic band model with the effective mass of 1.1, 1.5, 2.0, and 2.3 m0 were presented. Apparently, the effective mass of Bi doped GeTe samples drastically increases from 1.1 m0 to 2.3 m0, partly explaining the enhanced Seebeck coefficient. The DFT calculation with 7.4% Bi doping shows a reduced energy difference between the L band and the band in the X-Γ direction (the dashed yellow rectangle in the inset of Fig. 2(a) and Supplementary Fig. S231,32). This will lead to multiple band transport and enhancing the effective mass, which benefits for electrical transport that qualitatively consistent with the experimental result.
(a) DFT calculated Electronic band structure for rhombohedral GeTe with spin-orbital coupling, and the calculated band structure with 7.4% Bi doping shown in the inset figure. (b) Seebeck coefficient of Ge1−xBixTe as a function of carrier concentration at 300 K. The solid lines are derived from the single parabolic band model with the effective mass of 1.1, 1.5, 2.0, and 2.3 m0, respectively. The dashed line is DFT calculated Seebeck coefficient of GeTe as a function of carrier concentration at 300 K.
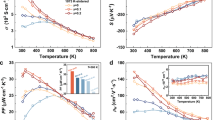
Figure 3 gives the thermoelectric properties of Ge1−xBixTe with x = 0–0.12 measured in 300–740 K. The σ of all samples decreases with increasing temperature, indicating a degenerated semiconductor behavior (Fig. 3(a)). At room temperature, the σ decreases from 8.02 × 105 S m−1 to 1.57 × 105 S m−1 as x increases from 0 to 0.1. As x further increases to 0.12, a dramatic reduction of ~97% in σ occurs. This can be attributed to the significant reduction in Fermi surface (or DOS) when the EF escapes the L band. Figure 2(a) shows that the Fermi level EF of Ge0.88Bi0.12Te merely intersects with the Σ band, represented by the orange line, where the DOS (with nH~0.75 × 1020 cm−3) is greatly reduced. Consequently, only a slight variation in hole concentration will cause a more pronounced EF shift. Besides, Bi alloyings do reduce the carrier mobility, and can be presumably attributed to the additional scattering of alloying effects (Supplementary Table S1). This phenomenon is normally seen in similar materials such as SnTe, PbSe, and PbTe. Contrary to the σ, the S shows an upward tendency with the increasing Bi content, as shown in Fig. 3(b). The S of all samples are positive in the whole temperature range, indicating that holes are the dominant charge carriers in this alloying system. In principle, the S of all samples increases with temperature increase. For Ge0.88Sb0.12, a flat S plateau is observed as T > 550 K, which infers the enhanced bipolar effect arisen from the massive carrier compensation. The point can be further confirmed by the σ, which starts to increase as T > 550 K and become nearly invariant for all Bi doped samples, the phenomenon is more obvious for x ≥ 0.06 specimens. It is noticed that the trade-off between the σ and S can significantly bring down the thermal conductivity of carriers while keeping the high value of PF (Fig. 3(c)). Compare to the undoped GeTe, the PF of x = 0.6, 0.8, 1.0 samples below 600 K are greatly enhanced, while for x = 0.12, the temperature-dependent PF curve drops dramatically due to the significant reduction in σ. The pristine GeTe has a high κ of ~8.6 W m−1 K−1 at room temperature, which decreases with increasing temperature and reaches the minimum value of 4.1 W m−1 K−1 near phase transition point at ~670 K which is clearly reflected in the discontinuity in κ (Fig. 3(d). With the increasing Bi content, the κ is substantially reduced. For instance, Ge0.88Bi0.12Te has the κ value of ∼1 W m−1 K−1 and 1.2 W m−1 K−1 at 300 K and 740 K respectively, which have about 88% and 71% reduction with respect to that of pristine GeTe. Such substantial reduction in thermal conductivity for Ge1−xBixTe crystals is very helpful in boosting the zT value. It is known that the total thermal conductivity κtot is the sum of the electronic contribution κe and the lattice contribution κlat. The plot of κe as a function of temperature for all samples is presented in Fig. 4(a), suggesting that the heat transport of pristine GeTe is mainly (~65%) from carrier contribution. With Bi doping, the κe was significantly decreased by reducing the p-type carrier concentrations. κlat is then calculated from κtot by subtracting κe (Fig. 4(b)). At 740 K, the κlat of pristine GeTe is ~1.9 W m−1 K−1, whereas it is only ~0.7 W m−1 K−1 for x = 0.1 of Bi, showing a 63% reduction in κlat. κlat decreases rapidly with increasing Bi doping, which can be attributed not only to the enhanced alloy scatterings but also to the lattice anharmonicity that will be discussed later.
In addition to the minimized carrier-contributed thermal conductivity and alloying effect, the anomalously low and nearly temperature independent thermal conductivity is also attributed to the large lattice anharmonicity introduced by long pair electrons of Bi cation33,34. The valence electronic configuration of Bi is 4f145d106s26p3 prefers to form stereochemically active lone pair electrons in many materials. The electrostatic repulsion between the lone pair electrons and the relevant bonding charges have been confirmed to the origin of strong anharmonic phonon-phonon interactions which is able to reduce the lattice thermal conductivity to the nearly amorphous limit. To understand the mechanism of strong anharmonic phonon-phonon interaction of Bi ions in GeTe, further systematical studies are required. Figure 5 shows the temperature dependence of zT for all Ge1−xBixTe specimens. Apparently the zT values are significantly boosted by Bi substitution at all temperatures. At highest available temperature T = 740 K, the zT remarkably achieve the values of 1.5, 1.6, 1.9 and 1.4 for x = 0.06, 0.08, 0.1, 0.12 respectively. Especially, a flat plateau of zT~1.9 is establish in Ge0.9Bi0.1Te when >700 K. It is also noted that the largest zT value in this paper is as high as 1.9, which is about 46% higher than zT = 1.3 reported25. The key point is that the elevated zT in Ge1−xBixTe specimens prepared by Bridgman method is realized by synergistically optimizing the power factor and downgrading the thermal conductivity of alloying effect and lattice anharmonicity caused by Bi doping. In addition, the thermoelectric data for Ge0.9Bi0.1Te were repeated for a couple of times, and the narrow statistic distribution of zT values clearly confirms the repeatability.
Conclusions
In summary, the substitution of Ge by Bi in GeTe enables an exquisite manipulation of carrier concentration n, Fermi level EF and thermal conductivity κ to optimum values that raise the zT of Bi-doped Ge1−xBixTe specimens for x = 0–0.12. The combination of theoretical calculations and experimental results elucidates the interrelations between σ, S and band valleys. Due to the substantial reduction in κ, the zT of all Bi doped Ge1−xBixTe specimens are greatly enhanced. A remarkable zT of 1.91 at 740 K is achieved in the specimen of Ge0.9Bi0.1Te, which is comparable to the state-of-the-art high performance thermoelectric material systems.
Methods
High purity elements of Ge (99.999%), Te (99.999%) and Bi (99.999%) were weighted according to the stoichiometric ratio of Ge1−xBixTe (x = 0, 0.06, 0.08, 0.10, 0.12), and sealed in evacuated silica tubes. The silica tubes were then heated at 1123 K for 48 hours followed by furnace cooling to room temperature. Ge1−xBixTe crystals were then grown by using Bridgman method from the pre-melt ingot, with a growth rate of 3 mm h−1 at 1123 K. The crystal structure of Ge1−xBixTe was determined by a PANalytical® X’Pert PRO X-ray diffraction diffractometer (λ = 1.54056 Å). The electrical conductivity and Seebeck coefficient were measured using the ULVAC ® ZEM-3 system. The uncertainty of the Seebeck coefficient and electrical conductivity measurements is about 2~4%. The thermal diffusivity of samples was measured on a NETZSCH LFA 457 laser flash instrument (Supplementary Fig. S3) and the thermal conductivity was calculated from the relationship κ = αCpd, where α is the thermal diffusivity, Cp is the heat capacity according to the Dulong-Petit law, and d is the mass density, measured by Archimedes’ method. The difference between calculated heat capacity and the measured value is less than 5%, and insure the validity of Dulong-Petit value for the Cp. The uncertainty of the thermal conductivity was estimated to be ~5%. Considering the uncertainties for Seebeck coefficient, electrical conductivity and thermal conductivity, the combined uncertainty of zT is less than 15%. The carrier concentration was estimated using the relation p = 1/eRH, where RH is the Hall coefficient measured by Quantum Design® Physical Properties Measurement System. The uncertainty of the Hall coefficient is ~3%. The first-principles density functional theory (DFT) calculations with spin-orbit coupling effect were performed using projector augmented-wave (PAW) potentials35,36,37, as implemented in the Quantum Espresso package38. The exchange-correlation functional was treated by the generalized gradient approximation with the Perdew–Burke–Ernzerhof form39. The experimental lattice constants was used with their atomic positions fully relaxed and the kinetic energy cutoff of 750 eV. The Seebeck coefficients were calculated using the BoltzTraP code30.
References
He, J. & Tritt, T. Advances in thermoelectric materials research: Looking back and moving forward. Science 357, 1369 (2017).
Pei, Y. Z. et al. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 473, 66–69 (2011).
Hicks, L. D. & Dresselhaus, M. S. Effect of quantum-well structures on the thermoelectric figure of merit. Phys. Rev. B 47, 12727–12731 (1993).
Heremans, J. P. et al. Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states. Science. 321, 554–557 (2008).
Pei, Y. Z., LaLonde, A. D., Wang, H. & Snyder, G. J. Low effective mass leading to high thermoelectric performance. Energy Environ. Sci. 5, 7963–7969 (2012).
Faleev, S. V. & Leonard, F. Theory of enhancement of thermoelectric properties of materials with nanoinclusions. Phys. Rev. B 77, 214304 (2008).
Chen, Z. W. et al. Lattice dislocations enhancing thermoelectric PbTe in addition to band convergence. Adv. Mater. 29, 1606768 (2017).
Ohta, H., Kim, S. W., Kaneki, S., Yamamoto, A. & Hashizume, T. High thermoelectric power factor of high-mobility 2D electron gas. Adv. Sci. 4, 1700696 (2017).
Zhang, J. et al. Extraordinary thermoelectric performance realized in n-Type PbTe through multiphase nanostructure engineering. Adv. Mater. 29, 1703148 (2017).
Su, X. L. et al. Multi-scale microstructural thermoelectric materials: transport behavior, non-equilibrium preparation, and applications. Adv. Mater. 29, 1602013 (2017).
Bansal, D. et al. Phonon anharmonicity and negative thermal expansion in SnSe. Phys. Rev. B 94, 054307 (2016).
Li, C. W. et al. Orbitally driven giant phonon anharmonicity in SnSe. Nat. Phys. 11, 1063–1073 (2015).
Christensen, M. et al. Avoided crossing of rattler modes in thermoelectric materials. Nat. Mater. 7, 811–815 (2008).
Liu, H. L. et al. Copper ion liquid-like thermoelectrics. Nat. Mater. 11, 422–425 (2012).
Ni, X. X., Liang, G. C., Wang, J. S. & Li, B. W. Disorder enhances thermoelectric figure of merit in armchair graphene nanoribbons. Appl. Phys. Lett. 95, 192114 (2009).
Snyder, G. J., Christensen, M., Nishibori, E., Caillat, T. & Iversen, B. B. Disordered zinc in Zn4Sb3 with phonon-glass and electron-crystal thermoelectric properties. Nat. Mater. 3, 458–463 (2004).
Wei, P. C. et al. Enhancement of thermoelectric figure of merit in β-Zn4Sb3 by indium doping control. App. Phys. Lett. 107, 123902 (2015).
Biswas, K. et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 489, 414–418 (2012).
Chang, C. et al. 3D charge and 2D phonon transports leading to high out-of-plane ZT in n-type SnSe crystals. Science 360, 778–782 (2018).
Chattopadhyay, T., Boucherle, J. X. & von Schnering, H. G. Neutron-diffraction study on the structural phase-transition in GeTe. J. Phys. C 20, 1431–1440 (1987).
Perumal, S., Roychowdhury, S., Negi, D. S., Datta, R. & Biswas, K. Thermoelectric performance and enhanced mechanical stability of p-type Ge0.9Sb0.1Te. Chem. Mater. 27, 7171–7178 (2015).
Davidow, J. & Gelbstein, Y. A. Comparison between the mechanical and thermoelectric properties of three highly efficient p-Type GeTe-rich compositions: TAGS-80, TAGS-85, and 3% Bi2Te3-doped Ge0.87Pb0.13Te. J. Electron. Mater. 42, 1542–1549 (2013).
Gelbstein, Y., Davidow, J., Girard, S. N., Chung, D. Y. & Kanatzidis, M. G. Controlling metallurgical phase separation reactions of the Ge0.87Pb0.13Te alloy for high thermoelectric performance. Adv. Energy Mater. 3, 815–820 (2013).
Wu, D. et al. Origin of the high performance in GeTe-based thermoelectric materials upon Bi2Te3 doping. J. Am. Chem. Soc. 136, 11412–11419 (2014).
Perumal, S., Roychowdhury, S. & Biswas, K. Reduction of thermal conductivity through nanostructuring enhances the thermoelectric figure of merit in Ge1−xBixTe. Inorg. Chen. Front. 3, 125–132 (2016).
Wei, P. C., Huang, T. S., Li, S. W., Guo, G. Y. & Chen, Y. Y. Thermoelectric properties optimization of Fe2VGa by tuning electronic density of states via titanium doping. J. Appl. Phys. 118, 165102 (2015).
Kuroki, K. & Arita, R. Pudding mold band drives large thermopower in NaxCoO2. J. Phys. Soc. Jpn. 76, 083707 (2007).
Kutorasinski, K., Wiendlocha, B., Kaprzyk, S. & Tobola, J. Electronic structure and thermoelectric properties of n- and p-type SnSe from first-principles calculations. Phys. Rev. B 91, 205201 (2015).
Lu, Q. S. et al. Unexpected large hole effective masses in SnSe revealed by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 119, 116401 (2017).
Madsen, G. K. H. & Singh, D. J. BoltzTraP. A code for calculating band-structure dependent quantities. Comput. Phys. Commun. 175, 67–71 (2006).
Medeiros, P. V. C., Stafström, S. & Björk, J. Effects of extrinsic and intrinsic perturbations on the electronic structure of graphene: Retaining an effective primitive cell band structure by band unfolding. Phys. Rev. B 89, 041407(R) (2014).
Medeiros, P. V. C., Tsirkin, S. S., Stafström, S. & Björk, J. Unfolding spinor wave functions and expectation values of general operators: Introducing the unfolding-density operator. Phys. Rev. B 91, 041116(R) (2015).
Nielsen, M. D., Ozolins, V. & Heremans, J. P. Lone pair electrons minimize lattice thermal conductivity. Energy Environ. Sci. 6, 570–578 (2013).
Kolobov, A. V., Fons, P., Tominaga, J. & Ovshinsky, S. R. Vacancy-mediated three-center four-electron bonds in GeTe-Sb2Te3 phase-change memory alloys. Phys. Rev. B 87, 165206 (2013).
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, a1133 (1965).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter. 21, 395502 (2009).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
This work is financially supported by Ministry of Science and Technology (MOST), Taiwan, Grant No. MOST 106-2112-M-001 -019 -MY3.
Author information
Authors and Affiliations
Contributions
P.C.W., C.L.C., and Y.Y.C. conceived the idea, analyzed the results and wrote the paper. C.X.C. prepared the samples and performed the thermoelectric property measurements. C.R.H., D.L.N. and C.M.W. carried out the theoretical calculations; S.H.Y., H.J.W., M.M.C.C. and D.H.W. provided the technical supporting for experiments.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41598_2019_45071_MOESM1_ESM.pdf
Enhancing thermoelectric performance by Fermi level tuning and thermal conductivity degradation in (Ge1-xBix)Te crystals
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wei, PC., Cai, CX., Hsing, CR. et al. Enhancing thermoelectric performance by Fermi level tuning and thermal conductivity degradation in (Ge1−xBix)Te crystals. Sci Rep 9, 8616 (2019). https://doi.org/10.1038/s41598-019-45071-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-45071-9
This article is cited by
-
Exploring the optoelectronic and thermoelectric properties of Ge1−xBixTe (at x = 12% and 24%) using GGA and GGA + SO approximation for renewable energy applications: a DFT study
Chemical Papers (2024)
-
Electronic structure and thermal conductance of the MASnI3/Bi2Te3 interface: a first-principles study
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.