Abstract
The ability to tune and enhance the properties of luminescent materials is essential for enlarging their application potential. Recently, the modulation of the photoluminescence emission of lanthanide-doped ferroelectric perovskites by applying an electric field has been reported. Herein, we show that the ferroelectric order and, more generally the polar order, has a direct effect on the photoluminescence of Eu3+ in the model BaZrxTi1−xO3 perovskite even in the absence of an external field. The dipole arrangement evolves with increasing x from long-range ferroelectric order to short-range order typical of relaxors until the non-polar paraelectric BaZrO3 is achieved. The cooperative polar interactions existing in the lattice (x < 1) promote the off-center displacement of the Eu3+ ion determining a change of the lanthanide site symmetry and, consequently, an abrupt variation of the photoluminescence emission with temperature. Each type of polar order is characterized by a distinct photoluminescence behaviour.
Similar content being viewed by others
Introduction
The ability to tune and enhance the properties of photoluminescent materials (phosphors) by changing the emission wavelengths, intensity, band-shape, emission quantum yields and excited states lifetime is essential for optimizing the performance of devices and understanding the luminescence mechanisms. A common type of highly efficient luminescent phosphors are rare-earth (RE) doped oxides, such as Eu3+:Y2O3, Nd3+:Y3Al5O12 and Er3+:glass1,2,3. For a given host structure, the photoluminescence (PL) and, in particular the color and brightness of the emitted light, can be tailored by changing the nature and the concentration of the RE ion as well as introducing a co-dopant as sensitizer. The incorporation of the same RE in different hosts also produces modifications of PL properties due to the variation of the crystal symmetry and crystal field around the active ion. More recently, efforts have been focused on the active, in-situ control of the emission of luminescent materials as this would represent a real breakthrough in the phosphor technology. Real-time modulation of PL can be realized by altering the local symmetry and the energy levels by the application of an external physical stimulus or field. The strong coupling existing in ferroelectrics between the lattice strain and external variables, such as electric field and mechanical stress, offers a unique opportunity to modify the crystal field around the active ions thus realizing an effective real-time PL tuning, as demonstrated in some recent papers for RE-doped ABO3 ferroelectric perovskites and LiNbO34,5,6,7,8,9. Although possible correlations between the PL response and parameters such as the remnant polarization and the poling field have been proposed and the occurrence of a field-induced phase transition has been claimed to play an important role8,10,11,12,13,14,15, the detailed mechanisms which control the luminescence in ferroelectric materials are not fully understood yet.
In the present paper we report strong evidence that the ferroelectric and, more generally, the polar order can control the luminescence properties of Eu3+ ions even without the application of an external field or stimulus and we propose a possible mechanism for explaining our observations.
The BaZrxTi1−xO3 (BZT) perovskite solid solution has been selected as a model host because the polar order can be tuned by changing x. The end-member BaTiO3 (x = 0) is one of the most carefully investigated ferroelectric compounds and, thanks to its high dielectric constant and low losses, is widely used as a ceramic material for the fabrication of multilayer ceramic capacitors in the microelectronic industry and other applications16,17. BaTiO3 exists in different crystallographic variants, depending on temperature18. At the Curie temperature, TC = 125–130 °C, it turns from the high temperature paraelectric cubic form (C, Pm-3m) to the ferroelectric tetragonal structure (T, P4mm). On further cooling, two other ferroelectric phases are observed: orthorhombic (O, Amm2), below 5–15 °C, and rhombohedral (R, R3m), below −80 –−90 °C. All polar forms originate from a small deformation of the prototype cubic lattice arising from the off-center displacement of the Ti ion (about 0.1 Å at room temperature) in the TiO6 octahedron. The cooperative, long-range ordering of the resulting electrical dipoles gives rise to macroscopic spontaneous polarization, spontaneous lattice strain and ferroelectricity19. Differently from BaTiO3, the crystal structure of the end-member BaZrO3 (x = 1) corresponds to the prototype Pm-3m cubic perovskite up to the melting point20,21. Barium zirconate is a nonpolar, paraelectric solid which has attracted attention in recent years as an efficient proton conductor when doped with acceptor impurities22,23. BaTiO3 and BaZrO3 show complete solid solubility. In the BZT solid solution the extent of polar order decreases with increasing x24,25,26 as Zr4+ (0.720 Å) is bigger than Ti4+ (0.605 Å) and does not move off the center of the BO6 octahedron. Long-range order typical of conventional ferroelectrics prevails for 0.0 ≤ x ≤ 0.15, whereas the correlation length of polar order is reduced for 0.15 < x ≤ 0.25 corresponding to a diffuse ferroelectric to paraelectric transition. Relaxor or dipolar glass state with only short-range polar order is observed for higher values of x, up to 0.95, and finally weak paraelectric behavior dominates in BaZrO3. The relaxor state is characterized by the presence of polar nanoregions (PNRs) embedded in a paraelectric matrix and an average cubic structure27. According to recent investigations24,25, the PNRs in BZT essentially correspond to frozen BaTiO3 clusters with Ti off-centering.
Eu3+ was chosen as a dopant because of the well-known bright emissions and for its powerful ability to act as a spectroscopic local probe for the determination of the symmetry of the first coordination sphere of a lanthanide ion in organometallic molecules and crystals28. Furthermore, Eu3+ has an ionic radius (c.n. 12) of 1.226 Å and, therefore, its crystallo chemical behavior can be considered as representative of other trivalent lanthanide ions with intermediate size, from Sm3+ to Er3+.
Six Eu-doped Ba(Ti, Zr)O3 ceramics with composition Ba1−yEuyTi1−x−y/4ZrxO3 (y = 0.01; x = 0, 0.05, 0.15, 0.30, 0.50, 0.70) and Ba1−yEuyZr1−y/4O3 (y = 0.01) were investigated. The different samples are labelled as BZX, where X = 100x.
Results and Discussion
Dielectric properties and polar order
The dielectric constant (real part of permittivity) of the BZ0-BZ30 ceramics is reported in Fig. 1. The phase transitions are indicated by anomalies of the dielectric constant. When x = 0 (Fig. 1a), there are three peaks at −70, 15 and 125 °C corresponding to R/O, O/T and T/C transitions, respectively.
The sharp permittivity peak at TC is typical of conventional ferroelectrics with first-order ferro/para transition. For ceramic BZ5 (Fig. 1b), TC decreases to 108 °C and the temperature of the O/T transition increases to 50 °C.
The R/O transition is no longer detected in Fig. 1b but can still be identified from the anomaly of the dielectric loss (the ratio of the imaginary and real part of dielectric permittivity, see Figure S1, Supporting Information) at about −10 °C. A single and broad permittivity peak at 50 °C, corresponding to a diffuse R/C phase transition, is observed in Fig. 1c when x = 0.15. Accordingly, the dielectric loss also reveals a single transition (Figure S1, Supporting Information). The sample BZ30 (Fig. 1d) displays a typical relaxor behavior: the temperature corresponding to the maximum permittivity shifts at higher temperatures with increasing frequency. The permittivity maximum no longer corresponds to a phase transition but is determined by the relaxation dynamics of the PNRs27. Comparison with literature data29,30,31 indicates that the dielectric properties of the Eu-doped samples are rather similar to those reported for BZT materials likely due to the low concentration of the dopant. The phase transition temperatures of ferroelectric samples are very close (within a few degrees) to those of the undoped ceramics.
The polarization - electric field (E) loops reported in Fig. 1e confirm the results of dielectric measurements. BZ0, BZ5 and BZ15 show typical hysteretic ferroelectric behavior. Both the maximum polarization and the remnant polarization (intercept with the vertical axis) decrease with increasing x as expected from the progressive lowering of TC. BZ30 sample shows a non-linear behavior without hysteresis, a feature representative of relaxors.
Crystal structure
The splitting of the (200) peak in the XRD pattern of the BZ0 ceramic (Figure S2, Supporting Information) indicates a typical P4/mm tetragonal structure and the refinement gives a c/a ratio of the lattice parameters of 1.0096, only slightly smaller than that of undoped BaTiO3 (1.0109). The unit cell volume, 64.35 Å3, is virtually the same of undoped barium titanate (64.34 Å3) being the difference within the experimental error. Although peak splitting is no longer observed, the broadening of some lines (compare the 111 and 200 peaks) indicates a non-cubic structure for BZ5 (Figure S2, Supporting Information), in agreement with the existence of long-range ferroelectric order at room temperature. The assignment of the crystal symmetry is not straightforward given the absence of splitting. Refinement with P4mm tetragonal structure with a lower c/a ratio of 1.0041 results in a marginally better fit than orthorhombic Pbnm structure. XRD pattern of BZ15 indicates a cubic Pm-3m symmetry (Figure S2) though this composition is expected to be ferroelectric at room temperature as indicated by the dielectric measurements (Fig. 1c). This apparent discrepancy is determined by the proximity of the phase transition (TC = 50 °C) and, consequently, the small deviation of the polar structure from the cubic arrangement not detectable with a conventional diffractometer. The ceramics with x = 0.30, 0.50 and 0.70 show the cubic Pm-3m structure, as expected from their relaxor nature. Relaxors possess an average cubic structure but their local symmetry is lower and characterized by the existence of PNRs with short-range polar order. The unit cell volume increases linearly with x (Figure S2, Supporting Information) as a result of the larger ionic radius of Zr4+ (0.720 Å, c.n. 6) in comparison to Ti4+ (0.605 Å, c.n. 6). The unit cell volume of the ceramic with x = 1 is 73.71 Å3 to be compared with 73.83 Å3 of undoped BaZrO3.
Photoluminescence properties
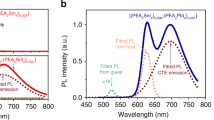
PL spectra of the investigated ceramics are reported in Fig. 2. Panel a) displays the stability range of crystal phases and polar variants as determined from the study of the dielectric properties. The drawings serve as a quick eye guide to correlate structure and polar order with luminescence properties.
(a) schematic representation of the stability range of the different crystal phases or polar variants in the Ba1−yEuyZrxTi1−x−y/4O3 and Ba1−yEuyZr1−y/4O3 (y = 0.01; x = 0, 0.05, 0.15, 0.30, 0.50, 0.70) ceramics. The drawings serve only as a quick eye guide to correlate structure and polar order with luminescence properties. Labels: C-P = cubic-paraelectric; C-R = cubic-relaxor; R-FE, O-FE, and T-FE = ferroelectric materials having rhombohedral, orthorhombic or tetragonal structure, respectively. Photoluminescence spectra of Eu:BZT ceramics at (b) room temperature, (c) −20 °C and (d) −100 °C. The curves color in panels (b-d) denotes the crystal phase and polar order according to panel (a). The numbers in panels b), c) and d) label the 5D0 → 7FJ (J = 0, 1, 2, 3, 4) Eu3+ transitions.
The shape of room temperature emission spectra (Fig. 2b), obtained exciting the 5L6 ← 7F0 transition at 395 nm, strongly depends on sample composition. The PL spectrum of BZ0 shows four groups of bands that are characteristics for europium emission from the 5D0 excited state to the 7FJ (J = 0, 1, 2, 3, 4) manifolds located at: 578 nm (7F0), 590–596 nm (7F1), 613–623 nm (7F2) and 680–720 nm (7F4)28. The 5D0 → 7F3 band, if any, is quite faint. HR spectra of the 5D0 → 7F1 (Figure S3) band evidence four components indicating the presence of at least two nonequivalent Eu3+ centers. In fact, considering the degeneration of the J = 1 level, a maximum of three components can be observed for a single site.
To verify the absence in the emission spectra of contributions coming from interface/foreign sites, sample BZ0 was annealed at 1450 °C for 48 h. This prolonged thermal treatment determined the exaggerated growth of some grains up to a size of 300–400 μm, thus allowing the intrinsic luminescence of Eu3+ in the perovskite lattice to be separated from other extrinsic contributions, such as the segregation of secondary phases (e.g. Eu2Ti2O7) and/or glassy phase films at grain boundaries, if any. Exaggerated grain growth during prolonged sintering is quite common in pure and slightly doped BaTiO3 ceramics and related to the formation of a liquid phase due to local stoichiometry variations or localized impurities32,33,34.
PL spectra collected by means of a microscope on a polished cross-section at the center of a large grain and on the fine-grained matrix (Figure S4) are virtually identical. Therefore, the non-equivalent Eu3+ sites are associated with the perovskite lattice. Although the ionic radius of Eu3+ in octahedral coordination (0.947 Å) is rather large and the stoichiometry was designed for exclusive Ba-site substitution, a small amount of the rare-earth could be incorporated at the B site. The probability of Eu3+ incorporation in perovskite B-site increases with increasing Zr content, as the unit cell volume expands of about 15% moving from BaTiO3 to BaZrO3. Alternative and complementary explanations for the existence of multiple sites will be discussed further on studying the emission spectra as a function of temperature.
As x increases from 0 to 0.7, the intensity of the 5D0 → 7F4 band decreases, the 5D0 → 7F2 emission gets stronger and overcomes the intensity of the 5D0 → 7F1 transition in BZ50 and BZ70. The 5D0 → 7F2 emission is strongly reduced in sample with composition x = 1, and the spectrum is dominated by the sharp 5D0 → 7F1 transition. Noteworthy, a significant band broadening is observed for BZ30, BZ50 and BZ70 ceramics. These shapes closely resemble those of Eu3+ doped glasses in which Eu3+ ions occupy multiple sites having small differences in the coordination environment35. Indeed, for intermediate compositions a significant contribution to PL is given by several sites corresponding to a different number of ZrO6 (TiO6) octahedra surrounding the Eu3+ ion. Moreover, the heterogeneous local structure of the relaxor ceramics, corresponding to Ti-rich PNRs embedded in a cubic paraelectric matrix26,27, further increases the disorder of the europium sites.
The narrowing of the 5D0 → 7F1 line and the drop of the intensity of 5D0 → 7F2 transition observed in the emission spectra of BZ100 suggests a decrease of the number of spectroscopic sites determined by the simpler composition and the disappearance of the PNRs. Very similar spectra are reported for BaZrO3 and BaSnO3 (cubic Pm-3m) in which Eu3+ is incorporated at the Ba site36,37,38,39. Indeed, the 5D0 → 7F1 transition is the most intense when Eu3+ occupies a centrosymmetric position such as Oh site of Ba in BaZrO3 for which all transitions but 5D0 → 7F1 are forbidden.
Not only the composition but also the temperature has a strong influence on the Eu3+ emission. At −20 °C (Fig. 2b) the spectra of the ferroelectric ceramics (BZ0, BZ5 and BZ15) are dominated by the 5D0 → 7F4 bands whose integrated intensity is three and a half times larger compared to the 5D0 → 7F1 transition that is the most intense at room temperature. All other bands, and in particular the 5D0 → 7F2 one, have a much lower intensity. The 5D0 → 7F4 transition is the strongest even in sample BZ30 in comparison to RT. The spectra of BZ50, BZ70 and BZ100 are instead very similar to those observed at room temperature. At −100 °C (Fig. 2c), the 5D0 → 7F4 transition is the most intense for all ceramics except BZ100, for which it has the same order of magnitude as 5D0 → 7F1 and 5D0 → 7F2. No significant changes in the shape of PL spectra of ferroelectric ceramics are observed between −20 and −100 °C. It is worth noting that band broadening in the PL spectra of relaxors is unaffected by temperature variations.
The detailed evolution of the PL spectra for some representative samples (BZ0, BZ15, BZ50 and BZ100) over the whole investigated temperature range, −100 to 140 °C, is illustrated in the color maps reported in Fig. 3. The maps of BZ5, BZ30 and BZ70 samples are shown in Figure S5.
Among other features, in ferroelectric Ti-rich ceramics (BZ0, BZ5 and BZ15) the main temperature-induced spectral modification is represented by the inversion of the intensity of the 5D0 → 7F1 and 5D0 → 7F4 transitions at about 10 °C, irrespective of composition. Moreover, in BaTiO3 the 5D0 → 7F4 transition remains strong up to 140 °C. Conversely, for relaxors we observed the rapid increase of the intensity of 5D0 → 7F4 transition, at temperatures that progressively decrease upon increasing Zr4+ content (x ≥ 0.30), and hence decreasing the number and/or the size of the Ti-rich PNRs.
It is worth noting that the spectrum of BZ100 is dominated by the 5D0 → 7F1 transition in the whole temperature range except at −100 °C. The PL variations are not determined by crystallographic modifications, as there is no correlation with the phase transitions (evidenced by white horizontal lines in Figs 3 and S5) in the ferroelectric samples while no transitions occur in relaxors.
It is evident that the emission properties of the solid solutions are mainly affected by the nature of polar order: ferroelectric, relaxor or paraelectric. The evolution of the PL spectra with temperature and polar order can be better quantified by plotting the first temperature derivative (D14) of the 5D0 → 7F1/5D0 → 7F4 integrated intensities ratio (Figs 4 and S6).
The temperature at which D14 reaches its maximum value is sensitive to the polar order of BaZrxTi1−xO3. For ferroelectric ceramics (BZ0, BZ5 and BZ15), the maximum of D14 is at ca. 10 °C and does not change with composition. By contrast, it progressively shifts to lower temperatures in relaxor and paraelectric ceramics on increasing Zr4+ content: −13 °C for BZ30, −55 °C for BZ50, −60 °C for BZ70, −65 °C for BZ100.
The absence of correlation between crystal phase transitions and modifications of PL emission with temperature is not surprising. The local symmetry of the Eu3+ site and, consequently, the relative intensities and shape of 5D0 → 7FJ manifolds in europium emission spectra are indeed essentially determined by the geometry of the first and second coordination sphere of Eu3+ rather than by the long-range crystallographic structure. There is increasing evidence that the local structure of BaTiO3 remains rhombohedral at all temperatures as indicated by the results of EXAFS, NMR and the pair-distribution function investigations40,41,42,43,44,45. According to the largely accepted eight-site model46, the Ti ions in the paraelectric cubic phase exhibit off-center local displacement along the eight [111] directions but the average polarization is null because of the random distribution among the 8 split sites. Below the Curie temperature partial ordering occurs. Thus O, T and C long-range structures are the result of the averaging [111] displacements of octahedral Ti over 2, 4 and 8 local rhombohedral directions, respectively. Only for the rhombohedral phase the local and long-range structures are equivalent. It is worth noting that the deformation of the R phase with respect to the cubic unit cell is quite small. At −93 °C the rhombohedral angle α is 89.85°18, i.e. there is only a deviation of 0.15° from the cubic prototype perovskite. Noteworthy, the position of Ba2+ ions is not affected by the off-center displacement of Ti4+ ions.
According to the above results (see Figs 2, 3 and S6), the ferroelectric ceramics show PL emission dominated by the 5D0 → 7F4 transitions over a broad temperature range, from −100 °C up to room temperature or even higher (up to 60–80 °C for x = 0). Emission spectra characterized by an abnormally high intensity of 5D0 → 7F4 transition are reported for Eu3+ occupying D4d (or distorted D4d) sites with coordination geometry close to square antiprism28,47,48,49,50 as well as distorted D2d sites51. For an undistorted D4d symmetry the 5D0 → 7F2 transition is forbidden whereas the transitions 5D0 → 7F1 and 5D0 → 7F4 are allowed28. This situation is uncommon and occurs only for the point groups D4d and O.
The ionic radius (c.n. 12) of Eu3+ (1.226 Å) is much smaller than that of Ba2+ (1.610 Å) and, consequently, the lanthanide ion is over-coordinated when it is positioned at the Ba site and the possibility of occupying a lower symmetry site has to be considered. Very recent investigations including careful crystal structure determination from synchrotron X-ray diffraction data and first-principle calculations on Gd- and Dy-doped BaTiO352,53 as well as the study of dielectric relaxations in Gd- and Dy-doped SrTiO354,55 have provided some evidence about the off-center displacement of trivalent lanthanide ions with average size at A-site of these perovskites.
As illustrated in Fig. 5, and referring to the cubic structure for the sake of simplicity, a displacement of about 1.0 Å along one of the six [100] directions (towards the center of any of the cube faces) drives Eu3+ from the regular dodecahedral Ba site, with Oh symmetry, to an acentric C4v site, with approximate D4d symmetry corresponding to a distorted 8-coordinated square antiprism.
Evolution of local symmetry during the off-center displacement of Eu3+ along one of the [100] directions of cubic BaTiO3. See text for details. Red spheres: O2−. Green sphere Eu3+. The images were realized using VESTA56.
The distortion arises from the existence of two groups of Eu-O distances: 2.240 and 3.000 Å (the first value is similar to the Eu-O distance in Eu2O3 and Eu2Ti2O7, 2.2–2.3 Å). In principle, the lanthanide can also move in other directions. Off-center displacement of Eu3+ along the crystallographic directions [110] (i.e. along a straight line parallel to the diagonal of the cube face) and [111] (towards a corner of the unit cell) will result in a reduction of the coordination number to 7 and 9, respectively. The local symmetry will be C2v for displacement in the [110] direction and C3v for displacement in the [111] direction.
When Eu3+ ions occupy sites with this punctual symmetry, the 5D0 → 7F0 transition is allowed and can be observed in the emission spectra. In our case, at room temperature the 5D0 → 7F0 transition is present only in PL spectra of ferroelectric materials and between −20 °C and −100 °C in relaxors depending on their composition, indicating a non-zero probability for displacements along [110] and [111] directions.
From a purely geometric point of view, the volume (5.34 Å3) of the pyramidal cavity available to host Eu3+ when moving along the [100] and [110] directions is twice that of the space available in the [111] direction and, consequently, this latter option is less likely. It is worth noting that no displacement would be expected if Eu3+ were incorporated at the Ti/Zr site, as its ionic radius in octahedral coordination (0.947 Å) is exceedingly large. The geometry depicted in Fig. 5b is only a first approximation as the oxygen ions around Eu3+ will undergo some relaxation from their ideal positions.
According to the previous discussion, the behavior of Eu3+ in the two perovskites BaTiO3 and BaZrO3 is, at a first glance, counterintuitive. The unit cell volume of BaZrO3 (73.83 Å3 at room temperature) is significantly larger (+15%) compared to BaTiO3 (64.34 Å3), but in BaZrO3 Eu3+ mainly occupies the Oh site of Ba2+ from 140 °C down to at least −60 °C. The spectra are dominated by the 5D0 → 7F1 transition and no 5D0 → 7F0 and 5D0 → 7F4 emissions were detected in this temperature range for pure zirconate (see Figs 2 and 3). At variance, in Ti-rich BaZrxTi1−xO3 ceramics (x = 0–0.15) there is convincing evidence of the displacement of Eu3+ along the [100] direction in the 8-fold square antiprism coordination site (Fig. 5), over a broad temperature range. Likewise, some displacements along [110] and [111] can be achieved.
The much smaller ionic radius of Eu3+ (1.226 Å) in comparison to Ba2+ (1.61 Å) is not enough by itself to explain the off-centering of the lanthanide in the ferroelectric ceramics and an additional driving force must exist. The investigation of the strikingly different behavior of CaxBa1−xTiO3 and SrxBa1−xTiO3 solid solutions provide some suggestions. While the incorporation of Sr2+ determines a continuous decrease of Curie temperature and unit cell volume, in the case of Ca2+ substitution the Curie temperature remains unaffected (stabilization of the ferroelectric phase) though the cell volume decreases. A combination of experimental techniques, first-principle calculations and atomistic modelling57,58,59 revealed the off-center displacement of Ca2+. Furthermore, the Ca2+ displacement amplifies the ferroelectric off-centering of Ti cations nearest to the Ca2+ site in a cooperative process thus enhancing ferroelectricity despite volume decrease. Atomistic simulations using large supercells59 showed that [100] displacement is preferred over [111]. Opposite, the position of Sr cations is largely central. The different behavior of the two earth-alkaline cations is essentially determined by their different ionic radius (c.n. 12), 1.34 Å for Ca2+ and 1.44 Å for Sr2+, being their chemical properties similar. It is worth noting that Ca2+ in CaTiO3 (orthorhombic Pbnm perovskite structure) occupies 8-coordinated distorted sites with Ca-O distances between 2.36 and 2.67 Å. The remaining 4 distances are >3 Å.
Following the same reasoning, the additional driving force determining off-centering of Eu3+ in ferroelectric ceramics is the enhancement of polar order and ferroelectricity resulting from the correlated movement of Eu3+ and Ti4+ ions. The off-center displacement of Eu3+ will give rise to an electrical dipole. If Eu3+ preferentially moves along one of the [100] directions in such a way that the component of the associated dipole moment will positively contribute to the dipole moment corresponding to the [111] relaxation of the Ti ions, the europium displacement will concur to the overall polarization and ferroelectricity. This mechanism can be amplified by the deformation of the TiO6 octahedra nearest to Eu3+ as happens with Ca2+. Opposite, if Eu3+ moved randomly, there would be no net contribution to ferroelectricity and no extra energy gain determined by off-centering. Hence, the absence of polar order in BaZrO3 prevents a correlated displacement of Eu3+ and Zr4+ and the lanthanide will largely stay in central position. It should be kept in mind that the concentration of Eu3+ ions is as low as 1% and, consequently, their mutual interaction will be negligible thus hampering a cooperative behavior of the lanthanide ions alone.
The evolution of the PL spectra with temperature is mainly ascribed to the change of the population of the different Eu3+ sites. For ferroelectric ceramics, the off-centering of Eu3+ occurs over a broad temperature range (up to 60–80 °C for BaTiO3) by the cooperative polar interactions discussed above and made possible by the existence of ferroelectric order. The polar interactions counteract the thermal motion which would favor the occupation of the central sites or more disordered distributions. In the absence of polar interactions, as in BaZrO3, off-centering of some Eu3+ can only occur at low temperature (≤−80 °C), as indicated by the increasing contribution of the 5D0 → 7F4 transition to the overall emission (Figs 2 and 3), thanks to the reduced thermal motion. In relaxors (BZ30, BZ50, BZ70), Eu3+ off-center displacement should be confined within PNRs, whereas a behavior similar to that exhibited by BaZrO3 is expected in the paraelectric matrix. However, the PL spectra of BZ30 below −40 °C are very similar to those of the ferroelectric samples (Figs 2, 3 and S5). This observation supports the idea that the ferroelectric to relaxor crossover in BaZrxTi1−xO3 occurs over the composition range 0.25 ≤ x < 0.35 with coexistence of PNRs and ferroelectric domains, the latter originated by percolation of polar clusters on cooling27,60. The rapid increase of the 5D0 → 7F4 emission at lower temperature in the other two relaxors (Figs 2–4 and S5) is again attributed to the suppression of thermal motion and off-centering of some Eu3+ ions.
One can wonder if the evolution of the PL spectra with temperature might be determined by a change of defect chemistry, for example by a redistribution of Eu3+ ions between A and B sites in the perovskite. However, owing to the very low mobility of cation and oxygen vacancies in the investigated temperature range, the defect chemistry of BaTiO3 and BaZrO3 is essentially frozen. Oxygen vacancies, the most mobile kind of ionic defects, start to be mobile above 400 °C61. A change in the distribution of Eu3+ between Ba and Ti sites is unlikely because this would imply a complete re-equilibration of the bulk defect chemistry and in particular the concentration of the charge compensating defects (cation vacancies for Ba-site incorporation, oxygen vacancies for B-site substitution) which can only occur by long-range diffusional transport. In contrast, the change of the Eu3+ position from the center of the dodecahedron to a nearby acentric site occurs over a very short distance (≈1 Å) and does not require diffusion.
Conclusions
An effective tuning of the photoluminescence of rare-earth ions incorporated in ferroelectric perovskites has recently been achieved by exploiting the strong coupling between the lattice strain and the electric field (or the mechanical stress) typical of ferroelectric materials. However, as shown in the present paper, the polar order and, in particular, the ferroelectric order, has a direct and remarkable impact on the photoluminescence of Eu3+ in the BaZrxTi1−xO3 perovskite even in the absence of an external field.
In the ferroelectric ceramics (x = 0–0.15), the photoluminescence spectra display a crossover from a dominating 5D0 → 7F1 emission above room temperature to a dominating 5D0 → 7F4 emission at lower temperature. This behavior provides strong evidence of the off-center displacement of Eu3+ along one of the [100] directions of the lattice into a site with approximate D4d symmetry with a coordination polyhedron close to a square antiprism with decreasing temperature. The off-centering of the lanthanide from the regular dodecahedral Oh site of Ba2+ can be attributed to the cooperative polar interactions with the ferroelectric lattice, i.e. the correlated displacement of Eu3+ and Ti4+ ions aided by the smaller ionic radius of Eu3+ (1.226 Å) in comparison to Ba2+ (1.610 Å). Conversely, in BaZrO3 the absence of ferroelectric order prevents a correlated displacement of Eu3+ and Zr4+ and the lanthanide will largely occupy the central dodecahedral Oh site in spite of the larger unit cell of the zirconate in comparison to BaTiO3. Only at low temperature (−100 °C) the suppression of thermal motion allows off-centering of some Eu3+ ions.
Materials with compositions x = 0.30–0.70 have a short-range polar order typical of relaxors and their photoluminescence shows a distinct crossover but a more complex behavior. The complexity partly arises from the heterogeneous nature of the relaxors at the nanoscale, corresponding to BaTiO3 polar nanoregions embedded in a paraelectric matrix. Moreover, for these intermediate compositions several Eu3+ sites corresponding to a different number of ZrO6 (TiO6) octahedra surrounding the lanthanide will give a significant contribution to the luminescence.
It is expected that other RE3+ ions with intermediate size (Sm3+ to Er3+), when incorporated at the Ba site of the perovskite, can exhibit a behavior similar to that of Eu3+ as the underlying mechanism is rather general and not restricted to a specific ion. However, the magnitude of the off-center displacement is likely to depend on the ionic radius of the dopant producing a systematic trend. Furthermore, a ferroelectric/polar order control of photoluminescence could be observed in other perovskites.
Experimental Section
Sample preparation
Six Eu-doped Ba(Ti,Zr)O3 ceramics with composition Ba1−yEuyTi1−x−y/4ZrxO3 (y = 0.01; x = 0, 0.05, 0.15, 0.30, 0.50, 0.70) and Ba1−yEuyZr1−y/4O3 (y = 0.01) were prepared by the classical solid-state route using industrial electronic grade precursors: BaCO3 (Solvay Bario e Derivati, Italy), TiO2 (Evonik Degussa grade P25, Germany), ZrO2 (Toho grade TZ0, Japan) and Eu2O3 (Metall Rare Earth Ltdl, China) powders as raw materials. The compositions correspond to Eu3+ substitution at the Ba site with Ti vacancy compensation (0 ≤ x ≤ 0.7) and Zr vacancy compensation (x = 1). The different samples are labelled as BZX, where X = 100x. Predominant substitution at the Ba site of BaTiO3 is reported for Ba/Ti < 1 up to 2–3 at.% europium,62,63 the solubility limit of trivalent europium. The low dopant concentration adopted (1 mol.%) guarantees that the structural and physical properties of the materials are not significantly affected. Precursor powders were wet-mixed in polypropylene jars using water as liquid and a solution of ammonium polyacrylate (pH = 10) as dispersant. After drying, the mixed powder was calcined for 4 h at 1000 °C and then compacted in cylinders (length: 1 cm, diameter: 1 cm) by isostatic pressing at 1500 bar. The resulting greens were sintered in air for 4 h at different temperatures depending on composition: 1450 °C (BZ0-BZ30), 1550 °C (BZ50-BZ70) and 1600 °C (BZ100). The relative density of the final samples was determined by the Archimedes’ method. The ceramics are well densified with relative density ≥94%. Ceramic disks with a thickness of about 1 mm were cut from the sintered body and characterized by different techniques.
Crystal structure, dielectric and ferroelectric properties
The phase composition and crystal structure was investigated by X-ray diffraction (XRD) using a CubiX diffractometer (Panalytical, The Netherlands) with Cu Kα radiation (30 kV, 30 mA). The lattice parameters were determined using FullProf 2000. For dielectric measurements, Ag-Pd electrodes were deposited on the plane-parallel polished surfaces of the disks followed by annealing in air at 500 °C for 12 h. The dielectric properties were measured by an impedance bridge E4980A Precision LCR Meter (Agilent, Santa Clara, CA) and a dielectric spectrometer CONCEPT40 (Novocontrol Technologies, Hundsangen, Germany) in the temperature range −150–150 °C at 102–106 Hz. Polarization – electric field ferroelectric loops were recorded at room temperature on the electroded ceramics immersed in transformer oil bath by a Sawyer–Tower modified circuit fed by triangular high voltage wave (frequency: 10 Hz) by using a TREK amplifier.
Photoluminescence
Room temperature luminescence spectra were recorded on solid samples in a front-face acquisition geometry with a spectrofluorimeter (Fluorolog-3, Horiba JobinYvon) equipped with double-grating monochromator in both the excitation and emission sides, coupled to a R928P Hamamatsu photomultiplier and a 450 W Xe arc lamp as the excitation source. The emission spectra were corrected for detection and optical spectral response of the spectrofluorimeter supplied by the manufacturer.
HR spectra and temperature dependent experiments (−100–140 °C) were carried out in backscattering geometry using a Horiba T64000 triple spectrometer equipped with a Peltier-cooled charge-coupled device detector (Horiba Synapse). The scattered radiation was collected through a 10× microscope objective (Olympus MPLAN, 10×/0.25). The spectrograph, equipped with 2400 lines/mm gratings for high resolution and 300 lines/mm for temperature dependent experiments, was used as a single stage spectrograph. Temperature dependent experiments were performed by means of a Linkam THMS600 heating/freezing microscope stage having temperature stability <0.1 °C over −196 °C to 600 °C temperature range.
Data Availability
All data generated or analysed during this study are included in this published article (and its Supplementary Information files).
References
Feldmann, C., Jüstel, T., Ronda, C. R. & Schmidt, P. J. Inorganic luminescent materials: 100 Years of research and application. Adv. Funct. Mater. 13, 511–516 (2003).
Eliseeva, S. V. & Bünzli, J. C. G. Lanthanide luminescence for functional materials and bio-sciences. Chem. Soc. Rev. 39, 189–227 (2010).
Bai, G., Tsang, M. K. & Hao, J. Tuning the luminescence of phosphors: Beyond conventional chemical method. Adv. Opt. Mater. 3, 431–462 (2015).
Hao, J., Zhang, Y. & Wei, X. Electric-induced enhancement and modulation of upconversion photoluminescence in epitaxial BaTiO3:Yb/Er thin films. Angew. Chemie - Int. Ed. 50, 6876–6880 (2011).
Yao, Q. et al. Electric field-induced giant strain and photoluminescence-enhancement effect in rare-earth modified lead-free piezoelectric ceramics. ACS Appl. Mater. Interfaces 7, 5066–5075 (2015).
Sun, H. L., Wu, X., Chung, T. H. & Kwok, K. W. In-situ Electric Field-Induced Modulation of Photoluminescence in Pr-doped Ba0.85Ca0.15Ti0.90Zr0.10O3 Lead-Free Ceramics. Sci. Rep. 6, 1–8 (2016).
Wang, F. et al. In situ reversible tuning of photoluminescence of an epitaxial thin film via piezoelectric strain induced by a Pb(Mg1/3Nb2/3)O3-PbTiO3 single crystal. J. Mater. Chem. C 5, 9115–9120 (2017).
Sun, H., Wu, X., Peng, D. F. & Kwok, K. W. Room-temperature large and reversible modulation of photoluminescence by in situ electric field in ergodic relaxor ferroelectrics. ACS Appl. Mater. Interfaces 9, 34042–34049 (2017).
Tu, D. et al. LiNbO3:Pr3+: A Multipiezo Material with Simultaneous Piezoelectricity and Sensitive Piezoluminescence. Adv. Mater. 29, 1–4 (2017).
Zhang, P. et al. Pr3+photoluminescence in ferroelectric (Ba0.77Ca0.23)TiO3 ceramics: Sensitive to polarization and phase transitions. Appl. Phys. Lett. 92, 3–6 (2008).
Tian, X. et al. Remanent-polarization-induced enhancement of photoluminescence in Pr3+-doped lead-free ferroelectric (Bi0.5Na0.5)TiO3 ceramic. Appl. Phys. Lett. 102, 7–10 (2013).
Du, P., Luo, L., Li, W., Zhang, Y. & Chen, H. Photoluminescence and piezoelectric properties of Pr-doped NBT-xBZT ceramics: Sensitive to structure transition. J. Alloys Compd. 559, 92–96 (2013).
Wei, Y. et al. Dual-enhancement of ferro-/piezoelectric and photoluminescent performance in Pr3+ doped (K0.5Na0.5)NbO3 lead-free ceramics. Appl. Phys. Lett. 105, 1–5 (2014).
Yao, Y., Luo, L., Li, W., Zhou, J. & Wang, F. An intuitive method to probe phase structure by upconversion photoluminescence of Er3+ doped in ferroelectric Pb(Mg1/3Nb2/3)O3-PbTiO3. Appl. Phys. Lett. 106, 1–5 (2015).
Khatua, D. K., Kalaskar, A. & Ranjan, R. Tuning Photoluminescence Response by Electric Field in Electrically Soft Ferroelectrics. Phys. Rev. Lett. 116, 2–6 (2016).
Haertling, G. H. Ferroelectric Ceramics: History and Technology. J. Am. Ceram. Soc. 82, 797–818 (1999).
Hiroshi, K., Youichi, M. & Hirokazu, C. Base-Metal Electrode-Multilayer Ceramic Capacitors: Past, Present and Future Perspectives. Jpn. J. Appl. Phys. 42, 1 (2003).
Kwei, G. H., Lawson, A. C., Billinge, J. L. & Cheong, S.-W. Structure of the Ferroelectric Phase of Barium Titanate. J. Phys. Chem. 97, 2368–2377 (1993).
Damjanovic, D. Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics. Reports Prog. Phys. 61, 1267 (1998).
Akbarzadeh, A. R., Kornev, I., Malibert, C., Bellaiche, L. & Kiat, J. M. Combined theoretical and experimental study of the low-temperature properties of BaZrO3. Phys. Rev. B 72, 205104 (2005).
Laulhé, C., Hippert, F., Bellissent, R., Simon, A. & Cuello, G. Local structure in BaTi1−xZrxO3 relaxors from neutron pair distribution function analysis. Phys. Rev. B 79, 064104 (2009).
Kreuer, K. D. Proton-Conducting Oxides. Annu. Rev. Mater. Res. 33, 333–359 (2003).
Fabbri, E., Pergolesi, D. & Traversa, E. Materials challenges toward proton-conducting oxide fuel cells: A critical review. Chem. Soc. Rev. 39, 4355–4369 (2010).
Petzelt, J. et al. Broadband dielectric spectroscopy of Ba(Zr,Ti)O3: Dynamics of relaxors and diffuse ferroelectrics. Ferroelectrics 469, 14–25 (2014).
Nuzhnyy, D. et al. Broadband dielectric response of Ba(Zr,Ti)O3 ceramics: From incipient via relaxor and diffuse up to classical ferroelectric behavior. Phys. Rev. B 86, 14106 (2012).
Buscaglia, V. et al. Average and local atomic-scale structure in BaZrxTi1−3O3 (x = 0.10, 0.20, 0.40) ceramics by high-energy x-ray diffraction and Raman spectroscopy. J. Phys. Condens. Matter 26, 13 (2014).
Shvartsman, V. V. & Lupascu, D. C. Lead-Free Relaxor Ferroelectrics. J. Am. Ceram. Soc. 95, 1–26 (2012).
Binnemans, K. Interpretation of europium(III) spectra. Coord. Chem. Rev. 295, 1–45 (2015).
Maiti, T., Guo, R. & Bhalla, A. S. Structure-property phase diagram of BaZrxTi1−xO3 system. J. Am. Ceram. Soc. 91, 1769–1780 (2008).
Dobal, P. S. et al. Micro-Raman scattering and dielectric investigations of phase transition behavior in the BaTiO3 –BaZrO3 system. J. Appl. Phys. 89, 8085–8091 (2001).
Farhi, R., Marssi, M., El, Simon, A. & Ravez, J. A Raman and dielectric study of ferroelectric Ba(Ti1−xZrx)O3 ceramics. Eur. Phys. J. B 9, 599–604 (1999).
Drofenik, M. Origin of the Grain Growth Anomaly in Donor-Doped Barium Titanate. J. Am. Ceram. Soc. 76, 123–128 (1993).
Lee, H.-Y., Kim, J.-S. & Kim, D.-Y. Fabrication of BaTiO3 single crystals using secondary abnormal grain growth. J. Eur. Ceram. Soc. 20, 1595–1597 (2000).
Rios, P. R., Yamamoto, T., Kondo, T. & Sakuma, T. Abnormal grain growth kinetics of BaTiO3 with an excess TiO2. Acta Mater. 46, 1617–1623 (1998).
Reisfeld, R., Velapoldi, R. A., Boehm, L. & Ish-Shalom, M. Transition probabilities of europium in phosphate glasses. J. Phys. Chem. 75, 3980–3983 (1971).
Guan, L. et al. Luminescent properties of Eu3+-doped BaZrO3 phosphor for UV white light emitting diode. J. Rare Earths 28, 292–294 (2010).
Sun, D. et al. Photoluminescence properties of europium and titanium co-doped BaZrO3 phosphors powders synthesized by the solid-state reaction method. Opt. Mater. 34, 1890–1896 (2012).
Patel, D. K., Vishwanadh, B., Sudarsan, V. & Kulshreshtha, S. K. Difference in the Nature of Eu3+ Environment in Eu3+ -Doped BaTiO3 and BaSnO3. J. Am. Ceram. Soc. 96, 3857–3861 (2013).
Kanie, K., Seino, Y., Matsubara, M., Nakaya, M. & Muramatsu, A. Hydrothermal synthesis of BaZrO3 fine particles controlled in size and shape and fluorescence behavior by europium doping. New J. Chem. 38, 3548–3555 (2014).
Comes, R., Lambert, M. & Guinier, A. The chain structure of BaTiO3 and KNbO3. Solid State Commun. 6, 715–719 (1968).
Kwei, G. H., Billinge, S. J. L., Cheong, S. W. & Saxton, J. G. Pair-distribution functions of ferroelectric perovskites: Direct observation of structural ground states. Ferroelectrics 164, 57–73 (1995).
Ravel, B., Stern, E. A., Vedrinskii, R. I. & Kraizman, V. Local structure and the phase transitions of BaTiO3. Ferroelectrics 206, 407–430 (1998).
Zalar, B., Laguta, V. V. & Blinc, R. NMR Evidence for the Coexistence of Order-Disorder and Displacive Components in Barium Titanate. Phys. Rev. Lett. 90, 4 (2003).
Levin, I., Krayzman, V. & Woicik, J. C. Local structure in perovskite (Ba, Sr)TiO3: Reverse Monte Carlo refinements from multiple measurement techniques. Phys. Rev. B 89, 24106 (2014).
Senn, M. S., Keen, D. A., Lucas, T. C. A., Hriljac, J. A. & Goodwin, A. L. Emergence of Long-Range Order in BaTiO3 from Local Symmetry-Breaking Distortions. Phys. Rev. Lett. 116, 207602 (2016).
Pirc, R. & Blinc, R. Off-center Ti model of barium titanate. Phys. Rev. B 70, 134107 (2004).
Zhiran, H. & Blasse, G. Energy transfer phenomena in luminescent materials based on GdB3O6. Mater. Chem. Phys. 12, 257–274 (1985).
Blasse, G. Luminescence from the Eu3+ ion in D4d symmetry. Inorg. Chim. Acta 142, 153–154 (1988).
Sá Ferreira, R. A. et al. A theoretical interpretation of the abnormal 5D0 → 7F4 intensity based on the Eu3+ local coordination in the Na9[EuW10O36]·14H2O polyoxometalate. J. Lumin. 121, 561–567 (2006).
Bettinelli, M., Speghini, A., Piccinelli, F., Neto, A. N. C. & Malta, O. L. Luminescence spectroscopy of Eu3+ in Ca3Sc2Si3O12. J. Lumin. 131, 1026–1028 (2011).
Ananias, D., Paz, F. A. A., Yufit, D. S., Carlos, L. D. & Rocha, J. Photoluminescent thermometer based on a Phase-transition lanthanide silicate with unusual structural disorder. J. Am. Chem. Soc. 137, 3051–3058 (2015).
Takeda, S. et al. Off-centering of rare-earth ion in (Ba,R)(Ti,Mg)O3 (R = Gd, Dy) Jpn. J. Appl. Phys. 55, 10TC08 (2016).
Takeda, S. et al. Structure fluctuation in Gd- and Mg-substituted BaTiO3 with cubic structure. Jpn. J. Appl. Phys. 56, 10PB10 (2017).
Tkach, A., Amaral, J. S., Zlotnik, S., Amaral, V. S. & Vilarinho, P. M. Enhancement of the dielectric permittivity and magnetic properties of Dy substituted strontium titanate ceramics. J. Eur. Ceram. Soc. 38, 605–611 (2018).
Tkach, A., Amaral, J. S., Amaral, V. S. & Vilarinho, P. M. Dielectric spectroscopy and magnetometry investigation of Gd-doped strontium titanate ceramics. J. Eur. Ceram. Soc. 37, 2391–2397 (2017).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Levin, I., Krayzman, V. & Woicik, J. C. Local-structure origins of the sustained Curie temperature in (Ba,Ca)TiO3 ferroelectrics. Appl. Phys. Lett. 102, 162906 (2013).
Fu, D., Itoh, M., Koshihara, S. Y., Kosugi, T. & Tsuneyuki, S. Anomalous phase diagram of ferroelectric (Ba,Ca)TiO3 single crystals with giant electromechanical response. Phys. Rev. Lett. 100, 227601 (2008).
Dawson, J. A., Sinclair, D. C., Harding, J. H. & Freeman, C. L. A-site strain and displacement in Ba1−xCaxTiO3 and Ba1−xSrxTiO3 and the consequences for the Curie temperature. Chem. Mater. 26, 6104–6112 (2014).
Kleemann, W., Miga, S., Dec, J. & Zhai, J. Crossover from ferroelectric to relaxor and cluster glass in BaTi1−xZrxO3(x = 0.25–0.35) studied by non-linear permittivity. Appl. Phys. Lett. 102, 232907 (2013).
De Souza, R. A. Oxygen Diffusion in SrTiO3 and Related Perovskite Oxides. Adv. Funct. Mater. 25, 6326–6342 (2015).
Lu, D. Y., Sun, X. Y. & Toda, M. Electron spin resonance investigations and compensation mechanism of europium-doped barium titanate ceramics. Jpn. J. Appl. Phys. 45, 8782–8788 (2006).
Mizuno, Y., Kishi, H., Ohnuma, K., Ishikawa, T. & Ohsato, H. Effect of site occupancies of rare earth ions on electrical properties in Ni-MLCC based on BaTiO3. J. Eur. Ceram. Soc. 27, 4017–4020 (2007).
Acknowledgements
L.C. and L.M. acknowledge the Romanian grants PNIII-P1-1.1-TE-2016-1951 and PN-III-P4-ID-PCE-2016-0817.
Author information
Authors and Affiliations
Contributions
All the authors contributed to the experiments. In particular G.C., M.T.B., C.C. and V.B. prepared the samples and made structural characterization. G.B. and L.A. performed the luminescence study. O.C., L.C., L.M. performed the electrical characterization of the samples. G.B. and V.B. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
To Paolo Nanni
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Canu, G., Bottaro, G., Buscaglia, M.T. et al. Ferroelectric order driven Eu3+ photoluminescence in BaZrxTi1−xO3 perovskite. Sci Rep 9, 6441 (2019). https://doi.org/10.1038/s41598-019-42897-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-42897-1
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.