Abstract
The major concern of current pagination is to report the doubly stratified medium subject to both magnetized and non-magnetized flow fields. For this purpose both the Newtonian and non-Newtonian liquids are considered in a double stratified medium having magnetic field interaction. To be more specific, a generally accepted rheological liquid around a cylindrical surface having constant radius embedded in magnetized doubly stratified media is taken into account. Additionally, flow field is manifested with various pertinent physical effects. The flow problem statement is defended through generalized formulation via fundamental laws. A computational scheme is executed and stream lines topologies are constructed for the both magnetized and non-magnetized stratified medium to explore the interesting features. It is observed that the Casson fluid velocity towards cylindrical surface is higher in magnitude as compared to flat surface. Such observation is same for the both the magnetized and non-magnetized flow fields. Our general formulation yields some existing attempts in the literature. The variations in local skin friction coefficient (LSFC), local Nusselt number (LNN) and local Sherwood number (LSN) are provided with the aid of tabular forms. It is trusted that the obtain observations via stream lines topologies will serve a clear insight to the said flow problem.
Similar content being viewed by others
Introduction
The fluid flow having interaction with applied magnetic field is termed as magneto-hydrodynamic flow. The engaged fluid can be from Newtonian and non-Newtonian models. The Newtonian fluids possesses linear relation between shear stress and shear rate. This relation is well-known by Newton’s law of viscosity. It is named after Sir Issac Newton. The common examples subject to Newtonian are alcohol, mineral, gasoline and water to mention just a few. The non-Newtonian do not possesses linear relation between shear stress and shear rate. The non-Newtonian class can be explore by dividing into subclasses, namely Dilatant (when viscosity is increasing function of shear like in silly putty, quicksand, water and cornflour), Pseudoplastic (when viscosity is decreasing function of shear for instance in ketchup), Thixotropic (when viscosity is time dependent decreasing function of shear like in glue, paint, asphalt and cosmetics) and Rheopectic (when viscosity is time dependent increasing function of applied shear like cream and gypsum paste). The movement of electrical conductor (EC) in existing magnetic field results EMF (electromotive force). Such force namely EMF is direct relation with both strength of magnetic field and speed of moving EC. The generated EMF along with applied magnetic field yields a resistive force that opposes the motion of EC. As far as the study of the magnetohydrodynamics (MHD) is concern, the assumed fluid model will play the role of EC. To explore the importance of MHD flows scientists proposed the coupling of applied magnetic field by means of Naviers stokes equations and ultimate results predicts acceptable remarks regarding practical involvements in both industrial and engineering areas like plasma welding, liquid metals subject to casting processes, (EHCs) electrolytic Hall cells, shielding individualities and significant heat transfer characteristics are few examples. Owing the importance of magnetic field involvement various scientist and researchers shared their views like Hua and Walker1 discussed magnetic field interaction via rectangular ducts. In this problem an inclined applied magnetic field is taken into account. The recorded observations were presented with both analytical and numerical approaches. The impact of magnetic field on fluid flow due to flat surface was identified by Chaturvedi2. In this problem viscous fluid is considered as EC along with porous flat surface assumption while the induced magnetic effect is neglected in this attempt. Aldoss3 studied the effects of magnetic field by way of vertical cylinder. The non-Darcian model is assumed in porous medium. He found that both natural and forced convection regime have opposite results against applied magnetic field. The impact of magnetic field on unsteady flow regime is reported by Nanousis4. The incompressibility condition is implemented on viscous fluid being acted as an EC in this study. Moreover, he assumed oscillatory flat surface. Chamkha5 explored the effects of magnetic field subject to vertical surface. In this analysis a surface is considered in thermally stratified medium. Both the Halls and Hartmann impacts are reported numerically. Bhattacharyya and Gupta6 identified magnetic field individualities for stagnation point flow in a three dimensional frame. In this study they also entertained heat transfer properties. A viscous fluid is taken as an EC with arbitrary velocity gradients. The influence of magnetic field and the corresponding involvement namely Joule heating towards microplar fluid was taken by Hakiem et al.7. The micropolar fluid is taken as EC in this study. They found that both the SFC (skin friction coefficient) and HRT (heat transfer rate) reflects decline values for the positive values of magnetic field parameter. Mansour et al.8 addressed the effects of magnetic field in the presence of both heat and mass transfer characteristics. In this study they consider micropolar as an EC by way of circular cylinder. The impact of magnetic field along with variable viscosity was examined by Seddeek9. In this study heat transfer properties are considered in the presence of radiations. They found that the fluid velocity is decreasing function of magnetic field parameter but temperature profile is found to be increasing one. Amin10 considered micropolar fluid as an EC with constant suction assumption. The transverse magnetic field in assumed in this analysis. The impact of magnetic field was provided with the aid of both tables and graphs. The impact of magnetic field on an Oldroyd-B fluid was examined by Hayat et al.11. In this attempt Oldroy-B was taken as an EC and exact solution in this regard was presented. The magnetic interaction towards shrinking surface was discussed by Nadeem et al.12. In this work they considered Casson fluid as an EC and shrinking was exponentially proportional. Adomian decomposition method was utilized to report analytical solution and the outcomes in this regard were offered in terms of both tables and graphs. The Eying-Powell fluid was taken as an EC and magnetic characteristics were reported by Hayat et al.13. They presented series solution and graphical trends are provided to elaborate impact of magnetic field parameter. Since than many attempts were with respect MHD flows. The past and recent developments in this direction can be assessed in refs 14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31.
The strength of current pagination is generalized mathematical formulation and interpretation in both magnetized and non-magnetized frames. In this article Casson fluid is taken as an EC with doubly stratified medium. The Casson fluid flow regime is further manifested with various physical effects namely stagnation point, applied magnetic field, mixed convetion, thermal radiation, heat generation/absorption, Joule heating, chemical reaction and suspended nanoparticles. It is noticed that the mutual mathematical modelling subject to flow narrating differential equations that is Navier-Stokes equations and Maxwell equations generates complex structures and it seems impossible to obtain exact solutions. Therefore a computational algorithm is developed to report numerical results in terms of both tables and graphs. To be more specific, Section-1 is devoted to skimmed the limited literature survey regarding magneto-hydrodynamic boundary layer flows which includes both Newtonian and non-Newtonians models. The generalized mathematical treatment for Casson fluid model is structured in Section-2. The detail analysis after implementation of computational algorithm is discussed in Section-3. In addition, Section-3 is further divided into sub sections (key to the graphs, key to the tables etc.) to facilitate readers. The stream lines patterns for both magnetized and non-magnetized cases are provided as a graphical outcomes in Section-4. The sub cases subject to said problem are retraced and discussed in Section-5. The summary of analysis is offered as an itemized points in Section-6. An adopted procedure is trustful and it can be extended to some useful fluid models like Tangent hyperbolic fluid model, Williamson fluid model, Powell-Eyring fluid model, Jeffrey fluid model etc.
Generalized Formulation
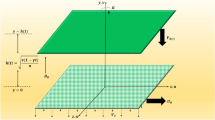
The flow model for the Casson fluid is mathematically modelled when various effects are taken into account namely, mixed convection, stagnation point, magnetic field, Joule heating, nonlinear radiations, heat generation/absorption, nanoparticles, temperature stratification, concentration stratification and chemical reaction. The fluid flow is achieved due to an inclined stretching cylindrical surface. For clarity the axial cylinder line is supposed to be parallel to x-axis and the perpendicular axis to the x-axis is taken as r-axis (radial direction). Through generally accepted mathematical laws, one can obtained the following flow narrating differential equations:
after using the Roseland radiative heat flux that is \({q}_{r}=-\,(\frac{4}{3})\frac{{\sigma }^{\cdot }}{{k}^{\cdot }}\frac{\partial {\bar{T}}^{4}}{\partial r}\), one can conclude the modification:
with end point conditions:
since the mathematical problem given in Eqs (1–5) with an endpoint conditions by Eq. (6) is highly non-linear therefore to report an exact solution seems impossible. Therefore, to seek the numerical solution we need an equivalent system of ordinary differential equations. It can be attained by using set of similarity transformation. This approach is scientifically and mathematically proven and considered by various prolific investigators like Sakiadis, Blasius, Prandtl and up-to today, see refs32,33,34. One of application of Lie symmetry analysis is order reduction towards differential equations. Ferdows et al.35 carried Lie symmetry approach to find set of similarity transformation for conversion of partial differential equations into ordinary differential system. Some recent trustful attempts subject to similarity transformation can assessed in refs36,37,38,39,40,41,42. Our attention is to solve the system of ordinary differential equations, therefore the widely used set of transformation37,38,39,40,41,42 for the cylindrical surface is given as
the velocity relations towards stream function are written by form:
use of Eq. (8) gives:
with transformed conditions:
The involved parameters are defined as below:
and the local skin friction coefficient at the surface of cylinder is given by:
in dimensionless practice, it is written as:
with \({{\rm{Re}}}_{x}=\frac{{U}_{0}{x}^{2}}{vL}\) be the local Reynolds number. The expression for the both local Nusselt and the local Sherwood numbers are given as:
the dimensionless form of these expression are pre-arranged as:
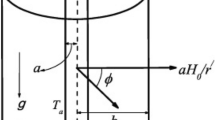
For the numerical solution the shooting method with Runge-Kutta algorithm is utilized. The complete description in this regard is provided by way of Fig. 2.
Analysis
Key to the graphs
Figures 3–20 are plotted to examine the flow field pattern of Casson liquid in both magnetized (γ ≠ 0) and non-magnetized (γ = 0) double stratified medium (δ1 ≠ 0, δ2 ≠ 0). Figure 1 provides the flow illustration of present problem. Figure 2 provides schematic diagram of numerical scheme. Figures 3 and 4 depicts stream lines pattern of Casson fluid in magnetized stratified medium for both flat (K = 0) and cylinder geometry (K ≠ 0) while Figs 5 and 6 are plotted against non-magnetized stratified medium subject to Casson liquid for both flat and cylinder geometry. It is important to note that Fig. 3–6 are examine without the assumption of stagnation point (A = 0) but Figs 7–16 are provided in the presence of stagnation point (A ≠ 0). In detail, Figs 7–12 are plotted for (A < 1), (A = 1) and (A > 1) respectively. Lastly, Figs 13 and 14 offered Casson fluid model stream lines topologies while Figs 15 and 16 depicts viscous fluid model (β → ∞). Figures 17–20 are provided to offer the variations in fluid velocity, temperature and nano-concentration profiles towards flow controlling parameters.
Key to the tables
Tables 1–8 are constructed to offer the variations in local skin friction coefficient (LSFC), local Nusselt number (LNN) and local Sherwood number (LSN) via curvature parameter (K), Casson fluid parameter (β), mixed convection parameter (λm), Prandtl number (Pr), heat generation parameter (Q+), temperature stratification parameter (δ1), Schmidt number (Sc), concentration stratification parameter (δ2), chemical reaction parameter (Rc) and Lewis number (Le). To be more specific, Tables 1, 3 and 6 reports the variations in LSFC. Further, Tables 2, 4 and 7 offer variations in LNN while the numerical values towards various parameters for LSN is reported in Tables 5 and 7.
Discussion
The generalized flow problem for the Casson fluid flow around a cylindrical geometry is controlled by mathematical formulation given in Eqs (2–6) in terms of partial differential equations. For solution purpose an acceptable set of transformation given in Eq. (7) is used to reduce partial differential equations into set of coupled ordinary differential equations. Since the reduced problem is boundary value problem therefore to meet the criteria of computational algorithm a dummy substitution is introduced and initial value problem is established. A shooting method along with Runge-Kutta scheme is implemented and the obtained observations are offered in terms of both tabular and graphical trends. One can easily check that our results are in excellent match with existing literature subject to local skin friction coefficient, local Nusselt and Sherwood numbers, see all of the tables in this regard. The stream lines topologies for the Casson liquid towards various involved physical parameters namely, magnetic field parameter (γ), curvature parameter (K), velocity ration parameter (A) and Casson fluid parameter (β) are presented. In detail, Figs 3 and 4 reports the stream lines patterns of Casson fluid in a magnetized (γ ≠ 0) doubly stratified (δ1 ≠ 0, δ2 ≠ 0) medium for both cylindrical (K ≠ 0) and flat (K = 0) surfaces. Particularly, Fig. 3 shows the stream lines pattern for cylindrical surface when K = 0.7 and Fig. 4 is examine for flat surface that is K = 0.0. Both patterns depicts magnetized stratified medium for Casson fluid and one can observed that the streamlines for γ = 0.5, K = 0.7 are significantly close as compared to γ = 0.5, K = 0.0. This fact is due to cylindrical surface and hence Casson fluid velocity enlarged for the case of cylindrical geometry with respect to flat surface even the fluid flow regime is magnetized. Figures 5 and 6 provided stream lines topologies when fluid flow regime is independent of applied magnetic field. It is observed that in non-magnetized stratified medium the stream lines are enough closer for cylindrical surface as compared to flat plate. Moreover, one can validated from Figs 3 and 4 being plotted in magnetized stratified medium (γ ≠ 0) in contrast to non-magnetized stratified medium (γ = 0) In this direction it is observed that the existence of magnetic field is the cause of wider distance between stream lines (Figs 3 and 4) with that of stream lines patterns (Figs 5 and 6) for without the influence of magnetic field. Therefore, a turbulence character can be avoid by considering magnetized flow field. In general, the presence of magnetic field parameter is the cause of increment in Lorentz force. It is resistive force and may cause resistance to fluid flow as a result the average velocity diminishing. The variations in Casson fluid velocity under the region of stagnation point for both magnetized and non-magnetized stratified medium is tested for (A < 1, A = 1, A > 1). The Figs 7–12 are provided in this direction. Figures 7 and 8 are plotted for A < 1, when the free stream velocity is lower in strength as compared to stretching rate in both magnetized and non-magnetized stratified medium. One can observed that the for magnetized case γ = 0.5 the stream lines patterns are wider than that of non-magnetized case γ = 0.0 as expected. The case A = 1, when both free stream and stretching velocities are equivalent is examined and observation in this regard is provided by means of Figs 9 and 10 for both magnetized and non-magnetized frame. In magnetized frame the velocity seems suppressed than that of non-magnetized. This is due to opposing force termed as Lorentz force. When free stream velocity exceeded the strength with that of stretching one we interpret this with A > 1. Figures 11 and 12 are given with respect to A > 1 in both magnetized and non-magnetized stratified medium. It can be seen that for A > 1 the impact of magnetic field parameter still remains significant that is the free stream lines patterns depicts larger distance between them as compared to non-magnetized frame which implies the suppress nature of velocity against magnetic flow field. Figures 13 and 14 are plotted to report flow pattern of Casson liquid (β = 1.3) under the region of stagnation point (A ≠ 0) flow in both magnetized (γ = 0.5) and non-magnetized (γ = 0) stratified medium. It is seen that the Casson fluid particles momentum is significant in non-magnetized (γ = 0) stratified medium than that of magnetized (γ = 0.5). The application of magnetic field brings the resistive role of Lorentz force as results the average velocity of Casson liquid suffers. It can be observed from Eq. (9), when Casson fluid parameters approaches the infinite value (β → ∞) we have viscous fluid via doubly stratified medium having suspended nanoparticles in flow regime. Therefore, Figs 15 and 16 reports the flow pattern of viscous fluid in both in both magnetized (γ = 0.5) and non-magnetized (γ = 0) stratified medium. Similar trends are observed for the existing of magnetized stratified medium with that of non-magnetized frame. The viscous fluid momentum is decreasing function of magnetic field parameter. On another hand when the Casson fluid parameter increases the fluid becomes more dense as a result the velocity increases. This fact is validated through stream lines patterns that is for β → 1.3 the distance between stream lines are less as compared to stream lines pattern given in Fig. 16. The extreme limit of Casson fluid parameter (β → ∞) yields Newtonian fluid model as an especial case.
Graphical outcomes
Additionally, Figs 17–20 are plotted to provide the impact of flow controlling parameters namely, mixed convection parameter (λm), thermal radiation parameter (RT), temperature stratification parameter (δ1) and chemical reaction parameter (Rc). To be more specific, the impact of mixed convection parameter on fluid velocity is examined and provided by way of Fig. 17. It is noticed that when we iterate λm = 0.1, 0.3, 0.4 the fluid velocity enhances. Figure 18 is plotted to offer the effect of thermal radiation parameter on fluid temperature. It can be seen that when we iterate RT = 0.1, 0.2, 0.4 the fluid temperature shows an inciting values. Further, it is noticed that the fluid temperature is decreasing function of temperature stratification parameter. Figure 19 is evident in this direction that is for positive values of δ1 = 0.1, 0.2, 0.3 the fluid temperature reflects decline nature. The effect of chemical reaction parameter on nano-concentration profile is examined and offered by means of Fig. 20. It is observed that the nano-concentration profile is decreasing function of Rc = 0.1, 0.3, 0.4.
Sub attempts
Since an article contains proposed generalized mathematical modelling for the stratified medium towards Casson fluid flow around a cylindrical geometry. The existing literature subject to the Casson flow field via stratified medium becomes over sub-study. The detail in this direction structured through section wise.
Case-1
In the absence of concentration equation and ignoring the stagnation point, thermal radiations, Joule heating and suspended nanoparticles assumptions, the generalized problem reduced to Problem reported in ref.31. In this problem a magnetohydrodynamic Casson fluid flow towards both flat and cylindrical surfaces via thermally stratified medium. It was concluded that the obtained variations were remarkably enormous for cylindrical geometry as compared to plane surface. The local skin friction coefficient was found as an increasing function of curvature parameter, Casson fluid parameter, Prandtl number and thermal stratification parameter while opposite trends were noticed towards mixed convection parameter and heat generation parameter. The local Nusselt number was an increasing function for greater values of curvature parameter, mixed convection parameter and Prandtl number while inverse values are noticed for Casson fluid parameter, thermal stratification parameter and heat generation parameter. An excellent comparison is noticed with ref.31 for both local skin friction coefficient and local Nusselt number. Tables 1 and 2 are constructed in this regard. The flow narrating formulation in this regard is given as:
Case-2
In absence of thermal radiations, Joule heating, suspended nanoparticles and stagnation point assumptions our generalized mathematical formulation meet with formulation reported in ref.43. In this problem doubly stratified mixed convection flow of Casson fluid due to an inclined cylindrical surface was examined. It was reported that in absolute sense the local skin friction shows an inciting nature towards curvature parameter, Casson fluid parameter, Prandtl number, Schmidt number, thermal stratification parameter while opposite attitude wasobserved for the positive values of mixed convection parameter, solutal stratification parameter and heat generation parameter. It was seen that Nusselt number was decreasing function of Casson fluid parameter, thermal stratification parameter and heat generation parameter but an inverse trends were found for the higher values of mixed convection parameter, curvature parameter and Prandtl number. Additionally, it was observed that Sherwood number reflected an inciting attitude for higher values of curvature parameter, Schmidt number, solutal stratification parameter and chemical reaction parameter. Tables 3, 4 and 5 are constructed in this direction and we have an excellent match with observation recorded in ref. 43. The corresponding mathematical formulation are prearranged as follows:
with transformed conditions:
Case-3
One can confirm from mathematical formulation given by Eqs (9–12), that the generalized problem meets with ref.44 when we ignore stagnation point, magnetic field, suspended nanoparticles, thermal radiations, heat generation and Joule heating effects along additional condition that is β → ∞. In this problem mixed convection effects towards thermally stratified media were presented. The corresponding mathematical formulation in this problem is as follows:
with transformed conditions:
Case-4
The effectiveness subject to velocity gradients due to viscous stresses was consider very small therefore in this attempt45 the impact of Joule heating was ignored. Since our flow problem contains the influence of Joule heating so by ignoring this fact our findings exactly matched with results reported in ref.45. For comparison purpose we have constructed Tables 6, 7 and 8. To be more specific, Table 6 is constructed for comparative values of local skin friction coefficient. It was found In absolute sense, it was noticed that the skin friction coefficient reflected increasing values via both K, and β. On the other hand it shows an opposite trends for the increasing values of λm. Moreover, the local skin friction coefficient in independent of Prandtl number. The negative sign of local skin friction implies the drag forced exerted by cylindrical surface towards Casson fluid particles. It has been observed through the local Nusselt number shows an increasing values for the greater values of K and Pr, however opposite variations are observed for the increasing values of the parameter δ1. The negative sign in local Nusselt number relates the transfer of heat normal to the cylindrical surface. The local Sherwood number depicts an increasing attitude for the increasing values of the parameters K, and Le. On the other hand, it shows a decreasing nature towards δ2. Further, the recent developments on the surface quantities can be assessed in refs46,47.
Summary
The realistic Casson fluid model via both magnetized (γ ≠ 0) and non-magnetized (γ = 0) stratified (δ1 ≠ 0, δ2 ≠ 0) media is investigated. The stream lines topologies are limited to magnetic field parameter (γ), curvature parameter (K), velocity ratio parameter (A) and Casson fluid parameter (β). The key outcomes are itemized as follows:
-
1.
A generalized mathematical formulation is proposed for the non-Newtonian fluid model.
-
2.
The Casson liquid around cylindrical surface (K = 0.7) claims larger momentum values with respect to Casson liquid via flat surface (K = 0.0). This variation is invariant subject to both magnetized and non-magnetized stratified medium.
-
3.
The flow momentum of Casson liquid found suppress for magnetized stratified medium as compared to non-magnetized medium.
-
4.
Both Newtonian (β → ∞) and non-Newtonian (β = 1.3) fluids flow reflects decline nature in magnetized (γ ≠ 0) stratified (δ1 ≠ 0, δ2 ≠ 0) medium than that of non-magnetized (γ = 0) one.
-
5.
The momentum of viscous fluid flow in stratified medium is significantly lower as compared to momentum of Casson fluid flow. Such variation holds in both magnetized and non-magnetized stratified medium.
-
6.
The Casson fluid temperature is increasing function of thermal radiation parameter.
-
7.
The nano-concentration profile is decreasing function of chemical reaction parameter.
-
8.
The LSFC, LNN and LSN are offered in a systematic design via comparison with some interesting existing results.
References
Hua, T. Q. & Walker, J. S. MHD flow in rectangular ducts with inclined non-uniform transverse magnetic field. Fusion Eng. Des. 27, 703–710 (1995).
Chaturvedi, N. On MHD flow past an infinite porous plate with variable suction. Energy Convers. Manag. 37, 623–627 (1996).
Aldoss, T. K. MHD mixed convection from a vertical cylinder embedded in a porous medium. Int. Commun. heat mass Transf. 23, 517–530 (1996).
Nanousis, N. D. The unsteady hydromagnetic thermal boundary layer with suction. Mech. Res. Commun. 23, 81–90 (1996).
Chamkha, A. J. MHD-free convection from a vertical plate embedded in a thermally stratified porous medium with Hall effects. Appl. Math. Model. 21, 603–609 (1997).
Bhattacharyya, S. & Gupta, A. S. MHD flow and heat transfer at a general three-dimensional stagnation point. Int. J. Non. Linear. Mech. 33, 125–134 (1998).
El-Hakiem, M. A., Mohammadein, A. A., El-Kabeir, S. M. M. & Gorla, R. S. R. Joule heating effects on magnetohydrodynamic free convection flow of a micropolar fluid. Int. Commun. heat mass Transf. 26, 219–227 (1999).
Mansour, M. A., El-Hakiem, M. A. & El Kabeir, S. M. Heat and mass transfer in magnetohydrodynamic flow of micropolar fluid on a circular cylinder with uniform heat and mass flux. J. Magn. Magn. Mater. 220, 259–270 (2000).
Seddeek, M. A. The effect of variable viscosity on hydromagnetic flow and heat transfer past a continuously moving porous boundary with radiation. Int. Commun. Heat Mass Transf. 27, 1037–1046 (2000).
El-Amin, M. F. Magnetohydrodynamic free convection and mass transfer flow in micropolar fluid with constant suction. J. Magn. Magn. Mater. 234, 567–574 (2001).
Hayat, T., Hutter, K., Asghar, S. & Siddiqui, A. M. MHD flows of an Oldroyd-B fluid. Math. Comput. Model. 36, 987–995 (2002).
Nadeem, S., Haq, R. U. & Lee, C. MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. 19, 1550–1553 (2012).
Hayat, T., Awais, M. & Asghar, S. Radiative effects in a three-dimensional flow of MHD Eyring-Powell fluid. J. Egypt. Math. Soc. 21, 379–384 (2013).
Khan, W. A., Makinde, O. D. & Khan, Z. H. MHD boundary layer flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with Navier slip. Int. J. Heat Mass Transf. 74, 285–291 (2014).
Shahzad, A. & Ramzan, A. L. I. MHD flow of a non-Newtonian Power law fluid over a vertical stretching sheet with the convective boundary condition. Walailak J. Sci. Technol. 10, 43–56 (2012).
Shahzad, A. & Ali, R. Approximate analytic solution for magneto-hydrodynamic flow of a non-Newtonian fluid over a vertical stretching sheet. Can J Appl Sci 2, 202–215 (2012).
Masood, K., Ramzan, A. L. I. & Shahzad, A. MHD Falkner-Skan flow with mixed convection and convective boundary conditions. Walailak J. Sci. Technol. 10, 517–529 (2013).
Ahmed, J., Shahzad, A., Khan, M. & Ali, R. A note on convective heat transfer of an MHD Jeffrey fluid over a stretching sheet. AIP Adv. 5, 117117 (2015).
Hayat, T., Muhammad, T., Shehzad, S. A., Chen, G. Q. & Abbas, I. A. Interaction of magnetic field in flow of Maxwell nanofluid with convective effect. J. Magn. Magn. Mater. 389, 48–55 (2015).
Nejad, M. M., Javaherdeh, K. & Moslemi, M. MHD mixed convection flow of power law non-Newtonian fluids over an isothermal vertical wavy plate. J. Magn. Magn. Mater. 389, 66–72 (2015).
Eid, M. R. Chemical reaction effect on MHD boundary-layer flow of two-phase nanofluid model over an exponentially stretching sheet with a heat generation. J. Mol. Liq. 220, 718–725 (2016).
Babu, D. H. & Narayana, P. V. S. Joule heating effects on MHD mixed convection of a Jeffrey fluid over a stretching sheet with power law heat flux: A numerical study. J. Magn. Magn. Mater. 412, 185–193 (2016).
Ahmed, J., Begum, A., Shahzad, A. & Ali, R. MHD axisymmetric flow of power-law fluid over an unsteady stretching sheet with convective boundary conditions. Results Phys. 6, 973–981 (2016).
Ahmed, J., Shahzad, A., Begum, A., Ali, R. & Siddiqui, N. Effects of inclined Lorentz forces on boundary layer flow of Sisko fluid over a radially stretching sheet with radiative heat transfer. J. Brazilian Soc. Mech. Sci. Eng. 39, 3039–3050 (2017).
Ali, F., Sheikh, N. A., Khan, I. & Saqib, M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 423, 327–336 (2017).
Shankar, B. M., Kumar, J. & Shivakumara, I. S. Magnetohydrodynamic stability of natural convection in a vertical porous slab. J. Magn. Magn. Mater. 421, 152–164 (2017).
Rashad, A. M. Impact of thermal radiation on MHD slip flow of a ferrofluid over a non-isothermal wedge. J. Magn. Magn. Mater. 422, 25–31 (2017).
Pal, D. & Mandal, G. Thermal radiation and MHD effects on boundary layer flow of micropolar nanofluid past a stretching sheet with non-uniform heat source/sink. Int. J. Mech. Sci. 126, 308–318 (2017).
Soid, S. K., Ishak, A. & Pop, I. MHD flow and heat transfer over a radially stretching/shrinking disk. Chinese J. Phys. 56, 58–66 (2018).
Rehman, K. U., Malik, M. Y., Zahri, M. & Tahir, M. Numerical analysis of MHD Casson Navier’s slip nanofluid flow yield by rigid rotating disk. Results Phys. 8, 744–751 (2018).
Rehman, K. U., Qaiser, A., Malik, M. Y. & Ali, U. Numerical communication for MHD thermally stratified dual convection flow of Casson fluid yields by stretching cylinder. Chinese J. Phys. 55, 1605–1614 (2017).
Blasius, H. Laminare stromung in kanalen wechselnder breite. Zeitschrift Fur Math. u Phys. 58, 225–233 (1910).
Sahoo, B. Flow and heat transfer of a non-Newtonian fluid past a stretching sheet with partial slip. Commun. Nonlinear Sci. Numer. Simul. 15, 602–615 (2010).
Fang, T., Zhang, J. & Zhong, Y. Boundary layer flow over a stretching sheet with variable thickness. Appl. Math. Comput. 218, 7241–7252 (2012).
Ferdows, M., Uddin, M. J. & Afify, A. A. Scaling group transformation for MHD boundary layer free convective heat and mass transfer flow past a convectively heated nonlinear radiating stretching sheet. Int. J. Heat Mass Transf. 56, 181–187 (2013).
Abdel-Wahed, M. S., Elbashbeshy, E. M. A. & Emam, T. G. Flow and heat transfer over a moving surface with non-linear velocity and variable thickness in a nanofluids in the presence of Brownian motion. Appl. Math. Comput. 254, 49–62 (2015).
Hayat, T., Saeed, Y., Asad, S. & Alsaedi, A. Convective heat and mass transfer in flow by an inclined stretching cylinder. J. Mol. Liq. 220, 573–580 (2016).
Merkin, J. H., Najib, N., Bachok, N., Ishak, A. & Pop, I. Stagnation-point flow and heat transfer over an exponentially stretching/shrinking cylinder. J. Taiwan Inst. Chem. Eng. 74, 65–72 (2017).
Tamoor, M., Waqas, M., Khan, M. I. & Alsaedi, A. Hayat, T. Magnetohydrodynamic flow of Casson fluid over a stretching cylinder. Results Phys. 7, 498–502 (2017).
Bakar, N. A. A., Bachok, N. & Arifin, N. M. Stability analysis on the flow and heat transfer of nanofluid past a stretching/shrinking cylinder with suction effect. Results Phys. 9, 1335–1344 (2018).
Usman, M., Soomro, F. A., Haq, R. U., Wang, W. & Defterli, O. Thermal and velocity slip effects on Casson nanofluid flow over an inclined permeable stretching cylinder via collocation method. Int. J. Heat Mass Transf. 122, 1255–1263 (2018).
Alamri, S. Z., Khan, A. A., Azeez, M. & Ellahi, R. Effects of mass transfer on MHD second grade fluid towards stretching cylinder: A novel perspective of Cattaneo-Christov heat flux model. Phys. Lett. A (2018).
Rehman, K. U., Malik, A. A., Malik, M. Y., Sandeep, N. & Saba, N. U. Numerical study of double stratification in Casson fluid flow in the presence of mixed convection and chemical reaction. Results Phys. 7, 2997–3006 (2017).
Mukhopadhyay, S. & Ishak, A. Mixed convection flow along a stretching cylinder in a thermally stratified medium. J. Appl. Math. 2012, https://doi.org/10.1155/2012/491695 (2012).
Rehman, K. U., Saba, N. U., Malik, M. Y. & Zehra, I. Nanoparticles individualities in both Newtonian and Casson fluid models by way of stratified media: A numerical analysis. Eur. Phys. J. E 41, 37 (2018).
Saif, R. S., Hayat, T., Ellahi, R., Muhammad, T. & Alsaedi, A. Darcy–Forchheimer flow of nanofluid due to a curved stretching surface. Int. J. Num. Meth. Heat Fluid Flow 29, 2–20 (2019).
Suleman, M. et al. A Numerical Simulation of Silver–Water Nanofluid Flow with Impacts of Newtonian Heating and Homogeneous–Heterogeneous Reactions Past a Nonlinear Stretched Cylinder. Symmetry 11, 295 (2019).
Acknowledgements
The authors would like to express their gratitude to King Khalid University, Abha 61413, Saudi Arabia, Air University Islamabad 44000, Pakistan and University of Sharjah 27272, UAE for providing administrative and technical support. In addition, authors also would like to acknowledge and express their gratitude to the United Arab Emirates University, Al Ain, UAE for providing the financial support with Grants Nos. 31S363-UPAR (4) 2018 and 31S240-UPAR (2) 2016.
Author information
Authors and Affiliations
Contributions
Khalil Ur Rehman develop the mathematical equations. M.Y. Malik wrote and approved the manuscript. The self-coded numerical algorithm is constructed by Qasem M. Al-Mdallal and the line graphs are obtained by Mostafa Zahri.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rehman, K.U., Malik, M.Y., Al-Mdallal, Q.M. et al. On both magnetized and non-magnetized dual stratified medium via stream lines topologies: A generalized formulation. Sci Rep 9, 6306 (2019). https://doi.org/10.1038/s41598-019-42726-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-42726-5
This article is cited by
-
Stratified Casson Fluid Flow Past a Riga-plate with Generative/Destructive Heat Energy
International Journal of Applied and Computational Mathematics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.