Abstract
The decrease in electronic device size necessitates greater understanding of gas breakdown and electron emission at microscale to optimize performance. While traditional breakdown theory using Paschen’s law (PL), driven by Townsend avalanche, fails for gap distance d \(\lesssim \) 15 μm, recent studies have derived analytic equations for breakdown voltage when field emission and Townsend avalanche drive breakdown. This study derives a new analytic equation that predicts breakdown voltage VB within 4% of the exact numerical results of a previously derived theory and new experimental results at subatmospheric pressure for gap distances from 1–25 μm. At atmospheric pressure, VB transitions to PL near the product of pressure and gap distance, pd, corresponding to the Paschen minimum; at lower pressures, the transition to PL occurs to the left of the minimum. We further show that the work function plays a major role in determining which side of the Paschen minimum VB transitions to PL as pressure approaches atmospheric pressure while field enhancement and the secondary emission coefficient play smaller roles. These results indicate that appropriate combinations of these parameters cause VB to transition to PL to the left of the Paschen minimum, which would yield an extended plateau similar to some microscale gas breakdown experimental observations.
Similar content being viewed by others
Introduction
Gas breakdown in the presence of electric fields is desirable for generating microplasmas for combustion1, electric propulsion2, or medical and environmental applications3,4,5,6,7 and deleterious in accelerators8, fusion devices9, micro and nanoelectronics10,11, and pulsed power biological experiments12. All these scenarios require accurately predicting gas breakdown at microscale gaps or smaller; however, the standard theory for predicting gas breakdown voltage VB given by Paschen’s law (PL)13 fails because field emission (FE), rather than Townsend avalanche (TA), drives breakdown at these scales14,15. Given by \({V}_{B}={B}_{p}pd/[\,\mathrm{ln}({A}_{p}pd)-\,\mathrm{ln}\,[\,\mathrm{ln}(1+{\gamma }_{SE}^{-1})]],\) where p is the pressure, d is the gap distance, γSE is the secondary electron emission coefficient, and Ap and Bp are gas constants, PL13 is characterized by a minimum VB that occurs when \(pd=\exp (1){A}_{p}^{-1}\,\mathrm{ln}(1+{\gamma }_{SE}^{-1});\) however, at microscale, this minimum vanishes or is replaced by an extended plateau14,15.
Several mathematical models and simulations15,16,17,18,19,20,21,22,23 have predicted VB as a function of gap distance and/or pressure to demonstrate the transition to FE. Because many of these models must be solved numerically—and those that are analytic often do not fully incorporate all mechanisms to elucidate limiting behavior—more recent studies have applied matched asymptotic theory to analytically unify FE and TA for argon at atmospheric pressure24, any gas at atmospheric pressure25, and any gas at any pressure for FE or TA driven breakdown26. These models can also quantify the relative contributions of FE and TA to breakdown25,26,27, demonstrate the transitions between the mechanisms, and yield an analytic expression similar to traditional vacuum breakdown27,28. More recent simulations have shown that electrodes with multiple sharp protrusions yielded an effective PL that combined the individual PL for each protrusion29. While potentially contributing to the observed extended plateau, these simulations did not fully incorporate field emission. Furthermore, real electrodes, even when polished to control surface roughness, may not necessarily have distinct, well-defined, sharp tips.
Many (albeit not all) microscale gas breakdown experiments focus on breakdown at atmospheric pressure, which is critical for the aforementioned biomedical6,7, environmental5, and combustion applications1. However, gas breakdown plays a major role in limiting the power levels of high power microwave devices from 1 to 100 GHz30,31,32. Additionally, electric field distribution plays a critical role in low-pressure gas breakdown33,34. While most vacuum electronics studies focus on device failures due to space-charge limited emission35,36,37,38 and multipactor39,40,41, vacuum breakdown has also been examined28. The development of carbon nanotube systems for vacuum electron emission42,43,44 and the potential for nanoscale systems at higher pressures45 motivates additional characterization of electron emission experimentally at subatmospheric pressure. While some studies have assessed pressure on the order of a few torr21, a study detailing the impact of pressure on the intersection of the combined FE/TA breakdown regime with PL has not been performed. This letter measures breakdown voltage at microscale for several subatmospheric pressures and assesses this behavior using a universal, matched asymptotic solution26. As we shall show, this universal model gives the conditions under which FE and TA driven breakdown transition to PL to the left of the Paschen minimum, yielding the appearance of an extended plateau.
Results
Experimental description and results
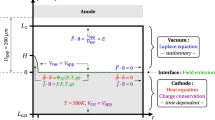
A detailed description and block diagram of the experimental setup can be found in ref.27. Briefly, the experimental system consists of a nanosecond pulse generation unit, a synchronous and delay triggering unit, an in-situ optical imaging unit, and an electrical parameter measurement unit. We generated the nanosecond pulse by feeding DC voltage into a high voltage solid-state switch (BEHLKE HTS-50-08-UF), which delivered adjustable nanosecond pulses with a maximum amplitude up to 5 kV. Synchronous triggering was performed by a function generator (RIGOL DG3101A). We integrated an in-situ optical imaging unit with an optical microscope to achieve micron-scale spatial resolution and a high-speed gated ICCD camera to attain nanosecond-scale temporal resolution. A metallographic microscope (OLYMPUS BX51M) with a long work distance objective lens (50×) magnified the micron-scale test specimen. We used a high-speed gated ICCD camera (ANDOR iStar 334 T) to detect light emission during gas breakdown with a minimum gate width of 2 ns. A current coil (Pearson 6585) monitored pulse current, an attenuator probe (100:1) measured pulsed voltage, and a digital oscilloscope (LeCroy 104MXs-B) reported the signal. This letter focuses on breakdown measurements; further experimental assessments will be reported elsewhere.
Figure 1 shows the experimental results for breakdown voltage in air at pressures of 3, 50, and 101 kPa for gap distances from 1–25 μm. When plotted as a function of d, VB is relatively insensitive to p at smaller gap distances where one anticipates field emission driven breakdown. Measured VB diverges with p for \(d\gtrsim 5{\rm{\mu }}m\). While our previous theoretical studies have examined VB as a function of either p or d24,25,26, the relatively large difference in p here suggests that collisionality, or pd, may elucidate the experimental behavior. Thus, we will assess VB(pd) when we apply the matched asymptotic theory to the experimental data.
Theoretical analysis and results
We start from the general, nondimensional, universal (true for any gas) breakdown equation, given by26
where \(\bar{\varphi }=\varphi /{\varphi }_{\ast }\) is the dimensionless work function of the electrode material with \({\varphi }_{\ast }={[{(3.79\times {10}^{-4})}^{2}{B}_{FN}]}^{2}\) in eV, β is the field enhancement factor, \(\bar{E}=E/{E}_{\ast }\) is the dimensionless breakdown electric field with \({E}_{\ast }=0.95{B}_{FN}{\varphi }_{\ast }^{3/2}\) in V/m, \(\bar{p}=p/{p}_{\ast }\) is the dimensionless pressure with \({p}_{\ast }={E}_{\ast }{B}_{p}^{-1}\) in Torr, \(\bar{d}=d/L\) is the dimensionless gap distance with \(L={p}_{\ast }^{-1}{A}_{p}^{-1}\) in m, \(\bar{T}=T/{T}_{\ast }\) is the dimensionless temperature with \({T}_{\ast }=[(\pi m{\sigma }_{CE}{B}_{p})/(8ek)]{\{{A}_{FN}/[{\varepsilon }_{0}{A}_{p}{t}^{2}(y){\varphi }_{\ast }]\}}^{2}\) in K, γSE is the secondary emission coefficient, \(\bar{\alpha }=\alpha L\) is the dimensionless ionization coefficient with \(\alpha ={A}_{p}p\exp (-{B}_{p}p/E)\) in m−1, and all terms without bars correspond to the dimensional (measured) quantities of those with bars. Additionally, AFN and BFN are Fowler-Nordheim constants, Ap and Bp are gas constants, m is the mass of the gas atom in kg, σCE isthe charge exchange cross section, e is the electron charge, k is Boltzmann’s constant, \({\varepsilon }_{0}\) is the permittivity of free space, and t2(y) ≈ 1.146 is a Fowler-Nordheim correction factor used since the Schottky reduction factor, y, is sufficiently less than one for the data considered here. Table 1 summarizes typical values.
We numerically solve Equation (1) and choose β to fit to the nondimensionalized experimental data from Fig. 1 as a function of \(\bar{p}\bar{d}\), with γSE = 10−5 and \(\bar{V}=\bar{E}\bar{d}\). Figure 2a shows the fitting of Equation (1) and the universal PL (UPL)26, given by
to the measured data with β shown in Fig. 3. We note that the experimental data for 50 kPa and 101 kPa actually intersects with the UPL, indicating the transition from the combined FE/TA regime to the traditional PL. Moreover, the 50 kPa data intersects the UPL to the left of the Paschen minimum, while the 101 kPa data intersects the UPL near the minimum, as observed in previous applications of this theory to atmospheric pressure data26,27. This stands to reason since previous results47 indicate the transition should occur around 18 μm. Since the curves in Fig. 2a are universal, they hold for any combination of parameters that yield these intersections, so the intersection with the UPL could occur on either side of the minimum at atmospheric pressure depending upon gas and electrode conditions.
(a) Dimensionless breakdown voltage, \(\bar{V}\), as a function of the product of dimensionless pressure and gap distance, \(\bar{p}\bar{d}\), for various pressures compared to results from the universal Paschen’s law (UPL) determined from (2) with γSE = 10−5 using β from Fig. 3. The symbols represent experimental data points and the dashed lines represent the numerical solution of (1), using field enhancement factor β as a fitting parameter. (b) Dimensionless breakdown voltage, \(\bar{V}\), as a function of dimensionless gap distance, \(\overline{d.}\,\,\)Numerical results from (1) are shown as the dashed lines and the limiting results of equation (5) are shown as symbols with γSE = 10−5 using β from Fig. 3. There is an average percent difference between equations (1) and (5) of 3.71%.
(a) Field enhancement factor, β, as a function of the product of the dimensionless pressure and gap distance, \(\bar{p}\bar{d}\), obtained by fitting the experimental data from Fig. 2. (b) Field enhancement factor, β, as a function of the dimensionless electric field, \(\bar{E}\).
We can analytically assess this intersection since \(\bar{\alpha }\bar{d}\gg 1\) generally for the data considered here, allowing us to simplify \(\bar{V}\) to obtain26
where
and Λ2 = 1 × 105. Analogous to ref.27, we can further simplify (3) to obtain a limiting equation for \(\bar{V}\), given by
Figure 2b compares the limiting results from equation (5) to the numerical calculations from equation (1) using β from Fig. 3. The limiting results agree well with equation (1) at low \(\bar{p}\bar{d}\) and deviate as \(\bar{p}\bar{d}\) increases. The numerical results of equation (1) and analytic results of equation (3) have an average percent difference of 3.97% while the results of equation (1) and the limiting results of equation (5) differ by an average of 3.71%. Thus, we use equation (5) in Fig. 2b and the remainder of the analytic assessment without sacrificing accuracy. Also important concerning global universality, Fig. 2 emphasizes that the breakdown voltage scales differently in the different regimes. Upon satisfying the PL condition (transitioned from the FE/TA combined regime to the conventional PL regime), the behavior the breakdown voltage scales with pd and one recovers the UPL. At smaller gaps, Fig. 2a shows that breakdown voltage scales with \(\bar{d}\). Thus, while breakdown exhibits universal behavior, the scaling of this universal behavior varies depending upon the dominant breakdown mechanism.
Figure 3 shows β for fitting equation (1) to the data in Fig. 2 as functions of the product of dimensionless pressure and gap distance, \(\bar{p}\bar{d}\), and the dimensionless electric field, \(\bar{E}\). For 50 kPa and 101 kPa, β increases linearly with increasing \(\bar{p}\bar{d},\) as observed previously in the FE dominant regime at atmospheric pressure26,27. Eventually, β approaches a constant, which corresponds to the transition from the FE to TA regimes, as also observed previously26,27. Interestingly, this occurs at a lower \(\bar{p}\bar{d}\) for 50 kPa. Previous results indicate that this transition is not solely driven by \(\bar{p}\bar{d}\), but by \(\bar{p}\) and \(\bar{d}\) independently, which is supported by this work. For 3 kPa, β also increases linearly at low \(\bar{p}\bar{d},\) but much more rapidly. While the current experiments cannot achieve sufficient voltage to measure VB at larger d for 3 kPa, the theory suggests that the intersection with the UPL will occur at a much higher β than either of the other pressures studied. Figure 3b indicates that β is a function of \(\bar{E}\), which is also supported by previous work48,49. Interestingly, β at the two highest pressures studied here is identical when plotted as a function of \(\bar{E},\) suggesting potential universality in this regime. Future work at lower pressures and larger gap distances can better characterize these transitions and further characterize the dependence of β on \(\bar{E}\).
Finally, we consider the impact of γSE, β, and \(\bar{\varphi }\), on the transition from the FE/TA regime to the UPL. Understanding how these parameters affect breakdown is vital for developing a predictive model, since γSE and β are difficult to determine a priori and the asymptotic prediction of VB is very sensitive to variations in β and \(\bar{\varphi }\) in the FE/TA regime50. Thus, elucidating the influence of these terms on VB will clarify the transition to UPL under different p and d. The transition from the FE/TA regime to the UPL occurs when the limiting expression of equation (5) matches the UPL from equation (2), so we numerically solve
for \(\bar{d}\,\,\)with a given γSE, β, and \(\bar{p}\). Figure 4 shows the ratio of \(\bar{p}\bar{d}\) for the transition, \({(\bar{p}\bar{d})}_{int}\), to the value corresponding to the standard “Paschen minimum” of Equation (2) by setting \(d\bar{V}/d(\bar{p}\bar{d})=0\) to give
When \({(\bar{p}\bar{d})}_{int}/{(\bar{p}\bar{d})}_{PL,min} < (\, > \,)1\), Equations (2) and (3) intersect to the left (right) of the traditional Paschen minimum. For example, at atmospheric pressure, β = 60, ϕ = 4.7 eV, and γSE = 10−4 the FE/TA model and the UPL intersect to the left of the Paschen minimum. However, reducing ϕ to 3 eV shifts the intersection to the right of the Paschen minimum. Figure 4a shows \({(\bar{p}\bar{d})}_{int}/{(\bar{p}\bar{d})}_{PL,min}\) as a function of \(\bar{p}\) for β = 60 and γSE = 10−6 considering ϕ = 2, 3.5, 5, and 6 eV \((\bar{\varphi }=0.0207,\,0.0362,\,0.0516,\,{\rm{and}}\,0.0620)\) and Fig. 4b shows \({(\bar{p}\bar{d})}_{int}/{(\bar{p}\bar{d})}_{PL,min}\,\)as a function of \(\bar{p}\) for various β at γSE = 10−6. We note that ϕ does not have a significant effect on the transition point until \(\bar{p}\approx 2\times {10}^{-6}\) (which corresponds to 380 Torr). We also observe the same behavior for any small value of γSE, such as γSE = 10−6 This is analogous to previous observations that γSE does not play a vital role until TA dominates breakdown (often occurring somewhere around atmospheric pressure)26,50. Figure 4b indicates that increasing β from 15 to 60 does not influence the transition point until \(\bar{p}\approx 5\times {10}^{-6}\,\)(950 Torr). Reducing ϕ can shift the transition to the left of the PL minimum at subatmospheric pressures, but changing β does not shift the transition to the left of the minimum until the pressure exceeds atmospheric pressure. Varying γSE yielded similar behavior on the intersection with PL as changing β.
The ratio of the product of dimensionless pressure and gap distance, \(\bar{p}\bar{d}\), causing the transition to Paschen’s law, \({(\bar{p}\bar{d})}_{int}\), to \(\bar{p}\bar{d}\) corresponding to the Paschen minimum, \({(\bar{p}\bar{d})}_{PL,min}\), as a function of \(\bar{p}\) for various values of (a) \(\bar{\varphi }\) with β = 60 and γSE = 10−6, and (b) β with γSE = 10−5 and \(\bar{\varphi }=0.0465\).
Conclusion
In summary, we applied a gas breakdown theory26,27 to assess experimental results for breakdown voltage at various pressures. Using β as a fitting parameter, we achieved excellent agreement between the exact numerical solution of the theory and the experimental results, and demonstrated that the analytic model differed from experiment by an average of 3.71%. We showed that experimental conditions, particularly electrode work function, can drive the intersection between the coupled FE/TA model and the UPL to the left or the right of the traditional Paschen minimum, providing a potential contributing factor determining whether VB decreases with decreasing pd or an extended plateau occurs. Furthermore, the results showed that β and γSE have little influence on the location of the transition below atmospheric pressure, but ϕ has a greater influence. Future studies quantifying the change in work function51 with multiple breakdown events will further elucidate how breakdown behavior changes with constant gap distance. For example, one can envision an initial work function leading to a transition to the UPL to the right of the minimum, with subsequent breakdown events occurring to the left after electrode surface damage potentially decreases work function if it enhances surface roughness51. Future work quantifying how changes in work function due to surface roughness or chemical roughness52 effect the system and incorporating thermionic emission53 into the model will enhance the utility and completeness of the model across multiple operating regimes. A more thorough understanding of this behavior is vital to accurately predict breakdown behavior and electron emission overall.
References
Ju, Y. & Sun, W. Plasma assisted combustion: Dynamics and chemistry. Prog. Energy and Comb. Sci 48, 21–83 (2015).
Martinez-Sanchez, M. & Pollard, J. E. Spacecraft electric propulsion—An overview. J. Propul. Power 14, 688–699 (1998).
Becker, K. H., Schoenbach, K. H. & Eden, J. G. Microplasmas and applications. J. Phys. D: Appl. Phys. 39, R55–R70 (2006).
Schoenbach, K. H. & Becker, K. 20 years of microplasma research: a status report. Eur. Phys. J. D 70, 29 (2016).
Becker, K. et al. Environmental and biological applications of microplasmas. Plasma Phys. Control. Fusion 47, B513–B523 (2005).
Kong, M. et al. Plasma medicine: an introductory review. New J. Phys. 11, 115012 (2009).
Laroussi, M. Low-temperature plasma jet for biomedical applications: a review. IEEE Trans. Plasma Sci. 43, 703712 (2015).
Rezvykh, K. A. & Romanov, V. A. Gases breakdown voltage calculation for the case of accelerator nonuniform fields by the method of base. Nuc. Instrum. Meth. Phys. Res. A. 423, 203–212 (1999).
Welch, D. R., Cuneo, M. E., Olson, C. L. & Mehlhorn, T. A. Gas breakdown effects in the generation and transport of light ion beams for fusion. Phys. Plasmas 3, 2113–2121 (1996).
Bogue, R. MEMS sensors: Past, present, and future. Sens. Rev. 27, 7–13 (2007).
Craighead, H. Nanoelectromechanical systems. Science 290, 1532–1535 (2000).
Garner, A. L. et al. Experimental validation of a compact, flexible pulsed power architecture for ex vivo platelet activation. PLoS ONE 12, e0181214 (2017).
Paschen, F. Ueber die zum Funkenübergang in Luft, Wasserstoff und Kohlensäure bei verschiedenen Drucken erforderliche Potentialdifferenz. Ann. Phys. 273, 69–96 (1889).
Boyle, W. S. & Kisliuk, P. Departure from Paschen’s law of breakdown in gases. Phys. Rev. 97, 255–259 (1955).
Go, D. B. & Venkattraman, A. Microscale gas breakdown: ion-enhanced field emission and the modified Paschen’s curve. J. Phys. D. 47, 503001 (2014).
Venkattraman, A. & Alexeenko, A. A. Scaling law for direct current field emission-driven microscale gas breakdown. Phys. Plasmas 19, 123515 (2012).
Semnani, A., Venkattraman, A., Alexeenko, A. & Peroulis, D. Frequency response of atmospheric pressure gas breakdown in micro/nanogaps. Appl. Phys. Lett. 103, 063102 (2013).
Radmilović-Radjenović, M. & Radjenović, B. An analytical relation describing the dramatic resuction of the breakdown voltage for the microgap devices. Europhys. Lett. 83, 25001 (2008).
Go, D. B. & Pohlman, D. A. A mathematical model of the modified Paschen’s curve for breakdown in microscale gaps. J. Appl. Phys. 107, 103303 (2010).
Tirumala, R. T. & Go, D. B. An analytical formulation for the modified Paschen’s curve. Appl. Phys. Lett. 97, 151502 (2010).
Torres, J. M. & Dhariwal, R. S. Electric field breakdown at micrometer separations. Nanotechnology 10, 102–107 (1999).
Chen, C. H., Yeh, J. A. & Wang, P. J. Electrical breakdown phenomena for devices with micron separations. J. Micromech. Microeng. 16, 1366–1373 (2006).
Radmilović-Radjenović, M., Radjenović, B., Matejčik, S. & Klas, M. The breakdown phenomena in micrometer scale direct-current gas discharges. Plasma Chem. Plasma Process. 34, 55–64 (2014).
Loveless, A. M. & Garner, A. L. Scaling laws for gas breakdown for nanoscale to microscale gaps at atmospheric pressure. Appl. Phys. Lett. 108, 234103 (2016).
Loveless, A. M. & Garner, A. L. Generalization of microdischarge scaling laws for all gases at atmospheric pressure. IEEE Trans. Plasma Sci. 45, 574–583 (2017).
Loveless, A. M. & Garner, A. L. A universal theory for gas breakdown from microscale to the classical Paschen law. Phys. Plasmas 24, 113522 (2017).
Meng, G. et al. Demonstration of field emission driven microscale gas breakdown for pulsed voltages using in-situ optical imaging. Phys. Plasmas 25, 082116 (2018).
Little, R. P. & Smith, S. T. Electrical breakdown in vacuum. IEEE Trans. Electron Dev. 12, 77–83 (1965).
Fu, Y., Krek, J., Zhang, P. & Verboncoeur, J. P. Gas breakdown in microgaps with a surface protrusion on the electrode. IEEE Trans. Plasma Sci., in press, https://doi.org/10.1109/TPS.2018.2878011.
Booske, J. H. Plasma physics and related challenges of millimeter-wave-to-terahertz and high power microwave generation. Phys. Plasmas 15, 055502 (2008).
Neuber, A. A., Krile, J. T., Edmiston, G. F. & Krompholz, H. G. Dielectric surface flashover at atmospheric conditions under high-power microwave excitation. Phys. Plasmas 14, 057102 (2007).
Braun, H. H., Döbert, S., Wilson, I. & Wuensch, W. Frequency and temperature dependence of electrical breakdown at 21, 30, and 39 GHz. Phys. Rev. Lett. 90, 224801 (2003).
Fu, Y., Yang, S., Zou, X., Luo, H. & Wang, X. Effect of distribution of electric field on low-pressure gas breakdown. Phys. Plasmas 24, 023508 (2017).
Fu, Y., Krek, J., Zhang, P. & Verboncoeur, J. P. Evaluating microgap breakdown mode transition with electric field non-uniformity. Plasma Sources Sci. Technol. 27, 095014 (2018).
Child, C. D. Discharge from hot CaO. Phys. Rev. (Series I) 32, 492–511 (1911).
Langmuir, I. The effect of space charge and residual gases on thermionic currents in high vacuum. Phys. Rev. 2, 450–486 (1913).
Benilov, M. S. The Child-Langmuir law and analytical theory of collisionless to collision-dominated sheaths. Plasma Sources Sci. Technol. 18, 014005 (2009).
Lau, Y. Y., Liu, Y. & Parker, R. K. Electron emission: From the Fowler-Nordheim relation to the Child-Langmuir law. Phys. Plasmas 1, 2082–2085 (1994).
Kishek, R. A., Lau, Y. Y., Ang, L. K., Valfells, A. & Gilgenbach, R. M. Multipactor discharge on metals and dielectrics: Historical review and recent theories. Phys. Plasmas 5, 2120–2126 (1998).
Gopinath, V. P., Verboncoeur, J. P. & Birdsall, C. K. Multipactor electron discharge physics using an improved secondary emission model. Phys. Plasmas 5, 1535–1540 (1998).
Kishek, R. A. Ping-pong modes and higher-periodicity multipactor. Phys. Plasmas 20, 056702 (2013).
She, J. C., Xu, N. S., Deng, S. Z. & Chen, J. Vacuum breakdown of carbon-nanotube field emitters on a silicon tip. Appl. Phys. Lett. 83, 2671–2673 (2003).
Descoeudres, A., Levinsen, Y., Calatroni, S., Taborelli, M. & Wuensch, W. Investigation of the dc vacuum breakdown mechanism. Phys. Rev. Accel. Beams 12, 092001 (2009).
Collins, P. G., Hersam, M., Arnold, M., Martel, R. & Avouris, P. Current saturation and electrical breakdown in multiwalled carbon nanotubes. Phys. Rev. Lett. 86, 3128–3131 (2001).
Li, M., Tang, H. X. & Roukes, M. L. Ultra-sensitive NEMS-based cantilevers for sensing, scanned probe and very high-frequency application. Nature Nanotech. 2, 114–120 (2007).
Spindt, C. A., Brodie, I., Humphrey, L. & Westerberg, E. R. Physical properties of thin-film field emission cathodes with molybdenum cones. J. Appl. Phys. 47, 5248–5263 (1976).
Meng, G. et al. Spatio-temporal dynamics of pulsed gas breakdown in microgaps. Phys. Plasmas 26, 014506 (2019).
Venkattraman, A. Electric field enhancement due to a saw-tooth asperity in a channel and implications on microscale gas breakdown. J. Phys. D: Appl. Phys. 47, 425205 (2014).
Buendia, J. A. & Venkattraman, A. Field enhancement factor dependence on electric field and implications on microscale gas breakdown: Theory and experimental interpretation. Europhys. Lett. 112, 55002 (2015).
Dynako, S. D., Loveless, A. M. & Garner, A. L. Sensitivity of modeled microscale gas breakdown voltage due to parametric variation. Phys. Plasmas 25, 103505 (2018).
Li, W. & Li, D. Y. On the correlation between surface roughness and work function in copper. J. Chem. Phys. 122, 064708 (2005).
Kim, K. S., Hurtado, J. A. & Tan, H. Evolution of a surface-roughness spectrum caused by stress in nanometer-scale chemical etching. Phys. Rev. Lett. 83, 3872–3875 (1999).
Jensen, K. L. A tutorial on electron sources. IEEE Trans. Plasma Sci. 46, 1881–1899 (2018).
Acknowledgements
This work was supported by the Office of Naval Research (Grant No. N00014-17-1-2702), the National Natural Science Foundation of China (Grant No. 51607138, 51521065), China Postdoctoral Science Foundation (Grant No. 2016M602820), Research Foundation of State Key Laboratory of Intense Pulsed Radiation Simulation and Effect (Grant No. SKLIPR.1512). A. M. L. also gratefully acknowledges funding from a graduate scholarship from the Directed Energy Professional Society.
Author information
Authors and Affiliations
Contributions
A.M.L., G.M. and A.L.G. designed the study. A.M.L. and A.L.G. conceived the theory and A.M.L. carried out the theoretical calculations. Y.C. and G.M. conceived and planned the experiment. Q.Y., F.W. and K.W. performed the experiment. A.M.L., G.M. and A.L.G. interpreted the results and wrote the manuscript. All authors reviewed and approved the manuscript
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Loveless, A.M., Meng, G., Ying, Q. et al. The Transition to Paschen’s Law for Microscale Gas Breakdown at Subatmospheric Pressure. Sci Rep 9, 5669 (2019). https://doi.org/10.1038/s41598-019-42111-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-42111-2
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.