Abstract
The clinical impact of drug-drug interactions based on time-dependent inhibition of cytochrome P450 (CYP) 3A4 has often been overpredicted, likely due to use of improper inhibitor concentration estimates at the enzyme. Here, we investigated if use of cytosolic unbound inhibitor concentrations could improve predictions of time-dependent drug-drug interactions. First, we assessed the inhibitory effects of ten time-dependent CYP3A inhibitors on midazolam 1′-hydroxylation in human liver microsomes. Then, using a novel method, we determined the cytosolic bioavailability of the inhibitors in human hepatocytes, and used the obtained values to calculate their concentrations at the active site of the enzyme, i.e. the cytosolic unbound concentrations. Finally, we combined the data in mechanistic static predictions, by considering different combinations of inhibitor concentrations in intestine and liver, including hepatic concentrations corrected for cytosolic bioavailability. The results were then compared to clinical data. Compared to no correction, correction for cytosolic bioavailability resulted in higher accuracy and precision, generally in line with those obtained by more demanding modelling. The best predictions were obtained when the inhibition of hepatic CYP3A was based on unbound maximal inhibitor concentrations corrected for cytosolic bioavailability. Our findings suggest that cytosolic unbound inhibitor concentrations improves predictions of time-dependent drug-drug interactions for CYP3A.
Similar content being viewed by others
Introduction
Harmful drug-drug interactions (DDIs) are often caused by inhibition of cytochrome P450 (P450) enzymes in hepatocytes. Inhibition of these enzymes depends on roughly two types of mechanisms: reversible (direct) and irreversible (time-dependent). Because time-dependent inhibition can manifest itself in a slow onset and a long-lasting inhibition in vivo1, a correct assessment of in vitro inhibition values and an accurate prediction of the clinical consequences are important. Static predictions of time-dependent inhibition of P450 enzymes have frequently been associated with overestimations2,3. In recent years, however, improved system data (e.g. P450 turnover) and experimental settings have led to better confidence in time-dependent inhibition predictions for some compounds4. Another explanation for the overestimations associated with time-dependent inhibition of P450 enzymes has been suggested to be conservative inhibitor concentration estimates3. Here, we investigate if the use of cytosolic unbound drug concentrations can be used to improve the predictions further.
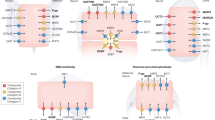
Basic static prediction models are usually used to initially screen the risk of inhibition for a worst-case constant exposure of the inhibitor, e.g., its total or unbound maximal systemic concentration at steady state ([I]max or [I]max,u)5,6. Mechanistic static models, which incorporate several interaction mechanisms, provide more quantitative predictions. However, no consensus has been reached on which inhibitor concentrations to use in these predictions, and several alternatives are available. These include total or unbound [I]max, time-averaged ([I]ave), or calculated liver-specific ([I]inlet) concentrations (Fig. 1a)3,5,6. In addition, although arbitrary, different concentrations are sometimes used for different interaction mechanisms (mixed term approach)2,3, i.e., in the same prediction, one concentration is used for reversible inhibition and another for time-dependent inhibition. Nevertheless, all these static approaches are based on systemic concentrations, which function as rough surrogates for the actual concentrations available for binding to the active site of P450 enzymes – the cytosolic unbound concentrations. Recently, a simple, robust, and label-free method was developed in our lab for determination of the intracellular bioavailability (Fic) of drugs7. Fic expresses the ratio between the intracellular unbound drug concentration and the extracellular drug concentration (Fig. 1b)8. Our methodology, which is based on parallel intracellular accumulation and binding experiments, has been successfully used to determine drug access to intracellular targets in multiple cell systems (including primary human cells)8,9. Fic provides a measurement of the net impact of all cellular drug disposition processes on intracellular bioavailable drug levels8. It correlates well with target engagement10,11 and pharmacological response in several therapeutic areas including cancer, inflammation and dementia9,12.
Schematic drawing of the models and the inhibitor concentrations used in the DDI predictions. (a) Time-dependent inhibitors can alter the activity of CYP3A in both intestine and liver. Measured or estimated total and unbound inhibitor concentrations in blood are commonly used as surrogates for the inhibitor concentrations affecting CYP3A inside cells. More realistic estimates of the intracellular unbound concentrations affecting CYP3A are obtained by correcting these concentrations for intracellular (Fic) or cytosolic bioavailability (Fcyto). (b) Difference between Fic and Fcyto. CYP3A is located in the endoplasmic reticulum with its binding sites facing the cytosol. As the pH inside lysosomes is below that of the cytosol, basic lipophilic compounds tend to get trapped in the lysosomes. Since Fic also includes drugs in the acidic endo-lysosomal compartment, Fic (left) gives an overestimation of the basic lipophilic inhibitor compound available at the active site of CYP3A. Fcyto (right), is determined in the presence of chloroquine, which increases the lysosomal pH and eliminates the trapping of bases inside acidic compartments. As drugs access CYP3A from the cytosol, correction for Fcyto gives a better estimate than Fic of the actual unbound drug concentration binding to the enzyme. Fcyto, cytosolic bioavailability; Fic, intracellular bioavailability; [I]ave,u, unbound average inhibitor concentration; [I]g, intestinal inhibitor concentration; [I]inlet,ave,u, unbound hepatic inlet inhibitor concentration based on [I]ave; [I]inlet,max,u, unbound hepatic inlet inhibitor concentration based on [I]max; [I]max,u, unbound peak inhibitor concentration; P450, cytochrome P450.
The use of Fic-adjusted drug concentrations, i.e. intracellular unbound concentrations, in DDI predictions based on time-dependent inhibition of P450 enzymes has not yet been evaluated. CYP3A4, the most important drug-metabolizing enzyme, is primarily expressed in liver and intestinal cells13. More specifically, it is located on the outer membrane of the endoplasmic reticulum, facing the cytosol14,15,16. A limitation of the Fic method is that it provides an average estimate of intracellular bioavailability and no information on the subcellular drug distribution. For instance, positively charged compounds with lipophilic moieties tend to accumulate in lysosomes and acidic subcellular compartments where they are inaccessible to cytosolic targets (Fig. 1b)17. Hence, the Fic of such compounds becomes inflated, resulting in an overestimation of the cytosolic bioavailability7. Determination of the intracellular bioavailability in the presence of chloroquine or other compounds that increase the lysosomal pH and eliminate the trapping of basic drugs inside endo-lysosomal compartments12,18,19 could give a better estimate for the relevant concentration at the CYP3A4 enzyme metabolic site, since it should better reflect the cytosolic bioavailability (Fcyto).
The aim of this work was to evaluate the impact of hepatic intracellular unbound (Fic-corrected) and cytosolic unbound (Fcyto-corrected) concentrations of time-dependent CYP3A inhibitors in DDI predictions. First, we determined the in vitro reversible and time-dependent microsomal inhibition properties of ten time-dependent CYP3A inhibitors with clinically known DDIs. Then, we determined the Fic and Fcyto of the inhibitors in human hepatocytes. Finally, we carried out interaction predictions based on the inhibition data and a range of different inhibitor concentration combinations, which were either uncorrected or corrected for Fic or Fcyto, and compared the results to interaction data from clinical studies. We show that Fcyto-correction of hepatic inhibitor concentrations results in predictions of the highest accuracy and precision, followed by Fic-corrected concentrations, and lastly uncorrected concentrations. Our data suggest that use of cytosolic and intracellular unbound inhibitor concentrations improves predictions of time-dependent DDIs.
Results
Drug-metabolizing enzyme inhibition
To characterize the inhibitory effects of the selected drugs on the CYP3A-mediated 1′-hydroxylation of midazolam in human liver microsomes (HLM), we first measured reversible inhibition, i.e., the inhibitory concentration causing 50% inhibition (IC50) of each drug, and corrected it for the measured non-specific binding to HLM. Reversible IC50 values ranged from 1.31 µM for the most potent inhibitor (nilotinib), to >100 µM for the weakest ones (azithromycin and crizotinib) (Table 1; Supplementary Figs S1–S2).
Then, we determined time-dependent inhibitory effects on CYP3A for the compounds (the maximal inactivation rate (kinact) and concentration resulting in half of kinact (KI)). After correction for measured non-specific binding to HLM, the calculated KI,u ranged from 0.09 to 19.2 µM, and kinact from 0.016 to 0.103 1/min, which is accordance with previously published data (Table 1; Figs 2 and S2). Crizotinib had the lowest KI,u value (0.09 µM), while nefazodone exhibited the highest inactivation rate (0.103 1/min). Unexpectedly, azithromycin, which has previously been classified as a time-dependent inhibitor of CYP3A20, did not exhibit time-dependent inhibition (data not shown). It was therefore excluded from further experiments and DDI predictions.
Time-dependent inhibition of CYP3A by the ten tested inhibitors in human liver microsomes (HLM). KI and kinact values of the inhibitors (crizotinib, diltiazem, erythromycin, imatinib, nefazodone, nilotinib, pazopanib, roxithromycin, telithromycin, verapamil) were determined in pooled HLM with midazolam 1′-hydroxylation as the marker reaction for CYP3A activity. The rate of inactivation of CYP3A activity by each inhibitor concentration (kobs) was determined by linear regression analysis of the natural logarithm of the percentage of activity remaining versus preincubation time data for each drug (inserts). The KI and kinact were then calculated by non-linear regression analysis of the kobs versus inhibitor concentration. The incubations were carried out in triplicate, and the results are given as mean ± standard deviation. KI, inactivation rate constant; kinact, maximal inactivation rate; Kobs, initial inactivation rate.
Intracellular and cytosolic bioavailability (Fic and Fcyto)
To predict the inhibitor concentrations available to bind CYP3A, we determined their Fic and Fcyto values. Fcyto was determined similar to Fic, but the intracellular accumulation (Kp) experiment was carried out in the presence of chloroquine (Kpcyto). Chloroquine increases lysosomal pH, and thereby reduces the trapping of lipophilic bases in this compartment12,17. We reasoned that this would allow a more accurate estimation of the unbound concentration in the cytoplasm.
The Fcyto values ranged from 0.010 (nilotinib) to 0.73 (imatinib) or 73-fold (Fig. 3, Table 2). Kp was significantly larger than Kpcyto (p ≤ 0.05 in Student’s t-test) for diltiazem, imatinib, nilotinib, verapamil and roxithromycin. Fcyto differed by more than two-fold to Fic for diltiazem, imatinib, nilotinib, and verapamil. In general, Fic values were low, in line with previous data in metabolically competent hepatocyte suspensions8.
Intracellular drug accumulation in the absence (Kp) and presence (Kpcyto) of chloroquine (a) and intracellular drug bioavailability (Fic) and cytosolic bioavailability (Fcyto) (b) of the tested inhibitors in hepatocytes. The signs within brackets in (a) denote charge at physiological pH. Lipophilic cationic drugs showed higher Kp than Kpcyto. The neutral drugs telithromycin and pazopanib had comparable Kp and Kpcyto, while nilotinib displayed higher Kp than Kpcyto, likely due to precipitation and accumulation in the lysosomes26. The numbers in (b) refer to the inhibitors listed in (a). Results are given as geometrical means (a,b) ± standard deviation (a) of triplicate measurements.
Interaction predictions
The reversible and time-dependent inhibition values for each inhibitor were combined with hepatic and intestinal inhibitor concentrations for the DDI predictions. In total, 12 hepatic and intestinal inhibitor concentration combinations were used to predict the change in AUCs of the victim drugs in 21 clinically documented interaction studies (Fig. 4, Supplementary Table S1). The different hepatic inhibitor concentrations used in the mechanistic static model (see Equation 6) were [I]max,u, [I]ave,u, [I]inlet,max,u, and [I]inlet,ave,u, respectively. The hepatic inhibitor concentrations were either used as they were (Fig. 4, left panels), or corrected for Fcyto (Fig. 4, right panels). The intestinal inhibitor concentrations used in the modelling were [I]g, [I]max,u, and [I]ave,u, respectively. The intestinal inhibitor concentrations were left uncorrected as no Fcyto was determined in enterocytes in this study. In addition, the effects of Fic-correction of hepatic inhibitor concentrations were evaluated (Supplementary Table S2).
Comparison of the effects of twelve inhibitor concentration combinations on the predictions of increase in the AUCs in clinical DDI studies. Reversible inhibition and time-dependent inhibition of CYP3A were predicted using uncorrected intestinal inhibitor concentrations, and uncorrected (left panel) or Fcyto-corrected (right panel) hepatic inhibitor concentrations. Twelve intestinal and hepatic inhibitor concentration combinations were evaluated for prediction bias (GMFE) (a,b), precision (RMSE) (c,d), and for the percentage of the predictions that were within two-fold of the observed AUC values (e,f). A perfect prediction of all actual values would give a GMFE value of 1, and a lower RMSE value denotes a greater precision of the prediction. Input parameters are given in Methods and in Supplementary Table S5. See Supplementary Table S2 for more details and results of predictions based on the mixed term approach. GMFE, geometric mean-fold error; Fcyto, cytosolic bioavailability; [I]ave,u, unbound average inhibitor concentration; [I]g, intestinal inhibitor concentration; [I]inlet,ave,u, unbound hepatic inlet inhibitor concentration based on [I]ave; [I]inlet,max,u, unbound hepatic inlet inhibitor concentration based on [I]max; [I]max,u, unbound peak inhibitor concentration; RMSE, root-mean square error.
Next, the combination of inhibitory concentrations recommended by the EMA and FDA ([I]inlet,max,u in combination with [I]g), were used as driving concentrations in the mechanistic static modelling of the AUCs obtained in the clinical interaction studies. This resulted in geometric mean fold error (GMFE; accuracy measurement) and root mean square error (RMSE; precision measurement) values of 5.28 and 16.4, respectively, and only 5% (1/21) of the interaction predictions were within 2-fold of the observed values (Figs 4–5, Supplementary Table S2). The non-physiological, mixed-term concentration combination (see above) gave slightly lower GMFE and RMSE values of 3.05 and 11.2. Twenty-nine percent (6/21) of the predictions were within 2-fold of the clinical interaction values (Fig. 5, Supplementary Table S2)2,3.
Effect of Fcyto-correction of hepatic inhibitor concentrations on prediction accuracy. The inhibitor concentration combination in (a) is the one recommended in drug authority guidelines, ([I]inlet,max,u + [I]g). The concentration combination in (b) corresponds to a mixed term approach, ([I]inlet,max,u for reversible inhibition in the liver, [I]max,u for time-dependent inhibition in the liver, and [I]g for intestinal inhibition). Our data suggest that if no Fcyto values are available, [I]ave,u for inhibition of both hepatic and intestinal CYP3A could be used (c). In the present study, the best prediction (GMFE closest to 1) was obtained with Fcyto-corrected [I]max,u in combination with [I]g (d). The full line denotes no difference between predicted and observed interactions and the dashed lines indicate a prediction within two-fold of the observed values. Input parameters are given in Methods and in Supplementary Table S5. See Supplementary Table S2 for detailed results of the predictions, and Supplementary Fig. S4 for an identical figure with references to the corresponding clinical trials. AUCR, the area-under-the-concentration-time curve of the substrate in the presence vs absence of the inhibitor; Fcyto, cytosolic bioavailability; [I]ave,u, unbound, average inhibitor concentration; [I]g, intestinal inhibitor concentration; [I]inlet,max,u, unbound hepatic inlet inhibitor concentration based on [I]max; [I]max,u, unbound, peak inhibitor concentration.
Fcyto corrections resulted in more accurate predictions of the changes in AUC and reduced the GMFE and RMSE values (Fig. 4, Supplementary Table S2). A combination of Fcyto-corrected [I]max,u for hepatic inhibition and [I]g for intestinal inhibition resulted in the GMFE value closest to 1 (1.06), while the RMSE was 3.18. Further, the frequency of predictions within two-fold of the observed DDIs increased to 67% (14/21; Figs 4–5). In addition, Fcyto-corrected [I]ave,u in combination with [I]g gave good results with 14/21 interactions within two-fold of the clinical data (GMFE 0.85, RMSE 2.39) (Fig. 4, Supplementary Table S2).
Although they were better than uncorrected predictions, Fic-corrections generally did not give as good predictions as Fcyto (Supplementary Table S2). This can be attributed to the overestimation of the bioavailable concentration of the positively charged compounds to CYP3A. However, it should be noted that predictions based on Fic-corrected [I]ave,u for hepatic inhibition, and [I]g for intestinal inhibition resulted in predictions with 14/21 interactions within two-fold of actual data, and GMFE and RMSE values of 0.97 and 2.65 (Supplementary Table S2).
To summarize, application of Fcyto-correction of hepatic inhibitor concentrations resulted in improved DDI predictions as compared to current recommendation for static modelling that are not corrected for Fcyto.
Discussion
We determined the cytosolic bioavailability (Fcyto) and in vitro reversible and time-dependent inhibition properties of a range of known time-dependent inhibitors of CYP3A with documented clinical interactions (Tables 1–2). Data from these experiments were used, together with literature data, to predict DDIs using a mechanistic static prediction model recommended by the regulatory agencies in Europe and the US5,6. Twelve combinations of hepatic and intestinal inhibitor concentrations, with and without Fcyto-correction of hepatic concentrations alone, were evaluated to identify the most accurate predictions. As a general trend, Fcyto-correction of inhibitor concentrations led to improved predictions (Figs 4 and 5). Inhibitor concentration combinations where inhibition of hepatic CYP3A was based on Fcyto-corrected [I]max,u concentrations resulted in the best predictions. Furthermore, interaction predictions based on the inhibitor concentration combination recommended by the drug regulatory agencies ([I]inlet,max,u in combination with [I]g)5,6 were markedly improved by Fcyto-correction.
Previously, we have used intracellular bioavailability (Fic) to calculate intracellular concentrations9. Fic is the net result of all processes in a living cell that determine the intracellular drug concentration, including unknown uptake and efflux mechanisms8. Our Fic-methodology requires fewer experiments, cells, and data collection than previous methods that determine intracellular drug concentrations21,22,23. However, the Fic method does not provide information on the subcellular distribution of drugs. In particular, compounds with log P > 2 and a basic pKa between 6.5 and 11 tend to accumulate in acidic intracellular organelles such as lysosomes24, which leads to a higher Fic. As CYP3A enzymes are located on the cytosolic side of the endoplasmic membrane15,16, Fic leads to an overestimation of the concentration of lysosomotropic drugs available to this enzyme. Therefore, we also determined the cellular accumulation of the inhibitors in the presence of chloroquine, which increases the lysosomal pH and eliminates the trapping of a positively charged drug inside the endo-lysosomal compartments18, and used it to calculate Fcyto7,12. Chloroquine particularly affected the intracellular accumulation of compounds with log P values of >3 and a basic pKa around 8; these compounds exhibited Fic/Fcyto ratios of more than 1.6-fold (Table 2, Figs 3 and S3). Given that, the endo-lysosomal volume in cells is only 0.5% as compared to the total cellular volume, this represents a substantial accumulation25. Also the bioavailability of nilotinib was markedly reduced by chloroquine, despite a relatively low pKa (pKa 5.5, log P 5). However, this is in line with previous findings showing that nilotinib accumulates in lysosomes because of its poor solubility at acidic pH, leading to precipitation inside the lysosome26.
While Fcyto-corrected (cytosolic unbound) concentrations resulted in better overall predictions than Fic-corrected (intracellular unbound) concentrations (Supplementary Table S2), a limitation of our approach is the possible interaction of chloroquine with drug transporters and enzymes that might affect the intracellular disposition of the inhibitors (apart from that resulting from differences in the endo-lysosomal pH; Supplementary Table S3). As alternatives, other endo-lysosomal pH modulators (e.g. monensin or ammonium chloride)19,27, subcellular fractionation22, pH partition theory7, or electrochemical modeling23 can be used. Further studies are necessary to assess which approach gives the most accurate estimates of Fcyto. Another limitation of our and all other studies predicting DDIs after oral administration is that we did not determine Fic and Fcyto values of the inhibitors in primary enterocytes. Because the Fic and Fcyto of a drug depends on multiple cell-specific processes, these values can differ between different cell types8. An attempt was made to evaluate the effects of intestinal inhibitor concentrations corrected with the present Fcyto values obtained from hepatocytes. Although these predictions were better than those based on uncorrected hepatic and intestinal concentrations (data not shown), the predictions where only hepatic concentrations had been Fcyto-corrected were still superior. It should be noted that Fcyto-correction of intestinal concentrations is complicated by 1) availability of primary enterocytes with physiologically relevant expression of CYP3A, 2) the fact that the levels of drug in the cell interior are influenced by both intestinal and blood drug concentrations.
Physiologically-based pharmacokinetic (PBPK) modelling can also be used for DDI predictions, and recent drug authority guidelines allow the use of PBPK models for the assessment of DDI potential of new drugs. Although not as straightforward as static models, the strength of PBPK predictions is that they consider the dynamic changes in drug concentrations with time. However, the development of an adequate PBPK model requires time and extensive information on the pharmacokinetics and physicochemical properties of the drug. We suggest that Fcyto and Fic values could be valuable parameters for incorporation also into PBPK models of DDIs. As Fic and Fcyto represent the net result of all cellular drug disposition processes, single mechanisms do not have to be identified when building a new PBPK model. For instance, the Simcyp Simulator, a commonly used platform for PBPK predictions, includes an optional term called ‘active hepatic scalar’, which in its essence describes the ratio between the ‘unbound intra-hepatocyte fluid concentration of drug and the unbound blood concentration of the drug’28. Fcyto and/or Fic provide exact experimental data to this parameter. Indeed, the clinical effects of several of the inhibitor compounds tested here, e.g. diltiazem, telithromycin and verapamil, have previously been predicted in PBPK simulations based on microsomal inhibition data very similar to ours (Fig. 6)29,30,31. In general, these simulations predicted the observed interactions very accurately. The exception was crizotinib, which was markedly overpredicted by microsomal data but not by hepatocyte data. Although our prediction for telithromycin resulted in a 2-fold overprediction of the observed interaction, our Fcyto–based predictions were generally in line with those obtained by PBPK modelling. Based on this analysis, we speculate that Fcyto and Fic could reduce the need for unnecessary parameter estimations and inclusion of undefined correction factors in PBPK models in order to obtain realistic predictions.
Comparison between observed clinical interaction data and predicted interaction data from PBPK simulations available in the literature and the current static model using Fcyto-corrected hepatic concentrations ([I]max,u for hepatic inhibition and [I]g for intestinal inhibition) or the inhibitor concentration combination recommended by drug authorities ([I]inlet,max,u + [I]g). The numbers within brackets on the x-axis refer to individual clinical trials listed in Supplementary Table S1. The dotted line indicates the threshold where an interaction is classified as strong (≥5-fold increase in AUC of the victim drug). References for PBPK data: crizotinib49; diltiazem50,51; erythromycin51; telithromycin30; verapamil29,52.
In the present study, no attempt was made to differentiate between inhibition of CYP3A4 or CYP3A5. The pooled microsomes used were from donors of predominantly Caucasian origin (86%), whom typically have low CYP3A5 expression levels in comparison to CYP3A4 levels, and a higher prevalence of the less ‘functional’ CYP3A5*3/*332,33. Therefore, we assumed that the inhibition parameters determined were mainly reflective of CYP3A4 inhibition. However, if the role of CYP3A5 inhibition was not accurately represented or that of CYP3A4 over accounted for, this may have implications for the clinical interaction risk predictions.
Given the limited number of interactions (n = 21) evaluated, we cannot confidently propose which of the inhibitor concentration combinations that should be used in the mechanistic static DDI predictions. Nevertheless, the Fcyto-corrected hepatic inhibitor concentrations led to improved predictions, with the combination of Fcyto-corrected [I]max,u for hepatic CYP3A inhibition and [I]g for intestinal CYP3A inhibition resulting in the best prediction. Hepatic inhibitor concentrations corrected for Fic also gave better predictions than those based on uncorrected concentrations only (Supplementary Table S2). Thus, our data suggest that Fcyto provides a good estimate of the biorelevant inhibitor concentrations in time-dependent interaction predictions.
In conclusion, we show that the overpredictions of DDIs based on time-dependent inhibition of CYP3A can be overcome by applying cytosolic unbound inhibitor concentrations in the predictions. A combination of Fcyto determination and inhibition experiments could thus become a powerful tool for DDI predictions. The unbound drug concentration at the site of the action is the concentration that engages the target (CYP3A), and this concentration should be used in static and dynamic prediction models and also in other pharmacokinetic models.
Methods
Chemicals and reagents
Crizotinib, diltiazem, erythromycin, imatinib, nilotinib, pazopanib, roxithromycin, and verapamil were obtained from Sigma-Aldrich (St. Louis, MO). Nefazodone and azithromycin were purchased from Toronto Research Chemicals (Toronto, ON) and telithromycin from Cayman Chemical Company (Ann Arbor, MI). Midazolam was obtained from Cerilliant Corporation (Round Rock, TX), 1′-hydroxymidazolam from Ultrafine Chemical Co. (Manchester, England) and nicotinamide adenine dinucleotide phosphate (NADPH) from AppliChem (Darmstadt, Germany). HLM from 50 individual mixed-sex donors were purchased from Xenotech (Lenexa, KS). Human hepatocytes were isolated in house from liver tissue obtained from a female donor undergoing surgical resection at the Department of Surgery, Uppsala University Hospital (Sweden) and cryopreserved as described previously34,35. Ethical approval was granted by the Uppsala Regional Ethics Committee (ethical Approvals Nos 2009/028 and 2011/037). Donors gave informed consent and all studies were performed in accordance with the current national regulations and ethical guidelines.
Selection of drugs
Eleven time-dependent inhibitors of CYP3A were selected on the basis of data from the University of Washington Drug Interaction Database (http://www.druginteractioninfo.org/). These inhibitors were selected because they have documented, clinically relevant effects on the plasma concentrations of the commonly used in vivo CYP3A substrate drugs midazolam and simvastatin (Supplementary Table S1). The eleven compounds were: nefazodone and telithromycin (strong inhibitors of CYP3A, causing a ≥5-fold increase in the area under the concentration-time curve (AUC) of the probe drug); crizotinib, diltiazem, erythromycin, imatinib, nilotinib and verapamil (medium inhibitors causing a ≥2 but <5-fold increase); and azithromycin, pazopanib and roxithromycin (weak inhibitors causing a ≥1.25 but <2-fold increase).
Inhibition in human liver microsomes
Given that all time-dependent inhibitors also affect the enzyme by reversible inhibition, the reversible IC50 value of each inhibitor was determined. Various concentrations of the inhibitors (or solvent control) were premixed with midazolam at its Michaelis-Menten concentration (Km; 2 µM) and HLM (0.1 mg/ml) in potassium phosphate buffer (0.1 M, pH 7.4) for 3 min (37 °C). Following inclusion of NADPH (1 mM), which initiated the reactions, the mixtures were further incubated for 5 min. Finally, the reactions were stopped by adding ice-cold acetonitrile (150 µl) containing internal standard (warfarin) to the incubation wells. The plates were put on ice for at least 10 min before further sample handling and analysis.
Time-dependent inhibition was assessed by first pre-incubating various inhibitor concentrations (or solvent control) with HLM (0.5 mg/ml) and NADPH (1 mM) in 100 mM potassium phosphate buffer, pH 7.4 for 0, 3, 6, 12, 20 and 30 min. At the determined time points, aliquots of the mixtures were transferred to separate wells containing a high concentration of midazolam (20 µM; to minimize reversible inhibition) and NADPH (1 mM), diluting the pre-incubation mixtures 20-fold. The resulting mixtures were further incubated for 5 min before addition of ice-cold acetonitrile containing internal standard (warfarin), to terminate the reactions.
Then, the unbound fraction of the inhibitors in microsomes (fu,mic) was determined as described below.
Non-specific binding of drugs in human liver microsomes
The unbound fraction of the inhibitors in the microsomes (fu,mic) was determined using two-chambered Rapid Equilibrium Dialysis (RED) devices (Thermo Fisher Scientific Inc., Rockford, IL). Triplicate mixtures (200 µl) of 6–8 inhibitors at a final concentration of 1 µM and HLM (0.1 or 0.5 mg/ml) were added to one chamber, and Hank’s buffered salt solution (HBSS) (350 µl) to the other chamber. The dialysis units were incubated at 37 °C for 4 h on an orbital shaker. At the end of the incubation, 20 μl of each sample from the homogenate and buffer chambers was transferred to a 96-well plate. Blank buffer or blank microsomes (20 μl) were added to the samples from the homogenate or buffer chambers, respectively, to yield identical matrices before further sample handling and analysis. The fu,mic values were calculated as the ratio of the drug concentration in the buffer chamber (containing drug that has passed through the dialysis membrane) to the drug concentration in the microsome chamber. To ensure that no drug had been metabolized/hydrolyzed during incubation, a stability test was performed. Here, drug-HLM mixture (100 µl) was transferred to an empty well of the dialysis unit and incubated for the same time. The remaining HLM solution (without drug) was kept as a blank sample. The mass balances calculated at the end of the experiment were consistently >80%.
Intracellular and cytosolic drug bioavailability
Intracellular drug binding (fu,cell, fraction of unbound drug inside cells) and intracellular drug accumulation (Kp) were measured in two separate experiments for all inhibitors8, as described in the following sections. Intracellular drug bioavailability (Fic) expresses the ratio between the intracellular unbound drug concentration (Cu,cell) to the drug concentration in the medium (Cmedium). Fic can be calculated as the product of fu,cell and Kp9:
If incubations for determining Kp are performed in buffer, Fic is equivalent to the unbound drug accumulation ratio (Kpuu), assuming that binding in the medium is negligible7,36. Fcyto was calculated similarly as Fic (Equation 1), but the Kp value used was the one determined in the presence of chloroquine (Kpcyto):
Determination of intracellular fraction of unbound drug (fu,cell)
Cryopreserved human hepatocytes were thawed at 37 °C and transferred to phosphate-buffered saline (PBS). The cells were centrifuged for 5 min at 100 × g and the pellet was suspended to 10 × 106 cell/ml in PBS (viability 85%) and homogenized for 10 seconds with a VCX-500 ultrasonic processor (Sonica & Materials. Newton, CT) at 20% intensity. The fu,cell values were measured using two-chambered Rapid Equilibrium Dialysis (RED) devices. Cell homogenate (200 µl) containing 6–7 of the tested inhibitors, chosen at random, was transferred to one chamber and 350 µl HBSS to the other, before incubation at 37 °C for 4 h on an orbital shaker37. At the end of the incubation, 20 μl of each sample from the homogenate and buffer chambers was transferred to a 96-well plate. Blank buffer or blank homogenate (20 μl) was added to the samples from the homogenate or buffer chambers, respectively, to yield identical matrices. For the stability test, the cell homogenate and drug mixture (100 µl) was transferred to an empty well of the dialysis unit. The mass balances were generally >80%. After incubation, 10-fold and 100-fold dilutions of cell homogenate were prepared on 96-well plates and a mixture of acetonitrile/water (60:40) with internal standard (warfarin) was added to the samples before further sample handling and analysis, which was performed as described above. The fu,hom values were calculated as the ratio of the concentration of the drug in the HBSS chamber (Cbuffer) vs. the cell homogenate chamber (Chom).
The protein concentration in the cell homogenate was measured using a BCA Protein Assay Reagent Kit (Pierce Biotechnology, Rockford, IL), according to the manufacturer’s instruction. The total cell volume in each well for 10 × 106 primary human hepatocytes was estimated from the protein concentration. As one mg of protein in primary human hepatocytes approximates to a volume of 6.5 µl8, the dilution factor, D, was calculated according to D = 1/(mg of protein × 6.5 µl/mg). Finally, fu,cell values were calculated according to Equation 3:
Determination of intracellular drug accumulation ratio (Kp) and cytosolic drug accumulation ratio (Kpcyto)
Cryopreserved human hepatocytes were thawed as described above and suspended to 1 × 106 cell/ml in HBSS (viability 85%). Cell suspension (100 µl) was transferred to 96-well plates (100,000 cell/well), and drug diluted in HBSS was added to give a final drug concentration of 0.5 µM. The plates were incubated on an orbital shaker (300 rpm) at 37 °C for three time points (15, 30, 45 min), to ensure sufficient time to reach steady-state. At the end of the incubation, the plates were centrifuged for 5 min at 100 × g, and medium samples (20 µl) were collected from the supernatant (Cmedium). Drug uptake was terminated by addition of ice-cold PBS followed by a washing step. Finally, the cells were lysed with acetonitrile/water (60:40) containing internal standard (warfarin) before further sample handling and analysis. The total amount of drug in the cells (Acell) was calculated based on the determined drug concentrations.
The protein concentration in the cell samples was measured as described above and the cell volume (Vcell) calculated. Finally, the Kp was calculated for each drug as the ratio between the total drug concentration in the cell vs. the drug concentration in the medium (Cmedium):
Kpcyto was measured similarly as Kp described above; however, the incubations included chloroquine (100 µM) for 45 min to reduce the lysosomal trapping of lipophilic bases. We have previously shown that 100 µM of chloroquine is sufficient to eliminate lysosomal trapping of basic compounds7,12.
Sample handling and determination of drug concentrations
The sample plates were centrifuged for 20 min at 3,500 rpm (4 °C) before analysis. The concentrations of the inhibitors and 1′-hydroxymidazolam were analyzed by ultra-performance liquid chromatography coupled to tandem mass spectrometry (UPLC-MS/MS) (Acquity, Waters Corp., USA). The compounds were separated on a BEH C18 column (2.1 × 50 mm, 1.7 µm, Waters, Ireland) at 60 °C. The mobile phases were formic acid 0.1% and acetonitrile 5% in water (mobile phase A) and formic acid 0.1% in acetonitrile (mobile phase B). The flow rate was 500 µL/min and the following gradient was used (min/%B): 0.0/5, 0.5/5, 1.2/100, 1.6/100, 2.0/5. The compounds were quantified with a triple quadrupole mass spectrometer (Xevo TQ MS, Waters Corp., USA). Transitions, cone voltages, and collision energies used are given in Supplementary Table S4.
Data analysis
The in vitro incubations were carried out in triplicate. Reversible IC50 values were determined by non-linear regression using GraphPad Prism (version 7, Systat Software, Inc., Chicago, IL). To determine time-dependent inhibition parameters, metabolite formation in the absence of inhibitor was used as a control, and the observed rates in the presence of inhibitor were adjusted to the control for each pre-incubation time. KI and kinact values were estimated using nonlinear regression (Equation 5)38,39:
where kobs is the initial rate of inactivation and [I] is the initial inhibitor concentration in the incubation.
Prediction of drug-drug Interactions
Interaction predictions were carried out for the inhibitors that exhibited time-dependent inhibition of CYP3A in the in vitro experiments. Clinical DDI studies with the inhibitors and the CYP3A probe drugs midazolam or simvastatin (http://www.druginteractioninfo.org/) were included as reference studies (n = 21; Supplementary Table S1). For interaction predictions, all reversible IC50 and time-dependent KI values were corrected for non-specific binding of the drugs to HLM by multiplying the value by fu,mic, measured at either 0.1 mg/ml HLM (IC50) or 0.5 mg/ml HLM (KI). IC50,u were further divided by 2 to obtain unbound reversible inhibition constants (Ki,u)40. The corrected values were assumed to be independent of drug concentration for the range used41.
The mechanistic static net effect model was used for interaction predictions2,6, to account for simultaneous reversible and time-dependent inhibition (Equation 6). The induction term has been excluded in Equation 6 as only one of the ten inhibitors tested (verapamil) has been reported to affect CYP3A by induction in vitro (Supplementary Table S3).
where AUCR represents the area under the plasma concentration-time curve of the affected drug in the presence and absence of the inhibitor. A and B represent reversible and time-dependent inhibition, respectively, and subscripts H and G denote liver and intestine, respectively2. The degradation rate (kdeg) values corresponded to 0.019 1/h (half-life of 36 h) for hepatic CYP3A4 degradation and 0.030 1/h (half-life of 23 h) for intestinal CYP3A4 degradation4. The fraction metabolized by CYP3A4 (fm) and the fraction of drug escaping CYP3A4-mediated gut metabolism (FG) were 0.94 and 0.51, respectively, for midazolam42,43, and 0.90 and 0.66, respectively, for simvastatin44,45.
Twelve combinations of hepatic and intestinal inhibitor concentrations were tested to evaluate the effects of Fcyto-correction on interaction predictions. As Fcyto describes the fraction of extracellular drug concentration that is bioavailable in the cytosol, the extracellular inhibitor concentration can be multiplied by Fcyto to obtain the concentration available at the enzyme. Thus, Fcyto-correction was performed by multiplying the hepatic inhibitor concentrations with the Fcyto value of each inhibitor. In addition, predictions were carried out with Fic-corrected hepatic inhibitor concentrations. Intestinal inhibitor concentrations were left uncorrected, since we did not determine Fcyto (or Fic) in enterocytes. The hepatic inhibitor concentrations in the predictions included the maximum unbound-inhibitor concentation at steady state in blood, [I]max,u; the average unbound-inhibitor concentation at steady state in blood, [I]ave,u,; the unbound-inhibitor blood concentration in the portal vein based on [I]max, [I]inlet,max,u; and the unbound-inhibitor blood concentration in the portal vein based on [I]ave,u, [I]inlet,ave,u.
[I]inlet,max,u and [I]inlet,ave,u were calculated according to Equations 9 and 10 5,6,46.
where fu,B is the unbound fraction of drug in blood (calculated as fu in plasma divided by the blood to plasma ratio); ka represents the absorption rate constant, dose and freq denote the inhibitor dose and frequency; fa is the fraction of drug absorbed; and Qh is the hepatic blood flow (97 l/h)47.
The intestinal inhibitor concentrations included the total enterocytic concentration, [I]g; the maximum unbound-inhibitor concentation at steady state in blood, [I]max,u; and the average unbound-inhibitor concentation at steady state in blood, [I]ave,u. Unless available in the literature, [I]ave,u was calculated according to Equation 11:
where τ is the dose interval (h).
[I]g was estimated using Equation 12 47:
where Qg represents the blood flow in the enterocytes (18 l/h)48. The inhibitor-specific input parameters are given in Supplementary Table S5.
Furthermore, an inhibitor concentration combination based on the mixed term approach, i.e., using different hepatic inhibitor concentrations for reversible and time-dependent inhibition3 was tested.
Each individual prediction was assessed by comparing the predicted AUCR to the corresponding one in the clinical reference study (predicted AUCR/observed AUCR). To assess the precision of each concentration combination, for a total of 21 individual predictions, the mean-square error (RMSE) of the predicted interactions (AUCR) compared to the observed AUCR was calculated according to Equation 13 3:
A lower RMSE value indicates a greater precision of the prediction. Moreover, to determine the accuracy of the predictions, the geometric mean fold error (GMFE) of each combination was calculated according to Equation 143:
A combination that predicts all values perfectly would thus have a GMFE value of 1; one that over- or underpredicts values on average by 2-fold would have GMFE values of 2 and 0.5, respectively.
Data Availability
All data generated or analyzed during this study are included in this published article or available from the corresponding author upon reasonable request.
References
Silverman, R. B. Mechanism-based enzyme inactivators. Methods Enzymol 249, 240–283 (1995).
Fahmi, O. A. et al. A combined model for predicting CYP3A4 clinical net drug-drug interaction based on CYP3A4 inhibition, inactivation, and induction determined in vitro. Drug Metab Dispos 36, 1698–1708 (2008).
Vieira, M. L. et al. Evaluation of various static in vitro-in vivo extrapolation models for risk assessment of the CYP3A inhibition potential of an investigational drug. Clin Pharmacol Ther 95, 189–198 (2014).
Rowland Yeo, K., Walsky, R. L., Jamei, M., Rostami-Hodjegan, A. & Tucker, G. T. Prediction of time-dependent CYP3A4 drug-drug interactions by physiologically based pharmacokinetic modelling: impact of inactivation parameters and enzyme turnover. Eur J Pharm Sci 43, 160–173 (2011).
EMA. European Medicines Agency, Guideline on the Investigation of Drug Interactions, http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2012/07/WC500129606.pdf [Accessed: August 4, 2017] (2012).
FDA. U.S Food and Drug Administration, In vitro metabolism- and transporter- mediated drug-drug interaction studies guidance for industry, https://www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/UCM581965.pdf [Accessed: November 12, 2017] (2017).
Mateus, A., Matsson, P. & Artursson, P. Rapid measurement of intracellular unbound drug concentrations. Mol Pharm 10, 2467–2478 (2013).
Mateus, A. et al. Intracellular drug bioavailability: a new predictor of system dependent drug disposition. Sci Rep 7, 43047, https://doi.org/10.1038/srep43047 (2017).
Mateus, A. et al. Prediction of intracellular exposure bridges the gap between target- and cell-based drug discovery. Proc Natl Acad Sci USA 114, E6231–E6239, https://doi.org/10.1073/pnas.1701848114 (2017).
Almqvist, H. et al. CETSA screening identifies known and novel thymidylate synthase inhibitors and slow intracellular activation of 5-fluorouracil. Nat Commun 7, 11040, https://doi.org/10.1038/ncomms11040 (2016).
Rimpela, A. K., Hagstrom, M., Kidron, H. & Urtti, A. Melanin targeting for intracellular drug delivery: Quantification of bound and free drug in retinal pigment epithelial cells. J Control Release 283, 261–268 (2018).
Treyer, A. et al. Intracellular drug bioavailability: Effect of neutral lipids and phospholipids. Mol Pharm 15, 2224–2233 (2018).
Zanger, U. M. & Schwab, M. Cytochrome P450 enzymes in drug metabolism: regulation of gene expression, enzyme activities, and impact of genetic variation. Pharmacol Ther 138, 103–141 (2013).
Korzekwa, K. R. In Drug-drug interactions (ed. A. D. Rodrigues) (Informa Healthcare USA, Inc, 2008).
Liao, M., Faouzi, S., Karyakin, A. & Correia, M. A. Endoplasmic reticulum-associated degradation of cytochrome P450 CYP3A4 in Saccharomyces cerevisiae: further characterization of cellular participants and structural determinants. Mol Pharmacol 69, 1897–1904 (2006).
Miyauchi, Y. et al. Suppression of cytochrome P450 3A4 function by UDP-glucuronosyltransferase 2B7 through a protein-protein interaction: Cooperative roles of the cytosolic carboxyl-terminal domain and the luminal anchoring region. Mol Pharmacol 88, 800–812 (2015).
Logan, R., Funk, R. S., Axcell, E. & Krise, J. P. Drug-drug interactions involving lysosomes: mechanisms and potential clinical implications. Expert Opin Drug Metab Toxicol 8, 943–958 (2012).
Ohkuma, S., Chudzik, J. & Poole, B. The effects of basic substances and acidic ionophores on the digestion of exogenous and endogenous proteins in mouse peritoneal macrophages. J Cell Biol 102, 959–966 (1986).
Schmitt, M. V., Lienau, P., Fricker, G. & Reichel, A. Quantitation of lysosomal trapping of basic lipophilic compounds using in vitro assays and in silico predictions based on the determination of the full pH profile of the endo-/lysosomal system in rat hepatocytes. Drug Metab Dispos 47, 49–57 (2019).
Ito, K., Ogihara, K., Kanamitsu, S. I. & Itoh, T. Prediction of the in vivo interaction between midazolam and macrolides based on in vitro studies using human liver microsomes. Drug Metabolism and Disposition 31, 945–954 (2003).
Yabe, Y., Galetin, A. & Houston, J. B. Kinetic characterization of rat hepatic uptake of 16 actively transported drugs. Drug Metab Dispos 39, 1808–1814 (2011).
Pfeifer, N. D., Harris, K. B., Yan, G. Z. & Brouwer, K. L. Determination of intracellular unbound concentrations and subcellular localization of drugs in rat sandwich-cultured hepatocytes compared with liver tissue. Drug Metab Dispos 41, 1949–1956 (2013).
Chien, H. C. et al. Rapid method to determine intracellular drug concentrations in cellular uptake assays: Application to metformin in organic cation transporter 1-transfected human embryonic kidney 293 cells. Drug Metab Dispos 44, 356–364 (2016).
Nadanaciva, S. et al. A high content screening assay for identifying lysosomotropic compounds. Toxicol In Vitro 25, 715–723 (2011).
de Duve, C. et al. Commentary. Lysosomotropic agents. Biochem Pharmacol 23, 2495–2531 (1974).
Fu, D. et al. Imaging the intracellular distribution of tyrosine kinase inhibitors in living cells with quantitative hyperspectral stimulated Raman scattering. Nat Chem 6, 614–622 (2014).
Friden, M. et al. Measurement of unbound drug exposure in brain: modeling of pH partitioning explains diverging results between the brain slice and brain homogenate methods. Drug Metab Dispos 39, 353–362 (2011).
Certara U. K. Simcyp division, Simcyp Simulator Version 17 Manual. (2017).
Neuhoff, S. et al. Application of permeability-limited physiologically-based pharmacokinetic models: part II - prediction of P-glycoprotein mediated drug-drug interactions with digoxin. J Pharm Sci 102, 3161–3173 (2013).
Vieira, M. L. et al. Predicting drug interaction potential with a physiologically based pharmacokinetic model: a case study of telithromycin, a time-dependent CYP3A inhibitor. Clin Pharmacol Ther 91, 700–708 (2012).
Rowland Yeo, K., Jamei, M., Yang, J., Tucker, G. T. & Rostami-Hodjegan, A. Physiologically based mechanistic modelling to predict complex drug-drug interactions involving simultaneous competitive and time-dependent enzyme inhibition by parent compound and its metabolite in both liver and gut - the effect of diltiazem on the time-course of exposure to triazolam. Eur J Pharm Sci 39, 298–309 (2010).
Lin, Y. S. et al. Co-regulation of CYP3A4 and CYP3A5 and contribution to hepatic and intestinal midazolam metabolism. Mol Pharmacol 62, 162–172 (2002).
Xie, H. G., Wood, A. J., Kim, R. B., Stein, C. M. & Wilkinson, G. R. Genetic variability in CYP3A5 and its possible consequences. Pharmacogenomics 5, 243–272 (2004).
Alexandre, E. et al. Influence of pre-, intra- and post-operative parameters of donor liver on the outcome of isolated human hepatocytes. Cell Tissue Bank 3, 223–233 (2002).
Lecluyse, E. L. & Alexandre, E. Isolation and culture of primary hepatocytes from resected human liver tissue. Methods Mol Biol 640, 57–82 (2010).
Gupta, A., Chatelain, P., Massingham, R., Jonsson, E. N. & Hammarlund-Udenaes, M. Brain distribution of cetirizine enantiomers: comparison of three different tissue-to-plasma partition coefficients: K(p), K(p,u), and K(p,uu). Drug Metab Dispos 34, 318–323 (2006).
Mateus, A., Matsson, P. & Artursson, P. A high-throughput cell-based method to predict the unbound drug fraction in the brain. J Med Chem 57, 3005–3010 (2014).
Kitz, R. & Wilson, I. B. Esters of methanesulfonic acid as irreversible inhibitors of acetylcholinesterase. J Biol Chem 237, 3245–3249 (1962).
Jones, D. R. et al. Diltiazem inhibition of cytochrome P-450 3A activity is due to metabolite intermediate complex formation. J Pharmacol Exp Ther 290, 1116–1125 (1999).
Brandt, R. B., Laux, J. E. & Yates, S. W. Calculation of inhibitor Ki and inhibitor type from the concentration of inhibitor for 50% inhibition for Michaelis-Menten enzymes. Biochem Med Metab Biol 37, 344–349 (1987).
McLure, J. A., Miners, J. O. & Birkett, D. J. Nonspecific binding of drugs to human liver microsomes. Br J Clin Pharmacol 49, 453–461 (2000).
Galetin, A., Burt, H., Gibbons, L. & Houston, J. B. Prediction of time-dependent CYP3A4 drug-drug interactions: impact of enzyme degradation, parallel elimination pathways, and intestinal inhibition. Drug Metab Dispos 34, 166–175 (2006).
Gertz, M., Harrison, A., Houston, J. B. & Galetin, A. Prediction of human intestinal first-pass metabolism of 25 CYP3A substrates from in vitro clearance and permeability data. Drug Metab Dispos 38, 1147–1158 (2010).
Houston, J. B. & Galetin, A. Methods for predicting in vivo pharmacokinetics using data from in vitro assays. Curr Drug Metab 9, 940–951 (2008).
Obach, R. S. et al. The utility of in vitro cytochrome P450 inhibition data in the prediction of drug-drug interactions. J Pharmacol Exp Ther 316, 336–348 (2006).
Ito, K. et al. Which concentration of the inhibitor should be used to predict in vivo drug interactions from in vitro data? AAPS PharmSci 4, E25, https://doi.org/10.1208/ps040425 (2002).
Rostami-Hodjegan, A. & Tucker, G. ‘In silico’ simulations to assess the ‘in vivo’ consequences of ‘in vitro’ metabolic drug-drug interactions. Drug Discov Today Technol 1, 441–448 (2004).
Yang, J., Jamei, M., Yeo, K. R., Tucker, G. T. & Rostami-Hodjegan, A. Prediction of intestinal first-pass drug metabolism. Curr Drug Metab 8, 676–684 (2007).
Mao, J., Johnson, T. R., Shen, Z. & Yamazaki, S. Prediction of crizotinib-midazolam interaction using the Simcyp population-based simulator: comparison of CYP3A time-dependent inhibition between human liver microsomes versus hepatocytes. Drug Metab Dispos 41, 343–352 (2013).
Zhang, X., Quinney, S. K., Gorski, J. C., Jones, D. R. & Hall, S. D. Semiphysiologically based pharmacokinetic models for the inhibition of midazolam clearance by diltiazem and its major metabolite. Drug Metab Dispos 37, 1587–1597 (2009).
Budha, N. R. et al. Evaluation of cytochrome P450 3A4-mediated drug-drug interaction potential for cobimetinib using physiologically based pharmacokinetic modeling and simulation. Clin Pharmacokinet 55, 1435–1445 (2016).
Wang, J. et al. A semi-physiologically-based pharmacokinetic model characterizing mechanism-based auto-inhibition to predict stereoselective pharmacokinetics of verapamil and its metabolite norverapamil in human. Eur J Pharm Sci 50, 290–302 (2013).
Cheng, Y. & Prusoff, W. H. Relationship between the inhibition constant (K1) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem Pharmacol 22, 3099–3108 (1973).
Acknowledgements
The authors thank Sibylle Neuhoff for insightful discussions, and Andrea Treyer, Richard Svensson and Aljona Saleh for help with experiments and analytical methods. SimulationsPlus is acknowledged for access to the ADMET Predictor Software. This work was supported by Swedish Research Council Grant 01951 (P.A.). A.M. was supported by Fundação para a Ciência e Tecnologia PhD Training Grant SFRH/BD/68304/2010. Uppsala Drug Optimization and Pharmaceutical Profiling Platform (UDOPP) was supported by the Helleday Laboratory at Karolinska Institutet, Sweden. This work was included in the Master’s thesis in Biomedicine of Rezvan Parvizi. Some parts of the work were presented at the FIP 6th Pharmaceutical Sciences World Congress in Stockholm in May 2017.
Author information
Authors and Affiliations
Contributions
R.P., A.M.F. and A.M. conducted the in vitro experiments of the study. A.M.F. and R.P. performed DDI predictions. A.M.F., R.P., A.M., P.B. and P.A. designed the study, performed data analysis and wrote the manuscript. P.B. and P.A. supervised the study.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Filppula, A.M., Parvizi, R., Mateus, A. et al. Improved predictions of time-dependent drug-drug interactions by determination of cytosolic drug concentrations. Sci Rep 9, 5850 (2019). https://doi.org/10.1038/s41598-019-42051-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-42051-x
This article is cited by
-
Clinical Trial Data-Driven Risk Assessment of Drug–Drug Interactions: A Rapid and Accurate Decision-Making Tool
Clinical Pharmacokinetics (2024)
-
Applications, Challenges, and Outlook for PBPK Modeling and Simulation: A Regulatory, Industrial and Academic Perspective
Pharmaceutical Research (2022)
-
K-means clustering analysis, ADME/pharmacokinetic prediction, MEP, and molecular docking studies of potential cytotoxic agents
Structural Chemistry (2021)
-
Inhibition and induction of CYP enzymes in humans: an update
Archives of Toxicology (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.