Abstract
The temperature dependence of the resistivity (ρ) of Ag-doped Bi2Se3 (AgxBi2−xSe3) shows insulating behavior above 35 K, but below 35 K, ρ suddenly decreases with decreasing temperature, in contrast to the metallic behavior for non-doped Bi2Se3 at 1.5–300 K. This significant change in transport properties from metallic behavior clearly shows that the Ag doping of Bi2Se3 can effectively tune the Fermi level downward. The Hall effect measurement shows that carrier is still electron in AgxBi2−xSe3 and the electron density changes with temperature to reasonably explain the transport properties. Furthermore, the positive gating of AgxBi2−xSe3 provides metallic behavior that is similar to that of non-doped Bi2Se3, indicating a successful upward tuning of the Fermi level.
Similar content being viewed by others
Introduction
Topological insulators are currently one of the most attractive research subjects in solid state physics because they are a new type of material characterized by gapless edge (surface) states and a finite energy gap1,2,3. These features are completely protected by time-reversal symmetry. The Bi compound Bi1-xSbx was the first to be confirmed as a ‘three-dimensional (3D) topological insulator’4, which had been theoretically predicted by Fu and Kane5. Since that discovery, many 3D topological insulators have been reported among Bi compounds6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. Among these, Bi2Se3 has been extensively studied because its simple surface states consist of a single Dirac cone6. However, the electronic state of real Bi2Se3 single crystals as prepared is not so simple, since electrons are naturally accumulated due to the deficiency of Se16,17,18, i.e., the Fermi level reaches the conduction band of the bulk crystal, leading to difficulty in detecting surface states. Consequently, the Fermi level tuning is very important for topological insulator, Bi2Se3.
One way to solve this problem is the doping of Bi2Se3 (substituting another element for Bi). Ca doping of Bi2Se3 enabled the tuning of the Fermi level downward so that it approached the Dirac point19,20. Furthermore, Bi2Te1.95Se1.05 showed the insulating behavior characteristic of having the Fermi level lying on the Dirac point9. This ternary compound was followed by a quaternary compound, Bi2−xSbxTe3−ySey21,22. This compound’s Fermi level could be tuned by adjusting the value of x, which was determined by angle-resolved photoemission spectroscopy (ARPES)22; at x = 1.0 the Fermi level reached the Dirac point.
Thus, pursuing techniques for detecting surface states that are hidden by bulk states is important in the study of real single crystals of topological insulators. Furthermore, the Ca doping of Bi2Se3 described above leads not only to the tuning of the Fermi level but the scattering of carriers20. Therefore, various ways must be investigated to detect surface states without any additional damage. Thus, the successful discovery of new dopant for tuning the Fermi level is of significance, even if the Fermi level does not yet reach surface states. Furthermore, an upward tuning of the Fermi level for the electron-depleted (or hole-doped) Bi2Se3 is also important for the control of not only electronic structure but also electric transport. The Fermi level tuning by combination of metal doping and electrostatic carrier doping is an important way in materials design to induce novel physical properties.
In this study, we have doped Bi2Se3 with a small quantity of Ag atoms and characterized its transport properties in field-effect transistor (FET) structured devices. The transport properties were measured over a wide temperature range from 300 to 1.5 K, and the Hall effect was measured from 250 to 10 K to follow the transport properties.
Results
Characterization of AgxBi2Se3
Commercially available single crystals of Bi2Se3 were used for this study. The stoichiometry of one single crystal was checked by energy dispersive X-ray spectroscopy (EDX) (not shown), which provided the chemical composition of Bi2Se2.55. Also we evaluated the stoichiometry of other Bi2Se3 single crystals, showing that the chemical composition is expressed ‘Bi2Se3.3(1)’. Figure 1a and b show a typical optical image of Ag0.05Bi2Se3 single crystal, and an atomic force microscope (AFM) image of exfoliated Ag0.05Bi2Se3 single crystal (135-nm thick). The preparation of AgxBi2Se3 is described in Methods. The exfoliated single crystal was placed on a Si substrate with a 300-nm thick SiO2 gate dielectric. The EDX showed only peaks assignable to Ag, Bi, and Se atoms on the single crystal of Ag0.05Bi2Se3 (Fig. 1c). The averaged stoichiometry of the surface of five Ag0.05Bi2Se3 single crystals was determined to be Ag0.11(1)Bi2Se3.2(6) in which the stoichiometry of Bi was fixed at 2, indicating doping with Ag atoms and an excess of Se. Here, it should be noticed that the scattering in stoichiometry of Se is too large, and the stoichiometry of Se in five single crystals is scattered from 2.1 to 3.8. The EDX of Ag0.2Bi2Se3 single crystals suggested that the chemical composition was expressed ‘Ag0.2(1)Bi2Se3.3(3)’ in which the stoichiometry of Bi was also fixed at 2, also demonstrating the Ag doping and an excess of Se atom, in the same manner as Ag0.05Bi2Se3. As described later, the electric transport for Bi2Se3±δ single crystals with various Se amounts was similar to each other (metallic), while that was also same for Ag doped Bi2Se3±δ single crystals (inverse V-shaped R–T plot).
(a) Photograph of typical Ag0.05Bi2Se3 single crystal and (b) AFM image of exfoliated Ag0.05Bi2Se3 single crystal (135-nm thick). (c) EDX spectrum of Ag0.05Bi2Se3 single crystal. In (c), Cu Lα and Kα peaks with an asterisk originate from the Cu tape used for fixing the single crystal to the sample folder. (d) Schematic representations of Ag0.05Bi1.95Se3 single crystal FET with 300-nm thick SiO2 gate dielectric used for transport measurement.
Single crystal X-ray diffraction (XRD) also yielded information on the structure and chemical composition of Ag0.05Bi2Se3 crystal. Table S1 of Supplementary Information lists the crystallographic data of Ag0.05Bi2Se3. Furthermore, Bragg spots obtained from the XRD of Ag0.05Bi2Se3 single crystal are shown in Figure S1 of Supplementary Information, which exhibits clear Bragg spots without diffusing, indicating the high crystallinity of single crystal. The crystal structure was rhombohedral (space group: R \(\bar{3}\,\)m) which is consistent with that of Bi2Se323. The lattice constants, a and c, were determined to be 4.146(6) and 28.66(4) Å, respectively, with being close to those of Bi2Se3 (4.18 and 28.7 Å)23. However, it is unclear whether Ag is not intercalated, because the lattice constant c does not so increase even in case of both the intercalation and the substitution for Bi24,25. Furthermore, the refinement of crystal structure also shows that no Ag atoms appear in any location other than the 6c and 3a sites which are occupied by Bi and Se, indicating that Ag may not be intercalated into the Bi2Se3 lattice. Namely, the difference Fourier map calculated from XRD for Ag doped Bi2Se3, where Ag, Bi and Se atoms are located at only the above sites, showed no electron density at other sites. Considering that Bi and Ag atoms become cations (Ag+ and Bi3+), Bi must be replaced by Ag, implying that hole is doped in Bi2Se3 by the replacement of Bi3+ with Ag+. Our recent experiment of X-ray fluorescence holography suggested that Ag was substituted for Bi, i.e., Ag0.05Bi1.95Se326. Furthermore, the X-ray photoelectron holography provided the same conclusion27. As described later, hole accumulation due to Ag doping was further supported by the transport measurement. As a consequence, the chemical formula of Ag-doped Bi2Se3 can be expressed as ‘AgxBi2−xSe3’ where x is experimental nominal value, although the exact chemical formula is ‘AgxBi2−xSe3±δ’ owing to not only the partial replacement of Bi with Ag but also a deficiency or excess of Se. If considering the above EDX’s values (Ag0.11(1)Bi2Se3.2(6) for Ag0.05Bi2Se3 and Ag0.2(1)Bi2Se3.3(3) for Ag0.2Bi2Se3), the exact chemical formulae are re-expressed ‘Ag0.10(1)Bi1.90Se3.0(6)’ and ‘Ag0.2(1)Bi1.8(1)Se3.0(3)’, respectively, by considering a partial substitution of Bi with Ag, but we expressed as AgxBi2−xSe3 for nominal x through this paper. Exactly saying, it is unclear whether Se is deficient or excessive because of a large scattering of stoichiometry for Se, but the transport suggests deficiency as described later. Furthermore, a preliminary experiment of X-ray photoemission spectrum (XPS) of Ag0.05Bi2Se3 showed only a single peak ascribable to Ag+ (not shown)27, indicating that the valence of Ag is 1. To sum up, the information on the quality of Ag doped Bi2Se3 single crystals obtained from these studies guarantees that the used single crystal of AgxBi2−xSe3 is sufficiently available for the study on transport properties of hole doped (or electron-depleted) Bi2Se3.
Transport properties of Ag0.05Bi1.95Se3
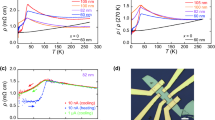
Figure 1d shows the structure of an Ag0.05Bi1.95Se3 single-crystal FET with a 300-nm thick SiO2 gate dielectric. The transport properties were measured using this device structure. The values of resistivity (ρ (=RWt/L), sheet resistivity (ρs (=RW/L)) and sheet conductance (σs (=1/ρs)) were evaluated from the slope (or R) derived by the linear fitting of the V–I plots in four-terminal or two-terminal measurement mode where R, L, W, and t are resistance, channel length, channel width, and thickness of the single crystal, respectively, shown in Fig. 1d. Details of measurement are described in Methods, and the measurement mode for each graph (transport property) is described in each Figure caption. The ρ (=RWt/L) of Ag0.05Bi1.95Se3 single crystal (105-nm thick) is plotted as a function of temperature (T), showing a clear transition at 35 K (Fig. 2a). The ρ of Ag0.05Bi1.95Se3 (x = 0.05, Fig. 2a) first increases with decreasing temperature, then rapidly decreases below 35 K, showing an inverse V-shaped ρ–T plot. This behavior is quite unlike the ρ–T plot of non-doped Bi2Se3 single crystal (60-nm thick, x = 0 in Fig. 2a), which exhibits simple metallic behavior. The observation of such metallic behavior implies that the transport properties reflect the conduction band because the Fermi level crosses the conduction band. As seen from Fig. 2a, the ρ of Ag0.05Bi1.95Se3 is higher than that of Bi2Se3. Thus, the transport properties of Ag0.05Bi1.95Se3 show that the Fermi level shifts downward in the conduction band.
(a) ρ – T plots of single crystals of Bi2Se3 (60-nm thick), Ag0.05Bi1.95Se3 (105-nm thick) and Ag0.2Bi1.8Se3 (110-nm thick). (b) Device structure used for measuemnt of Hall effect. Jx refers to current density along x direction, and Ey refers to electric field along y direction. Here, B is applied along z direction. (c) n–T plot of Ag0.05Bi1.95Se3 (82-nm thick) determined from Hall effect measurement. (d) ρ/ρ(270 K) – T plots of single crystals of Bi2Se3 (60-nm thick), Ag0.05Bi1.95Se3 (105-nm thick) and Ag0.2Bi1.8Se3 (110-nm thick). (e) Schematic representations of electronic structures in Bi2Se3, Ag0.05Bi1.95Se3, and Ag0.2Bi1.8Se3. All transport properties were measured in four-terminal measurement mode.
As described in the section of characterization of this paper, the ρ–T plot was always the same (metallic) in the Bi2Se3±δ single crystals with different Se amounts used in this study, and that of Ag doped Bi2Se3±δ was also the same (inverse V-shaped ρ–T plot), guaranteeing that the reliable comparison in electric transport between Bi2Se3 and Ag doped Bi2Se3. From this study, the inhomogeneity of Se within δ seems not to affect the transport property. Namely, we can discuss only the effect of Ag doping on transport property in this study.
Carrier density of Ag0.05Bi1.95Se3
To pursue this inverse V-shaped ρ–T plot more precisely, we measured Hall effect of 82 nm-thick Ag0.05Bi1.95Se3 single crystal; the device structure used for Hall effect measurement is shown in Fig. 2(b). Hall effect was measured by applying perpendicular magnetic field B to the substrate from −1 to 1T. Hall resistance, Ryx, was a linear function of B in this range, and Hall coefficient RH was obtained from RH = t dRyx/dB. The RH shows carrier type and carrier density because of RH = -(ne)−1 for electron and RH = (ne)−1 for hole, where n (>0) and e (>0) refer to carrier density and elementary charge, respectively; the RH is given in SI unit. The observed RH value was negative, showing that the carrier is still electron. Figure 2c shows n–T plot, which completely provides the V-shaped structure. This is consistent with the ρ–T plot. Here, we must stress that the inverse V-shaped ρ–T plot is completely reproduced in the sample (82-nm thick Ag0.05Bi1.95Se3 single crystal) used for the Hall effect measurement. As a consequence, the increase in ρ can be well explained by the decrease in n, and the n value exactly becomes minimum at the transition temperature, Tcr, in ρ–T plot (Tcr = 35 K in Fig. 2a). This unambiguous consistence means that the ρ–T plot reflects the variation of electron density against temperature. Here, we must comment on the n value for Ag0.05Bi1.95Se3. The minimum n is 4.7 × 1018 cm−3 at 35 K, which corresponds to the carrier density per area, ns (=nt), of 3.8 × 1013 cm−2. The value of the minimum ns further exceeds ~1 × 1013 cm−2 which is the maximum density for pure surface conduction in Bi2Se312,28. Therefore, the n meaningfully includes bulk carrier density in the conduction band at all temperatures. This suggests that the decrease in the resistivity below Tcr originates from the increase in bulk conductivity.
Recently, the variability of the transport properties of Sb-doped Bi2Se3 was investigated in FET structured devices12, showing metallic behavior in non-doped Bi2Se3 and non-metallic behavior in 6–7% Sb-doped Bi2Se3. The ρ–T plot of Ag0.05Bi1.95Se3 (Fig. 2a) is similar to the Rs - T of 6–7% Sb-doped Bi2Se3; Rs is sheet resistance (Rs = RW/L = ρs). Moreover, the Rs of Sb-doped Bi2Se3 increased by an order of magnitude12. The behavior is similar to the case of Ag-doped Bi2Se3 (Fig. 2a), although the ratio of increase is less than twice. As suggested for Sb-doped Bi2Se312, the Ag doping of Bi2Se3 must reduce the contribution from bulk conductivity. However, there are points of difference between Ag0.05Bi1.95Se3 and 6–7% Sb-doped Bi2Se3: (1) the Tcr is different (35 K for Ag0.05Bi1.95Se3 and 100 K for Sb-doped Bi2Se3), and (2) for Sb-doped Bi2Se3, saturation is observed below 50 K, rather than a rapid decrease in Rs below Tcr. In addition, application of positive and negative Vg to Sb-doped Bi2Se3 produced a rapid decrease in Rs below Tcr12. Therefore, it is suggested that the Fermi level in Ag0.05Bi1.95Se3 lies farther from the Dirac point than in 6–7% Sb-doped Bi2Se3.
Considering transport property of Sb-doped Bi2Se312 and the n determined from Hall effect, we concluded that the Fermi level of Ag0.05Bi1.95Se3 probably lied on the bottom area of conduction band or the top of surface states. Admittedly, preliminary ARPES suggests the crossing of the Fermi level to the bottom of conduction band (not shown); the ARPES of this sample changed gradually under the irradiation of light during the measurement. Thus, the ARPES study must be more precisely examined because the ARPES easily varies under various conditions29. Moreover, the transfer plot at 60 K shown in Fig. 3(a) exhibited different slope above/below Vg = 0 V, indicating that the Fermi level is located near the bottom of conduction band at Vg = 0 V. This result significantly supports the Fermi level’s location near bottom of the conduction band.
(a) σs–Vg plots at 272 and 60 K and (b) ρs–T plots of Ag0.05Bi1.95Se3 single-crystal FET with 300-nm thick SiO2 gate dielectric; thickness of single crystal is 105 nm. In (b), Vg values are fixed to −50, 0, and 50 V. In (a) and (b), transport properties are measured in four-terminal measurement mode. (c) Schematic representations of Ag0.05Bi1.95Se3 single crystal EDLT with bmim[PF6] ionic liquid used for transport measurement. (d) σs–Vg plot of Ag0.05Bi1.95Se3 single crystal EDLT at 242 K; thickness of single crystal is 105 nm. In (d), transport properties are measured in two-terminal measurement mode.
To sum up, the location of the Fermi level determined from Hall effect and comparison between transport properties in Ag doped Bi2Se3 (our study) and Sb doped Bi2Se3 (ref.12) is consistent with that determined from the preliminary ARPES and the FET data (Fig. 3(a)). Therefore, the transport data (R–T plot and n–T plot) achieved in this study is complementary for the ARPES and FET data. In addition, the Hall effect measurements of Bi2Se3 and possible more hole-doped Bi2Se3 such as Ag0.2Bi1.8Se3 may be necessary for pursuing exact position of the Fermi level and for understanding the transport properties. These are future tasks.
Transport properties of Ag0.2Bi1.8Se3
Figure 2a shows the temperature dependence of ρ in Ag0.2Bi1.8Se3 single crystal (110-nm thick, x = 0.2 in AgxBi2−xSe3). The ρ–T plot for Bi2Se3 (metallic behavior) is changed to the inverse V-shape by Ag doping. The ratio ρ/ρ-at-270-K (abbreviated as ρ(270 K)) shows almost the same behavior above 100 K between Ag0.2Bi1.8Se3 and Ag0.05Bi1.95Se3 (Fig. 2d), implying that the Fermi level is located at almost the same position. At 35–100 K, the ρ/ρ(270 K) was slightly higher in Ag0.2Bi1.8Se3 than that in Ag0.05Bi1.95Se3. The Tcr was also the same between x = 0.05 and 0.2. Furthermore, the ρ value in Ag0.2Bi1.8Se3 above Tcr is slightly smaller than that in Ag0.05Bi1.95Se3 (Fig. 2a). These results indicate that the larger amount of Ag doping than x = 0.05 in AgxBi2−xSe3 is not so effective to tune the Fermi level downward, indicating no hole doping at more than 0.1 (=0.05 × 2), i.e., no substitution of Ag for Bi. Recent photoelectron holography measurement suggests the occurrence of not only substitution but also intercalation for x = 0.227, although only a substitution is suggested for x = 0.0526,27, indicating both electron and hole doping for Ag0.2Bi1.8Se3. If it is the case, the low ρ in Ag0.2Bi1.8Se3 may be reasonably explained, because electron accumulation cancels the effect of hole doping. Schematic representations of the suggested electronic states of AgxBi2−xSe3 (x = 0.05 and 0.2) and Bi2Se3 are also shown in Fig. 2e.
Electrostatic carrier doping of Ag0.05Bi1.95Se3
Figure 3a shows σs as a function of Vg of −60 to 60 V recorded for Ag0.05Bi1.95Se3 single-crystal FET using a SiO2 gate dielectric (Fig. 1d) at 272 K. The σs–Vg plot exhibits n-channel normally-on properties; the single crystal was 105-nm thick. Thus, the single crystals are made electron-rich without any application of Vg, and the quantity of electrons in the channel region is weakly tuned by applying Vg. The σs–Vg plot at 60 K is also shown in Fig. 3a. The plot shows a steeper slope than that at 272 K when applying negative Vg, implying an effective depletion of the channel region when applying negative Vg. These results suggest the presence of significant bulk conductance even in Ag0.05Bi1.95Se3. This problem is discussed later. Figure 3b shows the ρs–T plots at different Vg values of −50, 0, and 50 V, with 105-nm thick Ag0.05Bi1.95Se3. Three ρs–T plots show no difference at 200 K, but the difference increases near Tcr (=35 K), and the ρs decreases with increasing Vg from −50 to 50 V, consistent with the σs–Vg plot at 60 K (Fig. 3a). The difference disappears below Tcr, implying a small gate-voltage modulation of transport properties.
The schematic representation of the Ag0.05Bi1.95Se3 single-crystal FET with an ionic liquid gate capacitor (105-nm thick Ag0.05Bi1.95Se3 single-crystal electric-double-layer transistor (EDLT)) is shown in Fig. 3c. Figure 3d shows the σs–Vg plot at 242 K for the Ag0.05Bi1.95Se3 EDLT, which exhibited n-channel normally-on properties and clearly showed low-voltage operation.
Figure 4a shows the ρs–T plots for the Ag0.05Bi1.95Se3 single-crystal EDLT over a Vg range from 0 to 5 V with a 105-nm thick single crystal. The ρs value decreased with an increase in Vg, and non-metallic behavior (an inverse V-shaped ρs–T plot) at 0–2 V changed very markedly to metallic behavior at 5 V. The transition of the ρs–T plot observed around 35 K becomes ambiguous with increasing Vg. The ρs–T plot at Vg = 5 V is similar to that of non-doped Bi2Se3 (see Fig. 2a), indicating that the Fermi level reaches the conduction band as shown in Fig. 4b. Clearly, the applied gate-voltage tunes the Fermi level.
(a) ρs–T plots of Ag0.05Bi1.95Se3 single crystal EDLT; thickness of single crystal is 105 nm. The applied Vg is in 0–5 V. Transport properties are measured in two-terminal measurement mode. (b) Schematic representations of electronic structures in Ag0.05Bi1.95Se3 single crystal at different Vg values. (c) ρ–T plots of 60-nm and 105-nm thick Ag0.05Bi1.95Se3 single crystals, which are measured in four-terminal measurement mode.
The field-effect mobility, μ, of the Ag0.05Bi1.95Se3 single-crystal FET with a SiO2 gate dielectric was found to be 35(2) cm2 V−1 s−1 at 272 K. The μ value was slightly suppressed by Ag doping, as the reported lower limit of μ for a non-doped Bi2Se3 single crystal FET with a SiO2 gate dielectric30 is 50–100 cm2 V−1 s−1. The μ value in an Ag0.05Bi1.95Se3 single crystal EDLT was 40(1) cm2 V−1 s−1, which is smaller by an order of magnitude than the 692 cm2 V−1 s−1 reported in a non-doped Bi2Se3 single-crystal EDLT31, indicating the suppression of μ due to scattering by Ag doping.
Discussion
The inverse V-shaped ρ–T (or ρs–T) plot in AgxBi2−xSe3 is the most interesting observation in this study. As illustrated in Fig. 2e, the Fermi level of AgxBi2−xSe3 is located on the bottom area of the conduction band or near the top of the surface states. Therefore, the ρ–T plot should reflect the surface states to some extent, in which the density of states (DOS) is much smaller than in the conduction band. In Ag0.05Bi1.95Se3, the bulk region of crystal is an insulator-like and the surface is metallic, which is different from that of non-doped Bi2Se3 with the complete crossing of the Fermi level to conduction band. This situation should lead to insulating behavior at high temperatures, because the bulk contribution may predominate for thick crystal and the transport property should be governed by the thermal excitation to the conduction band. In other words, the surface transport is hidden by the bulk conduction. This is the first scenario for explaining the insulating behavior above Tcr.
Here, it should be noticed that the temperature dependence of ρ reflecting surface states may slowly decrease at low temperature, because the ρ–T plot of non-doped graphene, which were measured with/without applying Vg, showed a very slow decrease with decreasing temperature below 150 K32,33. Therefore, the rapid decrease in ρ–T plot below Tcr (=35 K) found for AgxBi2−xSe3 may not be explained by considering the conduction through the surface states. Therefore, we assumed that the Fermi level shifted upward to cross the conduction band at Tcr. In this case, the bulk transport should suddenly change from insulating to metallic behaviour. If it is the case, the inverse-V shaped ρ–T plot mainly reflects a bulk transport in a whole temperature range (1.5–270 K), although the surface states indirectly affects the ρ–T plot. The n value determined from Hall effect (Fig. 2c) shows the drastic increase with decreasing temperature below Tcr, which correlates with ρ–T plot, showing that the variation of ρ can be substantially explained by electron density. Such a drastic increase in n may be easily explained by the upward moving of the Fermi level. However, it is still unclear whether such a Fermi level shift takes place below the Tcr, and why it happens. We must investigate whether the structural transition or the electronic variation occurs at Tcr, using various probe techniques such as temperature-dependent XRD, temperature dependent X-ray emission spectroscopy and so on.
We may comment on the other scenario for insulating behaviour of ρ–T plot in the high-temperature range above the Tcr. The insulating behaviour in AgxBi2−xSe3 may originate from the crossing of the Fermi level to surface states, since the defective graphene provides an insulating behaviour for the ρ–T plot34. If the surface region of AgxBi2−xSe3 will be much defective, the insulating behaviour may be observed in the ρ–T plot. This is the second scenario. Even in this scenario, we must assume the Fermi level shift for explaining the ρ–T plot below the Tcr.
Figure 4c shows the ρ–T plots from 60-nm and 105-nm thick Ag0.05Bi1.95Se3 single crystals. The slope of the temperature dependence curve of ρ in thick single crystal (105 nm) both above and below Tcr is steeper than that of thin single crystal (60 nm). In case of thick single crystal, the bulk transport should contribute significantly to the transport properties in comparison with thin single crystal. Therefore, the change of transport properties between thin and thick single crystals suggests that the ρ–T plot may mainly reflect the bulk transport in all temperature range, since the surface states should provide a constant contribution to the ρ–T plot regardless of thickness of crystal. As a consequence, we insist that the first scenario may explain the inverse-V shaped ρ–T plots observed in this study, although the second scenario must be more fully examined.
Conclusion
This study reports the FET properties as well as transport property and Hall effect of single crystals of Ag doped Bi2Se3. The Ag doping of Bi2Se3 provided a drastic change of transport property from metallic behavior in non-doped Bi2Se3, i.e., the characteristic inverse V-shaped ρ– T plot was observed in AgxBi2−xSe3 (x = 0.05 and 0.2). This behavior should be due to the successful tuning of the Fermi level downward through hole doping, because Ag is substituted for Bi in AgxBi2−xSe3 (x = 0.05 and 0.2), although the intercalation of Ag to Bi2Se3 lattice may also take place for x = 0.2 in addition to the substitution of Ag for Bi. The temperature-dependent Hall effect measurement showed that the ρ – T plot correlated with the n–T plot, i.e., the electron density plays an important role for the ρ–T plot. Two different scenarios were suggested to explain the inverse V-shaped ρ–T plot. As a consequence, we insisted that the ρ–T plot may mainly reflect the bulk transport in all temperature range and reflect the thermal electron excitation to conduction band at high temperature, and that the Fermi level upward-shift may happen at Tcr and the metallic property is observed below Tcr. The positive Vg application (or electron accumulation) for Ag0.05Bi1.95Se3 successfully changed the inverse V-shaped ρ–T plot to metallic one, suggesting an upward tuning of the Fermi level. Thus, this study evidenced the successful and free tuning of the Fermi level by doping of Ag atom and positive gating in Ag doped Bi2Se3 with ionic liquid. In additon, the pressure application for Sb2Se3, BiTeI and HfTe5 provided the variation of electric transport from semiconducting/semimetallic to metallic behavior through an instesting topological quantum transition35,36,37, which can be recognized as ‘physical tuning of the Fermi level’. Therefore, the element doping may be termed as ‘chemical tuning of the Fermi level or the Fermi surface’. Both combination of physical and chemical tuning may enable the wide tunig of the Fermi level and the Fermi surface to induce novel physical properties. To sum up, this study may provide us with a fruitful knowledge of physics of topological materials and experience for manufacturing practical transistor devices based on topological insulators.
Methods
The crystals of AgxBi2Se3 were grown by a conventional melt-growth method using stoichiometric amounts of Ag, Bi, and Se powders. The detailed experimental process was as follows: the powders were sealed in a quartz tube which was heated at 800 °C for 12 h. It was slowly cooled down to 650 °C at the rate of 30 °C/h, and then quenched with ice-water. The obtained crystals showed a clear basal plane structure. Their crystal structures were determined by single-crystal XRD measurements, using a Rigaku Saturn 724 diffractometer equipped with a Mo Kα source (wavelength λ = 0.71073 Å); measurement was performed at 100 K. Thickness and surface morphology of single crystals were determined by AFM equipment (SII technology, SPA400-DFM). The EDX spectrum was recorded with an EDX spectrometer equipped with a scanning electron microscope (SEM) (KEYENCE VE-9800 - EDAX Genesis XM2). The AFM and EDX measurements were made at room temperature.
In the measurements of electric transport and Hall effect, the I was applied with a KEITHLEY-220 Programmable current source. The exact value of I was monitored by an Advantest R-8240 digital electrometer. The V was measured with an Agilent 34420 A nano-voltmeter. For Hall effect measurement, the magnetic field, B, was controlled with Oxford Instruments, MercuryiPS. The gate voltage (Vg) was applied to a heavily doped Si substrate for the Ag0.05Bi2Se3 single-crystal FET with a 300-nm thick SiO2 gate dielectric, and to the side gate electrode (Au electrode) for the Ag0.05Bi2Se3 single-crystal EDLT with ionic liquid, using a KEITHLEY 2635 A sourcemeter. Device structures (top-contact type) are illustrated in Figs 1d, 2b and 3c; top-contact electrodes and side-gate electrodes were formed by 100-nm thick Au, and 5-nm thick Cr was inserted between the Au electrode and the single crystal. Temperature was controlled using an Oxford superconducting magnet system with a variable temperature insert. The ionic-liquid 1-butyl-3-methylimidazolium hexafluorophosphate (bmim[PF6]) was levigated by adding poly(styrene-b-ethylene oxide-b-styrene), and was placed across the side gate electrode and Ag0.05Bi2Se3 single crystal. All single crystals used for transport measurements were exfoliated using the scotch tape under air.
References
Kane, C. L. & Mele, E. J. Z2 Topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306(R) (2007).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–975 (2008).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys. 5, 398–402 (2009).
Chen, Y. L. et al. Experimental Realization of a Three-Dimensional Topological Insulator, Bi2Te3. Science 325, 178–181 (2009).
Hsieh, D. et al. Observation of Time-Reversal-Protected Single-Dirac-Cone Topological-Insulator States in Bi2Te3 and Sb2Te3. Phys. Rev. Lett. 103, 146401 (2009).
Ren, Z., Taskin, A. A., Sasaki, S., Segawa, K. & Ando, Y. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Phys. Rev. B 82, 241306(R) (2010).
Taskin, A. A., Ren, Z., Sasaki, S., Segawa, K. & Ando, Y. Observation of Dirac Holes and Electrons in a Topological Insulator. Phys. Rev. Lett. 107, 016801 (2011).
Zhang, J. S. et al. Band structure engineering in (Bi1−xSbx)2Te3 ternary topological insulators. Nature Commun. 2, 574 (2011).
Hong, S. S., Cha, J. J., Kong, D. & Cui, Y. Ultra-low carrier concentration and surface-dominant transport in antimony-doped Bi2Se3 topological insulator nanoribbons. Nature Commun. 3, 757 (2012).
Kuroda, K. et al. Experimental realization of a three-dimensional topological insulator phase in ternary chalcogenide TlBiSe2. Phys. Rev. Lett. 105, 146801 (2010).
Schafgans, A. A. et al. Landau level spectroscopy of surface states in the topological insulator Bi0.91Sb0.09 via magneto-optics. Phys. Rev. B 85, 195440 (2012).
Xu, S.-Y. et al. Discovery of several large families of topological insulator classes with backscattering-suppressed spin-polarized single-Dirac-cone on the surface. Preprint at https://arxiv.org/abs/1007.5111 (2010).
Butch, N. P. et al. Strong surface scattering in ultrahigh-mobility Bi2Se3 topological insulator crystals. Phys. Rev. B 81, 241301(R) (2010).
Analytis, J. G. et al. Bulk Fermi surface coexistence with Dirac surface state in Bi2Se3: A comparison of photoemission and Shubnikov–de Haas measurements. Phys. Rev. B 81, 205407 (2010).
Scanlon, D. O. et al. Controlling bulk conductivity in topological insulators: Key role of anti-site defects. Adv. Mater. 24, 2154–2158 (2012).
Wang, Z. Y. et al. Tuning carrier type and density in Bi2Se3 by Ca-doping. Appl. Phys. Lett. 97, 042112 (2010).
Checkelsky, J. G. et al. Quantum interference in macroscopic crystals of nonmetallic Bi2Se3. Phys. Rev. Lett. 103, 246601 (2009).
Ren, Z., Taskin, A. A., Sasaki, S., Segawa, K. & Ando, Y. Optimizing Bi2−xSbxTe3-ySey solid solutions to approach the intrinsic topological insulator regime. Phys. Rev. B 84, 165311 (2011).
Arakane, T. et al. Tunable Dirac cone in the topological insulator Bi2−xSbxTe3-ySey. Nature Commun. 3, 636 (2012).
Zargarova, M. I., Babaeva, P. K., Azhdarova, D. S., Melikova, Z. D. & Mekhtieva, S. A. A Study of the systems CuInSe2InSe (SnSe2, Bi2Se3). Inorg. Mater. 31, 263–264 (1995).
Hor, Y. S. et al. Superconductivity in CuxBi2Se3 and its implications for pairing in the undoped topological insulator. Phys. Rev. Lett. 104, 057001 (2010).
Liu, Z. et al. Superconductivity with topological surface state in SrxBi2Se3. J. Am. Chem. Soc. 137, 10512–10515 (2015).
He, T. et al. Pressure-induced superconductivity in AgxBi2−xSe3. Phys. Rev. B 97, 104503 (2018).
Matsui, F., Kobayashi, K., Goto, H. & Kubozono, Y. Photoelectron holography of Ag doped Bi2Se3. to be submitted (2019).
Kim, D. et al. Intrinsic electron-phonon resistivity of Bi2Se3 in the topological regime. Phys. Rev. Lett. 109, 166801 (2012).
Wray, L. A. et al. Spin-orbit ground states of superconducting doped topological insulators: A Majorana platform. Phys. Rev. B 83, 224516 (2011).
Steinberg, H., Gardner, D. R., Lee, Y. S. & Jarillo-Herrero, P. Surface state transport and ambipolar electric field effect in Bi2Se3 nanodevices. Nano Lett. 10, 5032–5036 (2010).
Eguchi, R. et al. Electric-double-layer transistors with thin crystals of FeSe1−xTex (x = 0.9 and 1.0). Appl. Phys. Lett. 102, 103506 (2013).
Chen, J.-H., Jang, C., Xiao, S., Ishigami, M. & Fuhrer, M. S. Intrinsic and extrinsic performance limits of graphene devices on SiO2. Nature Nanotech. 3, 206–209 (2008).
Morozov, S. V. et al. Giant intrinsic carrier mobilities in graphene and its bilayer. Phys. Rev. Lett. 100, 016602 (2008).
Chen, J.-H., Cullen, W. G., Jang, C., Fuhrer, M. S. & Williams, E. D. Deffect scattering in graphene. Phys. Rev. Lett. 102, 236805 (2009).
Kong, P. P. et al. Superconductivity in strong spin orbital coupling compound Sb2Se3. Sci. Rep. 14, 6679 (2014).
Jin, M. L. et al. Superconductivity bordering Rashba type topological transition. Sci. Rep. 7, 39699 (2017).
Liu, Y. et al. Superconductivity in HfTe5 across weak to strong topological insulator transition induced via pressures. Sci. Rep. 7, 44367 (2017).
Acknowledgements
The authors greatly appreciate Prof. Justin Ye of University of Groningen and Prof. Harald O. Jeschke of Okayama University for their valuable discussion. Also the authors are debted Ms. Tong He for her valuable assistance for sample characterization. This study was partly supported by Grants-in-aid (26105004, 26400361, 14J00228 and 17K05500) from MEXT, by the ACT-C program (No. JPMJCR12YW) of JST, and by the Program for Promoting the Enhancement of Research Universities.
Author information
Authors and Affiliations
Contributions
K.K. and Y.K. suggested the idea for this research, and designed this study. K.K. and T.U. prepared Ag-doped Bi2Se3 single crystals. E.U. and T.U. carried out experiments on characterization, transport properties and Hall effect. H.O. measured X-ray diffraction of the sample and determined its structure. H.F., K.T. and T.Y. carried out ARPES measurements and provided the electronic states of Ag-doped Bi2Se3. F.M. carried out X-ray photoelectron hologram. H.G., T.Y., J.A. and Y.K. discussed all experimental results with K.K. and E.U. With continuing discussion with all authors, Y.K. and E.U. prepared the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Uesugi, E., Uchiyama, T., Goto, H. et al. Fermi level tuning of Ag-doped Bi2Se3 topological insulator. Sci Rep 9, 5376 (2019). https://doi.org/10.1038/s41598-019-41906-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-41906-7
This article is cited by
-
Cobalt-doped double-layer α-Fe2O3 nanorod arrays for enhanced photoelectrochemical reduction of Cr(VI)
Discover Nano (2023)
-
Semiconductor–metal transition in Bi2Se3 caused by impurity doping
Scientific Reports (2023)
-
Tuning of charge carriers in Bi2Te3 thin films via swift heavy ion irradiation
Journal of Materials Science: Materials in Electronics (2023)
-
Tuning of fermi level in antimony telluride thin films by low-energy Fe−-ion implantation
Applied Physics A (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.