Abstract
Using first principles theory, we investigated the behavior of the one-dimensional (1D) topological edge states of high temperature superconductiviing FeSe/SrTiO3 films with Te atoms substitution to Se atoms in the bottom (top) layer in single-layer FeSe, as a function of strain. It was discovered that the 1D topological edge states are present in single-unit-cell FeSe film on SrTiO3, but are absent when more than 50% Se atoms are replaced by Te atoms. Stress induced displacive phase transformation exists in FeSe/SrTiO3 film when Te atoms substitute Se atoms in the bottom (top) layer in single-layer FeSe under 3% strain respectively. The 1D topological edge states are present under 3% (1.8%) strain in FeSe/SrTiO3 films with Te substitution Se in the bottom (top) layer in single-layer FeSe, even up to 5%, respectively. This indicates that the bonding angle of Se-Fe-Se (Te) and the distance of Te (or Se) atoms to the Fe plane are correlated with the topological edge states. Our findings provide an effective interface system that provides both superconducting and topological states, opening a new route for realizing 2D topological superconductors with proximity effect.
Similar content being viewed by others
Introduction
Single-unit-cell (UC) FeSe films have been successfully grown on SrTiO3 (STO) substrate with a superconducting gap up to 20 meV1 and possible superconducting transition temperature above 100 K2. The Fermi surface of single-layer FeSe/STO have been measured by angle-resolved photoemission spectroscopy (ARPES) experiments, showing electron pockets at the M point and no hole pockets at the Γ point. This experimental observation is inconsistency with theory in band structure. Despite intense experimental3,4,5,6,7,8,9 and theoretical efforts9,10 have been devoted, some of the essential fascinating new-style class of 2D superconductor is still elusive. Recently, much attention has been paid to the potential being of topological phases in FeSe11,12,13. Theoretical and experimental results have presented for an antiferromagnetic (AFM) quantum spin Hall (QSH) state in FeSe14. Previous low-temperature scanning tunneling microscopy (STM) and scanning tunneling spectroscopy (STS) study have demonstrated that the superconducting transition temperature (Tc) increases with the substitution of Se composition by Te which reaches 14.5 K at about 40% Se substitution15,16, which is higher than the maximum Tc ~9 K of bulk FeSe. 1UC FeTe1−xSex films (0 < x < 0.6) on STO(001) substrates were prepared by molecular beam epitaxy (MBE) and the superconducting properties were studied by in situ STS study and ex situ transport measurement17.
Considering the fact of both theoretical and experimental results for an AFM QSH state in FeSe14, it’s necessary to test the potential existence of topological phases in high-temperature superconductiving FeSe/STO films with Te substitution to Se. The properties of FeSe films with Te substitution could be affected by the key factors including interfacial strain, structural deformation, interfacial charge transfer and so on. However, the interfacial strain is the most dominant factor amongst these. The in-plane lattice constant of FeSe exactly matches the substrate with a perfect coherent interface. While Se atoms are substituted by Te, strain will be induced to the film, so that strain is suggested to play an important role in affecting the interaction of topological band states.
Motivated by these recent discoveries, we have carried out a systematic study of the topoelectronic properties of 1UC FeSe/STO films with Te substitution as a function of concentration change of Te substituting and strain, based on first-principles calculations. More than 50% Te substitution Se atoms in both top and bottom layers in single-layer FeSe will lead to the disappear of the 1D Dirac edge state. These calculation results allow us to conclude that tensile strain induces displacive phase transformation when Te atoms substitute Se atoms in the bottom (top) layer in single-layer FeSe under 3% strain respectively. 1D topological edge states of 1UC FeSe/STO films with Te substituting Se on bottom (top) layer is presented under tensile strain 3% (1.8%), respectively, even up to 5% strain. This study provides a good foundation for experimental study that leads to potential applications in spintronics.
Methods
The experimental interface configuration of FeSe/STO is complex. There are two possible atomic structures of FeSe/STO: the bottom Se atom in single-layer FeSe is directly above the top of either O or Ti atom in the STO substrate as can be seen in Fig. 1(a,b), respectively. These two interface configurations of FeSe/STO lead to equivalent result14. In our calculation, we assumed that the bottom Se atom in single-layer FeSe is directly above the top of O atom in the STO substrate. Its electronic band structures and topoelectronic properties were calculated with the framework of the PBE-type generalized gradient approximation using VASP package as described before18,19,20,21. Spin orbit coupling (SOC) was included in the self-consistent electronic structure calculations. All calculations were implemented with a plane-wave cutoff of 400 eV on a 9 × 9 × 1 Monkhorst-Pack k-point mesh, and a vacuum layer that is over 15 Å to avoid the interaction between neighboring slabs. For structural relaxation, all the atoms are allowed to relax until atomic forces are smaller than 0.01 eV/Å. The experimental lattice constant is a = 3.90 Å22. In order to test the influence of SrTiO3 antiferrodistortion on surface electronic structures, we chosen 2 × 2 × 1 supercell. Previous study indicated that the band structure of FeSe/STO with chequerboard AFM configuration coincides exactly with the ARPES spectra within the whole Brillouin zone, so that we chosen chequerboard AFM configuration in our calculations (neighbouring Fe atoms have opposite spin directions). Figure 1(c) shows the spin configurations of the chequerboard AFM state that are schematically along z, x and xy, respectively. z direction is the vertical normal to FeSe plane, x direction is along next nearest-neighbor Fe-Fe bond, and xy direction is along nearest-neighbor Fe-Fe bond. Our calculations shown that the differential energies among above three spin configurations are very small. On the other hand, previous work has proved that the in-plane spin configuration cannot leads to a sizeable gap at the M point in FeSe/STO14, so we set the z spin direction for Fe atoms in our calculation. We used the Wannier90 package23 to calculate the topoelectronic edge states of 1D zigzag nanoribbon as described previously20,21. The tight-binding Hamiltonian with maximally localized Wannier functions (MLWFs) was fitted to the first-principles band structures. The Coulomb repulsion is characterized by a spherically averaged Hubbard parameter U, which depends on the spatial extension of the wave functions. In our calculation the U was set to be 0.6 eV14. Considering that GGA is usually regarded to underestimate the binding in weakly bonded systems of inhomogeneous systems, we used van der Waals (vdw) correction in our calculations and applied the semiempirical DFT-D2 method proposed by Grimme24.
Unit cell of FeTe on SrTiO3 subtract with six atomic layers: (a) the bottom Se atom in single-layer FeSe is directly above the top O in the STO substrate, and (b) the bottom Se atom in single-layer FeSe is directly above the top Ti atom in the STO substrate, brown, light green, red, dark green and blue balls represent Fe, Se(Te), O, Sr and Ti atoms, respectively. (c) Fe atoms with chequerboard AFM spin configuration. Spin in z direction is the normal to FeSe plane denoted by blue arrows. Spin in x direction is along next-nearest-neighbor Fe-Fe bond and xy direction is along nearest-neighbor Fe-Fe bond denoted by red arrows. (d) Brillouin zone of unit cell of FeTe on SrTiO3 subtract with high symmetry point Γ, X, X′ and M.
Results and Discussion
We first modeled the interface structure of FeSe monolayer on TiO2-terminated SrTiO3 (001) surface in six atomic layers, where the bottom Se atom in single-layer FeSe is directly above the top O atom in the STO substrate. The vertical distance between O and Se atoms is 3.188 Å. The bond length between top (bottom) Se and Fe atoms is 2.389 (2.387) Å. The Fe-Se-Fe angle for top (bottom) Se atoms is 109.338° (109.520°). The calculated magnetic moment is 2.37 μB on each Fe atom.
Figure 1(d) shows the supercell brillouin zone with high-symmetry k points including Γ, M, X and X΄. In our calculations, the monolayer lattice constants a and b of FeSe/Te on STO are same. Duo to the effect of substrate, the symmetry of this system would be lowered, the electronic structures maybe have a small difference along MX and MX΄ directions. The corresponding band structures with Hubbard-U and vdw corrections are shown in Fig. 2(a). An obvious characteristic is that no hole pocket at the Γ point and electron pocket at the M point in FeSe/STO system, which is in agreement with the ARPES data4 and previous calculations14,22. The outspread flat bands below the Fermi level come from the dz2, dxz and dyz orbitals of the Fe atoms, and the pz orbital of the Se atoms. We demonstrate the band of free standing 1UC FeSe monolayer in Fig. 2(b) to compare the energy bands with substrate effects, thus further examining the influence of the substrate on the band. The STO substrate enhances the feature of electron pockets at the M point, showing that the hybridization between FeSe and STO substrate is negligible and the parabolic bands overlapping with the FeSe bands are most from the STO substrate.
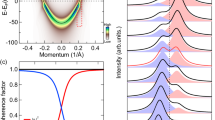
1D ferromagnetic (FM) edge states of a FeSe/STO ribbon indicated in Fig. 2(c) were studied using the Wannier functions25,26,27. Spin symmetry breaking along the FM edge leads to two asymmetric edge states for both the left and right edges. The edge states with bright lines are presented around Fermi level and Dirac point with the valence and conduction bands connecting is appeared in Fig. 2(d). Most importantly, the pair of gapless Dirac edge states inside the SOC gap demonstrates AFM QSH state. Figure 2(e) shows the edge states of free standing FeSe, exhibiting 1D Dirac edge state inside the “bulk” band gap. This verifies that the 1D Dirac edge states of 1UC FeSe/STO originate in the 1UC FeSe. Compared with Fig. 2(d), the interaction between SrTiO3 substrate and FeSe monolayer induces charge transfer and an interfacial electric field, which slightly modify the relative shape in “bulk” band structures while keep Dirac edge state.
1UC FeTe1−xSex films (0 < x < 0.6) on STO (001) substrates were reported with superconducting properties examined by combined in-situ STS study and ex-situ transport measurements17. In experiments, atom doping is an out of order distribution. The simulation modeling of such disorder is very complicated and time consuming. For simplicity, we firstly assumed that the Te replaces either the bottom or top Se atoms in 1UC FeSe. In this substitution we could distinguish which one between Se and Te atoms is benefit to induce 1D Dirac edge state in this system. Firstly, we consider that Te atoms completely substitute bottom Se atom in single-layer FeSe (The system is denoted as FeSeTe/STO, see Supplementary Fig. 1(a)). The vertical distance between O and Te atoms is 3.328 Å. This confirms that the Te atom substituting Se atom lowers the interaction between FeSeTe and STO substrate. The bond length between top (bottom) Se (Te) and the Fe atoms is 2.368 (2.542) Å. The Fe-Se (Te)-Fe angle for top Se and (bottom Te) atoms is 107.66° (97.92°). The calculated magnetic moment is 2.23 μB on each Fe atom. Te atom substituting changes bond length and bond angle with Fe atom, and decreases interaction in FeSeTe/STO interfacial system slightly.
The bands for FeSeTe/STO film are shown in Fig. 3(a). We could see that the band at Γ point shows electron pocket, which is the typical dz2 feature, whereas the bands along X- M line still show hole pockets, which are the dxz and dyz features. The Te substitution enhances the feature of electron pockets at Γ point slightly. In addition, this Te substitution induces the spatial inversion symmetry breaking. This is similar to the external electric field induced Rashba band splitting in the surface state of system. The 1D edge states of a FeSeTe/STO ribbon with FM edge shown in Fig. 3(b) were calculated using the Wannier functions. The valence and conduction bands is not connecting with a pair of gapless Dirac edge states in interior illustration to guide eyes, which could be seen in Fig. 3(b).
Subsequently, we considered Te atom substituting Se atom on the top layer of FeSe (denoted as FeSeTe/STO, as indicated in Supplementary Fig. 1(b)). The vertical distance between O and Se atoms is 3.217 Å, which is the less than that between O and Te atoms in FeSeTe/STO by 0.111 Å. The bond length between top (bottom) Te (Se) atoms and the Fe atom is 2.53 (2.36) Å. The Fe-Te(Se)-Fe angle for top Te and (bottom Se) atoms is 97.92° (107.66°). The calculated magnetic moment is 2.24 μB on each Fe atom which is almost same as 2.23 μB in FeSeTe/STO interface system.
Comparing the bands of FeSeTe/STO interfacial system in Fig. 3(a,c), we can realize an obvious characteristic that electron pockets at the M point and no hole pocket at the Γ point seen from Fig. 3(c) for FeSeTe/STO interfacial system, which is similar to FeSe/STO interfacial system (Fig. 1(c)). Bands at Γ point have lower energy with increased dz2 orbital, except Rashba band splitting in the surface state of system. The 1D edge states FeSeTe/STO ribbon with FM edge were also calculated using the Wannier functions. The original Dirac point opens a tiny gap appeared in Fig. 3(d) for FeSeTe/STO ribbon. The interior enlarged view could confirm that. Supplementary Fig. 2 shows the edge states of free standing FeSe with Te atom substituting Se atom in top layer, exhibiting 1D Dirac edge state inside the “bulk” band gap. This verifies that the 1D Dirac edge states are originated in the 1UC FeSe with Te substituting and the interaction between SrTiO3 substrate and FeSeTe monolayer induces original Dirac point opening a tiny gap.
Next we focused on the effect of Te substitution concentration (variation of x) on the band details. In our calculation, we assumed that Te atoms substitute Se atoms (on both top and bottom layers) with 0.25%, 50%, 50% and 75% concentration in single-layer FeSe of 2 × 2 × 1 supercell as shown in Fig. 4(a,c,e,g), respectively. Among these four atomic configurations, Fig. 4(c,e) are with same substitution concentration but with different atomic configurations. Figure 4(b,d,f,h) present the 1D band structure for Fig. 4(a,c,e,g), respectively. Figure 4(b) shows the edge states of FeSe0.75Te0.25/STO, exhibiting 1D Dirac edge state inside the “bulk” band gap, while others do not show the Dirac edge states. Figure 4(d) indicates the original Dirac point opens a tiny gap, which is in interior illustration to guide eyes. Our calculations confirm that Te atomic substitution more than 50% will lead to the disappearing of the original Dirac point due to the local structure change induced spin-up and spin-down channels coupling from each other.
(a) 2 × 2 × 1 supercell of FeSe0.75Te0.25/SrTiO3 film and (b) 1D band structure for a; (c) 2 × 2 × 1 supercell of FeSe0.50Te0.50/SrTiO3 film and (d) 1D band structure for c; (e) 2 × 2 × 1 supercell of FeSe0.50Te0.50/SrTiO3 film and (f) 1D band structure for e; (g) 2 × 2 × 1 supercell of FeSe0.25Te0.75/SrTiO3 film and (h) 1D band structure for g.
Experimental and theoretical analysis reveal there are two key effects dominant the properties of the system. The first is the Rashba effect introduced by internal electrical field with interfacial charge transfer when the films are grown on the substrate21,28,29. The second is the strain effect on the thin film. The thin film can form a perfect coherent interface with the substrate21,28,29 so that strain plays an important role in affecting the topological band states in addition to internal electrical field effect29. While generally they may be considered as negative factors, we may also work them to our advantage. In fact, strain and interfacial engineering have already become a common strategy to modulate the properties of thin films30. It is anticipated that introducing tensile biaxial strain will tune the helical Dirac points existing in the gap of bulk bands. As shown in Fig. 5(a), the two bands below the Fermi level between X′- Γ are nearly cross with the increasing tensile biaxial strain in FeSeTe/STO ribbon while the strain is under 1.8% (lattice constant a = 3.972 Å). When the strain increases to 3% (with lattice constant a = 4.018 Å), e.g. the bond length between Te (Se) atoms and the Fe atom is 2.57 (2.40) Å and the Fe-Te(Se)-Fe angle is 102.90° (113.41°). The interfacial distance decreases to 2.943 Å with an increased interface energy of 0.05 eV. The decreased interfacial distance and the increased interface energy enhance the interfacial coupling. In particular, stress-induced displacive phase transformation could be found while the thin film is under a strain of 3%, where the bottom Te atom in single-layer FeSe is directly above the top Ti atom in the STO substrate (see Fig. 3(a) in Supplementary). Band structures long M- Γ- X- M- X′- Γ directions under 3% strain show that electron pockets along X- M line and no hole pocket at the Γ point (see Fig. 4(a) in Supplementary). 1D Dirac edge states of FeSeTe/STO ribbon occurs under this strain as presented in Fig. 5(b). More importantly, under a strain of 5% (lattice constant a = 4.096 Å), two Dirac edge points could formed in 1D band structure of 1UC FeSeTe/STO film as shown in Fig. 5(c). The position of VBM and CBM connect between X′- Γ, forming a spin-polarized Dirac point inside the “bulk” band gap. Therefore, the topological Dirac states and their peculiar properties could be accessed by quantum control. We would emphasize that the increase of interfacial coupling induces Dirac states. Te substituting Se breaks the symmetry of system. The position where the band gap closes in the Brillouin zone depends on the symmetry of the system. In an inversion symmetric system, the gap closes at time-reversal invariant momenta, such as the Γ point, while in an inversion asymmetric system the gap vanishes at other points instead of at time-reversal invariant momenta. Similarly, stress-induced displacive phase transformation of FeSeTe/STO film is also found under a strain of 3% (see from Fig. 3(b) in Supplementary), where the bond length between Te (Se) atoms and the Fe atom is 2.58 (2.40) Å and the Fe-Te(Se)-Fe angle is 102.46° (113.98°). The interfacial distance decreases to 2.866 Å with an increased interface energy of 0.24 eV. Band structures (Supplementary Fig. 4(b)) long M- Γ- X- M- X′- Γ directions under 3% strain show that electron pockets along X- M line and hole pocket at the M point. For the strained FeSeTe/STO ribbon, their corresponding band structures are shown in Fig. 5(d–f) under a strain of 1.8%, 3% and 5%, respectively. The 1D edge states appear as the strain 1.8% case, except for the relative shape change. But there is no Dirac edge state within the band gap (see Fig. 5(a)) under same strain for FeSeTe/STO ribbon. Therefore, the FeSeTe/STO ribbon remains 1D Dirac edge states under less strain conditions, even up to 5% strain. The atomic structure changing under the strain results in the different shape of the edge states as shown in Fig. 5.
1D band structure for 1UC FeSeTe/STO film (a) under 1.8% strain with a = 3.972 Å, (b) under 3% strain with a = 4.018 Å, (c) under 5% strain with a = 4.096 Å. 1D band structure for 1UC FeSeTe/STO film (d) under 1.8% strain with a = 3.972 Å, (e) under 3% strain with a = 4.018 Å, (f) under 5% strain with a = 4.096 Å.
The time-reversal symmetry is preserved in the conventional QSH state while it is broken in the AFM system. However, AFM QSH state is presented if spin-up and spin-down channels are decoupled from each other. 3D AFM topological insulators31,32 has been studied under the combined symmetry of time-reversal and primitive-lattice-translation. On the basis of the Bernevig_Hughes_Zhang model with an AFM stagger potential, the edge states in the AFM QSH state are still robust against non-magnetic disorder33 though the non-magnetic disorder can break this combined symmetry. Berry Curvature and Chern number are the key factors to determine whether the gap induced by SOC is topological nontrivial. The Berry curvature Ω (k) is calculated by the equation34,35
where fn is the Fermi distribution, ψnk is the eigenstate of eigenvalue \({\varepsilon }_{n^{\prime} k}\) of band n, \({\nu }_{{\boldsymbol{x}}}/{\nu }_{{\boldsymbol{y}}}\) is the velocity operator. We use the WANNIER90 package to calculate the Berry curvature for the whole valence bands along the high-symmetry directions. The calculated spin Berry curvature for the Fermi level within the SOC gap is non-zero around four M points in reciprocal-space as can be seen from Fig. 6(a) for 1UC FeSeTe/STO film under 3% strain with a = 4.018 Å. The Chern number (C) is expressed as
Where Cs is spin Chern number and it is expressed as
(a) Spin Berry curvature within the SOC gap in reciprocal-space. (b) Spin Hall conductance as a function of the Fermi level within SOC gap. Differential charge density (c) corresponding 1UC FeSe/SrTiO3 film (d) corresponding 1UC FeSeTe/SrTiO3 film, (e) corresponding 1UC FeSeTe/SrTiO3 film. (f) Corresponding 1UC FeSeTe/SrTiO3 film with 1.8% strain. The charge density isosurface is set to be 0.0005 e/Å3.
By integrating the Berry curvatures over the first Brillouin zone (BZ), we can gain the spin Chern number with −1 and then the spin Hall conductance can be obtained from the spin Chern number as
Correspondingly, an AFM QSH state is confirmed with quantized value of spin Hall conductance within the energy range of the SOC gap in Fig. 6(b). In a FeSe/Te monolayer grown on STO substrate, the spatial inversion symmetry is indeed already broken, but the topological edge state still exists because of the finite coupling between the monolayer and the substrate where spin-up and spin-down channels are decoupled from each other. When Te replaces the bottom or top Se atoms in 1UC FeSe this disorder changes the electric potential and decreases the spin degeneracy of the AFM state, hence increases the gap of spin-split band, leading to the open of Driac edge state. Tensile strain will destroy coupling between spin-up and spin-down channels. When spin-up and spin-down channels are decoupled from each other again under large tensile strain, the Driac edge states present again.
It was found that the QSH state characterized by nonzero spin Chern numbers ±1 persists when the time reversal symmetry is broken with exchange field36. The quantum spin Hall phase could exist until the exchange field strength reaches a critical value. When the bulk band gap closes and then opens, the system enters the quantum anomalous Hall phase37 characterized by 1 (or −1). The non-trivial spin Chern number requires the existence of an edge state at the sample boundary without considering any symmetry36. Spin Chen Number is an effective tool to characterize the different topological phases of quantum spin Hall system without time inversion symmetry.
Although the superconducting properties of 1UC FeSe/STO films originate in the 1UC FeSe film without Te or with Te substituting, the STO substrate provides possibly a triggering mechanism that induces the superconducting states in the systems. When the FeSe film is attached on SrTiO3 substrate, local tension exists at the interface of heterojunction materials, which leads to charge transfer. This leads to a Rashba effect that is resulted from the internal electrical field which is introduced by interfacial charge transfer when they are grew on the STO substrate. The differential charge density at the interface is defined as ρ = ρFeSe/STO − ρFeSe − ρSTO, where, ρFeSe/STO, ρFeSe, and ρSTO are the charge density of FeSe/STO respectively, and FeSe and STO are at the same surface lattice constant. The differential charge density at the interface of FeSe/STO film is presented in Fig. 6(c). Our Bader analysis identifies a charge transfer of 10−3 e per cell from STO substrate to FeSe film. In practice, the actual charge transfer is larger because defects in substrate results in additional charge transfer. The differential charge density at the interface of two mentioned systems FeSeTe/STO and FeSeTe/STO are presented in Fig. 6(d–f). It confirms that Te atoms have less ability to acquire electrons in comparison with Se atoms, resulting in a decreased electron-phonon coupling. This might be one of the reasons that 1UC FeSe/STO film exhibits a superconducting state, while 1UC FeTe/STO doesn’t. Figure 6(f) also shows that FeSeTe monolayer has a different charge density due to more electrons transfer from Fe atoms to Se and Te under 1.8% strain. This is confirmed in our Bader analysis showing a charge transfer of 0.03 e from Fe atom to Se and Te atoms. This charge transfer generates an internal electric field at the interface region. The electric field leads to bands along M-X and M-X′ directions with an obvious band splitting around M point. The amplitude of this splitting is enhanced in FeSeTe/STO and FeSeTe /STO films than that in FeSe/STO. In order to further verify the charge transfer and dipole effect of SrTiO3 substrate, we also calculated electronic structure for a free-standing monolayer FeSeTe (see Fig. 5 in Supplementary). Our calculation clearly reveals that the splitting of energy bands decreases along M-X and M - X′ directions without the presence of electric field.
The strain-induced different Rashba states, that originate from their different response to strain, can be understood from deformation potential theory38,39. The surface state is presented by defining the surface deformation potential40
where EF and ε represent the Fermi energy and the applied strain, respectively. As Fermi energies of different strained systems are different, the deformation potential of the band in FeSeTe/STO system is smaller than that in FeSeTe/STO system. This indicates that the 1D band of the FeSeTe/STO system is more sensitive to strain than that in FeSeTe/STO system. Therefore, FeSeTe/STO system is more superior and more practical than FeSeTe/STO system to tune the quantum phase with a spin-polarized Dirac edge states inside the band gap under tensile strain. This indicates that the bonding angle of Se-Fe-Se (Te) and the distance of Te or Se atoms away from the Fe plane are correlated with the topological edge states.
In conclusion, we have studied the electronic properties of high-temperature superconductiving FeSe/SrTiO3 films without and with Te substitution by first-principles theory. Our calculations show that, although the bands are changed by interface electronic field, the 1D topological edge states appear within the gap without Te substitution. Interfacial Se atom layer is beneficial to form the1D topological edge states. Te substitution to Se atoms larger than 50% in both top and bottom layers in single-layer FeSe will lead to absence of original Dirac point. Stress-induced displacive phase transformation occurs in FeSe/SrTiO3 films with Te substitution under 3% strain. For the case of Te submitting the Se atom on the bottom layer of FeSe, the films on SrTiO3 exhibit no 1D topological edge states with a strain less than 3%. For the case of Te submitting the Se atom on the top layer of FeSe, the films on SrTiO3 exhibit 1D topological edge states under a strain of 1.8–5%. Since the 1D topological edge states of FeSeTe/SrTiO3 film are more sensitive to strain than that of FeSeTe /SrTiO3 film, we propose that Se atom layer should be used as a more practical interfacial atom layer on STO than Te atom layer. We also found that the bonding angle of Se-Fe-Se (Te) and the distance of Te or Se atoms away from the Fe plane are correlated with the topological edge states. These results provide an effective interface system that supports both superconducting and topological states, shedding light on realizing 2D topological superconductors on oxide substrate.
References
Wang, Q. et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 29, 037402 (2012).
Ge, J. et al. Superconductivity above 100 K in singlelayer FeSe films on doped SrTiO3. Nat. Mater. 13, 4153 (2014).
Liu, D. et al. Electronic origin of high-temperature superconductivity in single-layer FeSe superconductor. Nat. Commun. 3, 931 (2012).
He, S. et al. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nat. Mater. 12, 605 (2013).
Tan, S. et al. Interface-induced superconductivity and strain-dependent spin density wave in FeSe/SrTiO3 thin films. Nat. Mater. 12, 634 (2013).
Zhang, W. et al. Direct observation of high temperature superconductivity in one-unit-cell FeSe films. Chin. Phys. Lett. 31, 017401 (2014).
Zhang, W. et al. Interfacial charge doping effect on superconductivity of single unit-cell FeSe films on SrTiO3 substrates. Phys. Rev. B 89, 060506(R) (2014).
Lee, J. et al. Interfacial mode coupling as the origin of the enhancement of Tc in FeSe films on SrTiO3. Nature 515, 245 (2014).
Liu, K., Lu, Z. & Xiang, T. Atomic and electronic structures of FeSe monolayer and bilayer thin films on SrTiO3(001):Firstprinciples study. Phys. Rev. B 85, 235123 (2012).
Xiang, Y., Wang, F., Wang, D., Wang, Q. & Lee, D. High-temperature superconductivity at the FeSe/SrTiO3 interface. Phys. Rev. B 86, 134508 (2012).
Hao, N. & Hu, J. Topological phases in the single-layer FeSe. Phys. Rev. X 4, 031053 (2014).
Wang, Z. et al. Topological nature of the FeSe0.5Te0.5 superconductor. Phys. Rev. B 92, 115119 (2015).
Hao, N. & Shen, S. Topological superconducting states in monolayer FeSe/SrTiO3. Phys. Rev. B 92, 165104 (2015).
Wang, Z. et al. Topological edge states in a high-temperature superconductor FeSe/SrTiO3(001) film. Nature Materials 15, 9684 (2016).
Wu, M., Wang, M. & Yeh, K. Recent advances in β-FeSe1−x and related superconductors. Sci. Technol. Adv. Mater. 14, 014402 (2013).
Hanaguri, T., Niitaka, S., Kuroki, K. & Takagi, H. Unconventional s-wave superconductivity in Fe(Se,Te). Science 328, 474 (2010).
Li, F. et al. Interface-enhanced high-temperature superconductivity in single-unit-cell FeTe1−xSex films on SrTiO3. Physical Review B 91, 220503(R) (2015).
Chen, L., Yu, D. & Liu, F. Magnetism in nanopatterned graphite film. Appl. Phys. Lett. 93, 223106 (2008).
Chen, L. et al. Atomic chemisorption on graphene with Stone–Thrower–Wales defects. Carbon 49, 3356 (2011).
Wang, Z., Chen, L. & Liu, F. Tuning Topological Edge States of Bi(111) Bilayer Film by Edge Adsorption. Nano Lett. 14, 2879 (2014).
Chen, L., Wang, Z. & Liu, F. Robustness of two-dimensional topological insulator states in bilayer bismuth against strain and electrical field. Phys.Rev. B 87, 235420 (2013).
Zheng, F., Wang, Z., Kang, W. & Zhang, P. Antiferromagnetic FeSe monolayer on SrTiO3: the charge doping and electric field effects. Sci. Rep. 3, 2213 (2013).
Mostofi, A. et al. Wannier90: A Tool for Obtaining Maximally-Localised Wannier Functions. Comput. Phys. Commun. 178, 685 (2008).
Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 27, 1787 (2006).
Mostofi, A. A. et al. Wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Wang, Z. F., Liu, Z. & Liu, F. Organic topological insulators in organometallic lattices. Nature Commun. 4, 1471 (2013).
Wang, Z. F., Chen, L. & Liu, F. Tuning topological edge states of Bi (111) bilayer film by edge adsorption. Nano Lett. 14, 2879 (2014).
Hirahara, T. et al. Atomic and electronic structure of ultrathin Bi (111) films grown on Bi2Te3 (111) substractes: evidence for a strain-induced topological transition. Phys. Rev. Lett. 109, 227401 (2012).
Wang, Z. F. et al. Creation of helical Dirac fermions by interfacing two gapped systems of ordinary fermions. Nat. Commun. 4, 1384 (2013).
Chen, L., Zhuang, Q., Chen, Y., Shi, C. & Wang, D. Quantum phase transitions in Sn bilayer based interfacial systems by an external strain. Phys.Chem.Chem.Phys. 18, 24350 (2016).
Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).
Essin, A. M. & Gurarie, V. Antiferromagnetic topological insulators in cold atomic gases. Phys. Rev. B 85, 195116 (2012).
Guo, H., Feng, S. & Shen, S.-Q. Quantum spin Hall e_ect induced by nonmagnetic and magnetic staggered potentials. Phys. Rev. B 83, 045114 (2011).
Yao, Y. G. et al. First Principles Calculation of Anomalous Hall Conductivity in Ferromagnetic bcc Fe. Phys. Rev. Lett. 92, 037204 (2004).
Yao, Y. G. & Fang, Z. Sign Changes of Intrinsic Spin Hall Effect in Semiconductors and Simple Metals: First-Principles Calculations. Phys. Rev. Lett. 95, 156601 (2005).
Yang, Y. et al. Time-Reversal-Symmetry-Broken Quantum Spin Hall Effect. Phys. Rev. Lett. 107, 066602 (2011).
Haldane, F. D. M. Model for a Quantum Hall Eff’ect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 61, 2015 (1988).
Herring, C. & Vogt, E. Transport and Deformation-Potential Theory for Many-Valley Semiconductors with Anisotropic Scattering. Phys. Rev. 101, 944 (1956).
Hu, H. et al. Quantum Electronic Stress: Density-Functional-Theory Formulation and Physical Manifestation. Phys. Rev. Lett. 109, 055501 (2012).
Zhou, M. et al. Two-dimensional time-reversal-invariant topological superconductivity in a doped quantum spin-Hall insulator. Phys. Rev. Lett. 111, 246801 (2013).
Acknowledgements
We thank financial support from the National Natural Science Foundation of China (Grant Nos 1(Grants 11634007, 51431004 and 197309). We also thank the Linyi University for providing the computing resources.
Author information
Authors and Affiliations
Contributions
L.C. conceived the study, performed the D.F.T. calculations and wrote the manuscript, H.L. provided the valuable advice, C.J. revised the manuscript, C.S., D.W., G.C., X.L. provided the valuable discussion, Q. Zhuang revised manuscript. All authors approved the final manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, L., Liu, H., Jiang, C. et al. Topological edge states in high-temperature superconductiving FeSe/SrTiO3 films with Te substitution. Sci Rep 9, 4154 (2019). https://doi.org/10.1038/s41598-019-40644-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-40644-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.