Abstract
A stable BiI3 monosheet has been grown for the first time on the (0001) surface of the topological insulator Bi2Se3 as confirmed by scanning tunnelling microscopy, surface X-ray diffraction, and X-ray photoemision spectroscopy. BiI3 is deposited by molecular beam epitaxy from the crystalline BiTeI precursor that undergoes decomposition sublimation. The key fragment of the bulk BiI3 structure, \({{\rm{a}}}_{\infty }^{2}\)[I—Bi—I] layer of edge-sharing BiI6 octahedra, is preserved in the ultra-thin film limit, but exhibits large atomic relaxations. The stacking sequence of the trilayers and alternations of the Bi—I distances in the monosheet are the same as in the bulk BiI3 structure. Momentum resolved photoemission spectroscopy indicates a direct band gap of 1.2 eV. The Dirac surface state is completely destroyed and a new flat band appears in the band gap of the BiI3 film that could be interpreted as an interface state.
Similar content being viewed by others
Introduction
Two-dimensional (2D) metal halides have been of interest since a long time for their intriguing and tunable properties. Bulk BiI3 has been studied intensely as a material for nuclear radiation detection applications and its photovoltaic properties1,2.
The periodic structure of BiI3 belongs to the inversion symmetric space group \(R\bar{3}\) (no. 148) and consists of \({{\rm{a}}}_{{\rm{\infty }}}^{2}\)[I—Bi—I] trilayers (TL’s) which are stacked in a rhombohedral ABC sequence3. Bulk BiI3 is an indirect band gap semiconductor with a gap width of 1.67 eV1 which is favorable for potential energy harvesting4. Owing to the presence of a high-Z element (Bi) spin-orbit coupling (SOC) is significant and new functionalities are expected by reducing the crystal’s dimensionality to the ultra-thin film limit which might involve a symmetry lowering, for instance by the loss of the inversion center induced by atomic relaxations.
Up to now, only theoretical studies on BiI3 monosheets have been carried out which have predicted its stability and the possibility to tune the band structure by strain4,5. However, no experimental investigation concerning structure and physical properties of BiI3 monosheets are available. One standard way to prepare a thin film of a layered material is cleaving the bulk crystal which in the case of BiI3 consists of weakly van-der-Waals (vdW) connected sheets. Its disadvantage is that this method neither allows precise control of the film thickness nor the preparation of a single monosheet. Furthermore, handling of bulk BiI3 is hindered due to its notable moisture-sensitivity.
Here we establish a different approach by depositing a monosheet of BiI3 on the (0001) surface of the topological insulator (TI) Bi2Se3 by using molecular beam epitaxy (MBE) from a Knudsen cell filled with presynthesized BiTeI single crystals heated to 380 °C. As a result, a stoichiometrically almost exact BiI3 film is deposited by decomposition sublimation of BiTeI, as corroborated by X-ray photoemission spectroscopy (XPS), scanning tunnelling microscopy (STM) and surface X-ray diffraction (SXRD). In addition, momentum resolved photoemission spectroscopy6 demonstrates the instability of the Dirac topological surface state (TSS) of the Bi2Se3 substrate upon BiI3 deposition and the appearance of flat band interface states in the direct band gap of BiI3.
Results
Deposition of BiI3 on Bi2Se3(0001)
Experiments were carried out in-situ in ultra-high-vacuum systems equipped with standard surface physics analytical tools.
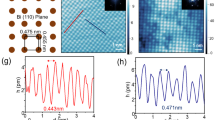
Figure 1(a) shows the BiTeI single crystal which was grown by chemical vapor transport (CVT) (see methods). BiI3 was MBE-deposited onto the substrate that was kept at room temperature. The underlying mechanism can be rationalized by decomposition sublimation of BiTeI7,8,9: \(3\,{\rm{BiTeI}}({\rm{s}})\rightleftharpoons {{\rm{Bi}}}_{2}{{\rm{Te}}}_{3}({\rm{s}})+{{\rm{BiI}}}_{3}({\rm{g}})\) . It is well established that solid BiTeI congruently melts at 555 °C and its volatilization commences above approximately 300 °C primarily by an incongruent decomposition into solid Bi2Te3 and gaseous BiI37,8. This is a typical behavior of chalcogenide halides9. The remaining Bi2Te3 may decompose further, forming subsidiary BiTe and Te2 gas species: \(\frac{2}{5}\,{{\rm{Bi}}}_{2}{{\rm{Te}}}_{3}({\rm{s}})\rightleftharpoons \frac{4}{5}\,{\rm{BiTe}}({\rm{g}})+\frac{1}{5}\,{{\rm{Te}}}_{2}({\rm{g}})\).
Vapor transport of both BiTeI and Bi2Te3 can proceed as an alternative reaction with these species:
However, the partial pressures of BiI(g) and Te2(g) increase sufficiently only above 410 °C and can then promote efficient vapor transport7. At our working temperatures, the total pressure is largely dominated by BiI3 gas species for a broad range of compositions in the ternary Bi-Te-I phase diagram10.
Formation of a BiI3 film on the Bi2Se3 substrate was observed via appearance of new LEED spots that closely corresponded to a √3 × √3-R30° superstructure, as shown in Fig. 1(b), in which the substrate and the adlayer spots are highlighted by the large and small hexagon, respectively. Epitaxial growth of BiI3 on Bi2Se3 is feasible thanks to a close structural match between the bulk structures. Both crystal structures can be viewed as hexagonal close-packed arrangements of anions (either iodine or selenium) with cations (bismuth) occupying the octahedral voids in a regular fashion. In the tetradymite-type structure, like Bi2Se3, two consecutive rows of octahedral voids along the c axis are fully populated and each third row remains empty, thus forming a van der Waals (vdW) gap between the quintuple layers (QL), \({{\rm{a}}}_{{\rm{\infty }}}^{2}\)[Se–Bi–Se–Bi–Se]. The latter are stacked in the ABC-sequence11,12. In BiI3, 2/3 of the octahedral sites within each second row of cations along the stacking direction are occupied. In the case of ideally matching lattices, BiI3 would exhibit a √3 × √3-R30° superstructure in the ab-plane with respect to the Bi2Se3 (0001) − (1 × 1) surface unit cell. But the existing difference in the van der Waals radii (Se: 1.82 Å vs. I: 2.04 Å) constitutes a mismatch between the anionic lattices, that becomes evident from the comparison of the respective unit cell parameters a: whereas a(Bi2Se3) = 4.134(2) Å13, a(BiI3) = 7.5249(3) Å3 is about 0.3 Å larger than a(Bi2Se3)√3. The detailed SXRD analysis of the deposited BiI3 indicates that the first order spot is located at h = k = 0.316 units of the hexagonal Bi2Se3 reciprocal surface lattice, rather than at \(h=k=\frac{1}{3}\) for the ideal √3 × √3-R30° superstructure. Hence, the BiI3 film is incommensurate with the substrate just like in the bulk case. Moreover, the mismatch is even stronger in the film, since the adlayer has an in-plane lattice parameter of a0 = 7.56 Å as compared to the reported range of bulk values which lie between a0 = 7.5249 Å and 7.50 Å3,14,15. We note that the lateral strain is only +0.8% at most and is thus well below the computed breaking strain of 13% for a free standing monosheet5.
Figure 2(a) shows a 500 × 500 nm2 STM image (U = −2 V, I = 50 pA) of a single-layer BiI3 film. The profile along the white line (labelled by “1”) is plotted in (b). The surface of the Bi2Se3 single crystal is characterized by 9.5 Å high steps which correspond to a full QL. The BiI3 monosheet has about 7 Å high steps corresponding to 1/3 of the bulk c0 lattice parameter of 20.72 Å related to three triple layers (TL)3,14. The wetting of the Bi2Se3 terraces proceeds from the step edges, leaving 3 Å high steps between the BiI3 layer and the next terrace.
Surface X-ray diffraction
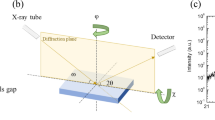
The atomic structure of the deposited film was analyzed by SXRD experiments which were carried out at the beamline SpLine BM25b of the European Synchrotron Radiation Facility in Grenoble (France) using a UHV six-circle diffractometer equipped with a two-dimensional pixel detector. During BiI3 deposition, the first-order (h = k = 0.316) reflection intensity was monitored until saturation. Subsequently, reflection intensities along several lattice rods were collected under grazing incidence (αi = 2°) of the incoming beam. In total 1042 symmetry independent reflections were collected along six lattice rods which are shown as symbols in Fig. 3. The intensities were fitted using the program “Prometheus”16 that enables refinement of anisotropic and anharmonic displacement parameters17 and crystal twinning. The latter is especially relevant in the present case owing to the two possible orientations of the adsorbate lattice relative to the substrate lattice, that forge the 6 mm point symmetry of the experimental diffraction pattern. In the plane group p3, bismuth atoms occupy the Wyckoff positions 1a, 1b, 1c, while iodine atoms reside in the general position 3d. Note that the plane group p3 lacks inversion symmetry in contrast to the space group \(R\bar{3}\) of the bulk structure and in contrast to the \(p\bar{3}\) plane group of individual BiI3 layers in the periodic structure3. The refined atomic coordinates and the isotropic displacement parameters (B = 8π2 <u>2) for the adlayer are listed in Table 1. The best fits to the experimental data according to these parameters are shown as solid lines in Fig. 3. The fit quality is quantified by the goodness of fit (GOF) and the un-weighted residuum which is given by: \({R}_{{\rm{U}}}=\sum |{I}_{{\rm{o}}{\rm{b}}{\rm{s}}}-{I}_{{\rm{c}}{\rm{a}}{\rm{l}}{\rm{c}}}|/\sum {I}_{{\rm{o}}{\rm{b}}{\rm{s}}}\). Here, Iobs, Icalc are the experimental and calculated intensities, respectively and the summation runs over all datapoints. The GOF is given by: \({\rm{GOF}}=\sqrt{1/(N-P)\cdot \sum [({I}_{obs}-{I}_{calc}{)}^{2}/{\sigma }^{2}]}\), where the difference between observed and calculated intensities is normalized to the uncertainties expressed by the standard deviation (σ) and to (N − P), i.e. the difference between the number of independent data points (N) and the number of parameters (P) which are varied. Here, we derive GOF = 1.40 and RU = 0.14, which are very reasonable values in view of the weak intensities scattered by the monosheet.
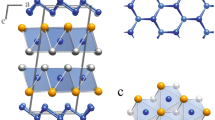
Figure 4 shows a side view of the resultant structure model of the thin film in comparison with the periodic bulk structure of BiI33. At first, the analysis shows that there is one complete TL and approximately one half of a second TL on the Bi2Se3 surface. Thus, in comparison with the STM experiments which indicated a single TL only, this sample is covered by BiI3 at its saturation coverage at 300 K. It can be concluded that the interlayer interaction is very weak which is also corroborated by the fact that desorption of the whole film sets in at about 360 K as evidenced by the rapid loss of the BiI3 reflection intensities. Correspondingly, the vertical spacing between the first and the half filled second TL is considerably enlarged as compared to the bulk. For instance, the closest interlayer I–I distance across the vdW gap increases from 4.14 Å in the bulk to 4.8 Å in the film.
Crystal structure of bulk BiI3 (left) compared to the experimentally elucidated structure model of BiI3 film on Bi2Se3(0001) (right). The film consists of a complete first TL adjacent to the Bi2Se3 (0001) surface and a second TL, which is only half filled. Iodine atoms are depicted in red, the bismuth atoms are color-coded in accordance with their shifts from the central position within the octahedra (traced by a dotted line). Atoms are numbered according to Table 1. Interplanar distances and shifts of the bismuth atoms are given in Å. We estimate the uncertainty of the distance determination equal to 0.1 Å.
The SXRD analysis also finds considerable relaxations within the TL’s. The first TL adjacent to the substrate is notably stretched as compared to its bulk counterpart, namely, the interplanar distance between the terminating iodine atoms (in other words, the height of a TL) increases from 3.61 Å (bulk) to 3.89 Å. The interatomic Bi–I distances towards the substrate (3.32–3.44 Å) are considerably longer than in the opposite direction (2.94–3.00 Å). All bismuth atoms (light and dark grey #2, 3 atoms in Fig. 4) are strongly displaced from the central position within the coordination octahedra towards the same side, namely, away from the substrate. The driving force of this movement cannot be pinpointed in a straightforward way, since the difference in electronegativity between iodine (2.66) and selenium (2.55) is not large, and both values are much higher than that for bismuth (2.02). One may tentatively assume that the I/Se interaction at the film/substrate interface -although weak- might lead to a weakening of the I–Bi bond and with it to an elongation of the corresponding bonds. Consideration of the van der Waals (Bi: 1.82 Å vs. I: 2.01 Å) and the (effective) ionic (Bi3+: 1.03 Å vs. I−: 1.70 Å) radii18,19 imposes limits of 3.86 Å and 2.73 Å for the Bi–I interatomic distance for atomic and ionic bonds, respectively. The distances derived from the SXRD analysis suggest a considerable ionicity of the Bi–I bond.
The second TL, which is only about half filled has a height of 3.57 Å which is much closer to the respective bulk value. The crystal structure of bulk BiI3 shows two distinct sets of Bi–I interatomic distances alternating in the first coordination polyhedron of each bismuth atom, i.e. 3.054 Å and 3.125 Å3. Such distortions ensure the highest density of TL packing3. Furthermore, the lone-pair effect on bismuth manifests itself in symmetrical shifts of adjacent Bi atoms in the opposite directions from the ideal site in the middle of the octahedral iodine environment (see Fig. 4). The same effects but with a larger magnitude are observed in the second TL. For instance, the Bi # 7 atom shifts by 0.4 Å from the middle position within an octahedron, and variations in the alternating longer and shorter interatomic Bi–I distances reach 0.5 Å. In general, the second TL of the BiI3 film demonstrates a bonding pattern characteristic for the bulk structure. One may argue that the formation of the bulk structure already commences as the second TL grows atop of the first TL, and that with it the accompanying bulk effects associated with the optimum packing emerge. The weak interlayer interaction nevertheless defines the mutual arrangement of the TL’s and their distortions, just like in the periodic crystal structure.
Photoemission Spectroscopy
Owing to their very similar atomic number, X-ray diffraction is not capable to separate the atomic species iodine (Z = 53) and tellurium (Z = 52). X-ray photoemission spectroscopy was used to analyze the chemical composition of the film. All photoemission spectroscopy experiments were carried out at the NanoESCA beamline20 of the Elettra Synchrotron in Trieste (Italy). After film deposition at room temperature until saturation as in the case of the SXRD experiments the sample was kept at 130 K using s-polarized light and a photon energy of hν = 200 eV. Figure 5 compares two XPS spectra collected for the pristine and the BiI3 saturated Bi2Se3 (0001) surface. In the case of the pristine sample, the spin-orbit split Bi-5d (experimental binding energy EB = 25.0 and 28.0 eV for 5d5/2 and 5d3/2, respectively) and the Se-3d (EB = 53.5 and 54.3 eV for 3d5/2 and 3d3/2, respectively) are observed.
Comparison of X-ray photoemission spectra collected for pristine and BiI3-covered Bi2Se3 (0001) collected at a photon energy of hν = 200 eV. The photoemission intensities are plotted on a log-scale and are shifted for clarity. Solid areas below the core level photoemission peaks indicate the fitted line shapes. Note the very low Te-4d emission indicating the presence of almost pure BiI3. The spin-orbit split Bi-5d lines exhibit a chemical shift of about 0.6 eV related to different Bi environments.
After film deposition in addition the 4d lines of iodine (EB = 49.0 [4d5/2] and 50.8 eV [4d3/2]) and tellurium (EB = 40.1 [4d5/2] and 41.6 eV [4d3/2]) appear. For a quantitative evaluation, the core level peaks were fitted using Voigt line shapes, taking into account the natural line width and the instrumental resolution, on top of a Shirley background. The fitted peak areas were subsequently corrected on the basis of tabulated photoionization cross sections and by a polarization factor for the photon energy of hν = 200 eV used for the XPS measurement21. This results in the normalized intensities of I(Se-3d3/2) = 1, I(I-4d3/2) = 2.2, I(Te-4d3/2) = 0.07, and I(Bi-5d3/2) = 2.3. Thus, the tellurium contribution in the film equals to only about 3% of that of the iodine contribution, indicating that the film is almost pure BiI3. In particular, the tellurium concentration is far away from that in stoichiometric BiTeI, for which the tellurium and iodine 4d signals are expected to be very similar.
Finally, the Bi-5d lines consist of totally three components, exhibiting a chemical shift due to a different bismuth environment in the film and in the substrate. The two most pronounced components are attributed to Bi in the Bi2Se3 substrate (\({{\rm{E}}}_{B}^{3/2}\) = 28.0 eV and \({{\rm{E}}}_{B}^{\mathrm{5/2}}\) = 24.9 eV) and Bi atoms in the BiI3 film (\({{\rm{E}}}_{B}^{\mathrm{3/2}}\) = 28.7 eV and \({{\rm{E}}}_{B}^{\mathrm{5/2}}\) = 25.7 eV). In addition, a third component can be identified at lower binding energy (\({{\rm{E}}}_{B}^{\mathrm{3/2}}\) = 27.16 eV and \({{\rm{E}}}_{B}^{\mathrm{5/2}}\) = 24.1 eV), leading to a small shoulder of the Bi-5d line. The total contribution of this bismuth component in the spectrum is in the order of 9% of the Bi spectral weight. The binding energy of the shoulder shifts towards metallic Bi22. Thus, we attribute this component to a small contribution of Bi atoms in a sub-stoichiometric environment such as e.g. in BixTe phase.
Figures 6(a,b) compare the band dispersion along the \(\bar{M}\)-\(\bar{{\rm{\Gamma }}}\)-\(\bar{K}\) high-symmetry direction of pristine and BiI3-saturated Bi2Se3 (0001), respectively. The latter corresponds to a complete BiI3 triple layer plus a second one which covers about a half of the surface area as found in the SXRD analysis. For pristine Bi2Se3(0001), the nearly linearly dispersive Dirac topological surface state (TSS) is clearly observed. Owing to the selenium vacancy induced n-doping, the Dirac point (DP) lies approximately 400 meV below the Fermi energy (EF).
Band structure of pristine Bi2Se3(0001) (a) and BiI3 with saturation (b) coverage (about 1.5 monosheets) on Bi2Se3 measured along the \(\bar{M}\)-\(\bar{{\rm{\Gamma }}}\)-\(\bar{K}\) direction. Spectra were collected at 130 K sample temperature at a photon energy of hν = 40 eV and p-polarized light of the incoming beam. Calculated band structure for a free standing two (2TL) and single TL (1TL) thick film is shown in (c) and (d), respectively. The arrow emphasizes the difference in the band structure decisive for the presence of the indirect band gap. (e) Measured photoemission momentum map of pristine Bi2Se3(0001) and at full coverage of BiI3 on Bi2Se3 (f) at EF = -1.8 eV. Note that, for a clear visualization of the band dispersion, the normalized intensity plot is presented in (b) and (f). The dashed white line in (e) and (f) indicates the substrate surface Brillouin zone.
Upon BiI3 adsorption, strong modifications of the band structure are observed. Fist of all, the TSS as such is destroyed and a new almost dispersion-less band appears at a binding energy (EB) of approximately −1.2 eV below EF. In the energy range between E = EF and E = −0.7 eV two states at \(\bar{{\rm{\Gamma }}}\) are observed which might be attributed to the conduction band (CB) of BiI3. For comparison Fig. 6(c) shows the calculated band structure for a 2TL thick BiI3 film including the atomic relaxations derived by the SXRD experiments. Our SXRD data suggest that the saturation film thickness is about one and a half TL’s. That is why we have chosen the calculation related to the two TL thick film for direct comparison with experiment.
The calculation for the free-standing 2TL film cannot reproduce all the interface- formation related new features, which are the new flat band interface states as well as the modification of the TSS. The energetic position of the calculated valence band (VB) maximum is aligned at \(\bar{{\rm{\Gamma }}}\) so as to match the experiment in (b). This is emphasized by the dashed horizontal line. The VB is related to iodine states5 and is separated from the conduction band (CB) by a gap of approximately Eg = 1.2 eV, which can be considered to be direct owing to the flat band conditions in the vicinity of the \(\bar{{\rm{\Gamma }}}\) point. The CB of BiI3 can also be identified in the momentum resolved photoemission experiment, which has a considerably smaller dispersion as the calculated one for the free-standing two TL thick film. We note that the calculated band structure for a single TL film [see Fig. 6(d)] -albeit similar to the 2TL band structure- exhibits some differences such as a smaller number of bands, a somewhat smaller band gap (Eg = 1.08 eV as compared to 1.18 eV for the 2TL film) and -most importantly- an indirect gap, in good agreement with the calculations in ref.5. In the experiment there is no evidence for an indirect gap mediated by a CB state between the \(\bar{{\rm{\Gamma }}}\) and the \(\bar{K}\) point [see arrow in Fig. 6(d)], thus the experiment is in closer correspondence with the 2TL calculation as expected.
The substantial change in electronic states is also found in the two-dimensional (2D) (kx, ky) photoelectron momentum map. As an example we have chosen the energy E = −1.8 eV below EF. Figure 6(e,f) compare the 2D momentum map of the pristine Bi2Se3(0001) and the BiI3 covered Bi2Se3(0001) surface. Upon film deposition the photoemission intensity is greatly suppressed near surface BZ boundary but a new six-fold star shaped VB state appears centered at the \(\bar{{\rm{\Gamma }}}\)-point which is related to the iodine-derived VB. The sixfold instead of threefold symmetry is due to the presence of two rotational domains.
Thus, the momentum resolved photoemission experiment indicates a considerable modification of the electronic structure of both, the Bi2Se3(0001) surface and of the BiI3-film. At first view this comes as a surprise given the rather weak structural modification of the Bi2Se3(0001) surface, but recent theoretical studies have predicted the appearance of interface states even in vdW epitaxial interfaces23,24.
Conclusions
We have shown that a stabile BiI3 monosheet can be grown on the Bi2Se3(0001) surface. The geometric structure of the BiI3 film -although basically reminiscent of the bulk- is characterized by strong relaxations along the vertical direction. Similarly, the electronic structure of the film and the Bi2Se3 surface are significantly modified. The TSS of the pristine Bi2Se3(0001) surface is instable against BiI3 adsorption and a new non-dispersing interface state appears in the direct band gap (1.2 eV) of BiI3.
Methods
Sample preparation
The Bi2Se3 single crystal was cleaned by mild Ar+ ion sputtering followed by annealing up to about 500 °C leading to a clean surface and to a sharp contrasted (1 × 1) low energy electron diffraction (LEED) pattern11,12. Presynthesized BiTeI was loaded into a Knudsen cell and heated up to 380 °C. Single crystals of BiTeI were obtained by the chemical vapor transport (CVT) technique starting from a stoichiometric mixture of Bi, BiI3 and Te. A sealed quartz ampoule with the reactants was placed into a two-zone furnace with a temperature gradient for 5 days. The reactants were held at 500 °C and the hexagonal platelets of BiTeI up to 5 mm in diameter have grown (Fig. 1a), by autotransport, directly on the batch. We used the optimum temperature gradient 500/450 °C reported for the gas-phase transport of BiTeI on the basis of comprehensive phase-diagram studies7,8. The chemical purity of the product was confirmed by X-ray energy dispersive analysis and powder X-ray diffraction that yielded, respectively, a slightly Te-deficient composition and a strong preferred orientation of the powdered sample in consistence with its high crystallinity.
Surface X-ray diffraction
Surface X-ray diffraction experiments were carried out at the beamline BM25b of the European Synchrotron Radiation Facility in Grenoble (France) using a six-circle UHV diffractometer. Samples were prepared in-situ in the same way as in the LEED, STM, XPS and photoemission experiments. In total the integrated intensities of 2786 reflections were collected by performing scans along the reciprocal qz = l × c* direction in reciprocal space and collecting the reflected beam by using a two-dimensional pixel detector. The Iobs(hkl) were then multiplied by instrumental correction factors Ccorr as outlined in detail in refs.25,26 yielding the experimental structure intensities [|Fobs(hkl)|2] via: |Fobs(hkl)|2 = Iobs(hkl) × Ccorr. Subsequently, the |Fobs(hkl)|2 were averaged according to the p3 plane group symmetry of the (0001) surface leading to in total 1042 symmetry independent |Fobs(hkl)|2. The total uncertainty (1 σ) is estimated by the quadrature sum of the statistical and the systematic error as outlined e.g. in ref.27. We find the reproducibility of symmetry equivalent |Fobs(hkl)|2 is equal to 17%.
Momentum resolved photoemission
Momentum-resolved photoemission spectroscopy experiments were carried out to study the electronic states upon BiI3 deposition on pristine Bi2Se3(0001) surface. Here, p-polarized light with a photon energy of hν = 40 eV was used. The incident photon beam lies in the ky–kz plane at an angle of 25° above the surface plane. By utilizing momentum microscopy, the wide acceptance angle of photoelectrons of ±90° can be simultaneously collected over a hemispherical region in real space. This provides full access to directly probe two-dimensional (kx, ky) reciprocal-space momentum maps of the photoemission intensity throughout the entire surface Brillouin zone (SBZ). Furthermore, by scanning the binding energy EB, the complete information of three-dimensional EB(kx, ky) maps, containing band dispersion along all directions of the SBZ, can be obtained28.
First-principles calculations
First-principles simulations have been carried out using a full-potential full-relativistic Green function method within the multiple scattering theory, specially designed as for bulks and for semiinfinite systems such as surfaces and interfaces29,30. The calculations were performed within the density functional theory in a generalized gradient approximation31. The angular momentum cutoff was taken to be lmax = 3 and a Γ-centered (30 × 30 × 12) k-mesh was used.
References
Lehner, A. J. et al. Electronic structure and photovoltaic application of BiI3. Applied Physics Letters 107, 131109 (2015).
Brandt, R. E. et al. Investigation of bismuth triiodide (BiI3) for photovoltaic applications. The Journal of Physical Chemistry Letters 6, 4297–4302 PMID: 26538045 (2015).
Ruck, M. Darstellung und Kristallstruktur von fehlordnungsfreiem Bismuttriiodid. Z. Kristallogr. 210, 650 (1995).
Zhang, W.-B., Xiang, L.-J. & Li, H.-B. Theoretical perspective of energy harvesting properties of atomically thin bii3. J. Mater. Chem. A 4, 19086–19094 (2016).
Ma, F. et al. Single layer bismuth iodide: Computational exploration of structural, electrical, mechanical and optical properties. Scientific Reports 5, 1–9 (2015).
Tusche, C., Krasyuk, A. & Kirschner, J. Spin resolved bandstructure imaging with a high resolution momentum microscope. Ultramicroscopy 159, 520–529 (2015).
Oppermann, H., Petasch, U., Schmidt, P., Keller, E. & Krämer, V. On the pseudobinary systems Bi2Ch3/BiX3 and the ternary phases in these systems (Ch=S, Se, Te; X=Cl, Br, I). ii: Bismuthselenidehalides Bi2Se3/BiX3 and bismuthtelluridehalides bi2te3/bix3. Z. Naturforsch. 59b, 727 (2004).
Oppermann, H., Schmidt, M. & Schmidt, P. Autotransport oder Selbsttransport Systeme mit Gasphasentransporten unter dem eigenen Zersetzungsdruck. Z. Anorg. Allg. Chem. 631, 197 (2005).
Binnewies, M., Glaum, R., Schmidt, M. & Schmidt, P. Chemical Vapor Transport Reactions (De Gruyter, Berlin, 2012).
Zeugner, A. et al. Modular design with 2d topological-insulator building blocks: Optimized synthesis and crystal growth and crystal and electronic structures of BixTei (x = 2; 3). Chem. Mater. 29, 1321 (2017).
Roy, S. et al. Tuning the Dirac point position in Bi2Se3(0001) via surface carbon doping. Phys. Rev. Lett. 113, 116802 (2014).
Roy, S. et al. Atomic relaxations at the (0001) surface of Bi2Se3 single crystals and ultrathin films. Phys. Rev. B 90, 155456 (2014).
Gardes, B., Brun, G. & Tedenac, J. Contribution to the study of the bismuth–selenium system. Eur. J. Solid State Inorg. Chem. 26, 221 (1989).
Trotter, J. & Zobel, T. The crystal structure of SbI3 and BiI3. Zeitschrift f. Kristallographie 123, 67–72 (1966).
Devidas, T. R. et al. Pressure-induced structural changes and insulator-metal transition in layered bismuth triiodide, BiI3: a combined experimental and theoretical study. Journal of Physics: Condensed Matter 26, 275502 http://stacks.iop.org/0953-8984/26/i=27/a=275502 (2014).
Zucker, U. H., Perenthaler, E., Kuhs, W. F., Bachmann, R. & Schulz, H. PROMETHEUS. a program system for investigation of anharmonic thermal vibrations in crystals. Journal of Applied Crystallography 16, 358 (1983).
Kuhs, W. F. Generalized atomic displacements in crystallographic structure analysis. Acta Cryst. A 48, 80–98 (1992).
Shannon, R. D. & Prewitt, C. T. Effective ionic radii in oxides and fluorides. Acta Crystallographica Section B 25, 925–946, https://doi.org/10.1107/S0567740869003220 (1969).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallographica Section A 32, 751–767, https://doi.org/10.1107/S0567739476001551 (1976).
Schneider, C. et al. Expanding the view into complex material systems: From micro-arpes to nanoscale haxpes. Journal of Electron Spectroscopy and Related Phenomena 185, 330–339 (2012).
Yeh, J. J. & Lindau, I. Atomic subshell photoionization cross sections and asymmetry parameters: 1 ≤ Z ≤ 103. Atomic Data and Nuclear Data Tables 32, 1–155 (1985).
Gibson, Q. D. et al. Termination-dependent topological surface states of the natural superlattice phase Bi4Se3. Phys. Rev. B 88 (2013).
Eremeev, S. V., Tsirkin, S. S., Nechaev, I. A., Echenique, P. M. & Chulkov, E. V. New generation of two-dimensional spintronic systems realized by coupling of rashba and dirac fermions. Science Reports 5, 2517–2520 (2015).
Eremeev, S., Menshov, V., Tugushev, V. & Chulkov, E. Interface induced states at the boundary between a 3D topological insulator Bi2Se3 and a ferromagnetic insulator EuS. Journal of Magnetism and Magnetic Materials 383, 30–33 http://www.sciencedirect.com/science/article/pii/S0304885314008518. Selected papers from the sixth Moscow International Symposium on Magnetism (MISM-2014) (2015).
Vlieg, E. Integrated Intensities Using a Six-Circle Surface X-ray Diffractometer. J. Appl. Crystallogr. 30, 532–543 (1997).
Schlepütz, C. M. et al. Improved data acquisition in grazing-incidence X-ray scattering experiments using a pixel detector. Acta Cryst. Section A 61, 418–425 (2005).
Robinson, I. K. & Tweet, D. J. Surface X-ray diffraction. Reports Prog. Phys. 55, 599–651 (1992).
Suga, S. & Tusche, C. Photoelectron spectroscopy in a wide hν region from 6 eV to 8 keV with full momentum and spin resolution. Journal of Electron Spectroscopy and Related Phenomena 200, 119–142 (2015).
Lüders, M., Ernst, A., Temmerman, W. M., Szotek, Z. & Durham, P. J. Ab initio angle-resolved photoemission in multiple-scattering formulation. Journal of Physics: Condensed Matter 13, 8587–8606 (2001).
Geilhufe, M. et al. Numerical solution of the relativistic single-site scattering problem for the Coulomb and the Mathieu potential. Journal of Physics: Condensed Matter 27, 435202 (2015).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
This work is supported by the DFG through SPP 1666 (Topological Insulators) and ERANET Chemistry program. The authors thank Arthur Ernst for providing the DFT calculations of the relaxed BiI3 double-layer film. We thank F. Weiss for technical support. The authors thank the staff of the ESRF and Elettra for their help and hospitality during their visit in Grenoble and Trieste, and G. Zamborlini, M. Jugovac and V. Feyer (PGI-6) for assistance, in using the NanoESCA beamline.
Author information
Authors and Affiliations
Contributions
H.L.M. and A.P. devised the X-ray diffraction experiment, A.I. and A.Z. prepared the BiTeI crystals. H.L.M., K.M., G.C. and J.R.-Z. carried out the X-ray experiments at the ESRF. Data analysis was done by K.M. and H.L.M. The momentum microscopy and XPS experiments at Elettra were carried out by C.T., H.L.M. and Y.J.C. H.L.M., A.I. and C.T. wrote the manuscript. All authors have read and approved the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Polyakov, A., Mohseni, K., Castro, G.R. et al. A bismuth triiodide monosheet on Bi2Se3(0001). Sci Rep 9, 4052 (2019). https://doi.org/10.1038/s41598-019-40506-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-40506-9
This article is cited by
-
Solution-grown BiI/BiI3 van der Waals heterostructures for sensitive X-ray detection
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.