Abstract
Recent studies point out that there exists some rough scaling relations for dark matter and some tight connections between dark matter and baryons. However, most of the relations and tight connections can only be found in galaxies, but not in galaxy clusters. In this article, we consider a new expression that can characterize the properties of dark matter-baryon interplay for both galactic and galaxy cluster scales. By using the archival observational data of galaxies and galaxy clusters, we show that the value \({\boldsymbol{K}}{\boldsymbol{=}}{\bar{{\boldsymbol{n}}}}_{{\boldsymbol{D}}}{\bar{{\boldsymbol{n}}}}_{{\boldsymbol{B}}}{{\boldsymbol{r}}}_{{\boldsymbol{o}}}{\boldsymbol{V}}{\boldsymbol{/}}{{\boldsymbol{v}}}^{{\bf{4}}}\) is almost a constant and scale independent within the optical radius ro, where \({\bar{{\boldsymbol{n}}}}_{{\boldsymbol{D}}}\) is the average dark matter number density, \({\bar{{\boldsymbol{n}}}}_{{\boldsymbol{B}}}\) is the average baryon number density, v is the characteristic velocity and V is the interacting volume. This would be the first universal relation between dark matter and baryons on both galactic and galaxy cluster scales. We anticipate this result to be a starting point to explain the small-scale problem and the scaling relations for dark matter in galaxies. The constant K discovered may reveal some underlying global interaction between dark matter and baryons.
Similar content being viewed by others
Introduction
It is commonly believed that dark matter particles exist in galaxies and galaxy clusters. However, we know very little about the properties of dark matter. Some studies point out that there exists some rough scaling relations for dark matter. For example, the product of the central density and the characteristic scale radius of dark matter is almost a constant1,2,3. However, these relations can only apply for galaxies, but not for galaxy clusters4. Besides, based on the assumption of collisionless behavior of dark matter particles, computer simulations show that dark matter density would follow the Navarro-Frenk-White (NFW) profile5, which is usually regarded as a universal density profile for dark matter. However, this profile only gives good agreement with the data of galaxy clusters6 and some galaxies7,8, but not for dwarf galaxies9,10. Therefore, it does not have any universal relation for dark matter which is true for both galactic and galaxy cluster scales. Some suggestions have been proposed to explain the discrepancies between the results of observations and computer simulations, such as baryonic feedback from supernovae and star formation11,12, and self-interacting dark matter model13,14,15. However, it is doubtful that the baryonic matter can rigorously control the dark matter density profile in many dwarf galaxies16. Also, recent observations give stringent constraints on self-interacting cross section of dark matter such that some tension still exists between predictions and observations (for a review of this problem, see17).
On the other hand, there are some interesting relations which relate dynamical mass (or dark matter halo mass) with baryonic mass, such as the Tully-Fisher relation18,19,20, the mass-discrepancy-acceleration relation21, the central-surface-densities relation22 and the radial acceleration relation23. These relations indicate some specific connection between dark matter and baryonic matter, which reveal some forms of interplay between dark matter and baryons. Recent 21-cm radio observations indicate a stronger absorption signal than expected at cosmic dawn (the EDGES result)24, which may reveal a non-zero interaction between dark matter and baryons25. However, further studies show that the EDGES result is unlikely to be solved by a dominant component of millicharged dark matter, allowing only to consist of 1% of the total dark matter26. Some studies even show that only less than 0.4% fraction is allowed for millicharged dark matter27,28. Therefore, the millicharged dark matter model cannot play a significant role on galactic and cluster scales.
In this article, we show that there exists a universal relation between dark matter and baryons on both galactic and galaxy cluster scales. The universal relation can be described by a constant which characterizes the properties of dark matter-baryon interplay. The value of the constant is almost universal for both galactic and galaxy cluster scales. This constant may reveal some underlying global properties of dark matter-baryon interaction or self-organization, which may also be used to explain the ‘core-cusp problem’10, ‘the mass-discrepancy-acceleration relation’23 and the ‘halo-disk conspiracy problem’29.
Method
The effect of dark matter-baryon interplay inside an ‘interacting region’ would depend on the average dark matter number density \({\bar{n}}_{D}\), average baryon number density \({\bar{n}}_{B}\) and the volume of the interacting region V which depends on the optical radius ro. Since most of the galaxies are disk-dominated at ro, the enclosed interacting volume would be a disk-like thin cylinder with radius ro (see Fig. 1). Consider the following product (unit: cm−2)
where \({\bar{\rho }}_{D}={m}_{D}{\bar{n}}_{D}\), \({\bar{\rho }}_{B}={m}_{B}{\bar{n}}_{B}\), v is the characteristic velocity, mD is the dark matter mass and mB is the average mass of a baryonic particle. Here, we have assumed that all dark matter can interact with baryons. The potential interaction can be gravitational only, or including some other forms of interactions such as scattering.
The schematic diagram of the interacting region in a dwarf galaxy. The large sphere is the dark matter core halo with radius r = rs. The grey thin cylinder with base radius ro indicates the interacting volume V (the effective volume of baryonic matter in a galaxy). The small yellow and black shaded circles represent the baryonic particles and dark matter particles respectively.
The constant for galaxies
For spiral galaxies, the Tully-Fisher relation relates the total baryonic mass with velocity as \({M}_{B}=\mathrm{(47}\pm \mathrm{6)}{M}_{\odot }{{\rm{km}}}^{-{\rm{4}}}\,{{\rm{s}}}^{-{\rm{4}}}\,{v^{\prime} }^{4}\) 19, where v′ is the asymptotic circular velocity. Since most of the galactic rotation curves rise to a constant v′ quickly within ro, we assume that the value of v′ is equal to the characteristic velocity v of a galaxy.
Besides, the optical radius ro is closely related to the scale radius of dark matter rs. By using the data of the local volume catalog (LVC) dwarf galaxies3,30, a very strong correlation between rs and ro is found (see Fig. 2). Although the relation is not a perfect linear relation, their ratio is close to a constant rs = (2.59 ± 0.55)ro. Since \({M}_{B}={\bar{\rho }}_{B}V=\)\(\mathrm{(47}\pm \mathrm{6)}{M}_{\odot }{{\rm{km}}}^{-{\rm{4}}}\,{s}^{-4}\,{v}^{4}\), the term v in Eq. (1) is canceled. Furthermore, putting rs = (2.59 ± 0.55)ro into Eq. (1) and taking mB = 1.2 mp, where mp is the proton mass, we can calculate the value and the uncertainty of K:
The graph of ro versus rs. The data (indicated by squares) are taken from3. The red line indicates the tight correlation between the two quantities.
On the other hand, the product K can also be understood as follow. Since \(v=\sqrt{G{M}_{D}(r)/r}\), where MD(r) is the enclosed dynamical mass of a galaxy, we have \({v}^{4}\propto {M}_{D}^{2}{r}_{o}^{-2}\). Assuming \({M}_{D}({r}_{o})\propto {\bar{\rho }}_{D}{r}_{o}^{3}\), we get
Therefore, K is directly proportional to the ratio of the baryonic mass and the enclosed dynamical mass at radius ro. Note that this ratio is not necessarily equal to the cosmic baryon fraction f = 0.156 ± 0.00331. For different sizes and types of galaxies, it is possible to have entirely different ratios at radii ro (see the discussion below).
Furthermore, the above relation is obtained by using the Tully-Fisher relation, which is formulated based on the data of spiral galaxies. For elliptical galaxies, many of them satisfy another relation called the Faber-Jackson relation32. This relation indicates a close relationship between the luminosity L and the stellar velocity dispersion vb of elliptical galaxies: \(L\propto {v}_{b}^{4}\), which is similar to the form of the Tully-Fisher relation. Recent studies show that the data of some elliptical galaxies also fall on the spiral baryonic Tully-Fisher relation if one assumes a certain value of mass-to-luminosity ratio33. Therefore, the above result may also be applicable for elliptical galaxies.
The constant for galaxy clusters
The above deduction method can only be applied for galaxies. It is because there is no Tully-Fisher relation for galaxy clusters. Also, the product \({\bar{\rho }}_{D}{r}_{s}\) is not a constant for galaxy clusters4. Fortunately, we can relate the velocity of baryons v′ by the temperature T of hot gas in galaxy clusters, which can be given by Virial relation \(v\approx \sqrt{3kT/{m}_{p}}\). The baryonic component in a large galaxy cluster is dominated by the spherical hot gas halo within the core radius of the hot gas rc. Therefore, we consider the spherical interacting region inside r = ro = rc so that \(V=4\pi {r}_{c}^{3}\mathrm{/3}\). Besides, the hot gas is in hydrostatic equilibrium so that the total mass can be determined34:
where \(P={\rho }_{B}kT/(\mu {m}_{p})\) is the pressure of hot gas, μ = 0.61 is the molecular weight and M(r) is the total enclosed mass. Recent studies show that the x-ray hydrostatic mass measurements are remarkably robust and method-independent35. The overall percentage error of mass estimation is about 10–30% if we assume that T is a constant34,36. The hot gas surface brightness profile can be determined by x-ray observations. It is usually described by a β-model34:
where S0 is the central surface brightness, rc is the core radius and β is a fitted parameter. These parameters can be used to construct the density profile of hot gas36:
where ρB0 is the central baryon density. Combining Eqs (4) and (6), we get
The total mass density can be obtained by
Taking r → 0, we can get the central total mass density ρt0. Since dark matter dominates the mass in a galaxy cluster, the central dark matter density is close to the central mass density:
Note that for most of the galaxy clusters, the density profiles are close to the NFW profile (a cuspy profile). Here, the density ρD0 represents the average dark matter density for r ≤ rc (i.e. \({\bar{\rho }}_{D}\approx {\rho }_{D0}\)). Using Eq. (9), the value of ρD0 for each galaxy cluster can be calculated by the parameters T, β and rc, including their uncertainties.
Putting all the above relations to Eq. (1), the term v and rc would be cancelled naturally. Therefore, we get
Result
For galaxies
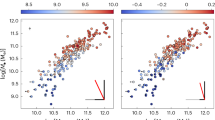
In many dark matter-dominated galaxies, the mass density of dark matter for r ≤ rs is close to constant (cored structure: \({\bar{\rho }}_{D}\approx {\rho }_{D0}\))10,37. Also, recent analyses suggest that the central dark matter column density (the product of the central dark matter mass density and the scale radius) is almost a constant. Early analysis using ∼1000 galaxies gives \({\rho }_{D0}{r}_{s}={141}_{-52}^{+82}{M}_{\odot }\,{{\rm{pc}}}^{-{\rm{2}}}\) 1 while later analysis using Milky Way spheroidal dwarf galaxies gives \({\rho }_{D0}{r}_{s}={75}_{-45}^{+85}{M}_{\odot }\,{{\rm{pc}}}^{-{\rm{2}}}\) 2. After that, using a sample of the LVC dwarf galaxies, the resultant central surface mass density gives \({\rho }_{D0}{r}_{s}\sim 100{M}_{\odot }\,{{\rm{pc}}}^{-{\rm{2}}}\) 3, which is consistent with the previous studies. By combining the data of the Milky Way spheroidal dwarf galaxies2 and the sample of disc galaxies in3, we get \({\bar{\rho }}_{D}\propto {r}_{s}^{-0.97\pm 0.14}\) and \({\bar{\rho }}_{D}{r}_{s}={95}_{-40}^{+70}{M}_{\odot }\,{{\rm{pc}}}^{-{\rm{2}}}\) (see Fig. 3). Therefore, using this result, we get
The central dark matter column density (in \({M}_{\odot }\,{{\rm{pc}}}^{-2}\)) as a function of total galactic mass of dark matter. The data (indicated by circles) are taken from2 and3. The regions bounded by the red dashed lines and bounded by the blue dotted lines are the ranges of the central dark matter column density obtained in1 and2 respectively.
The narrow range of K (or the ratio of baryonic mass to the enclosed dynamical mass) for galaxies has been known for a decade. The almost constant central dark matter column density for a wide range of galaxies1,2,3 and the constant luminous-to-dark matter ratio within one halo scale-length38 suggest the narrow range of K. Therefore, the almost constant value of K for galaxies is expected.
For galaxy clusters
By using the x-ray data of 64 large galaxy clusters (with rc ≥ 100 kpc)34, we get \({\rho }_{D0}\propto {\rho }_{B0}^{1.00\pm 0.06}\) (see Fig. 4), where \({\rho }_{B0}\approx {\bar{\rho }}_{B}\) is the central mass density of hot gas. It means that the ratio \({\rho }_{D0}/{\rho }_{B0}\approx 8.70\pm 3.42\) is roughly a constant. This correlation has not been discovered and discussed in previous studies. Although the average dark matter density to average baryonic density ratio for a galaxy cluster should be close to \({f}^{-1}\approx 6.41\), the ratio at the central region for all galaxy clusters may not be a constant and equal to f−1 because the density profiles for dark matter and hot gas are entirely different (see the discussion below). This approximately constant ratio of ρD0 to ρB0 at rc may reveal some global interplay between dark matter and baryons.
The graph of ρD0 versus ρB0 for 64 galaxy clusters (data are taken from34). The red dashed line indicates the slope of the fit: 1.00 ± 0.06.
Although different galaxy clusters have different values of β34, we approximate the distribution of β by a Gaussian function with an average value β = 0.65 and a dispersion of 0.13 (see Fig. 5). Putting the relation of ρD0 and ρB0 to Eq. (10) and using β = 0.65 ± 0.13, we get a scale invariant constant for galaxy clusters:
where \({\bar{\rho }}_{D}/{\bar{\rho }}_{B}\approx {\rho }_{D0}/{\rho }_{B0}\). We can see that the values of K for galaxies and galaxy clusters give excellent agreement with each other, within a factor of 2–3. This constant can be regarded as a universal constant for dark matter-baryon interplay because it is independent of scale.
The distribution of β for the 64 galaxy clusters (data are taken from34). The black line indicates the Gaussian fit with β = 0.65 ± 0.13.
Here, note that the x-ray data used have assumed the hubble parameter h = 0.534. To match the current observed hubble parameter h = 0.6831, we have re-scaled the parameters rc and ρB0. Besides, using the data of large galaxy clusters can minimize the errors because the uncertainties of the central hot gas temperature significantly affect the mass determination of small galaxy clusters. Therefore, we only choose the large galaxy clusters (with rc ≥ 100 kpc) to perform the analysis.
The relation between the constant and the cosmic baryon fraction
As mentioned above, the value of K is directly proportional to the ratio MB/MD(ro) (for galaxies) or ρB0/ρD0 (for galaxy clusters). One may claim that it is not surprising to have a similar constant value of K for galaxies and galaxy clusters because MB/MD(ro) or ρB0/ρD0 should be close to the cosmic baryon fraction f = 0.156 ± 0.003, which should be almost a constant for various structures. However, previous studies show that the baryon fractions in various structures are entirely different and the ratios quite depend on the positions of the structures39,40. In Fig. 6, we follow the study in39 and show the corresponding baryon fractions for different structures (from dwarf galaxies to galaxy clusters). We can see that the ratio can be ranging from 10−3 to 10−1, which spans 3 orders of magnitude.
The graph of baryon fraction versus total baryonic mass for different structures (from dwarf galaxies to galaxy clusters) (data are taken from39). The red line indicates the correlation \(f\propto {M}_{B}^{0.23}\).
If we assume the NFW profile for dark matter distribution in galaxy clusters and fix the baryon fraction f = MB/(MB + MD) = 0.156 at a large radius r = 1 Mpc, we can predict the baryon fraction at the characteristic radius rs for various total dynamical mass using hydrostatic equilibrium. In Fig. 7, we can see that the baryon fraction at rs = 100 kpc ranges from 10−3 to 10−1 (not close to f = 0.156 ± 0.003) for just a short range of dynamical mass if we consider a fix hot gas temperature (T = 5 keV) and scale radius of dark matter rs = 100 kpc. For various temperature of hot gas and scale radii of different galaxy clusters, the variation of the baryon fraction can be much larger. This large variation can also be seen in galaxies by examining the radial acceleration relation23. Therefore, theoretically, the baryon-dark matter density ratio is not necessarily a constant for various structures, but possibly spans at least 2 orders of magnitude. Furthermore, the characteristic radii of the galaxies (∼1–10 kpc) and galaxy clusters considered (∼100–500) kpc are different. There is no reason why the baryon fractions for galaxies and galaxy clusters are close to each other at different characteristic radii. Nevertheless, our results show that this ratio is almost constant at the characteristic radii ro or rc. Based on the result of Fig. 7, it seems that gravitational interaction between dark matter and baryonic matter alone is not enough to provide a satisfactory explanation for the constant value of K. This may reveal the existence of some interplay or self-organizing processes between baryons and dark matter particles within the ‘interacting region’.
Discussion
Previous studies have claimed some relations for dark matter. For example, as mentioned above, the central dark matter column density ρD0rs is almost a constant for a wide range of galaxies3. Some explanations have been given to account for this relation, such as the self-interacting dark matter model17,41. However, this relation is not correct for galaxy clusters4. Therefore, such scaling relation is not universal at all. Besides, the alleged universal NFW density profile for dark matter only gives good agreement with the data of galaxy clusters6 and some galaxies7,8, but not for dwarf galaxies9,10. Therefore, it does not have any universal relation for dark matter which is true for both galactic and galaxy cluster scales. Our result, K is a constant, would be the first universal relation of dark matter for both galactic and galaxy cluster scales. Although this constant is proportional to the ratio of baryon fraction in galaxies and galaxy clusters at the optical radii or core radii, it is not necessarily a constant. As shown in Fig. 6, the baryon fractions can span 3 orders of magnitude variation for different structures. Therefore, our results suggest that some interplay between baryons and dark matter particles may exist so that the constant K or the baryon fraction is almost a constant for galaxies and galaxy clusters within the ‘interacting region’.
Note that the choice of the characteristic radius (ro or rc) in this analysis is not arbitrary. The overlapping regions of dark matter and baryons for galaxies and galaxy clusters are characterized by the optical radii ro and the core radii rc respectively. The size of the interacting volume V also depends on ro or rc. If we consider the scale radius of dark matter rs as the characteristic radius, the volume considered would be much larger, which includes some non-interacting regions. Therefore, it is justified to use ro or rc as the characteristic radius for this analysis.
Although the range of baryon fraction can be very large, in this analysis, we mainly examine the value of K (proportional to the central baryon fraction) within the ‘interacting region’ (i.e. within ro or rc). As mentioned above, the narrow range of K in the central regions of galaxies has been known for a decade38. However, the narrow range of K in the core regions of galaxy clusters has not been discussed extensively. Many studies only focus on the total baryon fraction for the whole galaxy clusters40,42, not for the central regions. Some studies have examined the central baryon fraction of some galaxy clusters43,44. However, no extensive discussion about the range of the central baryon fraction has been made. Besides, some discrepancies exist between numerical simulations and observational data for galaxy clusters near the central regions. Previous studies using computer simulations suggest a very wide range of baryon fraction for different radii45. However, the simulated baryon fraction is somewhat smaller than that of the observed data43,44,45. For rc = 100–500 kpc, the corresponding baryon fraction should be ∼0.02–0.1 based on the simulated results45. This gives ρD0/ρB0 ∼ 10–50. Nevertheless, our results suggest a narrower and smaller ratio ρD0/ρB0 = 8.70 ± 3.42 (or a larger value of K) compared with the simulated results, which generally agree with the observed ranges of the central baryon fraction in43,44. We explicitly analyze the baryon fraction distribution at core radii of galaxy clusters and quantify the results to get the value of K. It is surprising to see the value of K for galaxy clusters being close to that for galaxies within the ‘interacting region’, which has not been discussed and discovered in the early works. Therefore, our analysis gives some new hints to investigate the alleged interplay between dark matter and baryons.
It has been suggested that dark matter-baryon interaction can explain the observed ‘mass-discrepancy-acceleration relation’46. This relation is closely related to the ‘Tully-Fisher relation’47. Some recent studies also discover some correlations between dark matter and baryonic component in galaxy clusters48. We anticipate that the global properties of dark matter-baryon interaction can give a holistic picture to account for these relations, as well as the ‘halo-disk conspiracy problem’29. Since the constant K links up the baryon fractions with some of the scaling relations in galaxies, it may provide a more fundamental ground to account for the constant dark matter column density (or \({\rho }_{D0}\propto {r}_{s}^{-1}\)) and the Tully-Fisher relation. Note that the dimension of the constant K is cm−2, which is the dimension of 1/cross section. This constant may be closely related to the cross section of the interplay between dark matter and baryons.
It seems that gravitational force only cannot provide a satisfactory account for this interplay. Since baryonic matter is self-interacting while dark matter particles are believed to be collisionless, the density profiles for baryonic matter and dark matter would be different. There is no reason why the values of K (or the baryon fraction) within different characteristic radii are close to each other. Some suggest that baryonic feedback mechanisms can account for the core formation in galaxies12. If baryonic feedback can have some self-organizing properties, it may be able to explain the universal nature of K.
Data Availability
The datasets generated during and/or analysed during current study are available from the corresponding author on reasonable request.
References
Donato, F. et al. A constant dark matter halo surface density in galaxies. Mon. Not. R. Astron. Soc. 397, 1169 (2009).
Burkert, A. The structure and dark halo core properties of dwarf spheroidal galaxies. Astrophys. J. 808, 158 (2015).
Karukes, E. V. & Salucci, P. The universal relation curve of dwarf disk galaxies. Mon. Not. R. Astron. Soc. 465, 4703 (2017).
Chan, M. H. A tight scaling relation of dark matter in galaxy clusters. Mon. Not. R. Astron. Soc. 442, L14 (2014).
Navarro, J. F., Frenk, C. S. & White, S. D. M. A universal density profile from hierarchical clustering. Astrophys. J. 490, 493 (1997).
Viola, M. et al. Dark matter halo properties of GAMA galaxy groups from 100 square degrees of KiDS weak lensing data. Mon. Not. R. Astron. Soc. 452, 3529 (2015).
Iocco, F., Pato, M. & Bertone, G. Evidence for dark matter in the inner Milky Way. Nature Physics 11, 245 (2015).
Sofue, Y. Dark halos of M31 and the Milky Way. Publ. Astron. Soc. Jpn. 67, 75 (2015).
Zackrisson, E., Bergvall, N., Marquart, T. & Östlin, G. The dark matter halos of the bluest low surface brightness galaxies. Astron. Astrophys. 452, 857 (2006).
De Blok, W. J. G. The core-cusp problem. Adv. Astron. 2010, 789293 (2010).
Governato, F. et al. Cuspy no more: how outflows affect the central dark matter and baryon distribution in Λ cold dark matter galaxies. Mon. Not. R. Astron. Soc. 422, 1231 (2012).
Pontzen, A. & Goverato, F. Cold dark matter heats up. Nature 506, 7487 (2014).
Spergel, D. N. & Steinhardt, P. J. Observational evidence for self-interacting cold dark matter. Phys. Rev. Lett. 84, 3760 (2000).
Burkert, A. The structure and evolution of weakly self-interacting cold dark matter halos. Astrophys. J. 534, L143 (2000).
Koda, J. & Shapiro, P. R. Gravothermal collapse of isolated self-interacting dark matter haloes: N-body simulation versus the fluid model. Mon. Not. R. Astron. Soc. 415, 1125 (2011).
Merritt, D. Cosmology and convention. Studies in History and Philosophy of Modern Physics 57, 41 (2017).
Tulin, S. & Yu, H.-B. Dark matter self-interactions and small scale structure. Phys. Rept. 730, 1 (2018).
Tully, R. B. & Fisher, J. R. A new method of determining distances to galaxies. Astron. Astrophys. 54, 661 (1977).
McGaugh, S. S. The baryonic Tully-Fisher relation of gas-rich galaxies as a test of ΛCDM and MOND. Astron. J. 143, 40 (2012).
Lelli, F., McGaugh, S. S. & Schombert, J. M. The small scatter of the baryonic Tully-Fisher relation. Astrophys. J. 816, L14 (2016).
McGaugh, S. S. The mass discrepancy-acceleration relation: disk mass and the dark matter distribution. Astrophys. J. 609, 652 (2004).
Lelli, F., McGaugh, S. S., Schombert, J. M. & Pawlowski, M. S. The relation between stellar and dynamical surface densities in the central regions of disk galaxies. Astrophys. J. 827, L19 (2016).
McGaugh, S. S., Lelli, F. & Schombert, J. M. Radial acceleration relation in rotationally supported galaxies. Phys. Rev. Lett. 117, 201101 (2016).
Bowman, J. D., Rogers, A. E. E., Monsalve, R. A., Mozdzen, T. J. & Mahesh, N. An absorption profile centred at 78 megahertz in the sky-averaged spectrum. Nature 555, 67 (2018).
Barkana, R. Possible interaction between baryons and dark matter particles revealed by the first stars. Nature 555, 71 (2018).
Barkana, R., Outmezguine, N. J., Redigolo, D. & Volansky, T. Signs of dark matter at 21-cm? Phys. Rev. D 98, 103005 (2018).
Kovetz, E. D. et al. Tighter limits on dark matter explanations of the anomalous EDGES 21cm signal. Phys. Rev. D 98, 103529 (2018).
Boddy, K. K. et al. A critical assessment of CMB limits on dark matter-baryon scattering: new treatment of the relative bulk velocity. Phys. Rev. D 98, 123506 (2018).
Battaner, E. & Florido, E. The rotation curve of spiral galaxies and its cosmological implications. Fund. Cosmic. Phys. 21, 1 (2000).
Salucci, P., Turini, N. Evidences for collisional dark matter in galaxies? ArXiv:1707.01059 (2017).
Ade, P. A. R. et al. Planck 2015 results. XIII. Cosmological parameters Astron. Astrophys. 594, A13 (2016).
Faber, S. M. & Jackson, R. E. Velocity dispersions and mass-to-light ratios for elliptical galaxies. Astrophys. J. 204, 668 (1976).
den Heijer, M. et al. The HI Tully-Fisher relation of early-type galaxies. Astron. Astrophys. 581, A98 (2015).
Chen, Y., Reiprich, T. H., Böhringer, H., Ikebe, Y. & Zhang, Y.-Y. Statistics of x-ray observables for the cooling-core and non-cooling core galaxy clusters. Astron. Astrophys. 466, 805 (2007).
Bartalucci, I., Arnaud, M., Pratt, G. W. & Le Brun, A. M. C. Resolving the hydrostatic mass profiles of galaxy clusters at z ∼ 1 with XMM-Newton and Chandra. Astron. Astrophys. 617, A64 (2018).
Reiprich, T. H. & Böhringer, H. The mass function of an x-ray flux-limited sample of galaxy clusters. Astrophys. J. 567, 716 (2002).
Contenta, F. et al. Probing dark matter with star clusters: a dark matter core in the ultra-faint dwarf Eridanus II. Mon. Not. R. Astron. Soc. 476, 3124 (2018).
Gentile, G., Famaey, B., Zhao, H. & Salucci, P. Universality of galactic surface densities within one dark halo scale-length. Nature 461, 627 (2009).
McGaugh, S. S., Schombert, J. M., de Blok, W. J. G. & Zagursky, M. J. The baryon content of cosmic structures. Astrophys. J. 708, L14 (2010).
Gonzalez, A. H., Sivanandam, S., Zabludoff, A. I. & Zaritsky, D. Galaxy cluster baryon fractions revisited. Astrophys. J. 778, 14 (2013).
Chan, M. H. Scaling relations of the slightly self-interacting cold dark matter in galaxies and clusters. Mon. Not. R. Astron. Soc. 433, 2310 (2013).
Laganà, T. F. et al. A comprehensive picture of baryons in groups and clusters of galaxies. Astron. Astrophys. 555, A66 (2013).
Allen, S. W. et al. Improved constraints on dark energy from Chandra X-ray observations of the largest relaxed galaxy clusters. Mon. Not. R. Astron. Soc. 383, 879 (2008).
Pratt, G. W. et al. Gas entropy in a representative sample of nearby X-ray galaxy clusters (REXCESS): relationship to gas mass fraction. Astron. Astrophys. 511, A85 (2010).
Young, O. E., Thomas, P. A., Short, C. J. & Pearce, F. Baryon fractions in clusters of galaxies: evidence against a pre-heating model for entropy generation. Mon. Not. R. Astron. Soc. 413, 691 (2011).
Famaey, B., Khoury, J. & Penco, R. Emergence of the mass discrepancy acceleration relation from dark matter-baryon interactions. J. Cosmol. Astropart. Phys. 03, 038 (2018).
Wheeler, C., Hopkins, P. F. & Dorè, O. The radial acceleration relation is a natural consequence of the baryonic Tully-Fisher relation. ArXiv:1803.01849 (2018).
Del Popolo, A., Umetsu, K., Le Delliou, M. & Lee, X. Correlations between the dark matter and baryonic properties of CLASH galaxy clusters. ArXiv:1808.02136 (2018).
Acknowledgements
The work described in this paper was partially supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region, China (Project No. EdUHK 28300518).
Author information
Authors and Affiliations
Contributions
Design of the study, analysis of the results and writing of the manuscript were performed by Man Ho Chan.
Corresponding author
Ethics declarations
Competing Interests
The author declares no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chan, M.H. A universal constant for dark matter-baryon interplay. Sci Rep 9, 3570 (2019). https://doi.org/10.1038/s41598-019-39717-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-39717-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.