Abstract
Each plane of layered ReS2 and ReSe2 materials has 1D chain structure, from which intriguing properties such as 1D character of the exciton states and linearly polarized photoluminescence originate. However, systematic studies on the 1D character of charge carriers have not been done yet. Here, we report on systematic and comparative studies on the energy-momentum dispersion relationships of layered transition metal dichalcogenides ReS2 and ReSe2 by angle resolved photoemission. We found that the valence band maximum or the minimum energy for holes is located at the high symmetric Z-point for both materials. However, the out-of-plane (\({k}_{z}\)) dispersion for ReSe2 (20 meV) is found to be much smaller than that of ReS2 (150 meV). We observe that the effective mass of the hole carriers along the direction perpendicular to the chain is about 4 times larger than that along the chain direction for both ReS2 and ReSe2. Remarkably, the experimentally measured hole effective mass is about twice heavier than that from first principles calculation for ReS2 although the in-plane anisotropy values from the experiment and calculations are comparable. These observation indicate that bulk ReS2 and ReSe2 are unique semiconducting transition metal dichalcogenides having strong one-dimensional characters.
Similar content being viewed by others
Introduction
Layered transition-metal dichalcogenides (TMDs) have been extensively studied in recent years because of their potential as electronic materials for future devices. Their intriguing characters of the electronic structures such as the valley degeneracy1 and spin-valley-layer locking2,3,4, provide added value for valley- and spintronic applications. While some of them even exhibit superconductivity and charge density waves originating from the electron-phonon and electron-electron interactions due to their low electronic dimensionality (e.g. in NbSe25,6), most of the studies have been focused on Mo and W compounds due to their semi-conducting properties and close to ideal 2 dimensionality7,8,9,10,11.
Very recently, layered ReS2 and ReSe2 began to draw attention as their layer-layer interactions are much weaker than other layered TMDs12. More interestingly, ReS2 and ReSe2 have one-dimensional (1D) characters in their structure as well as optical and electrical properties due to the formation of Re chain structure stemming from the distortion in the 1T structural phase12,13,14. High-resolution transmission electron microscopy and electron diffraction studies reveal distorted 1T structure with Re chain formation12. Such structure distortion is directly related to the high anisotropy in the Raman response from in-plane lattice vibrations14,15,16,17,18,19. It also affects optical properties, e.g., anisotropic character in optical absorption or photoluminescence comes from that of excitons20,21,22,23,24. Electrical conductivity is also found to be much higher along the chain direction than the direction perpendicular to the chain13,25,26.
As the above-mentioned intriguing 1D properties are determined by the characteristics of hole and electron band dispersions, electronic structure studies by angle resolved photoemission spectroscopy (ARPES) are naturally desired. Especially, the effective mass is a fundamental parameter that can be obtained from the energy and momentum dispersion relationship and governs the electrical and optical properties such as mobility, conductivity, light absorption and photoluminescence. In fact, a couple of ARPES studies on ReS2 and ReSe2 have been reported and the results indicate an in-plane anisotropy in the hole band dispersion as expected from the chain structures in ReS227,28,29 and in ReSe230. However, obtaining very high-quality data needed to determine the effective mass for all directions turned out to be challenging. For example, the photon energy dependence of the valence band dispersion for ReS2 appears to be very different among the reported results27,29. In addition, direct comparison between measured valence band dispersions of ReS2 and ReSe2, for which lattice parameters are quite different31, are difficult because the data were taken in different Brillouin zones for ReS2 and ReSe229,30.
In order to resolve aforementioned issues, we have performed systematic ARPES studies on ReS2 and ReSe2. Our goal is to take data for the entire momentum space which is good enough to do quantitative analysis and obtain in-plane anisotropy in the effective hole mass for the two materials for a comparative study. Our data show a striking difference from what were reported in previous experimental and theoretical studies29,30,32. (1) The valence band maximum (VBM) is located at the Z-point for both systems, while it was reported in a previous ARPES study reported that VBM of ReSe2 may be located at non-high-symmetric momentum point30,33. (2) The \({k}_{z}\) dispersion of ReSe2 is much smaller than that of published quasiparticle band structure within the LDA + GdW approximation32. (3) The effective hole masses along and perpendicular to the chain direction are quite different from the reported experimental and theoretical values29,30,34.
Results and Discussion
Valence band maximum of ReSe2 and ReS2
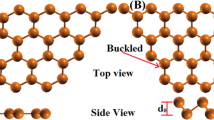
ReS2 and ReSe2 are layered materials in which the van der Waals interaction between layers is extremely weak, even weaker than other TMDs12. The crystal structure for both ReS2 and ReSe2 is the so-called distorted 1T structure. Re atoms show a hexagonal network but the structure is distorted to have chain structures as indicated by black lines in Fig. 1(a). The 1D chain structure makes these materials unique among TMDs in that optical and electrical properties carry 1D characteristics14,15,16,17,18,19,20,21,22,23,24,25,26.
Crystal structure and out-of-plane valence band dispersions. (a) Top and side views of the crystal structure of ReX2 (X = S, Se). It shows distorted 1 T structure with Re chains indicated by black solid lines. (b,c) Intensity plots of ReS2 and ReSe2 ARPES data in the energy and momentum space, respectively. kZ dependent intensities are taken by using different photon energies from 60 eV to 110 eV with 2 eV step. kZ is obtained with inner potentials of 17.8 and 12.4 eV for ReS2 and ReSe2, respectively. \({{\boldsymbol{k}}}_{\parallel }\) and \({{\boldsymbol{k}}}_{\perp }\) are in-plane momentum parallel and perpendicular to the chain, respectively. Red dashed lines are guides to eye for \({{\boldsymbol{k}}}_{{\boldsymbol{z}}}\) dispersion of the top-most valence bands. Insets are 2D constant energy (E = EVBM) intensity map in the momentum-space (as functions of \({{\boldsymbol{k}}}_{\parallel }\) and \({{\boldsymbol{k}}}_{\perp }\)) at the \({{\boldsymbol{k}}}_{{\boldsymbol{z}}}\) = Z-point. Note that there is a single peak at the zero in-plane momentum point (Z-point).
The inner potential can be estimated from the \({k}_{z}\) dispersion of electronic band (Fig. 1(b) and (c)) with the reciprocal lattice vector c*. Based on the results of reported X-ray diffraction measurements31, the reciprocal lattice vector c* is calculated to be 1.032 Å−1 (0.984 Å−1) for ReS2 (ReSe2). The inner potential is estimated to be V0 = 17.8 and 12.4 eV for ReS2 and ReSe2. These estimated values are similar to those of other TMDs35,36.
ARPES experiments are performed on ReS2 and ReSe2 to obtain the energy-and-momentum dispersion of the hole carriers. ARPES intensities as a function of the energy referenced to the valence band maximum (EVBM) are mapped along two momentum directions, parallel to chain (\({k}_{\parallel }\)) and perpendicular to the layer (\({k}_{z}\)) (Fig. 1(b,c)). While several band dispersions are observed within the energy range, the top-most valence band is of interest as it determines the low energy properties of the materials such as electrical conductivity. Due to the layered structure, the top-most bands of ReS2 and ReSe2 show relatively weak dispersions along \({k}_{z}\) than along in-plane momentum. Interestingly, we observed as shown in Fig. 1 that the \({k}_{z}\) dispersion of ReSe2 (about 20 meV) is even weaker compared to that of ReS2 (about 150 meV) which is known as a material with very weak inter-layer interaction12. Therefore, our results show an evidence for even smaller interaction between layers in ReSe2.
Our photon energy dependence data reveal that VBM is located at Z for both ReS2 and ReSe2 as indicated by the red dashed lines in Fig. 1(b,c). While previous ARPES studies also showed that VBM of ReS2 is located at Z, VBM of ReSe2 has been under debate. Hart et al. reported that the \({k}_{z}\) for VBM of ReSe2 is the same as the Z-point but the in-plane momentum was reported to be non-zero30. More recently, Eickholt et al. reported two VBM of ReSe233. One of them is at Z and the other is away from Z. But their experiment could not decide which is global VBM, since data quality is not good enough. The global VBM of ReSe2 can be decided to be located at Z due to high quality data. Please refer to the supplementary materials for more details. In fact, we find that ReSe2 result about VBM is consistent with a recent theoretical prediction as well32.
Directional dependence of effective hole masses in ReS2 and ReSe2
In order to investigate the effective mass of the hole carrier, we analyze ARPES data obtained in the in-plane momentum space that includes the Z-point. As shown in Fig. 2(a,c), constant energy maps of ARPES intensities of ReS2 and ReSe2 at E-EVBM = − 0.2 eV show two-fold symmetry and strong anisotropic band contours which are not closed along the direction perpendicular to the chain. These observations indicate much smaller band dispersion along the direction perpendicular to the chain. The top-most band dispersions, which we are interested in, along the chain are much stronger than those along the other for both ReS2 and ReSe2. For quantitative analysis, we try to fit the band dispersions with a quadratic function for which the effective mass is a free parameter32. The dotted lines in Fig. 2(b,d) indicate the fit functions. So, obtained effective masses along the direction perpendicular to the chain (4.63 me for ReS2 and 4.14 me for ReSe2) are much heavier than the effective masses along chain (1.08 me for ReS2 and 1.13 me for ReSe2). That is, the effective mass along the chain is about 4 times lighter than that perpendicular to the chain for both ReS2 and ReSe2. This in-plane anisotropy value in the effective hole mass is the largest among semiconducting TMDs37,38.
In-plane valence band dispersions near the valence band maximum. Constant energy (E-EVBM = − 0.2 eV) ARPES maps of ReS2 (a) and ReSe2 (c). The photon energy used for the experiment was 70 eV for ReS2 and 68 eV for ReSe2. For these photon energies, \({{\boldsymbol{k}}}_{{\boldsymbol{z}}}\) = Z point (white dot) where VBM is located is included in the data. Red solid and dashed lines in (a,c) indicate the direction parallel and perpendicular to the Re chain direction, respectively. θ is defined as the relative angle from the direction along the chain as shown in the figure. The honey comb structured line indicates the projected Brillouin zone boundary. (b,d) High symmetric cuts along (θ = 0°) and perpendicular (θ = 90°) to the Re chain. The dotted lines in (b,d) are quadratic fit to the top-most bands. The effective masses of hole carriers of ReX2 extracted from the fitting functions are shown in the figures.
The valence band dispersion can also be analyzed for different theta angle and corresponding effective hole mass can be obtained. Shown in Fig. 3(a,b) are ARPES data along in-plane momentum set by the θ angle defined in Fig. 2(a). The data are subsequently analyzed and the corresponding effective hole mass is obtained for a systematic study of direction dependence. We notice the top-most band can be fitted well with a quadratic function indicated by dotted lines, which makes us confident in our analysis. The extracted effective mass from the quadratic function is plotted in polar coordinate as a function of the theta angle in Fig. 3(c). The plot clearly shows two-fold symmetry and strong in-plane anisotropy of the effective hole mass for both ReS2 (red) and ReSe2 (blue). There is an important point to discuss in comparison with the results of first principles calculations on ReS2. The experimentally observed effective mass is about twice larger than that from the first principles calculations. The effective mass from the first principles calculations is 2.4 me along the direction perpendicular to the chain and 0.8 me along the chain27. The electron-electron and electron-phonon interactions or atomic spin-orbit coupling of Re atom which were not considered in the calculation may play a crucial role in the clear enhancement of the effective hole mass.
Anisotropic effective hole masses. ARPES cut data along the in-plane momentum defined by the angle θ (see Fig. 2(a) for definition) for (a) ReS2 and (b) ReSe2. All the data sets are centered around the Z-point at which VBM is located. The dotted lines indicate a quadratic function fitting the dispersions of the top-most bands. The effective mass from the quadratic fit function for each angle can be extracted and is plotted for ReS2 and ReSe2 in (c). Arrows indicate crystallographic orientation of ReX2.
Conclusions
In this study, we performed systematic ARPES studies of ReS2 and ReSe2 to reveal the energy-momentum dispersion relationships of the top most valence bands. We found that ReSe2 have much smaller \({k}_{z}\,\)dispersion than ReS2, indicating the more 2D-like feature in ReSe2 than in ReS2. We systematically investigated in-plane directional dependence of the effective hole masses of ReS2 and ReSe2. The effective masses show strong anisotropy, about 4 times lighter along the chain than the direction perpendicular to the chain. In-plane anisotropy of the hole effective masses in ReS2 and ReSe2 is larger than that in black phosphorus which also shows anisotropic electrical and optical properties39,40. Therefore, ReS2 and ReSe2 are quasi 1D materials in terms of the low energy hole carrier dynamics, which makes ReS2 and ReSe2 promising bulk materials for 1D semiconducting electronics. The effective mass of ReS2 observed by ARPES is found to be significantly enhanced compared to that from first principles calculations. Electron-electron and electron-phonon interactions or atomic spin-orbit coupling of Re atom may be attributed to the mass enhancement41. The quasi 1D character of the hole carriers as well as possibility of the electron-electron and electron-phonon interactions may lead to charge density wave order if enough amount of hole carriers are doped into ReS2 and ReSe242.
Methods
ARPES measurement
We performed ARPES experiments at the beamline 4.0.3.2 (MERLIN) of the Advanced Light Source at the Lawrence Berkeley National Laboratory equipped with VG-Scienta R8000 electron analyzer. All samples are cleaved in-situ and data were taken at 200 K to avoid the charging effect in a vacuum better than 6 × 10−11 Torr. with linearly polarized light. For the kz dependence experiment, photon energies between 60 and 110 eV with 2 eV energy step were used. The total energy resolution was better than 20 meV with a momentum resolution of 0.004 Å−1.
References
Xiao, D., Liu, G.-B., Feng, W. X., Xu, X. & Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Jones, A. M. et al. Spin-layer locking effects in optical orientation of exciton spin in bilayer WSe2. Nat. Phys. 10, 130–134 (2014).
Yao, W. et al. Direct observation of spin-layer locking by local Rashba effect in monolayer semiconducting PtSe2 film. Nat. Commun. 8, 14216 (2017).
Frindt, R. F. Superconductivity in Ultrathin NbSe2 Layers. Phys. Rev. Lett. 28, 299 (1972).
Arguello, C. J. et al. Visualizing the charge density wave transition in 2H-NbSe2 in real space. Phys. Rev. B 89, 235115 (2014).
Jin, C. H. et al. Ultrafast dynamics in van der Waals heterostructures. Nat. Nanotech. 13, 994–1003 (2018).
Rivera, P. et al. Interlayer valley excitons in heterobilayers of transition metal dichalcogenides. Nat. Nanotech. 13, 1004–1015 (2018).
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V. & Kis, A. 2D transition metal dichalcogenides. Nat. Rev. Mater. 2, 17033 (2017).
Wang, G. et al. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Chhowalla, M. et al. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 5, 263–275 (2013).
Tongay, S. et al. Monolayer behavior in bulk ReS2 due to electronic and vibrational decoupling. Nat. Commun. 5, 3252 (2014).
Tiong, K. K., Ho, C. H. & Huang, Y. S. The electrical transport properties of ReS2 and ReSe2 layered crystals. Solid State Commun. 111, 635–640 (1999).
Wolverson, D., Crampin, S., Kazemi, A. S., Ilie, A. & Bending, S. J. Raman Spectra of Monolayer, Few-layer, and bulk ReSe2: An Anistropic Layered Semiconductor. ACS Nano 8, 11154–11164 (2014).
Lorchat, E., Froehlicher, G. & Berciaud, S. Splitting of Interlayer Shear Modes and Photon Energy Dependent Anisotropic Raman Response in N-Layer ReSe2 and ReS2. ACS Nano 10, 2752–2760 (2016).
Chenet, D. et al. In-Plane Anisotropy in Mono- and Few-Layer ReS2 Probed by Raman Spectroscopy and Scanning Transmission Electron Microscopy. Nano Lett. 15, 5667–5672 (2016).
He, R. et al. Coupling and Stacking Order of ReS2 Atomic Layers Revealed by Ultralow-Frequency Raman Spectroscopy. Nano Lett. 16, 1404–1409 (2016).
Nagler, P., Plenchinger, G., Schüller, C. & Korn, T. Observation of anisotropic interlayer Raman modes in few-layer ReS2. Phys. Status Solidi RRL 10, 185–189 (2016).
Li, L. et al. Strong In-Plane Anisotropies of Optical and Electrical Response in Layered Dimetal Chalcogenide. ACS Nano 11, 10264–10272 (2017).
Ho, C. H., Huang, Y. S., Tiong, K. K. & Liao, P. C. Absorption-edge anisotropy in ReS2 and ReSe2 layered semiconductors. Phys. Rev. B 58, 16130 (1998).
Zhong, H.-X., Gao, S. Y., Shi, J.-J. & Yang, L. Quasiparticle band gaps, excitonic effects, and anisotropic optical properties of the monolayer distorted 1T diamond-chain structures ReS2 and ReSe2. Phys. Rev. B 92, 115438 (2015).
Aslan, O. B., Chenet, D. A., van der Zande, A. M., Hone, J. C. & Heinz, T. F. Linearly Polarized Excitons in Single- and Few-Layer ReS2 Crystals. ACS Photonics 3, 96–101 (2016).
Sim, S. et al. Selectively tunable optical Stark effect of anisotropic excitons in atomically thin ReS2. Nat. Commun. 7, 13569 (2016).
Sim, S. et al. Ultrafast quantum beats of anisotropic excitons in atomically thin ReS2. Nat. Commun. 9, 351 (2018).
Ho, C. H., Huang, Y. S. & Tiong, K. K. In-plane anisotropy of the optical and electrical properties of ReS2 and ReSe2 layered crystals. J. Alloys Comp. 317, 222–226 (2001).
Hu, S. Y., Liang, C. H., Tiong, K. K., Huang, Y. S. & Lee, Y. C. Electrical Anisotropy of W-Doped ReSe2 Crystals. J. Electrochem. Soc. 153, J100–J102 (2006).
Biswas, D. et al. Narrow-band anisotropic electronic structure of ReS2. Phys. Rev. B 96, 085205 (2017).
Gehlmann, M. et al. Direct Observation of the Band Gap Transition in Atomically Thin ReS2. Nano Lett. 17, 5187–5192 (2017).
Webb, J. L. et al. Electronic band structure of ReS2 by high-resolution angle-resolved photoemission spectroscopy. Phys. Rev. B 96, 115205 (2017).
Hart, L. S. et al. Electronic bandstructure and van der Waals coupling of ReSe2 revealed by high-resolution angle-resolved photoemission spectroscopy. Sci. Rep. 7, 5145 (2017).
Ho, C. H., Huang, Y. S., Liao, P. C. & Tiong, K. K. Crystal structure and band-edge transition of ReS1−xSex layered compounds. J. Phys. Chem. Solids 60, 1797–1804 (1999).
Arora, A. et al. Highly Anisotropic in-Plane Excitons in Atomically Thin and Bulklike 1T′-ReSe2. Nano Lett. 17, 3202–3207 (2017).
Eickholt, P. et al. Location of the valence band maximum in the band structure of anisotropic 1T′-ReSe2. Phys. Rev. B 97, 165130 (2018).
Yu, S. et al. Strain-engineering the anisotropic electrical conductance in ReS2 monolayer. Appl. Phys. Lett. 108, 191901 (2016).
Kim, B. S., Rhim, J.-W., Kim, B. Y., Kim, C. & Park, S. R. Determination of the band parameters of bulk 2H-MX2 (M = Mo, W; X = S, Se) by angle-resolved photoemission spectroscopy. Sci. Rep. 6, 36389 (2016).
Bovet, M. et al. Interplane coupling in the quasi-two-dimensional 1T-TaS2. Phys. Rev. B 67, 125105 (2003).
Miró, P., Audiffred, M. & Heine, T. An atlas of two-dimensional materials. Chem. Soc. Rev. 43, 6537–6554 (2014).
Zibouche, N., Philipsen, P., Kuc, A. & Heine, T. Transition-metal dichalcogenide bilayers: Switching materials for spintronic and valleytronic applications. Phys. Rev. B 90, 125440 (2014).
Xia, F., Wang, H. & Jia, Y. Rediscovering black phosphorus as an anisotropic layered material for optoelectronic and electronics. Nat. Commun. 5, 4458 (2014).
Akahama, Y., Endo, S. & Narita, S.-I. Electrical Properties of Black Phosphorus Single Crystals. J. Phys. Soc. Jpn. 52, 2148–2155 (1983).
Mahan, G. D. Many-Particle Physics (New York 1990).
Grüner, G. Density Waves in Solids (New York 1994).
Acknowledgements
This work was supported by the Incheon National University Research Grant in 2014. B.S.K. and C.K. acknowledges the support from research program of Institute for Basic Science (Grant No. IBS-R009-G2).
Author information
Authors and Affiliations
Contributions
B.S.K. and W.S.K. performed ARPES measurements with the support from J.D.D.; B.S.K. analyzed the ARPES data; B.S.K., C.K. and S.R.P. wrote the paper; C.K. and S.R.P. are responsible for project direction and planning.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, B.S., Kyung, W.S., Denlinger, J.D. et al. Strong One-Dimensional Characteristics of Hole-Carriers in ReS2 and ReSe2. Sci Rep 9, 2730 (2019). https://doi.org/10.1038/s41598-019-39540-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-39540-4
This article is cited by
-
Progress on material characterization methods under big data environment
Advanced Composites and Hybrid Materials (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.