Abstract
Levees are critical in providing protection against catastrophic flood events, and thus require continuous monitoring. Current levee inspection methods rely on limited information obtained by visual inspection, resulting in infrequent, localized, mostly qualitative and subjective assessments. This hampers the timely detection of problematic locations and the assessment of levee safety in general. Satellite radar interferometry yields weekly observations of levee conditions with high precision which complement current inspection methods. Here we show that levees are susceptible to short-term swelling and shrinkage associated with meteorological conditions, and assess how deformations can be related to the geohydrological properties and the safety of the levee. Our findings allow to understand the sub-seasonal behaviour of the levee in greater detail and to predict swelling and shrinkage due to variation of the loading conditions. This will improve the detection of anomalous levee responses which contributes to the development of reliable early warning methods using continuous deformation monitoring.
Similar content being viewed by others
Introduction
Failures of flood defence systems often lead to significant human, economic, social, and environmental losses, with the risk being highest in densely populated areas1,2. Earthen levees form a large part of the existing flood defence systems. Depending on the natural or man-induced driving mechanisms, levees can fail due to hydraulic failures (e.g., overtopping) and/or geotechnical failures (e.g., instability, erosion)3,4. Consequently, the monitoring of these levees is critical in achieving safety standards and avoiding catastrophic flooding events. Being able to identify if, where, and when a failure would suddenly occur is an important aspect to consider with respect to safety. However, current conventional levee inspection methods mostly rely on expert observers3,5, which result in infrequent, qualitative and labour intensive assessments6,7,8. During these inspections, the integrity of the structures is assessed using visual inspection parameters, in order to check the presence of any damage, cracks, seepage, animal burrows, or irregular vegetation on the levees9. Thus, visual inspection by expert’s judgement is not effective in detecting small (mm- to cm-level) and gradual changes in the structural behaviour of the levee10, which may be indicative of an imminent failure. Common remote sensing (e.g. LiDAR, thermal infrared) and in-situ monitoring methods (e.g. levelling, GNSS, creep/strain meters) are also costly and time-consuming, and are therefore usually only applied to locations considered to be at high risk by a visual inspection. Hence, there is a need for innovative and cost-effective complementary techniques, especially in countries with an extensive amount of flood defence infrastructure, such as the Netherlands, China, UK, and US among many others. These techniques could be most beneficial if they contribute to detecting which locations are most prone to sudden failures and estimating far in advance whether a levee would fail. This can be done by analysing the response of a levee under normal loading conditions in order to identify locations at risk of failing during extreme loading conditions, such as storm, high river discharge or drought.
The deformation behaviour of a levee can be divided into two main categories. Long-term, interannual deformation, such as the subsidence of the levee occurring over a period of years, mainly depends on the type and composition of the soil and can be considered irreversible. Apart from this, levees show short-term, sub-seasonal deformation, e.g. due to changing water levels, precipitation, and temperature, occurring over periods of days to weeks depending on the soil and loading conditions. The change in soil volume due to variations in soil moisture content is denoted as the swelling and shrinking behaviour of the soil11, which has been studied for different soil types, such as clay12,13, peat14,15,16 and others17,18,19.
Understanding and monitoring levee behaviour over an extended area, however, requires the availability of frequent deformation data with high resolution4, which are not provided by current inspection methods. In recent years, satellite radar interferometry, also known as Interferometric Synthetic Aperture Radar (InSAR)20,21, has become an efficient tool to monitor the surface displacements, referred to as deformations in the rest of the paper. The technique provides millions of observations with meter-level spatial resolution and millimetre-level measurement precision at reasonably low costs2,4. SAR satellites allow day and night monitoring of the Earth’s surface in all weather conditions, with up to a sub-weekly repeat interval. Persistent Scatterer InSAR (PS-InSAR) is a processing technique to estimate deformation time-series of points in the interferometric data stack with a coherent reflection over time20. It has been successfully applied on urban areas22, railways23, dams24, highways25, landslides26, tectonic movements27, and land subsidence28. Applications on levees have been limited to interannual deformations to monitor subsidence of the levees4,7,29,30,31. However, as most geotechnical failure mechanisms are related to dynamic levee responses to changes in loading conditions happening on a time scale of days to weeks4, a better understanding of the short-term behaviour of levees is required. Understanding the levee responses in normal conditions can then help to detect or predict the levee response to more extreme conditions, which would increase our capability of detecting anomalies that could identify unsafe situations. In this study, we assess how sub-seasonal patterns due to swelling and shrinkage can be identified from continuous levee deformation observations obtained with PS-InSAR, and we analyse how these patterns are related to meteorological variations and levee safety. By determining whether the observed deformation is in line with the response predicted from loading conditions experienced by levees and relating it to geohydrological properties of levees, it would become possible to identify problematic locations and apply the appropriate countermeasures. Here we focus on earthen canal levees in Delft, located in the Netherlands, where almost 12 million people live in flood prone areas, and reliable flood defences are essential to prevent catastrophic flood events32.
Modelling the Swelling and Shrinkage Behaviour of Levees
Swelling and shrinkage result from changes in the pore water pressures inside the levee, which are due to variations in hydrological loading conditions. When the soil saturates, the pore water pressure in the soil increases, reducing effective stresses in the soil matrix and results in swelling. In turn, a reduction in pore pressures due to drying leads to shrinkage of the soil33.
The swelling and shrinkage behaviour of the soil is especially relevant for the safety of the canal levees. Water levels in these canals are fairly constant and typically exceed surface levels of adjacent polders, posing a continuous flooding threat to the hinterland, even under normal conditions. These canal levees were often built centuries ago and strengthened several times using local peat and clay, amply available materials in the Netherlands34. Changes in precipitation and temperature can lead to significant swelling and shrinkage behaviour of these types of soil. In addition, cracks can form when the levee dries and the soil shrinks. Through these cracks water can enter the levee, reducing the soil strength. Another concern is that other materials or debris may enter the crack, preventing it from closing properly when the soil returns to a wet condition again3. Hence, the resulting changes in the geohydrology of the levee, which is loaded by a fairly constant water level, can directly lead to instability and failure. Many failures of the canal levees in the Netherlands have been recorded due to the heavy rainfall, e.g. a failure close to Wilnis in 187435 or extreme warm and dry weather, such as failures in Zoetermeer in 1947, Oostzaan near Amsterdam in 1990, Bleiswijk in 199036 and near Wilnis in 2003. Hence, extreme conditions, i.e. too dry (high temperature and low precipitation) or highly saturated soil (mainly heavy precipitation with low temperatures) cause a reduction in the soil strength of the levee, which can lead to a failure.
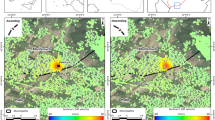
In order to analyse the deformation behaviour of the canal levees, we used 168 images recorded from the TerraSAR-X satellite, covering the case study area (see Methods for the details). We first estimate the deformation time-series of each measurement point (hereafter called PS point) on the canal levees of Delft using the PS-InSAR technique21,37 with an approach based on geodetic estimation theory38. Deformation time-series are created spanning a period of 6 years (2009–2015) (Fig. 1(a)). Although the results are visualized by linear deformation velocity [mm/year], every PS point has a complete time-series of deformation estimates in the Line-of-Sight (LOS) direction.
Analysis of deformation behaviour of the levees in Delft, the Netherlands. (a) Deformation behaviour of the canal levees has been analysed based on data acquired by TerraSAR-X, descending orbit (2009–2015) and visualized in the deformation velocity [mm/year] map. (b) A part of the levee segment in the monitored area. (c) A comparison is given between time-series of observed deformation d(t) and estimated deformation, \(\hat{d}(t)\) using the steady-state model with an MSE of 4 mm2 and the vPT-model with an MSE of 2.1 mm2 for this specific PS point. The period of summer 2011 is shown in a dashed rectangle. (d) Cumulative precipitation [mm] and average temperature [°C] data used in the vPT-model. The figure was generated using the QGIS software, (version 2.18.27, https://qgis.org). The background image from Map data ©2015 Google is added using the QGIS QuickMapServices (version 0.19.10.1, https://plugins.qgis.org/plugins/quick_map_services/).
To examine the swelling and shrinkage behaviour of the levees, we developed a predictive deformation model, called vPT-model (see Methods for the details), considering the meteorological loading conditions (i.e., precipitation and temperature) as indirect indicators of the water content inside the levee. The model is used to analyse the swelling and shrinkage behaviour, and to assess whether these sub-seasonal patterns can be identified in the deformation time-series. Figure 1(b) shows a part of the levee segment in the monitored area, and an associated time-series. A comparison between the time-series of observed deformation from satellite, d(t) and the deformation \(\hat{d}(t)\) estimated using the vPT-model, is given in Fig. 1(c) for a random PS point and compared with the steady-state model. It can be seen how the steady-state model only describes the interannual subsidence trend, whereas the vPT-model, which uses the meteorological data shown in Fig. 1(d), also follows the sub-seasonal swelling-shrinkage variations of the deformation time-series.
Nevertheless, deviations from the vPT-model occur, e.g., in December 2010 and in summer 2011, see Fig. 1(c). For example, the summer period of 2011, indicated by a dashed rectangle in Fig. 1(c), was very dry. During this period, surface of the levees was sprayed with water in order to avoid excessive drying of the soil due to the extreme drought conditions. This situation may explain the unexpected deformation of the levee which showed a swelling behaviour not predicted by the model.
Application of the vPT deformation model
The developed vPT-model has been applied on each PS point along the canal levees in Delft, comprising of 1184 PS points. To assess how well the vPT-model describes the deformation compared to the steady-state model, we apply hypothesis testing to both models independently. Firstly, the significance of the vPT-model is tested using an Overall Model Test (OMT) (see Methods, for the details) and compared with the steady-state model for different values of the assumed variance of the observations, \({\sigma }_{d}^{2}\). A lower value for \({\sigma }_{d}^{2}\) increases the value of the test statistic and thus the probability that the null hypothesis, H0, is rejected. The results are given in Fig. 2, showing the percentage of PS points for which H0 is sustained. It can be seen that, already for \({\sigma }_{d}^{2}=9\,{{\rm{mm}}}^{2}\), the vPT-model is providing a higher number of PS time-series that can be well modelled compared to the steady-state model. By decreasing the value of \({\sigma }_{d}^{2}\), the difference in significance between the two models gets even larger. This higher significance is the result of the improved modelling capability of the vPT-model, which results in better estimates of the observed deformation time-series.
In order to quantify this improved modelling capability, we then evaluate the quality of the estimations by calculating the mean square error (MSE) for each PS time-series. In Fig. 3, the MSE value per PS point for the entire area is given for both steady-state and vPT-model. The reduction in the MSE for the vPT-model compared to the steady-state model can be clearly observed on the two maps, with green points representing the PS time-series showing a low MSE, and red points representing PS time-series giving high MSE. The MSE values are also given in the histograms, which illustrates the error distribution for the PS points considered. The comparison between the two distributions highlights a clear shift of the MSE towards lower values.
Modelling results for the deformation behavior of the canal levees in Delft, the Netherlands, cf. Fig. 1. MSE values per PS point and distribution of MSE are shown for (a) steady-state model, (b) vPT-model. The comparison between the two maps shows how the vPT-model generally provides a lower MSE over the entire levee structure.
The reduction in the MSE also allows to assume a lower variance \({\sigma }_{d}^{2}\) for the observations. For instance, assuming an a-priori variance of 7 mm2, the vPT-model gives 79% of the PS points with \({\rm{MSE}} < {\sigma }_{d}^{2}\), while the steady-state model gives only 39%. Hence, for a large number of points, the deformation data can be modelled using the vPT-model with higher quality of the estimations. Thus, for those points that have low MSE, the vPT-model can also provide better indications of the swelling and shrinkage patterns.
However, deformation estimations with low precision (e.g. MSE above 7 mm2) are still included in the results. In general, a high MSE could be related to several factors, such as radar signal decorrelation20,38 (e.g., vegetation, maintenance), or unmodelled deformation behaviour due for instance to problematic locations or soil compositions responding differently to meteorological changes4.
Relation with soil types of the levee
The deformation behaviour of a levee depends on its soil characteristics. In order to assess whether any deformation pattern related to the type of soil can be observed from the model parameters, we focus on a levee segment (Fig. 4(a)) for which the soil profiles are provided by the local water authority, Water Board Delfland. Given these soil profiles, we defined three specific levee locations given in Fig. 4, whose main soil type for the first 2 meters of depth are considered. Location A is predominantly made of clay, location B shows different mixtures of clay and sand, and location C has sand as its primary soil type. These three locations have been investigated further based on the vPT-model results for those PS points giving an MSE lower than 7 mm2. First, we compared the reaction time of the soil, i.e. time delay parameters τP and τT. Then, we analysed the scaling coefficients cP and cT, which are expected to provide an indication about the reaction magnitude of the different soil types.
The relation between the soil types and the vPT-model parameters. The analysis of the estimated vPT-model parameters for those PS point with MSE lower than 7 mm2 within (a) the selected locations A, B and C (indicated by the rectangles) on the east levee in the study area with their predominant soil types. (b) time delay for P(t), τP [day], (c) time delay for T(t), τT [day], (d) scaling coefficient for P(t), cP [mm/mm], (e) scaling coefficient for T(t), cT [mm/°C]. The figure in (a) was generated using the QGIS software, (version 2.18.27, https://qgis.org). The background image from Map data ©2015 Google is added using the QGIS QuickMapServices (version 0.19.10.1, https://plugins.qgis.org/plugins/quick_map_services/).
Considering the swelling-shrinkage behaviour of the types of soil, sandy soil is expected to react faster than clayey soil for the same amount of precipitation received due to larger porosity and higher hydraulic conductivity. On the other hand, clayey soil would react with bigger magnitude compared to the sandy soil due to the organic components in its composition. Large pore volumes in between sand particles would allow the water to drain quicker, which would result in smaller volume changes compared to clayey soil.
In order to verify if these expected behaviours are observed in the parameters of the estimated vPT-model, Fig. 4(a) shows the different PS points within the selected locations (indicated by the rectangles), where the estimated values of the vPT-model parameters are given on a colour scale in Fig. 4(b–e). Figure 4(b) shows the values for the time delay τP related to the precipitation data. Location A shows longer τP compared to locations B and C. This is in accordance with the expected faster reaction of sandy soil compared to clayey soil. On the other hand, the values of the τT parameter (Fig. 4(c)) are almost always zero. This is an indication that the levee reacts almost instantaneously with respect to temperature (averaged over 10 days) regardless of the soil type. The few PS points showing higher values for τT are considered to be outliers, for which the parameters might have been poorly estimated due to some of the issues discussed before.
The values of the scaling coefficient related to the precipitation data cP provide no clear indication about the reaction magnitude of the different soil types. A better idea is however provided by the scaling coefficient for the temperature cT in Fig. 4(e). In this case, it is more evident that the influence of the temperature on the clayey soil (location A) is stronger than on sandy soil (location C).
In general, these results are in accordance with the expected behaviour of different soil types to precipitation and temperature changes, regardless of the fact that only a small number of PS points with low MSE is available in each location considered. The variability of the parameter values within the same locations is most likely due to differences in levee characteristics (e.g. different slopes), and heterogeneity of the soil profiles in between two boring measurement locations and other factors. More quantitative results and a better validation of the vPT-model for different soil types would thus require a larger amount of data available and of better quality, and more detailed information about the soil type at specific locations.
Enhancing Flood Protection
The strength of the proposed vPT-model lies in the ability of describing not only the interannual subsidence phenomenon, but also the sub-seasonal deformation behaviour using meteorological data, i.e., precipitation and temperature, as indirect indicators of the water content inside the levee. This also allows analysing the influence of the meteorological conditions on the swelling and shrinkage behaviour on a weekly basis, thus enabling predictions of the expected behaviour of the levee due to variations in the loading conditions. Being able to model and predict the sub-seasonal behaviour of a levee based on recorded extreme meteorological events would thus increase our ability of identifying critical situations.
In addition, the observed deformation can also be related to changes in geohydrological properties of a levee, such as the moisture content, weight and phreatic line (i.e. groundwater table in an unconfined aquifer). An instability or sliding of the landside slope can in fact occur when the levee loses weight due to drying and/or due to changes in effective stress in the soil. In order to illustrate the potential of satellite monitoring to detect stability problems, we consider the canal levee failure that occurred near Wilnis, the Netherlands, in 2003, as an example. Extreme drying out of this peat levee during the hot summer led to its loss of weight, triggering levee instability which consequently lead to flooding of the neighbourhood behind it39. Using the documented information by Van Baars39 on the weight changes from saturated to unsaturated conditions of the levee and assuming isotropic deformation, we roughly estimate 2 to 10% of shrinkage on the crest before the actual failure. In case of a deformation mostly on the vertical direction, this range can increase up to 20% during a dry period of 100 days (see Methods for the details). Expected deformations in the first phases of the drying process are estimated to be already in the range of few centimetres. While no SAR satellite data were available in the period of failure, this range of deformation is well within the observability capabilities of current SAR sensors and PS-InSAR algorithms. The monitoring and modelling of this kind of deformation behaviour, which normally takes place over a period of several weeks to months and eventually leads to a failure, could help to flag the extreme shrinkage of the levee. This would allow levee managers to apply timely countermeasures, such as watering or installing stability berms, to prevent instability.
A related possible future application of the proposed vPT-model is the detection of deformation anomalies in the framework of an early warning system. For example, when the soil has dried, the shrinkage and the volume change may result in cracks in the soil. In this case, the deformation behaviour of the levee will deviate from the expected deformation. This particular event would then be regarded as an anomaly with respect to the normal behaviour of the levee, which should be an indication for a potential weakness and a call for more in-depth analysis of the situation.
It is noted that levee deformation and its effect on safety will be highly dependent on local soil and geohydrological conditions of the levee. Further research on these aspects would need to address the relationship between deformation and geohydrological levee properties and the effects on levee stability for a number of representative situations.
In conclusion, this study shows that (a) sub-seasonal deformations obtained from monitoring a levee with the PS-InSAR technique can be observed on the time scale of weeks, that (b) these deformations are strongly correlated with the changes in meteorological conditions, that (c) deformation changes in time can be estimated using a relatively simple regression model, and that (d) deformations can be directly related to geohydrological properties and the safety of the levee. Even though the examples are given for the Netherlands, this technology is applicable to other parts of the world, thus supporting levee management especially in countries with extensive flood defence systems. Findings of this study will assist the future development of reliable early warning methods using continuous deformation monitoring, thus enhancing flood protection.
Methods
Study area
This paper focuses on a 10 × 10 km area south of Delft, the Netherlands. The levees used in this study are regional flood defences, as they are situated along regional rivers and canals. The canals are used to drain excess water from the lower-lying polders to the main rivers and the sea.
Meteorological data
Precipitation [mm/day] and temperature [°C] data are obtained from meteorological station 344 from the Royal Dutch Meteorological Institute near Rotterdam. Both precipitation and temperature are measured hourly with electronic sensors with a precision of 0.1 mm and 0.1 °C, respectively. The distance from the meteorological station to the study area is approximately 4 km. Hence, the measured data are expected to differ slightly from the meteorological conditions at the study area. However, since cumulative and average meteorological values are used in our model, the effect is assumed to be negligible.
Soil data
Soil profiles were obtained from borings performed in 2011 by Water Board Delfland at 17 different locations along the levee. Taking into account the non-uniformity of the soil compositions and the changes in soil moisture content of unsaturated zone, the dominant soil type from 0 to 2 meters below the surface level is being considered.
Deformation data from PS-InSAR processing
The case study area has been monitored using data from TerraSAR-X to estimate the deformation time-series of each PS point between 8 April 2009 and 8 January 2015. This satellite provides X-band high resolution data with a wavelength of 31 mm, 3 × 3 m pixel size and a repeat cycle of 11 days.
The main principle of satellite radar imaging can be described as follows. Radar sensors transmit pulses of high-frequency electromagnetic waves from space to Earth and record the strength and the fractional phase of the back-scattered signals that are reflected from the surface to construct SAR images. By interfering at least two radar images acquired at different times over the same location, the combined effect of surface deformation, topography and atmospheric signal delay is obtained. In order to estimate and isolate the surface deformation from the other phase contributions, a large stack of SAR images acquired by the same satellite is analysed by interferometric time-series methods. All deformations are projections of the real deformation [mm] onto the Line-of-Sight (LOS) direction. This direction from satellite to object is determined by the heading angle of the satellite, αh, and the incidence angle of the radar, θinc.
Various time-series processing techniques can be applied to estimate the deformations from the satellite data. The most suitable approach depends on a number of factors, such as the number of available radar images, satellite characteristics, the area of interest (e.g., surface cover), and the expected deformation signal. Regardless of the specific approach used, PS-InSAR analysis typically includes three main steps; 1) stack processing: creating the multiple interferograms from complex data, 2) PSI analysis: detecting Persistent Scatterers (PS) and separating deformation phase from other contributions (such as topography, atmospheric delay20) and 3) quality assessment: evaluating the quality of the results38. In this study, the interferometric stack processing of the radar data has been performed using the Delft Object-oriented Radar Interferometric Software (DORIS)40. The Delft implementation of Persistent Scatterer InSAR (DePSI)38 has been applied on 168 TerraSAR-X strip-map images in order to estimate the Line-of-Sight (LOS) deformation time-series. The main principles of PS-InSAR and a general overview of the past studies can be found in a review41, whereas another study4 discusses the applicability of the technique to continuous levee monitoring.
Deformation Modelling
In order to describe this deformation behaviour of earth-filled levees, we consider its relation with respect to those meteorological data, i.e. precipitation and temperature, which are expected to give an indication of soil moisture changes. For this reason, the steady-state model, which considers the interannual trend, due to the long-term irreversible behaviour of the levee (e.g. subsidence), is extended with the introduction of precipitation, P, and temperature, T, time-series. In this way, it is also possible to evaluate the sub-seasonal and reversible behaviour of the levee, i.e. its swelling and shrinkage. Hence, the proposed model, hereafter called vPT-model, is defined as
where the first term corresponds to the steady-state model,
with v the slope in [mm/day] and b the intercept in [mm] of the long-term linear trend. This intercept accounts for the atmospheric signal delay and scattering noise in the master acquisition, which is common in all single-master interferograms38. The second term describes the swelling-shrinkage behaviour of the levee as a linear combination of precipitation and temperature time-series. We expect the soil to react to variations in precipitation and temperature only after a certain period of time. This requires a regression model which includes a time delay τ between the meteorological data and the observed levee deformation. The second term of equation (1) is then defined as
where the time-series at time t are indicated as d(t) in [mm] for deformation, P(t) for the cumulative precipitation, in [mm], over a time interval ΔtP, starting at t − ΔtP and ending at t, and T(t) for the average temperature, in [°C], over a time interval ΔtT, starting at t − ΔtT and ending at t. The offsets for precipitation and temperature time-series are represented by δP in [mm] and δT in [°C], respectively, while the time delay parameters for P(t) and T(t) with respect to d(t) are denoted as τP and τT, with their units in [day]. Lastly, cP in [mm/mm] and cT in [mm/°C] are the scaling coefficients of the linear combination, between d(t) and P(t) and between d(t) and T(t), respectively.
Model parameter estimation
Soil deformation is expected to result from cumulative and smooth variations in precipitation and temperature. For this reason, the mean temperature and the cumulative precipitation data over time periods ΔtT = 10 days and ΔtP = 30 days are considered, respectively. The time period for the cumulative precipitation was chosen to be longer than the time resolution of the deformation data to take into account for the long-term effect of precipitation.
The vPT-model in equation (1) can be simplified as
where d(t), P(t) and T(t) are the deformation and meteorological data preprocessed as described above, and the global offset coefficient is defined as δ = (cPδP + cTδT − b). This model is non-linear due to the products cPτP and cTτT. For this reason, we use the cross-correlation method42 to estimate the τP and τT parameters. This approach is used to shift P(t) and T(t) with respect to d(t) (after removing the steady-state trend v⋅t) and to compare the two records at each possible time delay, where \({\hat{\tau }}_{P}\) and \({\hat{\tau }}_{T}\) are selected as the values providing the maximum absolute value in the cross-correlation function. Hence, the precipitation and temperature time-series are aligned to the deformation data (i.e. shifted by \({\hat{\tau }}_{T}\) and \({\hat{\tau }}_{P}\), respectively).
After the time alignment, the vPT-model is simplified as
where the aligned time-series are defined by
The optimal values for the linear parameters of the vPT-model are estimated by minimizing the mean square error between the deformation data and the model estimate
where d is the m × 1 vector containing the LOS deformation observations, A is the m × n design matrix whose columns are the time vector t, the vectors \(\tilde{{\boldsymbol{P}}}\) and \(\tilde{{\boldsymbol{T}}}\) containing respectively the aligned precipitation \(\tilde{P}\) and temperature data \(\tilde{T}\), 1 is a vector containing only ones, and x is the n × 1 vector of the model parameters (the symbol ′ indicates the transpose). The estimated optimal values of x are then given by the least squares solution43 as
where the covariance matrix Qd specifies the dispersion of the measured deformation data. The observations in the time-series are assumed to be uncorrelated, each having a fixed variance of unit weight \({\sigma }_{d}^{2}\). Thus, the variance matrix can be factorized as \({{\boldsymbol{Q}}}_{d}={\sigma }_{d}^{2}{{\boldsymbol{I}}}_{m}\), with Im an m × m identity matrix.
Once the model parameters are obtained as explained above, they are used in the vPT-model of equation (4) to obtain the estimated (adjusted) deformation time-series \(\hat{{\boldsymbol{d}}}={\boldsymbol{A}}\hat{{\boldsymbol{x}}}\). The error between the measured deformation time-series and the estimated one is given by the residual \(\hat{{\boldsymbol{e}}}={\boldsymbol{d}}-\hat{{\boldsymbol{d}}}\) and the quality of the estimation is then evaluated by the mean square error (MSE).
Hypothesis testing: Overall Model Test (OMT)
The Overall Model Test (OMT)44 is used to check the validity of the models. Testing is usually performed by comparing a null hypothesis, H0, versus an alternative hypothesis, Ha, where H0 represents the model under investigation and Ha corresponds to the case where no restrictions are imposed on the observations, as in
where E{⋅} and D{⋅} denote expectation and dispersion, respectively. To reject or sustain H0 depends on the test statistic,
which follows a central χ2-distribution with q = m − n degrees of freedom, and corresponds to a weighted sum-of-squares of the least squares residual vector \({\hat{{\boldsymbol{e}}}}_{0}\) under H0. Given a chosen level of significance α, the critical value kα follows from the χ2-distribution to test the null hypothesis,
Rejection of H0 indicates that the deformation behaviour is not significantly well described by the chosen model, given the assumed level of significance. For InSAR time-series, α is typically defined in the range of 0.2% < α < 2%, as we prefer to stick to a relatively simple null hypothesis if possible45. In this study, we assumed an α value of 1%, but in practice this is a decision to be taken by the local authorities. The variance of unit weight for TerraSAR-X with a 31 mm wavelength is conservatively assumed to be \({\sigma }_{d}^{2}={3}^{2}\,{{\rm{mm}}}^{2}\) 38,45.
Deformation estimation for the levee failure at Wilnis, the Netherlands
In the assessment of the failed levee at Wilnis39, two scenarios for changes of the phreatic line in the peat levee are considered: (a) fully saturated (phreatic line is at the crest), and (b) unsaturated (phreatic line drops 1 m below the crest level). Relevant information and the cross section of the levee can be found in the original study39. Here we estimate the expected deformation of the crest in case the phreatic line drops from scenario (a) to scenario (b), using the data documented by Van Baars39. In scenario (a), the volume of saturated soil, Vsoil-sat = 1 m3. The gravimetric water content, Θ, is described as the ratio between the mass of the water, Mw, and the mass of solids, Msolids. For the saturated peat soil at the Wilnis levee, Θ was varying between 600% to 800%, and the unit weight of the saturated peat soil, γsat = 11 kN/m3, and the unit weight of unsaturated peat soil, γunsat = 5 kN/m3 39,46,47. The ratio between mass and volume of the solids is assumed to be constant.
In the case of fully saturated soil (scenario (a)), the mass of soil, Msoil-sat, is equal to sum of mass of water, Mw-sat and mass of solids, Msolid-sat. Thus, for the given Θ of the saturated soil, Msoil-sat = γsat.Vsoil-sat = 11 kN. Using an average Θ of 700%, Mw-sat = 9.63 kN and Msolid-sat = 1.38 kN. Considering the unit weight of water, γw = 9.81 kN/m3, the volume of water in the saturated soil is calculated as Vw-sat = Mw-sat/γw = 0.98 m3 and the volume of solids in the saturated soil is then Vsolid-sat = Vsoil-sat − Vw-sat = 0.02 m3.
After a dry period of approximately 100 days, soil samples taken from the crest of the levee show that Θ of the unsaturated soil (scenario (b)) was around 200%39,46. In this case, the mass of water, Mw-unsat reduces to 2.75 kN and the corresponding volume of water in the unsaturated soil is Vw-unsat = 0.28 m3. The mass of solids in the unsaturated soil remains unchanged, Msolid-unsat = 1.38 kN.
Hence, the volume change of the soil, ΔV, between the two scenarios is estimated as 0.175 m3 in the case of a 1 m drop in the phreatic line with the reduction of Θ from 700% to 200%. This correspond to a deformation of 6% of the total height (i.e., 6 cm) assuming an isotropic shrinkage of the soil. For an initial Θ of 800% and 600%, about 2% to 10% of shrinkage can be observed, respectively. In case of an anisotropic deformation, mostly on the vertical direction, this range can increase up to approximately 20% in a drought period of 100 days.
References
Jonkman, S. N. Global perspectives on loss of human life caused by floods. Nat. Hazards 34, 151–175 (2005).
Özer, I. E., van Damme, M., Schweckendiek, T. & Jonkman, S. N. On the importance of analyzing flood defense failures. In Proc. 3rd Eur. Conf. Flood Risk Manag., vol. 7, 03013, https://doi.org/10.1051/e3sconf/20160703013 (Lyon, France, 2016).
Sharp, M. et al. The International Levee Handbook (CIRIA, London, England, 2013).
Özer, I. E., van Leijen, F., Jonkman, S. N. & Hanssen, R. F. Applicability of satellite radar imaging to monitor the conditions of levees. J. Flood Risk Manag. e12509, https://doi.org/10.1111/jfr3.12509 (2018).
Cundill, S. L., van der Meijde, M. & Hack, H. R. G. Investigation of remote sensing for potential use in dike inspection. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 7, 733–746 (2014).
Rijkswaterstraat. Hydraulische randvoorwaarden 2001 voor het toetsen van primaire waterkeringen. Tech. Report (in Dutch), Rijkswaterstraat, Delft, The Netherlands (2001).
Hanssen, R. F. & van Leijen, F. J. Monitoring water defense structures using radar interferometry. In Proc. 2008 IEEE Radar Conf., 1–4 (Rome, Italy, 2008).
Bakkenist, S. W. & Zomer, W. S. Inspectie van waterkeringen: een overzicht van meettechnieken. Tech. Report (in Dutch) 2010–31, STOWA, Amersfoort, The Netherlands (2010).
Bakkenist, S. [dl.2]: Inspectiewijzers waterkeringen: technische informatie uitvoering inspecties. Tech. Report (in Dutch), STOWA, Amersfoort, The Netherlands (2012).
Tarrant, O., Hambidge, C., Hollingsworth, C., Normandale, D. & Burdett, S. Identifying the signs of weakness, deterioration, and damage to flood defence infrastructure from remotely sensed data and mapped information. J. Flood Risk Manag. 10, 1–14 (2017).
Peng, X. & Horn, R. Identifying six types of soil shrinkage curves from a large set of experimental data. Soil Sci. Soc. Am. J. 77, 372–381 (2013).
Al-Homoud, A., Basma, A., Husein Malkawi, A. & Al Bashabsheh, M. Cyclic swelling behavior of clays. J. Geotech. Eng. 121, 562–565 (1995).
Tripathy, S., Rao, K. S. & Fredlund, D. Water content-void ratio swell-shrink paths of compacted expansive soils. Can. Geotech. J. 39, 938–959 (2002).
Price, J. S. & Schlotzhauer, S. M. Importance of shrinkage and compression in determining water storage changes in peat: the case of a mined peatland. Hydrol. Process. 13, 2591–2601 (1999).
Camporese, M., Ferraris, S., Putti, M., Salandin, P. & Teatini, P. Hydrological modeling in swelling/shrinking peat soils. Water Resour. Res. 42 (2006).
Gebhardt, S., Fleige, H. & Horn, R. Shrinkage processes of a drained riparian peatland with subsidence morphology. J. Soils Sediments 10, 484–493 (2010).
Peng, X. & Horn, R. Modeling soil shrinkage curve across a wide range of soil types. Soil Sci. Soc. Am. J. 69, 584–592 (2005).
Peng, X. & Horn, R. Anisotropic shrinkage and swelling of some organic and inorganic soils. Eur. J. Soil Sci. 58, 98–107 (2007).
Leong, E. & Wijaya, M. Universal soil shrinkage curve equation. Geoderma 237, 78–87 (2015).
Hanssen, R. F. Radar Interferometry: Data Interpretation and Error Analysis, vol. 2 (Springer Science + Business Media, Dordrecht, the Netherlands, 2001).
Ferretti, A., Prati, C. & Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote. Sens. 39, 8–20 (2001).
Gernhardt, S., Adam, N., Eineder, M. & Bamler, R. Potential of very high resolution SAR for persistent scatterer interferometry in urban areas. Ann. GIS 16, 103–111 (2010).
Chang, L., Dollevoet, R. P. & Hanssen, R. F. Nationwide railway monitoring using satellite SAR interferometry. IEEE. J. Sel. Top. Appl. Earth Obs. Remote. Sens. 10, 596–604 (2017).
Perissin, D. & Wang, T. Time-series InSAR applications over urban areas in China. IEEE. J. Sel. Top. Appl. Earth Obs. Remote. Sens. 4, 92–100 (2011).
Perissin, D., Wang, Z. & Lin, H. Shanghai subway tunnels and highways monitoring through Cosmo-SkyMed persistent scatterers. ISPRS J. Photogramm. Remote. Sens. 73, 58–67 (2012).
Cigna, F., Bianchini, S. & Casagli, N. How to assess landslide activity and intensity with persistent scatterer interferometry (PSI): the PSI-based matrix approach. Landslides 10, 267–283 (2013).
Hooper, A., Segall, P. & Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 112 (2007).
Cigna, F. et al. Monitoring land subsidence and its induced geological hazard with synthetic aperture radar interferometry: A case study in Morelia, Mexico. Remote. Sens. Environ. 117, 146–161 (2012).
Dixon, T. H. et al. Space geodesy: subsidence and flooding in New Orleans. Nature 441, 587–588 (2006).
Barends, F., Dillingh, D., Hanssen, R. & van Onselen, K. Bodemdaling langs de Nederlandse kust: case Hondsbossche en Pettermer zeewering, (in Dutch) 4–5 (IOS Press, Amsterdam, the Netherlands, 2008).
Brooks, B. A. et al. Contemporaneous subsidence and levee overtopping potential, Sacramento-San Joaquin Delta, California. San Francisco Estuary Watershed Sci. 10 (2012).
Jorissen, R., Kraaij, E. & Tromp, E. Dutch flood protection policy and measures based on risk assessment. In Proc. 3rd Eur. Conf. Flood Risk Manag., vol. 7, 20016 (Lyon, France, 2016).
Mitchell, J. K. et al. Fundamentals of Soil Behavior, vol. 3 (John Wiley & Sons, New York, US, 2005).
TeBrake, W. H. Taming the waterwolf: hydraulic engineering and water management in the Netherlands during the Middle Ages. Technol. Cult. 43, 475–499 (2002).
Grundmann, P. Een incident tijdens de droog making in 1874. (in Dutch). De Proostkoerier 3, 4–9 (1996).
Vonk, B. Some aspects of the engineering practice regarding peat in small polders. In den Haan, E., Termaat, R. & Edil, T. (eds) Advances in understanding and modelling mechanical behaviour of peat, 389–402 (A.A. Balkema, Rotterdam, the Netherlands, 1994).
Kampes, B. M. Radar interferometry, vol. 12 (Springer, Dordrecht, the Netherlands, 2006).
van Leijen, F. J. Persistent scatterer interferometry based on geodetic estimation theory. Ph.D. thesis, Delft University of Technology, Delft, the Netherlands (2014).
Van Baars, S. The horizontal failure mechanism of the Wilnis peat dyke. Géotechnique 55, 319–323 (2005).
Kampes, B. M., Hanssen, R. F. & Perski, Z. Radar interferometry with public domain tools. In Proc. FRINGE 2003, vol. 3 (Frascati, Italy, 2003).
Crosetto, M., Monserrat, O., Cuevas-González, M., Devanthéry, N. & Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote. Sens. 115, 78–89 (2016).
Zabihi Naeini, E., Hoeber, H., Poole, G. & Siahkoohi, H. R. Simultaneous multivintage time-shift estimation. Geophysics 74, V109–V121 (2009).
Teunissen, P. J. G. Adjustment Theory; An Introduction, first edn (VSSD, Delft, the Netherlands, 2000).
Teunissen, P. J. G. Testing Theory; An Introduction, second edn (VSSD, Delft, the Netherlands, 2006).
Chang, L. & Hanssen, R. F. A probabilistic approach for InSAR time-series postprocessing. IEEE Trans. Geosci. Remote. Sens. 54, 421–430 (2016).
Dekker, J. et al. Achtergrondrapport sterkteonderzoek oorzaak kadeverschuiving Wilnis. Tech. Report (in Dutch) CO-411242-0025, GeoDelft (2004).
Bezuijen, A., Kruse, G. & Van, M. Failure of peat dikes in the Netherlands. In Proc. Int. Conf. Soil Mech. Geotech. Eng., vol. 16, 1857 (Osaka, Japan, 2005).
Acknowledgements
This research was performed as part of the NWO TTW project SAFElevee (project:13861). The authors would like to thank the German Aerospace Centre (DLR) for providing the TerraSAR-X data and Water Board Delfland for making the soil data available. Dr. Phil Vardon, Dr. Anne-Catherine Dieudonné and Dr. Giacomo Vairetti are acknowledged for their feedbacks.
Author information
Authors and Affiliations
Contributions
S.N.J. and R.F.H. conceived the project. I.E.Ö. conducted the data analysis. I.E.Ö., S.J.H.R., F.J.L., S.N.J. and R.F.H. interpreted the results. I.E.Ö. wrote the original paper while all the authors contributed significantly to the final version.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Özer, I.E., Rikkert, S.J.H., van Leijen, F.J. et al. Sub-seasonal Levee Deformation Observed Using Satellite Radar Interferometry to Enhance Flood Protection. Sci Rep 9, 2646 (2019). https://doi.org/10.1038/s41598-019-39474-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-39474-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.