Abstract
The Framingham Risk Score (FRS) has been reported to predict coronary heart disease (CHD), but its assessment has been unsuccessful in Asian population. We aimed to assess FRS and Suita score (a Japanese CHD prediction model) in a Japanese nation-wide annual health check program, participants aged 40–79 years were followed up longitudinally from 2008 to 2011. Of 35,379 participants analyzed, 1,234 had new-onset CHD. New-onset CHD was observed in diabetic men [6.00%], non-diabetic men [3.96%], diabetic women [5.51%], and non-diabetic women [2.86%], respectively. Area under the curve (AUC) of receiver operating characteristic (ROC) curve for CHD prediction were consistently low in Suita score (TC), FRS (TC) and NCEP-ATPIII FRS (TC), suggesting that these scores have only a limited power. ROC, net reclassification improvement (NRI), integrated discrimination improvement (IDI), and decision curve analysis (DCA) and Hosmer–Lemeshow goodness-of-fit test did not show clear differences between Suita score (TC) and FRS (TC). New models combining waist circumference ≥85 cm in men or proteinuria ≥1+ in women to Suita score (TC) was superior in diabetic men and women. New models could be useful to predict 3-year risk of CHD at least in Japanese population especially in diabetic population.
Similar content being viewed by others
Introduction
The prevalence of diabetes mellitus is increasing worldwide, particularly in Asian countries1. The risk for cardiovascular disease (CVD) or coronary heart diseases (CHD) in patients with diabetes is assumed to be approximately 2–3 times higher than that in patients without diabetes in Japan2,3 as in Western countries4. The Framingham Risk Score (FRS) and the SCORE risk have been reported to predict CHD in Western countries5,6,7,8; however, its assessment in the Japanese population has been unsuccessful9. Thus, original predictive models in Japan are required10,11,12.
The Suita score is a CHD-predictive model score based on the Suita study, a prospective cohort study evaluating new-onset CHD in Suita City, Osaka, Japan9. In 2017, the Japan Atherosclerosis Society committee revised the Japanese guideline for prevention of atherosclerotic cardiovascular diseases: risk estimation outcome has been changed from total death because of CHD, based on Nippon Data 802, to new-onset CHD, based on the Suita study9. Hereafter, the Suita score is expected be used widely in Japan. However, several issues remain unsolved. Assessment of the Suita score in other large Japanese populations has not been performed9. Also, assessments in patients with diabetes have not been examined in such CHD-predictive model scores13,14.
In the present study, we evaluated the following: (1) assessments of FRS and Suita score in a large Japanese population using receiver operating characteristic (ROC) curve method and the Hosmer–Lemeshow test; (2) assessments of FRS and Suita scores in men and women with or without diabetes; (3) development of newly modified CHD-predictive models based on Suita score in participants with and without diabetes; (4) assessments of two scores by ROC curve, net reclassification improvement (NRI), integrated discrimination improvement (IDI), and decision curve analysis (DCA).
Results
Baseline characteristics and CHD onset in total participants, men, and women
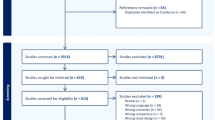
The flow chart of the participants’ recruitment is shown in the Supplementary Fig. 1. The baseline characteristics of participants are shown in Table 1. The study included 35,379 participants (mean age, 62.1 years [SD 7.5]), including 14,072 men (mean age, 61.9 years [8.0]), 21,307 women (mean age, 62.3 years [7.2]), and 2,926 participants with diabetes (8.3%). The Suita score (based on total cholesterol (TC) and low-density lipoprotein cholesterol level (LDL-C)), FRS (based on TC), and NCEP-ATPIII FRS (based on TC) for total participants, men and women were shown in Table 2. Risk scores were higher in men than in women. During three years of follow up, 1,234 participants (3.49%; 589 men [4.19%], 645 women [3.03%]) developed new-onset CHD.
Baseline characteristics and CHD onset in men and women with and without diabetes
The study had 2,926 participants with diabetes (men [1,566], women [1,360]). Of participants without diabetes, 12,506 were men and 19,947 were women (Table 1). The following variables were higher in men and women with diabetes than those in their counterparts: age, body weight (BW), body mass index (BMI), waist circumference, systolic blood pressure (SBP), diastolic blood pressure (DBP) (in women), glucose, HbA1c, triglyceride (TG), alanine aminotransferase (ALT), γ-glutamyl transpeptidase (γ-GTP), uric acid (in women), estimated glomerular filtration rate (e-GFR) (in women), proportion of proteinuria, smoking (in men), prevalence of hypertension, hyperlipidemia, and use of anti-hypertensive, lipid-lowering, and anti-diabetic drugs. Suita score (based on TC and LDL-C), FRS (based on TC), and NCEP-ATPIII FRS (based on TC) for non-diabetic and diabetic men and non-diabetic and diabetic women were shown in Table 2. Those risk scores were all higher in diabetic men and women than in their counterparts. New-onset CHD between 2008 and 2011 was observed in men with diabetes [6.00%], men without diabetes [3.96%], women with diabetes [5.51%], and women without diabetes [2.86%], respectively.
Assessment of FRS and Suita score in total participants, men and women
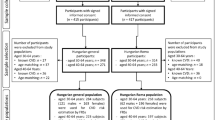
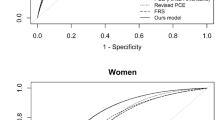
In ROC curves for CHD risk prediction, the areas under the curves (AUCs) of the Suita score (TC and LDL-C), FRS, and NCEP-ATPIII FRS were shown in the upper panel of Fig. 1(a) and values of AUC (95% CI) and cutoff (sensitivity, 1-specificity) were in the lower panel in Fig. 1(a). Discrimination of ROC curves was slightly different between Suita (TC) vs FRS (TC) or vs NCEP-ATPIII FRS (TC) in total participants, but that of three scores was almost equivalent when the population was divided into men and women (Fig. 1(a)).
ROC curve of Suita scores (TC and LDL-C), FRS (TC), and NCEP-ATPIII FRS (TC) for coronary heart disease (CHD) prediction in total participants, men and women (a) and in men and women with and without diabetes. (b) Receiver operating characteristic (ROC) curves in Suita scores total cholesterol (TC, black line) and low-density-lipoprotein cholesterol (LDL-C, yellow line), Framingham risk score (FRS) TC (FRS TC, red line), and NCEP-ATPIII FRS TC (green line) are shown. The area under the curve (AUCs) of new-onset coronary heart disease (CHD) and cutoff values (sensitivity, 1 – specificity) and P values are shown in the lower left panel. P values for model comparisons are also shown in the lower right panel.
Next, we conducted the Hosmer–Lemeshow test to evaluate the model’s calibration (Table 3). In total participants, Suita score (TC) and Suita score (LDL-C) showed a good fit, and FRS and NCEP-ATPIII FRS did not. When the population was divided into men and women, Suita, FRS and NCEP-ATPIII risk scores equivalently showed a good fit.
In total, men and women, NRI and IDI of ROC curves were slightly better in Suita score (TC) than in those of FRS (TC) (Tables 4 and 5). DCA of two scores was almost equally distributed (Fig. 2(a)).
Decision curve analysis (DCA) for coronary heart disease (CHD) prediction in total participants, men and women (a) and in men and women with and without diabetes. (b) Horizontal dotted lines are net benefit of treating no participants, assuming that all would not develop CHD; gray line is net benefit of treating all participants similarly, assuming that all would develop CHD; net benefit of treating participants based on Suita score (TC) is black line and those based on FRS (TC) is red line. Dotted lines are 95% confidential intervals.
Assessment of FRS and Suita score in men and women with and without diabetes
AUCs of the Suita score (TC), Suita score (LDL-C), FRS (TC) and NCEP-ATPIII FRS (TC) in non-diabetic and diabetic men and women were shown in Fig. 1(b). AUC of Suita score (TC) was slightly better in diabetic men compared to NCEP-ATPIII FRS (TC)(P = 0.029), however the AUCs were not different in non-diabetic men and non-diabetic and diabetic women as compared to the other scores. In Hosmer–Lemeshow test (Table 3), the values for Suita score (TC and LDL-C), FRS (TC) and NCEP-ATPIII FRS (TC) all indicated a good-fit model in men and women with or without diabetes, except for Suita score (TC) in non-diabetic men. Discrimination abilities, when assessed by NRI, IDI (Tables 4 and 5) and DCA (Fig. 2(b)), were better in Suita score (TC) than in FRS (TC), in non-diabetic and diabetic men and in non-diabetic women.
New risk prediction model 1: Suita score (TC) + new covariates
Selection of new covariates
Since AUC of ROC was low in Suita score (TC) as well as in FRS (TC) and NCEP-ATPIII FRS (TC), we attempted to create a new risk prediction model by adding new covariates to Suita score (TC). Candidates of covariates in new risk prediction models are shown in Supplementary Table 1A and newly selected covariates were compared with FRS Original and the Suita score (TC) in Supplementary Table 1B. Crude odds ratio of covariates for CHD prediction was shown in Table 6. Waist circumference (≥85 cm) and BMI were significant in non-diabetic and diabetic men and proteinuria (≥± or ≥1+) was in non-diabetic and diabetic women. Calculations for Suita score (LDL-C) resulted in almost the same that in the Suita score (TC) (data not shown). Variance inflation factor (VIF) of waist circumference and proteinuria with Suita score variables were all <2.5, indicating no evidence for strong multicollinearity. Odds ratios adjusted for all covariates of Suita score, waist circumference in diabetic men (2.160; 1.290–3.617; P < 0.01) and proteinuria in diabetic women (3.252; 1.731–6.110; P < 0.01), were almost comparable with their crude odds ratios.
Developing new risk prediction model 1
We implemented a new risk prediction model as follows. The β coefficients calculated using multiple logistic regression in diabetic men were Suita score 0.3, waist circumference 7, and intercept −5. Then, the formula for modified Suita score in diabetic men was 0.3 × Suita score (TC) + 7 × waist circumference. Although the intercept was omitted in this formula for simplification, the intercept was used to calculate the probability of CHD onset. In the same way, the β coefficients calculated using multiple logistic regression in women with diabetes were Suita model score 0.1, proteinuria 12, and intercept −4. Thus, the formula for modified Suita score in diabetic women was 0.1 × Suita score (TC) + 12 × proteinuria ≥1+ (0 or 1). In non-diabetic men, the formula = 0.3 × Suita score (TC) + 1.2 × waist circumference ≥85 cm (0 or 1), whereas that for non-diabetic women was 0.2 × Suita score (TC) + 4.3 × proteinuria ≥1+ (0 or 1). The results for Suita score (LDL-C) were almost the same as those for Suita score (TC) (data not shown).
Hosmer–Lemeshow goodness-of-fit test
Hosmer–Lemeshow test (Table 3) for Suita score (TC) new covariates indicated a good-fit model in total, men and women, and in non-diabetic and diabetic men and women.
ROC curve, NRI, IDI and DCA
We weighed the discrimination ability of the new risk prediction model by comparing AUC (Delong test), NRI, IDI and DCA. Addition of new covariates, waist circumference or proteinuria, to Suita score (TC) significantly improved AUCs in total and women (Fig. 3(a)), however showed a borderline difference (P = 0.068) in diabetic men and a significant difference in diabetic women (P = 0.042) (Fig. 3(b)). Meanwhile, the overall category-free NRI and IDI of Suita score (TC) new covariates indicated significance or borderline differences as compared to Suita score (TC) in total, men and women, and in non-diabetic and diabetic men and diabetic women (Tables 4 and 5). The DCA (Fig. 4) showed that curves of Suita score (TC) new covariates had a good discrimination in diabetic men and women, but not in non-diabetic men and women.
ROC curves of FRS, Suita score (TC) and its modified scores for coronary heart disease (CHD) prediction in total participants, men and women (a) and in men and women with and without diabetes. (b) Receiver operating characteristic (ROC) curves in FRS (light green lines), Suita score (TC) (black lines), New risk prediction model 1 (orange lines), Suita score (TC) new coefficients (blue lines), New risk prediction model 2 (light blue lines), and New risk prediction model 3 are shown. The area under the curve (AUCs) of new-onset coronary heart disease (CHD) and cutoff values (sensitivity, 1 – specificity) and P values are shown in the lower left panel. P values for model comparisons are also shown in the lower right panel. New risk prediction model 1: Suita score (TC) + new covariates*, New risk prediction model 2: Suita score (TC) new coefficients + new covariates*, New risk prediction model 3: Suita score (TC) new coefficients + new covariates 2**, *new covariates: Waist circumference (≥85 cm) in men and proteinuria (≥1+) in women were included, **new covariates 2: Triglyceride, drug of diabetes, hypertension, and dyslipidemia, waist circumference (≥85 cm), and proteinuria (≥+−) in men, and triglyceride, drug of diabetes, hypertension, and dyslipidemia, waist circumference (≥90 cm), and proteinuria (≥1+) in women were included.
Decision curve analysis (DCA) for coronary heart disease (CHD) prediction in men and women with and without diabetes. Horizontal dotted lines are net benefit of treating no participants, assuming that all would not develop CHD; gray line is net benefit of treating all participants similarly, assuming that all would develop CHD; net benefit of treating participants based on Suita score (TC) is black line and those based on New risk prediction model 1 (orange), Suita score (TC) new coefficients (blue lines), New risk prediction model 2 (light blue lines), and New risk prediction model 3 (light pink lines)are also shown. Dotted lines are 95% confidential intervals. (New risk prediction model 1: Suita score (TC) + new covariates*, New risk prediction model 2: Suita score (TC) new coefficients + new covariates*, New risk prediction model 3: Suita score (TC) new coefficients + new covariates 2**, *new covariates: Waist circumference (≥85 cm) in men and proteinuria (≥1+) in women were included, **new covariates 2: Triglyceride, drug of diabetes, hypertension, and dyslipidemia, waist circumference (≥85 cm), and proteinuria (≥+−) in men, and triglyceride, drug of diabetes, hypertension, and dyslipidemia, waist circumference (≥90 cm), and proteinuria (≥1+) in women were included.
Probability of new-onset CHD
The probability of new-onset CHD for 3 years using Suita score (TC or LCL-C) covariates were calculated in diabetic men and women. If waist circumference was positive in men, the probability of CHD was increased approximately 2-fold, whereas if proteinuria was positive in women, the probability was increased approximately 3-fold (Supplementary Tables 2 and 3).
New risk prediction model 2: Suita score (TC) new coefficients + new covariates
New coefficients for Suita score (TC) covariates
We developed another new risk model in which all the variables included in the Suita score were reassessed to obtain better model performance.β-coefficients of Suita score (TC) variables9 such as age, TC, HDL-C, SBP, current smoking, HbA1c and e-GFR were recalculated in the-sex specific models to obtain best fit models.
In non-diabetic men: Suita score (TC) new coefficients = 0.44 × age (years) + 0.05 × SBP (mmHg) + 0.01 × TC (mg/dL) − 0.05 × HDL-C (mg/dL) − 0.96 × current smoking (0 or 1) − 0.07 × eGFR + 2.5 × HbA1C (%).
In diabetic men: Suita score (TC) new coefficients = 0.38 × age (years) + 0.04 × SBP (mmHg) + 0.001 × TC (mg/dL) − 0.03 × HDL-C (mg/dL) + 1.38 × current smoking (0 or 1) − 0.12 × eGFR + 0.10 × HbA1C (%).
In non-diabetic women: Suita score new coefficients = 0.36 × age (years) + 0.08 × SBP (mmHg) − 0.06 × TC (mg/dL) + 0.02 × HDL-C (mg/dL) − 2.73 × current smoking (0 or 1) + 0.03 × eGFR + 1.2 × HbA1C (%).
In diabetic women: Suita score new coefficients = 0.48 × age (years) − 0.01 × SBP (mmHg) − 0.11 × TC (mg/dL) + 0.00 × HDL-C (mg/dL) + 1.35 × current smoking (0 or 1) − 0.11 × eGFR + 2.64 × HbA1C (%).
Suita score (TC) new coefficients + new covariates
New risk prediction model 2 was implemented adding waist circumference in men and proteinuria ≥1 in women to Suita score (TC) new coefficients scores as follows.
In non-diabetic men: Suita score (TC) new coefficients + new covariates = 0.98 × Suita score (TC) new coefficients + 1.11 × waist circumference ≥85 cm (0 or 1).
In diabetic men: Suita score (TC) new coefficients + new covariates = 0.96 × Suita score new coefficients + 7.40 × waist circumference ≥85 cm (0 or 1).
In non-diabetic women: Suita score (TC) new coefficients + new covariates = 0.98 × Suita score new coefficients + 4.48 × proteinuria ≥1+ (0 or 1).
In diabetic women: Suita score (TC) new coefficients + new covariates = 0.96 × Suita score new coefficients + 11.1 × proteinuria ≥1+ (0 or 1).
Hosmer–Lemeshow goodness-of-fit test
As shown in Table 3, performance of Suita Score (TC) new coefficients and Suita Score (TC) new coefficients + covariates were good in total, men and women, were also good when divided to non-diabetic and diabetic men and women.
ROC curve, NRI, IDI, and DCA
As compared Suita score (TC), Suita score (TC) new coefficients with or without new covariates significantly improved AUCs in total, men and women (Fig. 3(a)), in non-diabetic men and non-diabetic and diabetic women (Fig. 3(b)). The overall category-free NRI and IDI of Suita score (TC) new coefficients with or without new covariates also showed improvement in total, men and women, non-diabetic men and non-diabetic and diabetic women. (Tables 4 and 5). DCA indicated that curve discrimination of Suita score (TC) new coefficients with or without covariates was improved compared to those of Suita score (TC) in diabetic men and women (Fig. 4).
New risk prediction model 3: Suita score (TC) new coefficients + new covariates 2
Suita score (TC) new coefficients + new covariates 2
Finally, to obtain the best risk prediction models, we reconsidered a set of new comprehensive candidates of covariates: sex, age, BW, BMI, waist circumference, waist circumference (≥85 cm in men and ≥90 cm in women), SBP, DBP, FPG, HbA1c, AST, ALT, γ-GTP, HDL-C, LDL-C, triglyceride, uric acid, serum creatinine, eGFR, proteinuria, proteinuria (≥±), proteinuria (≥1+), smoking habits, drinking habits, drug information of diabetes, hypertension, and dyslipidemia (Supplementry Table 1A). We selected the newly selected covariates as new covariates 2 (Supplementry Table 1B).
In detail, new models are as follows; Age, SBP, TC, HDL, HbA1c, current smoking, and e-GFR (Suita score (TC) new coefficients), adding waist circumference ≥85 cm, the use of drug of diabetes, hypertension, and dyslipidemia, triglyceride, and proteinuria ≥+− (new covariates 2) in men: meanwhile, Age, SBP, TC, HDL, HbA1c, current smoking, and e-GFR(Suita score (TC) new coefficients), adding proteinuria ≥1+, the use of drug of diabetes, hypertension, and dyslipidemia, triglyceride, and waist circumference ≥90 cm (new covariates 2) in women, respectively. Next, we calculated β-coefficients of Suita score (TC) new coefficients and new covariates 2 in the-sex specific models to obtain best fit models.
In non-diabetic men: Suita score (TC) new coefficients + new covariates 2 = 0.86 × Suita score (TC) new coefficients + 0.52 × waist circumference ≥85 cm (0 or 1) + 3.74 × the use of drug of hypertension (0 or 1) + 3.22 × the use of drug of dyslipidemia (0 or 1) + 0 × triglyceride + 0.16 × proteinuria ≥+− (0 or 1).
In diabetic men: Suita score (TC) new coefficients + new covariates 2 = 0.87 × Suita score new coefficients +8.02 × waist circumference ≥85 cm (0 or 1)+ 1.08 × the use of drug of hypertension(0 or 1), +1.98 × the use of drug of diabetes (0 or 1), −1.88 × the use of drug of dyslipidemia, (0 or 1) −0.03 × triglyceride + 3.84 × proteinuria ≥+− (0 or 1).
In non-diabetic women: Suita score (TC) new coefficients + new covariates 2 = 0.75 × Suita score new coefficients + 3.42 × proteinuria ≥1 (0 or 1) + 5.03 × the use of drug of hypertension(0 or 1), +1.44 × the use of drug of dyslipidemia(0 or 1), + 0 × triglyceride −1.01 × waist circumference ≥90 cm (0 or 1).
In diabetic women: Suita score (TC) new coefficients + new covariates 2 = 0.9 × Suita score new coefficients + 11.03 × proteinuria ≥1 (0 or 1) + 1.54 × the use of drug of hypertension(0 or 1), +2.38 × the use of drug of diabetes (0 or 1) + 1.30 × the use of drug of dyslipidemia,(0 or 1), −0.02 × triglyceride +0.29 × waist circumference ≥90 cm (0 or 1).
Hosmer–Lemeshow goodness-of-fit test
As shown in Table 3, performance of Suita score (TC) new coefficients + covariates 2 were good in total, men, and women, in non-diabetic and diabetic men and women.
ROC curve, NRI, IDI, and DCA
As compared FRS or Suita score (TC), Suita score (TC) new coefficients + new covariates 2 significantly improve AUCs in total, men and women (Fig. 3(a)), also significantly improved AUCs in non-diabetic and diabetic men and women (Fig. 3(b)). As compared FRS or Suita score (TC), the overall category-free NRI and IDI of Suita score (TC) new coefficients with new covariates 2 also showed improvement in total, men, women and in non-diabetic and diabetic men and women (Tables 4 and 5). DCA indicated that curve discrimination of Suita score (TC) new coefficients with covariates 2 was improved compared to those of Suita score (TC) in diabetic men and women (Fig. 4).
Discussion
In the current study, we assessed how accurately the risk scores which were originally developed for predicting 10-year risk of CHD9 could predict 3-year risk of CHD in a large Japanese population. We obtained three major findings in the study. First, ROC curve distribution of Suita score (TC) was slightly different between vs FRS (TC) and NCEP-ATPIII FRS (TC) in total participants, but was almost equivalent when the population was divided into men and women. The AUCs were consistently low in Suita score (TC), FRS (TC) and NCEP-ATPIII FRS (TC), suggesting that these risk scores have only a limited power for CHD risk prediction in Japanese population. Second, ROC curve distribution, NRI and IDI, and DCA did not show clear differences between Suita score (TC) and FRS (TC)/ NCEP-ATPIII FRS (TC) in men and women with or without diabetes. Third, new models combining waist circumference ≥85 cm or proteinuria ≥1+ to Suita score (TC) or Suita score new coefficients (TC) (new risk prediction model 2) was proven better than its respective models, when assessed by AUC, NRI, IDI, and Hosmer–Lemeshow test. In addition, the AUCs of new risk prediction model 3 (Suita score (TC) new coefficients + new covariates 2) were also superior to those of the FRS and Suita scores in total, men and women, but the superiority was observed especially when population were subdivided to non-diabetic and diabetic men and women. Two new models could be useful to predict 3-year risk of CHD at least in Japanese population especially in diabetic population.
Epidemiological studies in Japan, such as Nippon Data 802,3 and the Hisayama Study9, reported that current risk prediction models are not adequate. Nakai et al.15 reported that, the expected CHD mortality rate was rather higher than the observed CHD onset in Nippon Data 80. The guidelines for prevention of atherosclerotic cardiovascular diseases in 2017, which had been established based on the Suita study, are increasingly used in Japan. However, the issue whether Suita score can be used satisfactory in real practice remains not fully evaluated. To the best of our knowledge, our study is the first to assess the utility of Suita score using a large Japanese population and clarified the limited ability discussed below. Nishimura et al.9 reported: FRS might overestimate CHD incidence in a Japanese general population, while Suita score (TC or LDL-C) could improve the estimation power. In our Japanese population, discrimination of Suita score (TC) for estimating CHD was slightly better compared to FRS (TC) and NCEP-ATPIII FRS (TC) in total participants, but the performance was comparable, when the population was divided into men and women. Also, Hosmer–Lemeshow test indicated that FRS (TC) did not fit in total participants but did in men and women subgroups as well as in FRS (TC), suggesting that both scores may be equivalent in the sex-specific risk prediction (Table 3). We assessed discrimination ability of Suita score (TC) in non-diabetic and diabetic men and women. ROC curve distribution, NRI and IDI, and DCA were partially better in Suita score (TC) than FRS (TC) or NCEP-ATPIII FRS (TC) in several subcategory, but the results were not consistent among ROC, NRI and IDI, and DCA. Because the CHD predictive models of Japanese especially in general population are limited10,12, we further sleeked a risk prediction model in participants with or without diabetes as discussed below.
Since the power of Suita score (TC) for CHD risk prediction was limited, we tried to create new models. Interestingly, combining waist circumference ≥85 cm or proteinuria ≥1+ to Suita score (TC) or Suita score new coefficients (TC) was proven superior to its respective models (new risk prediction model 2). Gender difference in covariates for CHD risk prediction has been discussed16.
Waist circumference is a useful and convenient substitute index for visceral fat, which is associated with insulin resistance17. In general, visceral fat accumulates more easily in men, and subcutaneous fat accumulates more easily in women18,19. Therefore, adding waist circumference tended to increase AUC in diabetic men (Suita score (TC) new covariates vs Suita score (TC), P = 0.068, Fig. 3(b)) is consistent with that of previous studies18,19. We reported that men with increased waist circumference was closely related to endothelial dysfunction, an early feature of CHD20,21. Insulin resistance is the other important residual risk factor of CHD22. We previously proved that endothelial dysfunction was correlated with individual metabolic risk components, such as diabetes, dyslipidemia, hypertension or visceral obesity, but most strongly with clustering of the components under a condition with low insulin sensitivity23. Although markers for visceral fat obesity and/or insulin resistance are not included in Suita score19, waist circumference is reported to be one such marker. Therefore, adding waist circumference to the CHD predictive model can be valuable.
In contrast, proteinuria was recently reported to be an independent cardiovascular disease (CVD) risk factor, which is different from e-GFR24. Irie et al.25 reported that the combination of proteinuria and e-GFR was an efficient predictor of CVD in the Japanese general population. Accordingly, adding proteinuria and including e-GFR to the Suita score were not contradicted in their report. Meanwhile, in our study, adding proteinuria to the Suita score demonstrated different results between men and women with diabetes, although the reasons for this remain unclear. Irie et al.25 also found that the age-adjusted relative CHD risk because of proteinuria was 2.90 (95% CI, 1.94–4.34) and 4.54 (95% CI, 2.93–7.04) in men and women, suggesting that the relative CVD risk with proteinuria was higher in women. The sex difference of CVD risk with proteinuria remains undetermined and further study is needed to clarify the issue. The utility of urinary microalbumin levels rather than considering proteinuria in the model might be more informative for CHD risk assessment26,27. We could not measure microalbuminuria due to limitation of cost. Alternatively, we compared the impact of proteinuria (±) and proteinuria (1+) on ROC: in diabetic men, Suita score (TC) AUC = 0.586 (95%CI 0.523–0.650, P = 0.005), plus proteinuria (±), AUC = 0.598 (95%CI 0.539–0.657, P < 0.001), plus proteinuria (+) AUC = 0.586 (0.524–0.648, P = 0.005); in diabetic women, Suita score (TC) AUC = 0.544 (95%CI, 0.475–0.613, P = 0.199), plus proteinuria (±) AUC = 0.573 (0.504–0.643, P = 0.033, plus proteinuria (+) AUC = 0.597 (0.526–0.668, P = 0.005). AUC was increased by addition of proteinuria (±) greatly in men, but slightly in women. Utility of dipstick proteinuria and albuminuria for CHD risk prediction need to be discussed in further studies28.
We also created new risk prediction model 3 (Suita score (TC) new coefficients + new covariates 2), in which the AUCs of were also superior to those of the FRS and Suita scores in total, men and women, but the superiority was observed especially when population were subdivided to non-diabetic and diabetic men and women. Addtiion of triglyceride, and drug of diabetes, hypertension, and dyslipidemia may increase the power of CHD prediction in thesubdivided groups. There are risk prediction scores for diabetic patients in the world29,30,31 and in Japan11. As compared to c-statics in CHD (male 0.65, female 0.71) in UK database30, CHD (0.74) in Hong Kong Diabetes Registry (HKDR)31, CHD (0.725) in JJ risk enjine11, AUC (c-statics) of current new Suita score (TC) (0.660 in diabetic men, 0.691 in diabetic women) was still low. It is suggested that including other potential covariates such as nutritional16 and genetic risk factors32,33 or family history of premature myocardial infarction34 to the model will be beneficial for a better risk prediction.
Our study has several limitations
First, the duration of observation was 3 years, which was shorter than that in previous studies. Also, the number of censored cases was large, and the reason of censoring could not be obtained by limitations of study design. It could give bias of samplings, which considerably influence statistical analysis. Although time-to-event analysis could not be obtained in the current analysis, we are planning to elongate periods of observations (~7 years) in the same population to validate our risk prediction model. Second, past medical history of diseases was determined only by medical interview, and evaluations were not fully objective. To compensate for the medical interview, the study physicians conducted a physical evaluation of each subject and reassessed their medical history. Third, the definition of CHD differed between the Suita study and ours. In the Suita study, CHD was defined as acute myocardial infarction, CHD followed by coronary artery bypass or angioplasty, and sudden cardiac death within 24 h after acute onset of symptoms, not including angina9. Meanwhile, we defined CHD as angina or myocardial infarction. The difference in definition of CHD can cause a difference in the prevalence of new-onset CHD. In fact, the prevalence of CHD was higher in our study. The new onset CHD cases could serve as an index of performance of Suita score, if this scoring is compared with percentage stenosis of coronary arteries. Our recent study indicated that FRS used in the current study was not largely associated with significant coronary stenosis (r = 0.197, P = 0.006) and Gensini score, an index of coronary atherosclerosis severity (r = 0.200, P = 0.005)35 on computed tomography angiography. Associations between CHD onset and coronary atherosclerosis need to be evaluated in terms of risk prediction scores in future studies. Fourth, types of medicines and diabetes duration could not be evaluated fully in an annual health check program. In diabetes, the past state of glycemic control, so-called “metabolic memory” or “legacy effect” can strongly affect onset of CHD, but that information cannot be obtained by our study, limiting our interpretation. Fifth, the assessment of our new prediction models should be done in other Japanese diabetic population databases. The features of the Suita study and annual health check program (SHCG) (this study) are compared in Supplementary Table 4, indicating two different Japanese population.
Conclusion
We demonstrated the differential assessment of the Suita score in a large population of Japanese men and women with and without diabetes. Adding waist circumference and proteinuria to the Suita score in men and women with diabetes, respectively, resulted in better discrimination. Because the costs are limited in an annual health check program, development of a low-cost and convenient marker is very important. We have shown a benefit of new Suita scores for CHD prediction as compared to original Suita score in diabetic participants. However, the discrimination ability of the scores remains unsatisfactory and thus future studies are warranted to develop better models.
Methods
Study population
This study was conducted as a part of the ongoing “Research on the Positioning of Chronic Kidney Disease in Specific Health Check and Guidance in Japan (SHCG)” project36,37. To determine external validations of the Suita and FRS scores, we analyzed data from participants who were followed up longitudinally from 2008 to 2011 based on the SHCG. The annual health check program, SHCG, was started by the Japanese government in 2008, targeting early diagnosis and intervention for metabolic syndrome in Japanese citizens aged 40–74 years. If necessary, public health nurses provide lifestyle interventions in participants who are at high risk for metabolic syndrome38. Data were collected and confirmed by the NPO Japan Clinical Research Support Unit (Tokyo, Japan).
Primary outcome and study design
The primary outcome was defined as new-onset CHD (angina or myocardial infarction). The flow chart of the participants’ recruitment is shown in the Supplementary Fig. 1. Of 667,218 participants with available data at baseline in 2008, 109,653 were available for longitudinal data until 2011. Of these, 41,301 were selected after 68,352 were excluded because of the missing data. We excluded 2673 participants because of baseline history of CHD (n = 1767) and/or cerebrovascular disease (n = 1065) and 2935 because of missing data on CHD in 2009, 2010, and 2011. Participants with TG ≥400 mg/dL (n = 314) were also excluded39. Finally, 35,379 participants (14,072 men; 21,307 women) were selected and analyzed.
FRS (original or National Cholesterol Education Program Adult Treatment Panel III [NCEP-ATPIII] version) and Suita score (TC or LDL-C version)
We calculated the FRS5 and NCEP-ATPIII FRS6, using data on age, sex, TC, high-density lipoprotein cholesterol level (HDL-C), SBP, smoking, DBP (FRS), diabetes (FRS)5, and anti-hypertensive drug intake (NCEP-ATPIII)6. Suita scores were calculated similarly to that in the Suita study (TC or LDL-C version), using data on age, sex, TC or LDL-C, HDL-C, SBP, DBP, smoking, diabetes, and e-GFR9.
Covariates
Trained staff measured height, BW, waist circumference, and SBP and DBP using a standard sphygmomanometer or an automated device on the right arm after resting for 5 min in a sitting position based on the recommendations of the Japanese Ministry of Health, Labor and Welfare40. The participants described age; sex; smoking and alcohol intake; anti-hypertensive, anti-diabetic, and anti-dyslipidemia medication intake; and history of CHD, cerebrovascular disease, and kidney dysfunction on a questionnaire. CHD was defined as angina or myocardial infarction; cerebrovascular disease, as cerebral hemorrhage or cerebral infarction; and kidney dysfunction, as chronic renal failure or need for dialysis. Blood samples were collected after overnight fasting. Centrifuged samples were analyzed by automatic clinical chemistry analyzer within 24 h of sampling. All blood samples were analyzed at local, rather than central, laboratories. Analyses were conducted by the methods for laboratory tests recommended by the Japan Society of Clinical Chemistry37. The analyzed factors were the following: fasting plasma glucose (FPG), HbA1c (JDS or National Glycohemoglobin Standardization Program [NGSP]), AST, ALT, γ-GTP, HDL-C, LDL-C, TG, uric acid (UA) and serum creatinine. In addition, HbA1c (JDS) was converted to HbA1c (NGSP), which was calculated as JDS + 0.4%41. e-GFR was calculated as follows: e-GFR (men) = 194 × Scr−1.094 × age−0.287 and e-GFR (women) = e-GFR (men) × 0.73942. Urine was tested using the dipstick method on spot urine specimens gathered from participants in the early morning after overnight fasting. Proteinuria was defined as positive ≥1+ and negative− or± 40. Alcohol consumption subgroups were classified as those who drink every day, drink sometimes, and drink almost never. Diabetes mellitus was determined by American Diabetes Association criteria43: FPG ≥ 126 mg/dL, HbA1c-NGSP ≥ 6.5%, or use of anti-diabetic medications. Hypertension was defined as SBP ≥ 140 mmHg, or DBP ≥ 90 mmHg, or anti-hypertensive medication intake. Dyslipidemia was defined as LDL-C 140 ≥ mg/dL, HDL-C ≤ 40 mg/dL, TG ≥ 150 mg/dL, or anti-dyslipidemic drug intake. If necessary, TC was calculated by the Friedewald’s method39, and participants whose TG was ≥400 mg/dL were excluded.
Statistical analyses
Subgroups of participants
We divided the participants into four subgroups of men and women with and without diabetes and assessed the risk prediction power of the Suita and FRS scores.
ROC curve, NRI, IDI and DCA
The risk score of new-onset CHD was calculated as the sum of the individual new coefficients in the Suita score (TC and LDL-C) and original and NCEP-ATPIII FRS. We then assessed the predictive performance for the risk score by drawing an ROC curve, by calculating the AUCs for ROC curve, and sensitivity, specificity, and positive and negative predictive values for cutoff values44. The cutoff value was determined by the maximum AUC value, and AUCS were compared by the DeLong test45.
Hosmer–Lemeshow test
We compared the predicted and observed incidence of new-onset CHD in each decile of risk score and performed the Hosmer–Lemeshow test to assess goodness-of-fit of the model. If P < 0.05, the model was regarded as no goodness of fit46.
New risk prediction model 1: Suita score (TC) +new covariates
Selection of covariates: Finally, to create a better predictive model, particularly in participants with diabetes, we evaluated the impact of adding covariates to the Suita score. As residuals in the Suita score, we selected potential covariates measured in the SHCG: abdominal obesity (waist circumference ≥85 cm in men, >90 cm in women)47, BMI,AST, ALT, γ-GTP, UA, proteinuria (≥+−),proteinuria (≥1+), FPG, HbA1c, and alcohol consumption (drinking every day, sometimes, and never). Crude odds ratio of new-onset CHD was calculated individually by adding a selected covariate to the Suita score, and the covariate (s) with the highest crude odds ratio was selected.
Assessment of covariates added to the Suita score: We assessed the influence of newly added covariates by comparing the adjusted odds ratio in multiple logistic regression. For an additional covariate, multicollinearity was checked with the VIF. If multicollinearity was less extent (VIF ≤ 2.5)48, we implemented the new covariate in the new model as bellow.
Developing modified Suita score: Using multiple logistic regression, we calculated the β-coefficients by adding new covariates to the Suita score. We multiplied the value 10 times and rounded the respective β-coefficients to create new coefficients primarily used β-coefficients:
Finally, we calculated the modified Suita score by adding a new covariate to the original Suita score.
Reclassification of new model of diabetes: Pencina et al.49 reported that NRI and IDI are valuable to evaluate the modified model’s ability of discrimination, which was assessed by evaluating AUC changes45. Finally, we drew a DCA of the Suita score and modified the score. DCA is the method of calculating the net benefit, which means the true positive value is subtracted from the false positive value50.
Calculation of the CHD probability by multiple logistic regression models: We calculated the probability of CHD for 3 years by multiple logistic regression based on the modified Suita score:
New risk prediction model 2: Suita score (TC) new coefficients +new covariates
Recalculation of regression coefficients: We developed the new prediction model by adding appropriate covariates to the Suita score as above [Suita score (TC) new covariates]. However, if the model performance of the original Suita score might be insufficient, which would possibly just come from “inaccurate” regression coefficients in the Suita score. Therefore, we develop another risk model in which all the coefficients included in the Suita score were entered as explanatory variables and check its model performance. The β-coefficients for CHD prediction, calculated using multiple logistic regression, were obtained for variables used in the Suita score (TC) [age, SBP, TC, HDL-C, HbA1c, eGFR, and current smoking]. Suita score (TC) new coefficients models were made based on results of discrimination (ROC, NRI, IDI and DCA) and calibration (Hosmer–Lemeshow test).
Adding covariates on Suita score (TC) new coefficients score: As in Suita score (TC) new covariates, other covariates other than Suita score (TC) new coefficients were tested. Crude odds ratio for new-onset CHD was calculated individually by adding a selected covariate to the Suita score (TC) new coefficients model, and the covariate(s) with the highest crude odds ratio was selected to the model. Furthermore, additionally develop risk models in which above coefficients included in the Suita score plus other covariates were entered as explanatory variables and check their model performance.
New risk prediction model 3: Suita score (TC) new coefficients +new covariates 2
Adding covariates 2 on Suita score (TC) new coefficients score: Finally, to obtain the best risk prediction models, we reconsidered a set of new comprehensive candidates of covariates: sex, age, BW, BMI, waist circumference, waist circumference (≥85 cm in men and ≥90 cm in women), SBP, DBP, FPG, HbA1c, AST, ALT, γ-GTP, HDL-C, LDL-C, triglyceride, uric acid, serum creatinine, eGFR, proteinuria, proteinuria (≥±), proteinuria (≥1+), smoking habits, drinking habits, drug information of diabetes, hypertension, and dyslipidemia (Supplementry Table 1A). We selected the newly selected covariates as new covariates 2 (Supplementry Table 1B) and the model performance were also assessed by Hosmer–Lemeshow test and ROC curve, NRI, IDI, and DCA.
Statistical applications
The data were expressed as mean ± standard deviation or %. For a two-group comparison, unpaired two-tailed t-test or Mann–Whitney U test were used for parametric or nonparametric distribution variables, respectively. The X2 test was used for non-continuous variables and the DeLong test was for AUC. P < 0.05 was considered statistically significant. Assessment in subgroups was completed by the model’s ability for discrimination (ROC curve and AUC)44 and calibration [the Hosmer–Lemeshow test]). For statistical analyses, we used SPSS (version 24.0; SPSS, Inc., Chicago, IL, USA) for basic descriptive statistics and R statistical package (R version 3.3.2) for ROC (pROC), NRI and IDI (PredictABEL), DCA (rmda) and Hosmer–Lemeshow test (ResourceSelection).
Ethics approval and consent to participate
All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee at which the studies were conducted (Fukushima Medical University; IRB Approval Number #1485, #2771) and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. This study was conducted according also to the Ethical Guidelines for Medical and Health Research Involving Human Subjects enacted by MHLW of Japan [http://www.mhlw.go.jp/file/06-Seisakujouhou-10600000-Daijinkanboukouseikagakuka/0000069410.pdf and http://www.mhlw.go.jp/file/06-Seisakujouhou-10600000-Daijinkanboukouseikagakuka/0000080278.pdf]. In the context of the guideline, the investigators shall not necessarily be required to obtain informed consent, but we made public information concerning this study on the web [http://www.fmu.ac.jp/univ/sangaku/data/koukai_2/2771.pdf] and ensured the opportunities for the research subjects to refuse utilizing their personal information.
Data Availability
The datasets during and/or analyzed during the current study available from the corresponding author on reasonable request.
References
Danaei, G. et al. National, regional, and global trends in fasting plasma glucose and diabetes prevalence since 1980: systematic analysis of health examination surveys and epidemiological studies with 370 country-years and 2·7 million participants. The Lancet 378, 31–40, https://doi.org/10.1016/S0140-6736(11)60679-X (2011).
Kadowaki, S. et al. Relationship of elevated casual blood glucose level with coronary heart disease, cardiovascular disease and all-cause mortality in a representative sample of the Japanese population. NIPPON DATA80. Diabetologia 51, 575–582, https://doi.org/10.1007/s00125-007-0915-6 (2008).
Ikeda, F. et al. Haemoglobin A1c even within non-diabetic level is a predictor of cardiovascular disease in a general Japanese population: the Hisayama Study. Cardiovasc Diabetol 12, 164, https://doi.org/10.1186/1475-2840-12-164 (2013).
Fox, C. S. et al. Trends in cardiovascular complications of diabetes. Jama 292, 2495–2499, https://doi.org/10.1001/jama.292.20.2495 (2004).
Wilson, P. W. et al. Prediction of coronary heart disease using risk factor categories. Circulation 97, 1837–1847 (1998).
The Examination Committee of Criteria for ‘Obesity Disease’ in Japan & Japan Society for the Study of Obesity. Executive Summary of The Third Report of The National Cholesterol Education Program (NCEP) Expert Panel on Detection, Evaluation, And Treatment of High Blood Cholesterol In Adults (Adult Treatment Panel III). Jama 285, 2486–2497 (2001).
Conroy, R. M. et al. Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J 24, 987–1003 (2003).
Collins, G. S. & Altman, D. G. An independent external validation and evaluation of QRISK cardiovascular risk prediction: a prospective open cohort study. Bmj 339, b2584, https://doi.org/10.1136/bmj.b2584 (2009).
Nishimura, K. et al. Predicting coronary heart disease using risk factor categories for a Japanese urban population, and comparison with the framingham risk score: the suita study. J Atheroscler Thromb 21, 784–798 (2014).
Arima, H. et al. Development and validation of a cardiovascular risk prediction model for Japanese: the Hisayama study. Hypertens Res 32, 1119–1122, https://doi.org/10.1038/hr.2009.161 (2009).
Tanaka, S. et al. Predicting macro- and microvascular complications in type 2 diabetes: the Japan Diabetes Complications Study/the Japanese Elderly Diabetes Intervention Trial risk engine. Diabetes care 36, 1193–1199, https://doi.org/10.2337/dc12-0958 (2013).
Yatsuya, H. et al. Development of a Risk Equation for the Incidence of Coronary Artery Disease and Ischemic Stroke for Middle-Aged Japanese- Japan Public Health Center-Based Prospective Study. Circulation journal: official journal of the Japanese Circulation Society 80, 1386–1395, https://doi.org/10.1253/circj.CJ-16-0081 (2016).
Tunstall-Pedoe, H. et al. Myocardial infarction and coronary deaths in the World Health Organization MONICA Project. Registration procedures, event rates, and case-fatality rates in 38 populations from 21 countries in four continents. Circulation 90, 583–612 (1994).
Ueshima, H. Explanation for the Japanese paradox: prevention of increase in coronary heart disease and reduction in stroke. J Atheroscler Thromb 14, 278–286 (2007).
Nakai, M. et al. Calibration between the Estimated Probability of the Risk Assessment Chart of Japan Atherosclerosis Society and Actual Mortality Using External Population: Evidence for Cardiovascular Prevention from Observational Cohorts in Japan (EPOCH-JAPAN). J Atheroscler Thromb 23, 176–195, https://doi.org/10.5551/jat.31286 (2016).
Lloyd-Jones, D. M. et al. Estimating Longitudinal Risks and Benefits From Cardiovascular Preventive Therapies Among Medicare Patients: The Million Hearts Longitudinal ASCVD Risk Assessment Tool: A Special Report From the American Heart Association and American College of Cardiology. Circulation 135, e793–e813, https://doi.org/10.1161/cir.0000000000000467 (2017).
Hiuge-Shimizu, A. et al. Absolute value of visceral fat area measured on computed tomography scans and obesity-related cardiovascular risk factors in large-scale Japanese general population (the VACATION-J study). Ann Med 44, 82–92, https://doi.org/10.3109/07853890.2010.526138 (2012).
Matsuzawa, Y. et al. Pathophysiology and pathogenesis of visceral fat obesity. Obes Res 3(Suppl 2), 187s–194s (1995).
Tchernof, A. & Despres, J. P. Pathophysiology of human visceral obesity: an update. Physiol Rev 93, 359–404, https://doi.org/10.1152/physrev.00033.2011 (2013).
Shimabukuro, M. et al. Hypoadiponectinemia is closely linked to endothelial dysfunction in man. J Clin Endocrinol Metab 88, 3236–3240 (2003).
Flammer, A. J. et al. The assessment of endothelial function: from research into clinical practice. Circulation 126, 753–767, https://doi.org/10.1161/circulationaha.112.093245 (2012).
DeFronzo, R. A. Insulin resistance, lipotoxicity, type 2 diabetes and atherosclerosis: the missing links. The Claude Bernard Lecture 2009. Diabetologia 53, 1270–1287, https://doi.org/10.1007/s00125-010-1684-1 (2010).
Shimabukuro, M., Higa, N., Masuzaki, H., Sata, M. & Ueda, S. Impact of individual metabolic risk components or its clustering on endothelial and smooth muscle cell function in men. Cardiovasc Diabetol 15, 77, https://doi.org/10.1186/s12933-016-0394-5 (2016).
Nagata, M. et al. Prediction of cardiovascular disease mortality by proteinuria and reduced kidney function: pooled analysis of 39,000 individuals from 7 cohort studies in Japan. Am J Epidemiol 178, 1–11, https://doi.org/10.1093/aje/kws447 (2013).
Irie, F. et al. The relationships of proteinuria, serum creatinine, glomerular filtration rate with cardiovascular disease mortality in Japanese general population. Kidney Int 69, 1264–1271, https://doi.org/10.1038/sj.ki.5000284 (2006).
Ali, M. K., Bullard, K. M., Saydah, S., Imperatore, G. & Gregg, E. W. Cardiovascular and renal burdens of prediabetes in the USA: analysis of data from serial cross-sectional surveys, 1988–2014. The lancet. Diabetes & endocrinology 6, 392–403, https://doi.org/10.1016/s2213-8587(18)30027-5 (2018).
Scirica, B. M. et al. Cardiovascular Outcomes According to Urinary Albumin and Kidney Disease in Patients With Type 2 Diabetes at High Cardiovascular Risk: Observations From the SAVOR-TIMI 53 Trial. JAMA cardiology 3, 155–163, https://doi.org/10.1001/jamacardio.2017.4228 (2018).
Iseki, K. et al. Dipstick proteinuria and all-cause mortality among the general population. Clinical and experimental nephrology, https://doi.org/10.1007/s10157-018-1587-x (2018).
Stevens, R. J., Kothari, V., Adler, A. I. & Stratton, I. M. The UKPDS risk engine: a model for the risk of coronary heart disease in Type II diabetes (UKPDS 56). Clinical science (London, England: 1979) 101, 671–679 (2001).
Bannister, C. A. et al. External validation of the UKPDS risk engine in incident type 2 diabetes: a need for new type 2 diabetes-specific risk equations. Diabetes care 37, 537–545, https://doi.org/10.2337/dc13-1159 (2014).
Yang, X. et al. Development and validation of a total coronary heart disease risk score in type 2 diabetes mellitus. The American journal of cardiology 101, 596–601, https://doi.org/10.1016/j.amjcard.2007.10.019 (2008).
Thanassoulis, G. & Vasan, R. S. Genetic cardiovascular risk prediction: will we get there? Circulation 122, 2323–2334, https://doi.org/10.1161/circulationaha.109.909309 (2010).
Houston, M., Minich, D., Sinatra, S. T., Kahn, J. K. & Guarneri, M. Recent Science and Clinical Application of Nutrition to Coronary Heart Disease. Journal of the American College of Nutrition 37, 169–187, https://doi.org/10.1080/07315724.2017.1381053 (2018).
Ridker, P. M., Buring, J. E., Rifai, N. & Cook, N. R. Development and validation of improved algorithms for the assessment of global cardiovascular risk in women: the Reynolds Risk Score. Jama 297, 611–619, https://doi.org/10.1001/jama.297.6.611 (2007).
Maimaituxun, G. et al. Local Thickness of Epicardial Adipose Tissue Surrounding the Left Anterior Descending Artery Is a Simple Predictor of Coronary Artery Disease- New Prediction Model in Combination With Framingham Risk Score. Circulation journal: official journal of the Japanese Circulation Society 82, 1369–1378, https://doi.org/10.1253/circj.CJ-17-1289 (2018).
Iseki, K. et al. Risk factor profiles based on estimated glomerular filtration rate and dipstick proteinuria among participants of the Specific Health Check and Guidance System in Japan 2008. Clinical and experimental nephrology 16, 244–249, https://doi.org/10.1007/s10157-011-0551-9 (2012).
Hasegawa, K. et al. Control Status of Atherosclerotic Cardiovascular Risk Factors Among Japanese High-Risk Subjects:Analyses of a Japanese Health Check Database from 2008 to 2011. J Atheroscler Thromb 23, 991–1003, https://doi.org/10.5551/jat.31906 (2016).
Wakasugi, M. et al. Association between combined lifestyle factors and non-restorative sleep in Japan: a cross-sectional study based on a Japanese health database. PLoS One 9, e108718, https://doi.org/10.1371/journal.pone.0108718 (2014).
Friedewald, W. T., Levy, R. I. & Fredrickson, D. S. Estimation of the concentration of low-density lipoprotein cholesterol in plasma, without use of the preparative ultracentrifuge. Clin Chem 18, 499–502 (1972).
Sato, Y. et al. Glycohemoglobin not as predictive as fasting glucose as a measure of prediabetes in predicting proteinuria. Nephrol Dial Transplant 27, 3862–3868, https://doi.org/10.1093/ndt/gfs324 (2012).
Kashiwagi, A. et al. International clinical harmonization of glycated hemoglobin in Japan: From Japan Diabetes Society to National Glycohemoglobin Standardization Program values. J Diabetes Investig 3, 39–40, https://doi.org/10.1111/j.2040-1124.2012.00207.x (2012).
Matsuo, S. et al. Revised equations for estimated GFR from serum creatinine in Japan. Am J Kidney Dis 53, 982–992, https://doi.org/10.1053/j.ajkd.2008.12.034 (2009).
Diagnosis and classification of diabetes mellitus. Diabetes care 34 Suppl 1, S62–69, https://doi.org/10.2337/dc11-S062 (2011).
Hanley, J. A. & McNeil, B. J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143, 29–36, https://doi.org/10.1148/radiology.143.1.7063747 (1982).
DeLong, E. R., DeLong, D. M. & Clarke-Pearson, D. L. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44, 837–845 (1988).
Hosmer, D. W., Hosmer, T., Le Cessie, S. & Lemeshow, S. A comparison of goodness-of-fit tests for the logistic regression model. Stat Med 16, 965–980 (1997).
The Examination Committee of Criteria for ‘Obesity Disease’ in Japan & Japan Society for the Study of Obesity. New criteria for ‘obesity disease’ in Japan. Circulation journal: official journal of the Japanese Circulation Society 66, 987–992 (2002).
Katz, M. H. In A Practical Guide for Clinicians and Public Health Researchers. 3rd ed. (Cambridge University Press, 2011).
Pencina, M. J., D’Agostino, R. B. Sr. & Steyerberg, E. W. Extensions of net reclassification improvement calculations to measure usefulness of new biomarkers. Stat Med 30, 11–21, https://doi.org/10.1002/sim.4085 (2011).
Vickers, A. J. & Elkin, E. B. Decision curve analysis: a novel method for evaluating prediction models. Med Decis Making 26, 565–574, https://doi.org/10.1177/0272989x06295361 (2006).
Nanri, A. et al. Development of Risk Score for Predicting 3-Year Incidence of Type 2 Diabetes: Japan Epidemiology Collaboration on Occupational Health Study. PLoS One 10, e0142779, https://doi.org/10.1371/journal.pone.0142779 (2015).
Sullivan, L. M., Massaro, J. M. & D’Agostino, R. B. Sr. Presentation of multivariate data for clinical use: The Framingham Study risk score functions. Stat Med 23, 1631–1660, https://doi.org/10.1002/sim.1742 (2004).
Acknowledgements
This study were supported by a Health and Labor Sciences Research Grant for the “Design of the comprehensive health care system for chronic kidney disease (CKD) based on the individual risk assessment by Specific Health Check” from the Ministry of Health, Labor and Welfare of Japan (K.A., K.I., T.M., K.Y., K.T., S.F., I.N., T.K., M.Ko., Y.S., M.Ka., and T.W.) and by a grant from the Ministry of Education, Culture, Sports, Science and Technology, Japan (MS, #16K01823).
Author information
Authors and Affiliations
Contributions
H.H. and M.S. explored the study concept, researched data, and wrote the manuscript. S.Y. and H.M. assisted statistical analysis. K.A., H.S., K.I., T.M., K.Y., K.T., S.F., I.N., T.K., M.Ko., Y.S., M.Ka. and T.W. collected data and constructed the database set. All authors discussed data and reviewed the manuscript and approved the final manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hirai, H., Asahi, K., Yamaguchi, S. et al. New risk prediction model of coronary heart disease in participants with and without diabetes: Assessments of the Framingham risk and Suita scores in 3-year longitudinal database in a Japanese population. Sci Rep 9, 2813 (2019). https://doi.org/10.1038/s41598-019-39049-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-39049-w
This article is cited by
-
Glucose variability and predicted cardiovascular risk after gastrectomy
Surgery Today (2022)
-
Utility of Liver Transplantation Within the Bounds of Non-futility
Current Transplantation Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.