Abstract
Escherichia coli have developed one of the most efficient regulatory response mechanisms to phosphate starvation. The machinery involves a cascade with a two-component system (TCS) that relays the external signal to the genetic circuit, resulting in a feedback response. Achieving a quantitative understanding of this system has implications in synthetic biology and biotechnology, for example, in applications for wastewater treatment. To this aim, we present a computational model and experimental results with a detailed description of the TCS, consisting of PhoR and PhoB, together with the mechanisms of gene expression. The model is parameterised within the feasible range, and fitted to the dynamic response of our experimental data on PhoB as well as PhoA, the product of this network that is used in alkaline phosphatase production. Deterministic and stochastic simulations with our model predict the regulation dynamics in higher external phosphate concentrations while reproducing the experimental observations. In a cycle of simulations and experimental verification, our model predicts and explores phenotypes with various synthetic promoter designs that can optimise the inorganic phosphate intake in E. coli. Sensitivity analysis demonstrates that the Pho-controlled genes have a significant influence over the phosphate response. Together with experimental findings, our model should thus provide insights for the investigations on engineering new sensors and regulators for living technologies.
Similar content being viewed by others
Introduction
Mechanisms of inorganic phosphate intake within the context of cellular processes is a topic of extensive research effort, also due to potential applications in enhanced biological phosphorus removal (EBPR) from wastewater. Phosphorous, which is one of the major causes of water quality problems, occurs in wastewater almost solely in the form of phosphates such as inorganic phosphate (Pi). Microorganisms, which are key players in bioremediation, have potential to treat large amounts of the pollutants and hold promise for renewable sources1. An in-depth understanding of the mechanisms controlling such processes should pave the way for metabolic engineering to lead to improvements in wastewater treatment.
The physiological characteristics of Pi transport in E. coli have been extensively studied2,3,4,5,6. Nonetheless, the regulatory interactions that control the Pi transport are complex, and they involve two major phosphate transport systems, depending on external Pi levels. The low affinity phosphate inorganic transport (Pit) system depends on the proton motive force; it is a coupled transporter of two different ions through the membrane2,7. The phosphate specific transport (Pst) system, on the other hand, is Pi-repressible, and it is induced when the external Pi concentration is depleted8,9,10.
Mechanistically, Pi signalling associated with the Pst system in E. coli, is a negative process, that is, excessive Pi is required for turning the system off. Activation is the default state and occurs in conditions of Pi limitation2,8,11. Signal transduction by environmental Pi requires seven proteins, which are thought to interact in a membrane associated signalling complex. These Pi signalling proteins include2,8.
-
Four components of the ABC transporter Pst (PstSCAB), which consist of an extracellular binding protein (PstS), two transmembrane proteins (PstC, PstA) that form the transmembrane domain (TMD), and a dimer of cytosolic peripheral proteins (PstB), i.e., the nucleotide-binding domain;
-
Two that are members of the large family of two component systems (TCS) that perform both positive and negative regulation, a sensor histidine kinase PhoR and a transcriptional response regulator PhoB;
-
The chaperone-like PhoR/PhoB inhibitory protein PhoU.
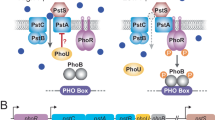
Figure 1 displays a schematic representation of the system in the starvation condition. When Pi is limited in quantity outside the cell, PstS binds to the Pi following its diffusion to the cell surface2,8,12. The transmembrane domain of the ABC transporter, that is, PstC and PstA are integral membrane proteins that span the entirety of the membrane. They regulate the translocation of Pi from PstS to the inner membrane2,3,8,12. Pi intake happens with the conformational changes in the PstB as a result of ATP binding, also known as ATP-switch model. This way, the ABC transporter provides the required increase in the amount of phosphate in the cell2,8.
The transmembrane signal transduction due to external Pi levels and the Pho regulon activity when extracellular inorganic phosphate (Pi) is in excess (left) and when it is depleted (right). The ABC transporter consists of the extracellular domain PstS, transmembrane domains PstA and PstC, and intracellular domains PstB (see the main text for the description). Left: when external Pi is in excess, the ABC transporter activity is limited as the cell does not consume ATP for the Pi transport. According to the current model in the literature, PhoR assesses Pi availability by monitoring the activity of Pst transporter, and relays the signal from PstB via PhoU to PhoR. When the Pi influx is increased, PhoU stabilises PhoR, which is depicted with the green bars around PhoU. This prevents PhoR dimers from autphosphorylating (red). Consequently, the tanscription factor PhoB does not become phosphorylated by PhoR. Right: Due to the ABC transporter activity, the external Pi binds to the PstS component of the ABC transporter. It is then translocated to the inner membrane domain of the transporter through PstC and PstA. Following this, PstB changes its conformation by consuming ATP. Pi is internalised and released to the cytosol. When the Pi influx through the ABC transporter decreases, PhoU does not stabilise PhoR, which is depicted with the red bar next to PhoU. As a result of this, PhoR becomes free to perform its auto-kinase-phosphotransferase activity, whereby it phosphorylates PhoB. Phosphorylated PhoB then forms a dimer to act as a transcription factor for the operons, resulting in PhoA, PhoB and PhoR expression.
The low activity of the ABC transporter PstSCAB causes, in a number of steps, the autophosphorylation of the sensor kinase PhoR, which relays the signal to the transcription factor PhoB. The current evidence suggests that PhoR and eventually PhoB assess Pi availability by monitoring the activity of Pst transporter via PhoU11,12. In mechanistic terms, when there is sufficient Pi flux, PhoU stabilizes PhoR. The resulting stable conformation prevents PhoR from auto-phosphorylation. This, in return, prevents the down-stream signalling that would otherwise result in the expression of the genes that feedback to the Pst system for further Pi intake. In fact, when PhoU is deleted, PstB does not only continue to spend ATP and transport Pi, but PhoR acts as a constitutive PhoB kinase, leading to high expression of the Pho regulon genes2,8, and thereby, activating the expression of the Pst system. On the other hand, when external Pi is limited, PhoU does not stabilise PhoR. Consequently, PhoR is freed to bind phosphoryl groups and passes to the active state. Active PhoR phosphorylates PhoB. Phosphorylated PhoB then acts as a transcription factor for the operon.
All experimental evidence indicates that Pho regulon is controlled by external phosphate limitation rather than internal3. When the surrounding environment has abundant phosphate, E. coli uses as few resources as possible to facilitate the phosphate intake. However, when Pi becomes low outside the cell, it turns into a growth limiting factor and the cell spends energy to up-regulate the expression of target genes that are used to acquire phosphate. Previous studies have shown that the TCS plays a central role in sensing the Pi level in the environment and regulating the expression of genes that are directly involved in the intake2,12.
Although much is known about the molecular aspects of this signal transduction pathway, a comprehensive and structured mechanistic model of the Pho regulon is currently unavailable3. Here, we investigate the relationship between Pi-starvation, the TCS signalling, and promoter activity by using a combination of wet lab experiments and dynamic modelling. This work introduces the proteins involved in phosphate starvation response mechanism. Our model describes the phosphate starvation response at the genetic level by considering all system variables that affect the phosphate starvation response. We consider components where phosphate starvation response of TCS model is described in terms of their interactions. The model is composed of a set of ordinary differential equations and the corresponding stochastic model that are derived from a chemical reaction network. The model provides a quantitative description of how different processes interact to form a positively-regulated biological control system. The mechanism is based on an E. coli Pi-starvation signalling system. Our model displays how specific TCS proteins work together to provide gene expression and increase in Pi intake, and provides a set up for identifying a wide family of promoter mechanisms that potentially have synthetic applications.
In recent years, significant advances have been made in understanding the role and the structure of TCS and signalling mechanisms. It is known that most bacteria species have more than 10 different TCS13. Moreover, in E. coli, 30 sensor kinases and 32 response regulators have been found14. Although there is large qualitative knowledge, especially for E. coli, quantitative research is still scarce. A model for PhoR/PhoB signal transduction was set up by Van Dien and Keasling earlier3, whereby the authors have determined a model for the induction of PhoA. Models for other signal transduction systems in E. coli are described by Wong et al., Fisher et al., and Koh et al.15,16,17. Recently, research groups have only just begun to use modelling in combination with experimental data to analyse the TCS especially PhoR and PhoB4,18. Gao et al. built quantitative analyses of PhoR and PhoB protein concentrations and activities. They showed that the experimental data and protein expression levels of TCSs matched. Recently, Gao and Stock et al.19 built a quantitative analyses of TCS switch off mechanism. However, to the best of our knowledge, there has been no focus on developing genetically encoded signal transduction pathways leading to transcription factors.
In this work, we have developed an approach combining wet-lab experiments and modelling to show that rates of histidine kinase and promoter activities can be used to tune TCS detection thresholds. We have described the steps in the design of a synthetic biological system based on the use of TCS. This should constitute a contribution to the research on genetically modified bacteria that detect environmental changes and respond to higher inorganic phosphate levels. In order to better understand the quantitative analyses of protein concentrations in response to modifications and activities in the environment, we have focused on the activation response of the TCS components PhoB and PhoR. Our model should thus help to better understand the dynamic behaviour of system activation, and to quantitatively evaluate the role of phosphatase activity under varying external Pi conditions.
The model includes TCS members and activation of the Pho regulon promoters pPhoB and pPhoA. Experimental data is used to fit the parameters to the feasible physiological range given in the literature, and to determine the relative sensitivity to the parameters. The simulations with our model provide a dynamic description of the mechanisms. With a combination of wet-lab experiments and computer simulations, we use our model to quantify dynamic mechanisms of auto-regulation in E. coli in response to varying external phosphate levels, and explore and verify emerging phenotypes with synthetic promoters. Simulations with the model do not only reproduce our experimental measurements, but also predict phenotypes with various synthetic promoter designs that can optimise the Pi intake in E. coli. Sensitivity analysis on the parameters demonstrate the influence on the expression of Pho-controlled genes and the gain of the system under variations in transcription efficiency in response to external phosphate concentration. The model can thus serve as a virtual lab, and can be used to test various promoter designs for enhanced Pi intake in biotechnology applications for phosphate sequestration.
Results
Phosphate intake at starvation requires rapid activation of PhoB dimers
Figure 2 provides a schematic representation of the control model set up with the experimental data and the formal model. The control model is set up with respect to the initial phosphate starvation in accordance with the experimental data and the parametrisation and fitting procedure described in Methods. In first of the two steps, the blue curves in Figs 2C and S2 are obtained by using only the experimental values of PhoA levels. When external Pi is abundant, the Pst system inhibits the activation of TCS, and consequently the Pi intake; PhoA is then expressed at a basal level. However, when Pi is limiting, inhibition of TCS is relieved, resulting in the activation of PhoA transcription. The alterations of PhoA expression can thus be interpreted to an extent as an indicator for the changes in external phosphate level and Pi intake.
Schematic representation of the experimental data and the control model, and its dynamics in response to varying external Pi concentrations. (A) The data for the PhoA and PhoB expression are obtained using PCR amplified DNA from E. coli MG1655 genome and transcriptionally fused to the translational coupler BCD2 and the fluorescent ms-fgfp gene. (B) The control model has been obtained from the experimental data and the chemical reaction network (CRN) described in Methods by applying a fitting procedure with the physiological ranges obtained from the literature in Table 1, and verified by sensitivity analysis. The deterministic ODE and stochastic simulations are performed by applying the standard translation from CRNs based on stoichiometry. The blue color denotes the proteins, orange denotes the promoters in their active and inactive forms, and purple denotes the mRNA molecules. Filled arrowheads denote the reversible reactions. The red arrows denote degradation reactions, the green arrows denote complexations, the black arrows denote phosphorylation and dephosphorylation, and the blue arrows denote the transcription and translation reactions. The model species that are plotted in C and D are distinguished with frames. (C) The dynamics of the highlighted species of the control model in panel B as a result of the fitting procedure together with the experimental data, as described in Methods, are plotted. In the first of the two steps, the blue curves are obtained by using only the experimental values of PhoA levels. In the second step, that delivers the control model, the red curves are obtained by using the experimental values of both PhoA and PhoB levels. Inclusion of the PhoB data highlights the contribution of the feedback mechanism to the response dynamics, which is otherwise not represented. The stochastic dynamics, plotted in grey, display the fluctuations in the control model that are due to small molecule numbers and are not observable in the deterministic simulations. (D) The response of the control model to variations in the external Pi levels, which are represented as fold change factors, applied to the autophosphorylation propensities of PhoR. A higher external Pi concentration corresponds to a smaller factor and vice versa.
In these simulations, in response to external Pi level at 0 μM, the system initiates the activation of PhoR, given by the autophosphorylation of both of the monomers in the stable dimer. This results in the subsequent transfer of phosphoryl groups. As a consequence, the response regulator PhoB rapidly becomes active and dimerises to form active transcription factors. The resulting rapid increase in the promoter activity delivers the mRNA transcription, and the consequent experimentally observed levels of PhoA.
At a second step in our analysis, to highlight and contrast the role of PhoB dynamics in the feedback mechanism, we have refined the model to include the experimental data on PhoB expression. The resulting red curves in Figs 2C and S2 are obtained by using the relative experimental levels of both PhoA and PhoB in the fitting procedure. The rates in Table 1 are obtained as a result of this fitting procedure that delivered the control model parameters, whereby we have enforced the displayed physiologically boundaries. The difference in the phenotype between red and blue curves in Fig. 2C should thus highlight the role of the feedback of the PhoB and PhoR expression to the system.
We have performed a large scale analysis of the system dynamics of the control model in terms of the fitted parameter values within a broader range. We have first analysed the broader effect of the TCS disassociation rates (r3r, r5r, r7r, r8r) on the dynamics and the PhoB transcription and translation parameters that deliver the expression of PhoB (r14, r15), which is a transcription factor. The cumulative output of different simulations with fold changes that cover the physiological intervals for r14 and r15 as well as a broad range for r3r, r5r, r7r, and r8r are depicted in Figs S3, S4, S5, S6, S7 and S8, respectively.
In these simulations, the dissociation rates of PhoR and PhoB, that is, r3r and r5r, have transient effects on the steady state concentrations of the complexes formed by these molecules. These rates do not modify the PhoB activity or the levels of PhoA and PhoB as shown in Figs S5 and S6. Variations in the dissociation rate of PhoB, given by r7r, affect the activity of PhoB as a transcription factor, however this has a minor effect on the transcription and translation of PhoB and none on PhoA (Fig. S7). On the other hand, the dissociation rate of the inactive PhoR from the active PhoB, given by r8r, affects the activation of PhoB as a transcription factor in a proportional way, yet its effect on promoter activity is negligible (Fig. S8). As it can be seen from Table 1, there are also other parameters that have an effect on both system dynamics and PhoB activity. Nonetheless, these are not suitable candidates for modification at this first analysis due to their physiologic ranges, and they are discussed below.
As it can be observed in Fig. 2, and supported by the analysis above, the simulations that include the PhoB data for parametrisation result in faster response dynamics, measured in terms of the time required to reach a peak state. This can be explained by the self-feeding role of the TCS, and the resulting increased requirement for the active transcription factors to sustain the experimentally observed protein levels due to their feedback to the network: because PhoR and PhoB are encoded by the same operon, not only PhoB levels, but also PhoR levels increase as a result of the changes in the reaction rates. This causes the cell to increase the sensor histidine kinase levels, resulting in a more immediate response. The response time thus decreases with an increase in the amount of sensor histidine kinase as well as an increase in its activity.
The deterministic ODE simulations lead to observations that describe the average dynamic behaviour of the variable concentrations for the simulated 4.5 hours. To observe the possible fluctuations in the system, we have performed stochastic simulations. This way, we have been able to compare the mean behaviour with the regulatory dynamics that incorporates the noise due to smaller molecular numbers. Figure 2 as well as Figure S2 include a comparison of the deterministic and the stochastic simulations. The stochastic simulations are performed by applying the standard conversion to obtain molecule numbers from the concentrations. The grey fluctuating lines show the stochastic results at a single representative simulation; the simulation shows the expected fluctuations in the model species with smaller numbers such as mRNA molecules as well as the qualitative agreement between the stochastic and the deterministic simulations.
Binding and unbinding of transcription regulators are a primary mechanism for gene regulation, whereby transcription factors operate at a fast time-scale. While the rate of binding of transcription regulators are known in many cells, little is known about how cells can modulate their unbinding for regulation20. The unbinding rate of an active transcription factor can thus vary over many orders of magnitude6,20. Therefore, in the initial analysis, we have fixed the transcription factor unbinding rates (r10r, r11r) to 1000 s−1 as shown in Table 1, and analysed the system behaviour with respect to variations.
To this end, we have experimented in stochastic simulations with different DNA unbinding rates, that is, r10r and r11r, from 100/s up to 5000/s. In accordance with the common practice, we have used stochasticity to quantify the noise that arises from the binding of a regulatory protein to a promoter21. The resulting amplification in oscillations in stochastic simulations, shown in Fig. 3 as well as Figs S9, S10 and S11, are due to the increase in the promoter unbinding rates. In Fig. 3, we have quantified the decrease in noise in the steady state distribution of mRNA and active promoter levels in terms of the ratio of the standard deviation over the mean. In this respect, the deterministic simulations display how DNA binding rates affect the mean behaviour, while the stochastic simulations bring about the loss of coherence due to noise in gene expression. Figure 3B displays the simulations with the rates of the control model. In Fig. 3A, DNA unbinding rate is decreased by an order of magnitude, whereas in Fig. 3C, the effect of a higher DNA unbinding rate of 5000/s is depicted. These results indicate that lower unbinding rates, as observed in saturation conditions, are required for stable gene regulation that is not affected by noise. This also reflects how both genetics and noise due to environmental factors can affect the development of targeted pathway interventions for faster Pi accumulation.
The variations in the mRNA and active promoter levels due to the unbinding rate of the promoter and the active transcription factor. An unbinding rate of 100/sec (A) results in much less spread in the steady state distributions in comparison to unbinding rates of 1000/sec (B) and 5000/sec (C). The variations are quantified as the ratio of the standard deviation and the mean.
The results above show that our control model provides detailed predictions about the complex effects of production pathways of the Pi accumulation system. The simulations are in good agreement with the experimental data and the general concepts described in the literature for the functionality of Pho regulon2,3. The control model proposed can thus serve as a virtual lab, which can be used to test and justify the theoretical approaches on the Pi intake system.
PhoR tunes the P i intake both up and down
Besides the chemical properties of the proteins in the regulatory system4, also the activity of the TCS proteins influence the Pi intake. Moreover, as displayed in Fig. 2C, the feedback mechanism due to the increased expression of sensor histidine kinase PhoR and the response regulator PhoB introduces a speed-up of an hour in comparison to the simulations, where this feedback mechanism is not taken into consideration. This indicates that a faster response in terms of Pi intake is delivered by an increase in the histidine kinase levels as well as the increase of its activity due to signalling.
A notable feature of the Pi response system is that the sensor histidine kinase is bifunctional: it participates in both phosphorylation and dephosphorylation of its cognate response regulator. In this respect, the TCS autoregulatory design is a distinct mechanism from the conventional positive feedback loops. The bifunctional PhoR component is an autokinase with concomitant opposing phosphatase activity22,23,24.
The dual role of PhoR is a mechanism that enhances signal robustness18,25. Moreover, it has also been shown that the phosphatase activity in TCS provides a rapid dephosphorylation mechanism that shuts off the system, and thereby restores it to the original state19. Such a dynamics can be triggered, for example, by an increase in the external Pi concentration and the consequent decrease in the autophosphorylation activity of PhoR.
We have analysed the effect of the changes in autophosphorylation rates to the system behaviour. Because autophosphrylation becomes possible when the starvation signal prevents PhoU from inhibiting PhoR, the propensity of autophosphorylation depends on the incoming signal, which is a function of the external Pi levels. By decreasing the autophosphorylation propensity by applying various fold changes, we can thus see the effect of an increase in external Pi concentration on the system as depicted in Figs 2D and S12. In these simulations, a decrease in PhoR activity due to increased external Pi concentration results in a proportional decrease in the active PhoB dimers, and a decrease in the promoter activity as well as the PhoR activity.
A complementary realisation of this mechanism is given by the association of PhoB to PhoR, that is, r8. Although the physiological range for this parameter is narrow, as a result of a hypothetical increase in the association rate of PhoB and PhoR, the PhoB concentration stays low for a longer time period and the levels of active PhoB dimers decrease proportionally as displayed in the fold change experiments in Fig. S13.
In our model, we assume that the growth in the cell culture within the considered time interval is negligible. However, due to cell cycle, which has a time scale in the order of an hour, the protein concentrations can be subject to dilution besides the active degradation of the molecules we have considered. To this end, Figs S14, S15 and S16 explore the effect of higher degradation rates due to dilution in growth conditions, (r17, r18, r19, r20, and r21), together with higher external Pi levels, given with a decrease in the rates r1 and r2. As it can be seen in Fig. S12, a decrease in the autophosphorylation rates does not only lower the steady state levels, but also slows down the activation of the transcription factor by preventing the formation of an initial peak in DiPhoBpp levels. A concomitant increase in the degradation and dilution rates delays reaching a steady state. However, this does not drastically alter the eventual active DiPhoBpp concentrations.
Starvation response can be obtained with synthetic promoters at higher external P i concentrations
The simulation results in Figs 2D and S12 demonstrate the system’s adaptation to the stimuli due to Pi concentration, whereby the autophosphorylation propensity of PhoR acts as a proxy for the external Pi levels. These simulations predict how changes in the external Pi concentration affect the Pho regulon, and in particular, how the promoter activity decreases with an increase in the external Pi concentration. These results thus confirm that the adaptation of gene expression is clearly dependent on the Pi response stimuli2,12. Moreover, the model provides a mechanistic explanation for the interplay between the system components under the conditions of varying external Pi concentrations, which result in variations in the promoter activity.
It is well established that the protein production rate is greatly influenced by the specific nucleotide sequence of the promoter26,27,28. In this respect, synthetic biology and genetic engineering methods aim at synthesising promoters with the desired strength. To this end, in order to observe the possible variations in gene expression due to variations in promoter strength, we have performed a class of simulations. The results of these simulations in Fig. 4 display measurements of the steady state levels of PhoA promoter activity (pPhoAa) as well as the PhoA yield of the system as the resulting product in terms of the area under the curve (PhoA AUC).
Heatmaps for the activity of various promoter designs for pPhoA and pPhoB, and the resulting PhoA expression (bottom-row) under different external Pi concentration conditions. The heatmaps are ordered decreasingly from left to right according to the external Pi concentration given by the fold changes applied to the PhoR autphosphorylation reactions r1 and r2. The left most column with 1 as the fold change value is the starvation condition with 0 μM external Pi. Each heatmap scans 100 simulations by applying 10 different fold change values to the promoter binding rates r10 and r11 as well as 10 different fold change values to the promoter unbinding rates r10r and r11r. The upper row displays the resulting steady state levels of the active promoter pPhoAa, whereas the lower row displays the yield of PhoA gene expression measured as the area under the curve (AUC). The intersection of the dashed lines in the left column delivers the experimentally observed regime observed in Fig. 2. The levels of this regime, that display the starvation response, are highlighted in all the heatmaps.
In these simulations, we have scanned regimes with varying external Pi concentrations simulated by applying fold changes to the rates r1 and r2 as in the simulations in Figs 2D and S12. We have applied a fold change of 1 for the control regime with 0 μM external Pi, and 0.5, 0.2 and 0.1 for increasing external Pi levels. For each external Pi regime, we have scanned 100 different promoter designs by means of simulations that apply 10 fold change values from 0 to 2.5 with steps of 0.25 to the promoter binding rates r10 and r11 as well as 10 such fold change values to the promoter unbinding rates r10r and r11r. The heatmaps resulting from these 100 simulations are depicted in Fig. 4, where the control values for 1 fold change for binding and unbinding rates are marked by dashed lines.
We have further assessed our analysis to factor for the possible effects of stress response in Pi starvation conditions. As depicted in Fig. S17, Pi limitation induces the general stress response regulated by RpoS, sigma factor29,30. Concomitantly, Pi limitation increases the intracellular level of guanosine tetraphosphate (ppGpp), which is known as stringent stress response12,30,31. RpoS and ppGpp are thought to maintain a balance between vegetative and stress/starvation states of E. coli. The ppGpp nucleotide induces RpoS accumulation32. The RpoS responds to stress and shifts transcription away from vegetative growth and towards stress resistance31,32,33,34. Accumulation of ppGpp triggers the stringent response and a radical decrease in ribosome and protein synthesis, even leading to growth arrest31. When the level of RpoS is higher, E. coli is more resistant to stress but grows more slowly under a variety of conditions32,33.
It is known that RpoS and ppGpp direct RNA polymerase to promoters, and negatively affect the expression of several PHO genes with varying effects18,35,36. We have assessed the effect of the RpoS and SpoT activity on the system by applying sensitivity analysis on the transcription rate of PhoB, as depicted in Fig. S3 for r14. In the light of this analysis, we have investigated the effect of stress response on the results depicted in Fig. 4, whereby the model is calibrated under varying stress response conditions due to Pi starvation. By repeating the analysis in Fig. 4 under these conditions, we have tested the activity of various promoter designs (Fig. S18). These results confirm the previous observations, and indicate that stress response can have a modulating effect, which can however be factored for by promoter design.
These results indicate that the steady state promoter activity and the PhoA yield are highly correlated in all the regimes and for all the promoter binding and unbinding rates. As expected, when the control system’s output in Pi starvation condition is compared with the output in regimes with increased external Pi, we observe a decrease in PhoA yield. Moreover, these results predict that in order to obtain the starvation response in the conditions with higher external Pi concentration, promoter binding rates need to be increased and unbinding decreased. Promoters that provide the required strengths can be obtained by modifying the nucleotide sequences, for example, as in28,37,38.
We have tested the predictions of the model on experimental data obtained with the synthetic promoter under starvation conditions with 0 μM external Pi concentration. Moreover, we have used the model to explore the effect of such synthetic promoters under various external Pi concentration conditions. The experimental data and the simulation results with our model are depicted in Fig. 5. The selected synthetic promoter verifies the model predictions as it has a similar behaviour as the control model for the pPhoA promoter in starvation conditions. Moreover, the model further predicts the synthetic promoters with increased strength, given with higher binding rates and lower unbinding rates, deliver responses similar to the starvation response, also in the presence of higher external Pi concentrations. Within a modular framework, the simulation results mechanistically quantify how changes in the genetic components affect the behaviour of the circuit.
Comparison of the experimental data on PhoA expression with the synthetic promoter together with the simulation results with varying external Pi concentrations and promoter parameters that model synthetic designs. The experimental data on the starvation response with the synthetic promoter is represented as hollow circles. As in Fig. 4, the plots are ordered decreasingly from left to right according to the external Pi concentration given by the fold changes applied to the PhoR autphosphorylation reactions r1 and r2. The left most column with 1 as the fold change value is the starvation condition with 0 μM external Pi. Each plot displays four simulations with varying fold change values applied to promoter binding and unbinding rates that model various promoter designs. A modified promoter (blue curve) can reproduce the starvation response in low as well as high external Pi concentration, and reproduce the experimental data under the synthetic promoter starvation conditions.
Sensitivity Analysis
To assess the sensitivity of our model to the parameters, we have performed a two-step analysis. In the first step, we have considered the physiological interval of the parameters given in Table 1. For this analysis, we have only included the rate parameters that have been taken from literature and have been estimated within a given range. For each parameter, we have run simulations by instantiating the model with the maximum and minimum values of its physiological range, and, for each species, we have computed the yield of the system in terms of the area under the curve (AUC). Figure 6 displays the results obtained by taking the difference of the AUC for the maximum and minimum parameter values, normalised with the AUC of the control model. The resulting heatmap quantifies the impact of each parameter on the system dynamics with respect to plausible variations within its physiological range. The results demonstrate that the changes in the translation parameters are more pronounced than in the others. Moreover, in accordance with the results above, the autophosphorylation rate of PhoR impacts the active transcription factor levels and the transient species that lead to it.
Heatmap displaying the results of the sensitivity analysis by considering the physiological interval in Table 1. For each parameter, the maximum and minimum values within its physiological range are considered for simulation, and the area under the curve (AUC) for each species is computed. The difference of the AUC for the maximum and minimum parameter values are then normalised with the AUC of the control model. Red represents the decreasing effect and green represents the increasing effect.
In the second step, we have performed a sweeping analysis by considering all the model reactions and species within a range of 3 orders of magnitude both up and down. That is, each reaction rate is multiplied with a fold-change factor within a spectrum of 6 orders of magnitude, that is, from 10−3 to 103. We have then computed the AUC for each species and normalised the outcome with the AUC of the control model. The heatmap depicted in Fig. S19 quantifies the impact of these changes and predicts the system behaviour under hypothetical conditions simulated by such variations in parameters.
Discussion
We have presented a computational model and its experimental validation for quantifying dynamic mechanisms of auto-regulation in Escherichia coli in response to external Pi levels. Our model provides a mechanistic explanation of the interplay between transcriptional regulatory network, given by a two-component system (TCS) and Pho regulon, and promoter efficiency under variations in external Pi concentrations. Being parameterised within the physiological ranges of its components, the output of the model in terms of gene regulation delivers the expected system dynamics. The results provided by the model are in good agreement with the theory and the general concepts described in the literature for the functionality of Pho regulon2,3. The model provides predictions for the complex effects of TCS activity and consequent dynamics, including synthetic promoters with varying affinities to their transcription factor. A direct validation of the predictions is provided by the good fit of the experimental data.
With these insights, this work offers a mechanistic understanding of inorganic phosphate intake, realised by Pho regulon in a way that connects signalling with the genetic level. It provides a quantitative description of how different proteins interact to form a biological control system. It also describes the control of the phosphate-starvation response at the genetic level. Our work provides measurements of protein, phosphorylation, and promoter activity levels that are fundamental to define features of TCS circuits. One of the major outcomes is that our results do not only explain the observed experimental data, but also provide predictions on the physiology of the Pho regulon and insights for the synthetic promoter design. Moreover, our work has implications for applications in artificial life and for others in biotechnology that exploit such mechanisms. As the model architecture is intrinsically open to integrate supplementary layers, together with experimental findings, it should provide insights in investigations on engineering new dynamic sensors and regulators for living technologies.
Our model describes the responsive structure of the TCS system, which can be used to synthesize bacteria that detect changes in their environment and respond by modulating the synthesis and intake. Applications of such an engineering approach for bacteria should provide a basis for a new generation of bio-materials. We have presented a recipe for the design process of such an application, which integrates gene expression data from E. coli into a computer model.
Our model, which includes 29 reactions that describe the dynamic behaviour of the key regulatory network components, provides a quantification of the phosphate starvation response by means of both deterministic and stochastic simulations. The deterministic simulations allowed us to estimate the missing parameters of the model and analyse the mean behaviour of the system dynamics. In particular, we have exposed the phosphorylation cycle in TCS signalling and its role in the positive feedback mechanism in determining the network yield in terms of PhoA. Moreover, the steady state properties of the system could be displayed by sensitivity analysis on deterministic simulations.
In accordance with the common practice, we have employed stochastic simulations to highlight the effect of noise in the system39. As expected, the stochastic simulations are consistent with the deterministic simulations, which display the mean behaviour. Stochastic simulations, on the other hand, capture the noise due to small species numbers and concomitant fast and slow reactions. As a result of this, stochastic simulations with our model display the fluctuations observed in experimental observations, thereby exposing the fluctuations due to binding and unbinding of the transcription factors with the promoters, which operate at a much faster time scale in comparison to the preceding signalling cascade40,41,42. In these simulations, higher unbinding rates result in greater fluctuations that correlate with the decrease in binding saturation, a requirement for a robust signal. While confirming the notion that the complex networks of interacting molecules within cells should be robust43,44, these results highlight the additional role of the transcription factor unbinding rate in tuning the protein synthesis. Our stochastic simulation results, together with the experimental data on PhoB concentration in wild-type, suggest that the noise at the level of promoters controls the phenotypic variability in the mean behaviour. Large levels of noise at the level of PhoA and PhoB promoters are results of DNA unbinding rates. Moreover, our model shows that the smaller DNA unbinding rates also reduce the response time.
Our results confirm that the dynamics of the TCS and its responsiveness to both genetic and environmental perturbations play a key role in tuning the E. coli Pi response. In this respect, with parameter values obtained by fitting the experimental data on PhoA and PhoB promoters, we have investigated and identified the response dynamics of individual system species. Moreover, we have analysed synthetic promoter affinities that reproduce the wild type response to Pi starvation. For this purpose, we have tested and verified the model with experimental data for the response regulator binding affinity to infer the functional relation between the fraction of bound response regulator and the transcriptional activity. We have then quantified the effect of each protein in the pathway, through sensitivity analysis, singling out the main regulator mechanisms of the TCS.
Our results indicate the extent to which synthetic promoters can be tuned for various TCS detection thresholds such that the organism adapts to various environmental conditions. In this regard, because our model includes mechanisms for quantifying the information E. coli has about its phosphate environment, the model can be used to perform further experiments on the Pi intake system. Moreover, it can be used to explore and test various promoter designs, for example, in biotechnology applications such as sensors for wastewater treatment or detecting environmental pollutants to relocate towards them.
In conclusion, our study reveals how the tight interplay between theory and wet-lab experiments greatly helps to improve our understanding of bacterial sensing and signalling pathways. In particular, the TCS component of our model, which relays the signal on environmental changes to the genetic components for tuning protein expression, belongs to one of the largest and most diverse families of sensory components in biology. In this respect, the TCS features examined in this work provide a template for the models of similar systems that regulate the response for various external signals. An improved and quantitative understanding of such systems by formal mechanistic models will likely contribute to our understanding of the engineering of biosensors for diverse synthetic biology applications.
Methods
The model is based on a mechanistic description of the system dynamics within a chemical reaction network representation with respect to mass action kinetics. To build the simulation model, we have selected the part of the system from the TCS to gene regulation, and used the promoter activity as well as the levels of active transcription factor as indicators for quantifying the response to external Pi levels.
In the following, to better illustrate the response of Pho regulon and TCS signalling to the Pi starvation, we describe the network in terms of the interactions of system components as a chemical reaction network. Figure 2B provides an alternative representation of the regulatory system interactions given by the chemical reaction network.
When the external Pi concentration is limited, PhoR is free to bind ATP. This allows PhoR to autophosphorylate itself. PhoR is stable as a dimer, which is denoted by DiPhoR. Therefore, it is doubly phosphorylated.
PhoR is essential for the control of the activity of PhoB2,8,45. It phosphorylates PhoB through an autokinase/phosphotransferase activity2,8. After autophosphorylating, PhoR relays the signal to the transcription factor PhoB. The bidirectional reactions 3 and 5 below model the association of phosphorylated PhoR dimer and PhoB, and the unidirectional reactions 4 and 6 model the phosphotransferase. PhoB has been reported to exist primarily as monomers and phosphorylation greatly enhances dimerisation of PhoB (DiPhoBpp), modelled by reaction 710.
In E. coli, the sensor histidine kinase PhoR is a bifunctional enzyme that paradoxically performs two opposed tasks: in one direction, it catalyzes the phosphorylation of response regulator PhoB, and in the other, it also performs the dephosphorylation of phosphorylated PhoB, which is PhoBp18,25. The association of PhoR dimers with phosphorylated PhoB is modelled by the bidirectional reaction 8, whereas the phosphatase activity is given by reaction 9.
Phosphorylated dimer structure PhoB (DiPhoBpp) is enabled for activating Pho regulon by binding to a consensus promoter region. PhoB and PhoR in Pho regulon are encoded by the same operon, that is, the phoBR operon. Thus, the synthesis of the regulatory proteins PhoB and PhoR is under Pho regulon control2,8,46.
Based on experimental data, we consider the PhoA and PhoB promoters (pPhoA, pPhoB), whereby the PhoB promoter provides feedback to the system as this results in the expression of both PhoB and PhoR. PhoR expression during Pi limitation is dependent on the upstream pPhoB; the operon structure indicates that PhoR gene function requires expression from the pPhoB46. For this, phosphorylated PhoB dimers (DiPhoBpp) bind to the promoter as active transcription factors.
Active promoters pPhoAa and pPhoBa lead to the transcription of mRNA, which carry the information for the subsequent translation, resulting in protein synthesis, which are PhoA, PhoB and DiPhoR2,8.
With the inclusion of the degradation/dilution terms, we obtain:
We have implemented the deterministic ordinary differential equation (ODE) model in Matlab by using the standard translation from the chemical reaction network above, based on stoichiometries. The ODEs and detailed descriptions of each system variable are listed in Fig. S1 and Table S1. We have also implemented a version of the model for stochastic simulation, again based on mass action kinetics. The stochastic simulations capture fluctuations due to small molecule numbers, which are not captured by the deterministic simulations. By using the standard conversion factors for mass action kinetics, we could use the same rates for the deterministic and stochastic simulations.
The initial concentrations of the model variables have been derived from the literature or obtained from our experiments, described below. The control model has been calibrated for an initial culture containing 0 μM external Pi. Prior to Pi starvation, the concentrations of proteins PhoR and PhoB are approximately 0.22 μM. The concentrations of active PhoR and active PhoB are \(4\cdot {10}^{-8}\,\mu M\) and \(6\cdot {10}^{-8}\,\mu M\), as determined by Keasling et al.3. With a single plasmid, average mRNA number is 2–3 in E. coli47. Therefore, the initial states of mRNAa and mRNAb are set to 0.00166 μM by taking E. coli volume as 1 μm3, and the initial promoters numbers are set to 10 for each. We assume that the ATP concentration stays constant throughout the considered time intervals.
The rates of chemical reactions are obtained in accordance with the variability of physiological ranges given in the literature5,6,47,48,49,50. The model includes 29 reactions, including the reverse reactions. The control model has been used to reproduce the data and the unknown parameters have been estimated by least square inference within the plausible physiological ranges. When possible, parameter values are fixed or estimated by using experimental measurements found in the literature. The parameter values taken from the literature and their physiological ranges for the rates, if applicable, are listed in Table 1. The parameters without a range are fitted to the experimental data by using the deterministic model to reproduce the response curves. The parameter estimation procedure has been carried out by using a multi-start approach. The rate values have been selected with respect to the best fit to the physiological ranges, also listed in Table 1, and the dynamics in accordance with the experimental findings in order to avoid discontinuities or states with unrealistic values.
The data for the PhoA and PhoB expression have been obtained using PCR amplified DNA from E. coli MG1655 genome and transcriptionally fused to the translational coupler BCD251 and the fluorescent ms-fgfp gene. Subsequently the PphoA-BCD2-msfgpf and PphoB-BCD2-msfgfp fragments were cloned using the PacI/HindIII restrictions sites in pSEVA234 plasmid (http://seva.cnb.csic.es/), generating the pSEVA237PphoA and pSEVA237PphoB vectors as depicted in Fig. 2A.
The synthetic promoter Pliar was obtained as in52,53 with modifications. Activities of the PphoA and PphoB promoters have been determined as follows. Cells were maintained on LB rich medium. For Pi assays, an overnight preculture of E. coli DH10B carrying pSEVA237PphoA, pSEVA237PphoB or pSEVA237PLiar00117 plasmids harbouring PhoA, PhoB or PLiar00117 promoters driving the expression of MsfGFP, respectively were grown in 10 ml MOPS medium (pH = 7.2), supplemented with 0.02% casamino acids and 5 mM KH2PO4 at 37 °C under constant shaking at 250 rpm. The activity of PhoB and PhoA promoters were analysed in resting cells, both in presence or absence of 50 μg/ml antibiotic kanamycin, which did not have any impact on the promoter activity as it can be seen in the Supplementary Figs S2 and S20. The bacterial precultures were used to inoculate 50 ml of the same medium reaching an OD600 of 0.1 and grown until mild-late exponential phase (OD600 of 0.6–0.9). At this point, the bacterial cells were pelleted at 1500 × g for 10 min at room temperature, and finally washed twice in MOPS medium without \({{{\rm{PO}}}_{4}}^{\underline{3-}}\). Subsequently, the cells were suspended in 250 μl of MOPS to reach a final OD600 of 2 with increasing concentrations of \({{{\rm{PO}}}_{4}}^{\underline{3-}}\) (from 0 to 50 mM). The bacterial cell suspensions were loaded in 96-well plates and the expression of MsfGFP (fluorescence) was measured at different times in a SpectraMax i3x (Molecular Device) at 30 °C. The excitation wavelength was set to 485 nm and the fluorescence emission was measured at different times at 525 nm.
References
Mosa, K., Saadoun, I., Kumar, K., Helmy, M. & Dhankher, O. Potential biotechnological strategies for the cleanup of heavy metals and metalloids. Front Plant Sci. 7 (2016).
Wanner, B. Phosphorus assimilation and control of the phosphate regulon. In Neidhardt, F. (ed.) Escherichia coli and Salmonella typhimurium cellular and molecular biology, 1357–1381 (ASM Press, Washington, DC, 1996).
Van Dien, S. J. & Keasling, J. D. A dynamic model of the Escherichia coli phosphate-starvation response. J. Theor. Biol 190, 37–49 (1997).
Gao, R. & Stock, A. Evolutionary tuning of protein expression levels of a positively autoregulated two-component system. PLoS Genet 9, e1003927 (2013).
Bloch, W. & Schlesinger, M. J. The phosphate content of Escherichia coli alkaline phosphatase and its effect on stopped flow kinetic studies. JBC 248, 5794–5805 (1973).
Alon, U. An introduction to system biology: design principles of biological circuits (Chapman and Hall/CRC, 2007).
Harris, R. M., Webb, D. C., Howitt, S. M. & Cox, G. B. Characterization of PitA and PitB from Escherichia coli. J Bacteriol. 183, 5008–5014 (2001).
Wanner, B. L. et al. Are the multiple signal transduction pathways of the Pho regulon due to cross talk or cross regulation? In Regulation of gene expression in Escherichia coli, 297–315 (R.G. Landes Company, Texas USA, 1995).
Chekabab, S. M., Harel, J. & Dozois, C. M. Interplay between genetic regulation of phosphate homeostasis and bacterial virulence. Virulence 5 (2014).
Jansson, M. Phosphate uptake and utilization by bacteria and algae. Kluwer Academic Publishers 170, 177–189 (1988).
Gardner, S. G., Johns, K. D., Tanner, R. & McCleary, W. The PhoU protein from Escherichia coli interacts with PhoR, PstB, and metals to form a phosphate-signaling complex at the membrane. J Bacteriol 196, 1741–1752 (2014).
Lamarche, M., Wanner, B., Crepin, S. & Harel, J. The phosphate regulon and bacterial virulence: a regulatory network connecting phosphate homeostasis and pathogenesis. Federation of European Microbiological Societies 32 (2008).
McCleary, W. R. Molecular mechanisms of phosphate homeostasis in Escherichia coli. In Samie, A. (ed.) Escherichia coli, chap. 17, https://doi.org/10.5772/67283 (IntechOpen, Rijeka, 2017).
Kremlinga, A., Heermannb, R., Centlerc, F., Jungb, A. & Gillesa, E. D. Analysis of two-component signal transduction by mathematical modeling using the KdpD/KdpE system of Escherichia coli. BioSystems 78, 23–37 (2004).
Wong, P., Gladney, S., Centlerc, F. & Keasling, J. D. Mathematical model of the lac operon: inducer exclusion, catabolite repression, and diauxic growth on glucose and lactose. Biotechnol. Prog. 13, 132–143 (1997).
Fisher, S., Kim, S. K. K., Wanner, B. & Walsh, C. Kinetic comparison of the specifity of the vanomycin resistance kinase VanS for two response regulators. VanR and PhoB. Biochemistry 35, 4732–4740 (1996).
Koh, B., Tan, R. & Yap, M. Genetically structured mathematical modeling of trp attenuator mechanism. Biotechnol. Bioeng. 58, 502–509 (1998).
Gao, R. & Stock, A. Probing kinase and phosphatase activities of two-component systems in vivo with concentration-dependent phosphorylation profiling. PNAS 110, 672–677 (2012).
Gao, R. & Stock, A. Quantitative kinetic analyses of shutting off a two-component system. mBio 8, e00412–17 (2017).
Chen, T. Y. et al. Concentration- and chromosome-organization-dependent regulator unbinding from DNA for transcription regulation in living cells. Nature Communications 6 (2015).
Karapetyan, S. & Buchler, N. E. Role of DNA binding sites and slow unbinding kinetics in titration-based oscillators. Physical review E Statistical, nonlinear, and soft matter physics 92, 062712 (2015).
Abreu, Rd. S., Penalva, L. O., Marcotte, E. M. & Vogel, C. Two-component signaling circuit structure and properties. Curr Opin Microbiol 13, 184–189 (2010).
Miyashiro, T. & Goulian, M. High stimulus unmasks positive feedback in an autoregulated bacterial signaling circuit. PNAS 105, 17457–17462 (2008).
Tiwari, A., Ray, J. C., Narula, J. & Igoshin, O. A. Bistable responses in bacterial genetic networks: designs and dynamical consequences. Math Biosci 231, 76–89 (2011).
Shinar, G., Milo, R., Matinez, M. R. & Alon, U. Input output robustness in simple bacterial signaling systems. PNAS 104, 19931–19935 (2007).
Hawley, D. K. & McClure, W. R. Compilation and analysis of Escherichia coli promoter DNA sequences. Nucleic Acids Research 11, 2237–2255 (1983).
Jensen, P. R. & Hammer, K. The sequence of spacers between the consensus sequences modulates the strength of prokaryotic promoters. Applied and Environmental Microbiology 64, 82–87 (1998).
Jensen, P. R. & Hammer, K. Artificial promoters for metabolic optimization. Biotechnology and Bioengineering 58, 191–195 (1998).
Bougdour, A., Wickner, S. & Gottesman, S. Modulating RssB activity: IraP, a novel regulator of σ S stability in Escherichia coli. Genes Dev. 20, 884–897 (2006).
Merrikh, H., Ferrazzoli, A. E. & Lovett, S. Growth phase and (p)ppgpp control of IraD, a regulator of RpoS stability, in Escherichia coli. Journal of Bacteriology 191, 7436–7446 (2009).
Ferenci, T., Galbiati, H., Betteridge, T., Phan, K. & Spira, B. The constancy of global regulation across a species: the concentrations of ppGpp and RpoS are strain-specific in Escherichia coli. BMC Microbiology 11, 62 (2011).
Spira, B., Hu, X. & Ferenci, T. Strain variation in ppGpp concentration and RpoS levels in laboratory strains of Escherichia coli K-12. Microbiology 154, 2887–2895 (2008).
Ferenci, B. Maintaining a healthy SPANC balance through regulatory and mutational adaptation. Mol. Microbiology 57, 1–8 (2005).
Wang, L. et al. Divergence involving global regulatory gene mutations in an Escherichia coli population evolving under phosphate limitation. Genome Biol. Evol. 2, 478–487 (2010).
Pasternak Taschner, N., Yagil, E. & Spira, B. A differential effect of σ S on the expression of the PHO regulon genes of Escherichia coli. Microbiology 150, 2985–2992 (2004).
Gao, R., Godfrey, K. A., Sufian, M. A. & Stock, A. Counterbalancing regulation in response memory of a positively autoregulated two-component system. Journal of Bacteriology 119, e00390–17 (2017).
De Mey, M., Maertens, J., Lequeux, G. J., Soetaert, W. K. & Vandamme, E. J. Construction and model-based analysis of a promoter library for E. coli: an indispensable tool for metabolic engineering. BMC Biotechnology 7 (2007).
Li, J. & Zhang, Y. Relationship between promoter sequence and its strength in gene expression. The European Physical Journal E 37 (2014).
Shahrezaei, V. & Swain, P. S. The stochastic nature of biochemical networks. Current Opinion in Biotechnology 19, 369–374 (2008).
Elowitz, M. B., Levine, A. J., Siggia, E. D. & Swain, P. S. Stochastic gene expression in a single cell. Science 297, 1183–1186 (2002).
Yu, J., Xiao, J., Ren, X., Lao, K. & Xie, X. S. Probing gene expression in live cells, one protein molecule at a time. Science 311, 1600–1603 (2006).
Raj, A. & van Oudenaarden, A. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell 135, 216–226 (2008).
Williams, C. L. & Cotter, P. A. Autoregulation is essential for precise temporal and steady-state regulation by the Bordetella BvgAS phosphorelay. J Bacteriol 189, 1974–1982 (2007).
Mukhopadhyay, A., Gao, R. & Lynn, D. G. Integrating input from multiple signals: the VirA/VirG two-component system of Agrobacterium tumefaciens. Chembiochem 5, 1535–1542 (2004).
Gao, R. & Stock, A. Biological insights from structures of two-component proteins. Annu Rev Microbiol. 63 (2009).
Warner, B. & Chang, B. The phoBR operon in Escherichia coli K-12. Bacteriol 169, 5569–5574 (1987).
OpenWetWare. Parameter estimation in E. coli. Available at http://www.openwetware.org/wiki/Computational_Biology/Gene_Expression_modeling (2007).
Dexter, J. & Gunawardena, J. Dimerization and bifunctionality confer robustness to the isocitrate dehydrogenase regulatory system in Escherichia col. J Biol Chem. 288, 5770–5778 (2013).
Thattai, M. & van Oudenaarden, A. Intrinsic noise in gene regulatory networks. PNAS 98, 8614–8619 (2001).
Milo, R., Phillips, R. & Orme, N. Cell Biology by the Numbers (Garland Science, 2015).
Mutalik, V. K. et al. Precise and reliable gene expression via standard transcription and translation initiation elements. Nature Methods 10, 354–360 (2013).
Uluşeker, C. et al. A dynamic model of the phosphate response system with synthetic promoters in Escherichia coli. Proc. of the International Conference on Artificial Life (2017).
Gilman, J. & Love, J. Synthetic promoter design for new microbial chassis. Biochem Soc Trans 44, 731–737 (2016).
Acknowledgements
This work has been partially funded by the European Union’s Horizon 2020 research and innovation programme under the grant agreement No 686585 - LIAR, Living Architecture.
Author information
Authors and Affiliations
Contributions
C.U. and O.K. designed the model and performed the simulations and the sensitivity analysis. J.T.-B., C.U., J.L.G. and J.N. designed and performed the experiments. C.U., O.K. and M.H. wrote and edited the manuscript. All the authors analysed the results and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Uluşeker, C., Torres-Bacete, J., García, J.L. et al. Quantifying dynamic mechanisms of auto-regulation in Escherichia coli with synthetic promoter in response to varying external phosphate levels. Sci Rep 9, 2076 (2019). https://doi.org/10.1038/s41598-018-38223-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-38223-w
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.