Abstract
Recent analysis of data, recorded on March 8th 2014 at the Comprehensive Nuclear-Test-Ban Treaty Organisation’s hydroacoustic stations off Cape Leeuwin Western Australia, and at Diego Garcia, has led to the development of an inverse model for locating impacting objects on the sea surface. The model employs the phase velocity of acoustic–gravity waves that radiate during the impact, and only considers their propagation in the water layer. Here, we address a significant characteristic of acoustic–gravity waves: the ability to penetrate through the sea-bottom, which modifies the propagation speed and thus the arrival time of signals at the hydrophone station. Therefore, we revisit some signals that are associated with the missing Malaysian Aeroplane MH370, and illustrate the role of sea-bottom elasticity on determining impact locations.
Similar content being viewed by others
Introduction
Motivated initially by locating the missing Malaysian Aeroplane MH370, ref.1 studied the radiation of acoustic–gravity waves from impacting objects. ref.1 presented a technique for locating objects impacting at the sea surface using an inverse approach. Data recorded at hydrophone stations were employed to calculate the location of events not only at the sea surface but also at the sea-bottom (i.e., earthquakes), which is found to be possible since the far-field solution of both problems is very similar. The proposed technique was validated by ref.1 by comparing the calculated locations of two earthquake epicentres with existing data from seismometers. Although the agreement was sufficient at such large distances (order of thousands kilometres), discrepancies were still found. These might be associated with the sea-bottom rigidity assumption postulated in the original model. When rigidity is assumed, acoustic–gravity waves propagate at speeds near 1500 m/s, i.e. the speed of sound in water. In this study, we discuss the role of sea-bottom elasticity on the propagation speed of acoustic–gravity waves, and how this alters location calculations of impacting objects. Note that the sound signals that were analysed here are standard sound waves of low frequency nature. They are referred to as acoustic–gravity waves to emphasise that gravitational effects, which can modulate them, are not neglected in the analysis.
It is now well established that acoustic–gravity waves can travel in the ocean2,3,4,5 for long distances6, yet they can also penetrate through the elastic layers such as sea-bottom7 or ice-sheets8,9. The transmission mechanism between layers is still not well developed, though it is believed that it could occur once a critical depth (or frequency) is reached7. It is also reasonable that transmissions and reflections occur between media (liquid and solid) when a sharp change in the sea-bottom bathymetry is observed, such as a trench, a hill, or a shelf-break6. The propagation through multiple layers results in different arrival times, or in the context of this work, would modify the calculated location of impacting objects. To this end, we revisit data that was recorded at the Comprehensive Test Ban Treaty Organisation’s (CTBTO) hydrophone stations HA01 and HA08s on March 7th and 8th 2014 between 23:00 and 04:00 UTC, a time window in which MH370 is believed to have crashed in the Southern Indian Ocean. The findings here not only modify possible impact locations from previously analysed signals on HA01, but also reveal new evidence of missing data on HA08s, which if found related to MH370 would suggest a completely different route and impact location north-east Madagascar, see Fig. 1.
Map of recorded signals on CTBTO hydrophone stations HA01 and HA08s on March 7th and 8th 2014 between 23:00 and 04:00 UTC. Purple: bearing of signals recorded on HA01 that could be associated with MH370, with white-grey polygons that present possible source locations corresponding to transmission routes combining water and sea-bottom following Tables 1 and 2. Cyan: bearing of signals recorded on HA08s that could be associated with MH370, based on Table 3 - bearings 170° and 234° could be related. White: satellite data of the last ‘handshake’ with MH370, known as the 7th arc. Red: bearings of military action that were recorded intermittently on HA08s between 23:00–04:00 UTC. Orange: two possible MH370 routes; only route I is in agreement with the 7th arc. Attribution: Data SIO, NOAA, U.S. Navy, NGA, GEBCO; ©2018 Basarsoft; US Dept of State Geographer; ©2018 Google.
Results
Upon impact, the generated acoustic–gravity waves radiate in the water layer at about cl = 1500 m/s. When they penetrate in the solid layer they travel at cs = 3350 m/s. Acoustic–gravity waves can transmit back and forth from one layer to another, depending on the critical depth/frequency and sharp changes in sea-bottom bathymetry, and that creates a complex matrix of possible routs for the recorded signals as summarised below. In the following we revisit some of the previously analysed signals recorded on station HA01, and introduce new signals recorded on station HA08s. Spectrograms of all signals indicate a significant amount of noise in the 0–4 Hz band. The signals in this band appear to have a broadband frequency content which is typical for low frequency AGWs that can travel long distances before dissipating. We therefore filtered low frequencies (below 5 Hz) with a high pass Butterworth IIR filter. Since the signal randomness measure will change when the signal’s nature changes, transient signals over a noisy background can be identified by calculating a windowed entropy value. Peaks in the entropy trace are present where transient signals are detected. These peaks were considered for the subsequent bearing calculation. After separating the signals, the bearing is calculated using time of arrival based triangulation, see ref.1 for detailed bearing calculations.
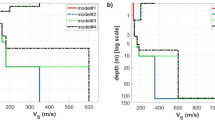
HA01
We address two possible impact events that were identified by ref.1 thats could be associated with MH370:
-
1.
E1: 301.4 ± 0.4°, 1900 ± 200 km from HA01, centred at −23.662°, 96.676°, recorded at 01:34:40 UTC (event source between 01:11 and 01:16)
-
2.
E2: 234.6 ± 0.4°, 1940 ± 200 km from HA01, centred at −43.487°, 94.469°, recorded at 00:50:00 UTC (event source between 00:25 and 00:31)
Transects along the bearings of E1 and E2 are given in Figs 2 and 3. Acoustic–gravity waves can transmit between layers at the highlighted regions T1j (j = 1, …, 8) in the case of bearing 301°, and T2k (k = 1, …, 6) in the case of bearing 234°. One possibility, in both E1 and E2, is that the recorded acoustic–gravity waves travelled only in the water layer, which results in the locations originally identified by ref.1. Another possibility is that acoustic–gravity waves couple with the elastic layer shortly after the impact and all along the way until the signals are received at the station. This scenario dictates farest location distance that is cs/cl (almost as twice) the distance originally calculated by ref.1. The second scenario is more likely when the water depth at impact is critical. Between these two marginal possibilities there are a number possible transmission between layers that result in different locations, as summarised in Tables 1 and 2.
HA08s
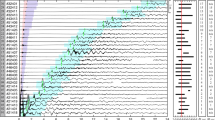
Analyses of signals recorded at station HA08s (−65.5445°, 32.4730°) were more challenging, partially due to disturbances in the recordings that are believed to be caused by military action in the region. A summary of identified signals of interest (see Fig. 4) is given in Table 3. Note that bearings if signals HA_30 and HA_32 fall within the military action bearings, so it is also possible that the signals are associated with the military action. Among the rest of the signals, it is remarkable that three have a bearing of 170.9°, and one 173°. The first occurred at 12:11 UTC whereas the other three followed about three hours later, all after 3.30. Last but not least, a fifth signal appears at 3:07 (see Fig. 5). This signal probably indicates restarting the system after it was shutdown for 25 minutes, i.e. there is a missing data in these specific CTBTO recordings.
Signal, cross-correlation, and bearings of recordings at HA08s reveals a few signals of interest (summarised in Table 3).
Discussion
Acoustic–gravity waves can travel at speeds near the speed of sound in water, yet they can double their speed when coupling with the elastic layer. As they propagate they carry information on their source and thus can be used, among others, for locating impacting objects at the sea surface by applying a proper inverse model1. However, since the location directly relies on the propagation speed, and the later depends on the medium, it is important to know the route travelled by acoustic–gravity waves. For example, signals E1 and E2 travel through different routs, as given in Tables 1 and 2, which can results in different calculated locations. In the case of multiple transmissions one expects teh signals to be composed of a number of smaller signals, which is not the case here unless if other signals are buried in the ambient noise. Since only one complete signal has been identified for each of E1 and E2, it is more likely that the signals either did not transmit at all into the elastic layer, or transmitted only once at the initial stage and coupled with the elastic layer all a long the way, i.e. the first and last possibilities of each table.
The locations of signals found on HA08s are with high uncertainty or unknown and require further analysis. Though, if related to MH370 that might suggest a location in the northern part of the Indian Ocean. Due to the sensitivity of the recorded data, it is unlikely that the three hydrophones on HA08s had a simultaneous technical failure and the reason behind the shut down is to-date unknown. The missing data might be related to the military action in the area (during or after the impact), but another argument is that a violent nearby activity (including impact, explosion) could have resulted in a shutdown of the system. Both the signal HA_30 of bearing 247° recorded at 11:57 on March 7th, and the missing data if related to MH370 could (independently) suggest that the impact location is closer to Diego Garcia’s station, as opposed to Cape Leeuwin’s station. With the absence of the recordings, there is currently no scientific evidence that an impact occurred during this time window. However, it might be possible to extract more information after processing hidden signals in the ambient noise. To study this possibility and to further assess the effects of elasticity and transmissions due to sea-bottom topography we intend to carry out a set of field experiments, while in parallel develop a depth-integrated, see10, sea-bottom elastic model for the radiation of acoustic–gravity waves from impacting objects.
Methods
Dispersion relation
The solution for the propagation of acoustic–gravity waves in compressible water under the effects of gravity, and an elastic half space was treated by ref.7, who derived the dispersion relation,
where r is the eigenvalue, h is the water depth, g is the acceleration due to gravity, k is the wavenumber, ω is the frequency, λ and μ are Lame’s elasticity constants, \({\rho }_{l}\) is the water density, and q and s are separation constants in the solid sea-bottom,
where \({c}_{p}=\sqrt{(\lambda +2\mu )/{\rho }_{s}}\) and \({c}_{s}=\sqrt{\mu /{\rho }_{s}}\) are pressure-wave and shear-wave velocities in the sea-bottom, respectively; and \({\rho }_{s}\) is the earth density. For our numerical examples we rely on average parameter-values taken from the entries for the crust and ocean in Table 1 of PREM11: \({\rho }_{l}\) = 1020 kg/m3, \({\rho }_{s}\) = 2750 kg/m3, cl = 1470 m/s, cs = 3550 m/s. Employing the dispersion relation allows transmission from the water layer into the elastic sea-bottom and vice-versa. Once coupled with the sea-bottom, the propagation speed increases from cl to cs. Note that for this main reason, and since we analyse low frequency acoustic–gravity waves that span the entire depth, the effects of stratification and variations of water density on the propagation speed where ignored.
Impact time and location
The measured frequency of the signal is dependant on the impact time and location, t0 and x0 as given by5,12:
By choosing pairs of instants \({\hat{t}}_{m}\) and \({\hat{t}}_{n}\) from the recordings and the corresponding frequencies at these instants \({\hat{{\rm{\Omega }}}}_{{\hat{t}}_{n}}\) and \({\hat{{\rm{\Omega }}}}_{{\hat{t}}_{m}}\), we can solve for x0 and t0 explicitly5:
and
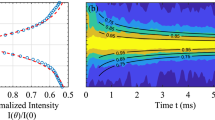
For each signal we fix \({\hat{t}}_{n}\) at some instant at the beginning of the signal, and calculate t0 and x0 with \({\hat{t}}_{m}\) running from \(m=n\,\mathrm{...}\,M\), where M denotes the location at the end of the signal. Thus, we obtain a probabilistic distribution of solutions that allow uncertainty about the most probable solution (see Fig. 6). Detailed signals processing and bearing calculations can be found in the methods section of ref.1.
Data Availability
Data can be accessed by direct inquiries to ukadri@mit.edu.
References
Kadri, U., Crivelli, D., Parsons, W., Colbourne, B. & Ryan, A. Rewinding the waves: tracking underwater signals to their source. Sci. Rep. 7, 13949 (2017).
Yamamoto, T. Gravity waves and acoustic waves generated by submarine earthquakes. Int. J. Soil Dyn. Earthq. Eng. 1, 75–82 (1982).
Stiassnie, M. Tsunamis and acoustic–gravity waves from underwater earthquakes. J. Eng. Math. 67, 23–32 (2010).
Kadri, U. Wave motion in a heavy compressible fluid: Revisited. Eur. J. Mech. - B/Fluids 49(A), 50–57 (2015).
Mei, C. C. & Kadri, U. Sound signals of tsunami from slender faults. J. Fluid Mech. 836, 352–373 (2017).
Kadri, U. & Stiassnie, M. Acoustic-gravity waves interacting with the shelf break. J. Geophys. Res. Ocean. 117 (2012).
Eyov, E., Klar, A., Kadri, U. & Stiassnie, M. Progressive waves in a compressible-ocean with an elastic bottom. Wave Motion 50, 929–939 (2013).
Kadri, U. Generation of hydroacoustic waves by oscillating ice block in arctic zones. Advances in Acoustics and Vibration, 8076108 (2016).
Abdolali, A., Kadri, U., Parsons, W. & Kirby, J. On the propagation of acoustic–gravity waves under elastic ice-sheets. J. Fluid Mech. 837, 640–656 (2017).
Abdolali, A., Kirby, J. T. & Bellotti, G. Depth-integrated equation for hydro-acoustic waves with bottom damping. J. Fluid Mech. 766, R1 (2015).
Dziewonshi, A. M. & D.L. Anderson, D. L. Preliminary reference earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981).
Hendin, G. & Stiassnie, M. Tsunami and acoustic-gravity waves in water of constant depth. Phys. Fluids 25, 86103 (2013).
Acknowledgements
The author is grateful to ATSB and their collaborators for providing the recordings, to A. Abdolali for assisting with Figures 2 and 3, and to D. Crivelli for technical discussions, to P. Caldairou & H. Schneider for confirming the missing time window, and to the reviewers for providing valuable comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing Interests
The author declares no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kadri, U. Effect of sea-bottom elasticity on the propagation of acoustic–gravity waves from impacting objects. Sci Rep 9, 912 (2019). https://doi.org/10.1038/s41598-018-37626-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-37626-z
This article is cited by
-
Effects of oceanic ice cover and density stratification on the propagation of hydroacoustic waves
Journal of Hydrodynamics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.