Abstract
We provide an evaluation of the paleolatitudinal dependence of the paleosecular variation throughout the Paleozoic-Mesozoic transition – linked to the high geomagnetic reversal frequency interval Illawarra Hyperzone of Mixed Polarity (IHMP; ~266.7–228.7 Myr). Our findings were compared with those for intervals of distinctive geomagnetic reversal frequencies within the Phanerozoic. Our results for the IHMP were conducted through estimates of angular dispersion (SB) of virtual geomagnetic pole (VGP) data groups, taken from a high quality paleomagnetic database. Model G was fitted to these data, providing its shape parameters a and b (respectively related to the antisymmetric and symmetric harmonic terms for the time-average geomagnetic field). Results for the IHMP exhibited compatible patterns with two well-known intervals of higher reversal frequency – Jurassic and the last 5 Myr. A comparison of b/a ratio results – considered as an efficient indicator for the relative contribution of the axial dipole field – for the last 270 Myr, indicated an inverse correspondence with the relative core-mantle boundary (CMB) heat flux, according to recent discussions, clarifying the physical meaning of the Model G shape parameters a and b.
Similar content being viewed by others
Introduction
The phenomenological aspects of geodynamo that imply long-term changes for the geomagnetic field behavior have been an important subject of debate in literature1,2,3,4. Important progress toward a better understanding of the geodynamo has been made by means of more realistic numerical modelings, which better emulated geodynamic conditions throughout geologic eras5,6,7,8,9,10. Nevertheless, some of the long-standing questions refer to the Earth’s magnetic field (EMF) reversibility and its large-scale variations in average reversal rate are still a demand. It is well-known that the geomagnetic polarity timescale (GPTS) for the last 160 Myr indicates wide changings for the rate of geomagnetic reversals, reflecting the variable stability of geodynamo – from around 4-5 Myr−1, with an average duration for the polarity chrons of ~200 kyr for the past 15 Myr, reaching down to ~0.05 Myr−1 during the so-called 84–125 Myr Cretaceous Normal Superchron (CNS)11,12,13,14.
Although a stochastic contribution to the high variable geomagnetic reversal spectra cannot be ruled out15,16, there is important evidence for long-term modulations on the reversal rates by mantle convection13,17,18,19,20, which is plausible, taking into account the timescale differences between the shorter term, outer core convection and the GPTS – the latter being compatible to the mantle convection timescale14,21. Some authors (e.g., refs 20,21,22,23) suggest that such changes in reversal rate would be a result of spatial variability of the heat flux at the core-mantle boundary (CMB) throughout the Phanerozoic, although the connections between the geomagnetic reversal frequency and long-term mantle dynamics are still far from being completely clarified16.
Additionally, it has been discussed by some authors (e.g., refs 9,24) that the geodynamo exhibited more stability conditions (i.e. lower geomagnetic reversal rates) in periods when the main contribution to the geomagnetic field is given by the axial dipole field – which can be given by the antisymmetric spherical harmonic terms, as a solution for a field generated by a spherical geodynamo – in relation to the non-axial dipole contribution. Such conditions have been linked to ‘superchrons’ (~107 yr, single geomagnetic polarity periods), as discussed by Biggin et al. (ref. 25) for the CNS, and for the 262–318 Myr Permian-Carboniferous Reversed Superchron (PCRS; ref. 26). Conversely, a lower dipolar contribution was reported for intervals of higher reversal frequency, such as the Jurassic25,27 and the last 5 Ma28.
Such information can be acquired by evaluations of the ancient geomagnetic field through analyses of paleosecular variation (PSV), related to the spatio-temporal variability in both direction and intensity of the EMF8,22. It provides an independent way of investigating the EMF evolution through geological time, hence it is adequate for assessing information on the time-averaged field, and its dipolar and non-dipolar contributors4,25,29,30. The PSV is commonly obtained by the angular dispersion (S) of virtual geomagnetic poles (VGPs) datasets, given by:
where N and Δi are, respectively, the number of VGPs and the angular difference between the ith VGP and the mean VGP. A phenomenological model that has been successfully employed for evaluation of S – which demonstrated a clear relation between reversal frequency and the latitudinal dependence of VGP dispersions24, was proposed by McFadden et al. (ref. 31). This approach (Model G) considers that the VGP angular dispersion results from the contribution of two independent “families” – dipole (SD) and quadrupole (SQ) families, which are respectively related to odd and even l–m spherical harmonic terms (i.e., asymmetric and symmetric around the equator region):
where λ is the paleolatitude, and a and b are the Model G shape parameters (which are empirical constants that are respectively related to the quadrupole (symmetric) and dipole (antisymmetric) families of the field).
From hemispherically averaged VGP dispersion datasets carried out from 0–5 Ma lava flows, McFadden et al. (ref. 27) reported a possible correspondence for the past 160 Myr between the reversal frequency and the ratio b/a – which provides an empirical evaluation of the relative contribution of antisymmetric (b) to symmetric (a) harmonics terms of the geodynamo. Furthermore, Coe and Glatzmaier (ref. 24) reported by means of modeling simulations of the geodynamo that the symmetry of the time-averaged field – which can also be indicated by the ratio b/a – can be a better predictor of reversal frequency in comparison to the intensity evaluations.
Nevertheless, some important questions are still far from being completely elucidated about the extension of the large-scale variations for the reversal frequency, and its connections to the CMB heat flux fluctuations (linked to the long-term mantle dynamics) throughout the Phanerozoic. For instance, there are no reported discussions so far for:
- (i)
a possible lower contribution of the antisymmetric family for the high reversal rate interval known as Illawarra Hyperzone of Mixed Polarity (IHMP; ~266.7–228.7 Myr). The IHMP is characterized by a high mean geomagnetic reversal frequency (comprising tens of polarity reversal events from the end of PCRS (Late Permian) to the lowermost Triassic32,33,34), and is possibly related to some of the prominent geodynamic events that took place during the Paleozoic-Mesozoic transition35,36;
- (ii)
the extension of the original evaluation by means of b/a ratio as a function of reversal frequency proposed by McFadden et al. (ref. 27) and Coe and Glatzmaier (ref. 24) for Pre-Jurassic times, to achieve a better description of such behavior throughout the Phanerozoic;
- (iii)
comparisons about the mean CMB heat flux and the b/a ratio, in order to verify a possible correspondence between both factors.
In this work, we aim to address these points, in order to provide new information for the discussions that linked the long-term variations of the geomagnetic reversals, the geodynamo’s stability and the geodynamic processes throughout the Phanerozoic.
Methods
IHMP: selection criteria for the paleomagnetic database
In order to assess of the paleolatitudinal dependence of the paleosecular variation for the IHMP interval (~266.7–228.7 Myr), we conducted a pre-selection of paleomagnetic studies available in literature for this time interval, comprising of 112 works published between 1990 and 2018 based on igneous rocks. Such preliminary database research was carried out by means of academic search engines (e.g., Web of Science (https://www.webofknowledge.com/) and Scopus (https://www.scopus.com/home.uri)) and the IAGA’s Global Paleomagnetic Database (http://www.ngu.no/geodynamics/gpmdb/). Regarding the scarcity of studies based on highly sensitive magnetometers, which were often associated to low accuracy rock magnetism investigations, we did not consider datasets prior to 1990, according to similar procedures adopted by De Oliveira et al. (ref. 26).
From the preliminary dataset, we built the “final” paleomagnetic database by means of the following selection criteria: (1) all works that did not provide directional, characteristic remanent magnetization (ChRM) data per site and site coordinates, as well as at least ten sampling sites (N < 10) were ruled out; (2) preference was given to the selection of works which provide high-quality paleomagnetic poles in accordance to the Van der Voo (ref. 37) quality criteria; (3) the selected studies shall be related to level ≥ 4 of the GPMDB Demagcode procedure protocol38,39 as reliable analyses of VGP dispersion datasets can be prevented due to the employment of inadequate demagnetization procedures40; (4) only studies that succeeded in the recalculation of its paleomagnetic pole (s) and associated paleolatitude (s) by means of its ChRM directional data and site coordinates were considered. In order to remove spurious data that could be possibly related to eventual excursional fields or lightning occurrences that may influence the VGP angular dispersion, due to the size of the paleomagnetic datasets De Oliveira et al. (ref. 26), all selected paleomagnetic datasets were submitted to the Vandamme (ref. 41) iterative method. We ruled out the usage of a fixed cut-off angle regarding it could lead to overestimation (underestimation) of the angular standard deviation for low (high) latitudes Tauxe et al. (ref. 42).
The resulting paleomagnetic database from application of selection criteria #1 – #4 is constituted of 16 VGP datasets, provided by 12 paleomagnetic studies (which corresponds to ~14.3% of the pre-selected works), from igneous-based lithologies (Table 1; Supplementary Information Tables S1 and S2). However, as some of the datasets exhibit considerably high k-values (>200), we adopted an additional procedure to evaluate whether such corresponding VGP distributions represent adequate PSV samplings, by means of application of the Deenen et al. (ref. 43) criteria. It provides a N-dependent A95 envelope defined by a range of upper (A95max) and lower (A95min) limits, in which the observed A95 shall be within for a sufficient PSV sampling. As discussed by some authors (e.g., ref. 43,44), datasets that provide A95 > A95max may contain additional scatter contributors, whereas A95 < A95min could be considered as an indicator for an EMF spot-reading record. It was noticed that four of the select datasets (datasets # 2, 8, 10 and 15) provided A95 values that fall out of the A95min/A95max range, and hence were not considered for the paleomagnetic data processing and the subsequent Model G curve fitting for the IHMP.
IHMP paleomagnetic data processing
From the paleomagnetic database, all VGP angular dispersion data were calculated by means of Eq. (1). Upper and lower limits for S (Su and Sl, respectively) were estimated as suggested by the bootstrap method. Obtaining angular dispersion data due to the PSV (SB) can be done by minimization of sampling and measurement errors25 by means of the following relationship:
where \(\bar{n}\,\,\)and Sw are, respectively, the average number of samples per site and the within-site dispersion. The relation \({S}_{w}^{2}/\bar{n}\) is the correction factor for the within-site dispersion of a given VGP dataset, which is given by42:
where \({\bar{\alpha }}_{95}\) is the mean value of α95 for the VGP dataset. SB data are also displayed in Table 1. The mean difference between S and SB is quite small (~1.9°), which could be an indirect indicator for the adequacy of the selection criteria adopted in this work. For the evaluation of VGP dispersion data regarding the paleolatitude for the IHMP, we considered the SB (λ) data.
Model G curve fitting
For evaluation of the paleolatitudinal dependence of the VGP dispersion data to the selected SB (λ) dataset for the IHMP, we performed a curve fitting based on the Model G (ref. 31) by means on the Levenberg–Marquardt method, which is an iterative regression method for solving nonlinear least square problems, by means of a stabilization parameter that assures the convergence of the goal function for a minimum value by choosing Steepest Descent or Gauss-Newton methods (ref. 45). It was done by means of the modulus “scipy.optimize.leastsq”, available at the Python online repository ScyPy (https://scipy.github.io/devdocs/generated/scipy.optimize.least_squares.html). From the best Model G fitted curve, we carried out the shape parameters a and b for the SB (λ) dataset to the IHMP, which will be discussed later.
Results
Evaluation of the paleolatitudinal dependence of the VGP dispersion data for the IHMP
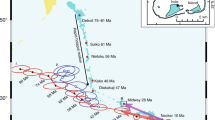
By the hemispheric representation of the selected database along with its corresponding paleolatitudes (Fig. 1), it was not possible to observe any evidence for an equatorial asymmetry between the SB dispersion datasets related to both Southern and Northern hemispheres (open and full circles, respectively) – which could be reasonably explained by the assumption of the GAD hypothesis, as previously discussed by Biggin et al. (ref. 25). The SB (λ) distribution, in association to its best fitted Model G curve (which resulted in shape parameters \({13.2}_{6.8}^{16.3}\) and \({0.12}_{0.11}^{0.13}\)), clearly exhibits a low paleolatitudinal dependence trending pattern (ranging from SB ~13.8° to ~17.0° at (paleo)latitudes = 0° and 90°, respectively). All the three SB (λ) curves exhibit similar shapes, which is compatible to a low (paleo)latitudinal dependence due to smaller antisymmetric contribution during high reversal rate intervals. Nevertheless, the IHMP interval (average reversal rate of ~5.9 Myr−1) exhibits higher SB values at low paleolatitudes in comparison to those reported for lower reversal frequency intervals, as the CNS25 (~8.7°) and the PCRS26 (~9.4°) – and similar to the observed to the 0–5 Myr and Jurassic intervals, of similar reversal frequency (4–5 Myr−1 and 4.6 Myr−1, respectively).
VGP dispersion only due to the PSV (SB) as a function of paleolatitude in hemispheric projection for the selected paleomagnetic database. Demonstrated together with the IHMP data is the best-fit Model G (ref. 31) (red line), associated to its 95% confidence limits (dashed lines). This curve is compared to the S(λ) curves for the last 5 Ma (green lines; ref. 28) and for the Group 1 dataset (blue) for Jurassic times provided by Biggin et al. (ref. 25). For each curve the correspondent b/a ratio is indicated on the right.
Furthermore, in order to compare the observed paleolatitudinal trending pattern and shape of the VGP dispersion curve for the IHMP with other high mean reversal frequency intervals we also demonstrated in Fig. 1, the Model G best-fit curves respectively provided for Jurassic times from Group 1 of Biggin et al. (ref. 25) and for the last 5 Myr28.
All curves exhibit the same low paleolatitudinal trending patterns, which has been discussed in literature (e.g., ref. 25 and ref. 27) as being due to a major symmetric family contribution in comparison to the influence from the antisymmetric family. Such effect leads to higher (lower) values for the shape parameter a (b) in comparison to low reversal frequency intervals, as the CNS (Johnson & McFadden, ref. 4). The IHMP (red) and Jurassic (blue) curves evolved similarly within the 0–90° paleolatitudinal interval, although the IHMP SB (λ) curve exhibit lower SB at lower and higher paleolatitudes. The VGP dispersion curves for both Jurassic and 0–5 Myr intervals provided shape parameters that are compatible to those found for IHMP (Jurassic: \(a={16.4}_{10.3}^{19.0}\) and \(b={0.19}_{0.00}^{0.46}\); 0–5 Myr: \(a={14.6}_{13.4}^{15.6}\) and \(b={0.20}_{0.13}^{0.24}\)).
It can be noticed that the b/a ratios – which can be considered as an empirical measure of the relative contribution of the antisymmetric/symmetric harmonic terms24 – for the Jurassic (\({0.012}_{0.000}^{0.028}\,)\) and 0–5 Myr (\({0.014}_{0.009}^{0.019})\,\,\)intervals are slightly higher than the b/a ratio found for the IHMP (\(={0.009}_{0.005}^{0.014})\). Additionally, the mean reversal rate for the Jurassic25 (~4.6 Myr−1) and the 0–5 Myr28 (~4–5 Myr−1) intervals are quite similar. We estimated the mean average reversal frequency for the IHMP (for more detail, see description in “Evaluation of the time evolution of the b/a ratio” section) as ~5.9 Myr−1, for the ~266.7–228.7 Myr suggested for this period, which is higher than the previous two intervals. By comparison, the higher (lower) values of mean average reversal frequency (b/a ratio) found for IHMP in comparison to the last 5 Myr and Jurassic could indicate the inverse relationship between mean reversal rate and b/a ratio, as expected, and the even lower influence of the antisymmetric family for the IHMP.
Evaluation of the time evolution of the b/a ratio
As discussed by several authors13,14,18,20, the timescale of the anharmonic variations verified along the GPTS are evocative of the mantle convection timescales – which is itself comparable to the variations of the heat flux patterns over the CMB, as suggested by numerical modeling works of mantle convection46,47.
In order to contribute to this debate, we also conducted an evaluation aiming to track the time evolution of the relative contribution of dipole/non-dipole fields derived from paleomagnetic data – by means of b/a ratios – and its possible correspondence with time variations in relative CMB heat flux throughout most of the Phanerozoic. The results for b/a ratios were provided both by this work and other studies, which together comprise contiguous, million-year scale intervals that exhibited high and low mean reversal rates throughout the Phanerozoic: (1) PCRS26; (2) IHMP (this study); (3) Jurassic25; (4) CNS25; (5) 45–80 Myr27; (6) 22.5–45.0 Myr27; (7) 5.0–22.5 Myr27; (8) 0–5 Myr28 (Table 2 and Fig. 2). It is important to highlight that, as discussed by Biggin et al. (ref. 25) the data provided by McFadden et al. (ref. 27) probably reflect a latitudinal dependence to the VGP scatter by application of a constant within-site error correction in pole-space. Estimates of the time evolution of the relative CMB heat flux for the past 270 Myr, based on temporal variations in relative geomagnetic reversal frequency, followed the recent model proposed by Olson & Amit (ref. 9). Their approach is supported by indications from convection-driven numerical dynamos16,47 of which the likelihood of the geomagnetic polarity reversals occur is proportion to the increasing of the CMB heat flux on the outer boundary. Additionally, we estimated the average reversal frequency based on the GPTS provided by Gradstein et al. (ref. 48), by application of a 3 Myr running window in steps of 2 Myr for the past 350 Myr.
Time evolution for the last 270 Myr between the b/a ratio (dark circles) (based on calculations provided by different studies – including the IHMP data, provided by this work) and the CMB heat flux variations relative to the present day according to the Olson & Amit (2015) model (smoothed curve in red). Estimates for the average reversal frequency (for the last 350 Myr) are also available for comparison (brown curve).
It is noticeable that the time evolution of the b/a ratio matches, in an inverse relationship, the smooth trending pattern for the relative CMB heat flux from the PCRS to the present times, as provided by Olson & Amit (ref. 9). It is important to highlight that the b/a ratios were carried out with PSV analyses from Model G fittings of VGP dispersion curves, which are not of straightforward interpretation in terms of physical processes, because their origins rely on a number of different factors19.
Nevertheless, our results point out that the relative contribution of equatorially antisymmetric to symmetric spherical harmonics terms, given by the Model G, could be inversely related to the CMB heat flux variations, indicating that higher axial (non-axial) dipole contributions may be expected for lower (higher) relative CMB heat flux intervals for the last 270 Myr. As discussed previously, high/low b/a ratios would be considered, for a given time interval, as a predictor of low/high reversal frequency states24 – which in turn could reflects high/low CMB heat flow conditions, as discussed by some authors47,49,50.
Such observations would shed some light on the physical meaning of the Model G shape parameters a and b, what can partially explain the adequacy of this phenomenological model for most of the Phanerozoic. Surely new investigations aiming to extend back in time the b/a ratio coverage herein presented, and with more time resolution, are demanded to verify the hypothesis.
Change history
15 January 2020
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Johnson, H. P., Van Patten, D., Tivey, M. & Sager, W. W. Geomagnetic polarity reversal rate for the Phanerozoic. Geophysical Research Letters 22, 231–234 (1995).
Hollerbach, R. The range of timescales on which the geodynamo operates. Geodynam. Series 31, 181–192 (2003).
Korte, M. & Constable, C. G. Centennial to millennial geomagnetic secular variation. Geophysical Journal International 167, 43–52 (2006).
Johnson, C. L., McFadden, P. & Kono, M. Paleosecular Variation and the Time-Averaged Paleomagnetic Field. In: G. Schubert (Ed.), Treatise on Geophysics 5, 417–453. Netherlands: Elsevier (2007).
Glatzmaier, G. A., Hollerbach, R. & Roberts, P. H. A study by computer simulation of the generation and evolution of the Earth’s magnetic field (No. LA-UR–95-4184). Los Alamos National Lab., NM (United States) (1995).
Aubert, J., Labrosse, S. & Poitou, C. Modelling the palaeo-evolution of the geodynamo. Geophysical Journal International 179, 1414–1428 (2009).
Aubert, J., Finlay, C. C. & Fournier, A. Bottom-up control of geomagnetic secular variation by the Earth/’s inner core. Nature 502, 219–223 (2013).
Lhuillier, F. & Gilder, S. A. Quantifying paleosecular variation: insights from numerical dynamo simulations. Earth and Planetary Science Letters 382, 87–97 (2013).
Olson, P. & Amit, H. Mantle superplumes induce geomagnetic superchrons. Frontiers in Earth Science 3 (2015).
Constable, C., Korte, M. & Panovska, S. Persistent high paleosecular variation activity in southern hemisphere for at least 10 000 years. Earth and Planetary Science Letters 453, 78–86 (2016).
Opdyke, M. D. & Channell, J. E. Magnetic stratigraphy 64. Academic press (1996).
Lowrie, W. & Kent, D. V. Geomagnetic polarity timescales and reversal frequency regimes. Timescales of the paleomagnetic field, 117–129 (2004).
Pétrélis, F., Besse, J. & Valet, J. P. Plate tectonics may control geomagnetic reversal frequency. Geophysical Research Letters 38 (2011).
Choblet, G., Amit, H. & Husson, L. Constraining mantle convection models with palaeomagnetic reversals record and numerical dynamos. Geophysical Supplements to the Monthly Notices of the Royal Astronomical Society 207, 1165–1184 (2016).
Ryan, D. A. & Sarson, G. R. Are geomagnetic field reversals controlled by turbulence within the Earth’s core? Geophysical Research Letters 34 (2007).
Amit, H. & Olson, P. Lower mantle superplume growth excites geomagnetic reversals. Earth and Planetary Science Letters 414, 68–76 (2015).
Courtillot, V. & Olson, P. Mantle plumes link magnetic superchrons to phanerozoic mass depletion events. Earth and Planetary Science Letters 260, 495–504 (2007).
Zhang, N. & Zhong, S. Heat fluxes at the Earth’s surface and core–mantle boundary since Pangea formation and their implications for the geomagnetic superchrons. Earth and Planetary Science Letters 306, 205–216 (2011).
Biggin, A. J., Strik, G. H. & Langereis, C. G. Evidence for a very-long-term trend in geomagnetic secular variation. Nature Geoscience 1, 395–398 (2008a).
Olson, P., Deguen, R., Hinnov, L. A. & Zhong, S. Controls on geomagnetic reversals and core evolution by mantle convection in the Phanerozoic. Physics of the Earth and Planetary Interiors 214, 87–103 (2013).
McFadden, P. L. & Merrill, R. T. Evolution of the geomagnetic reversal rate since 160 Ma: Is the process continuous? Journal of Geophysical Research: Solid Earth 105, 28455–28460 (2000).
Merril, R. T., McElhinny, M. W. & McFadden, P. L. The magnetic field of the Earth. International Geophysics Series 63 (1996).
Buffett, B. A. The thermal state of Earth’s core. Science 299, 1675–1677 (2003).
Coe, R. S. & Glatzmaier, G. A. Symmetry and stability of the geomagnetic field. Geophysical Research Letters 33 (2006).
Biggin, A. J., Van Hinsbergen, D. J., Langereis, C. G., Straathof, G. B. & Deenen, M. H. Geomagnetic secular variation in the Cretaceous Normal Superchron and in the Jurassic. Physics of the Earth and Planetary Interiors 169, 3–19 (2008b).
De Oliveira, W. P. et al. Behavior of the paleosecular variation during the Permian-Carboniferous Reversed Superchron and comparisons to the low reversal frequency intervals since Precambrian times. Geochemistry, Geophysics, Geosystems 19, 1035–1048 (2018).
McFadden, P. L., Merrill, R. T., McElhinny, M. W. & Lee, S. Reversals of the Earth’s magnetic field and temporal variations of the dynamo families. Journal of Geophysical Research: Solid Earth 96, 3923–3933 (1991).
Johnson, C. L. et al. Recent investigations of the 0–5 Ma geomagnetic field recorded by lava flows. Geochemistry, Geophysics, Geosystems 9 (2008).
Herrero-Bervera, E., Ubangoh, R., Aka, F. T. & Valet, J. P. Paleomagnetic and paleosecular variation study of the Mt. Cameroon volcanics (0.0–0.25 Ma), Cameroon, West Africa. Physics of the Earth and Planetary Interiors 147, 171–182 (2004).
Smirnov, A. V., Tarduno, J. A. & Evans, D. A. Evolving core conditions ca. 2 billion years ago detected by paleosecular variation. Physics of the Earth and Planetary Interiors 187, 225–231 (2011).
McFadden, P. L., Merrill, R. T. & McElhinny, M. W. Dipole/quadrupole family modeling of paleosecular variation. Journal of Geophysical Research: Solid Earth 93, 11583–11588 (1988).
Nawrocki, J., Wagner, R. & Grabowski, J. The Permian/Triassic boundary in the Polish Basin in the light of paleomagnetic data. Geological Quarterly 37, 565–578 (1993).
Yugan, J., Qinghua, S. & Changqun, C. Late Permian magnetostratigraphy and its global correlation. Science Bulletin 8, 698–705 (2000).
Hounslow, M. W. & Balabanov, Y. P. A geomagnetic polarity timescale for the Permian, calibrated to stage boundaries. Geological Society, London, Special Publications 450, (SP450–8 (2016).
Isozaki, Y. Integrated “plume winter” scenario for the double-phased extinction during the Paleozoic–Mesozoic transition: the G-LB and P-TB events from a Panthalassan perspective. Journal of Asian Earth Sciences 36, 459–480 (2009a).
Isozaki, Y. Illawarra Reversal: the fingerprint of a superplume that triggered Pangean breakup and the end-Guadalupian (Permian) mass extinction. Gondwana Research 15, 421–432 (2009b).
Van der Voo, R. The reliability of paleomagnetic data. Tectonophysics 184, 1–9 (1990).
McElhinny, M. W. & Lock, J. Global palaeomagnetic database project. Physics of the Earth and Planetary Interiors 63, 1–6 (1990).
Pisarevsky, S. A. & McElhinny, M. W. Global paleomagnetic data base developed into its visual form. Eos, Transactions American Geophysical Union 84, 192–192 (2003).
McElhinny, M. W. & McFadden, P. L. Palaeosecular variation over the past 5 Myr based on a new generalized database. Geophysical Journal International 131, 240–252 (1997).
Vandamme, D. A new method to determine paleosecular variation. Physics of the Earth and Planetary Interiors 85, 131–142 (1994).
Tauxe, L., Kodama, K. P. & Kent, D. V. Testing corrections for paleomagnetic inclination error in sedimentary rocks: A comparative approach. Physics of the Earth and Planetary Interiors 169, 152–165 (2008).
Deenen, M. H. L., Langereis, C. G., van Hinsbergen, D. J. J. & Biggin, A. J. Geomagnetic secular variation and the statistics of palaeomagnetic directions. Geophysical Journal International 186, 509–520 (2011).
Xu, Y., Yang, Z., Tong, Y.-B. & Jing, X. Paleomagnetic Secular Variation Constraints on the Rapid Eruption of the Emeishan Continental Flood Basalts in Southwestern China and Northern Vietnam. Journal of Geophysical Research: Solid Earth 123(4), 2597–2617 (2018).
Aster, R. C., Borchers, B. & Thurber, C. H. Parameter estimation and inverse problems, 2nd edition, Academic Press, 376 p. (2011).
Nakagawa, T. & Tackley, P. J. Influence of initial CMB temperature and other parameters on the thermal evolution of Earth’s core resulting from thermochemical spherical mantle convection. Geochemistry, Geophysics, Geosystems 11 (2010).
Olson, P. & Amit, H. Magnetic reversal frequency scaling in dynamos with thermochemical convection. Physics of the Earth and Planetary Interiors 229, 122–133 (2014).
Gradstein, F. M., Ogg, J. G., Schmitz, M. & Ogg, G. (Eds). The geologic time scale 2012. Elsevier (2012).
Biggin, A. J. et al. Possible links between long-term geomagnetic variations and whole-mantle convection processes. Nature Geoscience 5, 526–533 (2012).
Driscoll, P. & Olson, P. Effects of buoyancy and rotation on the polarity reversal frequency of gravitationally driven numerical dynamos. Geophysical Journal International 178, 1337–1350 (2009).
Acknowledgements
The authors are grateful to Dr. Jean-Marie Flexor (National Observatory, Brazil), Dr. Marcia Ernesto and Daniele Brandt (University of São Paulo, Brazil) and Ricardo Sant’Anna Martins (State University of Rio de Janeiro, Brazil) for valuable discussions that contributed to the development of the study. We thank the referees for thoughtful and thorough reviews that significantly improved the paper. This work was partially supported by the Brazilian agencies CAPES, CIEE, CNPq (grants 313253/2017-0 and 165161/2018-3) and FAPERJ (grant E-26/203.302/2017).
Author information
Authors and Affiliations
Contributions
D.R.F. initiated the project, advised and assisted throughout, as well as provided the interpretations of the Model G results and the correspondence with the CMB heat flux patterns (with special support of W.P.O. and F.B.V.F.). F.B.V.F. organized the paleomagnetic database and, together with D.T.T. and W.P.O., provided the Model G curve fitting and supplementary interpretation. C.F.P.N. participated in discussions about the interpretations of the Model G results and provided computational support when necessary. W.P.O. contributed for the improvement of this manuscript, working together with D.R.F. towards the proposition of a revaluation of the selection criteria for paleomagnetic datasets and data processing. I.M.C.P. also provided computational support when necessary.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Franco, D.R., de Oliveira, W.P., Freitas, F.B.V.d. et al. Paleomagnetic Evidence for Inverse Correspondence between the Relative Contribution of the Axial Dipole Field and CMB Heat Flux for the Past 270 Myr. Sci Rep 9, 282 (2019). https://doi.org/10.1038/s41598-018-36494-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-018-36494-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.